郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解(5-6章)【圣才出品】
郑君里《信号与系统》(第3版)配套题库【考研真题+模拟试题】【圣才出品】

第 7 章 离散时间系统的时域分析
一、填空题
1.周期分别为 3 和 5 的两个离散序列的卷积和的周期性为______。[北京航空航天大学
2007 研]
【答案】7
【解析】对于线性卷积,若一个周期为 M,另一个周期为 N,则卷积后周期为 M+N
-1,所以T T1 T2 1 3 5 1 7 。
2.某线性时不变(LTI)离散时间系统,若该系统的单位阶跃响应为
5 / 69
圣才电子书
十万种考研考证电子书、题库视频学习平台
Y z z 6z 1 8z 2 3z 3
根据时域卷积定理可得:
H
z
z
6 z 1 z
8z2 2 z1
3z 3
使用长除法可得:
H z 1 2z 1 3z 2
取逆变换可得:
h[n] n 2 n 1 3 n 2
圣才电子书 十万种考研考证电子书、题库视频学习平台
yzs (0) 1, yzs (1) 1/ 2, yzs (2) 5/ 4, yzs (3) 13/ 8, yzs (4) 29 /16, yzs (5) 93/ 32 (2)零输入响应 yzi (n) 的递推方程可以化简为
由于
x[n] u[n 1] u[n] u[n 1] u[n 2]
u[n 1] u[n 1] u[n] u[n 2]
此式又可以写成:
x[n] n 1 2 n n 1 X z z 2 z 1
由题意可知:
yn x n*h n n 1 6 n 1 8 n 2 3 n 3
yzi (n) 0.5 yzi (n 1)
(n)
1 0
(n (n
0)
。当
0)
郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解-第2章 连续时间系统的时域分析【圣才

Ri(t) v1(t) e(t)
Ri(t)
1 C
t
i(
)d
v1 (t )
e(t)
vo (t) v1(t)
消元可得微分方程:
6 / 59
圣才电子书
十万种考研考证电子书、题库视频学习平
1
台
C
d
dt
vo (t)
1 R
vo (t)
R
e(t)
2-2 图 2-2-2 所示为理想火箭推动器模型。火箭质量为 m1,荷载舱质量为 m2,两 者中间用刚度系数为 k 的弹簧相连接。火箭和荷载舱各自受到摩擦力的作用,摩擦系数分 别为 f1 和 f2。求火箭推进力 e(t)与荷载舱运动速度 v2(t)之间的微分方程表示。
M
di1 (t ) dt
Ri2 (t)
0
化简方程组可得微分方程:
(L2
M
2
)
d4 dt 4
vo
(t)
2RL
d3 dt 3
vo
(t)
2L C
R2
d2 dt 2
vo
(t)
2R C
d dt
vo
(t)
1 C2
vo
(t)
MR
d2 dt 2
e(t)
(3)由图 2-2-1(c)所示列写电路方程,得:
C
dv1 (t ) dt
b.自由响应由两部分组成,其中,一部分由起始状态决定,另一部分由激励信号决 定,二者都与系统的自身参数有关;当系统 0-状态为零,则零输入响应为零,但自由响应 可以不为零。
c.零输入响应在 0-时刻到 0+时刻不跳变,此时刻若发生跳变,可能为零状态响应分 量。
郑君里《信号与系统》(第3版)(上册)(课后习题 傅里叶变换)【圣才出品】

第3章 傅里叶变换3-1 求图3-1所示对称周期矩形信号的傅里叶级数(三角形式与指数形式)。
图3-1解:(1)三角形式由图3-1可知,f(t)为奇函数,故有所以三角形式的傅里叶级数为。
(2)指数形式因所以指数形式的傅里叶级数为。
3-2 周期矩形信号如图3-2所示。
若:重复频率f=5kHz脉宽τ=20μs幅度E=10V求直流分量大小以及基波、二次和三次谐波的有效值。
图3-2解:由图3-2可知,f(x)为偶函数,且f=5kHz,得:所以直流分量为1V基波分量为1sin() 1.3910Vπ=≈二次谐波为2sin( 1.325Vπ=≈三次谐波为。
33sin() 1.2110V π=≈3-3 若周期矩形信号f 1(t )和f 2(t )波形如图3-2所示,f 1(t )的参数为τ=0.5μs,T=1μs,E=1V ;f 2(t )的参数为τ=1.5μs,T=3μs,E=3V ,分别求:(1)f 1(t )的谱线间隔和带宽(第一零点位置)频率单位以kHz 表示;(2)f 2(t )的谱线间隔和带宽;(3)f 1(t )与f 2(t )的基波幅度之比;(4)f 1(t )基波与f 2(t )三次谐波幅度之比。
解:由题3-2的结论可知,f(t)的傅里叶级数可表示为其中,。
(1)f 1(t )的谱线间隔,则带宽:。
(2)f 2(t )的谱线间隔带宽:。
(3)由题3-2可知,所以f 1(t )的基波幅度为:f 2(t )的基波幅度为:故。
(4)的三次谐波幅度为:故。
3-4 求图3-3所示周期三角信号的傅里叶级数并画出频谱图。
图3-3解:由图3-3可知,f(t)为偶函数,故。
bn所以的傅里叶级数可表示为()f t其幅度谱如图3-4所示。
图3-43-5 求图3-5所示半波余弦信号的傅里叶级数。
若E=10V ,f=10kHz ,大致画出幅度谱。
图3-5解:由图3-5可知,f(t)为偶函数,因而b n =0,();所以其傅里叶级数可表示为若E=10V ,,则幅度谱如图3-6所示。
《信号与系统》(郑君里)课后习题答案
(t )
2
非线性:设 r1 ( t ) = e1
( t ) 、 r2 ( t ) = e2 2 ( t ) ,
2 2 2 2
则⎡ ⎣ c1e1 ( t ) + c2 e2 ( t ) ⎤ ⎦ = c1 e1 ( t ) + c2 e2
2
( t ) + 2c1c2e1 ( t ) e2 ( t ) ≠ c1r1 ( t ) + c2 r2 ( t )
5
即 输 入 x1 ( t ) , x2 ( t ) 得 到 的 输 出 分 别 为 y1 ( t ) , y2 ( t ) , T ⎡ ⎣ x1 ( t ) ⎤ ⎦ = y1 ( t ) ,
T⎡ 。 ⎣ x2 ( t ) ⎤ ⎦ = y2 ( t ) ,则 T ⎡ ⎣ c1 x1 ( t ) + c2 x2 ( t ) ⎤ ⎦ = c1 y1 ( t ) + c2 y2 ( t ) ( c1 , c2 为常数)
解题过程:
(a-1)
(a-2)
(a-3)
4
(a-4)
(b) f ( t ) 为偶函数,故只有偶分量,为其本身
(c-1)
(c-2)
(c-3)
(c-4)
(d-1)
(d-2)
(d-3)
(d-4)
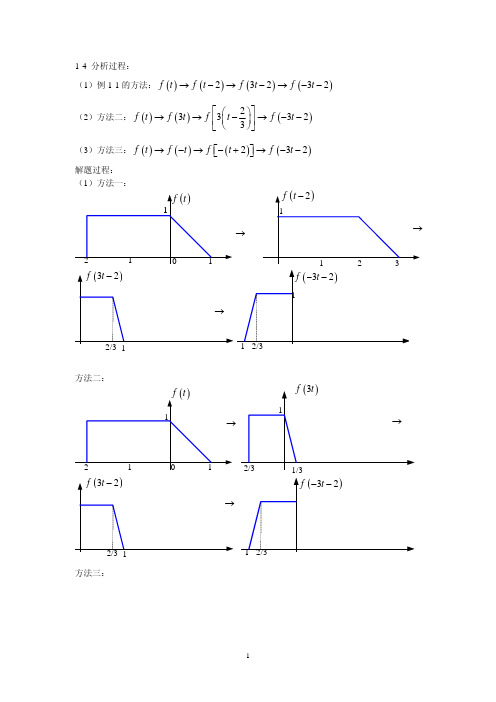
1-20 分析过程:本题为判断系统性质:线性、时不变性、因果性 (1)线性(Linearity) :基本含义为叠加性和均匀性
f (t )
1 1
f ( 3t )
→
→
-2
-1
0
1
-2/3
f ( 3t − 2 )
→
1/3
f ( −3t − 2 )
郑君里《信号与系统》(第3版)【教材精讲+考研真题解析】讲义 第5章 傅里叶变换应用于通信系统——

3 2
c
j)2 (
3 2
c
)
2
| H ( j) | e
j ( )
| H ( j) |
1
[1
(
c
)
2
]2
(
c
)
2
(
)
arctan[
1
c
(c
)
2
]
h(t) F 1[H ( j)]
2 c 3
ct
e 2 sin(
3 2
ct
)
波形及频谱图:
6 / 26
圣才电子书 十万种考研考证电子书、题库视频学习平台
衰减不能过于迅速;佩利-维纳准则是系统物理可实现的必要条件,而不是充分条件。
五、希尔伯特变换研究系统函数的约束条件
7 / 26
圣才电子书 十万种考研考证电子书、题库视频学习平台
希尔伯特变换对
R()
1
X
()
d
X
(
)
1
R( )
d
该变换对说明具有因果性的系统函数 H ( j) 的实部 R() 被已知的虚部 X () 唯一
轴上的相对位置产生变化;
(3)线性失真:幅度、相位变化,不产生新的频率成分;
(4)非线性失真:产生新的频率成分。
2.无失真传输条件
(1)无失真传输
系统的无失真传输是指响应信号与激励信号相比,只是大小与出现的时间不同,而无波
形 上 的 变 化 。 设 激 励 信 号 为 e(t) , 响 应 信 号 为 r(t) , 则 无 失 真 传 输 的 条 件 是 r(t) Ke(t t0) ,K 为常数, t0 为滞后时间,如图 5-1 所示。
郑君里《信号与系统》(第3版)名校考研真题(离散傅里叶变换以及其他离散正交变换)

,则
Y
e j
Y0 e j2kπ
k
,所以
yn
k
y0
n ej2kn
sin(πn/3) 2 πn
四、计算题
1.已知如图 9-2(a)所示的离散时间函数 x(n)
(1)求 x(n)的离散时间傅里叶变换
(2)以周期 N=100,把 x(2n)开拓为一个周期性信号
①画出周期信号
的波形图;
②把
展开成离散傅里叶级数,并画出频谱图。
8/8
再以 N=10 为周期开拓为周期序列
,如图 9-2(c)所示。
②令
,将
展开为离散傅里叶级数,即
式中,
,将 N=10 并令
数字角频率代入上式,得
当 k=0 时,
;k=1 时,
;k=2 时,
3/8
圣才电子书 十万种考研考证电子书、题库视频学习平台
当 k=3 时,
;k=4 时,
;k=5 时,
当 k=6 时,
;k=7 时,
;k=8 时,
当 k=9 时,
一个周期的图形如图 9-2(d)所示。
③系统的
,则由对称性质,该离散系统的频率响应函数
一
定是频域的周期函数,周期为 2n。
将
加 在 这样 一个 系统 的输 入端 ,只 有它 的直 流分 量, 基波 分量 (k=1),
,二次谐波分量(k=2),0.4πrad 可以通过该系统,其他的谐波分量均被滤除。
c
≤
≤π π c
,当
c
减小时,
该滤波器的单位冲激响应是更远离原点( )。[华南理工大学 2008 研]
1/8
圣才电子书 十万种考研考证电子书、题库视频学习平台
郑君里《信号与系统》(第3版)【教材精讲+考研真题解析】讲义 第6章 信号的矢量空间分析【圣才出品
(1)定义
假设有 n 个函数 g1(t), g2 (t)...gn (t) 构成的一个函数集,这些函数在区间 (t1,t2 ) 内满
足正交特性
t2 t1 t2 t1
gi (t)g j (t)dt 0,i
g
2 i
(t
)dt
Ki ,i
j
j
则称此函数集为正交函数集。
(2)特性
任意信号 f(t)可表示为 n 维正交函数之和,即
十万种考研考证电子书、题库视频学习平台
直角坐标平面内两矢量相对位置关系为
cos(f1 -f2 ) =
x1 y1 + x2 y2
1
1
(x12 + x22 )2 ( y12 + y22 )2
利用范数符号,将矢量长度分别写作
1
x 2 = (x12 + x22 ) 2
1
y 2 = ( y12 + y22 ) 2
必属
称为完备正交
9 / 21
圣才电子书 十万种考研考证电子书、题库视频学习平台
式中
为信号的能量,
为基底信号的能量,
为各信号分量的能量。
(2)物理意义 一个信号所含有的能量(功率)恒等于此信号在完备正交函数集中各分量能量(功率) 之和。 (3)数学本质 矢量空间信号正交变换的范数不变性。
圣才电子书 十万种考研考证电子书、题库视频学习平台
一、信号矢量空间的基本概念 1.线性空间 线性空间是指这样一种集合,其中任意两元素相加可构成此集合内的另一元素,任一元 素与任一数相乘后得到此集合内的另一元素。常见的线性空间有 N 维实数空间 与复数
空间 、连续时间信号空间 L、离散时间信号空间 l 等。
郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解(第4章)【圣才出品】
3.全通函数 如果一个系统函数的极点位于左半平面,零点位于右半平面,而且零点与极点对于 jω 轴互为镜像,这种系统函数称为全通函数,此系统则称为全通系统或全通网络。它的幅频特 性是常数。
4.最小相移函数 零点仅位于左半平面或 jω轴的网络函数称为“最小相移函数”,该网络称为“最小相 移网络”。非最小相移函数可以表示为最小相移函数与全通函数的乘积,即非最小相移网络 可以用最小相移网络与全通网络的级联来代替。
(1)部分分式展开法求解
首先将 F(s)展开成部分分式之和的形式,再对各部分分式分别取逆变换后叠加即可
得出 f(t)。
(2)留数定理求解
将拉氏逆变换的积分运算转化为求被积函数 F(s)est 在围线中所有极点的留数之和。
L 1[F (s)] 1 j F (s)estds [F (s)est的留数]
1 s
s2
s 2
,故
7 / 122
圣才电子书 十万种考研考证电子书、题库视频学习平台
L
[1 cos(t)]et
s
1
s (s )2 2
;
(7) L
[t 2
2t]
d2 ds2
1 s
d ds
2 s
2 s3
2 s2
(8) L [2 (t) 3e7t ] 2 3 s7
图 子书、题库视频学习平台
二、系统函数与系统特性 1.系统函数 系统的零状态响应的拉氏变换与激励的拉氏变换之比称为系统函数,即 H(s)=RZS (s)/E(s)。且冲激响应 h(t)↔H(s)。
2.零极点分布
H (s)
(9)e-αtsinh(βt);
(10)cos2(Ωt);
郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解(1-2章)【圣才出品】
第1章绪论
1.1复习笔记
本章作为《信号与系统》的开篇章节,是整个信号与系统学习的基础。
本章介绍了有关信号与系统的基本概念和术语,给出几种典型的信号和系统的表现形式,讲述了各信号与系统的特点以及信号之间的运算和转换。
通过本章学习,读者应掌握:如何判断信号类型、不同信号之间的运算、信号的分解以及系统类型的判断。
一、信号概述
1.信号的概念及分类(见表1-1-1)
表1-1-1信号的概念及分类
2.典型的连续信号(见表1-1-2)
表1-1-2典型的信号及表示形式
3.信号的运算(见表1-1-3)
表1-1-3信号的运算
4.阶跃函数和冲激函数
阶跃信号和冲激信号是信号与系统中最基础的两种信号,许多复杂信号皆可由二者或二者的线性组合表示。
具体见表1-1-4及表1-1-5。
(1)单位阶跃信号u(t)
表1-1-4单位阶跃信号u(t)
(2)单位冲激信号δ(t)
表1-1-5单位冲激信号δ(t)表示形式及性质
5.信号的分解
一个一般信号根据不同类型可分解为以下几种分量,具体见表1-1-6。
表1-1-6信号的分解
二、系统
1.系统概念及分类(见表1-1-7)
表1-1-7系统的概念及分类
系统模型如下:
输入信号经过不同系统可得到不同输出信号,具体见表1-1-8。
表1-1-8不同系统特性
1.2课后习题详解
1-1分别判断图1-2-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?
(a)
(b)
(c)
(d)
(e)
(f)。
信号系统(第3版)习题解答
《信号与系统》(第3版)习题解析高等教育目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?(c) (d)题1-1图解 (a)、(c)、(d)为连续信号;(b)为离散信号;(d)为周期信号;其余为非周期信号;(a)、(b)、(c)为有始(因果)信号。
1-2 给定题1-2图示信号f ( t ),试画出下列信号的波形。
[提示:f ( 2t )表示将f ( t )波形压缩,f (2t)表示将f ( t )波形展宽。
](a) 2 f ( t - 2 ) (b) f ( 2t )(c) f ( 2t)(d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示,R 、L 、C 元件可以看成以电流为输入,电压为响应的简单线性系统S R 、S L 、S C ,试写出各系统响应电压与激励电流函数关系的表达式。
题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i Lt u L L d )(d )(= ⎰∞-=tC C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成,系统属于何种联接形式?试写出该系统的微分方程。
S RS LS C题1-4图解 系统为反馈联接形式。
设加法器的输出为x ( t ),由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有)()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|,试判定该系统是否为线性时不变系统?解 设T 为系统的运算子,则可以表示为)()]([)(t f t f T t y ==不失一般性,设f ( t ) = f 1( t ) + f 2( t ),则)()()]([111t y t f t f T == )()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性,故为非线性时不变系统。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.脉冲编码调制(PCM) (1)脉冲调制概念 利用脉冲序列对连续信号进行抽样产生的信号称为脉冲幅度调制(PAM)信号。把连 续信号转换成数字(编码)信号进行传输或处理的调制方式称为脉冲编码调制(PCM)。PCM 通信系统的简化框图如图 5-1-2 所示。
图 5-1-2 PCM 通信系统简化框图 (2)PCM 通信特点(见表 5-1-4)
5-2 若系统函数H(jω)=1/(jω+1),激励为周期信号e(t)=sin(t)+sin(3t), 试求响应r(t),画出e(t),r(t)波形,讨论经传输是否引起失真。
解:激励信号 e(t)=sin(t)+sin(3t),则 E(jω)=F[e(t)]=jπ[δ(ω+1)-δ(ω-1)]+jπ[δ(ω+3)-δ(ω-3)]
一、系统函数 H(jω)
当且仅当 H(s)在虚轴上及右半平面无极点时,有 H ( j) H (s) s j ,也即,对于 H(s)在虚轴上有极点的系统,有 H ( j) H (s) s j 。
二、无失真传输 1.定义 系统无失真传输是指响应信号与激励信号相比,只是大小与出现的时间不同,而无波形 上的变化。 设激励信号为 e(t),响应信号为 r(t),则无失真传输的条件是 r(t)=Ke(t-t0), K 为常数,t0 为滞后时间,如图 5-1-1 所示。
6 / 107
圣才电子书 十万种考研考证电子书、题库视频学习平台
故响应为:
R( j) = E( j)×H ( j)
=
jπ j +
[ 1
(
+
1)
-
(
-
1)] +
jπ j +
[ 1
(
+
3)
-
(
-
3)]
= jπ ×e- [ jtan- 1 ( + 1) - ( - 1) + ( + 3) - ( - 3)] 1+ 2
= jπ [ejtan- 11 ( + 1) - e- ( jtan- 11 - 1)] + jπ ×[ejtan- 1 3 ( + 3) - e- ( jtan- 1 3 - 3)]
2
10
反变换,可得:
r(t) = F - 1[R( j )]
= 1 sin(t - tan- 1 1) + 1 sin(3t - tan- 1 3)
希尔伯特变换对:
R() 1
π
X
()
d
X () 1
π
R()
d
该变换对说明具有因果性的系统函数 H(jω)的实部 R(ω)被已知的虚部 X(ω)唯
一确定,反之亦然。
五、调制与解调 1.调制和解调(见表 5-1-3)
表 5-1-3 调制和解调
4 / 107
圣才电子书 十万种考研考证电子书、题库视频学习平台
5-3 无损LC谐振电路如图5-2-2所示,设 0 =
1 ,激励信号为电流源i(t),响应
LC
为输出电压v(t),若F[i(t)]=I(jω),F[v(t)]=V(jω),求:
(1)H(jω)=V(jω)/I(jω),h(t)=F-1[H(jω)];
(2)讨论本题结果与教材例5-1的结果有何共同特点。
解:激励信号 e(t)=e-3tu(t),则 E(jω)=F[e(t)]=F[e-3tu(t)]=1/(jω+3)
故响应Байду номын сангаас:
R( j) = E( j)×H ( j) = 1 ×1 = 1 - 1 j + 3 j + 2 j + 2 j + 3
反变换可得: r(t)=F-1[R(jω)]=(e-2t-e-3t)u(t)
表 5-1-4 PCM 通信特点
六、频分复用和时分复用(见表 5-1-5) 表 5-1-5 频分复用和时分复用
5 / 107
圣才电子书 十万种考研考证电子书、题库视频学习平台
5.2 课后习题详解
5-1 已知系统函数H(jω)=1/(jω+2),激励信号e(t)=e-3tu(t),试利用傅里 叶分析法求响应r(t)。
表 5-1-1 理想低通滤波器各类响应
2 / 107
圣才电子书 十万种考研考证电子书、题库视频学习平台
2.佩利-维纳准则
对于幅度函数|H(jω)|物理可实现的必要条件为:
ln H ( j) 12
d
改式称为佩利-维纳准则。
注意:
(a)该准则既不允许网络特性在一频带内为零,也限制了幅度特性的衰减速度;
圣才电子书 十万种考研考证电子书、题库视频学习平台
第 5 章 傅里叶变换应用于通信系统——滤波、调制与抽样
5.1 复习笔记
现代通信系统的发展处处伴随着傅里叶变换方法的运用。本章初步介绍了这些应用中最 主要的几个方面(滤波、调制、抽样),这是前两章基本内容的继续深入。通过本章学习, 读者应掌握:利用系统函数 H(jω)求响应、无失真传输的判断和实现、各种类型滤波器 的应用以及调制和解调在通信系统中发挥的作用。
(b)该准则只从幅度特性提出要求,在相位特性方面没有给出约束,因而该准则是系
统物理可实现的必要条件,而不是充分条件。
3.带通滤波器(见表 5-1-2) 表 5-1-2 带通滤波器特性及应用
3 / 107
圣才电子书 十万种考研考证电子书、题库视频学习平台
四、希尔伯特变换研究系统函数的约束条件
2
10
= 1 sin(t - 45°) + 1 sin(3t - arctan 3)
2
10
e(t)、r(t)的波形如图 5-2-1(a)、(b)所示。
7 / 107
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 5-2-1 由图 5-2-1 可知,传输引起了失真,r(t)既有幅度失真,也有相位失真。
1 / 107
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 5-1-1 线性网络的无失真传输 2.引起信号失真的原因 ①系统对信号中各频率分量幅度产生不同程度的衰减,使响应的各频率分量的相对幅度 发生变化,引起幅度失真; ②系统对各频率分量产生的相移与频率不成正比,使响应的各频率分量在时间轴上的相 对位置产生变化,引起相位失真。 三、滤波 1.理想低通滤波器(见表 5-1-1)
