第15讲一元一次不等式组培优专题

一元一次不等式组含参培优专题

一元一次不等式组含参培优专题1．若关于x 的不等式组0721x m x -⎧⎨-⎩＜≤的整数解共有3个，则m 的取值范围是（） A ．56m ＜＜ B ．56m ≤＜ C ．56m ≤≤ D ．67m ≤＜2．已知关于x 的不等式组：2123x a x b +⎧⎨-⎩＜＞的解集是32x -＜＜，则a b +的值为（） A ．3- B ．2 C ．0 D ．6-3．如果不等式组2223x a x b ⎧+⎪⎨⎪-⎩≥＜的解集是03x ≤＜，那么a b 的值为____________． 4．关于x 的不等式组352x a x a -⎧⎨-⎩＞＜无解，则a 的取值范围是____________． 5．若关于x 的不等式组01321x m x -⎧⎨-⎩＞≥的所有整数解的和是15，则m 的取值范围是____________．6．关于x 的不等式组30340x x a -⎧⎨+⎩＜＜的解集中为3x ＜，则a 的取值范围是____________． 7．不等式组1726m x m x ++⎧⎨⎩＜＜＜＜有解且解集是27x m +＜＜，则m 的取值范围为____________．8．方程组43165x y k x y -=+⎧⎨+=⎩的解x 、y 满足条件0783x y -＜＜，则k 的取值范围____________． 9．已知关于x 的不等式组211x m n x m ++⎧⎨--⎩＞＜，的解集为12x -＜＜，则2020()m n +的值是____________．10．若不等式组11324x x x m+⎧-⎪⎨⎪⎩＜＜有解，则m 的取值范围为____________． 11．若关于x 的一元一次不等式组1020x x a -⎧⎨-⎩＞＜有2个整数解，则a 的取值范围是____________．12．若不等式组11324x x x m+⎧-⎪⎨⎪⎩＜＜无解，则m 的取值范围是____________． 13．若不等式组11324x x x m+⎧-⎪⎨⎪⎩＜＜有解，则m 的取值范围为____________． 14．若不等式组420x a x ⎧⎨-⎩＞＜的解集是x a >，则a 的取值范围是____________． 15．若关于x 的不等式组6050x a x b ⎧-⎨-⎩≥＜的整数解仅有1，2，3，则a b +的最大值为____________． 16．若x 为实数，定义：[]x 表示不大于x 的最大整数．（1）例如[1.6]1=，[]π= ，[ 2.82]-= ．（请填空）（2）[]1x +是大于x 的最小整数，对于任意的实数x 都满足不等式[][]1x x x +≤＜，利用这个不等式，求出满足[]21x x =-的所有解．17．已知方程组317x y a x y a -=+⎧⎨+=--⎩．（1）求方程组的解（用含有a 的代数式表示）；（2）若方程组的解x 为负数，y 为非正数，且4a b +=，求b 的取值范围．18．已知关于x、y的方程组22324x y mx y m-=⎧⎨+=+⎩的解满足不等式组3050x yx y⎧+⎨+⎩≤＞，求满足条件的m的整数解．19．若关于x的不等式组23(3)1324x xxx a-+⎧⎪⎨++⎪⎩＜＞有四个整数解，求a的取值范围．20．对x ，y 定义一种新的运算A ，规定：()()()ax by x y A x y ay bx x y ⎧+⎪=⎨+⎪⎩，当时，，当时≥＜，（其中0ab ≠）．已知(11)0A =，，(02)2A =，．（1）求a ，b 的值；（2）若关于正数p 的不等式组(321)4(132)A p p A p p m -⎧⎨---⎩，，＞≤恰好有2个整数解，求m 的取值范围；（3）请直接写出()()22220A x y A y x +=，，时，满足条件的x ，y 的关系．21．对x 、y 定义一种新运算T ，记为：()T x y ，．（1）若()21T x y x y =+-，，如：(01)02111T =+⨯-=，，则(13)T =，；（2）若()1T x y ax by =+-，，（其中a 、b 为常数），且(11)2T -=-，，(42)3T =，． ①求a 、b 的值；②若关于m 的不等式组(254)4(32)T m m T m m P ⎧-⎨-⎩，，≤＞恰好有2个整数解，求实数P 的取值范围．。

七年级下册——不等式专题培优

七年级下册——不等式专题培优
七年级下册最难的章节莫过于方程组和不等式组的运用，以前教七年级的时候，很多同学都表示这一块没有思路，七年级下册——不等式专题培优
目录1
目录2
解一元一次不等式组时，可通过数轴来直观表示各不等式的解集，其公共部分即为不等式组的解集，也可通过口诀来确定不等式组的解集，口诀内容是：“同大取大，同小取小，大小小大中间找，大大小小找不到。

”
列一元一次不等式解应用题的关键是先根据题意找不等关系，列不等式，然后解不等式，求出未知数的解集，再根据题目的实际意义选择适合题意的未知数的值。

找不等关系时，要关注题中的关键词，如：超过、最多、不少于、至少、合算等等，特别是在设元时，如果能运用一定的技巧，可让问题化难为易，达到事半功倍的效果。

666
转发，赠送此文讲义。

(完整word)一元一次不等式(组)与二元一次方程(组)结合培优资料

一元一次不等式（组）与方程（组）的结合培优资料考点·方法·破译1．进一步熟悉二元一次方程组的解法，以及一元二次不等式组的解法．2．综合运用一元一次不等式组和二元一次方程组解决一些典型的实际问题．经典·考题·赏析【例1】求方程3x +27＝17的正整数解．【解法指导】一般地，一个二元一次方程有无数个解，但它的特殊解是有限个,如一个二元一次方程的正整数解，非负整数解都是有限个．求不定方程的正（非负）整数解时，往往借助不等式，整数的奇偶性等相关知识来帮助求解．解：将方程变形为2y ＝17－3x 即2317x y -= ∵y ＞0 ∴2317x -＞0 ∴x ＜317即x ＜325 又∵y 为正整数（即2317x -为整数） ∴17－3x 为偶数∴x 必为奇数∴x ＝1，3，5当x ＝1时，7213172317=⨯-=-=x y 当x ＝3时,4233172317=⨯-=-=x y 当x ＝5时，1253172317=⨯-=-=x y故原方程的正整数解为错误! 或错误! 或错误!【变式题组】01．求下列各方程的正整数解：⑴2x +y ＝10（2） 3x +4y ＝2102．有10个苹果，要分给两个女孩和一个男孩，要求苹果不得切开，且两个女孩所得的苹果数相等，每个孩子都有苹果吃，问有哪几种分法？【例2】足球联赛得分规定如下:胜1场得3分，平1场得1分,负1场得0分•某队在足球联赛的4场比赛中得6分，这个队胜了几场，平了几场，负了几场?【解法指导】本题中，所有的等量关系只有两个，而未知量有三个•因而所列方程的个数少于未知数的个数，即为不定方程组，但每个未知数量的数目必为非负整数•因此，此题的实质就是滶不定方程的非负整数解的问题．此方程组有两个方和，三个未知数，解法仍然是消元，即消去某一个未知数后，变为二元一次方程，再仿照例1的解法施行．解：设该队胜了x场,平了y场 ,负了z场，依题意可得：错误!②－①得：2x－z＝2 ③变形得：z＝2x－2∵0≤z≤2∴0≤2x－2≤2即1≤x≤2又x为正整数∴x＝1,2相应地，y＝3，0 z＝0，2答:这个队胜了1场，平了3场，或胜了2，负了2场．【变式题组】01．（佳木斯)为了奖励进步较大的学生，某班决定购买甲、乙、丙三种钢笔作为奖品，其单价分别为4元、5元、6元，购买这些钢笔需要花60元;经过协商，每种钢笔单价下降1元，结果只花了48元，那么可能购买甲种笔（）．A．11支B．9支C．7支D．5支02．一旅游团50人到一旅舍住宿，旅舍的客户有三人间、二人间、单人间三种•其中三人间的客房每人每晚20元,二人间的客房每人每晚30元，单人间的客房每人每晚50元．(1）若旅游团共住满了20间客房，问三种客房各住了几间？怎样住消费最低?（2）若该旅游团中,夫妻住二人间，单身住三人间，小孩随父母住在一起,现已知有小孩4人(每对夫妻最多只带1个小孩)，单身30人，其中男性17人，有两名单身心脏病患者要求住单人间,问这一行人共需多少间客房？【例3】已知：关于x、y的方程组错误!若x＞y，求a的取值范围．【解法指导】解本题的指导思想就是构建以a为未知数的不等式•解之即得a的取值范围，构建不等式的依据就是x＞y，而解方程组即可用a的代数式分别表示x和y，进而可得不等式．解：解方程组错误!得错误!∵x＞y∴2a＋1＞a－2 解得a＞－3故a的取值范围是a＞－3．【变式题组】01．已知：关于x的方程3x－（2a－3) ＝5x＋(3a＋6)的解是负数，则a的取值范围是_____．02．已知：关于x、y的方程组错误!的解为非负数．(1)求a的取值范围；(2)化简｜4a+5｜－｜a－4｜．03．当m 为何值时，关于x 的方程2153166--=--m x m x 的解大于1？4．已知方程组错误! 的解x 、y 都是正数,且x 的值小于y 的值,求m 的取值范围．【例4】(凉州）若不等式{x －a ＞2，b －2x ＞0 的解集是－1＜x ＜1，求（a +b ）2009的值．【解法指导】解此不等式组得a +2＜x ＜2b ，而依题意，该不等式的解集又是－1＜x ＜1,而解集是唯一的，因此两解集的边界点分别“吻合”，从而得两等式即得方程组，解之可得a 、b 之值．解：解不等式组错误! 得a +2＜x ＜2b 又∵此不等式组的解集是－1＜x ＜1∴ 错误! 解设错误!∴（a +b ）2009＝（－1)2009＝－1【变式题组】 01．若错误! 的解集为－1＜x ＜2，则a ＝___________，b ＝_____________．02．已知：关于x 的不等式组错误!的解集为3≤x ＜5，则a b 的值为（） A ．－2 B ．21- C ．－4 D ． 41- 03．若关于x 的不等式组错误! 的解集为x ＜2，则a 的取值范围是___________．04．已知：不等式组错误! 的解庥为－1＜x ＜2，求(a +b )2008的值．【例5】（永春）商场正在销售“福娃"玩具和徽章两种奥运商品，已知购买1盒“福娃”玩具和2盒徽章共需145元；购买2盒“福娃”玩具和3盒徽章共需280元•（1)一盒“福娃"玩具和一盒徽章的价格各是多少元?(2)某公司准备购买这两种奥运商品共20盒送给幼儿园（要求每种商品都要购买），且购买金额不能超过450元，请你帮该公司设计购买方案•【解法指导】本题属材料选择类的方程与不等式结合的实际应用题,但方程组与不等式组是分开的•分析可知:第（1）问只需依照题目主干所提供的两个等量关系即可列出二元一次方程组•第（2)问由题目所给不等关系“购买金额不能超过450元”及第(1)问所求出的数据列出不等式,从而求解•解：（1)设一盒“福娃"玩具和一盒徽章的价格分别为x元和y元．依题意,得错误!解得错误!答：一盒“福娃”玩具和一盒徽章的价格分别是125元和10元．(2)设购买“福娃”玩具m盒，则购买徽章(20－m）盒．由题意,得125m+10（20－m）≤450,解得m≤2。

初一下册数学讲义：一元一次不等式(组)复习培优

初一数学讲义一元一次不等式（组）一．教学衔接1.检查上周练习，并复习回顾考点。

2.引入新课。

课前检测1.若不等式组⎩⎨⎧ax x 3的解集是a x ,则a 的取值范围是( )A.3 a B 3=a . C.3 a D.3≥a2.不等式()()0352 x x -+的解集是( )A.253- x x 且B.253 x x 或-C.325 x -D.253 x - 3.若不等式组⎩⎨⎧b x a x 无解,则不等式组⎩⎨⎧--bx a x 22 的解集是( )A.a x b --22B.22--a x bC.b x a --22D.无解4.某冰箱厂为响应国家“家电下乡”号召，计划生产A 、B 两种型号的冰箱100台．经预算，两种冰箱全部售出后，可获得利润不低于 4.75万元，不高于4.8万元，两种型号的冰箱生产成本和售价如下表：型号A 型B 型成本（元/台）2200 2600 售价（元/台） 2800 3000（1）冰箱厂有哪几种生产方案？（2）该冰箱厂按哪种方案生产，才能使投入成本最少？“家电下乡”后农民买家电（冰箱、彩电、洗衣机）可享受13%的政府补贴，那么在这种方案下政府需补贴给农民多少元？（3）若按（2）中的方案生产，冰箱厂计划将获得的全部利润购买三种物品：体育器材、实验设备、办公用品支援某希望小学．其中体育器材至多买4套，体育器材每套6000元，实验设备每套3000元，办公用品每套1800元，把钱全部用尽且三种物品都购买的情况下，请你直接写出实验设备的买法共有多少种．二．本章知识梳理1．基本概念（1）不等式、不等式的解和不等式的解集、解不等式；（2）不等式的性质；（3）一元一次不等式、一元一次不等式组、不等式组的解集、解不等式组．2．方法与思考（1）解一元一次不等式的一般步骤：去分母、去括号、移项、合并同类项、（未知数）系数化为1．注意当去分母、系数化为1时，两边都乘以或除以负数时，不等号的方向要改变．（2）解一元一次不等式组的一般步骤：先分别解不等式组中的各个不等式，然后再求这几个不等式解集的公共部分．在数轴上表示不等式（组）的解集一方面要注意射线的方向，另外，解集中有等号时，用实心点表示，无等号时用空心圈表示．（3）列一元一次不等式（组）解决实际问题的方法步骤：①设未知数；②根据不等关系列出一元一次不等式（组）；③解一元一次不等式（组）；④对解的结果进行解释和检验，写出答案．三．例题解析1、不等式4（x -2）＞2（3x + 5）的非负整数解的个数为( )A ．0个B ．1个C ．2个D ．3个2、已知关于x 的方程x a x 34122-=+的解是非正数，求a 的取值范围.3、当a 在什么范围取值时，方程组 ⎩⎨⎧-=-=+123232a y x a y x 的解都是正数？4、若a 、b 、c 是△ABC 的三边，且a 、b 满足关系式|a －3|＋（b －4）＝0，c 是不等式组⎪⎪⎩⎪⎪⎨⎧++--21632433x x x x ＜＞的最大整数解，求△ABC 的周长。

第15讲一元一次不等式组培优专题

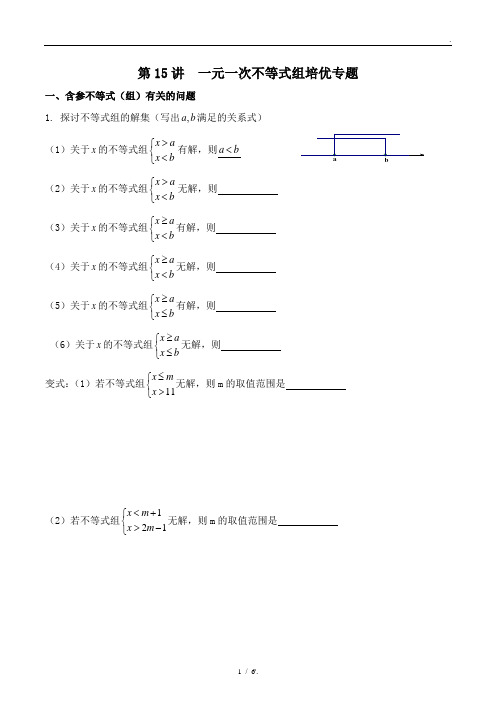
第15讲一元一次不等式组培优专题一、含参不等式（组）有关的问题1. 探讨不等式组的解集（写出,a b 满足的关系式）（1）关于x 的不等式组x a x b >⎧⎨<⎩有解，则a b < （2）关于x 的不等式组x a x b>⎧⎨<⎩无解，则（3）关于x 的不等式组x a x b ≥⎧⎨<⎩有解，则（4）关于x 的不等式组x a x b≥⎧⎨<⎩无解，则（5）关于x 的不等式组x a x b ≥⎧⎨≤⎩有解，则（6）关于x 的不等式组x a x b ≥⎧⎨≤⎩无解，则变式：（1）若不等式组⎩⎨⎧>≤11x m x 无解，则m 的取值范围是（2）若不等式组121x m x m <+⎧⎨>-⎩无解，则m 的取值范围是(3)若不等式组⎩⎨⎧>≤<kx x ,21有解，则k 的取值范围是(4)如果关于x 的不等式组x a x b >⎧⎨<⎩无解，则关于y 的不等式组11y a y b +>⎧⎨+<⎩的解如何？2. (1)若不等式组⎩⎨⎧>-<-3212b x a x 的解集为11<<-x ，那么)3)(3(+-b a 的值等于_______(2)如果关于x 的不等式组7060x m x n -≥⎧⎨-<⎩的整数解仅为1，2，3，那么适合这个不等式组的整数对(),m n 共有对.（3）已知关于x 的不等式x －2a ＜3的最大整数解是-5，求a 的取值范围3.已知不等式13a x ->的每一个解都是21122x -<的解，求a 的取值范围变式：如果关于x的不等式组224x ax a>-⎧⎨<-⎩有解，并且所有解都是不等式组－6＜x≤5的解，求a的取值范围．4. 若关于x的不等式组2113xxx k-⎧>-⎪⎨⎪-<⎩的解集为2x<，求k的取值范围5.不等式组1235a x ax-<<+⎧⎨<<⎩的解集是3x<<2a+，求a的取值范围6.已知不等式组111x x x k >-⎧⎪<⎨⎪<-⎩（1）当2k =-时，不等式组的解集是__ ___，当3k =时，不等式组的解集是___ __；（2）由（1）可知，不等式组的解集是随数k 的值的变化而变化．当k 为任意有理数时，写出不等式组的解集．二、不等式（组）与方程（组）7.已知关于x 的方程23x k kx -=-无负数解，求k 的取值范围.变式：已知关于x 的方程20142014a x x -=只有负数解，求a 的取值范围8.已知非负实数x ,y ,z 满足123234x y z ---==，记345W x y z =++，求W 的最大值与最小值.三.绝对值不等式（1）若x a <(0)a >，则a x a -<< 不等式2x <的解集为（2）若x a >(0)a >，则x a >或x a <- 不等式>5x 的解集为。

一元一次不等式(公开课优秀课件)

预算管理
使用不等式来控制开销，在有限预算内实现最大化利用。
运动训练
通过不等式来设定目标和限制，实现效果最优的运动训练计划。
投资决策
运用不等式进行资产配置和投资决策，最大化回报并保持风险可控。
一元一次不等式的综合应用
实际问题求解
强化练习题目演练
完成总结和回顾
运用所学不等式解决实际问题，如最优化、限制条件下的优化等。
减法法
2
பைடு நூலகம்
未知数的系数为1。
通过逐步减去等式两边的数值来求解不
等式，使得未知数的系数为1。
3
乘法法
通过逐步乘以一个合适的数来求解不等
分类讨论法
4
式，使得未知数的系数为1。
通过将不等式条件分为不同情况进行讨论，求解得到最终解集。
一元一次不等式的生活应用
发现不等式在生活中的实际应用，从解决日常问题到优化方案，学习如何将数学知识运用于实际场景。
一元一次不等式(公开课优秀课件)
在本课中，我们将探索一元一次不等式的基本概念、解决方法和实际应用。通过丰富的例子和图像，让我们一起追寻这个有趣的数学领域。
一元一次不等式的基本概念
了解一元一次不等式的定义和解集，并探索不等式的性质。通过实例分析和图像解释，深入理解这一重要概念。
不等式的定义
一元一次不等式是一个包含一个未知数的线性不等式，用于表示数值之间的不等关系。
通过大量练习题和实例分析，提高对一元一次不等式的运用能力。
总结所学知识，回顾解题思路，巩固对一元一次不等式的理解和应用。
不等式的解集
解集是满足给定不等式条件的所有数值的集合。
不等式的性质
不等式具有传递性、加法性和乘法性等性质，我们将一一探究它们。

一元一次不等式组含参培优专题-教师版

一元一次不等式组含参培优专题1．若关于x 的不等式组0721x m x -⎧⎨-⎩＜≤的整数解共有3个，则m 的取值范围是（） A ．56m ＜＜B ．56m ≤＜C ．56m ≤≤D ．67m ≤＜【答案】B 2．已知关于x 的不等式组：2123x a x b +⎧⎨-⎩＜＞的解集是32x -＜＜，则a b +的值为（） A ．3-B ．2C ．0D ．6-【答案】D 3．如果不等式组2223x a x b ⎧+⎪⎨⎪-⎩≥＜的解集是03x ≤＜，那么a b 的值为____________．【答案】94．关于x 的不等式组352x a x a -⎧⎨-⎩＞＜无解，则a 的取值范围是____________．【答案】12a -≤ 5．若关于x 的不等式组01321x m x -⎧⎨-⎩＞≥的所有整数解的和是15，则m 的取值范围是____________．【答案】34m ≤＜或43m --≤＜【解析】解：解不等式组01321x m x ->⎧⎨-⎩得：6m x <，所有整数解的和是15，15654=++， 6x ∴=，5，4，因此不等式组的整数解为①6，5，4，或②6，5，4，3，2，1，0，1-，2-，3-，34m ∴<或43m -<-；故答案为：34m <或43m -<-．6．关于x 的不等式组30340x x a -⎧⎨+⎩＜＜的解集中为3x ＜，则a 的取值范围是____________．【答案】94a -≤ 7．不等式组1726m x m x ++⎧⎨⎩＜＜＜＜有解且解集是27x m +＜＜，则m 的取值范围为____________．【答案】51m --≤＜8．方程组43165x y k x y -=+⎧⎨+=⎩的解x 、y 满足条件0783x y -＜＜，则k 的取值范围____________．【答案】112k ＜＜ 9．已知关于x 的不等式组211x m n x m ++⎧⎨--⎩＞＜，的解集为12x -＜＜，则2020()m n +的值是____________．【答案】110．若不等式组11324x x x m+⎧-⎪⎨⎪⎩＜＜有解，则m 的取值范围为____________．【答案】2m ＞11．若关于x 的一元一次不等式组1020x x a -⎧⎨-⎩＞＜有2个整数解，则a 的取值范围是____________．【答案】68a <≤12．若不等式组11324x x x m+⎧-⎪⎨⎪⎩＜＜无解，则m 的取值范围是____________．【答案】2m ≤13．若不等式组11324x x x m+⎧-⎪⎨⎪⎩＜＜有解，则m 的取值范围为____________．【答案】2m ＞14．若不等式组420x a x ⎧⎨-⎩＞＜的解集是x a >，则a 的取值范围是____________．【答案】2a ≥15．若关于x 的不等式组6050x a x b ⎧-⎨-⎩≥＜的整数解仅有1，2，3，则a b +的最大值为____________．【答案】26【解析】解：6050x a x b -⎧⎨-<⎩①②，解不等式①得：6a x，解不等式②得：5b x <， ∴不等式组的解集为65a b x <，关于x 的不等式组6050x a x b -⎧⎨-<⎩的整数解仅有1，2，3， 016a ∴<，345b <，解得：06a <，1520b <a ∴的最大值为6，b 的最大值为20， a b ∴+的最大值为26．16．若x 为实数，定义：[]x 表示不大于x 的最大整数．（1）例如[1.6]1=，[]π= ，[ 2.82]-= ．（请填空）（2）[]1x +是大于x 的最小整数，对于任意的实数x 都满足不等式[][]1x x x +≤＜，利用这个不等式，求出满足[]21x x =-的所有解．【答案】解：（1）[]3π=，[ 2.82]3-=-．（2）对任意的实数x 都满足不等式[][]1x x x <+，[]21x x =-， 21211x x x ∴-<-+，解得01x <，21x -是整数，0.5x ∴=或1x =，故答案为：3，3-．17．已知方程组317x y a x y a -=+⎧⎨+=--⎩．（1）求方程组的解（用含有a 的代数式表示）；（2）若方程组的解x 为负数，y 为非正数，且4a b +=，求b 的取值范围．【答案】解：（1）317x y a x y a -=+⎧⎨+=--⎩①②， ①+②得：226x a =-，解得：3x a =-，②-①得：248y a =--，解得：24y a =--，所以方程组的解是：324x a y a =-⎧⎨=--⎩；（2）方程组的解x 为负数，y 为非正数， ∴30240a a -<⎧⎨--⎩，解得：23a -<，∴乘以1-得：23a ->-，加上4得：641a ->，4a b +=，4b a ∴=-，b ∴的取值范围是16b <．18．已知关于x 、y 的方程组22324x y m x y m -=⎧⎨+=+⎩的解满足不等式组3050x y x y ⎧+⎨+⎩≤＞，求满足条件的m 的整数解．【答案】解：22324x y m x y m -=⎧⎨+=+⎩①②， ①+②，得：334x y m +=+，②-①，得：54x y m +=+，由3050x y x y +⎧⎨+>⎩可得34040m m +⎧⎨+>⎩，解得：443m -<-，则满足条件的m 的整数解为3-、2-．19．若关于x 的不等式组23(3)1324x x x x a -+⎧⎪⎨++⎪⎩＜＞有四个整数解，求a 的取值范围．【答案】解：由不等式①，得2391x x -<-+，解得8x >，由不等式②，得3244x x a +>+，解得24x a <-，不等式组有四个整数解，即：9，10，11，12， 122413a ∴<-，解得11542a -<-． 20．对x ，y 定义一种新的运算A ，规定：()()()ax by x y A x y ay bx x y ⎧+⎪=⎨+⎪⎩，当时，，当时≥＜，（其中0ab ≠）．已知(11)0A =，，(02)2A =，．（1）求a ，b 的值；（2）若关于正数p 的不等式组(321)4(132)A p p A p p m -⎧⎨---⎩，，＞≤恰好有2个整数解，求m 的取值范围；（3）请直接写出()()22220A x y A y x +=，，时，满足条件的x ，y 的关系．【答案】解：（1）根据题中的新定义得：022a b a +=⎧⎨=⎩，解得：11a b =⎧⎨=-⎩；（2）由（1）化简得：(A x ，(),),()x y x y y y x x y ⎧-=⎨-<⎩当时当时， ∴在关于正数p 的不等式组(3,21)4(13,2)A p p A p p m->⎧⎨---⎩中，3(21)10p p p --=+>，13(2)10p p p ----=--<，(3,21)32114A p p p p p ∴-=-+=+>，(13,2)2131A p p p p p m ---=-++=+， 3p ∴>，1p m -恰好有2个整数解，2∴个整数解为4，5．516m ∴-<67m ∴<．答：m 的取值范围为67m <．（3）2(A x ，22)(y A y +，2)0x =， ∴当22x y 时，22220x y x y -+-=， 22x y ∴=，x y ∴=或x y =-；当22y x 时，22220y x y x -+-=，x y ∴=或x y =-．答：满足条件的x ，y 的关系为x y =或x y =-．21．对x 、y 定义一种新运算T ，记为：()T x y ，．（1）若()21T x y x y =+-，，如：(01)02111T =+⨯-=，，则(13)T =，；（2）若()1T x y ax by =+-，，（其中a 、b 为常数），且(11)2T -=-，，(42)3T =，． ①求a 、b 的值；②若关于m 的不等式组(254)4(32)T m m T m m P ⎧-⎨-⎩，，≤＞恰好有2个整数解，求实数P 的取值范围．【答案】解：（1）(1,3)12316T =+⨯-=，故答案为：6；（2）①由题意，得：124213a b a b --=-⎧⎨+-=⎩，解得：1343a b ⎧=⎪⎪⎨⎪=⎪⎩；②由题意得()()45421433432133mmmmP-⎧+-⎪⎪⎨-⎪+->⎪⎩①②，解不等式①，得：514 m，解不等式②，得：937Pm-<，不等式组恰好有2个整数解，∴此整数解为1、2，则93237P-<，解得：543P-<-．。

一元一次不等式培优专题

一元一次不等式综合【例题求解】【例题1】（1）已知关于x 的不等式组⎩⎨⎧>-≥-0025a x x 无解，则a 的取值围是是___________。

思路点拨：从数轴上看，原不等式组种两个不等式的解集没有公共部分。

（2）已知不等式03≤-a x 的正整数解恰好是1、2、3，则a 的取值围是___________。

思路点拨：由题意，结合数轴，理解3a x ≤。

【例题2】如果关于x 的不等式组⎩⎨⎧<-≥-0607n x m x 的整数解仅为1、2、3，那么适合这个不等式组的整数m 和n 的值是多少。

思路点拨：借助数轴，分别建立m 、n 的不等式，确定整数m 、n 的值。

【例题3】解下列不等式（组）（1）n x m +<+332 （2）102≤-x（3）求不等式321≤-+-x x 的所有整数解。

思路点拨：与方程类似，解含有字母系数的不等式（组）需要对字幕系数进行讨论；解含有绝对值符号的不等式（组）的关键是去掉绝对值符号，化为一般的不等式求解。

【例题4】已知三个非负数a 、b 、c 满足132523=-+=++c b a c b a 和，若c b a m 73-+=。

求m 的最大值与最小值。

思路点拨：本体综合了方程、不等式组的丰富知识，解题的关键是通过解方程组，用含一个字母的代数式来表示m ，通过解不等式组，确定这个字母的取值围，在约束条件下，求m 的最大值与最小值。

【课堂练习】1、若关于不等式组⎪⎩⎪⎨⎧<++>+01456m x x x 的解集为4<x ，则m 的取值围是______________。

2、若不等式组⎩⎨⎧>-<-3212b x a x 的解集是11<<-x ，则)1)(1(-+b a 的值是_____________。

3、已知0<a ，且a x a ≤，则262---x x 的最小值是______________。

一元一次不等式(组)培优训练(参数问题)

一元一次不等式（组）培优训练（参数问题）拔高级训练：1、已知关于x ，y 的二元一次方程组⎩⎨⎧-=++=-222323t y x t y x ，当A=x -2y 且-1<t ≤2,求A 的取值范围.2、若关于x ，y 的二元一次方程组⎩⎨⎧=++=+333y x a t y x 的解满足x+y<505，则a 的取值范围是（）A. a>2016B.a<2016C.a>505D.a<5053、已知关于x ，y 的方程组⎩⎨⎧-=++=+m y x m y x 12312的解x ，y 满足x+y1<1，且m 为正数，求m 的取值范围.4、已知关于x ，y 的方程组⎩⎨⎧-=-+=+34272a y x a y x . （1）若a=2，求方程组的解；（2）若方程组的解x ，y 满足x>y ，求a 的取值范围并化简110118+-+a a5、若关于x 的不等式组⎩⎨⎧≥-≥-0250x m x 有解，则m 的取值范围是？6、关于x 的不等式组⎩⎨⎧->-<-)1(2130x x m x 无解，那么m 的取值范围为（） A. m ≤-1 B.m<-1 C.-1<m ≤0 D.-1≤m<07、（1）若不等于组⎩⎨⎧>≤<k x x 21无解，则k 的取值范围是（） A.k ≤2 B.k<1 C.k ≥2 D.1≤k<2（2）已知关于x 的不等式组⎩⎨⎧>-≥-1250x a x 只有四个整数解，则实数a 的取值范围是________. （3）定义[]x 表示不大于x 的最大整数，即x 的整数部分，例如[]47.4=.①根据定义，[][][]______;4.1_____,2_____,=-==π②比较[][]1,,1,++x x x x 的大小关系，按照从小到大的顺序用不等号连接的结果为____________________________； ③解方程：412213+=⎥⎦⎤⎢⎣⎡-x x8、若整数使关于的x 方程x ＋2a=1的解为负数,且使关于x 的不等式组⎪⎩⎪⎨⎧+≥->--31210)(21x x a x 无解,则所有满足条件的整数a 的值之和是（）A.5B.7C.9D.109、关于x 、y 的方程组⎩⎨⎧+=+-=+ky x k y x 13233的解满足x+y>0，且关于x 的不等式组⎪⎩⎪⎨⎧≥+≤--x x k x x 323)1(2有解，则符合条件的整数k 的值的和为（）A.2B.3C.4D.510、已知关于x 的不等式组⎩⎨⎧<+>-13430x a x 有且只有3个整数解，则a 的取值范围是（） A.a>-1 B.-1≤a<0 C.-1<a ≤0 D.a ≤0培优级训练：1、已知⎩⎨⎧+=+=+12242k y x k y x 且0<y -x<1,则k 的取值范围是（）A.211-<<-kB.210<<kC.10<<kD.121<<k 2、如果关于x 的不等式组⎩⎨⎧<->-0809b x a x 的整数解仅为1,2,3，那么适合这个不等式组的整数a ，b 的有序数对（a ，b ）共有______个.3、阅读以下材料：对于三个数a,b,c ，用M{a ，b ，c}表示这个三个数中最小的数，例如：M{-1,2,3}=343321-=++；⎩⎨⎧->--≤=--=-)1(1)1(},2,1min{;1}3,2,1min{a a a a 解决下列问题：（1）填空：如果min{2,2x+2,4-2x}=2，则x 的取值范围为_________.（2）如果M{2，x+1,2x}=min{2，x+1,2x}，求x.4、社会主义核心价值观"富强、民主、文明、和谐、自由、平等、公正、法治、爱国、敬业、诚信、友善"体现了社会主义核心价值理念.我们用"核心符号"[x]来表示不大于x 的最大整数(如[1.5]=1,[-1.5]=-2,我们把满足[x]=a （a 为常数）的x 取值范围叫做的核心范围)(如[x]=3的x 的核心范围为3≤x<4，[x]=-1的x 的核心范目-1≤ x<0).（1）请直接写出[2.6]的值和[x]=1的的核心范围;（2）己知关于x 的不等式⎩⎨⎧<->a x x ]2.1[有且只有两个整数解,写出这两个整数解并求出a 的取值范围.5、先阅读理解下面的例题,再按要求解答下列问题:例题:对于(x -2)(x -4)>0,这类不等式我们可以通过下面的解题思路来分析:由有理数的乘法法则"两数相乘,同号得正",可得①⎩⎨⎧<->-0402x x ，②⎩⎨⎧<-<-0402x x .从而将陌生的高次不等式化为学过的一元一次不等式年解不等式组，分别去解两个不等式组即可求得原不等式的解集,即:解不等式组①得x>4,解不等式组②得x<2,所以(x -2)(x -4)>0的解集为x>4或x<2.请利用上述解题思想解决下面的问题:（1）请直接写出(x -2)(x -4)<0的解集；（2）对于0>nm ，请根据除法法则化为我们学过的不等式（组）；（3）求不等式013>-+x x 的解集.6、先阅读理解下面的例题,再按要求解答下列问题:例题:解一元二次不等式x ²-4>0.解:∵x ²-4=(x ＋2)(x -2),∴x ²-4>0可化为(x ＋2)(x -2)>0.由有理数的乘法法则"两数相乘,同号得正",得①⎩⎨⎧>->+0202x x ，②⎩⎨⎧<-<+0202x x 解不等式组①,得x >2,解不等式组②,得x<-2.∴x ²-4>0的解集为x >2或x<-2,即一元二次不等式x ²-4>0的解集为x >2或x<-2.（1）一元二次不等式x ²-16>0的解集为______________.（2）分式不等式031>--x x 的解集为______________.课堂检测：1、已知关于x 、y 的方程组⎩⎨⎧=++=-ay x a y x 523的解满足x>y>0，求a 的取值范围.2、已知a>1,则a x x a -=-2)2(2中x 的取值范围是多少？3、若关于x 不等式组⎩⎨⎧≥-≥-0035m x x 有实数解，则实数m 的取值范围是（）A.35≤m B.35<m C.35>m D.35≥m4、若关于x 的不等式组⎩⎨⎧+≥++≤)1(341m x m x 无解，则m 的取值范围是__________.5、已知关于x 的不等式a ≤x<b 的整数解为7,8,9,10.当a 、b 为实数时，a 、b 的取值范围分别为________、__________.。

一元一次不等式及不等式组培优

兀一次不等式及不等式组培优一、一兀一次不等式和函数1.一次函数y=kx+b（k,b是常数，k丰0）的图象如图所示,是；不等式kx+b<2的解集是；当x<0时，y的取值范围是；当x>-2时，y的取值范围是.x 4.____________________________ 已知2x+y=5，当x满足条件时,5.如图，直线y=kx+b过A（-1，2），B（0W kx+b V4的解集为.6.如图，直线y=-x+m与y=nx+4n（n H O）的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的整数解是二、二元一次方程组和不等式1.已知方程组的解为负整数，求整数a的值.2.已知方程组的解x为非正数，y为负数，求符合条件的整数a的[x+3y=-7-a值.3.已知方程组的解满足x为非正数，y为负数.[x-y=l+3m(1)求m的取值范围；(2)化简：|m-3m+2|；(3)在第(1)小题的取值范围内，当m为何整数时，不等式2mx-x V2m-1的解为x>1?2x+14x—14.已知整数x满足不等式3x-4<6x-2和不等式―-—-1<^—，并且满足方程323(x+a)一5a+2=0，求a的值.、一元一次不等式组的解集：解下列不等式组1)2)3)4)（2）若关于x 的一）解不等式组（1）求3<5-2x <9的整数解（2）求不等式3<1-2x <5-2x 的解集.⑶IX ，3⑷解不等式13x -11<5I x 一4}⑸0已知「J —求关于的不等式的解集.（二）有解或者无解1-⑴若不等式组二魚无解’则a 的取值范围是多少？•I 瞥—m ~2>11元一次不等式组无解，则a 的取值范围是多少?（v "二・汨-L 1J 12,）若不等式组有解，则a 的取值范围是多少?1. 不等式组的解集为x V 2,则k 的取值范围为 16—3x >0(2)若不等式组f 、八有实数解，则实数m 的取值范围是,I x —m >0三)不等式的解集2-不等式组宀<。

一元一次不等式培优资料

《一元一次不等式（组）》培优辅导资料知识点1、不等式定义1、用不等式表示：⑴a 是非负数 ⑵m 的2倍与1的和小于7解：解：⑶a 与4的和的20%不大于－5 ⑷x 的61与x 的3倍的和是负数。

解：解：2、已知c b a ,,在数轴上如图所示，请用“＜”或“＞”填空（1）a 0 （2）c 0 （3）c b ____（4）c b c a ++____ （5）c b c a --_____ 知识点2、不等式的性质3、用a ＞b ，用“＜”或“＞”填空：⑴ a ＋2 b ＋2 ⑵ 3a 3b ⑶ －2a －2b⑷ a －b 0 ⑸ －a －4 －b －4 ⑹ a －2 b －2；4、用“＜”或“＞”填空：(1)若a －b ＜c －b ，则a c (2)若3a ＞3b ，则a b(3)若－a ＜－b ，则a b (4)若2a ＋1＜2b ＋1，则a b(5)若a －b ＞a ，则b 0 (6)若a ＜0，b 0时ab≥0(7)若a ＜－b ，则πa －πb （8）若a ＜b ，则a －b 0（9）若2ac ＞2bc ，则a b （10）若a ＞b ，则2ac 2bc5、已知a ＞b ，若a ＜0，则2a a b ，若a ＞0，则2a a b ；若a ＞b ，2b ab <，则b 0.6、若3a -＜2a -，则a 一定满足（） A.a ＞0 B.a ＜0 C.a ≥0 D.a ≤0 7、已知a<b<0,c>0，在下列空白处填上恰当的不等号：① (a-2)c (b-2)c ； ②||a ||b ③b 1 a 1 ④ac b c 。

8、若m ＜n ，则下列各式中正确的是（）。

A ．m －3＞ｎ－3 B.3m ＞3n C.－3m ＞－3n D.1313->-n m 9、若a ＜0，则下列不等关系错误的是（）。

A ．a ＋5＜a ＋7 B.5a ＞7a C.5－a ＜7－a D.75a a > 10、下列变形不正确的是（）。

一元一次不等式(组)与二元一次方程(组)结合培优资料

一元一次不等式（组）与方程（组）的结合培优资料考点·方法·破译1．进一步熟悉二元一次方程组的解法，以及一元二次不等式组的解法．2．综合运用一元一次不等式组和二元一次方程组解决一些典型的实际问题．经典·考题·赏析【例1】求方程3x +27＝17的正整数解．【解法指导】一般地，一个二元一次方程有无数个解，但它的特殊解是有限个，如一个二元一次方程的正整数解，非负整数解都是有限个．求不定方程的正（非负）整数解时，往往借助不等式，整数的奇偶性等相关知识来帮助求解．解：将方程变形为2y ＝17－3x 即2317x y -= ∵y ＞0 ∴2317x -＞0 ∴x ＜317即x ＜325 又∵y 为正整数（即2317x -为整数） ∴17－3x 为偶数∴x 必为奇数∴x ＝1，3，5当x ＝1时，7213172317=⨯-=-=x y 当x ＝3时，4233172317=⨯-=-=x y 当x ＝5时，1253172317=⨯-=-=x y故原方程的正整数解为⎩⎨⎧x =1y =7 或⎩⎨⎧x =3y =4 或⎩⎨⎧x =5y =1 【变式题组】01．求下列各方程的正整数解：⑴2x +y ＝10 (2) 3x +4y ＝2102．有10个苹果，要分给两个女孩和一个男孩，要求苹果不得切开，且两个女孩所得的苹果数相等，每个孩子都有苹果吃，问有哪几种分法？【例2】足球联赛得分规定如下：胜1场得3分，平1场得1分，负1场得0分•某队在足球联赛的4场比赛中得6分，这个队胜了几场，平了几场，负了几场？【解法指导】本题中，所有的等量关系只有两个，而未知量有三个•因而所列方程的个数少于未知数的个数，即为不定方程组，但每个未知数量的数目必为非负整数•因此，此题的实质就是滶不定方程的非负整数解的问题．此方程组有两个方和，三个未知数，解法仍然是消元，即消去某一个未知数后，变为二元一次方程，再仿照例1的解法施行．解：设该队胜了x 场，平了y 场，负了z 场，依题意可得：⎩⎨⎧x ＋y ＝4 ①3x ＋y ＝6 ②②－①得：2x －z ＝2 ③变形得： z ＝2x －2∵0≤z ≤2∴0≤2x －2≤2即1≤x ≤2又x 为正整数∴x ＝1，2相应地，y ＝3，0 z ＝0，2答：这个队胜了1场，平了3场，或胜了2，负了2场．【变式题组】01．（佳木斯）为了奖励进步较大的学生，某班决定购买甲、乙、丙三种钢笔作为奖品，其单价分别为4元、5元、6元，购买这些钢笔需要花60元；经过协商，每种钢笔单价下降1元，结果只花了48元，那么可能购买甲种笔（）．A ．11支B ．9支C ．7支D ．5支02．一旅游团50人到一旅舍住宿，旅舍的客户有三人间、二人间、单人间三种•其中三人间的客房每人每晚20元，二人间的客房每人每晚30元，单人间的客房每人每晚50元．(1)若旅游团共住满了20间客房，问三种客房各住了几间？怎样住消费最低？(2)若该旅游团中，夫妻住二人间，单身住三人间，小孩随父母住在一起，现已知有小孩4人（每对夫妻最多只带1个小孩），单身30人，其中男性17人，有两名单身心脏病患者要求住单人间，问这一行人共需多少间客房？【例3】已知：关于x 、y 的方程组⎩⎨⎧x －y =a +32x +y =5a若x ＞y ，求a 的取值范围．【解法指导】解本题的指导思想就是构建以a 为未知数的不等式•解之即得a 的取值范围，构建不等式的依据就是x ＞y ，而解方程组即可用a 的代数式分别表示x 和y ，进而可得不等式．解：解方程组⎩⎨⎧x －y ＝a ＋32x ＋y ＝5a 得 ⎩⎨⎧x ＝2a ＋1y ＝a －2∵x ＞y ∴2a ＋1＞a －2 解得a ＞－3故a 的取值范围是a ＞－3．【变式题组】01．已知：关于x 的方程3x －(2a －3) ＝5x ＋(3a ＋6)的解是负数，则a 的取值范围是_____．02．已知：关于x 、y 的方程组⎩⎨⎧x +y =3a +9x －y =5a +1的解为非负数． (1)求a 的取值范围；(2)化简｜4a +5｜－｜a －4｜．03．当m 为何值时，关于x 的方程2153166--=--m x m x 的解大于1？4．已知方程组⎩⎨⎧2x +y =5m +6x －2y =－17 的解x 、y 都是正数，且x 的值小于y 的值，求m 的取值范围．【例4】（凉州）若不等式⎩⎨⎧x －a ＞2b －2x ＞0 的解集是－1＜x ＜1，求（a +b ）2009的值．【解法指导】解此不等式组得a +2＜x ＜2b ，而依题意，该不等式的解集又是－1＜x ＜1，而解集是唯一的，因此两解集的边界点分别“吻合”，从而得两等式即得方程组，解之可得a 、b 之值．解：解不等式组⎩⎨⎧x －a ＞2a －2x ＞0 得a +2＜x ＜2b 又∵此不等式组的解集是－1＜x ＜1∴ ⎩⎪⎨⎪⎧a +2=－12b =1a 解设⎩⎨⎧a =－3a b =2a ∴（a +b ）2009＝（－1）2009＝－1【变式题组】01．若⎩⎨⎧2a +x ＞a 2－3x ＞a的解集为－1＜x ＜2，则a ＝___________，b ＝_____________． 02．已知：关于x 的不等式组⎩⎨⎧x －a ≥b 2x －a ＜2b +1的解集为3≤x ＜5，则ab 的值为（）A ．－2B ．21-C ．－4D ． 41- 03．若关于x 的不等式组⎩⎪⎨⎪⎧34+x ＞12+x x +a ＞0b的解集为x ＜2，则a 的取值范围是___________．04．已知：不等式组⎩⎨⎧x +2＞a +b x －1＜a －b 的解庥为－1＜x ＜2，求（a +b ）2008的值．【例5】（永春）商场正在销售“福娃”玩具和徽章两种奥运商品，已知购买1盒“福娃”玩具和2盒徽章共需145元；购买2盒“福娃”玩具和3盒徽章共需280元•(1)一盒“福娃”玩具和一盒徽章的价格各是多少元？(2)某公司准备购买这两种奥运商品共20盒送给幼儿园（要求每种商品都要购买），且购买金额不能超过450元，请你帮该公司设计购买方案•【解法指导】本题属材料选择类的方程与不等式结合的实际应用题，但方程组与不等式组是分开的•分析可知：第(1)问只需依照题目主干所提供的两个等量关系即可列出二元一次方程组•第(2)问由题目所给不等关系“购买金额不能超过450元”及第(1)问所求出的数据列出不等式，从而求解•解：(1)设一盒“福娃”玩具和一盒徽章的价格分别为x 元和y 元．依题意，得⎩⎨⎧x +2y =142x +3y =280 解得⎩⎨⎧x =125y =10答：一盒“福娃”玩具和一盒徽章的价格分别是125元和10元．(2)设购买“福娃”玩具m 盒，则购买徽章（20－m ）盒．由题意，得125m +10（20－m ）≤450，解得m ≤2.17．所以m 可以取1，2．答：该公司有两种购买方案．方案一：购买“福娃”玩具1盒，徽章19盒；方案二：购买“福娃”玩具2盒,徽章18盆．【变式题组】01．(益阳)开学初，小芳和小亮去学校商店购买学习用品,小芳用18元钱买了1支钢笔和3本笔记本;小亮用31元买了同样的钢笔2支和笔记本5本．(1)求每支钢笔和每本笔记本的价格；(2)校运会后，班主任拿出200元学校奖励基金交给班长，购买上述价格的钢笔和笔记本共48件作为奖品，奖给校运会中表现突出的同学，要求笔记本数不少于钢笔数，共有多少种购买方案？请你一一写出．02． (眉山)渔场计划购买甲、乙两种鱼苗共6000尾，甲种鱼苗每尾0.5元，乙种鱼苗每尾0.8元．相关资料表明：甲、乙两种鱼苗的成活率分别为90%和95%．⑴若购买这批鱼苗共用了 2600元，求甲、乙两种鱼苗各购买了多少尾？⑵若购买这批鱼苗的钱不超过4200元，应如何选购鱼苗？⑶若要使这批鱼苗的成活率不低于93%，且购买鱼苗的总费用最低，应如何选购鱼苗？ 03．（盐城）整顿药品市场，降低药品价格是国家的惠民政策之一．根据国家的《药品政府定价办法》，某省有关部门规定：市场流通药品的零售价格不得超过进价的15%根据相关信息解决下列问题：⑴降价前，甲乙两种药品每盒的出厂价格之和为6.6元．经过若干中间环节，甲种药品每盒的零售价格比出厂价格的5倍少2.2元，乙种药品每盒的零售价格是出厂价格的6倍，两种药品每盒的零售价格之和为33.8元．那么降价前甲、乙两种药品每盒的零售价格分别是多少元？⑵降价后，某药品经销商将上述的甲、乙两种药品分别以每盒8元和5元的价格销售给医院，医院根据实际情况决定：对甲种药品每盒加价15%对、乙种药品每盒加价10%后零售给患者．实际进药时，这两种药品均以每10盒为1箱进行包装．近期该医院准备从经销商处购进甲乙两种药品共100箱，其中乙种药品不少于40箱，销售这批药品的总利润不低于900元．请问购进时有哪几种搭配方案？【例6】认真阅读下面三个人的对话．小朋友：阿姨，我买一盒饼干和一袋牛奶（递上10元钱入）．售货员：本来你用10元钱买一盒饼干是多余的，但再买一袋牛奶就不够了．不过今天是儿童节，我给你买的饼干打九折，两样东西请拿好，还有找你的8角钱．旁边者：一盒饼干的标价可是整数哦！根据对话内容，试求出饼干和牛奶的标价各是多少？【解法指导】本题的条件蕴藏在对话中，应学会从对话中获取信息，“用10元钱买一盒饼干是多余的”，说明一盒饼干的售价小于10元，此不等关系之一；“但再买一袋牛奶就不够了 ”，说明一盒饼干和一袋牛奶的价格之和大于10元，此不等关系之二．对话中还包含有一个等量关系，就是用10元钱买上述两样东西剩余0.8 元钱，即是说一袋牛奶与一盒饼干的价格之和等于10元减去0.8元，由一个方程和两个不等式结合最终可求出答案．解：设饼干的标价为每盒x 元，牛奶的标价为每袋^元.根据题意，得⎩⎪⎨⎪⎧x ＋y ＞10 ①0.9x ＋y ＝10－0.8 ②x ＜10 ③由②，得y ＝9.2－9x 将其代入①，得x +9.2－9x ＞10，解得：x ＞8．所以综合③可知8＜x ＜10．又因为x 为整数，所以x ＝9，y ＝9.2－9x ＝1.1即饼干的标价为每盒9元，牛奶的标价为每袋1. 1元．【变式题组】01．某次足球联赛A 组共6队，比赛规定采取小组循环赛的形式，取前3名进人决赛，记分方法为胜1场得2 分，负1场扣1分，平1场不得分，问该小组共需比赛几场？某队得了 7分，则它是几胜几负？能否进人决赛？02．(杭州)宏志高中高一年级近几年来招生人数逐年增加，去年达到550名，其中有面向全省招收的“宏志班” 学生，也有一般普通班学生．由于场地、师资等条件限制，今年招生最多比去年增加100人，其中普通班学生可多招20%，“宏志班”学生可多招10%问今年最少可招收“宏志班”学生多少名？03．把一些书分给几个学生，如果每人分3本，那么余8本，如果前面的每个学生分5本，那么最后一个同学分不到3本，这些书有多少本？学生有多少人？【例7】(北京市竞赛题)已知：a 、b 、c 是三个非负数，并且满足3a +2b +c ＝5，2a +b －3c ＝1，设m ＝3a +b －7 c ，设x 为m 的最大值，y 为m 的最小值．求xy 的值．【解法指导】要求某一代数式的最大(或最小)值，往往依题意构建一个不等式组：若s ≤m ≤t ，则m 的最小值为s ，最大值为t ．本题思路亦类此，首先利用前两个等式，将c 看作已知量，解关于a 、b 的二元一次方程组，得到用含c 的式子表示a 、b 的形式，代入第三个等式，得到用含c 的式子表示m 的形式，同时依据a 、b 、c 均为非负数，得到c 的范围，代入m 与c 的关系式，得m 的范围，因而x 、y 可求．解：由条件得：解得： ⎩⎨⎧3a ＋2b =5－c 2a ＋b =1+3 c⎩⎨⎧a =7c －3b =7－11 c则m ＝3a +7－7c ＝3(7c －3)+ (7－11 c ) －7 c ＝3 c －2由a ≥0，b ≥0，c ≥0得⎩⎪⎨⎪⎧7c －3≥07－11c ≥0c ≥0解得，37≤c ≤711从而x ＝－57，y ＝－111故xy ＝577．【变式题组】01．若a 、b 满足3a +5∣b ∣＝7，S ＝2a 2－3∣b ∣，则 S 的取值范围是．02．已知：x 、y 、z 是三个非负有理数，且满足3 x +2 y +z ＝5，x +y －z ＝2，若S ＝3 x + y －z ，则S 的取值范围是．演练巩固反馈提高一、填空题01．方程3x +y ＝ 10的解有个，其正整数解有个．02．若关于x 的不等式(a －1)＜a +5和2x ＜4的解集相同，则a 的值为．03．已知：关于x 的不等式2x －a ≥－3的解集如图所示，则a ＝．04．已知方程组⎩⎨⎧2x －y =m 2y －x =1，若未知数x 、y 满足尤x +y ＞0，则m 的取值范围是． 05．若方程组⎩⎨⎧3x +2y =2k 2y －x =3的解满足无x ＜1且y ＞0，则整数k 的个数是． 06．若∣x －1∣ x －1＝－1则x 的取值范围是．二、选择题07．已知：关于尤的不等式组⎩⎨⎧x －y ≥b 2x －a ＜2b +1的解为3≤x ＜5，则b a 的值为( ) A ．－2 B ．－2 C ．2 D ．108．若∣x +1∣＝－1－x ，∣3x +4∣＝3x +4．则x 取值范围是( )A ．－43≤x ≤－1B ．x ≥－1C ．―43≤x ≤―1D ．―43＜x ＜―1 09．已知：m 、n 是整数，3 m +2＝5n +3，且3 m +2＞30，5n +3＜40，则mn 的值是〈〕A ．70B ．72C ．77D ．8410．某次测验共20道选择题，答对一题记5分，答错一题记―2分，不答记0分，某同学得48分，那么他答对的题目最多是（）道．A ．9B ．10C ．11D ．12三、解答题11．学校举办奥运知识竞赛，设一、二、三等奖共12名，奖品发放方案如下表：一等奖二等奖三等奖 1盒福娃和1枚徽章 1盒福娃 1枚徽章用于购买奖品的总费用不少于1000元但不超过1100元，小明在购买“福娃”和徽章前，了解到图所示的信息：⑴求一盒“福娃”和一枚徽章各多少元？⑵若本次活动设一等奖2名，则二等奖和三等奖应各设多少名？12．（宿迁）某花农培育甲种花木2株，乙种花木3株，共需成本1700元；培育甲种花木3株，乙种花木1 株，共需成本1500元．⑴求甲、乙两种花木每株成本分别为多少元；⑵据市场调研，1株甲种花木的售价为760元，1株乙种花木的售价为540元．该花农决定在成本不超过30000元的前提下培育甲乙两种花木，若培育乙种花木的株数是甲种花木的3倍还多10株，那么要使总利润不少于21600元，花农有哪几种具体的培育方案？13．—项维修工程，若由甲工程队单独做，则40天可以完成，需费用24万元；若由乙工程队单独做，则60天可以完成，需费用21万元•现打算由甲、乙两工程队共同完成，要使该项目的总费用不超过22万元，则乙工程队至少要施工多少天？14．足球联赛得分办法是胜一场得3分，平一场得1分，负一场得0分•在一次足球赛中，南方足球队参加了14场比赛，至少负了1场，共积分19分．试推算南方足球队胜、平、负各多少场．15．（温州）某工厂用如图甲所示的长方形和正方形纸板，做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒.⑴现有正方形纸板162张，长方形纸板340张．若要做两种纸盒共100个，设做竖式纸盒x个．①根据题意，完成以下表格：盒纸板竖式纸盒（个）横式纸盒（个）x正方形纸板（张）2(100－x)长方形纸板（张）4x②按两种纸盒的生产个数来分，有哪几种生产方案？(2)若有正方形纸板162张，长方形纸板a张，做成上述两种纸盒，纸板恰好用完．已知290＜a＜306．则求a的值．(写出一个即可)培优升级奥赛检测01．若方程组⎩⎨⎧4x +y =k +1x+4y =3的解满足条件0＜x+y ＜1，则k 的取值范围是( ) A ．－4＜k ＜1 B ．－4＜k ＜0 C ．0＜k ＜9 D ．k ＜－402．（浙江省竞赛题)要使方程组⎩⎨⎧3x +2y =a 2x+3y =2的解是一对异号的数，则a 的取值范围是( ) A ．43＜k ＜3 B ．a ＜43 C ．a ＞3 D ．a ＜43或a ＞3 03．已知a +b +c ＝0，a ＞b ＞c ，则 c a的取值范围是． 04．(新加坡竞赛题）正整数m 、n 满足8m +9n ＝mn +6，则m 的最大值是．05．（“希望杯”邀请赛初一试题）（中国古代问题）唐太宗传令点兵，若一千零一卒为一营，则剩余一人；若一千零二卒为一营，则剩余四人，此次点兵至少有人．06．（第15届“希望杯”邀请赛试题）若正整数x 、y 满足2004x ＝15y ，则x +y 的最小值为． 07．（北京市竞赛题）有8个连续的正整数，其和可以表示成7个连续的正整数的和，但不能表示为3个连续的正整数的和，那么这8个连续的正整数中最大数的最小值是．三、解答题08．已知:关于x 的方程组⎩⎨⎧x －y =a +32x+y =5a的解满足x ＞y ＞0，化简∣a ∣+∣3－a ∣．09．a 、b 、c 、d 是正整数，且a +b ＝20，a +c ＝24，a +d ＝22，设a +b +c +d 的最大值为M ，最小值为N ，求M －N 的值．10．在车站开始检票时，有a (a ＞0)名旅客在候车室排队等候检票进站，检票开始后，仍有旅客继续前来排队检票进站，设旅客按固定的速度增加，检票口检票的速度也是固定的，若开放一个检票口，则需30分钟才可将排队等候检票的旅客全部检票完毕；若开放两个检票口，则只需10分钟便可将排队等候检票的旅客全部检票完毕；如果要在5分钟内将排队等候检票的旅客全部检票完毕，以便后来到站的旅客能随到随检，至少要同时开放几个检票口？11．（河南省竞赛题）一个盒子里装有不多于200粒棋子，如果每次2粒、3粒、4粒或6粒地取出，最终盒内都剩一粒棋子；如果每次11粒地取出，那正好取完，求盒子里共有多少粒棋子？12．(“希望杯”初二竞赛题)一个布袋中有红、黄、蓝三种颜色的大小相同的木球，红球上标有数字1，黄球上标有数字2，蓝球上标有数字3，小明从布袋中摸出10个球，它们上面所标数字和等于21，则小明摸出的球中，红球的个数最多不超过多少个？13．（第20届香港中学数学竞赛题）已知：n 、k 皆为自然数，且1＜k ＜n ，若1+2+3+…+n －k n －1，及n +k ＝a ，求a 的值．。

一元一次不等式含参问题

一元一次不等式（组）专项培优【学习目标】1．理解不等式组的概念；2.会解一元一次不等式组，并会利用数轴正确表示出解集；3.会利用不等式组解决较为复杂的实际问题，感受不等式组在实际生活中的作用．要点一、不等式组的概念定义：一般地，关于同一未知数的几个一元一次不等式合在一起，就组成了一元一次不等式组．如，等都是一元一次不等式组．一元一次不等式的解法【学习目标】1．理解并掌握一元一次不等式的概念及性质；2.能够熟练解一元一次不等式；3. 掌握不等式解集的概念并会在数轴上表示解集.【要点梳理】要点一、一元一次不等式的概念只含有一个未知数，未知数的次数是一次的不等式，叫做一元一次不等式，例如，是一个一元一次不等式．要点诠释：(1)一元一次不等式满足的条件：①左右两边都是整式(单项式或多项式)；②只含有一个未知数；③未知数的最高次数为1.(2) 一元一次不等式与一元一次方程既有区别又有联系：相同点：二者都是只含有一个未知数，未知数的次数都是1，“左边”和“右边”都是整式．不同点：一元一次不等式表示不等关系，由不等号“＜”、“≤”、“≥”或“＞”连接，不等号有方向；一元一次方程表示相等关系，由等号“＝”连接，等号没有方向．要点二、一元一次不等式的解法1.解不等式：求不等式解的过程叫做解不等式．2.一元一次不等式的解法：与一元一次方程的解法类似，其根据是不等式的基本性质，将不等式逐步化为：（或）的形式，解一元一次不等式的一般步骤为：(1)去分母；(2)去括号；(3)移项；(4)化为（或）的形式（其中）；(5)两边同除以未知数的系数，得到不等式的解集.要点诠释：（1）在解一元一次不等式时，每个步骤并不一定都要用到，可根据具体问题灵活运用． 2562010x x ->⎧⎨-<⎩7021163159x x x ->⎧⎪+>⎨⎪+<⎩2503x >a x <a x >ax b >ax b <0a ≠（2）解不等式应注意：①去分母时，每一项都要乘同一个数，尤其不要漏乘常数项；②移项时不要忘记变号；③去括号时，若括号前面是负号，括号里的每一项都要变号；④在不等式两边都乘(或除以)同一个负数时，不等号的方向要改变．要点三、不等式的解及解集1.不等式的解：能使不等式成立的未知数的值，叫做不等式的解.2.不等式的解集：对于一个含有未知数的不等式，它的所有解组成这个不等式的解集．要点诠释：3.不等式的解集的表示方法（1）用最简的不等式表示:一般地，一个含有未知数的不等式有无数个解，其解集是一个范围，这个范围可用最简单的不等式来表示．如：不等式x-2≤6的解集为x ≤8．(2) 用数轴表示:不等式的解集可以在数轴上直观地表示出来，形象地表明不等式的无限个解．如图所示：(3)要点诠释：借助数轴可以将不等式的解集直观地表示出来，在应用数轴表示不等式的解集时，要注意两个“确定”：一是确定“边界点”，二是确定方向．(1)确定“边界点”：若边界点是不等式的解，则用实心圆点，若边界点不是不等式的解，则用空心圆圈；(2)确定“方向”：对边界点a 而言，x ＞a 或x ≥a 向右画；对边界点a 而言，x ＜a 或x ≤a 向左画．注意：在表示a 的点上画空心圆圈，表示不包括这一点．【典型例题】类型一、一元一次不等式的概念1．下列式子哪些是一元一次不等式？哪些不是一元一次不等式？为什么？（1）（2）（3）（4）（5）0x >1x1->2x 2>3y x ->+1x -=类型二、解一元一次不等式2.求不等式﹣≤的非负整数解，并把它的解在数轴上表示出来．举一反三：【变式1】解不等式：【变式2】代数式的值不大于的值，求x 的范围．3.m 为何值时，关于x 的方程：的解大于1？举一反三：【变式】已知关于方程的解是非负数，是正整数，则．4.（2016•杭州模拟）若关于x ，y 的二元一次方程组的解满足x ﹣y ＞﹣3.5，求出满足条件的m 的所有正整数解． 2x ]2)14x (32[23<---6151632x m m x ---=-x 3x 23m x 2x -=--m =m类型二、不等式的解及解集5.若关于的不等式只有三个正整数解，求的取值范围.举一反三：【变式】已知的解集中的最大整数为3，则的取值范围是．类型四、逆用不等式的解集6. 若关于的不等式的解集为，则关于的不等式的解集．一元一次不等式组【典型例题】类型一、解一元一次不等式组1.（2016•深圳）解不等式组：．x a x ≤a a x <a x n m x >53x <x 0n 5m x )n m 2(>-+-2. 不等式组是否存在整数解？如果存在请求出它的解；如果不存在要说明理由.举一反三：【变式】（2015•北京）解不等式组，并写出它的所有非负整数解．3.试确定实数a 的取值范围．使不等式组恰好有两个整数解．3(2)5(4) 2.......(1)562(2)1,........(2)32211............(3)23x x x x x x ⎧⎪++-<⎪+⎪+≥+⎨⎪++⎪-≤⎪⎩1023544(1)33x x a x x a +⎧+>⎪⎪⎨+⎪+>++⎪⎩类型二、解特殊的一元一次不等式组4.（2015•黔西南州）求不等式（2x﹣1）（x+3）＞0的解集．解：根据“同号两数相乘，积为正”可得：①或②．解①得x＞；解②得x＜﹣3．∴不等式的解集为x＞或x＜﹣3．请你仿照上述方法解决下列问题：（1）求不等式（2x﹣3）（x+1）＜0的解集．（2）求不等式≥0的解集．课堂练习类型一根据不等式租的整数解情况确定字母的取值范围例1．不等式组有3个整数解，则m的取值范围是．变式练习1．不等式组有3个整数解，则m的取值范围是．变式练习2．已知关于x的不等式组只有3个整数解，则实数a的取值范围是．变式练习3. 已知关于x 的不等式组{4x +2>3(x +a)2x >3(x −2)+5,仅有4个整数解，则实数a 的取值范围是．变式练习4. 已知关于x 的不等式组{5x +2>3(x −1)12x ≤8−32x +2a ,仅有4个整数解，则实数a 的取值范围是．类型二根据不等式组的解集确定字母的取值范围例2.已知关于x 的不等式组无解，则a 的取值范围是．变式练习1．若关于x 的不等式组有解，则实数a 的取值范围是．变式练习2．若不等式的解集为x ＞3，则a 的取值范围是．变式练习3．若关于x 的不等式的解集为x ＜2，则a 的取值范围是．变式练习4．已知不等式组无解，则a 的取值范围是．类型三根据未知数解集或者未知数间的关系确定字母的取值范围例3. 已知方程组⎩⎨⎧-=++=+my x m y x 12312满足x +y <0,求m 的取值范围变式练习1.若关于x ，y 的二元一次方程组的解满足x +y ＜2，则a 的取值范围为．2.已知⎩⎨⎧+=+=+12242k y x k y x 且的取值范围为则k y x ,01-〈-〈 ．例4. 已知关于x的不等式（1﹣a）x＞2的解集为x＜，则a的取值范围是．变式练习1．不等式（x﹣m）＞3﹣m的解集为x＞1，则m的值为．2．若关于x的不等式3m﹣2x＜5的解集是x＞3，则实数m的值为．3．若不等式ax+b＜0的解集是x＞﹣1，则a，b应满足的条件有．综合练习1．关于x的一元一次不等式≤﹣2的解集为x≥4，则m的值为（）A．14B．7C．﹣2D．22．不等式组的解集是x＞﹣1，则a的取值范围是．3．若关于x的一元一次不等式组无解，则a的取值范围是．4．若不等式组的解集为3≤x≤4，则不等式ax+b＜0的解集为．5．已知关于x的不等式组无解，则a的取值范围是．6.不等式组的解是0＜x＜2，那么a+b的值等于．7．已知关于x的不等式组只有3个整数解，则实数a的取值范围是．8．已知关于x的不等式组的整数解共有6个，则a的取值范围是．。

第15讲 一元一次不等式组培优专题

一元一次不等式组含参培优专题

七年级下册——不等式专题培优

(完整word)一元一次不等式(组)与二元一次方程(组)结合培优资料

初一下册数学讲义： 一元一次不等式(组)复习培优

第15讲 一元一次不等式组培优专题

一元一次不等式(公开课优秀课件)

一元一次不等式组含参培优专题-教师版

一元一次不等式培优专题

一元一次不等式(组)培优训练(参数问题)

一元一次不等式及不等式组培优

一元一次不等式培优资料

一元一次不等式(组)与二元一次方程(组)结合培优资料

一元一次不等式含参问题

第15讲一元一次不等式组培优专题

初一下册数学讲义：一元一次不等式(组)复习培优

第15讲一元一次不等式组培优专题