数值分析 第7章 非线性方程的数值解法
数值分析第七章非线性方程的数值解法

数值分析第七章非线性方程的数值解法在数值分析中,非线性方程和非线性方程组的求解是非常重要的问题。
线性方程是指变量之间的关系是线性的,而非线性方程则指变量之间的关
系是非线性的。
非线性方程的数值解法是通过迭代的方式逼近方程的解。
非线性方程的求解可以分为两类:一元非线性方程和多元非线性方程组。
接下来,我们将对这两类方程的数值解法进行介绍。
对于一元非线性方程的数值解法,最常用的方法是二分法、牛顿法和
割线法。
二分法是一种直观易懂的方法,其基本思想是通过迭代将方程的解所
在的区间逐渐缩小,最终找到方程的解。
二分法的缺点是收敛速度较慢。
牛顿法是一种迭代法,其基本思想是通过选择适当的初始值,构造出
一个切线方程,然后将切线方程与x轴的交点作为新的近似解,并不断迭代,直到满足精度要求。
牛顿法的优点是收敛速度较快,但其缺点是初始
值的选择对结果影响很大,容易陷入局部极值。
割线法是对牛顿法的改进,其基本思想是通过选择两个初始值,构造
出一条割线,然后将割线与x轴的交点作为新的近似解,并不断迭代,直
到满足精度要求。
割线法的收敛速度介于二分法和牛顿法之间。
对于多元非线性方程组的数值解法,最常用的方法是牛顿法和拟牛顿法。
牛顿法的思想同样是通过构造切线方程来进行迭代,但在多元方程组中,切线方程变为雅可比矩阵。
牛顿法的优点是收敛速度快,但同样受初
始值的选择影响较大。
拟牛顿法是对牛顿法的改进,其基本思想是通过逼近Hessian矩阵来进行迭代,从而避免了计算雅可比矩阵的繁琐过程。
拟牛顿法的收敛性和稳定性较好,但算法复杂度相对较高。
数值分析非线性方程的数值解法

数值分析非线性方程的数值解法数值分析是一种应用数学方法来分析和解决数学问题的领域。
非线性方程是数值分析中一类重要的问题,其解法包括了迭代法、牛顿法、割线法等。
本文将详细介绍这些数值解法及其原理和应用。
一、迭代法迭代法是解非线性方程的一种常用数值方法。
该方法的基本思想是通过不断迭代逼近方程的根,直到达到所需精度或满足停止准则为止。
迭代法的求根过程如下:1.选择适当的初始值x0。
2. 利用迭代公式xn+1 = g(xn),计算下一个近似根。
3.重复步骤2,直到满足停止准则为止。
常用的迭代法有简单迭代法、弦截法和牛顿法。
简单迭代法的迭代公式为xn+1 = f(xn),其中f(x)为原方程的一个改写形式。
该方法的收敛性要求函数f(x)在解附近有收敛性且导数在一个区间内收敛。
弦截法的迭代公式为xn+1 = xn - f(xn) * (xn-xn-1) / (f(xn)-f(xn-1))。
该方法通过连接两个点上的函数值的割线来逼近方程的根。
牛顿法的迭代公式为xn+1 = xn - f(xn) / f'(xn),其中f'(x)为f(x)的导数。
该方法通过用切线来逼近方程的根。
二、牛顿法牛顿法是解非线性方程的一种常用迭代法。
该方法通过使用方程的导数来逼近方程的根。
迭代过程如下:1.选择适当的初始值x0。
2. 利用迭代公式xn+1 = xn - f(xn) / f'(xn),计算下一个近似根。
3.重复步骤2,直到满足停止准则为止。
牛顿法的收敛速度较快,但要求方程的导数存在且不为0。
三、割线法割线法是解非线性方程的另一种常用迭代法。
该方法通过连接两个点上的函数值的割线来逼近方程的根。
迭代过程如下:1.选择适当的初始值x0和x12. 计算下一个近似根xn+1 = xn - f(xn) * (xn-xn-1) / (f(xn)-f(xn-1))。
3.重复步骤2,直到满足停止准则为止。
割线法的收敛速度介于简单迭代法和牛顿法之间。
第7章非线性方程组的数值解法

f 1 y f 2 2 y
2 y ( 1,1 ) 2
( 1,1 )
( y 3) ( 1, 1 )
( 1, 1 )
( x 1) ( 1 , 1 ) 2
( 1,1 )
f 1 f 2 2 2[ 2 * ( 3) ( 2 ) * ( 2 )] 4 f1 f2 g10 x ( 1,1) x ( 1,1) x f 1 f 2 g 2 2[ 2 * ( 3) 2 * ( 2 )] 20 20 y y f 1 y f 2 ( 1, 1 ) ( 1, 1 )
完
f ( x0 h, y0 k ) f ( x0 , y0 ) ( h k ) f ( x0 , y0 ) x y 1 2 ( h k ) f ( x 0 , y0 ) 2! x y 1 n ( h k ) f ( x 0 , y0 ) n! x y 1 n 1 ( h k ) f ( x0 h, y0 k ) ( n 1)! x y
2
2
令
0
得 f 1 f 1 ( g10 x g 20 y ) f 1 ( g10 ( g f 1 g f 1 ) 2 ( g 10 20 10 x y f 2 g 20 x f 2 g 20 x f 2 ) f2 y f 2 2 ) ( x y
1
f 1 ( x 0 , y0 ) f ( x , y ) 2 0 0
从n到n+1的迭代格式为:
f 1 ( x n , y n ) xn 1 x n x y y f 2 ( xn , yn ) n 1 n x
第7章 非线性方程的数值解法

设 0为给定精 度要求,试确定分半次 数k 使
x* xk
ba 2k
由 于2k , 两 边 取 对 数 , 即 得
ba
k ln(b a) ln
ln 2
数值分析
18/47
§例1: 5.用2 二二分分法 求 法x3 4x2 10 0在[1,2]内 的 根 ,
要 求 绝 对 误 差 不 超 过1 102。 2
第七章 非线性方程的数值解法
数值分析
本章内容
§7.1 方程求根与二分法 §7.2 不动点迭代及其收敛性 §7.4 牛顿法 §7.5 弦截法
数值分析
2/47
本章要求
1. 掌握二分法基本原理,掌握二分法的算法 流程;
2. 掌握理解单点迭代的基本思想,掌握迭代 的收敛条件;
3. 掌握Newton迭代的建立及几何意义,了解 Newton迭代的收敛性;
27/47
§ 7.2 不动点迭代法及其收敛性
不动点迭代的几个重要问题: 1、迭代格式的构造; 2、初值的选取; 3、敛散性的判断;☆ 4、收敛速度的判断。
数值分析
28/47
§ 7.2 不动点迭代法及其收敛性
三.压缩映射原理(整体收敛性)
考虑方程x g( x), g( x) C[a, b], 若
则f (x)=0在[a, b]内必有一根。
二. 过程
将区间对分,判别f (x)的符号,逐步缩小有根区 间。
数值分析
14/47
§7.1.2 二分法
三. 方法
取xmid=0.5*(a+b)
若f(xmid) < (预先给定的精度),则xmid即为根。
否则,若f (a)*f (xmid)<0,则取a1=a,b1=xmid 若f (a)*f (xmid)>0,则取a1=xmid,b1=b 此时有根区间缩小为[a1, b1],区间长度为 b1-a1=0.5*(b-a)
非线性方程数值求解法总结

(一)非线性方程的迭代解法1.非线性方程的一般形式:f(x)=02.非线性方程的分类:⎩⎨⎧=为其他函数。
超越方程,次代数多项式;为代数方程,)()(0)(x f n x f x f 3.方程的根:若存在常数s 使f(s)=0,则称s 是方程(4.1)的根,又称s 是函数f(x)的零点。
4.重根:若f(x)能分解为)()()(x s x x f m ϕ-= 则称s 是方程(4.1)的m 重根和f(x)的m 重零点。
当m=1时,s 称为方程(4.1)的单根和f(x)的单零点。
5.结论:(1)零点存在定理:设函数f(x)在闭区间[a,b]上连续,且f(a)•f(b)<0,那么在开区间(a,b )内至少有一点ξ,使f(ξ)=0.(2)根的唯一性判别:一阶导数不变号且不为零(3)n 次代数方程在复数域上恰有n 个根(4)高于4次的代数方程没有求根公式6.方法:(1)搜索根方法:①作图法:②逐步搜索法:确定方程根的范围的步骤:步骤1 取含f(x)=0根的区间[a,b],即f(a)•f(b)<0;步骤2 从a 开始,按某个预定的步长h ,不断地向右跨一步进行一次搜索, 即检查kh a x k +=上的函数)(k x f 值的符号。
若0)()(1<•-k k x f x f ,则可以确定一个有根区间],[1k k x x -.步骤3 继续向右搜索,直到找出[a,b]上的全部有根区间],[1k k x x -(k=1,2,…,n).(2)二分法①基本思想:含根区间逐次分半缩小,得到一个区间长度以1/2的比例减小的含根区间序列 {}k I ,在给定根的误差界时,利用长度趋于零的特点,可得到在某个区间中满足要求的近似根。
②迭代终止的条件ε<)(k x fε2<-k k a b或者ε<-≤-2k k k a b s x(3)简单迭代法及其收敛性)(0)(x x x f ϕ=⇔=,2,1,0),(1==+k x x k k ϕ迭代法是一种逐次逼近法,用某个固定公式反复校正根的近似值,使之逐 步精确化,最后得到满足精度要求的解。
数值分析第七章 非线性方程与方程组的数值解法0607)

一、二分法
3. 二分法的一个例题
例2 求x3 x 1 0在[1.0,1.5]内的一个实根,准确到
小数点后2位.
k ak
bk
xk
f(xk)符号
0 1.0
1.5
1.25
−
1 1.25
1.375
+
2
1.375 1.3125
−
3 1.3125
1.3438
+
4
1.3438 1.3281
+
5
1.3281 1.3203
续,并且
(x*) (x*) ( p1) (x*) 0, ( p) (x*) 0,
只要相邻两次 计算结果的偏
|
xk
x* |
Lk 1 L
|
x1
x0
|
.
(2.5)
差足够小即可
保证近似值xk 具有足够精度
|
xk
x* |
1 1 L
|
xk 1
xk
|
.
(2.6)
二、不动点迭代法
3. 存在性与收敛性
• 局部收敛性
- 定义1 设(x)有不动点x*,若对任意x0∈{ x*
的某个邻域R},迭代公式(2.2)产生的序列 {xk}∈R,且收敛到x*,则称迭代法(2.2)局部 收敛.
2). 存在正数L<1,使对任意x,y∈[a, b]都有
| (x) ( y) | L | x y |;
则(x)在[a, b]上存在唯一的不动点x*.
二、不动点迭代法
3. 存在性与收敛性
• 全局收敛的充分条件
- 定理2 设(x) 满足定理1中两条件,则对任意
x0∈[a, b],迭代法收敛,并有误差估计式
数值分析 第七章 非线性方程(组)的数值解法.
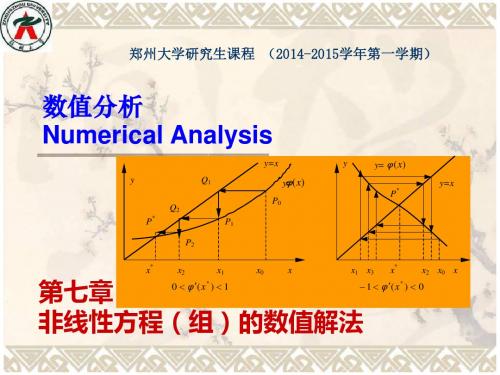
y
,这样就可得缩小有根区间 a1 , b1
y=f(x) y=f(x)
x* a a1 x1 a2 x* x0 b1 b2 b a x0 a1 x1 a2 b b1 b2
23/87 郑州大学研究生2014-2015学年课程 数值分析 Numerical Analysis
§7.2 二分区间法 ② 对压缩了的有根区间 a1 , b1 施行同样的手法, b 即取中点 x a 2 ,将区间 a1 , b1 再分为两半,然 后再确定有根区间 a 2 , b2 ,其长度是 a1 , b1 的 二分之一。
长h=(B-A)/n(n是正整数),在[A,B]内取定节点:xi=x0+ih (i=0,1,2,…,n),从左至右检查f (xi)的符号,如发现xi与端点x0 的函数值异号,则得到一个缩小的有根子区间[xi-1,xi]。
y
0 A
a1 b1 a2 b2
B
x
20/87 郑州大学研究生2014-2015学年课程 数值分析 Numerical Analysis
§7.1 引言
数值解法的三个步骤 ① 判定根的存在性。即方程有没有根?如果有 根,有几个根? ② 确定根的分布范围。即将每一个根用区间隔 离开来,这个过程实际上是获得方程各根的 初始近似值。(隔离根) ③ 根的精确化。将根的初始近似值按某种格式 逐步精确化,直到满足预先要求的精度为止。
10/87 郑州大学研究生2014-2015学年课程 数值分析 Numerical Analysis
3/87 郑州大学研究生2014-2015学年课程 数值分析 Numerical Analysis
§7.1 引言 当 f (x)不是x的线性函数时,称对应的函数方程
f (x)=0为非线性方程。
数值分析 李庆扬 第7章 非线性方程与方程组的数值解法
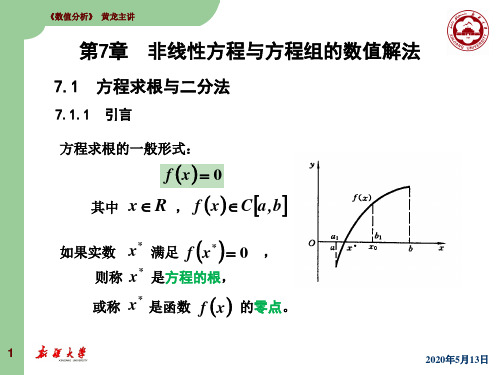
x x3 1
时,在区间
1,2
有:
x 3 x 2 1
不满足定理的条件,无法保证迭代收敛。
a , b
上)
(2) 存在正常数 L 1 ,使对任意
x , y a , b 都有
x y L x y
(迭代函数的增量小于自变量的增量) 则
14
x 在 a , b
上存在唯一的不动点 x 。
2017年1月4日
*
《数值分析》 黄龙主讲
证明:先证不动点存在性。 若
x , y a , b 有
x y x y L x y , a , b
因此,可将上述定理 1 和定理 2 中的条件(2)改为:
x L 1
21
2017年1月4日
《数值分析》 黄龙主讲
例如:
(2) 存在正常数 L 1 ,使对任意
x y L x y
则对任意 由
x0 a , b :
xk 1 xk 得到的迭代序列 xk
收敛到
x 的不动点 x*
,并有误差估计
k L x k x* x1 x0 1 L
17
2017年1月4日
*
最终取值: x
误差:取有根区间
ak , bk 的中点 (
ak bk xk 作为近似根,则: 2 b ak b a x* x k k k 1 2 2
特点:算法简单,可保证收敛,但收敛太慢。用于求近似解。
8
2017年1月4日
《数值分析》 黄龙主讲
P214例2 求方程 f x x 3 x 1 0 在区间 1.0 ,1.5 内的一个实根, 要求准确到小数点后的第二位。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
构造迭代格式 xk1 3 xk 1 (k 0,1,2, ) 取初值 x0 1.5
表7 3
k
xk
k
xk
0
1.5
5 1.32476
1 1.35721 6 1.32473
2 1.33086 7 1.32472
3 1.32588 8 1.32472
若 x满* 足 f (x*,) 则0
x;*反 之(亦x*然) ,称
x*
为函数 (的x)一个不动点.
求 f (x)的零点就等价于求 (x) 的不动点.
迭代格式 xk1 (xk ) (k 0,1, ).
(2.2)
(称x)为迭代函数.
➢格式的收敛性
如果对任何 x0 [,a, 由b]迭代 xk1 ( xk ) (k 0,1, ). 不动点迭代法
如果实数 x满* 足 f (x*,) 0 则称 x是* 方程(1.1)的根,或称 是x * 的f 零(x点) .
若f (可x)分解为
其中 m为正整数,
f ( x) ( x x*)m g( x),
g( x*) 0.
则称 x为*方程(1.1)的 重m根,或 为x *的f 重(x零) 点m,
m 时1为单根.
后来卡当的学生弗瑞里(Ferrari)又提出了四次方程的解法。 此成果更激发了数学家们的情绪,但在以后的二个世纪中, 求索工作始终没有成效,导致人们对高次代数方程解的存 在性产生了怀疑。
1799年,高斯证明了代数方程必有一个实根或复根的定理, 称此为代数基本定理,并由此可以立刻推理n次代数方程必 有n个实根或复根。
4 1.32494
如果仅取6位数字,
结果x7与 完x8全相同, x即7 为所求的根.
说明:①迭代函数不唯一,②迭代点列可能收敛,也可能 发散,迭代收敛与否不仅与迭代函数有关,还与初始 点有关。
➢不动点迭代的几何解释
x
(x)
y
y x
(x)
交点的横坐标
y=x
y (x)
( x0 )
( x2 ) ( x1 )
xi=x0+ih (i=0,1,2,……) 考察函数值f(xi)的符号,当f(x)连续且f(xi) .f(x i+1)<0,则区
间[xi , x i+1]为有根区间,若导数不变号有唯一根。
例2 求方程 f (x) x3 11.1x2 的38有.8x根区41间.77. 0
对 f (x) 的 0根进行搜索计算,
7.1 方程求根与二分法
7.1.1 引言 单变量非线性方程的一般形式
f (x) 0 其中 x R, f (x) C[也a,可b]以, [是a,无b]穷区间. ➢代数方程与超越方程 如果函数 f是(x多) 项式函数,即
(1.1)
f ( x) a0 xn a1 xn1 an1 x an (a0 0),
a
2
b
b1
b2
b3
由二分法的过程知
(1) [a, b] [a1, b1] [a2 , b2 ] [ak , bk ] , f (ak ). f (bk ) 0, x* [ak ,bk ],
(2)
bk ak
bk1 ak1 2
ba 2k
(3)
xk
ak
bk 2
作为根的近似
近似根的序列
后来伽罗华命运不佳,投考名校巴黎工科大学落榜,屈就高 等师院,并卷入政事两次入狱,被开除学籍,又决斗受伤, 死于1832年。决斗前,他把关于五次代数求解的研究成果写 成长信,留了下来。
十四年后,法国数学家刘维尔(J·Liouville)整理并发表了 伽罗华的遗作,人们才意识到这项近代数学发展史上的重 要成果的宝贵。
但在以后的几十年中仍然没有找出高次代数方程的公式解。 一直到18世纪,法国数学家拉格朗日用根置换方法统一了 二、三、四方程的解法。
但求解五次方程时未能如愿,开始意识到有潜藏其中的奥妙, 用现代术语表示就是置换群理论问题。
在继续探索5次以上方程解的艰难历程中,第一个重大突破 的是挪威数学家阿贝尔(N·Abel1802-1829) 1824年阿贝 尔发表了“五次方程代数解法不可能存在”的论文,但并 未受到重视,连数学大师高斯也未理解这项成果的重要意 义。
例1 求方程3x-1-cosx=0的有根区间。
方程等价变形为3x-1=cosx,
y=3x-1与y=cosx的图像只有一个交点位于[0.5,1]内。
(2)解析法
根据函数的连续性、介值定理和单调性寻找有根区间和唯一 根的区间。
(3)定步长搜索法
在某一区间[a,b]上,从x0=a 出发,以步长 h=(b-a)/n 其中n是正整数,在[a,b]内取定节点:
xk xk1
例5 求方程
f (x) x3 x 1 0
(2.3)
在 x0 附1.5近的根 x *.
解 构造迭代格式。
方法一: x x3 1 取迭代函数 1( x) x3 1
构造迭代格式 xk1 xk3 1 (k 0,1,2, ) 取初值 x0 1.5
k0 1
2
3
发散
xk 1.5 2.375 12.396 1904.002
➢基本思想
逐步将区间二等分, 通过判断区间端点f(x)的符号, 将有根区 间缩小,直至有根区间足够地小, 便可求出满足精度要求的近 似根。
➢具体做法
[a1, b1] [a2 , b2 ] [a3, b3]
y
a3
a2
b2 2
x2
a1
y f (x)
以
o
a
•••
x
bx
此
类 推
a2
a1
b1 2
x1
x0
首先取一个粗糙的近似值,然后用同一个递推公式,反复 校正这个初值,直到满足预先给出的精度要求为止。 7.2.1 不动点与不动点迭代法/*Fixed-Point Iteration*/
已知方程 f ( x)在 0区间[a,b] 内有一个根x*,在区间[a,b]
f ( x) 0 x ( x). (x) C[a,b] (2.1)
1828年17岁的法国数学家伽罗华(E·Galois 1811-1832)写出 了划时代的论文“关于五次方程的代数解法问题”,指出即 使在公式中容许用n次方根,并用类似算法求五次或更高次 代数方程的根是不可能的
文章呈交法兰西科学院后,因辈份太低遭到冷遇,且文稿丢 失。1830年伽罗华再进科学院递稿,得到泊松院士的判词 “完全不能理解”。
得到序列
{
x
k
}有极限 k0
lim
k
xk
x *. 则称迭代法收敛,
且 x* 为(x*) 的不 (动x)点。
不动点迭代是一种逐次逼近的方法,用某个固定公式反复校正根
的近似值,使之逐步精确化,最后得到满足精度要求的结果。
➢迭代终止的判定 对预先给定的精度要求ε,只要某个k满足 即可结束计算并取 x* xk
限为 102,问至少需对分多少次?
解: a 1, b 1.5, 102;
k ln(b a) ln 1
ln 2
ln(1.5 1) ln102 1 4.64
ln 2 k 5
➢二分法的算法
y
xb
开始 输 入 a , b,ε
(a+b)/2 x
f(a) f(x )<0 ?
|b-a|< ε
远在公元前1700年的古巴比伦人就已有关于一、二次方程 的解法。《九章算术》(公元前50~100年)其中“方程术” 有联立一次方程组的一般解法。
1535年意大利数学家坦特格里亚(TorTaglia)发现了三次方 程的解法,卡当(H·Cardano)从他那里得到了这种解法, 于1545年在其名著《大法》中公布了三次方程的公式解, 称为卡当算法。
得到新的有根区间 [a1, b1]. Nhomakorabea欲使
x*xk
(bk
ak
)
/
2
(b
a)
/
2k
1
1 2
1 2 k 1
0.005,
只需 k ,6 即只要二分6次,便能达到预定的精度.
k ak 0 1.0
bk
xk
f ( xk )符号
1.5 1.25
1 1.25
1.375
2
1.375 1.3125
3 1.3125
1.3438
4
1.3438 1.3281
5
1.3281 1.3203
6 0.3203
1.3242
优点 不管有根区间多大,总能求出满足精度要求的根, 且对函数f(x)的要求不高,只要连续即可,计算亦简单。
缺点 二分法对多个零点的情况,只能算出其中一个零点。 即使 f(x)在[a, b]上有零点,也未必有 f(a) f(b)<0。
➢结论若 是x * 的f (x重) 零点m,且 充分g光(x滑) ,则
f ( x*) f ( x*) f (m1)( x*) 0, f (m)( x*) 0.
n次方程在复数域有且只有 个n根(含重根, 重m根为 个根m).
本章将介绍常用的求解非线性方程的近似根的几种数值解法
通常方程根的数值解法大致分为2个步骤进行:
其中 a0 0, ai (i 为0,1实,数,, n则) 称方程(1.2)为 次代数方程.
(1.2)
n
超越函数 不能表示为多项式的函数
如 (x)=3x5-2x4+8x2-7x+1=0 (x)=e2x+1-xln(sinx)-2=0
高次代数方程
超越方程
➢方程的根与函数的零点
f ( x) 0 (1.1)
x0 , x1, x2 , xk , ,
