第5讲-二次函数轨迹问题
二次函数与运动轨迹问题

二次函数与运动轨迹问题二次函数是数学中一个非常重要的概念,它描述了一个物体的运动轨迹。
在实际生活中,我们经常遇到物体的运动问题,比如投篮、射门、跳高等等。
这些运动问题都可以用二次函数来描述。
首先,我们来了解一下什么是二次函数。
二次函数的一般形式是y=ax^2+bx+c(a≠0),其中a、b、c是常数,x是自变量,y是因变量。
这个函数的图像是一个抛物线,顶点是(−b/2a,c−b^2/4a),对称轴是x=−b/2a。
在运动轨迹问题中,物体的运动可以看作是重复的直线运动和曲线运动的组合。
直线运动是物体在一段时间内沿直线移动,可以用一次函数来描述;曲线运动是物体在一段时间内沿曲线移动,可以用二次函数来描述。
以投篮为例,当篮球离开手后,它会由于重力的作用沿一条弧线运动,这条弧线的形状可以用二次函数来描述。
具体来说,如果以t表示时间,x表示篮球的水平位移,y表示篮球的垂直位移,那么篮球的运动轨迹可以表示为y=kx^2+h(k≠0),其中k和h是常数。
通过这个例子,我们可以看出二次函数在描述物体的运动轨迹方面具有重要作用。
在实际应用中,我们可以通过测量物体的运动数据,比如时间、位置、速度、加速度等,来拟合出物体的运动轨迹方程,从而更好地预测和控制物体的运动。
除了投篮,二次函数还可以描述其他类型的运动轨迹问题。
比如跳高运动中,运动员的腾空高度随时间的变化可以用二次函数来描述;在发射卫星时,卫星的轨道高度随时间的变化也可以用二次函数来描述。
总之,二次函数是描述物体运动轨迹的一个重要工具。
通过掌握二次函数的性质和应用方法,我们可以更好地解决实际生活中的运动轨迹问题,提高我们的生活质量和工作效率。
二次函数的变换规律

二次函数的变换规律二次函数是高中数学中的重要内容,它是一种常见的数学函数形式。
在学习二次函数时,我们需要了解二次函数的变换规律,即通过对函数中的参数进行变化,能够改变函数的形状和位置。
在本文中,我将详细介绍二次函数的变换规律,以加深对该主题的理解。
1. 平移变换平移变换是指通过改变二次函数的平移量,使函数图像在坐标平面上上下左右移动。
二次函数的标准形式为f(x) = ax² + bx + c,在平移变换中,平移量为h和k,表示在横轴和纵轴上的平移距离。
1.1 沿x轴平移二次函数沿x轴正方向平移h个单位,相当于将函数图像向左移动h个单位;沿x轴负方向平移h个单位,相当于将函数图像向右移动h个单位。
平移后的函数可表示为f(x) = a(x-h)² + bx + c,其中h代表横轴的平移量。
1.2 沿y轴平移二次函数沿y轴正方向平移k个单位,相当于将函数图像向上移动k个单位;沿y轴负方向平移k个单位,相当于将函数图像向下移动k个单位。
平移后的函数可表示为f(x) = ax² + bx + (c-k),其中k代表纵轴的平移量。
2. 缩放变换缩放变换是指通过改变二次函数的参数a和导致函数图像的纵向和横向的缩放。
二次函数的标准形式为f(x) = ax² + bx + c,在缩放变换中,缩放因子为p和q,表示纵向和横向的缩放比例。
2.1 纵向缩放当缩放因子p大于1时,二次函数的图像会纵向收缩;当p在0和1之间时,二次函数的图像会纵向拉伸。
缩放后的函数可表示为f(x) = pax² + bx + c,其中p表示纵向缩放因子。
2.2 横向缩放当缩放因子q大于1时,二次函数的图像会横向拉伸;当q在0和1之间时,二次函数的图像会横向收缩。
缩放后的函数可表示为f(x) =a(qx)² + bx + c,其中q表示横向缩放因子。
3. 翻转变换翻转变换改变了二次函数图像的方向。
二次函数的平移与变形抛物线的移动之谜

二次函数的平移与变形抛物线的移动之谜二次函数是高中数学学习中的重要内容之一,它描述了一条抛物线的形状。
除了基本的抛物线方程y=ax²+bx+c外,平移与变形是二次函数的常见操作。
本文将探讨二次函数的平移与变形对抛物线的移动产生的影响。
一、平移操作平移是指将函数图像在平面上沿着x轴或y轴方向上移动固定的距离的操作。
对于二次函数y=ax²+bx+c来说,平移操作分别对应了c、b 和a的改变。
1. 沿x轴平移当函数图像沿x轴正方向平移h个单位长度时,抛物线向左平移h 个单位长度;而当函数图像沿x轴负方向平移h个单位长度时,抛物线向右平移h个单位长度。
平移操作的数学表达式如下:y=a(x-h)²+bx+c其中(h, k)为平移后抛物线的顶点坐标。
2. 沿y轴平移当函数图像沿y轴正方向平移k个单位长度时,抛物线向上平移k 个单位长度;而当函数图像沿y轴负方向平移k个单位长度时,抛物线向下平移k个单位长度。
平移操作的数学表达式如下:y=a(x-α)²+b(x-α)+c其中α为平移后抛物线的顶点的x坐标。
二、变形操作变形是指改变二次函数方程中的参数,从而改变抛物线的形状。
常见的变形操作包括改变a、b和c的值。
1. 改变a的值当a的值发生变化时,抛物线的开口方向和形状都会发生变化。
当a>0时,抛物线开口朝上;当a<0时,抛物线开口朝下。
同时,a的绝对值越大,抛物线越窄;而a的绝对值越小,抛物线越宽。
变形操作的数学表达式如下:y=ax²+bx+c2. 改变b的值当b的值发生变化时,抛物线的对称轴位置和形状都会发生变化。
当b>0时,抛物线的对称轴向右移动;当b<0时,抛物线的对称轴向左移动。
同时,b的绝对值越大,抛物线越陡;而b的绝对值越小,抛物线越平缓。
变形操作的数学表达式如下:y=ax²+bx+c3. 改变c的值当c的值发生变化时,抛物线的顶点位置和整体位置都会发生变化。
二次函数实际应用轨迹与路桥问题
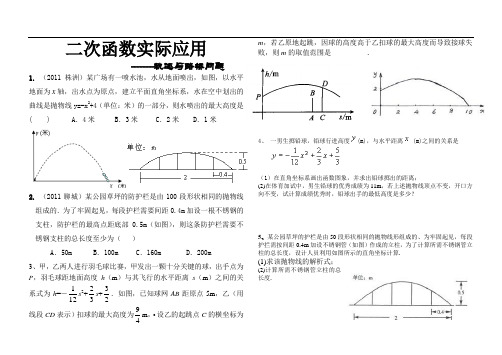
二次函数实际应用 --------轨迹与路桥问题1. (2011株洲)某广场有一喷水池,水从地面喷出,如图,以水平地面为x 轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x 2+4(单位:米)的一部分,则水喷出的最大高度是( ) A .4米 B .3米 C .2米 D .1米2. (2011聊城)某公园草坪的防护栏是由100段形状相同的抛物线组成的.为了牢固起见,每段护栏需要间距0.4m 加设一根不锈钢的支柱,防护栏的最高点距底部0.5m (如图),则这条防护栏需要不锈钢支柱的总长度至少为( )A .50mB .100mC .160mD .200m3、甲,乙两人进行羽毛球比赛,甲发出一颗十分关键的球,出手点为P ,羽毛球距地面高度h (m )与其飞行的水平距离s (m )之间的关系式为h =-112s 2+23s +32.如图,已知球网AB 距原点5m ,乙(用线段CD 表示)扣球的最大高度为94m ,•设乙的起跳点C 的横坐标为m ,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m 的取值范围是__________.4、 一男生掷铅球,铅球行进高度(m),与水平距离(m)之间的关系是(1)在直角坐标系画出函数图象,并求出铅球掷出的距离;(2)在体育加试中,男生铅球的优秀成绩为11m ,若上述抛物线顶点不变,开口方向不变,试计算成绩优秀时,铅球出手的最低高度是多少?5、某公园草坪的护栏是由50段形状相同的抛物线形组成的、为牢固起见,每段护拦需按间距0.4m 加设不锈钢管(如图)作成的立柱,为了计算所需不锈钢管立柱的总长度,设计人员利用如图所示的直角坐标计算.(1)求该抛物线的解析式;(2)计算所需不锈钢管立柱的总长度.6、一座拱桥的轮廓是抛物线型(如图所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.(1)在图上建立适当的平面直角坐标系,求抛物线的解析式;(2)求支柱E F的长度;(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说明你的理由.7、如图,河上有一座抛物线桥洞,已知桥下的水面离桥拱顶部3m时,水面宽A B为6m,雨季时水位上升0.5m.(1)求水面的宽度C D为多少米?(2)有一艘游船,它的左右两边缘最宽处有一个长方体形状的遮阳棚,此船正对着桥洞在上述河流中航行.①若游船宽(指船的最大宽度)为2m,从水面到棚顶的高度为1.8m,问这艘游船能否从桥洞下通过?②若从水面到棚顶的高度为74m的游船刚好能从桥洞下通过,则这艘游船的最大宽度是多少米?8、(2012武汉)如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成,已知河底ED 是水平的,ED=16米,AE=8米,抛物线的顶点C到ED距离是11米,以ED所在的直线为x轴,抛物线的对称轴y轴建立平面直角坐标系,(1)求抛物线的解析式;(2)已知从某时刻开始的40小时内,水面与河底ED的距离h(单位:米)随时间t(单位:时)的变化满足函数关系h=-8)19(12812+-t(0≤t≤40)且当水面到顶点C的距离不大于5米时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?9. (2012安徽)如图,排球运动员站在点O处练习发球,将球从O 点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
2019年九年级数学 第5讲—二次函数与特殊平行四边形的综合问题教案

知识讲解考点1 二次函数的基础知识1.一般地,如果y=ax 2+bx+c (a ,b ,c 是常数且a ≠0),那么y 叫做x 的二次函数,它是关于自变量的二次式,二次项系数必须是非零实数时才是二次函数,这也是判断函数是不是二次函数的重要依据.当b=c=0时,二次函数y=ax 2是最简单的二次函数.2.二次函数y=ax 2+bx+c (a ,b ,c 是常数,a ≠0)的三种表达形式分别为:一般式:y=ax 2+bx+c ,通常要知道图像上的三个点的坐标才能得出此解析式;顶点式:y=a (x -h )2+k ,通常要知道顶点坐标或对称轴才能求出此解析式;交点式:y=a (x -x 1)(x -x 2),通常要知道图像与x 轴的两个交点坐标x 1,x 2才能求出此解析式;对于y=ax 2+bx+c而言,其顶点坐标为(-2b a,244ac b a ).对于y=a (x -h )2+k 而言其顶点坐标为(h ,k ),•由于二次函数的图像为抛物线,因此关键要抓住抛物线的三要素:开口方向,对称轴,顶点. 考点2 矩形的性质及判定1. 矩形定义:有一角是直角的平行四边形叫做矩形. 注意:矩形(1)是平行四边形;(2)四个角是直角.2. 矩形的性质性质1 矩形的四个角都是直角;性质2 矩形的对角线相等,具有平行四边形的所以性质。
; 3. 矩形的判定矩形判定方法1:对角线相等的平行四边形是矩形.注意此方法包括两个条件:(1)是一个平行四边形;(2)对角线相等矩形判定方法2:四个角都是直角的四边形是矩形. 矩形判断方法3:有一个角是直角的平行四边形是矩形。
考点3 菱形的性质及判定1.菱形定义:有一组邻边相等的平行四边形叫做菱形. 注意: 菱形(1)是平行四边形;(2)一组邻边相等. 2.菱形的性质性质1 菱形的四条边都相等;性质2 菱形的对角线互相平分,并且每条对角线平分一组对角;3.菱形的判定菱形判定方法1:对角线互相垂直的平行四边形是菱形.注意此方法包括两个条件:(1)是一个平行四边形;(2)两条对角线互相垂直.菱形判定方法2:四边都相等的四边形是菱形.考点4 正方形的性质及判定1. 正方形是在平行四边形的前提下定义的,它包含两层意思:有一组邻边相等的平行四边形(菱形)有一个角是直角的平行四边形(矩形)都可以得到正方形;正方形不仅是特殊的平行四边形,并且是特殊的矩形,又是特殊的菱形.2.正方形定义:有一组邻边相等.......的平行四边形.....叫做正方形.......并且有一个角是直角正方形是中心对称图形,对称中心是对角线的交点,正方形又是轴对称图形,对称轴是对边中点的连线和对角线所在直线,共有四条对称轴;3. 因为正方形是平行四边形、矩形,又是菱形,所以它的性质是它们性质的综合,正方形的性质总结如下:边:对边平行,四边相等;角:四个角都是直角;对角线:对角线相等,互相垂直平分,每条对角线平分一组对角.注意:正方形的一条对角线把正方形分成两个全等的等腰直角三角形,对角线与边的夹角是45°;正方形的两条对角线把它分成四个全等的等腰直角三角形,这是正方形的特殊性质.正方形具有矩形的性质,同时又具有菱形的性质.4. 正方形的判定方法:(1)有一个角是直角的菱形是正方形;(2)有一组邻边相等的矩形是正方形.注意:1、正方形概念的三个要点:(1)是平行四边形;(2)有一个角是直角;(3)有一组邻边相等.2、要确定一个四边形是正方形,应先确定它是菱形或是矩形,然后再加上相应的条件,确定是正方形.考点5 探究特殊平行四边形的一般思路解答特殊平行四边形的存在性问题时,要具备分类讨论的思想及数形结合思想,要先找出特殊平行四边形的分类标准,一般涉及到动态问题要以静制动,动中求静,由于特殊平行四边形分为矩形、菱形和正方形,故我们可以从这些特殊平行四边形的性质及题干信息入手,具体如下:(1)假设结论成立,分情况讨论,抓住每类图形的特殊性质入手,由于特殊的平行四边形也是平行四边形,可先证明出是平行四边形,在适当加入一些特征便可以得到矩形、菱形或是正方形。
二次函数平移规律

二次函数平移规律二次函数的一般形式为:y = ax^2 + bx + c,其中a、b和c是常数,代表曲线的形状、位置和方向。
平移变换的规律可以分为以下几种情况:1.沿x轴平移:将整个图像沿x轴的正方向或负方向移动一个固定的距离。
将二次函数的公式中的x换成(x-h),其中h表示x轴的平移量。
例如,若h>0,则平移后的函数为y=a(x-h)^2+b(x-h)+c。
2. 沿y轴平移:将整个图像沿y轴的正方向或负方向移动一个固定的距离。
将二次函数的公式中的c换成c + k,其中k表示y轴的平移量。
例如,若k > 0,则平移后的函数为y = ax^2 + bx + (c + k)。
3.组合平移:同时沿x轴和y轴方向进行平移变换。
将二次函数的公式中的x换成(x-h),c换成(c+k)。
例如,若h>0且k>0,则平移后的函数为y=a(x-h)^2+b(x-h)+(c+k)。
需要注意的是,平移会改变函数的位置,但不会改变函数的形状和方向。
也就是说,平移前后的函数曲线是相似的,它们只是在坐标系中的位置不同。
平移变换也可通过绘制函数图像来观察和理解。
首先,绘制原始函数的图像,然后通过调整参数a、b、c、h和k,分别代表二次函数的系数和平移量,来获得不同位置的图像。
通过比较不同图像之间的差异,可以更好地理解平移变换的规律。
此外,可以通过数学的推导和计算来验证平移变换的规律。
对于给定的二次函数,通过代入不同的参数值,并计算出相应的函数值,可以验证函数图像在平移后是否符合平移变换的规律。
总结起来,二次函数的平移变换是通过改变函数的参数来实现的。
沿x轴平移可以通过更改x的值,沿y轴平移可以通过更改c的值,组合平移则同时改变x和c的值。
平移变换不仅可以通过绘制函数图像来观察和理解,还可以通过数学的推导和计算来验证和探索。
掌握了二次函数的平移规律,可以更好地理解二次函数的性质和变换。
暑期备课笔记-初三数学第5讲:实际问题与二次函数(教师版)

第5讲实际问题与二次函数实际问题与二次函数1、二次函数与一次函数的解析式形式;待定系数法求解析式2、二次函数与一次函数的综合题;(1)二次函数与一次函数交点个数问题此类问题解题思路:第一步,把二次函数与一次函数联立方程组第二步,整理成一元二次方程一般式第三步,求△,△>0,有两个交点△=0,有一个交点△<0,无交点(2)二次函数图像沿x轴或y轴或某条平行于x轴或y轴的直线翻折,得到新的函数图像,有一条直线与新图像有公共点,求b的取值范围;解题思路:1.先画出原函数图像2,再根据条件画出新函数图像3,观察图形,找出临界情况。
4. 带点求解析式,从而求出b的取值范围3、二次函数与三角形的综合;存在等腰三角形:两圆一线;存在直角三角形:两线一圆;1、二次函数与一次函数求解析式以及求交点个数问题;2、二次函数与一次函数相切问题;3、二次函数与三角形综合;存在等腰三角形或直角三角形;例1、函数2axy=与baxy+-=的图象可能是()A. B. C.D答案:B解析:分情况讨论:1)当a>0时,开口向上。
—a<0,下降趋势。
2)当a<0时,开口向上。
—a>0,上升趋势,所以应该选B例2、方程组⎩⎨⎧-+-=-=32422xxyxy的解为⎪⎩⎪⎨⎧-==321yx和⎩⎨⎧-=-=61yx,则一次函数42-=xy与二次函数322-+-=x x y 的图象交点坐标为___________答案:(12,-3) (-1,-6)解析:⎩⎨⎧-+-=-=32422x x y x y 的解即为42-=x y 42-=x y 与322-+-=x x y 的交点坐标。
例3、当b 为何值时,直线b x y +=3与抛物线122-+=x x y 有一个交点? 答案:b=−54解析:与只有一个交点,联立转化成b x x x +=-+3122整理成一般式012=---b x x ,求b 2-4ac =0,从而可得b 。
例4、(1)点A (2,-3)是抛物线3222--=mx x m y 上的点,求抛物线的解析式; (2) 在(1)的条件下,是否存在与抛物线只交于点A 的直线)0(≠+=k b kx y ?若存在,请求出直线的解析式;若不存在,请说明理由答案:(1) 322--=x x y (2) 存在 72-=x y解析:(1)把(2,-3)代入抛物线解析式-3=4m 2-4m -3, 解得m 1=0,m 2=1,舍掉m =0,所以m=1.(2) -3=2k+b,则b=-2k-3,联立x 2-2x -3=kx -2k -3,当b 2-4ac =0,求出k=2,b=-7.例5.如图,二次函数2y x bx c =++经过点(-1,0)和点(0,-3). (1)求二次函数的表达式;(2)如果一次函数4y x m =+的图象与二次函数的图象有且只有一个公共点,求m 的值和该公共点的坐标;(3)将二次函数图象y 轴左侧部分沿y 轴翻折,翻折后得到的图象与原图象剩余部分组成一个新的图象,该图象记为G ,如果直线4y x n =+与图象G 有3个公共点,求n 的值.答案:y =x 2-2x -3b x y +=3122-+=x x y解析:1)代入(-1,0)和点(0,-3),求出b 、c 的值2)联立与消掉y,整理得0)3(62=---m x x ,让△=0,解出m,从而得公共点坐标。
二次函数的图像和轨迹

二次函数的图像和轨迹二次函数是高中数学中的重要概念,它在代数、几何以及实际问题中都有广泛的应用。
本文将探讨二次函数的图像和轨迹,通过图形和数学方程来帮助读者更好地理解这个概念。
1. 二次函数的定义和一般形式二次函数是指形如f(x) = ax² + bx + c的函数,其中a、b、c是实数且a≠0。
这个函数的图像通常是一个开口朝上或朝下的抛物线。
当a>0时,抛物线开口朝上;当a<0时,抛物线开口朝下。
2. 抛物线的顶点和对称轴对于二次函数f(x) = ax² + bx + c,抛物线的顶点坐标可以通过求解方程-f(x) = ax² + bx + c的最值来得到。
顶点的横坐标是x = -b/(2a),纵坐标是f(-b/(2a))。
这个顶点处于抛物线的最低点或最高点,也是抛物线的中心。
抛物线的对称轴是通过顶点且垂直于x轴的直线。
它的方程为x = -b/(2a)。
对称轴将抛物线分成两个对称的部分。
3. 抛物线的开口方向和轨迹根据二次函数的系数a可以确定抛物线的开口方向。
当a>0时,抛物线开口向上;当a<0时,抛物线开口向下。
开口方向对应了二次函数的正负性质。
根据抛物线的开口方向,可以推测二次函数的图像在坐标系中的轨迹。
当a>0时,抛物线的轨迹在y轴的正半轴上方;当a<0时,抛物线的轨迹在y轴的负半轴上方。
4. 抛物线的焦点和直线的切线对于二次函数f(x) = ax² + bx + c,如果a≠0,那么抛物线将与y轴交于点(0, c)。
这个点称为抛物线的焦点。
抛物线上的每个点都有一条切线。
切线与抛物线在该点处相切,并且切线斜率等于抛物线在那点的导数。
对于二次函数,可以根据导数的定义来求解切线的斜率,并再结合该点的坐标得到切线的方程。
5. 抛物线在坐标系中的平移通过修改二次函数的系数b和c,可以使得抛物线在坐标系中进行平移。
当b≠0时,抛物线将在x轴方向上平移;当c≠0时,抛物线将在y轴方向上平移。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
,
(1)求x1·x2的值.
(2)分别过M,N作直线l:y=-1的垂线,垂足分别是M1,N1,连接FM1,FN1,判断△M1FN1的形状,并证明你的结论.
解:(1)∵直线y=kx+b过点F(0,1),∴b=1;
例3、例4、例5、例6
模块一抛物线特殊点轨迹问题
题型一抛物线顶点的轨迹
例1.(1)已知抛物线y= -4ax+4 +a-1,当实数a变化时,抛物线的顶点D都在某条直线l上,求直线l的解析式.
解:∵y= -4ax+4 +a-1= +a-1,∴D(2a,a-1).
x-1.
②若a=-1,点M坐标为(2,0)是x轴上的点,N为抛物线C1上的点,Q为线段MN的中点.设点N在抛物线C1上运动时,Q的运动轨迹为抛物线C2,求抛物线C2的解析式.
解:①∵y=ax2-4a+4=a(x2-4)+4,该函数图象过第一象限内的定点P,
∴x2-4=0,解得x=2或x=-2(舍去),则y=4,
(1)若-1<t<1,求证:OP+PM为定值,并求出该值.
(2)若t<-1或t>1,求证:OP-PM为定值,并求出该值.
证明:(1)P(t, t2- ),OP= = t2+ ,PM= t2- ,
∴OP+PM=t2.
(2)P(t, t2- ),OP= = t2+ ,PM= t2- ,
∴OP-PM=1.
【解】(1) ;
[
∵AO=2CO,C(0,-1),∴A(-2,0), 代入得抛物线方程 .
(2) 把D(4,-m) 代入抛物线方程 ,得m=3, ∴D(4,3),DO=5.∴d=5, ∴t=-2.
(3) 分别过点E、F作直线l的垂线,垂足分别为N、K,连接OE,OF.
由(2)知EN=EO,FK=FO.
;
(2)已知抛物线 :y= +2ax+2x-a+1,当实数a变化时,抛物线 的顶点D都在某条抛物线 上,求抛物线 的解析式.
解:∵ :y= +2ax+2x-a+1= - -a+1,∴D(-a-1,- -a+1).
∵抛物线 的顶点D都在某条抛物线 上,∴抛物线 的解析式为:y=- +x+2.
练习
(1)已知抛物线y=- +2ax- 的顶点为P,当a变化时,点P总在直线l上.求直线l的解析式;
∴点P( , ).
【
例4.如图1,P(m,n)是抛物线 上任意一点,l是过点(0,-2)且与x轴平行的直线,过点P作直线PH⊥l于点H.
(1)填空:m=0时,OP=______________,PH=_____________;当m=4,OP=____________,PH=____________.
(1)直接写出抛物线 的解析式;
(2)如图1,y轴上是否存在定点F,使得抛物线 上任意一点P到x轴的距离与PF的长总相等若存在,求出点F的坐标;
(3)如图2,D为抛物线 的顶点,P为抛物线 上任意一点,过点P作PH⊥x轴于点H,连接DP,求PH+PD的最小值及此时点P的坐标.
?
图1图2
【解】(1) 抛物线 的解析式 ;
①当EF不过O点时,在△EOF中,∵OE+OF>EF,∴EN+FK>EF=8.
②当AB过O点时,∵OE+OF=EF,∴EN+FK=OE+OF=EF=8.
∴EN+FK≥8.又MH= (EN+FK)≥4,∴MH的最小值为4
即点M纵坐标的最小值为2.
?
例5
如图,抛物线y= x2- 与x轴交于A、B两点(A在B的左侧),点P是抛物线上一动点(不包括A、B),PM⊥x轴于点M,点P的横坐标为t.
∴点P的坐标是(2,4);
②设点Q的坐标为(xQ,yQ),点N的坐标为(xN,yN).∵M(2,0).
-
由点Q是线段MN的中点,可以求得,xN=2xQ-2,yN=2yQ.
∵a=-1,∴抛物线C1的解析式为y=-x2+8.
∵点N在抛物线C1上,∴yN=-xN2+8.
∴2yQ=-(2xQ-2)2+8,即yQ=-2xQ2+4xQ+2,
解:(1)∵y=kx+2k+4=k(x+2)+4,令x+2=0,则x=-2,y=4,∴C(-2,4).
(2)当k=-2,y=-2x,设D(m,-2m),则E(m, ),P(m, -m),∴y= -x.
/
练习
(1)如图,抛物线y= -2x-3与x轴交于A、B两点,与y轴交于点C,点P在直线BC上,过点P作PQ∥y轴交抛物线于点Q,G是线段PQ的中点,求点G的轨迹的解析式.
解:∵y=- +2ax- =- +4a-4,∴P(a,4a-4).
∵当a变化时,点P总在直线l上,∴直线l的解析式为:y=4x-4.
/
(2)已知,直线 :y= x,抛物线 :y=a +6ax+7a的顶点A在直线 上.求抛物线 的解析式.
解:∵ :y=a +6ax+7a=a -2a,∴A(-3,-2a).
∵点A在直线 上,∴-2a= ×(-3),∴a=1,∴抛物线 的解析式为y= +6x+7.
题型二中点的轨迹问题
例2.如图,已知直线AB:y=kx+2k+4与抛物线 :y= 交于A、B两点.
(1)直线AB总经过一个定点C,请求出点C坐标;
(2)若k=-2,点D在直线AB上,过点D作y轴的平行线交抛物线 于点E,P是线段DE的中点,设点D在直线AB上运动时,P的运动轨迹为抛物线 ,求抛物线 的解析式.
(2)对任意点P,猜想OP与PH的大小关系,并证明你的猜想;
(3)如图2,若A、B是抛物线 上的两个动点且AB=6,求A、B两点到直线l的距离之和的最小值.
图1图2
【解】(1)OP=1,PH=1;OP=5,PH=5.
(2)OP=PH.
设点P(x, ),
@
则 . 即OP=PH.
(3)分别过点A、B作直线l的垂线,垂足分别为C、D,连接OA,OB.
(1)求抛物线方程;
(2)①若D(4,-m)为抛物线 上一定点,点D到直线l的距离记为d,当d=DO时,求t的值;
②若D为抛物线 上一动点,点D到①中的直线l的距离与OD的长是否恒相等,说明理由;
(3)如图2,若E、F为上述抛物线上的两个动点,且EF=8,线段EF的中点为M,求点M纵坐标的最小值.
图1图2
解:设P(x, ),则
= + = ,
= = ,
∴ = ,∴PF=PH.
(
(2)已知点M(2,3),F(0, ),点P(m,n)为抛物线y= 上一动点,则用含m的式子表示PF= ;PF+PM的最小值是 .
设P(m, ),则
= + = ,∴PF= .
^
练习
将抛物线 先向左平移4个单位,再向下平移2个单位,得到抛物线 .
∴抛物线C2的解析式为:y=-2x2+4x+2.
习2
(2)如图1,直线y=kx-k2(k>0)与抛物线y=ax2有唯一的公共点.
①求抛物线的解析式;
②已知点A(0,1),直线l:y=-1,如图2,P是抛物线上一个动点,PB⊥l于B点,连PA、PB,求证:AB平分∠OAP.
解:① ,ax2-kx+k2=0,△=k2-4ak2=0,a= ,y= x2.
②证明:设P(t, t2),
PA= = t2+1,PB= t2-(-1)= t2+1,
PA=PB,∴∠PAB=∠PBA,∵PB⊥l,∴PB∥y轴,∴∠PBA=∠OAB,
∴∠PAB=∠PAB,∴AB平分∠OAP.
M1N12=(x2-x1)2=x12+x22-2x1x2=x12+x22+8,∴FM12+FN12=M1N12,
∴△M1FN1是以F点为直角顶点的直角三角形.
(
课后作业 二次函数轨迹问题
习1
(1)在平面直角坐标系xOy中,抛物线C1:y=ax2-4a+4(a<0)经过第一象限内的定点P.
①直接写出点P的坐标;
(2)点F的坐标(0,2).
作PH⊥x轴于H,设得抛物线 上点P(x, ),
则 . 即PF=PH.
(3) 由(2)PH=PF,∴PH+PD=PF+PD,
∴当F,P,D在一直线上的,PF+PD值最小, 即PH+PD最小.
此时∵F(0,2),D(4,3),∴最小值为PF= ,
又直线DF为 , 由 , 得 ,
解:易知B(3,0),C(0,-3),可求BC解析式为y=x-3.
设P(m,m-3),则Q(m, -2m-3),G(m, - m-3),∴y= - x-3.
(2)如图,N为抛物线 :y=- +8上一动点,点M(2,0)在x轴上,Q为线段MN的中点,设点N在抛物线 上运动时,Q的运动轨迹为抛物线 ,求抛物线 的解析式.
解:设N(m,- +8),则M(2,0),Q( +1,- +4), :y=-2 +4x+2.
`
模块二焦点与准线
知识导航
抛物线的定义:平面内,到定点与定直线的距离相等的点的轨迹叫做抛物线,其中定点叫抛物线的焦点,定直线叫抛物线的准线.
例3(1)如图,抛物线y= 的焦点F(0, ),准线l的解析式为y=- ,求证:抛物线y= 上任意一点P到点F的距离等于它到直线l的距离,即PF=PH.
由(2)知OB=BD,OA=AC.
①当AB不过O点时,在△AOB中,∵OB+OA>AB,∴BD+AC>AB=6.
②当AB过O点时,∵OB+OA=AB,∴BD+AC=AB=6.
综上所述BD+AC≥6,
即A,B两点到直线l的距离之和的最小值为6.
<
练习
如图1,在以O为原点的平面直角坐标系中,抛物线 与x轴交于A、B两点,与y轴交于点C(0,-1),连接AC,AO=2CO,直线,过点G(0,t)且平行于x轴, .
∵直线y=kx+1与抛物线y= x2交于M(x1,y1)和N(x2,y2)两点,
