交流电路的功率课件
合集下载
电路原理3章 正弦交流电路的功率
p UI cos UI cos(2t )
UI cos [1 cos 2t] UI sin sin2t
Q UI sin 单位:乏 (var)
Q UI sin I 2 X
感性电路： Q > 0
容性电路： Q < 0
I
U
+
U X U
UR _
R jX
+ U_ R _+U X
视在功率、无功功率、平均功率关系：
电感在一个周期内吸收的平均功率 为：
P 1
T
pdt
1
T
UI sin 2tdt 0
T0
T0
电感是储能元件，不消耗能量，但是在某一
时间段内，它从外部电路吸收功率。
电感瞬时功率的最大值，定义为电感的无功
功率QL：
电感无功功率：QL UI
I2 XL
U2
XL
单位:乏 (var)
3.7.1.3 电容元件的功率
(1) 视在功率(apparent power)
•
Ii
一端口网络电压有效值与
电流有效值的乘积
Z
S UI 单位:伏安 (VA)
+
•
U
u
-
无 源 网 络
S UI Z I 2
注： SN＝UN IN 称为发电机、变压器 等供
电设备的额定视在功率，表示其容量。
(2) 无功功率(reactive power)
并联电容器是电网中用得最多的一种无功功 率补偿设备，目前国内外电力系统中90%的无 功补偿设备是并联电容器。
可以串电容吗？
串联电容器补偿，现在主要应用于超高 压、大容量的输电线路上，例如，山西大同 至北京的500kV输电电线路全长300km,加装 了串联电容补偿后,电网线损降低，电压质 量改善，电网运行的稳定性得到加强，而且 输电能力提高30%以上。
UI cos [1 cos 2t] UI sin sin2t
Q UI sin 单位:乏 (var)
Q UI sin I 2 X
感性电路： Q > 0
容性电路： Q < 0
I
U
+
U X U
UR _
R jX
+ U_ R _+U X
视在功率、无功功率、平均功率关系：
电感在一个周期内吸收的平均功率 为：
P 1
T
pdt
1
T
UI sin 2tdt 0
T0
T0
电感是储能元件，不消耗能量，但是在某一
时间段内，它从外部电路吸收功率。
电感瞬时功率的最大值，定义为电感的无功
功率QL：
电感无功功率：QL UI
I2 XL
U2
XL
单位:乏 (var)
3.7.1.3 电容元件的功率
(1) 视在功率(apparent power)
•
Ii
一端口网络电压有效值与
电流有效值的乘积
Z
S UI 单位:伏安 (VA)
+
•
U
u
-
无 源 网 络
S UI Z I 2
注： SN＝UN IN 称为发电机、变压器 等供
电设备的额定视在功率，表示其容量。
(2) 无功功率(reactive power)
并联电容器是电网中用得最多的一种无功功 率补偿设备，目前国内外电力系统中90%的无 功补偿设备是并联电容器。
可以串电容吗？
串联电容器补偿，现在主要应用于超高 压、大容量的输电线路上，例如，山西大同 至北京的500kV输电电线路全长300km,加装 了串联电容补偿后,电网线损降低，电压质 量改善，电网运行的稳定性得到加强，而且 输电能力提高30%以上。
《电工技术》课件 正弦交流电路的功率
P
1 T
0T
pdt
1 T
0TUI[cos
cos(2t
)]dt
UI
cos
P UI cos
单位为瓦（W）
u 与 i 的夹角，即阻抗角
= cos 称为功率 因数，用来衡量对电
源的利用程度。
一、一般计算公式
3.无功功率
Q UI sin 单位为乏（Var）
4.视在功率：电路中总电压与总电流有效值的乘积，表示用电设备的容量。
（3）视在功率： S UI
S
Q
φ
功率三角形
P
S UI 单位为伏安（VA）
注： SN＝UN IN 称为发电机、变压器 等供电设备的容量，可用来衡量发电机、变压器可能提供的最大有 功功率。
• 注意 （1）平均功率P、无功功率Q和视在功率S的关系
S2 P2 Q2
（2） P、Q、S 都不是正弦量，不能用相量表示。
S
Q
功率三角形
S PQ P
二、几种特例电路的功率计算
（3） R、 、X L X C
解：
（1）根据电压三角形，求得总电压
U UR2 (UL UC )2 152 (60 80)2 25V
（2）电路中只有电阻是耗能元件，因此电路有功功率就是电阻消耗的功率。
P U R I 151 15W Q QL Q C ULI (UC I ) 20Var S UI 251 25VA
（2）无功功率： Q UI sin
因为电路中只有电感元件和电容元件有无功功率，因此无功功率又可以用公式：
Q QL Q C ULI (UC I )
I2XL I2XC
U
2 L
UC2
XL XC
《交流电路的功率》课件
变压器
利用磁耦合原理将一次侧的交流 电变换为二次侧的交流电。
02
交流电路的功率计算
有功功率
01
02
03
定义
有功功率是指交流电路中 真正用于做功的功率，单 位为瓦特（W）。
计算公式
$P = frac{V^2}{R}$，其 中V为电压有效值，R为电 阻值。
意义
有功功率反映了交流电路 中实际消耗的能量，是衡 量电器设备效率的重要指 标。
节能技术介绍
高效电机
采用高效电机替换传统电机， 提高电机效率和功率因数，减
少能源浪费。
变频技术
通过变频器调节电机运行速度 ，实现能源的精确控制和节约 。
绿色照明
采用LED等高效照明设备，降低 照明能耗，提高照明质量。
能源管理系统
通过能源管理系统对能源使用 进行实时监测、分析和控制，
实现能源的有效管理。
节能技术的应用实例
建筑节能
在建筑设计中采用节能技术，如保温隔热、自然采光、太阳能利 用等，降低建筑能耗。
工业节能
在工业生产中采用高效电机、变频技术、余热回收等技术，降低 工业能耗。
交通节能
在城市交通中推广电动汽车、混合动力汽车等节能交通工具，建 设智能交通系统，提高交通能源利用效率。
THANKS
节能的意义
能源危机
随着能源资源的日益枯竭，节能已成为全球共同关注的问题。节能 可以减少对化石燃料的依赖，降低能源消耗，缓解能源危机。
环境保护
节能可以减少温室气体排放，降低环境污染，有助于保护环境，改 善空气质量，实现可持续发展。
经济利益
节能可以降低能源成本，提高能源利用效率，为企业和个人创造经济 利益。
感谢观看
利用磁耦合原理将一次侧的交流 电变换为二次侧的交流电。
02
交流电路的功率计算
有功功率
01
02
03
定义
有功功率是指交流电路中 真正用于做功的功率，单 位为瓦特（W）。
计算公式
$P = frac{V^2}{R}$，其 中V为电压有效值，R为电 阻值。
意义
有功功率反映了交流电路 中实际消耗的能量，是衡 量电器设备效率的重要指 标。
节能技术介绍
高效电机
采用高效电机替换传统电机， 提高电机效率和功率因数，减
少能源浪费。
变频技术
通过变频器调节电机运行速度 ，实现能源的精确控制和节约 。
绿色照明
采用LED等高效照明设备，降低 照明能耗，提高照明质量。
能源管理系统
通过能源管理系统对能源使用 进行实时监测、分析和控制，
实现能源的有效管理。
节能技术的应用实例
建筑节能
在建筑设计中采用节能技术，如保温隔热、自然采光、太阳能利 用等，降低建筑能耗。
工业节能
在工业生产中采用高效电机、变频技术、余热回收等技术，降低 工业能耗。
交通节能
在城市交通中推广电动汽车、混合动力汽车等节能交通工具，建 设智能交通系统，提高交通能源利用效率。
THANKS
节能的意义
能源危机
随着能源资源的日益枯竭，节能已成为全球共同关注的问题。节能 可以减少对化石燃料的依赖，降低能源消耗，缓解能源危机。
环境保护
节能可以减少温室气体排放，降低环境污染，有助于保护环境，改 善空气质量，实现可持续发展。
经济利益
节能可以降低能源成本，提高能源利用效率，为企业和个人创造经济 利益。
感谢观看
10-三相交流电路的功率PPT模板
P 3ULIL cos
同理3ULIL sin
S 3UPIP 3ULIL
【例3-2】有一对称三相负载，每相电阻为R＝6Ω，电抗 X＝8Ω，三相电源的线电压为380V。求：（1）负载星形连 接时的有功功率P；（2）负载三角形连接时的有功功率P′。
【解】每相阻抗的阻抗模为： Z 62 82 10（Ω）
功率因数为：
cos R 6 0.6
Z 10
（1）负载星形连接时，相电压为220V，线电流等于相 电流，即
IL
IP
UP Z
220 10
22（A）
有功功率P为：
P 3ULIL cos 3380220.6 8.7（kW）
（2）负载三角形连接时，相电压等于线电压，即UP′＝ UL＝380V，相电流为：
IP
UP Z
380 10
38（A）
线电流为相电流的 3 倍，即
IL 3IP 3 38 65.8（A）
有功功率P′为：
P 3ULIL cos 338065.80.6 26（kW）
电工电子技术
电工电子技术
三相交流电路的功率
在三相交流电路中，不论负载如何连接，电路总的有功 功率都等于各相有功功率之和，即
P P1 P2 P3
在对称三相电路中，由于各相电压、相电流及阻抗角都 相等，因此，上式可写为
P 3PP 3UPIP cos
由于实际工作中线电压和线电流的测量较为容易，因此， 三相功率的计算通常用线电压和线电流表示。当对称负载为星 形连接时，UL＝ 3 UP，IL＝IP；当对称负载为三角形连接时， UL＝UP，IL＝ 3 IP，于是，不论对称负载是星形连接还是三 角形连接，其有功功率都可写为：
同理3ULIL sin
S 3UPIP 3ULIL
【例3-2】有一对称三相负载，每相电阻为R＝6Ω，电抗 X＝8Ω，三相电源的线电压为380V。求：（1）负载星形连 接时的有功功率P；（2）负载三角形连接时的有功功率P′。
【解】每相阻抗的阻抗模为： Z 62 82 10（Ω）
功率因数为：
cos R 6 0.6
Z 10
（1）负载星形连接时，相电压为220V，线电流等于相 电流，即
IL
IP
UP Z
220 10
22（A）
有功功率P为：
P 3ULIL cos 3380220.6 8.7（kW）
（2）负载三角形连接时，相电压等于线电压，即UP′＝ UL＝380V，相电流为：
IP
UP Z
380 10
38（A）
线电流为相电流的 3 倍，即
IL 3IP 3 38 65.8（A）
有功功率P′为：
P 3ULIL cos 338065.80.6 26（kW）
电工电子技术
电工电子技术
三相交流电路的功率
在三相交流电路中，不论负载如何连接，电路总的有功 功率都等于各相有功功率之和，即
P P1 P2 P3
在对称三相电路中，由于各相电压、相电流及阻抗角都 相等，因此，上式可写为
P 3PP 3UPIP cos
由于实际工作中线电压和线电流的测量较为容易，因此， 三相功率的计算通常用线电压和线电流表示。当对称负载为星 形连接时，UL＝ 3 UP，IL＝IP；当对称负载为三角形连接时， UL＝UP，IL＝ 3 IP，于是，不论对称负载是星形连接还是三 角形连接，其有功功率都可写为：
电工学第三章三相交流电ppt课件
结论：电源 Y形联结时, 线电压Ul 3UP, 且超 前相应的相电压 30 , 三相线电压也是对称的 。
6
3.1.2 三相电路中负载的联结方法
1. 三相负载
分类
三相负载：需三相电源同时供电
负载
三相电动机等
单相负载：只需一相电源供电
照明负载、家用电器
对称三相负载：ZA=ZB= ZC
三相负载
如三相电动机
此时负载中性点N´即为 A, 因此负载各相电压为 N
UA 0 , UA 0
B
UB UB A, UB 380 V UC UC A , UC 380 V C
+
U A
iA
iC
– –
N´
–
iB
+ U C U B +
此情况下，B相和C相的电灯组由于承受电压上所加 的电压都超过额定电压（220V) ，这是不允许的。
(2) 相UA电B=流UBC=UIIICABCABCA=UUUUZZZClCAABB=AABBCCUP
A
+–
U AB
– U CA
B U+ BC C–
+
IB IC
ICA
ZCA
IAB
ZBC ZAB
IBC
相电流： 线电流：
IIAA、B、IIB、BC、IC ICA
线电流不等于相电流
20
(3) 线电流
IA IAB ICA
16
(2) A相断路
A
1) 中性线未断
B、C相灯仍承受220V N
电压, 正常工作。
2) 中性线断开
B
变为单相电路，如图(b) C 所示, 由图可求得
I UBC 380 12 .7 A RB RC 10 20
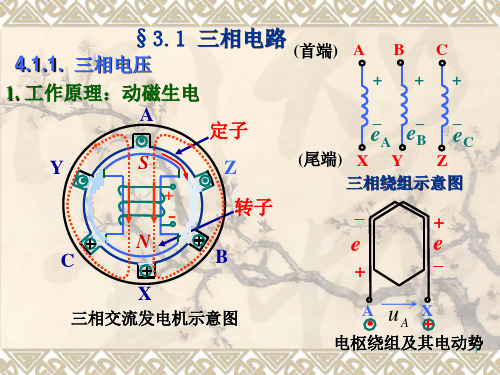
6
3.1.2 三相电路中负载的联结方法
1. 三相负载
分类
三相负载：需三相电源同时供电
负载
三相电动机等
单相负载：只需一相电源供电
照明负载、家用电器
对称三相负载：ZA=ZB= ZC
三相负载
如三相电动机
此时负载中性点N´即为 A, 因此负载各相电压为 N
UA 0 , UA 0
B
UB UB A, UB 380 V UC UC A , UC 380 V C
+
U A
iA
iC
– –
N´
–
iB
+ U C U B +
此情况下，B相和C相的电灯组由于承受电压上所加 的电压都超过额定电压（220V) ，这是不允许的。
(2) 相UA电B=流UBC=UIIICABCABCA=UUUUZZZClCAABB=AABBCCUP
A
+–
U AB
– U CA
B U+ BC C–
+
IB IC
ICA
ZCA
IAB
ZBC ZAB
IBC
相电流： 线电流：
IIAA、B、IIB、BC、IC ICA
线电流不等于相电流
20
(3) 线电流
IA IAB ICA
16
(2) A相断路
A
1) 中性线未断
B、C相灯仍承受220V N
电压, 正常工作。
2) 中性线断开
B
变为单相电路，如图(b) C 所示, 由图可求得
I UBC 380 12 .7 A RB RC 10 20
三相交流电电路分析PPT课件
第17页/共44页
U AN U p0V
Z Z
UBN U p 120
UCN U p120 IN IAN IBN ICN 0
IA
IAN
U AN Z
U P0
Z
Up Z
IB
IBN
Up Z
120
IC
ICN
Up Z
120
第18页/共44页
结论：三相电源对称， 负载对称且Y形连接， 则三个线电流也是对称 的。中线电流为0
B
•
•
Z
C
C
星形接法
三角形接法
第13页/共44页
4.2.1 三相对称负载星i形A 接法及计算
uA AN N
i Z AN
uCN C
uBN B
iZ
C
i Z
BN
iB iCN
相电流(负载上的电流)：
IAN 、IBN、ICN
线电流(火线上的电流)：
IA 、IB 、IC
第14页/共44页
一、星形接法特点
iA
N
eB
uBN B uCN C
U AN U P0 U BN U P 120 U CN U P120
U CN
120
120
120
U BN
U AN
UP代表电源相电压的有效值
三个相电压是对称的
第8页/共44页
线电压：火线间的电压。
A
u AB uBC uCA
u AN uAB
uCN
N
uBN
B C
uBC uCA
C
第6页/共44页
e eC A
ZX
ec Y
eB
A （火线）
第三讲：交流电路中的复数功率
交流电路中的复数功率一 节点与支路的功率平衡1 节点功率平衡－复数形式的基尔霍夫电流定律（KCL ）通过节点i 的电流为1I 、2I ……nI . 其正方向如图一所示（离开节点i 为正），应满足基尔霍夫电流定律：0n21＝＋＋＋I I I (1) 对应的共轭电流也必须是0ˆˆˆn 21＝＋＋＋I I I (2) (2)式两端同乘以节点i 的电压iU 得到 0ˆU ˆU ˆU n i 2i 1i ＝＋＋＋I I I 这就是节点i 的复数功率i S 的平衡方程。
0S S S n 21=+++ (3)根据复数功率的定义1S = P 1 + j Q 12S = P 2 + j Q 2……n S = P n + j Q nP i 为各支路的有功功率。
Q i 为各支路的无功功率最后得到各支路的有功功率和无功功率平衡方程为 P 1+P 2+……P n = 0Q 1+Q 2+……Q n = 0 (4)这里的有功功率无功功率方向与对应的电流方向一致，均定义成离开节点i 为正，反之为负。
如果屏幕上规定的功率方向不一致，应该在前面加一负号才能满足（4）式给出的平衡方程。
2 支路功率平衡—复数形式的欧姆定律与电功率电力系统中联络线的模型通常用π 型等值电路表示，如图2所示。
ZI j i U U -＝ Z ＝R +j X 线路的电阻与电抗，j B = 1/j X c 为线间电容对应的电纳，分别挂在线路的两侧各为j B /2。
支路功率方向的规定如图2所示。
支路功率平衡的意义是建立在能量守恒的基础上的，即输入线路的视在功率S i =P i +j Q i .应等于节点j 侧输出的视在功率S j =P j ＋j Q j 加上线路的损耗与充电无功功率： P i = P j + ΔP ij (5) Q i = Q j + ΔQ ij 其中： ΔP ij = I 2RΔQ ij = I 2X – U 2B (6)I 为通过R +j X 阻抗的电流，U 为联络线路的平均电压，X I 2为联络线路电抗的无功损耗，BU 2为线间电容的充电无功，二者差一负号，它与支路传送功率的大小无关，只与电压有关，而运行中电压变化不大，这一批无功损失近似不变。
交流电路中的功率
10 103 (tan tan 18 0 ) 213.7μF 2 2π 50 220
上页 下页 返回
第 2章
2.7
电路中的谐振
含有电感和电容的电路其电压与电流存 在相位差。若调节电源的频率或电路参数， 使u、i同相，则电路处于无功功率完全补偿， 电路的功率因数 ,称此电路处于谐 cos 1 振状态。 串联谐振 谐振 并联谐振
P 解: 1） 由公式 C (tan tan ) 1 2 2 U cos1 0.6 , 1 53 ; cos 2 0.95 , 2 18
10 10 得 C (tan tan ) 656 μ F 53 18 2 50 2202
I U
U I RL R jX L U I C 1 jC
谐振条件：
IRL
1 I I RL I C R jL jC U R L 2 j C U 2 2 2 R L R L 实部 虚部 上页 下页 返回
第 2章
5 . 有功功率、无功功率与视在功率间的关系 ---功率三角形 有功功率 P UI cos 无功功率 Q UI sin 视在功率
S UI
U
S
阻抗 三角形
Z
X L XC
R
U U L C
电压 三角形
P
功率 三角形
Q
U R
上页
下页
返回
第 2章
I
＋
1 1 … 1 1 U ) IU （ Z1 Z 2 Z n -1 Z n Z
n 1 1 1 1 1 1 Z Z1 Z 2 Z n-1 Z n k 1 Zk
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解：感抗为 X L ? ? L ? 314 ? 328 ? 10 ?3 ? 120?
容抗为 X C
?
1
?C
?
1 314 ? 40 ? 10? 6
? 80?
? ? 阻抗为 Z ? R 2 ? X L ? XC 2 ? 50?
因此电流为 I ? U ? 220 ? 4. 4A
Z
50
相位差为 ? ? arctan X L ? X C ? 53 .10 R
QC
? UCIC
?
U
2
C
XC
9
? IC2X C
纯电感电路的功率
10
纯电感电路的功率
由上图表明，电感元件瞬时功率的平均值也为零，即 P=0，说明电感线圈也不消耗功率，只是在线圈和电源 之间进行着可逆的能量转换。
瞬时功率的最大值，也叫做无功功率，它表示电感线 圈与电源之间能量交换的最大值，用符号Q表示，单位 也是乏。
13
功率三角形
?
?
arctan
XL
?
R
XC
?
arctan QL
? QC P
S ? P2 ? Q2
P ? S cos ? ? UI cos ?
Q ? QL ? QC ? S sin ? ? UI sin ?
Q>0，QL > QC ，电路呈感性；
Q>0，QL
<
14
QC
，电路呈容性。
功率因数
功率因数cos ? ，其大小等于有功功率与视在功 率的比值，在电工技术中，一般用? 表示。
电路的平均功率 P ? UI的无功功率 Q ? UI sin ? ? 220 ? 4.4 sin 53.1?var ? 774 var
电路的视在功率
S ? UI ? 220? 4.4VA ? 968VA
由上可见， ? >0，电压超前电流，因此电路为感性。 17
? = cos ? = P S
15
RLC串联电路的功率
纯电阻元件 P=S，Q=0，cosφ=1 纯电感元件 Q=S，P=0，cosφ=0 纯电容元件 Q=S，P=0，cosφ=0
16
例题分析
已知电阻R=30Ω，电感L=382mH，电容C=40μF，串联后接到 电压 u ? 220 2 sin(314t ? 300 )V的电源上。求电路的P、Q和S。
课堂练习
1.负载的端电压为u=-220 s（in314t-1600）V，通过的电 流i=4.4 co（s 314t-1300）A，试求此负载的功率因数即 输入的有功功率、无功功率和视在功率。
18
课堂练习
19
本课小结
1.掌握纯电阻、纯电感、纯电容元件及电源的功率及其计算 2.掌握电路功率因数的计算方法
QL
?
U LIL
?
U
2 L
XL
11
? IL2X L
思考题
无功功率？=无用功
12
RLC串联电路的功率
总电压有效值和电流有效值的乘积叫做视在功率，以符 号S表示，即
S=UI 视在功率常用来表示电器设备的容量，其单位为伏安。 视在功率不是表示交流电路实际消耗的功率，而只能表示电 源可能提供的最大功率，或指某设备的容量。
工程管理系 宣娜
1
复习
一、正弦交流电路中的欧姆定律是什么？
2
复习
二、RLC串并联电路的三角形有哪些？ 串联
并联
3
复习
三、直流电路的功率如何计算？
4
交流电路的功率
1．瞬时功率 p
设正弦交流电路的总电压 u 与总电流i的相位差(即阻抗角) 为 ? ，则电压与电流的瞬时值表达式为
u = Umsin(? t ? ? )，i = Imsin(? t) 瞬时功率为
P
?
1 2
Pm
?
1? 2
2U R ?
2I R
? U RIR
?
U
2 R
R
? I R2R
如果电路中存在多个电阻，则总有功功率为各个电阻上有 功功率之和。
7
纯电容电路的功率
8
纯电容电路的功率
在电容器和电源之间进行着可逆的能量转换而不消耗功率， 所以，电容元件有功功率为零，即P=0。
电容元件用无功功率来衡量其与电源间能量互换的规模， 规定电容元件的无功功率为瞬时功率的幅值（它并不等 于单位时间内互换了多少能量），因此也叫做最大值功 率，用符号Q来表示，它的单位是乏（var）。
p = ui = UmImsin(? t ? ? )sin(? t)
5
纯电阻电路的功率
电阻的瞬时功 率总是正值， 表示电阻总是 消耗功率，这 是不可逆的。
6
纯电阻电路的功率
瞬时功率在一个周期内的平均值叫做 平均功率，它反映 了交流电路中实际消耗的功率，所以又叫做有功功率，用 P 表示，单位是瓦特(W)。
20
作业
P143（1（10）（11）2（11）4（11））
21
22