网格中的勾股定理
网格线中的三角函数问题

・ . .
’ . .
由勾股 定理 得 B E =
AB=
・ . ・
, A E = 2
设B D为 , C D为 2 一 , 由勾 股 定理 得
AB - BD = AD , AC 一C D = AD。 ,
・
例 2 如图3 , 在 边 长相 同的小 正方 形 网 格 中, 点 A、 B、 C 、 D都 在 这 些 小 正 方 形 的 顶
点上, A B 、 C D相 交 于 点 P, 则t a n Z AP D的 值 为
( ) .
A. 1 B. 2 C_ 3 D.
故选 : B .
,
A D: T 9 . 3
.
二、 运用方 程 。 以数 解形
.
9
几何 图形 中 的问题转 化 为用代 数 的知识
.
・ .
求解 , 这 就 是数形 结合 思想 中的“ 以数解 形” ,
s i n 肚 A D 去
数 学语言与直观 的图像结合起来 , 关键是代数 问题 与图形之间的相 互转化 , 它可以使代数 问题 几 何化 , 几何问题 代数化. 数学 中的知识 , 有的本身就可以看作是数形 的结合 . 女 口 : 锐角三角函数 的定 义是借助 于直 角三 角形 来定 义的. 下面 我们就 网格线 中锐 角三 角函数 的 问题来 体会这 种数学思
、
-"
'--4 \Fra bibliotek"- - -
.
3
aB D P, 然后 由相似 三 角形 的对 应边 成 比例 . 易得 D P : C P = 1 : 3 , 即 可得 P F : C F = P F : B F = 1 : 2 ,
网格中的三角函数

1网格中的锐角三角函数网格是同学们从小就熟悉的图形,在网格中隐含的条件有:1.直角;2.单位长度。
所以在网格中可以求一个锐角的三角函数,是近几年中考的热点,下面举例说明。
一、在网格中与勾股定理现结合求一个锐角的三角函数。
【例1】 三角形在正方形网格纸中的位如图1,则sin α的值是( ).[解析] 本题在网格中考查锐角的正弦的意义,首先要用勾股定理计算直角三角形斜边的长.一般情况下,为了减小计算量,把小正方形的边长设为1.选C .练习1(广州市2014)如图2,在边长为1的小正方形组成的网格中,的三个顶点均在格点上,则( ).(A ) (B ) (C ) (D )练习2 (2014年福州)如图3,在边长为1个单位长度的小正方形所组成的网格中,△ABC 的顶点均在格点上,344543B .; C .35;D .A. 35图3图22sinB 的值是 .3.(2011四川)如图4,在4×4的正方形网格中, tanα= .A .1B .2C .12D4.(2011甘肃兰州)如图5,A 、B 、C 三点在正方形网格线的交点处,若将△ACB 绕着点A 逆时针旋转得到△AC’B’,则tanB’的值为 .A .12B .13C .14 D3. (2011江苏连云港)如图6,△ABC 的顶点都在方格纸的格点上,则sin A =_______.在网格中求一个锐角的三角函数时,根据图中角的位置。
充分利用网格中的直角和边,然后根据勾股定理求出相应的边长,最后利用三角函数公式进行计算,达到解决问题的目的。
二、在网格中与辅助线相结合求一个锐角的三角函数。
【例2】 (2014•贺州)如图7-1网格中的每个小正方形的边长都是1,△ABC 每个顶点都在网格的交点处,则sinA= .[解析] 虽然网格中隐含直角,但是∠A 是△ABC中图7-1图7-2图4图6图5的一个锐角,而△ABC不是直角三角形,不能直接运用三角函数公式进行计算,必须先做辅助线构造直角三角形,使∠A在一个直角三角形中,然后求出所对应的斜边和对边,而后解决问题。
中考专题复习:解直角三角形,正方形网格中直角三角形解法归纳
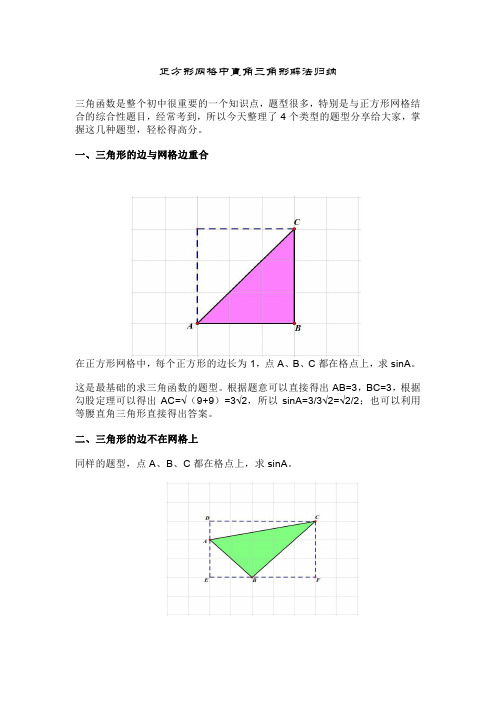
正方形网格中直角三角形解法归纳三角函数是整个初中很重要的一个知识点,题型很多,特别是与正方形网格结合的综合性题目,经常考到,所以今天整理了4个类型的题型分享给大家,掌握这几种题型,轻松得高分。
一、三角形的边与网格边重合在正方形网格中,每个正方形的边长为1,点A、B、C都在格点上,求sinA。
这是最基础的求三角函数的题型。
根据题意可以直接得出AB=3,BC=3,根据勾股定理可以得出AC=√(9+9)=3√2,所以sinA=3/3√2=√2/2;也可以利用等腰直角三角形直接得出答案。
二、三角形的边不在网格上同样的题型,点A、B、C都在格点上,求sinA。
这个题型需要先确定三角形ABC是不是直角三解形。
解题思路:先在RTAEB、RTCFB、RTADC中利用勾股定理把AB、BC、AC 求出来。
AB=2√2,BC=3√2,AC=√26,三条边满足勾股定理,所以这是一个直角三角形。
sinA=BC/AC=3√2/√26=√117/13。
不知道求AB、BC、AC的同学,要把三条边分别放在直角三角形中求。
正方形网格中所有在格点上的线段,都是可以构成直角三角形求出来的。
三、三边不在网格上也不是直角三角形在相同的已知条件下求sinC。
这种题型是三角形三边不在网格上,也不是直角三角形的类型。
一般要通过作图(要求:把要求的角放在直角三角形中),构成一个直角三角形。
然后利用端点在格点上的边都可以求出,这一性质,列出一个面积相等的式子求出BD,最后求sinC。
解题思路:过点B作BD⊥AC,根据同一个三角形的面积相同得出等式:1/2(2AB)=1/2(AC×DB)即3=1/2(2√5×DB),BD=3√5/5,在RTCBD中sinC=BD/BC=(3√5/5)/√5=3/5。
四、求不在同一直角三角形中两个角的正弦值相同的条件求sin(+)因为∠和∠不在同一个三角形中,所以要通过作图让它们在一起,而且必须是在直角三角形中,这样才能求sin(+)。
初中数学勾股定理教案 初中数学勾股定理教案优秀3篇

初中数学勾股定理教案初中数学勾股定理教案优秀3篇初中数学勾股定理教案优秀3篇由作者为您收集整理,希望可以在初中数学勾股定理教案方面对您有所帮助。
初中数学勾股定理教案篇一一、教案背景概述:教材分析:勾股定理是直角三角形的重要性质,它把三角形有一个直角的形的特点,转化为三边之间的数的关系,它是数形结合的榜样。
它可以解决许多直角三角形中的计算问题,它是直角三角形特有的性质,是初中数学教学内容重点之一。
本节课的重点是发现勾股定理,难点是说明勾股定理的正确性。
学生分析:1、考虑到三角尺学生天天在用,较为熟悉,但真正能仔细研究过三角尺的同学并不多,通过这样的情景设计,能非常简单地将学生的注意力引向本节课的本质。
2、以与勾股定理有关的人文历史知识为背景展开对直角三角形三边关系的讨论,能激发学生的学习兴趣。
设计理念:本教案以学生手中舞动的三角尺为知识背景展开,以勾股定理在古今中外的发展史为主线贯穿课堂始终,让学生对勾股定理的发展过程有所了解,让他们感受勾股定理的丰富文化内涵,体验勾股定理的探索和运用过程,激发学生学习数学的兴趣,特别是通过向学生介绍我国古代在勾股定理研究和运用方面的成就,激发学生热爱祖国,热爱祖国悠久文化的思想感情,培养他们的民族自豪感和探究创新的精神。
教学目标:1、经历用面积割、补法探索勾股定理的过程,培养学生主动探究意识,发展合理推理能力,体现数形结合思想。
2、经历用多种割、补图形的方法验证勾股定理的过程,发展用数学的眼光观察现实世界和有条理地思考能力以及语言表达能力等,感受勾股定理的文化价值。
3、培养学生学习数学的兴趣和爱国热情。
4、欣赏设计图形美。
二、教案运行描述:教学准备阶段:学生准备:正方形网格纸若干,全等的直角三角形纸片若干,彩笔、直角三角尺、铅笔等。
老师准备:毕达哥拉斯、赵爽、刘徽等证明勾股定理的图片以及其它有关人物历史资料等投影图片。
三、教学流程:(一)引入同学们,当你每天手握三角尺绘制自己的宏伟蓝图时,你是否想过:他们的边有什么关系呢?今天我们来探索这一小秘密。
勾股定理

勾股定理【知识点】1.勾股定理(只适用于直角三角形)内容:直角三角形两直角边的平方和等于斜边的平方;表示方法:如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么222a b c +=2.勾股定理的证明证明方法1:4EFGH S S S ∆+=正方形正方形ABCD ,2214()2ab b a c ⨯+-=,化简可证.证明方法2:四个直角三角形的面积与小正方形面积的和等于大正方形的面积.四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+大正方形面积为222()2S a b a ab b =+=++ 所以222a b c +=证明方法3:1()()2S a b a b =+⋅+梯形,2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形,化简得证3.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须注明所考察的对象是直角三角形4.勾股定理的应用①已知直角三角形的任意两边长,求第三边在ABC ∆中,90C ∠=︒,则c,bacbaHG F EDCBAbacbac cabcab a bc cbaED CBA②可运用勾股定理解决一些实际问题③利用勾股定理作长为 n (n 为大于1的整数)的线段5.勾股定理的逆定理如果三角形三边长a ,b ,c 满足222a b c +=,那么这个三角形是直角三角形,其中c 为斜边 注意:①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和22a b +与较长边的平方2c 作比较:若222a b c +=时,以a ,b ,c 为三边的三角形是直角三角形; 若222a b c +<时,以a ,b ,c 为三边的三角形是钝角三角形; 若222a b c +>时,以a ,b ,c 为三边的三角形是锐角三角形;②定理中a ,b ,c 及222a b c +=只是一种表现形式,不可认为是唯一的,如若三角形三边长a ,b ,c 满足222a c b +=,那么以a ,b ,c 为三边的三角形是直角三角形,但是b 为斜边③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形6.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即222a b c +=中,a ,b ,c 为正整数时,称a ,b ,c 为一组勾股数②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25等 ③用含字母的代数式表示n 组勾股数: 221,2,1n n n -+(2,n ≥n 为正整数); 2221,22,221n n n n n ++++(n 为正整数)2222,2,m n mn m n -+(,m n >m ,n 为正整数)考点例析考点1:已知直角三角形两边边长,求第三边边长1、如果直角三角形的两直角边长分别为1n 2-,2n (n>1),那么它的斜边长是( ) A 、2nB 、n+1C 、n 2-1D 、1n 2+2、直角三角形的斜边比一直角边长2 cm ,另一直角边长为6 cm ,则它的斜边长 A 、4 cmB 、8 cmC 、10 cmD 、12 cm3、已知一个Rt △的两边长分别为3和4,则第三边长的平方是( ) A 、25B 、14C 、7D 、7或254、在ABC ∆中,90C ∠=︒.⑴已知6AC =,8BC =.求AB 的长⑵已知17AB =,15AC =,求BC 的长考点2:已知直角三角形的一边以及另外两边的关系利用勾股定理求周长、面积等问题。
10 专题 勾股定理(逆定理)与网格画图
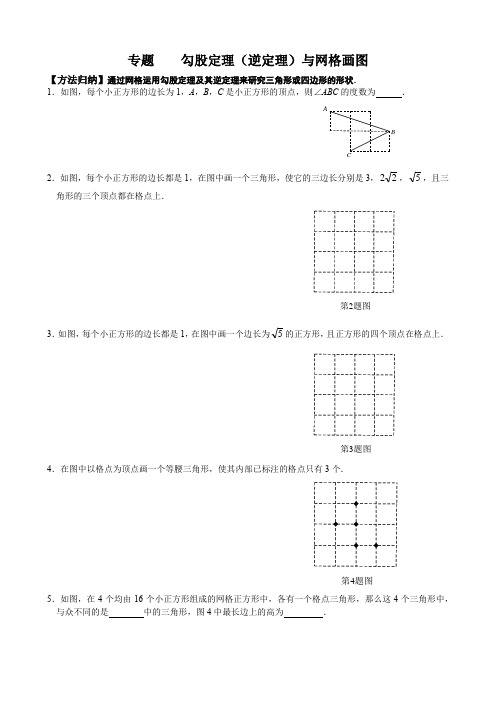
专题 勾股定理(逆定理)与网格画图
【方法归纳】通过网格运用勾股定理及其逆定理来研究三角形或四边形的形状.
1.如图,每个小正方形的边长为1,A ,B ,C 是小正方形的顶点,则∠ABC 的度数为 .
2.如图,每个小正方形的边长都是1,在图中画一个三角形,使它的三边长分别是3,22,5,且三角形的三个顶点都在格点上.
3.如图,每个小正方形的边长都是1,在图中画一个边长为5的正方形,且正方形的四个顶点在格点上.
4.在图中以格点为顶点画一个等腰三角形,使其内部已标注的格点只有3个.
5.如图,在4个均由16个小正方形组成的网格正方形中,各有一个格点三角形,那么这4个三角形中,与众不同的是 中的三角形,图4中最长边上的高为 . A
C
B
第2
题图第3题图
第4
题图
6.如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画图:
7.如图,在5×5的正方形网格中,每个小正方形的边长均为1,线段AB 的端点在格点上.
(1)图1中,以AB 为腰的等腰三角形有 个,画出其中的一个,并直接写出其
边长.
(2)图2中,以AB 为底边的等腰三角形有 个,画出其中一个,并直接写出其底边上的高.
图4图3图2图
1图2
图1图2图1
A
B A B。
北师大版八年级上册第一章探索勾股定理精讲

勾股定理第一节 探索勾股定理●应知 基础知识1、勾股定理(1)勾股定理的内容:在直角三角形中,两直角边的 等于 的平方.(2)勾股定理的表示方法:如果直角三角形的两直角边分别为,a b ,斜边为c ,那么有 。
2、理解(1)勾股定理存在和运用的前提条件是在直角三角形中,如果不是直角三角形,那么三边之间不存在这种关系。
(2)勾股定理把“图形”与“数量”有机地结合起来,即把直角三角形的“形”与三边关系的“数”结合起来,是数形结合思想的典型代表之一。
(3)利用勾股定理,可以在直角三角形中已知两边长的情况下,求出未知的第三边长。
一般情况下,用,a b 表示直角边,c 表示斜边,则有:222222222a b c b c a a c b +==-=- 在运用勾股定理求第三边时,首先应确定是求直角边还是求斜边,在选择利用勾股定理的原形公式还是变形公式。
【例1】在ABC ∆中,90C ︒∠=, (1)若3,4,a b ==则c = ; (2)若6,10a c ==,则b = ;(3)若:3:4,15a b c ==,则a = ,b = 。
【例2】已知直角三角形的两边长分别是3和4,如果这个三角形是直角三角形,求以第三边为边长的正方形的面积。
3、勾股定理的验证至少掌握勾股定理的三种验证方法,并从中体会到这种验证方法所体现的数学思想。
【例3】2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾 股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所 示).如果大正方形的面积是13,小正方形的面积是1,直角三角形较短直角边为a ,较长 直角边为b ,那么2()a b 的值为( ).A .13B .19C .25D .169 ●应会 基本方法1、如何利用勾股定理求长度利用勾股定理求长度,关键是找出直角三角形或构造直角三角形,把实际问题转化为直 角三角形问题。
在已知两边求第三边时,关键是弄清已知什么边,要求什么边,用平方和还 是平方差。
勾股定理的应用(六)在网格图形中的应用

祖π数学
新人教 八年级下册
之高分速成 1
【题型6】网格中的勾股定理
1.如图,正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC 中,边长为无理数的边数是( )
A.0
B.1
C.2
D.3
2.如图,正方形网格中的△ABC ,若小方格边长为1,则△ABC 是( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.以上答案都不对
3.如图,小方格都是边长为1的正方形,则四边形ABCD 的面积是 ( )
A.25
B.12.5
C.9
D.8.5
(第1题) (第2题) (第3题)
4.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点分别按下列要求画三角形:
①使三角形的三边长分别为3;
②使三角形为钝角三角形且面积为4(在图乙中画一个即可).
甲
乙
B C
A B C。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
网格中的勾股定理
正方形网格中的每一个角都是直角,所以在正方形网格中的计算都可以归结为求任意两个格点之间的长度问题,一般情况下都是应用勾股定理来进行计算。
例1、如图1所示,在一个有4×4个小正方形组成的正方形网格中,阴影部分的面积与正方形ABCD 的面积比是( )
A 、3:4
B 、 9:16
C 、5:8
D 、1:2
分析:可以设每一个小正方形的边长为1,则正方形ABCD 的面积就是4×4=16,小正方形的边长应该是直角三角形DEF 的斜边,另外两条直角边长度分别是1和3,根据勾股定
理可以求出EF=10,所以小正方形的面积就是2
)10(=10。
所以阴影部分的面积与正方形
ABCD 的面积比是10:16=5:8。
所以选择C
例2、如图2所示为一个6×6的网格,在△ABC、△A’B’C’、△A’’B’’C’’三个三角形中,直角三角形有( )
A 、3个
B 、2个
C 、1个
D 以上都不对
分析:要想判断是否为直角三角形,本题中可以根据勾股定理的逆定理来进行判断,前提条件是先求出三角形的三边的平方。
同样可以设每一个小正方形的边长为1,在直角三角形ABC 中,AB 2
=10,BC 2
=5,CA 2
=5,因为,BC 2
+CA 2
=AB 2
,所以该三角形是直角三角形。
同理可以求出,A’B’2
=10,B’C’2
=5,C’A’2
=13,因为A’B’2
+B’C’2
≠C’A’2
,所以该三角形不是直角三角形,同理可以判断△A’’B’’C’’是直角三角形。
所以选择B 。
例3、如图3,正方形网格的每一个小正方形的边长都是1,试求
122424454A E A A E C A E C ++∠∠∠的度数.
解:连结32A E .
32122222A A A A A E A E ==Q ,,
图1
图2
1A
2A 3A 4A
5A 5E
2E 1
1 1 1 4C
3C 2C
图3
32212290A A E A A E ∠=∠=o ,322122Rt Rt A A E A A E ∴△≌△(SAS ).
322122A E A A E A ∴∠=∠.
由勾股定理,得
4532C E C E ===
,4532A E A E ===,
44332A C A C ==Q ,445332A C E A C E ∴△≌△(SSS ). 323454A E C A E C ∴∠=∠.
122424454324424323224A E A A E C A E C A E C A E C A E C A E C ∴∠+∠+∠=∠+∠+∠=∠.
由图可知224E C C △为等腰直角三角形.
22445A E C ∴∠=o .即12242445445A E A A E C A E C ∠+∠+∠=o .
例4、阅读下列材料:
正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫格点三角形. 数学老师给小明同学出了一道题目:在图正方形网格(每个小正方形边长为1)中画出格点△ABC ,使,;
小明同学的做法是:由勾股定理,得,,于是画出线段AB 、AC 、BC ,从而画出格点△ABC . (1)请你参考小明同学的做法,在图23-2正方形网格(每个小正方形边长为1)中画出格点△(点位置如图所示),使==5,.(直接画出图形,不写过程);
(2
)观察△ABC 与△的形状..,猜想∠BAC 与∠有怎样的数量关系。
(不要求证明)
解:(1)正确画出△(画出其中一种情形即可) (2)猜想:∠BAC =∠
【参考】证明:∵,;
∴,
∴△ABC ∽ △, ∴∠BAC =∠
C
B
A
A '
'。
