高二数学选修44平面直角坐标系中极坐标系 (高考必修
合集下载
高二数学,人教A版,选修4-4 , 第2课时,极坐标,和直角坐标的互化 , 课件

7π 3,-1)化为极坐标为2, 6 .
[规律方法]
2
将点的直角坐标(x,y)化为极坐标(ρ,θ)时,
2
y 运用公式 ρ= x +y ,tan θ=x(x≠0)即可.在[0,2π)范围内,由 y tan θ=x(x≠0)求 θ 时, 要根据直角坐标符号特征判断出点所在的 象限.如果允许 θ∈R,再根据终边相同的角的意义,表示为 θ +2kπ(k∈Z)即可.
解析: (1)∵ρ=2,θ=0,
∴x=2cos θ=2,y=2sin θ=0, ∴将极坐标(2,0)化为直角坐标为(2,0). 0 (2)∵ρ= -2 +0 =2,tan θ= =0, -2
2 2
由于点(-2,0)在 x 轴的非正半轴上,所以 θ=π, ∴将直角坐标(-2,0)化为极坐标为(2,π).
(2)互化公式: 设 M 是平面内任意一点, 它的直角坐标是(x, y),极坐标是(ρ,θ)(ρ≥0), 于是极坐标与直角坐标的互化公式如表: 点M 互化 公式 直角坐标(x,y)
______ cos θ x=ρ sin θ ______ y=ρ
极坐标(ρ,θ)
x2+y2 ρ2=______
tan θ=-1,θ∈[0,2π), 3π 由于点(-1,1)在第二象限,所以 θ= 4 ,
∴直角坐标(-1,1)化为极坐标为
2 2
3π 2, 4 .
-1 3 (2)ρ= - 3 +-1 =2,tan θ= =3, - 3 7π 由于点(- 3,-1)在第三象限,所以 θ= 6 , ∴直角坐标(-
二 极坐标 第2课时 极坐标和直角坐标的互化
课标定位
1.了解极坐标系与直角坐标系的联系.
2.掌握极坐标和直角坐标的互化关系式.
[规律方法]
2
将点的直角坐标(x,y)化为极坐标(ρ,θ)时,
2
y 运用公式 ρ= x +y ,tan θ=x(x≠0)即可.在[0,2π)范围内,由 y tan θ=x(x≠0)求 θ 时, 要根据直角坐标符号特征判断出点所在的 象限.如果允许 θ∈R,再根据终边相同的角的意义,表示为 θ +2kπ(k∈Z)即可.
解析: (1)∵ρ=2,θ=0,
∴x=2cos θ=2,y=2sin θ=0, ∴将极坐标(2,0)化为直角坐标为(2,0). 0 (2)∵ρ= -2 +0 =2,tan θ= =0, -2
2 2
由于点(-2,0)在 x 轴的非正半轴上,所以 θ=π, ∴将直角坐标(-2,0)化为极坐标为(2,π).
(2)互化公式: 设 M 是平面内任意一点, 它的直角坐标是(x, y),极坐标是(ρ,θ)(ρ≥0), 于是极坐标与直角坐标的互化公式如表: 点M 互化 公式 直角坐标(x,y)
______ cos θ x=ρ sin θ ______ y=ρ
极坐标(ρ,θ)
x2+y2 ρ2=______
tan θ=-1,θ∈[0,2π), 3π 由于点(-1,1)在第二象限,所以 θ= 4 ,
∴直角坐标(-1,1)化为极坐标为
2 2
3π 2, 4 .
-1 3 (2)ρ= - 3 +-1 =2,tan θ= =3, - 3 7π 由于点(- 3,-1)在第三象限,所以 θ= 6 , ∴直角坐标(-
二 极坐标 第2课时 极坐标和直角坐标的互化
课标定位
1.了解极坐标系与直角坐标系的联系.
2.掌握极坐标和直角坐标的互化关系式.
高中数学第1章坐标系1.2.2点的极坐标与直角坐标的互化课件北师大版选修44

【 自 主 解 答 】 (1) 由 于 直 角 坐 标 原 点 (0,0) 与 极 点 重 合 , 所 以 限 定
ρ≥0,0≤θ<2π 时,其极坐标为(0,θ).
(2)∵ρ= x2+y2= -12+-12= 2,tan θ=yx=1,θ∈[0,2π).
由于点(-1,-1)在第三象限,所以 θ=54π.
第二十九页,共40页。
1.本例综合考查了点的极坐标与直角坐标的互化公式以及等腰直角三角形 的意义和性质.结合几何图形可知,点 C 的坐标有两解,设出点的坐标寻求等量 关系建立方程组求解是关键.
2.坐标平面内两点间的距离公式: (1)如果已知点的直角坐标 A(x1,y1),B(x2,y2), 那么|AB|= x1-x22+y1-y22; (2) 如 果 已 知 点 的 极 坐 标 A(ρ1 , θ1) , B(ρ2 , θ2) , 那 么 |AB| = ρ12+ρ22-2ρ1ρ2cosθ1-θ2.
且|AC|=|BC|,∴A→C ·B→C =0,
即(x- 2,y- 2)·(x+ 2,y+ 2)=0,
第二十五页,共40页。
∴(x- 2)(x+ 2)+(y- 2)(y+ 2)=0,
∴x2+y2=4.
①
又|AC|2=|BC|2,于是
(x- 2)2+(y- 2)2=(x+ 2)2+(y+ 2)2,
即 y=-x,代入①得 x2=2, 解得 x=± 2,
[构建·体系]
第二十三页,共40页。
在极坐标系中,如果点 A,B 的极坐标分别为 A2,π4,B2,54π, 且△ABC 为等腰直角三角形,求直角顶点 C 的极坐标与该三角形的面积.
【精彩点拨】 解答本题既可以把极坐标转化为直角坐标来解,也可以利 用余弦定理来解决.
人教版高中数学选修4-4课件:第一讲二极坐标

4.写出下图中各点的极坐标:
A________,B________,C________. 答案:(4,0) 2,π4 3,π2
5.极坐标系中,与点3,-π3关于极轴所在直线对 称的点的极坐标是________.
答案:3,π3
类型 1 极坐标系与点的极坐标(自主研析) [典例 1] (1)写出下图中各点的极坐标(ρ>0,0≤ θ<2π,且各线之间间距相等).
法二 将点 A 化为直角坐标为( 3,1),点 B 化为直 角坐标为( 3,-1).所以 A、B 两点间的距离
d= ( 3- 3)2+[1-(-1)]2=2. (2)如下图所示:
关于极轴的对称点为 B2,-π3. 关于直线 l 的对称点为 C2,23π. 关于极点 O 的对称点为 D2,-23π.
归纳升华 1.点(ρ,θ)关于极轴的对称点是(ρ,-θ)或(ρ,2π- θ),关于极点的对称点是(ρ,π+θ),关于过极点且垂直 于极轴的直线的对称点是(ρ,π-θ).
2.求极坐标系中两点间的距离应通过由这两点和极 点 O 构成的三角形求解,也可以运用两点间距离公式|AB| = ρ21+ρ22-2ρ1ρ2cos(θ1-θ2)求解,其中 A(ρ1,θ1), B(ρ2,θ2).注意当 θ1+θ2=2kπ(k∈Z)时,|AB|=|ρ1-ρ2|; 当 θ1+θ2=2kπ+π(k∈Z)时,|AB|=|ρ1+ρ2|.
2.点的极坐标
一般地,极坐标(ρ,θ)与(ρ,θ+2kπ)(k∈Z)表示同一 个点.特别地,极点 O 的坐标为(0,θ)(θ∈R).和直角坐 标不同,平面内一个点的极坐标有无数种表示方法.
如果规定 ρ>0,0≤θ<2π,那么除极点外,平面内的 点可用唯一的极坐标(ρ,θ)表示;同时,极坐标(ρ,θ)表 示的点也是唯一确定的.
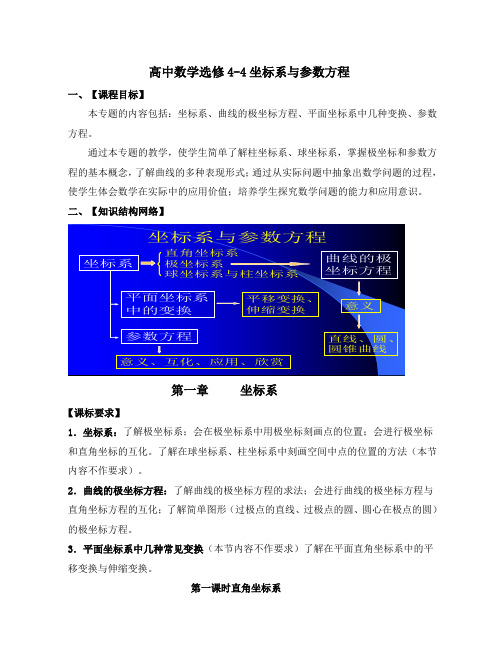
高二数学 4-4第一章坐标系全部教案
表示方法?(3)、坐标不唯一是由谁引起的?(4)、不同的极坐标是否可以写出统一
表达式。约定:极点的极坐标是 =0, 可以取任意角。
变式训练 :在极坐标系里描出下列各点
A(3,0) B(6,2 )C(3, )D(5, 4 )E(3, 5 )F(4, )G(6, 5 )
2
3
6
3
例 2 在极坐标系中,
特别强调:由极径的意义可知 ≥0;当极角 的取值范围是[0,2 )时,平面上的 点(除去极点)就与极坐标(,)建立一一对应的关系 .们约定,极点的极坐标是极 径 =0,极角是任意角. 3、负极径的规定:在极坐标系中,极径 允许取负值,极角 也可以去任意的正角 或负角,当 <0 时,点 M (,)位于极角终边的反向延长线上,且 OM= 。
(1)如果图形有对称中心,可以选对称中心为坐标原点;
(2)如果图形有对称轴,可以选择对称轴为坐标轴;
(3)使图形上的特殊点尽可能多的在坐标轴上。
(二)、平面直角坐标轴中的伸缩变换
1、在平面直角坐标系中进行伸缩变换,即改变 x 轴或 y 轴的单位长度,将会对图形
产生影响。
2、探究:(1)在正弦曲线 y=sinx 上任取一点 P(x,y),保持纵坐标不变,将横坐标 x
π 3
<0,解得 k=-1,
= 3
-2 =- 5 , 点 A 的坐标为(5,- 5 ).
3
3
变式训练:1、若 ABC的的三个顶点为 A(5, 5 ), B(8, 5 ),C(3, 7 ),判断三角形的形状.
2
6
6
答案:正三角形。2、若 A、B 两点的极坐标为 (1,1), (2 ,2 ) 求 AB 的长以及 AOB 的 面积。(O 为极点)
高考数学一轮复习选修44坐标系与参数方程课件新人教A版理

3
cos +sin
(2)C3 是一条过原点且斜率为正值的直线,
C3 的极坐标方程为 θ=α,α∈ 0,
π
2
,
= 2cos,
联立 C1 与 C3 的极坐标方程
= ,
得 ρ=2cos α,即|OA|=2cos α.
3
= cos +sin ,
联立 C1 与 C2 的极坐标方程
= ,
-11知识梳理
1
双基自测
2
3
4
5
2.若原点与极点重合,x 轴正半轴与极轴重合,则点(-5,-5√3)的极
坐标是(
)
π
A. 10, 3
2π
C. -10,- 3
4π
B. 10, 3
2π
D. 10, 3
关闭
设点(-5,-5√3)的极坐标为(ρ,θ),
-5 √3
则 tan θ=
-5
= √3.
4π
因为 x<0,所以最小正角 θ= ,
由圆 C1 与圆 C2 的方程相减可得公共弦所在的直线方程为
4x-2y+1=0.
圆心(1,1)到直线 4x-2y+1=0 的距离 d=
故弦长|AB|=2 1-
3 2
√20
=
√55
5
.
|4-2+1|
42 +(-2)2
=
3
,
√20
-24考点1
考点2
考点3
考点4
考点5
(2)解 ①圆 O:ρ=cos θ+sin θ,即 ρ2=ρcos θ+ρsin θ,
3
3
得 ρ=cos +sin ,即|OB|=cos +sin ,
高考数学冲刺讲义选修4-4坐标系与参数方程(选考)

解:把直线的参数方程代入圆的方程,得
(1 t ) (1 t ) 4,
2 2
因此t1 1, t2 1
t 1
2
x1 0 分别代入直线方程,得 y1 2 交点为A(0,2)和B(2,0)。
x2 2 y2 0
选修4-4
六.圆锥曲线的参数方程
x x0 lt ,t R y y0 mt
例10:直线过点A(1,3),且与向量(2,-4)共线: (1)求出直线的参数方程;(2)练习:求点P(-2,-1) 到此直线的距离。
x 1 2t y 3 4t
解:(1)
(2)解第二问的方法很多,最简单的方法就是把直线才 参数方程转换为直线的一般方程,然后利用点到直线 的距离公式求解。 答案: 2 2
又因为(t以s为单位),得参数方程
x 2 cos 60 t ,t 0 y 2 sin t 60
O
A 2 x
曲线的直角坐标方程常常可以转化为参数方程,转化的 关键是找到一个适当的参数。
曲线的普通方程和参数方程之间有些容易转化,有些则 较困难,有些无法转化。
由此可见,平面上的点与它的极坐标不是一一对应关系。这是极 坐标与直角坐标的 0 ,此时极坐标 ( , ) 对应的点M 的位置下面规则确定:点M在与极轴成 角的射线的反向 延长线上, 它到极点O的距离为 ,即规定当 0 时,点
M ( , ) 就是点M ( , ) 。
选修4-4
坐标系 与 参数方程
选修4-4
一.坐标系 在生产实践中,随着活动范围的扩大和对精度要 求的提高,为了更快,更准确的表述物体的位置, 我们通常要建立新的坐标系,叫做极坐标。
(1 t ) (1 t ) 4,
2 2
因此t1 1, t2 1
t 1
2
x1 0 分别代入直线方程,得 y1 2 交点为A(0,2)和B(2,0)。
x2 2 y2 0
选修4-4
六.圆锥曲线的参数方程
x x0 lt ,t R y y0 mt
例10:直线过点A(1,3),且与向量(2,-4)共线: (1)求出直线的参数方程;(2)练习:求点P(-2,-1) 到此直线的距离。
x 1 2t y 3 4t
解:(1)
(2)解第二问的方法很多,最简单的方法就是把直线才 参数方程转换为直线的一般方程,然后利用点到直线 的距离公式求解。 答案: 2 2
又因为(t以s为单位),得参数方程
x 2 cos 60 t ,t 0 y 2 sin t 60
O
A 2 x
曲线的直角坐标方程常常可以转化为参数方程,转化的 关键是找到一个适当的参数。
曲线的普通方程和参数方程之间有些容易转化,有些则 较困难,有些无法转化。
由此可见,平面上的点与它的极坐标不是一一对应关系。这是极 坐标与直角坐标的 0 ,此时极坐标 ( , ) 对应的点M 的位置下面规则确定:点M在与极轴成 角的射线的反向 延长线上, 它到极点O的距离为 ,即规定当 0 时,点
M ( , ) 就是点M ( , ) 。
选修4-4
坐标系 与 参数方程
选修4-4
一.坐标系 在生产实践中,随着活动范围的扩大和对精度要 求的提高,为了更快,更准确的表述物体的位置, 我们通常要建立新的坐标系,叫做极坐标。
高二数学选修4-4极坐标系

(2)在平面直角坐标系上,平面上所有点的集合与全体有序实数对 (x , y)的集合建立一一对应;
(3)在空间直角坐标系上,空间上所有点的集合与全体三元有序实数对 (x , y , z)的集合建立一一对应;
复习回顾
4.1.1 直角坐标系
数
平面直角
轴
坐标系
空间直角 坐标系
R
(x , y)
(x , y , z)
五、极坐标系下点的极坐标
探索点M(3,/4)的所有极坐标
P
M [1]极径是正的时候:
3,2k
4
O
X
[2]极径是负的时候:
( 3,2k )
4
新课讲解
六、极坐标系下点与它的极坐标的对应情况
[1]给定(,),就可以在极坐标平面 内确定唯一的一点M。
[2]给定平面上一点M,但却有无数个 极坐标与之对应。
π 4
练一练
题组2:在极坐标系里描出下列各点
A(3, 0)
B(6, 2 )
C(3, )
2
D(5, 4 )
3
E(3, 5 )
6
F (4, )
5
G(6, ) 3
解析: 2
5
6
C
E
F
A O
B X
4
D
3
G 5
3
新课讲解
四、1、负极径的定义
说明:一般情况下,极径都是正值;在某些必要 情况下,极径也可以取负值。
)重合
的点是(C)
A.(3, C. (3,
6
-
)
5
6
)
6
人教B版高二数学选修4-4_4.(2)极坐标与直角坐标互化课件

y
cos sin
2、 ( , ) (x,y)2tanx2xyy2
人教B版高二数学选修4-4_4.(2)极 坐标与 直角坐 标互化 课件
人教B版高二数学选修4-4_4.(2)极 坐标与 直角坐 标互化 课件
课外作业
人教B版高二数学选修4-4_4.(2)极 坐标与 直角坐 标互化 课件
练一练
某地区原计划经过B地沿着东北方向修建一条高速公路.但在A 村北偏西300方向距A村500米处,发现一古代文物遗址W, 经过初步勘测,文物管理部门将遗址W周围200米划为禁区。 已知B地位于A村的正西方向1千米处,试问:修建高速公路 的计划需要改变吗?如图示:
C
W
B
A
人教B版高二数学选修4-4_4.(2)极 坐标与 直角坐 标互化 课件
人教B版高二数学选修4-4_4.(2)极 坐标与 直角坐 标互化 课件
人教B版高二数学选修4-4_4.(2)极 坐标与 直角坐 标互化 课件
练一练
练习:已知点的直角坐标, 求它们的极坐标.
A (3, 3) C (5,0) E (3,3)
B (1, 3) D (0,2)
F (3, 0)
人教B版高二数学选修4-4_4.(2)极 坐标与 直角坐 标互化 课件
化成直角坐标.
解:由5, 2
则有 x5co2s35 y5sin2 5 3
32
32
所以, 点M的直角坐标为( 5 , 5 3 )
22
人教B版高二数学选修4-4_4.(2)极 坐标与 直角坐 标互化 课件
特此声明
由于一个点达 可式 有, 多 对 0种 时于 表 ,上
公式仍适用!
例如:上述点也的可极写坐 -成 5, 标 5( )
