初一数学上有理数与无理数的概念和练习(有详细的答案!)
乐乐课堂初一数学实数运算
乐乐课堂初一数学实数运算乐乐课堂：初一数学实数运算实数运算是数学学习的基础，也是数学应用的重要工具。
在初一数学中，实数运算涉及到有理数的运算、无理数的运算、实数的概念和运算等。
本文将通过实例和练习题，帮助同学们掌握初一数学实数运算的基本方法和技巧。
一、有理数运算1. 概念和性质：有理数运算包括加法、减法、乘法、除法四种基本运算。
在进行有理数运算时，需要注意符号的判断和运算法则的掌握。
2. 加法法则：同号两数相加，取相同的符号并把绝对值相加；异号两数相加，取绝对值较大的符号并把绝对值相减；互为相反数的两数相加得0；一个数与0相加仍得原数。
3. 减法法则：减去一个数等于加上这个数的相反数。
4. 乘法法则：两数相乘，同号得正，异号得负，并把绝对值相乘；任何数与0相乘都得0。
5. 除法法则：除以一个不为0的数等于乘以这个数的倒数；两数相除，同号得正，异号得负，并把绝对值相除；0除以任何一个不等于0的数都得0。
二、无理数运算1. 概念和性质：无理数是无限不循环小数，如π等。
在进行无理数运算时，需要注意小数点的位置和运算结果的精度。
2. 运算技巧：对于无理数的运算，可以采用分数指数幂的概念和性质，将其转化为有理数的运算或者实数的乘方运算。
三、实数概念和运算1. 概念：实数包括有理数和无理数，是数学中的基本概念之一。
实数可以表示长度、面积、体积等实际问题的数量关系。
2. 运算规则：实数的运算规则与有理数相同，但在处理无理数时需要注意小数点的位置和运算结果的精度。
四、练习题为了巩固初一数学实数运算的基本方法和技巧，下面提供一些练习题供同学们参考：1. (选择题)下列各式中正确的是（）A. (-3) + (-2) = - 5 B. (-3) + ( +2) = - 5 C. ( + 3) + ( + 2) = - 1 D. ( - 3) + ( - 2) = - 5 2. (填空题)计算(-4)÷( - 3)的结果是（）A. 1 B. - 1 C. －4 D. -4.3( )是真分数，（）是假分数．（）的绝对值最小．A．B．C．D． 3. （解答题）已知|a|=3，|b|=2，且a＞b，求a、b的值．五、总结初一数学实数运算包括有理数的运算、无理数的运算、实数的概念和运算等基本内容。
无理数的概念是什么
无理数的概念是什么
无理数是指实数范围内不能表示成两个整数之比的数。
简单的说，无理数就是10进制下的无限不循环小数，常见的无理数有：圆周长与其直径的比值，欧拉数e，黄金比例φ等等。
无理数最早由毕达哥拉斯学派弟子希伯索斯发现。
扩展资料
有理数和无理数的区别
（1）性质区别：
有理数是两个整数的'比，总能写成整数、有限小数或无限循环小数；无理数不能写成两个整数之比，是无限不循环小数。
（2）结构区别：
有理数是整数和分数的统称；无理数是所有不是有理数的实数。
（3）范围区别：
有理数集是整数集的扩张，在有理数集内，加法、减法、乘法、除法(除数不为零)4种运算均可进行；无理数是指实数范围内不能表示成两个整数之比的数。
向你推荐的相关文章
相关文章列表
微信扫码分享。
有理数与实数中考专题复习-含答案
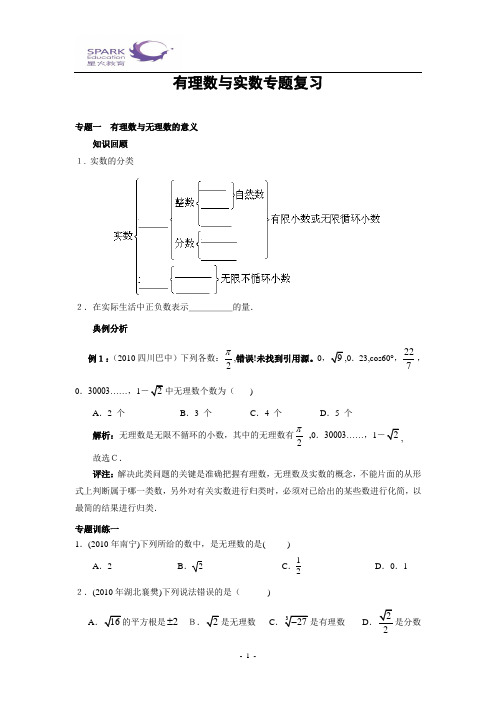
有理数与实数专题复习专题一 有理数与无理数的意义知识回顾１. 实数的分类２．在实际生活中正负数表示＿＿＿＿＿的量．典例分析例１：（2010四川巴中）下列各数：2π,错误！未找到引用源。
0．23·,cos60°，227，0．30003……，1 )A ．2 个B ．3 个C ．4 个D ．5 个解析：无理数是无限不循环的小数，其中的无理数有2π,0．30003……，1故选Ｃ． 评注：解决此类问题的关键是准确把握有理数，无理数及实数的概念，不能片面的从形式上判断属于哪一类数，另外对有关实数进行归类时，必须对已给出的某些数进行化简，以最简的结果进行归类．专题训练一1．(2010年南宁)下列所给的数中，是无理数的是( )A ．2B ． 2C ．12D ．0．1 ２．(2010年湖北襄樊)下列说法错误的是（ )A 2± 是无理数 C D ．2是分数３．（2010年上海）下列实数中，是无理数的为（ ）A ． 3．14B ． 13C ． 3D ． 9 ４．（2010安徽）在－1，0，1，2这四个数中，既不是正数也不是负数的是（ ）A ．1-B ．0C ．1D ．2专题二 实数的有关概念知识回顾１． 数轴：规定了＿＿＿、＿＿＿＿、＿＿＿的直线叫数轴．数轴上的点与＿＿＿是一一对应．２．相反数:到原点的距离相等且符号不同的两个数称为相反数,实数a 的相反数是＿＿,零的相反数是＿＿，a 与b 互为相反数，则＿＿＿＿＿；３．绝对值：在数轴上，表示一个数的点到原点的距离叫这个数的绝对值．⎪⎩⎪⎨⎧<=>=)0___()0(___)0(___||a a a a典例分析例1：（2010．湘潭）下列判断中，你认为正确的是（ )A ．0的绝对值是0B ．31是无理数 C ．|—2|的相反数是２ D ．1的倒数是1-解析：Ａ评注：解决本题的关键是弄清实数中的有关的概念，关于绝对值除了了解几何意义是表示点到原点的距离，还应理解“正数的绝对值是它本身，零的绝对值是零，负数的绝对值是它的相反数”的内涵；关于无理数应从概念上突破：表示无限不循环小数；|—2|＝２,２的相反数为－２；对于倒数，掌握它们的乘积为１．专题训练１．（2009年滨州）对于式子(8)--，下列理解：（1）可表示8-的相反数；（2）可表示1- 与8-的乘积；（3）可表示8-的绝对值；（4）运算结果等于8．其中理解错误的个数是（ ）A ．0B ．1C ．2D ．3 ２．（2010年内蒙古鄂尔多斯）如果a 与1互为相反数，则a 等于（ ）．A ．2B ．2-C ．1D ．1-３．（2010年山东菏泽）负实数a 的倒数是（ ）．A ．a -B ．1aC ．1a- D ．a ４．（2010年绵阳）－2是2的（ ）．A ．相反数B ．倒数C ．绝对值D ．算术平方根５．（2010年镇江）31的倒数是 ；21-的相反数是 ． ６．（2010年四川成都）若,x y 为实数，且20x ++=，则2010()x y +的值为________． 7．（2010吉林）如图，数轴上点A 所表示的数是_________．8（2010河南）若将三个数是 ．专题三 实数的大小比较知识回顾比较实数大小的一般方法：① 性质比较法：正数大于___,负数____0,正数_____任何负数；② 数轴比较法：在数轴上的实数，右边的数总是比左边的数___；差值法：③ 设a ，b 是任意实数，如a －b ．>0,则a ___b ，如a －b ．<0,则a b ，如a －b =0,则a ___b ;④ 商值法：如a ÷b ．>1,则a ___b ，如a ÷b ．<1,则a ___b ，如a ÷b ．=1,则a ___b ，⑤扩大法；⑥倒数比较法，当然还有分子、分母有理化和换元法等。
【绝对经典】初一数学有理数30题含详细答案
30．a、b、c三个数在数轴上位置如图所示，且|a|=|b|
（1）求出a、b、c各数的绝对值；
（2）比较a，﹣a、﹣c的大小；
（3）化简|a+b|+|a﹣b|+|a+c|+|b﹣c|．
参考答案
1．D
【解析】
【分析】
负数小于0，可将各项化简，然后再进行判断．
3．C
【解析】
【分析】
（25±0.2）的字样表明质量最大为25.2，最小为24.8，二者之差为0.4．
【详解】
解：根据题意得：标有质量为（25±0.2）的字样，
（3）如果点A、C表示的数互为相反数，求点B表示的数．
29．数轴上两点之间的距离等于相应两数差的绝对值，如2与3的距离可表示为|2﹣3|=1，2与﹣3的距离可表示为|2﹣（﹣3）|=5
（1）数轴上表示3和8的两点之间的距离是_____；数轴上表示﹣3和﹣9的两点之间的距离是_____；
（2）数轴上表示x和﹣2的两点A和B之间的距离是_____；如果|AB|=4，则x为_____；
2．B
【解析】
【分析】
根据有理数的分类逐一作出判断即可.
【详解】
解：A.0既不是正数也不是负数，故A错误；B.整数和分数统称为有理数；故B正确；C.若|a|＝|b|，则a=b或a与b互为相反数.故C错误；D.整数包括正整数、0和负整数，故D错误.
【点睛】
本题考查了有理数的分类，掌握有理数的分类是解题的关键.
A．0.2 kgB．0.3 kgC．0.4 kgD．50.4 kg
4．小丽在纸上画了一条数轴后，折叠纸面，使数轴上表示2的点与表示－4的点重合；若数轴上A、B两点之间的距离为10（A在B的左侧），且A、B两点经上述折叠后重合，则A点表示的数是（）
七年级有理数概念题
七年级有理数概念题有理数是整数和分数的统称，包括正整数、负整数、零以及正分数、负分数。
在学习有理数概念题时，需要掌握有理数的加减乘除运算规则、有理数的大小比较、有理数的绝对值等基本概念。
下面将为您介绍一些七年级有理数概念题的相关内容：1. 有理数的加减法：有理数的加减法遵循以下规则：- 同号相加，取绝对值相加，结果的符号与原数相同。
- 异号相加，取绝对值相减，结果的符号取绝对值较大的数的符号。
通过练习一些有理数的加减法题目，可以帮助学生掌握有理数的加减法规则，提高计算能力。
2. 有理数的乘法：有理数的乘法规则为：- 同号相乘，结果为正数。
- 异号相乘，结果为负数。
在乘法运算中，学生需要注意符号的运用，通过练习有理数的乘法题目，巩固乘法规则，提高计算水平。
3. 有理数的除法：有理数的除法也有相应的规则：- 除数不为0，被除数为0时，商为0。
- 同号相除，结果为正数。
- 异号相除，结果为负数。
在进行有理数的除法运算时，学生需要注意除数不能为0的情况，熟练掌握有理数的除法规则，避免出现计算错误。
4. 有理数的大小比较：在比较有理数的大小时，可以通过绝对值的大小来判断，绝对值大的数较大，绝对值小的数较小。
同时，注意有理数的正负情况，负数的绝对值大于正数的绝对值。
通过练习有理数的大小比较题目，可以帮助学生理解有理数的大小关系，提高比较能力。
5. 有理数的绝对值：有理数的绝对值是数的绝对值，即数到原点的距离，绝对值为正数，不考虑数的符号。
绝对值的概念在有理数的运算中有着重要的作用，通过练习有理数的绝对值题目，可以帮助学生理解绝对值的概念，提高数的理解能力。
通过练习以上的有理数概念题目，可以帮助学生巩固有理数的基本概念，提高有理数的运算能力，加深对数学知识的理解。
希望以上内容能对您有所帮助，有任何疑问，欢迎继续咨询。
人教初一数学上册知识点
人教初一数学上册知识点一、知识概述1. 《有理数》①基本定义：有理数就是能够写成两个整数之比的数，简单来说就是整数、有限小数还有无限循环小数这一类的数。
比如2是有理数，也是，因为可以写成1/2，…（无限循环）写成1/3也是有理数。
②重要程度：在初一数学里超级重要。
它是学习后面各种计算、方程的基础。
很多数学概念和实际问题的解决都是基于有理数的运算。
③前置知识：在学有理数之前，得知道整数的概念，会简单的加减法等算术运算。
④应用价值：在生活中算钱的时候就会用到，假如买东西花了元，就是有理数，还有计算距离、速度啥的也用到有理数运算。
2. 《整式》①基本定义：像3x、-4y²这种数与字母的乘积形式就是整式。
单独的一个数或者一个字母也叫做整式，就好比5是整式，a也是整式。
②重要程度：这是代数的起步知识，以后学各种函数、方程等都会涉及到整式的相关知识。
③前置知识：要对有理数运算比较熟，还有知道字母可以表示数这个概念。
④应用价值：举个例子，如果要计算长方形面积，设长为x，宽为y，面积就是xy，这就是整式在生活几何中应用的例子。
二、知识体系1. 《有理数》①知识图谱：有理数在初一数学上册中属于数的概念范畴，是基础的基础，很多其他数的学习都和它相关或基于它拓展。
②关联知识：和后面要学的无理数合起来就是实数了。
有理数的运算规则对整式运算也有启发意义。
③重难点分析：对有理数的正负性在运算中的影响是个难点，像两个负数相乘得正数这种规则有些同学一开始很难理解。
关键点就是得牢记运算规则，多做练习。
④考点分析：考试中经常单独出题考查有理数的运算，要么就是和后面的知识结合一起考查。
考查方式从单纯的计算，到在应用题中的运算都有。
2. 《整式》①知识图谱：整式在代数部分处于起始位置，往后的多项式、因式分解等都以整式为基础。
②关联知识：和方程关系紧密，比如一元一次方程中的未知数就是整式的形式。
③重难点分析：整式的系数、次数概念容易混淆，这是难点。
初一数学有理数试题答案及解析
初一数学有理数试题答案及解析1.若的相反数是3，5，则的值为_________.【答案】2或－8【解析】因为的相反数是3，所以.因为，所以．所以的值为2或－8．2.某初中校为每个学生编号，设定末尾用1表示男生，用2表示女生，若201103202表示“2011年入学的3班20号同学，是位女生”，则2012年入学的5班13号男生的编号是．【答案】201205131．【解析】根据编号的方法，前四位表示入学年份，第五、六位表示班级，第七、八位表示学号，末尾数表示性别，然后写出该同学的编号即可．2012年入学的5班13号男生的编号是：201205131；故答案为：201205131．【考点】用数字表示事件．3.（1）问题：你能比较和的大小吗？为了解决这个问题，首先写出它的一般形式，即比较和的大小（是正整数），然后我们从分析，，，…这些简单情况入手，从中发现规律，经过归纳，猜想出结论.通过计算，比较下列各组数的大小（在横线上填写“＞”、“＜”、“＝”号）：，，，，，…（2）从第（1）题的结果经过归纳，可以猜想出和的大小关系是什么？（3）根据上面的归纳猜想，尝试比较和的大小.【答案】（1）＜，＜，＞，＞，＞；（2）当时，＜，当≥3时，＞；（3）＞.【解析】仔细分析所给各组数的大小即可得到规律，再应用这个规律解题即可.（1），，，，；（2）当时，＜，当≥3时，＞；（3）＞.【考点】找规律-数字的变化点评：解答找规律的题目要求学生通过观察，分析、归纳发现其中的规律，并应用发现的规律解决问题．解决本题的难点在于找到“＜”、“＞”的临界点．4.下列式子一定成立的是（）A．x4+x4=2x8B．x4·x4 =x8C．(x4)4=x8D．x4÷x4=0【答案】B【解析】A．错误：x4+x4=2x4；C．错误：(x4)4=x16 D．错误：x4÷x4=1，选B正确。
【考点】整式运算点评：本题难度较低，主要考查学生对整式运算知识点的掌握。
初一数学有理数无理数题目
2.2有理数与无理数同步精练一、单选题1．下列说法中，正确的个数有()①－3.14既是负数，又是小数，也是有理数；②－25既是负数，又是整数，但不是自然数；③0既不是正数也不是负数，但是整数；④0是非负数．A．1个B．2个C．3个D．4个2．下列说法正确的个数有（）①负分数一定是负有理数②自然数一定是正数③﹣π是负分数④a一定是正数⑤0是整数A．1个B．2个C．3个D．4个3．下列各数：1.414，π，13-，0，其中是无理数的为（）A．1.414B．πC．13-D．04．对于 3.271-，下列说法不正确的是（）A．是负数，不是整数B．是分数，不是自然数C．是有理数，不是分数D．是负有理数，且是负分数5．下列说法正确的是（）A．有理数包括正有理数和负有理数B．2a是正数C．正数又可称为非负数D．有理数中有绝对值最小的数6．下列实数是无理数的是（）A．-2B．16C D7．下列说法正确的是（）A．所有的整数都是正数B．整数和分数统称有理数C．0是最小的有理数D．不是正数的数一定是负数8．下列四个数中，是正整数的是（）A．﹣1B．0C．12D．1 9．下列实数中的无理数是（）A BC D ．22710．在5-，2.3，0，π，123-五个数中，非负的有理数共有（）．A ．1个B ．2个C ．3个D ．4个11．下列实数为无理数的是（）A ．-5B ．72C ．0D ．π12．在3-，3π，1.62，0四个数中，有理数的个数为（）A ．4B ．3C ．2D ．1二、填空题13．是整数而不是正数的有理数是______．14．在－42，＋0.01，π，0，120这5个数中，正有理数是___________．15．在有理数﹣0.5，﹣3，0，1.2，2，312中，非负整数有____．16．在 3.5+，0，11，2-，23-，0.7-中，负分数有个______个．17．写出两个符合条件：是正数但不是整数的数，这两个数可以是____．三、解答题18．如图所示，将下列各数填入相应的集合圈内：12-，﹣7，+2.8，﹣900，﹣312，99.9，0，4．19．把下列各数分类，并填在表示相应集合的大括号里：-2，37+，0.8，12，0，-2.1，375-，17%，0.4．(1)正数集合：｛}(2)整数集合：｛}(3)分数集合：｛}(4)负数集合：｛}(5)正整数集合：｛}(6)负分数集合：｛}20．请把下列各数填入相应的集合中：﹣(＋4)，|﹣3.5|，0，3，10%，2018，＋(﹣5)，﹣2.030030003…（每两个3之间逐次加一个0）．正分数集合：{…}；负有理数集合：{…}；非负整数集合：{…}；参考答案1--10DBBCD DBDCB11--12DB13．非正整教殊性．14．+0.01，120.15．0，216．217．12和13（答案不唯一）．键．18．解：根据负数的定义，负数有1-2、﹣7、﹣900、﹣312；根据整数的定义，整数有﹣7、﹣900、0、4．根据正数的定义，正数有+2.8、99.9、4．∴既是负数又是整数的有﹣7、﹣900；既是整数又是正数的有4．19．（1）解：正数集合：｛37+，0.8，12，17%，0.4}（2）整数集合：｛-2，12，0}（3）分数集合：｛37+，0.8，-2.1，375-，17%，0.4}（4）负数集合：｛-2，-2.1，375 -}（5）正整数集合：｛12}（6）负分数集合：｛-2.1，375 -}20．正分数集合：{|﹣3.5|，10%，…}；负有理数集合：{﹣（+4），+（-5），…}；非负整数集合：{0，2018，…}；。
初一数学有理数知识点与经典例题
初一数学有理数知识点与经典例题一、有理数知识点。
（一）有理数的概念。
1. 有理数的定义。
- 整数和分数统称为有理数。
整数包括正整数、0、负整数；分数包括有限小数和无限循环小数。
例如：5是正整数，属于有理数； - 3是负整数，属于有理数；(1)/(2)是分数，属于有理数；0.25（有限小数，可化为(1)/(4)）也是有理数。
2. 有理数的分类。
- 按定义分类：- 有理数整数正整数 0 负整数分数正分数负分数- 按性质符号分类：- 有理数正有理数正整数正分数 0 负有理数负整数负分数（二）数轴。
1. 数轴的定义。
- 规定了原点、正方向和单位长度的直线叫做数轴。
2. 数轴上的点与有理数的关系。
- 所有的有理数都可以用数轴上的点来表示，但数轴上的点不都表示有理数（例如√(2)等无理数也可以用数轴上的点表示）。
一般地，设a是一个正数，则数轴上表示数a的点在原点的右边，与原点的距离是a个单位长度；表示数 - a的点在原点的左边，与原点的距离是a个单位长度。
（三）相反数。
1. 相反数的定义。
- 只有符号不同的两个数叫做互为相反数。
特别地，0的相反数是0。
例如，3和 - 3互为相反数，-(1)/(2)和(1)/(2)互为相反数。
2. 相反数的性质。
- 互为相反数的两个数的和为0，即若a与b互为相反数，则a + b=0。
（四）绝对值。
1. 绝对值的定义。
- 一般地，数轴上表示数a的点与原点的距离叫做数a的绝对值，记作| a|。
2. 绝对值的性质。
- 当a>0时，| a|=a；当a = 0时，| a|=0；当a<0时，| a|=-a。
例如，|3| = 3，| - 3|=3，|0| = 0。
- 非负性：| a|≥s lant0。
（五）有理数的大小比较。
1. 法则。
- 正数大于0，0大于负数，正数大于负数。
- 两个负数，绝对值大的反而小。
例如，比较 - 2和 - 3，| - 2|=2，| - 3| = 3，因为2<3，所以 - 2>- 3。
初一数学有理数试题答案及解析
初一数学有理数试题答案及解析1.一粒米的质量大约是0．000 021 kg，这个数字用科学记数法表示为( )A．21×10－4 kg B．2．1×10－6 kg C．2．1×10－5 kg D．2．1×10－4 kg【答案】C．【解析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10-n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．0．000021=2．1×10-5．故选C．【考点】科学记数法—表示较小的数．2.绝对值不大于3的整数的和是．【解析】绝对值不大于3的整数即为绝对值分别等于3、2、1、0的整数，据此解答．解：不大于3的整数绝对值有0，1，2，3．因为互为相反数的两个数的绝对值相等，所以绝对值不大于3的整数是0，±1，±2，±3；其和为0．故答案为：0．点评：考查了绝对值的定义和性质，注意掌握互为相反数的两个数的绝对值相等．3.数轴上原点表示的数是______，绝对值最小的有理数是_______.【答案】0，0【解析】根据数轴的知识、绝对值的规律求解即可.解：数轴上原点表示的数是0；绝对值最小的有理数是0.【考点】数轴的知识，绝对值的规律点评：解题的关键是熟练掌握绝对值的规律：正数和0的绝对值是它本身，负数的绝对值是它的相反数.4.很多代数原理都可以用几何模型解释．现有若干张如图所示的卡片，请拼成一个边长为(2a+b)的正方形（要求画出简单的示意图），并指出每种卡片分别用了多少张？然后用相应的公式进行验证．【答案】种卡片用了4张；种卡片用了4张；种卡片用了1张．；验证：【解析】解：拼图如下从图中可知：种卡片用了4张；种卡片用了4张；种卡片用了1张．验证如下：根据正方形面积公式：，成立【考点】几何模型点评：本题难度中等，主要考查学生使用几何模型验证代数原理的能力。
人教版七年级数学上册《有理数》易错题练习-有答案
人教版七年级数学上册《有理数》易错题练习-有答案【易错1例题】正数和负数1．（2021·四川中考真题）如果规定收入为正那么支出为负收入2元记作2+支出5元记作（）．A．5元B．5-元C．3-元D．7元【答案】B【分析】结合题意根据正负数的性质分析即可得到答案．【详解】根据题意得：支出5元记作5-元故选：B．【点睛】本题考查了正数和负数的知识解题的关键是熟练掌握正负数的性质从而完成求解．【易错2例题】有理数2．（2021·广西三美学校）已知下列各数：5-1340 1.5-513312-．把上述各数填在相应的集合里：正有理数集合：｛｝负有理数集合：｛｝分数集合：｛｝【答案】正有理数集合：11,4,5,333⎧⎫⎨⎬⎩⎭负有理数集合：15, 1.5,2⎧⎫---⎨⎬⎩⎭分数集合：111, 1.5,3,332⎧⎫--⎨⎬⎩⎭【分析】正有理数指的是除了负数0无理数的数字负有理数指小于0的有理数正分数负分数小数统称为分数．【详解】解：正有理数集合：11,4,5,3 33⎧⎫⎨⎬⎩⎭负有理数集合：15, 1.5,2⎧⎫---⎨⎬⎩⎭分数集合：111, 1.5,3,332⎧⎫--⎨⎬⎩⎭．【点睛】本题考查了有理数的分类熟练掌握各类数的属性和特点是解题的关键．【易错3例题】数轴3．（2021·广东七年级月考）已知下列有理数：－42－3.50－231－0.52（1）在数轴上标出这些有理数表示的点（2）设表示－0.5的点为A那么与A点的距离相差4个单位长度的点所表示的数是多少？【答案】（1）答案见解析（2）3.5或−4.5．【分析】（1）根据所给有理数画出数轴标出各数据即可．（2）直接利用数轴结合与A点的距离相差4个单位长度即可得出答案．【详解】（1）如图所示：（2）设表示−0.5的点为A则与A点的距离相差4个单位长度的点所表示的数是：−0.5+4=3.5或−0.5−4=−4.5.【点睛】本题考查数轴根据题意正确的在数轴上表示出各数据是解题关键．【易错4例题】相反数4．（2021·江苏七年级专题练习）2021的相反数为__________．-【答案】2021【分析】利用相反数的定义即可求解．【详解】-解：2021的相反数为2021-．故答案为：2021【点睛】本题考查相反数掌握相反数的定义是解题的关键．【易错5例题】绝对值5．（2021·浙江九年级三模）2021的绝对值是（）A．12021B．﹣12021C．2021D．﹣2021【答案】C【分析】根据绝对值的定义即可得出正确选项．【详解】解：2021的绝对值是2021故选：C．【点睛】本题考查求绝对值．正数的绝对值是它本身0的绝对值是0负数的绝对值是它的相反数．【专题训练】一、选择题1．（2021·江苏苏州市·九年级二模）π的相反数是（）A．π-B．πC．1π-D．1π【答案】A【分析】根据相反数的定义即可求解．【详解】解：π的相反数是π-故选：A【点睛】此题考查的是相反数的概念是：只有符号不同的两个数互为相反数掌握相反数的概念是解题的关键．2．（【新东方】初中数学20210625-022【初一上】）下列各对量中不具有相反意义的是（）A．胜2局与负3局B．盈利3万元与亏损3万元C．气温升高4℃与气温降低10℃D．转盘逆时针转3圈与向右转5圈【答案】D【分析】首先审清题意明确“正”和“负”所表示的意义再根据题意作答．【详解】解：A胜2局与负3局具有相反意义不符合题意B盈利3万元与亏损3万元具有相反意义不符合题意C气温升高4℃与气温降低10℃具有相反意义不符合题意D转盘逆时针转3圈与向右转5圈不具有相反意义符合题意故选D．【点睛】本题主要考查了正数和负数的意义解题关键是理解“正”和“负”的相对性明确什么是一对具有相反意义的量．在一对具有相反意义的量中先规定其中一个为正则另一个就用负表示．3．（【新东方】DY试卷解析初一下数学【00017】）下列关于数轴的图示画法不正确的有（）A．4个B．3个C．2个D．1个【答案】B【分析】根据数轴的定义逐一判断即可得到答案．【详解】（1）中数轴的单位长度不一致画法不正确符合题意（2）中数轴没有原点画法不正确符合题意（3）中数轴画法正确不符合题意（4）中数轴没有正方向画法不正确符合题意℃画法不正确的有3个故选B．【点睛】本题主要考查数轴的画法掌握画数轴的三要素：正方向单位长度原点是解题的关键．4．（2021·上海期中）在-125% 23250-0.30.67-4257-中非负数有（）A．2个B．3个C．4个D．5个【答案】C【分析】根据非负数的范围即非负数是大于等于零的数即可求解．【详解】解：非负数有：232500.67负数有：-125% -0.32 57 -非负数有4个．故选：C【点睛】本题主要考查了有理数的分类解题的关键是熟练掌握有理数的分类情况．5．（2021·江苏南京一中七年级月考）一个数的绝对值是7这个数是（）A．7B．﹣7C．7或﹣7D．不能确定【答案】C【分析】根据绝对值的定义即可求解．【详解】解：℃一个数的绝对值是7℃这个数是7或﹣7．故选：C．【点睛】此题主要考查绝对值的求解解题的关键是熟知绝对值的性质．二填空题6．（2021·福建七年级期末）﹣2的相反数是___．【答案】2【分析】根据一个数的相反数就是在这个数前面添上“-”号 求解即可． 【详解】解：-2的相反数是：-（-2）=2故答案为：2． 【点睛】本题考查了相反数的意义 一个数的相反数就是在这个数前面添上“-”号：一个正数的相反数是负数 一个负数的相反数是正数 0的相反数是0．不要把相反数的意义与倒数的意义混淆．7．（1.有理数（题型篇））如果节约20元钱 记作“＋20”元 那么浪费15元钱 记作_______元．【答案】-15 【分析】根据节约20元钱 记作“＋20”元 可知浪费记为负 可得结果． 【详解】解：根据题意 节约记为正 浪费记为负 那么浪费15元钱 记作-15元故答案为：-15． 【点睛】本题考查了正负数的意义 解题关键是明确正负数代表意义相反的两个量 节约记为正 浪费记为负． 8．（2021·江苏七年级期末）下列各数：﹣1 2 1.01001…（每两个1之间依次多一个0） 0 227 3.14 其中有理数有_____个．【答案】4．【分析】 根据有理数的定义逐一判断即可．【详解】解：在所列实数中 有理数有﹣1 0227 3.14 故答案为：4．【点睛】本题考查了有理数 掌握有理数的概念是解题的关键．9．（1.有理数（题型篇））如果若|x －2|＝1 则x ＝________．【答案】3或1根据绝对值的性质可得x-2=±1再求出x即可．【详解】解：℃|x-2|=1℃x-2=±1则x-2=1或x-2=-1解得：x=3或1故答案为：3或1．【点睛】此题主要考查了绝对值关键是掌握绝对值等于一个正数的数有两个它们互为相反数．10．（2021·湖南七年级期末）已知A B是数轴上的两点且AB＝4.5点B表示的数为1则点A表示的数为___________．【答案】﹣3.5或5.5【分析】根据AB＝4.5点B表示的数为1进行分类讨论A可以在B的左边或右边求得点A表示的数．【详解】解：℃AB＝4.5B表示1℃A表示的数为1﹣4.5＝﹣3.5或1+4.5＝5.5．故答案为：﹣3.5或5.5．【点睛】本题考查了数轴上两点之间的距离解题的关键是分类讨论借助数轴来分析．三解答题11．（2021·河北七年级期中）把下列各数填在相应的表示集合的大括号里：﹣2312﹣（﹣96）﹣|﹣3| ﹣4.50|﹣2.5|13．（1）正有理数集合{…} （2）非负整数集合{…} （3）负分数集合{…}．【答案】（1）12﹣（﹣96）|﹣2.5| 13（2）12﹣（﹣96）0|﹣2.5| （3）﹣23﹣4.5化简各数 进而分别利用正有理数 非负整数 负分数分析 再分类填写． 【详解】解：﹣（﹣96）＝96 ﹣|﹣3|＝﹣3 |﹣2.5|＝2.5（1）正有理数集合{12 ﹣（﹣96） |﹣2.5| 13…} （2）非负整数集合{12 ﹣（﹣96） 0 …}（3）负分数集合{﹣23 ﹣4.5 …}． 【点睛】本题主要考查了有理数的相关定义 正确化简各数是解题关键．12．（【新东方】初中数学1283-初一上）把下面的数填入它所属于的集合的大括号内（填序号） ① 5.3- ②5+ ③20% ④0 ⑤27- ⑥7- ⑦3--∣∣ ⑧( 1.8)-- 正数集合｛ ｝整数集合｛ ｝分数集合｛ ｝有理数集合｛ ｝【答案】见解析【分析】根据有理数的分类填空．【详解】解：-|-3|=-3 -（-1.8）=1.8．正数集合{②③⑧}整数集合{②④⑥⑦}分数集合{①③⑤⑧}有理数集合{①②③④⑤⑥⑦⑧}．【点睛】本题考查了有理数 认真掌握正数 负数 整数 分数 正有理数 负有理数 非负数的定义与特点．注意整数和正数的区别 注意0是整数 但不是正数．13．（2020·贵阳市清镇养正学校七年级期中）已知下列各有理数 2.5- 0 3- ()2-- 0.5 1-．（1）画出数轴 在数轴上标出表示这些数的点（2）用>符号把这些数连接起来．【答案】（1）见解析 （2）3-＞-（-2）＞0.5＞0＞-1＞-2.5【分析】（1）求出|-3|=3 -（-2）=2 在数轴上把各个数表示出来（2）根据数轴上右边的数总比左边的数大比较即可．【详解】解：（1）如图（2）3-＞-（-2）＞0.5＞0＞-1＞-2.5．【点睛】本题考查了有理数的大小比较和数轴的应用 关键是求出各个数的大小和在数轴上把各个数表示出来 注意：在数轴上右边的数总比左边的数大．14．（【新东方】初中数学20210625-022【初一上】）在数轴上 A B 两点的数分别用a b 表示 如果2a =- 2b a = 请你在给定的数轴上（1）画出B 点可能的位置 并标上字母（2）计算A B 两点的距离为多少？【答案】（1）见解析 （2）2或6【分析】（1）根据绝对值的意义求出b 值 在数轴上画出即可（2）根据b 值 利用两点间的距离计算方法计算即可．【详解】解：（1）℃a =-2℃2=a℃2224b a ==⨯=b=±℃4画图如下：（2）如图可知：当b=-4时AB=2即A B两点距离为2当b=4时AB=6即A B两点距离为6℃A B两点的距离为2或6．【点睛】本题考查了绝对值的意义数轴上两点之间的距离解题的关键是要进行分类讨论．15．（2021·河南七年级期末）点A B在数轴上所表示的数如图所示回答下列问题：（1）将A在数轴上向左移动1个单位长度再向右移动9个单位长度得到点C求出B C两点间的距离是多少个单位长度？（2）若点B在数轴上移动了m个单位长度到点D且A D两点间的距离是3求m的值．【答案】（1）B C两点间的距离是3个单位长度（2）m的值为2或8．【分析】（1）利用数轴上平移左移减右移加可求点C所表示的数为﹣3﹣1+9＝5利用绝对值求两点距离BC＝|2﹣5|＝3（2）分类考虑当点D在点A的左侧与右侧利用AD=3求出点D所表示的数再利用BD=m求出m的值即可．【详解】解：（1）点C所表示的数为﹣3﹣1+9＝5℃BC＝|2﹣5|＝3.（2）当点D在点A的右侧时点D所表示的数为﹣3+3＝0所以点B移动到点D的距离为m＝|2﹣0|＝2。
七年级数学上册1.2.1 有理数-有理数的概念及分类-填空题专项练习一(人教版,含解析)
2021-2022学年度人教版七年级数学上册练习一1.2.1 有理数-有理数的概念及分类1．将下列各数填入适当的括号内：9-，227，0.314-，2020，0，338-，π-，66．（1）整数集合______…}；（2）负分数集合______…}；（3）非负整数集合______…}．2．___________既不是正数，也不是分数，但它是整数．3．在数8．3，-4，-0．8，-15，0．9，0，-223，-|-2 4 |中，有______个数是正数，有______个数是非负数，有_________个数不是整数．4．大于－2而小于3的非负整数是_______．5．在“1，﹣0.3，13+，0，﹣3.3”这五个数中，非负有理数______（写出所有符合题意的数）.6．比3小的非负整数有 ________个，7．下列各数中﹣2，0，116，53-，2019，0.121221222…，﹣0.32，－π．非负有理数有______个．8．在数322180.27520 1.048100473++----，，，，，，，，，中，负分数有______________________，非负整数有__________________________．9．在有理数中，既不是正数也不是负数的数是________．10．下列各数中：127，-3.1416，0，58-，10%，17，••3.21-，-89，分数有_____个；非负整数有_______个．11．把下列各数填入相应的大括号内13.5-，2，0，3.14，27-，15%-，1-，227负数集合{_______________}整数集合{________________}分数集合{________________}12．在有理数﹣0.2，﹣3，0，312，﹣5，1中，非负整数有__．13．在3.14122,373π，0.2020020002…(每相邻两个2之间依次增加一个0)，__________________________，无理数有__________________________．14．在1.7，－17，0，257-，－0.001，π，92-，2003和－1中，有理数有_______个，负数有________个，其中负整数有___________个，负分数有_________个.15．在+8.3，－6，－0.8，－(－2)，0，12中，整数有_______个．16．在28,2020,3,07-，15,13,, 6.94-+-中，正整数有m 个，负数有n 个，则m n +的值为__________．17．最小的正整数是__________，最大的负整数是__________，最大的非正数________．18．下列各数：①12；②213；③0；④-4；⑤-227；⑥-0.3；⑦π；⑧25%，其中是分数的是___________(填序号）19．在﹣227，0，﹣0.010010001…，π四个数中，有理数有_____个． 20．下列说法中：①0是最小的整数；②有理数不是正数就是负数；③非负数就是正数；④2π-不仅是有理数，而且是分数；⑤237是无限不循环小数，所以不是有理数；⑥无限小数不都是有理数；⑦正数中没有最小的数，负数中没有最大的数．其中错误的说法的个数为_________个．参考答案1．（1）9-，2020，0，66；（2）30.314,38--；（3）2020，0，66．解析：根据整数、负分数、非负整数的意义，逐个进行判断即可．详解：解：（1）整数有：9-，2020，0，66，故答案为：9-，2020，0，66；（2）负分数有：30.314,38--，故答案为：30.314,38--；（3）非负整数有：2020，0，66，故答案为：2020，0，66．点睛：本题考查整数集合，负分数集合，非负整数集合，掌握有理数的分类是解题关键．2．0解析：根据有理数的分类可求解．详解：解：0既不是正数，也不是分数，但它是整数．故答案为0．点睛：本题主要考查有理数的分类，属于基础知识．3．2 3 5解析：试题分析：正数有8．3，0．9共2个，非负数有0，8．3，0．9共3个，8．3，-0．8，-15，0．9，-223不是整数，共5个．考点：有理数的分类．4．0,1,2．详解：试题分析：大于－2而小于3的整数是-1,0,1,2共4个，非负整数是0,1,2．考点：绝对值．5．1，+13，0详解：非负有理数包含0和正有理数，所以1，+13，0满足题意.6．3.解析：非负整数是大于或等于0的整数，根据小于3的条件即可得出答案.详解：解：因为非负整数是大于或等于0的整数，并且小于3，所以比3小的非负整数的是0，1，2．所以有3个，故答案为3．点睛：本题考查的是非负整数的概念，掌握非负整数是大于或等于0的整数是解答此题的关键．7．3解析：根据非负有理数的定义找出题目中给出的非负有理数，数其个数，即可得出答案. 详解：依题意可得，非负有理数有：0，116，2019，共3个，故答案为：3.点睛：本题考查的是有理数，理解非负有理数的概念是解决本题的关键，非负有理数包括0和正有理数.8．11.04,3--8,2,0+解析：按照有理数的分类填写．详解：解：负分数有1 1.04,3--，非负整数有8,2,0+，故答案为：11.04,3--；8,2,0+．点睛：本题考查了有理数的分类，解题的关键是掌握负分数和非负整数的定义．9．0解析：根据有理数分为：正数，0，负数，即可得到答案.详解：解：在有理数中，既不是正数也不是负数的数是0．故答案为0.点睛：本题考查了有理数的分类，熟记0既不是正数，也不是负数是解题的关键.10．5 2解析：根据有理数的分类可直接进行解答．详解：由下列各数中：127，-3.1416，0，58-，10%，17，••3.21-，-89，分数有127，-3.1416，58-，10%，••3.21-，共5个；非负整数有0，17，共2个；故答案为5，2．点睛：本题主要考查有理数的分类，熟练掌握有理数的概念是解题的关键．11．13.5-，27-，15%-，1-；2，0，27-，1-；13.5-， 3.14，15%-，22 7解析：根据有理数的分类，即可得到答案．详解：负数有：13.5-， 27-，15%-，1-；整数有： 2，0，27-，1-；分数有：13.5-， 3.14， 15%-， 227． 故答案是：13.5-， 27-，15%-，1-；2，0，27-，1-；13.5-， 3.14， 15%-，227． 点睛：本题主要考查有理数的分类，掌握负数，整数，分数的概念，是解题的关键．12．0，1解析：非负整数是0和正整数的统称，依据定义即可作出判断．详解：在有理数﹣0.2，﹣3，0，312，﹣5，1中，非负整数有0，1.点睛：本题主要考查了非负整数定义，熟悉掌握定义是关键.13．1223.14,,0.12,37,0.20200200023π解析：分别根据实数的分类及有理数、无理数的概念进行解答详解：根据有理数及无理数的概念可知，在这一组数中是有理数的有1223.14,,0.12,37,0.20200200023π.故答案为（1）1223.14,,0.12,372,0.20200200023π. 点睛： 本题考查的是实数的分类及无理数、有理数的定义，比较简单.14．8 5 2 3解析：根据负数的定义以及负整数、负分数的定义，求解即可求得答案详解：有理数：1.7，－17，0，257-，－0.001，92-，2003和－1共8个；负数为：-17，257-，-0.001，92-，-1共5个；负整数有：-17，-1共2个；负分数有：257-,－0.001，92-共3个．故答案为：8，5，2，3．点睛：此题考查了有理数的分类．熟练掌握有理数的分类是解题的关键.15．3解析：根据整数的定义进行判断即可．详解：解：整数有：－6，－(－2)，0，故整数有3个；故答案为:3.点睛：本题考查整数的定义与特点，掌握整数的定义是解题的关键.16．5解析：先根据正整数和负数的定义求出m、n的值，再求两者之和即可．详解：正整数有2020,13+，共2个负数有8,5, 6.9---，共3个2,3m n==∴235m n∴+=+=故答案为：5．点睛：本题考查了正整数的定义、负数的定义，熟记各定义是解题关键．17．1 -1 0解析：根据最小的正整数是1，最大的负整数是-1，最大的非正数0即可．详解：解：最小的正整数是1，最大的负整数是-1，最大的非正数0，故答案为：1，-1，0．点睛：本题考查了有理数的概念和性质，解题的关键是熟知最小的正整数是1，最大的负整数是-1，最大的非正数0．18．②⑤⑥⑧解析：根据分数的定义即可判断．详解：①12；②213；③0；④-4；⑤-227；⑥-0.3；⑦π；⑧25%，其中是分数的是②213、⑤-227、⑥-0.3、⑧25%，故答案为：②⑤⑥⑧．点睛：此题主要考查有理数的分类，解题的关键是熟知分数的定义．19．2解析：根据有理数是有限小数或无限循环小数,可得答案.详解：解: ﹣227，0是有理数故答案为:2.点睛：本题考查了实数,有理数是有限小数或无限循环小数,无理数是无限不循环小数.20．5解析：根据有理数的分类作出判断，即可得出答案．详解：解：①没有最小的整数，故该项说法错误；②有理数包括正数、0和负数，故该项说法错误；③非负数就是正数和0，故该项说法错误； ④2π-是无理数，故该项说法错误； ⑤237是无限循环小数，所以是有理数，故该项说法错误； ⑥无限小数不都是有理数，故该项说法正确；⑦正数中没有最小的数，负数中没有最大的数，，故该项说法正确；所以其中错误的说法的个数为5个，故答案为：5．点睛：本题考查了有理数的分类，掌握正数、负数、整数、分数、正有理数、负有理数、非负数的定义与特点是解题的关键．注意整数和正数的区别，注意0是整数，但不是正数．。
初一数学有理数试题答案及解析
初一数学有理数试题答案及解析1.―0.5的相反数是．【答案】0.5【解析】正数的相反数是负数，0的相反数是0，负数的相反数是正数，所以-0.5的相反数是0.5. 本题涉及了相反数，该题很简单，主要考查学生对相反数的理解和判断，除此以外，常考的还有绝对值和平方等。
2.下列计算中，正确的是（）A．30＋3－3＝－3B．C．(2a2)3＝8a5D．－a8÷a4＝－a4【答案】D【解析】根据有理数的乘方法则、二次根式的性质、幂的运算法则依次分析各选项即可.A、，B、不是同类项，无法合并，C、，故错误；D．，本选项正确.本题涉及了实数的运算，计算题是中考必考题，一般难度不大，学生要特别慎重，尽量不在计算上失分.3.下列结论正确的有（）（1）零是绝对值最小的实数；（2）π-3的相反数是3-π；（3）无理数就是带根号的数；（4）-的立方根为±；（5）所有的实数都有倒数；（6）的绝对值是。
A．5个B．4个C．3个D．2个【答案】C.【解析】（1）零是绝对值最小的实数；正确；（2）π-3的相反数是3-π，正确；（3）无理数就是带根号的数，错误；（4）-的立方根为±，错误；（5）所有的实数都有倒数，错误；（6）的绝对值是，正确.共有3个正确的，故选C.【考点】1.绝对值；2.无理数；3.立方根.4.已知两数在数轴上的位置如图所示，则化简代数式的结果是（）A．1B．C．D．－1【答案】B【解析】由数轴可知，且，所以，故.5.有理数在数轴上表示的点如图所示，则的大小关系是（）A．B．C．D．【答案】D【解析】由数轴可知，所以其在数轴上的对应点如图所示，则，选D.6.有理数a、b在数轴上位置如图所示，试化简.【答案】－5－2b.【解析】由有理数a、b在数轴上位置可得1＜a＜2，-3＜b＜-1.正数和零的绝对值是它本身，附属的绝对值是它的相反数，所以，︱1-3b︱=1－3b; ︱2+b︱=-(2+b),︱3b-2︱=3b－2,试题解析：原式＝1－3b－4－2b＋3b－2＝－5－2b【考点】1.数形结合.2.绝对值.3.整式加减.7.如果数轴上的点A对应的数为，那么与A点相距3个单位长度的点所对应的有理数为_________________.【答案】或2.【解析】如果数轴上的点A对应的数为，那么与A点相距3个单位长度的点所对应的有理数为：或.【考点】实数与数轴.8.﹣|﹣|的倒数是（）A．B．﹣C．2D．﹣2【答案】D【解析】根据绝对值和倒数的定义作答．解：∵﹣|﹣|=﹣，﹣的倒数是﹣2，∴﹣|﹣|的倒数是﹣2．故选：D．点评：此题主要考查了倒数与绝对值的性质，根据一个负数的绝对值是它的相反数．若两个数的乘积是1，我们就称这两个数互为倒数得出是解决问题的关键．9.利用整式乘法公式计算：2014×2012-20132=_________．【答案】【解析】2014×2012-20132=（2013+1）（2013-1）-20132=20132-1-20132=-1【考点】整式运算点评：本题难度较低，主要考查学生对整式运算知识点的掌握。
数学分析课本-习题及答案01
第一章 实数集与函数习题§1实数1、 设a 为有理数，x 为无理数。
证明：（1）a+ x 是无理数；（2）当a ≠0时，ax 是无理数。
2、 试在数轴上表示出下列不等式的解：（1）x （2x -1）>0；（2）|x-1|<|x-3|；（3）1-x -12-x ≥23-x 。
3、 设a 、b ∈R 。
证明：若对任何正数ε有|a-b|<ε，则a = b 。
4、 设x ≠0，证明|x+x1|≥2，并说明其中等号何时成立。
5、 证明：对任何x ∈R 有（1）|x-1|+|x-2|≥1；（2）|x-1|+|x-2|+|x-3|≥2。
6、 设a 、b 、c ∈+R （+R 表示全体正实数的集合）。
证明 |22b a +-22c a +|≤|b-c|。
你能说明此不等式的几何意义吗7、 设x>0，b>0，a ≠b 。
证明x b x a ++介于1与ba 之间。
8、 设p 为正整数。
证明：若p 不是完全平方数，则p 是无理数。
9、 设a 、b 为给定实数。
试用不等式符号（不用绝对值符号）表示下列不等式的解：（1）|x-a|<|x-b|；（2）|x-a|< x-b ；（3）|2x -a|<b 。
§2数集、确界原理1、 用区间表示下列不等式的解：（1）|1-x|-x ≥0；（2）| x+x1|≤6； （3）（x-a ）（x-b ）（x-c ）>0（a ，b ，c 为常数，且a<b<c ）；（4）sinx ≥22。
2、 设S 为非空数集。
试对下列概念给出定义：（1）S 无上界；（2）S 无界。
3、 试证明由（3）式所确定的数集S 有上界而无下界。
4、 求下列数集的上、下确界，并依定义加以验证：（1）S={x|2x <2}；（2）S={x|x=n ！，n ∈+N }；（3）S={x|x 为（0，1）内的无理数}；（4）S={x|x=1-n21，n ∈+N }。
七年级上数学：有理数和无理数(提优练习有答案)
2．2有理数与无理数1．下列各数：…(每相邻两个1之间0的个数一次加1)，，其中有理数有 ( )A．3个 B．4个 C．5个 D．6个2．(2020独家原创试题)将分数化为小数是，则小数点后第2 020位上的数是 ( )A．8 B ．7 C．1 D．23．写出5个数同时满足以下三个条件：(1)其中3个数属于非正数集合；(2)其中3个数属于非负数集合；(3)5个数都属于整数集合．4．在 (每相邻的两个1之间依次多一个3)中，无理数的个数是 ( )A．1 B．2 C．3 D．45．(2020江苏徐州期中，4，★☆☆)在这5个数中，无理数有 ( )A．0个 B．1个 C．2个 D.3个6．(2020江苏南京鼓楼期中，12，,★☆☆)写出一个负有理数_____________ 7．(2020江苏南京雨花台期中，10，★☆☆)下列各数：其中是无理数的是_________(填写序号)．8.&(2020江苏镇江句容月考，22，★☆☆)把下列各数填在相应的括号内．(每相邻两个l之间0的个数依次加l)．①自然数集合：{ …}；②整数集合：{ …}；③非正数集合：{ …}；④正分数集合：{ …}；⑤正有理数集合：{ …}；⑥无理数集合’：{ …}．9．(2018辽宁锦州中考，1，★☆☆)下列各数为无理数的是 ( )10．(2015江苏扬州中考，1，★☆☆)0是 ( )A．有理数 B ．无理数 C．正数 D．负数11．(2017江苏盐城中考，7，★☆☆)请写出一个无理数_______________ 12．500多年前．数学各学派的学者都认为世界上的数只有整数和分数，直到有一天，大数学家毕达哥拉斯的一个名叫希帕索斯的学生．在研究1和2的比例中项(如果l：X=X：2，那么X叫1和2的比例中项)时，怎么也想不出这个比例中项值．后来，他画出了一个边长为1的正方形，设该正方形的对角线长为x，由毕达哥拉斯定理得，他想省代表对角线的长，而，那么x必定是确定的数，这时他又为自己提出了几个问题：(1)x是整数吗?为什么?(2)x可能是分数吗?如果是，请找出来；如果不是，请说明理由．13．无限循环小数如何化为分数呢?请你仔细阅读下列资料：由于小数部分位数是无限的，所以不可能写成十分之几、百分之几、干分之几等等的数．转化时需要先去掉无限循环小数的“无限小数部分”．一般是用扩倍的方法，把无限循环小数扩大十倍、一百倍、一千倍、…，使扩大后的无限循环小数与原无限循环小数的“无限小数部分”完全相同，然后这两个数相减，这样“大尾巴”就减掉了．例题：例如把化为分数(如图2—2—1①②所示)．。
七年级上册数学有理数练习题及答案
七年级上册数学有理数练习题及答案导语：数学是一门需要重复练习和不断巩固的学科，特别是对于初中的学生来说，在学习有理数的过程中，练习题是非常重要的。
本文将为你提供一些七年级上册数学有理数的练习题及答案，希望能够帮助你巩固知识点，提高解题能力。
一、填空题1. 将-5.2表示成有理数的形式是 ____________。
2. 一个负数和一个正数相加的结果可能是 _____________。
3. 已知a是负有理数，b是正有理数，那么a乘以b的结果是_____________。
4. 这个数，负有理数，和它的相反数的和是 ___________。
5. -2.5减去6.8，结果是 ____________。
答案：1. -5 2/102. 一个正数3. 负有理数4. 05. -9.3二、选择题1. -7.5的相反数是：A. 7.5B. -7.5C. -6.5D. 6.5答案：B2. 下列哪个是负有理数：A. 0B. 3/4C. -1D. 5/6答案：C3. 两个负有理数相加的结果可能是：A. 正有理数B. 负有理数C. 0D. 无法确定答案：B4. 两个相反数相加的结果是：A. 正有理数B. 负有理数C. 0D. 无法确定答案：C5. -1.5加上0.9的结果是：A. -2.4B. -0.6C. 0.6D. 2.4答案：B三、计算题1. 用分数表示下列数：-2.8，-4.6，3.75。
答案：-2 4/5，-4 3/5，3 3/42. 计算：-7.3 +3.5 - 1.8。
答案：-5.63. 计算：(-1.5) × (-4.2)。
答案：6.34. 计算：-9.2 ÷ (-0.5)。
答案：18.45. 计算：-3.6 - 7.5 × (1/2)。
答案：-7.35四、应用题1. 有一冰柜的温度为-5.2摄氏度，经过一段时间后，温度下降了3.6摄氏度，求现在冰柜的温度。
答案：-8.8摄氏度2. 小明在学校时，距离家2.5千米，他走了1.8千米后转了个弯，又走了3.6千米才到了学校，求小明走到学校一共走了多远。
初一数学上有理数与无理数的概念和练习(有详细的答案!)
有理数和无理数的概念与演习 【1 】常识清单1界说：有理数：我们把可以或许写成分数情势nm (m.n 是整数,n≠0)的数叫做有理数. 无理数：①无穷②不轮回小数叫做无理数.2有理数的分类整数和分数都可以写成分数的情势,它们统称为有理数.零既不是正数,也不是负数.有限小数和无穷轮回小数是有理数.3无理数的两个前提前提： （1） 无穷（2）不轮回4两者的差别：（1）无理数是无穷不轮回小数,有理数是有限小数或无穷轮回小数.（2）任何一个有理数后可以化为分数的情势,而无理数则不克不及. 经典例题例1：下列各数中,哪些是有理数？哪些是无理数？ -3,3π,-61,0.333…,3.30303030…,42,-3.1415926,0,3.101001000……（相邻两个1之间0的个数逐个加1）,面积为π的圆半径为r.例2：下列说法准确的是：（）A.整数就是正整数和负整数B.分数包含正分数.负分数闯关全练一.填空题：（1）我们把可以或许写成分数情势nm (m.n 是整数,n≠0)的数叫做. （2）有限小数和都可以化为分数,他们都是有理数.（3）小数叫做无理数.（4）写出一个比-1大的负有理数.（1）无理数与有理数的差都是有理数;（2）无穷小数都是无理数;（3）无理数都是无穷小数;（4）两个无理数的和不一定是无理数.（5）有理数不一定是有限小数.答案例1： 无理数有：3π,0,3.101001000……,（相邻两个1之间0的个数逐个加1） 有理数有：-3,-61,0.333…,3.30303030…,42,-3.1415926,0,面积为π的圆半径为r 例2：B （A,还有0 C,还有0 D,无穷不轮回） 闯关全练一.（1）有理数（2）无穷轮回小数.（3）无穷不轮回小数.（4）答案不独一,如：-0.5二.（1）错,如3π-0=3π （2）错,如：0.333…（3）对,无理数的两个前提前提之一无穷（4）对,3π+（-3π）=0 （5）对,如：0.333…。
初一数学暑假第01讲-有理数的定义
第一讲 有理数的基本概念及运算一、正数、负数1.正数【概念】像220.123π+，，，…这样大于0的数都是正数。
2.负数【概念】像47-，-3.14，-2015…这样在正数前加上“－”（读作负）号的数，叫做负数。
【注意】：（1）正数大于0，负数小于0；（2）0既不是正数，也不是负数；（3）正数前面的“＋”可以省略，注意3与3+表示是同一个正数，负号不能省略。
3.相反意义的量【概念】如果正数表示某种意义，那么负数表示它的相反的意义，反之亦然。
【举例】用正数表示向东，那么向西3km 可以用负数表示为-3km 。
【注意】“相反意义的量”包括两个方面的含意：一是相反意义；二是相反意义的基础上要有量。
（1）如果收入500元，记作+500元，那么支出237元记作________。
（2）甲，乙两地海拔高度分别是+500米，-250米，那么甲地比乙地高出 。
（3）汽车向东行驶5千米记作+5千米，那么向西行驶3千米记作 。
（4）牛牛最喜欢吃方便面，有一次他连续吃了5包的方便面。
已知方便面外包装上印有 “1005±(g )”字样，细心的牛牛老师对每包方便面都进行称重，质量分别为103g ，101g ， 99g ，105g ，95g ，请问，牛牛老师吃的方便面合格吗？知识点1例1（5）下面说法正确的是（）A．带正号的数就是正数，带负号的数就是负数B．任何一个正数前面加上“—”，就是一个负数C．0是最小的正数D．a既是正数，又是负数练一练1（1）向南走-23米表示。
（2）成都地区6月平均温度为25℃，记录表上有6月份5天的记录分别为+2.7，0， +1.4， -3，-4.7，那么这5项记录表示的实际温度分别是（3）七名同学的体重以48kg为标准,超过记为正,不足记为负,记录如下编号1234567与标准体重的差(kg) -3.0+1.5+0.80+0.3+1.2+0.5最接近标准体重的学生体重是多少?按体重的轻重排列时,恰好居中的是哪位同学?二、有理数1．有理数【概念】整数与分数统称有理数。
初一数学有理数无理数题目
初一数学有理数无理数题目【实用版】目录一、有理数与无理数的概念二、有理数与无理数的性质三、有理数与无理数的运算规则四、初一数学有理数无理数题目的解题方法与技巧五、总结正文一、有理数与无理数的概念有理数指的是可以表示为两个整数之比的数，包括整数、分数和小数（有限小数和循环小数）。
而无理数指的是不能表示为两个整数之比的数，它的小数部分既不是有限小数也不是循环小数，例如圆周率π和自然对数的底数 e 等。
二、有理数与无理数的性质有理数具有如下性质：1) 有理数可以表示为分数形式，即 a/b（a、b 为整数，b≠0）；2) 有理数可以表示为小数形式，包括有限小数和循环小数；3) 有理数可以进行加、减、乘、除等运算。
无理数具有如下性质：1) 无理数不能表示为分数形式，即无法表示为 a/b（a、b 为整数，b≠0）；2) 无理数的小数部分既不是有限小数也不是循环小数；3) 无理数可以进行加、减、乘、除等运算。
三、有理数与无理数的运算规则有理数与无理数的运算规则与实数的运算规则相同，包括加法、减法、乘法、除法。
在运算过程中，需要注意以下几点：1) 运算顺序，先乘除后加减；2) 同号相乘为正，异号相乘为负；3) 除数不能为零。
四、初一数学有理数无理数题目的解题方法与技巧在初一数学中，有理数与无理数的题目主要涉及有理数的大小比较、有理数的混合运算、无理数的估算等。
解题时，可以采用以下方法与技巧：1) 利用数轴进行有理数大小比较；2) 将有理数混合运算转化为简单的加减运算；3) 利用近似值估算无理数的大小；4) 注意运算过程中的符号和精度。
五、总结有理数与无理数是初中数学中的基本概念，掌握它们的性质和运算规则对于解决相关题目至关重要。
初一数学有理数与无理数
有理数与无理数1.有理数我们把能够写成分数形式n m （m 、n 是整数，n ≠0）的数叫做有理数．2.无理数无限不循环小数叫无理数，例如π．3.有理数的分类()⎧⎧⎫⎪⎬⎪⎨⎭⎪⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩正整数自然数整数零有理数按定义分类负整数正分数分数负分数()()⎧⎧⎪⎨⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩正整数正有理数正分数有理数按符号分类零零既不是正数,也不是负数负整数负有理数负分数常见题型：区分有理数和无理数；有理数与无理数分类．易错点：1．正数和零统称为非负数；2．负数和零统称为非正数；3．正整数和零统称为非负整数；4．负整数和零统称为非正整数．中考回顾：基础知识，是运算的基础.例1在+2017，﹣3.2，0，227-，π，0.010010001…，﹣49这七个数中，有理数的个数为（）A ．4B ．5C ．6D ．7例2按要求选择下列各数：3，π，0， 3.5-，13，0.03-，0.26+，1-，132，94-，1，7-，2.4．（1）属于整数的有________________________________________________（2）属于分数的有________________________________________________（3）属于非正数的有______________________________________________（4）属于非负数的有______________________________________________（5）属于非负整数的有____________________________________________（6）属于有理数的有______________________________________________参考答案1.【答案】B【考点】有理数的概念【解析】在+2017，﹣3.2，0，227-，π，0.010010001…，﹣49这七个数中，有理数有+2017，﹣3.2，0，227-，﹣49，有理数的个数为5；其中0.010010001…只是小数部分有规律并不是循环小数，是无限不循环小数，即无理数．2.【答案】（1）属于整数的有3、0、1-、1、7-（2）属于分数的有 3.5-、13、0.03-、0.26+、132、94-、2.4（3）属于非正数的有0、0.03-、1-、94-、7-（4）属于非负数的有3、π、0、13、0.26+、132、1、2.4（5）属于非负整数的有1-、7-（6）属于有理数的有3、0、 3.5-、13、0.03-、0.26+、1-、132、94-、1、7-、2.4【考点】有理数的分类【解析】主要是其中的非正数包括0和负数，非负数包括0和正数，非负整数包括0和正整数.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
有理数和无理数
1.什么是有理数？我们把能够写成分数形式
n
m (m 、n 是整数，n≠0)的数叫做有理数。
2.有理数的分类？
整数和分数都可以写成分数的形式，它们统称为有理数。
零既不是正数，也不是负数。
有限小数和无限循环小数是有理数。
2.什么是无理数？①无限②不循环小数叫做无理数。
3无理数的两个前提条件是什么？
（1） 无限（2）不循环
4两者的区别是什么？
（1）无理数是无限不循环小数，有理数是有限小数或无限循环小数。
（2）任何一个有理数后可以化为分数的形式，而无理数则不能。
1：下列各数中，哪些是有理数？哪些是无理数？ -3，3π，-6
1，0.333…，3.30303030…，42，-3.1415926,0，3.101001000……（相邻两个1之间0的个数逐个加1），面积为π的圆半径为r 。
答：无理数有：3
π，0，3.101001000……，（相邻两个1之间0的个数逐个加1） 有理数有：-3，-6
1，0.333…，3.30303030…，42，-3.1415926,0，面积为π的圆半径为r
2：下列说法正确的是：（ ）
A.整数就是正整数和负整数
B.分数包括正分数、负分数
C.正有理数和负有理数统称有理数
D.无限小数叫做无理数 答：B 因为：A 、C 的答案里缺少 0这一部分 D ，无限小数循环小数是有理数，
无限不循环小数才是无理数
3：我们把能够写成分数形式n
m (m 、n 是整数，n≠0)的数叫做 有理数 。
4：有限小数和无限循环小数都可以化为分数，他们都是有理数。
5：无限不循环小数叫做无理数。
6：无理数与有理数的差都是有理数；答：错，如3π-0=3
π 7：无限小数都是无理数；答：错，如：0.333…
8：无理数都是无限小数；答：对，无理数的两个前提条件之一无限
9：两个无理数的和不一定是无理数。
答：对，3π+（-3
π）=0 10：有理数不一定是有限小数。
答：对，如：0.333…
（注：文档可能无法思考全面，请浏览后下载，供参考。
可复制、编制，期待你的好评与关注）。