第1章 1.5 力的时间和空间积累效应
1第1章 理论力学基础
A D B E 1m
M A 0
Fx F1x F2 x F3x F4 x Fx
在垂直方向的合力:
F1Y F2Y
Fy F1 y F2 y F3 y F4 y Fy
(4)根据勾股求合力F:
F4Y
F4X
F1X F2X
F3X
F (Fx ) (Fy )
2
2019年1月14日星期一 2019/1/14
2019年1月14日星期一 2019/1/14
22 ‹#›
例5
作受力图。
T
G A B o
G NA
O
NB
圆柱O
2019年1月14日星期一 2019/1/14
23 ‹#›
例6
作受力图。(不计摩擦) P
A
B E D C P
A
B
o
W F
NE
C
YA
NE
XA
ND
折杆ABC、圆柱体O
ND
O
W
NF
2019年1月14日星期一 2019/1/14
2019年1月14日星期一 2019/1/14
绳索是重物的约束
轴承是轴的约束。
5 ‹#›
3.约束力:约束对被约束物体的作用力 (约束反力,或反力) 工程中常见的约束:
1、 柔体约束 柔性体 (绳索、皮带、链条等拉住物体,限制其运动。)
TA
A
A T1’ T1
P 柔绳约束动画
P
T2’
T2
作用线:沿柔性体
1.4 力矩和力偶
Mo(F)=±Fd +
- O
.
d F
若“F”为分力F1、F2、· · · Fn的合力,则它也等 于各分力对同一点力矩的代数和。即:
怎么理解力对空间的积累

怎么理解力对空间的积累力是物理学的基本概念,它是描述物体运动状态的量。
在我们日常生活中,力也是一个经常被提及的词汇。
力的作用可以对物体产生影响,也可以对我们的身体产生影响。
但是,力还有一个非常重要的作用,那就是对空间的积累。
本文将从以下几个方面来探讨力对空间的积累的意义。
一、力对空间的影响首先,我们需要了解力对空间的影响。
力的作用可以改变物体的位置、形状和速度等。
这些变化会对空间造成影响。
例如,一个重物落地时,它的重力会对地面产生压力,这个压力会使地面产生一个凹陷的形状。
这个凹陷的形状就是力对空间的影响。
此外,力还可以改变空间中物体的运动轨迹。
例如,一个弹簧可以将物体向上弹起,这个弹起的轨迹就是力对空间的影响。
力还可以改变物体的方向和速度,这些变化也会对空间产生影响。
例如,一个车辆在高速行驶时,它的速度和方向会对周围的空间产生影响。
二、力对空间的积累力对空间的影响是不断积累的。
当一个物体受到力的作用时,它会对周围的空间产生影响。
这些影响会随着时间的推移而不断积累,最终形成一个稳定的形态。
例如,一座大桥的建造就是力对空间的积累。
在建造过程中,桥梁承受着巨大的重力和风力,这些力会对周围的空间产生影响。
但是,经过多年的积累,这些影响逐渐稳定下来,形成了一座坚固的大桥。
此外,力对空间的积累还可以表现在自然界中。
例如,一座山峰的形成就是力对空间的积累。
在地球的漫长历史中,地壳运动、地质变化、水流侵蚀等力的作用会不断改变山峰的形态。
但是,这些影响逐渐积累,最终形成了我们看到的山峰。
三、力对空间的美学价值力对空间的积累不仅仅是一个物理过程,它还具有美学价值。
当我们欣赏一座大桥或者一座山峰时,我们所看到的不仅仅是一个物理结构,更是一个经过力对空间积累的艺术品。
例如,一座古老的城墙,它经历了多年的风雨侵蚀和人类的战争摧毁,但它依然屹立在那里,成为城市的标志性建筑。
这个城墙所承载的不仅仅是历史的记忆,更是力对空间积累的美学价值。
力的时间累积效应冲量动量动量定理

4-3 角动量 角动量守恒定律
mvM
l 2
J
2mu
l 2
1 12
ml 2
1 2
ml 2
解得
mvMl ml 2 12
2 ml 2
6m(2gh)1 2 2 (m 6m)l
演员N以u起跳,到达旳高度:
h u2 l 2 2 ( 3m )2 h
2g 8g m 6m
第四章 刚体的转动
28
解 碰撞前M落在 A点旳速度
vM (2gh)1 2
碰撞后旳瞬间,M、N具有相同旳线速度
u l
2
第四章 刚体的转动
26
物理学
第五版
4-3 角动量 角动量守恒定律
M、N和跷板构成旳系统,角动量守恒
mvM
l 2
J
2mu
l 2
1 12
ml 2
1 2
ml 2
M
h
N
C
A
B
l
l/2
第四章 刚体的转动
27
物理学
➢ 在冲击等问题中 M in M ex L 常量
➢ 角动量守恒定律是自然界旳一种基本定律.
第四章 刚体的转动
19
物理学
第五版
4-3 角动量 角动量守恒定律
许多现象都能 够用角动量守恒来 阐明.
➢把戏滑冰 ➢跳水运动员跳水
第四章 刚体的转动
20
物理学
第五版
4-3 角动量 角动量守恒定律
自然界中存在多种守恒定律
开始时静止于圆环上旳 点 A (该点在经过环心 O 旳水平面上),然后 点从开A 始下滑.设小球与圆环间旳摩擦力略 去不计.求小球滑到点 B 时对环心 O 旳角 动量和角速度.
大学物理学-力的空间积累

质点系的功能原理
W 外 W 内 E k末 E k初
W 外 W 非保守内力 W 保守内力 E K E K 0
W 保守内力 ( E P E P 0 ) E P
W 外 W 非保守内力 ( E K E K 0 ) ( E P E P 0 )
总动量,但增大总动能。
大学物理学
章目录
节目录
上一页
下一页
2.3 力在空间上的积累
质点系的动能定理
质点系的动能
一对内力 做功之和不一定为零
W 外 W 内 E k末 E k初
质点系的动能定理:
质点系总动能的增量等于外力的功和内力的功之和。
大学物理学
章目录
节目录
上一页
下一页
2.3 力在空间上的积累
此势能曲线可分析系统
状态的变化。
大学物理学
势垒
E
ra 势阱 rb
•A
章目录
节目录
rc
上一页
X
下一页
2.3 力在空间上的积累
四、质点系的动能定理和功能原理
内力矢量和为零,但内力做功之和可不为零。
作用于不同质点,质点位移可能不同。
W W 0
f
f
例:物体间摩擦力矢量和为零,对总动量没影响
,但做功可以减小总动能。炸弹爆炸时爆炸力不改变
2GM
c
R
星体即使发光,引力也会把光吸引回来,远处
的观察者根本接收不到该星体发出的任何信息。这
W 外 W 非保守内力 E E0
功能原理:质点系在运动过程中,所受外力的功与系
统内非保守力的功的总和等于其机械能的增量。
大学物理学
力的三种效应及应用

求解力学问题的三把金钥匙——力的三种效应及应用力学是物理学的基础和重要的组成部分,在中学物理教材中,力学知识的核心可以概括为力的三种效应即力的瞬时效应、力的时间积累效应、力的空间积累效应。
力的这三种效应从三个不同的视角揭示了自然界中最普遍的现象之一---运动现象的内在本质及其遵循的规律,为力学问题的解决提供了三种求解方法。
下面就力的三种效应及其应用做以粗浅探讨:1、力的瞬时效应:牛顿第二定律的微分形式为d(mv)/dt=F, mv表示物体的“运动量”,简称动量,d(mv)/dt为动量对时间求导,即动量随时间改变的快慢程度。
在宏观、低速情况下,物体的质量m为定值,d(mv)/dt可写作mdv/dt,dv/dt为速度对时间求导,即速度随时间改变地快慢程度——加速度;如果物体做匀变速运动,加速度为恒量,记做dv/dt=a,则d(mv)/dt=F可写作ma=F,该式就是中学物理教材中牛顿第二定律的数表达式。
F=ma给出了力F与加速度a的瞬时定量关系,称为力的瞬时效应。
应用中可以从物体的受力分析出发,求出物体的加速度a,进而求解位移s、速度v等运动学问题;也可以从分析物体的运动情况出发,求出物体的加速度,进而解决物体的受力问题。
2、力的时间积累效应:力的时间积累效应就是求力F对时间t的积分,由d(mv)/dt=F可得Fdt=mdv则有ʃFdt=ʃmdv 即ʃFdt=mv2-mv1当F为恒力时有F(t2– t1 )= m(v2– v1 ) 即F△t = m△V这就是动量定理:在一段时间内物体动量的变化(m△V),等于物体在同一时间内所受外力的冲量(F△t)。
力的时间积累效应在应用中与力的瞬时效应的应用类似,也是双向的。
3、力的空间积累效应:力的时间积累效应就是求力对位移的积分,其微分形式为Fds ,由d(mv)/dt=F可得Fds = d(mv)ds/dt ,又ds/dt = v则有Fds = vd (mv) , 对其积分ʃFds =ʃvd(mv) 当F为恒力时有F(s2 – s1) = m(v22– v12)/2这就是动能定理:物体动能的增加,等于外力对物体所做的功。
15力的时间和空间积累效应
l
v0
y
v
x
m
M
解:(1)子弹、物体系统:穿透过程水平向未受外力 系统在水平方向动量守恒。设子弹穿出时物体的水 平速度为v
T
M
Mg
V
y
x
x : mv0 0 mv MV
V2 y:T Mg M l
V 3.13(m / s) T 26.5( N )
(2)
I x mv mv0 1.0 102 (30 500) 4.7(N s)
1. 质点动量定理与动量守恒 Principal of partical momentum
冲量(Impulse)
d (mv ) F dt dI Fdt d (mv )
质点动量定理
(力的时间积累效应, N· s)
t1
t2 I Fdt mv2 mv1
t1 0
t2
2
I = mv2 - mv1 140 = 10( v2 -10)
v2 24( m/ s)
2. 质点系动量定理与动量守恒 ※质点系(m1 m2 ) ※质点系的内力与外力 ※质点系的动量
P pi
i
① 质点系
由分立质点 mi 组成
由质量元 dm 组成
dm
mi
② 质点系的内力与外力
例1. 质量为m的质点,以不变速率v沿图中正三角形 ABC的水平光滑轨道运动.质点越过A角时,轨道作 用于质点的冲量为
I 3mvj
A
B
x
y
C
例2 图示一圆锥摆,质量为m的小球在水平面 内以角速度w匀速转动.在小球转动一周的过程 中, (1) 小球动量增量等于__________. (2) 小球所受重力的冲量_______. (3) 小球所受绳子拉力的冲量大小等于_____.
力的空间累积效应
W P t
瞬时功率
ΔW dW P lim F v t 0 Δt dt
P Fv cos
6
2-3 力的空间累积效应
(1) 内力的矢量和为零,内力作功之的和不 一定为零? f2 B B f1 A A f1f 2 f 0
W 1 f 1L
2-3 力的空间累积效应
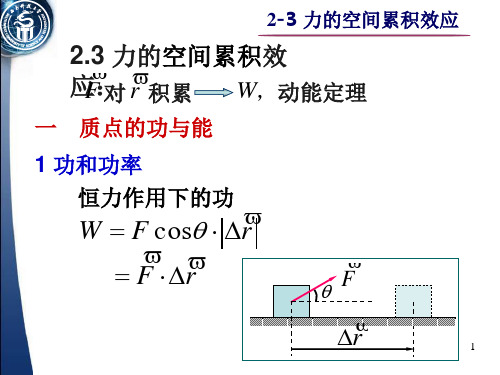
2.3 力的空间累积效 应: F 对 r 积累 W,动能定理
一 质点的功与能 1 功和功率 恒力作用下的功
W F cos r F r
F
r
1
2-3 力的空间累积效应
变力的功
dW F cos dr dW F dr
l
C
D
B
质点沿任意闭合路径运动一周时,保守力 对它所作的功为零. 非保守力:力所作的功与路径有关. (例如摩擦力)
20
2-3 力的空间累积效应
(4) 势能
与质点位置有关的能量. 引力的功
m' m m' m W ( G ) (G ) rB rA
引力势能
m' m Ep G r
m 'm m 'm 引力的功 W (G ) (G ) rB rA 1 2 1 2 弹力的功 W ( kxB kx A ) 2 2
19
2-3 力的空间累积效应
F d r F d r A ACB ADB l F dr ACB F dr BDA F dr W F dr 0
解: l
m
8
2-3 力的空间累积效应
l
m
9
力对物体的时间累积效应

c
c c
➢ 其余点的运动=随C点的平动+绕C点的转动
质心的位置
由n个质点组成 的质点系,其质心 的位置:
m2
mi
c
m1
➢对质量离散分布的物系:
➢对质量连续分布的物体: 说明 对密度均匀、形状对称的物体,质 心在其几何中心.
例1 水分子H2O的结构如图.每个氢原 子和氧原子之间距离均为d=1.0×10-10 m,氢 原子和氧原子两条连线间的夹角为θ=104.6o.
求水分子的质心.
H
d oC Od
H
52.3o 52.3o
解 yC=0
H
d oC Od
H
52.3o 52.3o
P66例2.2.7求半径为 R 的匀质半圆薄片的质心. 例2 求半径为 R 的匀质半薄球壳的质心.
Rθ O
解 选如图所示的坐标系. 在半球壳上取一如图圆环
➢ 圆环的面积
Rθ O
➢ 圆环的质量 由于球壳关于z 轴对称,故xc= 0
非完全弹性碰撞 可以证明:恢复系数等于恢复过程与压 缩过程的冲量之比
讨论
(1)若
碰前
则
(2)若
,则
碰后
讨论
(3)若
,则
碰前
碰后
1、教材p61 例2.2.2; 2.2.3;2.2.4;2.2.5分析
1 动量定理微分形式的应用举例
o
例3、一质量均匀分布的柔软细绳
铅直地悬挂着,绳的下端刚好触到水平
为0.05 s.求在此时间内钢板
所受到的平均冲力.
解 由动量定理得:
O
方向与 轴正向相同.
弹性和非弹性碰撞
一般情况碰撞
1 完全弹性碰撞 动量和机械能均守恒
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
?
微分、积分
F
B
dr
A
dA F cos dr F dr
元过程力的功:
dA F dr
宏观过程力的功: A
S A
B
dA
B
A
F dr
例1:如果一质点位置的时间函数是 (m),质点受到的力中有一个力是 (N)。求:当质点从 t 1 秒位置运动到 秒位置过程中这个力的功。
解: dA F dr (3 xi ) (3dxi 3dyj )
9 xdx
9 2 A 9 xdx x 18( J ) 0 2 0
Fi外1
成对出现; 大小相等方向相反。
f
i
i内
0
mj
mi
外力:系统外部对质点系 内部质点的作用力
Fi外
③ 质点系的动量
F1外
m1.v11
f1内
m1.v11
dr1
F1外
过程
m1.v12
I
f 2内
II
m2 .v22
dr2
f1内
m2 .v21
F2外 F2外
P系1 ( pi1 ) (mi1vi1 )
I 3mvj
A
B
x
yห้องสมุดไป่ตู้
C
例2 图示一圆锥摆,质量为m的小球在水平面 内以角速度w匀速转动.在小球转动一周的过程 中, (1) 小球动量增量等于__________. (2) 小球所受重力的冲量_______. (3) 小球所受绳子拉力的冲量大小等于_____.
0
I mg mg
IG+IT=ΔP
l
v0
y
v
x
m
M
解:(1)子弹、物体系统:穿透过程水平向未受外力 系统在水平方向动量守恒。设子弹穿出时物体的水 平速度为v
T
M
Mg
V
y
x
x : mv0 0 mv MV
V2 y:T Mg M l
V 3.13(m / s) T 26.5( N )
(2)
I x mv mv0 1.0 102 (30 500) 4.7(N s)
1. 质点动量定理与动量守恒 Principal of partical momentum
冲量(Impulse)
d (mv ) F dt dI Fdt d (mv )
质点动量定理
(力的时间积累效应, N· s)
t1
t2 I Fdt mv2 mv1
例1. 质量为m的质点,以不变速率v沿图中正三角形 ABC的水平光滑轨道运动.质点越过A角时,轨道作 用于质点的冲量为
六. 动能定理与机械能守恒定律(标量角度) (Kinetic energy theorem) (convercation of mechenical energy )
(§1.5.2)
1. 功(work) (1)力对质点的功 中学:直线位移常力的功 大学:曲线、变力的功
F
A F x cos
r 2i 3tj F 2ti
t2
解:
dA F dr (2ti ) (3dtj ) 0
A dA 0
例2:一力 F 3xi ( N )
而质点运动函数 r 3xi 3 yj (m)
求质点在 (0,0)
(2,3)
空间位置变化过程中力的功。
2
j
j
y
IT mg
2
例3. 一物体质量为10 kg,受到方向不变的力F= 30+40t (SI)作用,在开始的两秒内,此力冲量的大 小等于________________;
I F d t (30 40t ) d t 140( N s)
t1 0
t2
2
I = mv2 - mv1 140 = 10( v2 -10)
五. 动量定理与动量守恒定律(矢量角度) (conservation of momentum)
(§1.5.1)
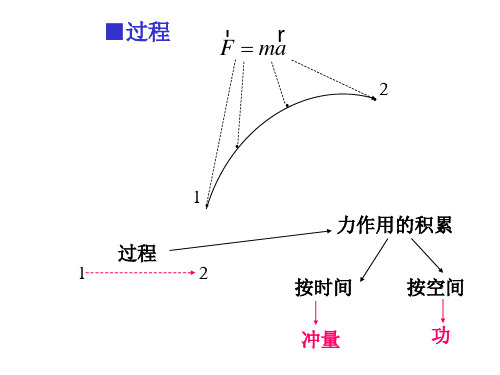
■过程
F ma
2
1
力作用的积累
过程
1 2
按时间
按空间 功
冲量
■三个定理与三个守恒定律(过程)
*. 动量定理与动量守恒定律 (conservation of momentum) *. 动能定理与能量(机械能)守恒定律 (conservation of mechanical energy *. 角动量定理与角动量守恒定律 (conservation of angular momentum)
⑤ 质点系的动量守恒定律 :
dI外 ( Fi外)dt dP系
i
F
i
i外
0
P系 pi mi vi 常矢量
i i
Fx外 0, Fy外 0, F 0, z外
m v
i
i ix
Px C1 Py C2 Pz C3
m2 .v21
F2外 F2外
m2 :
(m1 m2 ) :
dI内 (f1 内 f2内 )dt 0
( F1,外 F2,外)dt d (m1v1 m2v2 )
dI外 ( Fi外)dt dP系
i
I外 P系2 P系1
质点系动量定理
内力不改变系统的动量但可改变系统内质点的动量
i i
P系2 ( pi 2 ) (mi 2vi 2 )
i i
F1外
m1.v11
m1.v11
dr1
F1外
④ 质点系动量定理
m1 :
f1内
过程
m1.v12
I
f 2内
II
m2 .v22
dr2
f1内
(f1内 F1,外 )dt d (m1v1 ) (f2内 F2,外 )dt d (m2v2 )
v2 24( m/ s)
2. 质点系动量定理与动量守恒 ※质点系(m1 m2 ) ※质点系的内力与外力 ※质点系的动量
P pi
i
① 质点系
由分立质点 mi 组成
由质量元 dm 组成
dm
mi
② 质点系的内力与外力
内力: 系统内部各质点间的相互作用力
F jj 外
f i j f j i
m v m v
i i
i iy
三个方向必 须同时满足 时系统动量 守恒
i iz
m
v
人在船上行走
例. 质量为M=1.5 kg的物体,用一根长为l=1.25 m的 细绳悬挂在天花板上.今有一质量为 m= 10 g的子弹 以v0=500 m/s的水平速度射穿物体,刚穿出物体时子 弹的速度大小v =30 m/s,设穿透时间极短.求: (1) 子弹刚穿出时绳中张力的大小; (2) 子弹在穿透过程中所受的冲量.
