青海省西宁市第四高级中学高一数学上学期第一次月考试题
青海省西宁市第四高级中学2022-2023学年高一数学第一学期期末经典模拟试题含解析

B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
6.某几何体的三视图如图所示,则该几何体的体积为( )
1 / 15
A.8π
B.16π
8
C.
3
16
D.
3
7.若 a 1,则 a 1 有( ) a 1
A.最小值为 3
B.最大值为 3
C.最小值为 1
D.最大值为 1
8.若用二分法逐次计算函数 f x ln x x 在区间0.5,1 内的一个零点附近的函数值,所得数据如下:
其中甲、乙两名志愿者选择同一个比赛小项进行志愿服务工作共 种,
种情况,
所以甲、乙两名志愿者选择同一个比赛小项进行志愿服务工作的概率是
,
故选:C. 11、C 【解析】由空间中直线与平面的位置关系逐项分析即可
【详解】当 m / /, n / /, / / 时,m, n 可能平行,也可能相交或异面,所以①不正确;当 , 时,, 可
5、B 【解析】先根据“关于 的不等式 【详解】设 :“关于 的不等式 则由 知一元二次函数 所以对于一元二次方程
对 恒成立”得
对 恒成立”,
的图象开口向上,且 轴无交点.
必有
,
,再根据集合关系判断即可得答案.
解得
,
由于
,
所以“
”是“关于 的不等式
对 恒成立”的必要不充分条件.
故选:B.
【点睛】结论点睛:本题考查充分不必要条件的判断,一般可根据如下规则判断:
8、B
【解析】利用零点存在性定理和精确度要求即可得解.
【详解】由表格知在区间 0.5625,0.625两端点处的函数值符号相反,且区间长度不超过 0.1,符合精度要求,
青海省西宁四中2015-2016学年高一上学期第一次月考数学试卷

西宁市第四高级中学15—16学年第一学期第一次月考试卷高 一 数 学出题人: 黄红娟一、 选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.集合}80|{<<∈=+x N x M ,{1,3,5,7,8}N =,则=⋂N M ( )A.{1,3,5,7}B.}7,5,3{C.{3,5,7,8}D.{1,3,5,7,8}2.下列四组函数中表示同一个函数的是( )A.0()f x x =与()1g x =B.()||f x x =与()g x =C.()f x x =与2()x g x x =D.()f x =与2()g x =3.函数1()1f x x =+- )A.[1,)-+∞B.),1()1,1[+∞⋃-C.(1,)+∞D.(,)-∞+∞4.已知集合},{2a a A =,}1{=B ,若A B ⊆,则实数a 的取值集合为()A.}1,1{-B.}1{C.}1{-D.∅5.设函数211()21x x f x x x ⎧+≤⎪=⎨>⎪⎩,则((3))f f =() A.15 B.3 C.139 D.236.下列函数中为偶函数的是( )A.x y 2=B.]4,4(,2-∈=x x yC.3x y =D.0x y =7.下列函数中,在区间)1,0(上是增函数的是( ) A.xy 1= B.||y x = C.42+-=x y D.x y -=3 8.设}20|{≤≤=x x A ,}21|{≤≤=y y B ,能表示从集合A 到集合B 的函数关系的图象是( )9.设偶函数()f x 的定义域为R ,()f x 在区间]0,(-∞上为增函数,则)3(),(),2(f f f π-的大小关系是( )A.)3()2()(f f f >->πB.)2()3()(->>f f f πC.)3()2()(f f f <-<πD.)2()3()(-<<f f f π10.已知函数2)(3-+=bx ax x f ,3)2014(=f ,则=-)2014(f ( )A.7-B.5-C.3-D.2-11.若函数2(1) 1 (1)()1 1 (1)2a x x f x ax ax x +-≥⎧⎪=⎨--<⎪⎩在),(+∞-∞上单调递增,则实数a 的取值范围是( ) A.)0,32(- B.)0,1(- C.)0,32[- D.)0,1[- 12.已知)(x f 是定义在R 上的函数,且)(x f 的图像关于坐标原点对称;当0<x 时,x x x f 2015)(2+-=.若0)()2(2<+-a f a f ,则实数a 的取值范围是( )A.),2()1,(+∞⋃--∞B.),1()2,(+∞⋃--∞C.)2,1(-D.)1,2(-二.填空题:(本大题共4小题,每小题5分,共20分)13.若集合M 满足M ≠⊂}2,1{,则这样的集合M 有____________个.14.已知函数)(x f y =由右表给出,若3)(=a f ,则a =____________15.若))(2()(m x x x f --=是定义在R 上的偶函数,则=m __________.16. 下列叙述正确的有①集合}5|),{(=+=y x y x A ,}1|),{(-=-=y x y x B ,则}3,2{=⋂B A ②若函数34)(2-+-=x ax xx f 的定义域为R ,则实数121-<a ③函数)0,2(,1)(-∈-=x x x x f 是奇函数④函数b x x x f ++-=3)(2在区间),2(+∞上是减函数三.解答题:(本大题共6小题,共70分)17.(本小题满分10分)已知集合}63|{<≤=x x A ,}92|{≤<=x x B .(Ⅰ)求B A ⋃,B A C R ⋂)(;(Ⅱ)已知{|}C x x a =<,若C B ⊆,求实数a 的取值范围.18.(本小题满分12分)已知函数21)(-+=x x x f ,其中]5,3[∈x .(Ⅰ)用定义证明函数)(x f 在]5,3[上单调递减; (Ⅱ)结合单调性,求函数21)(-+=x x x f 在区间]5,3[上的最大值和最小值.19.(本小题满分12分)已知函数()f x 是定义在R 上的偶函数.若0≥x 时,x x x f 2)(2-=.(Ⅰ)当0<x 时,求函数()f x 的解析式;(Ⅱ)画出()f x 的简图;(要求绘制在答题卷的坐标纸上.............);(Ⅲ)结合图像写出()f x 的单调区间(只写结论....,不用证明....).20.(本小题满分12分)已知函数3)(2--=kx x x f ,(1,5]x ∈-.(Ⅰ)当2=k 错误!未找到引用源。
青海省西宁市2021_2022学年高一数学上学期第一次月考试题

青海省西宁市2021-2022学年高一数学上学期第一次月考试题一、选择题((本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1、设集合}1|{x ->∈=x Q A ,则( )A . A ∅∉B .2A ∉C .2A ∈D .}2{⊆A 2、已知集合A 到B 的映射f:x →y=2x+1,那么集合A 中元素2在B 中对应的元素是: A 、2 B 、5 C 、6 D 、8 3、设集合{|12},{|}.A x x B x x a =<<=<若,A B ⊆则a 的范围是( )A .2a ≥B .1a ≤C .1a ≥D .2a ≤ 4、函数12-=x y 的定义域是( )1111. (,) . [,) . (,) . (,]2222A B C D +∞+∞-∞-∞5、全集U ={0,1,3,5,6,8},集合A ={ 1,5, 8 }, B ={2},则集合)A B =U (C ( )A .{0,2,3,6}B .{ 0,3,6}C .{2,1,5,8}D . ∅ 6、已知集合{}{}13,25A x x B x x AB =-≤<=<≤=,则( )A. ( 2, 3 )B. [-1,5]C. (-1,5)D. (-1,5]7、设偶函数f(x)的定义域为R,当x ∈[0,+∞)时,f(x)是增函数,则 f(-2),f(π),f(-3)的大小关系是( )A .f(π)>f(-3)>f(-2)B .f(π)>f(-2)>f(-3)C .f(π)<f(-3)<f(-2)D .f(π)<f(-2)<f(-3) 8、化简:2(4)ππ-+=( )A . 4B . 2 4π-C .2 4π-或4D . 4 2π-9、设集合{}22≤≤-=x x M ,{}20≤≤=y y N ,给出下列四个图形,其中能表示以集合M 为定义域,N 为值域的函数关系的是( )10、已知f (x )=g (x )+2,且g(x)为奇函数,若f (2)=3,则f (-2)=( )A 、 0B 、-3C 、1D 、311、 有下列命题:①偶函数的图象一定与y 轴相交;②奇函数的图象一定过原点; ③1()(1)1xf x x x+=--是偶函数④ 22()11f x x x =-+-既是奇函数又是偶函数. 其中,正确命题的个数是( )A 、1B 、2C 、3D 、412、已知函数()x f 是R 上的增函数,()1,0-A ,()1,3B 是其图像上的两点,那么()1f x <的解集是( ) A 、()3,0-B 、()0,3C 、(][),13,-∞-⋃+∞D 、(][),01,-∞⋃+∞二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上) 13、已知25(1)()21(1)x x f x x x +>⎧=⎨+≤⎩,则[(1)]f f = . 14、已知2(1)f x x -=,则 ()f x = .15、 定义在R 上的奇函数()f x ,当0x >时, ()2f x =;则奇函数()f x 的值域是 . 16、 如图下面的四个容器高度都相同,将水从容器顶部一个孔中以相同的速度注入其中,注满为止。
青海省西宁四中高三数学上学期第一次月考试卷 理(含解
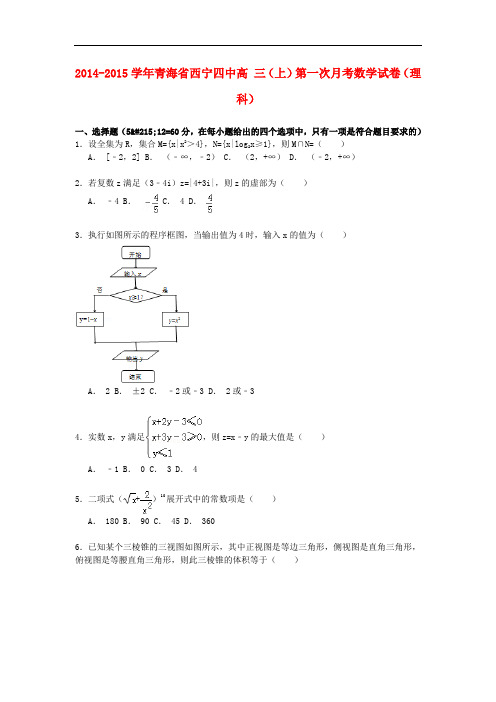
2014-2015学年青海省西宁四中高三(上)第一次月考数学试卷(理科)一、选择题(5×12=60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集为R,集合M={x|x2>4},N={x|log2x≥1},则M∩N=()A. [﹣2,2] B.(﹣∞,﹣2) C.(2,+∞) D.(﹣2,+∞)2.若复数z满足(3﹣4i)z=|4+3i|,则z的虚部为()A.﹣4 B. C. 4 D.3.执行如图所示的程序框图,当输出值为4时,输入x的值为()A. 2 B.±2 C.﹣2或﹣3 D. 2或﹣34.实数x,y满足,则z=x﹣y的最大值是()A.﹣1 B. 0 C. 3 D. 45.二项式(+)10展开式中的常数项是()A. 180 B. 90 C. 45 D. 3606.已知某个三棱锥的三视图如图所示,其中正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形,则此三棱锥的体积等于()A. B. C. D.7.已知双曲线的离心率为,则双曲线的渐近线方程为()A.y=±2x B. C. D.8.等比数列{a n}的前n项和为S n,若S3+3S2=0,则公比q=()A.﹣2 B. 2 C. 3 D.﹣39.有10件不同的电子产品,其中有2件产品运行不稳定.技术人员对它们进行一一测试,直到2件不稳定的产品全部找出后测试结束,则恰好3次就结束测试的方法种数是() A. 16 B. 24 C. 32 D. 4810.已知函数f(x)=,若对于任意x∈R,不等式f(x)≤﹣t+1恒成立,则实数t的取值范围是()A.(﹣∞,1]∪[2,+∞) B.(﹣∞,1]∪[3,+∞) C. [1,3] D.(﹣∞,2]∪[3,+∞)11.点A,B,C,D均在同一球面上,且AB、AC、AD两两垂直,且AB=1,AC=2,AD=3,则该球的表面积为()A.7π B.14π C. D.12.已知函数y=f(x)是定义在R上的偶函数,对于任意x∈R都f(x+6)=f(x)+f(3)成立;当x1,x2∈[0,3],且x1≠x2时,都有>0.给出下列四个命题:①f(3)=0;②直线x=﹣6是函数y=f(x)图象的一条对称轴;③函数y=f(x)在[﹣9,﹣6]上为增函数;④函数y=f(x)在[0,2014]上有335个零点.其中正确命题的个数为()A. 1 B. 2 C. 3 D. 4二、填空题(5×4=20分,把答案填在答题纸的相应位置上)13.已知⊥,||=2,||=3,且+2与λ﹣垂直,则实数λ的值为.14.如图,矩形OABC内的阴影部分由曲线f(x)=sinx及直线x=a(a∈(0,2π)与x轴围成.向矩形OABC内随机掷一点,该点落在阴影部分的概率为,则a= .15.曲线在点M(,0)处的切线的斜率为.16.数列{a n}的前n项和记为S n,a1=1,a n+1=2S n+1(n≥1),则{a n}的通项公式为.三、解答题(本大题6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.在△ABC中,角A,B,C的对边分别是a,b,c,其面积为S,且b2+c2﹣a2=S.(1)求A;(2)若a=5,cosB=,求c.18.如图五面体中,四边形CBB1C1为矩形,B1C1⊥平面ABB1N,四边形ABB1N为梯形,且AB⊥BB1,BC=AB=AN==4.(1)求证:BN⊥平面C1B1N;(2)求此五面体的体积.班级甲乙丙丁志愿者人数45 60 30 1550名参加问卷调查.(1)从参加问卷调查的50名志愿者中随机抽取两名,求这两名来自同一个班级的概率;(2)在参加问卷调查的50名志愿者中,从来自甲、丙两个班级的志愿者中随机抽取两名,用X表示抽得甲班志愿者的人数,求X的分布列和数学期望.20.已知椭圆C的中心在原点,焦点在x轴上,左右焦点分别为F1,F2,且|F1F2|=2,点(1,)在椭圆C上.(1)求椭圆C的方程;(2)过F1的直线l与椭圆C相交于A,B两点,且△AF2B的面积为,求直线l的方程.21.已知函数在点(﹣1,f(﹣1))的切线方程为x+y+3=0.(Ⅰ)求函数f(x)的解析式;(Ⅱ)设g(x)=lnx,求证:g(x)≥f(x)在x∈[1,+∞)上恒成立.四、解答题(共1小题,满分8分)22.已知直线L的参数方程:(t为参数)和圆C的极坐标方程:ρ=2sin(θ+)(θ为参数).(1)求圆C的直角坐标方程.(2)判断直线L和圆C的位置关系.五、解答题(共1小题,满分10分)【选修4-5:不等式选讲】23.已知函数f(x)=|x﹣2|﹣|x﹣5|(Ⅰ)证明:﹣3≤f(x)≤3;(Ⅱ)求不等式f(x)≥x2﹣8x+15的解集.2014-2015学年青海省西宁四中高三(上)第一次月考数学试卷(理科)参考答案与试题解析一、选择题(5×12=60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集为R,集合M={x|x2>4},N={x|log2x≥1},则M∩N=()A. [﹣2,2] B.(﹣∞,﹣2) C.(2,+∞) D.(﹣2,+∞)考点:交集及其运算.专题:计算题;不等式的解法及应用;集合.分析:求出M中二次不等式的解集确定出M,求出N中对数不等式的解集确定出N,再求出两集合的交集即可.解答:解:由于M={x|x2>4}={x|x>2或x<﹣2},N={x|log2x≥1}={x|l og2x≥log22}={x|x≥2},则M∩N={x|x>2}.故选C.点评:此题考查了交集及其运算,同时考查二次不等式和对数不等式的解法,熟练掌握交集的定义是解本题的关键.2.若复数z满足(3﹣4i)z=|4+3i|,则z的虚部为()A.﹣4 B. C. 4 D.考点:复数代数形式的乘除运算;复数求模.专题:数系的扩充和复数.分析:由题意可得 z==,再利用两个复数代数形式的乘除法法则化简为+i,由此可得z的虚部.解答:解:∵复数z满足(3﹣4i)z=|4+3i|,∴z====+i,故z的虚部等于,故选:D.点评:本题主要考查复数的基本概念,两个复数代数形式的乘除法法则的应用,属于基础题.3.执行如图所示的程序框图,当输出值为4时,输入x的值为()A. 2 B.±2 C.﹣2或﹣3 D. 2或﹣3考点:程序框图.专题:算法和程序框图.分析:根据程序框图,得到x的可能取值,逐个判断是否满足条件即可得到答案.解答:解:当输出值为4时,由程序框图知x的取值为﹣3或2或﹣2,x=﹣3,x≥1不成立,执行y=1﹣x=4,正确.x=2,x≥1成立,执行y=x2=4,正确.x=﹣2,x≥1不成立,执行y=1﹣x=3,不正确.故选:D.点评:本题主要考察程序框图和算法,属于基础题.4.实数x,y满足,则z=x﹣y的最大值是()A.﹣1 B. 0 C. 3 D. 4考点:简单线性规划.专题:不等式的解法及应用.分析:作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求z的最大值.解答:解:作出不等式对应的平面区域,设z=x﹣y,得y=x﹣z,平移直线y=x﹣z,由图象可知当直线y=x﹣z经过点B(3,0)时,直线y=x﹣z的截距最小,此时z最大.此时z的最大值为z=3﹣0=3,故选:C.点评:本题主要考查线性规划的应用,利用数形结合是解决线性规划题目的常用方法.5.二项式(+)10展开式中的常数项是()A. 180 B. 90 C. 45 D. 360考点:二项式定理的应用.专题:二项式定理.分析:在二项展开式的通项公式中,令x的幂指数等于0,求出r的值,即可求得常数项.解答:解:二项式(+)10展开式的通项公式为 T r+1=•2r•,令5﹣=0,求得 r=2,可得展开式中的常数项是•22=180,故选:A.点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于基础题.6.已知某个三棱锥的三视图如图所示,其中正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形,则此三棱锥的体积等于()A. B. C. D.考点:由三视图求面积、体积.专题:计算题.分析:由三视图知几何体是一个侧面与底面垂直的三棱锥,底面是斜边上的高是1的直角三角形,则两条直角边是,斜边是2与底面垂直的侧面是一个边长为2的正三角形,求出面积.解答:解:由三视图知几何体是一个侧面与底面垂直的三棱锥,底面是斜边上的高是1的直角三角形,则两条直角边是,斜边是2,∴底面的面积是=1,与底面垂直的侧面是一个边长为2的正三角形,∴三棱锥的高是,∴三棱锥的体积是故选B.点评:本题考查由三视图还原几何体,本题解题的关键是求出几何体中各个部分的长度,特别注意本题所给的长度1,这是底面三角形斜边的高度.7.已知双曲线的离心率为,则双曲线的渐近线方程为()A.y=±2x B. C. D.考点:双曲线的简单性质.专题:计算题.分析:由离心率的值,可设,则得,可得的值,进而得到渐近线方程.解答:解:∵,故可设,则得,∴渐近线方程为,故选C.点评:本题考查双曲线的标准方程,以及双曲线的简单性质的应用,求出的值是解题的关键.8.等比数列{a n}的前n项和为S n,若S3+3S2=0,则公比q=()A.﹣2 B. 2 C. 3 D.﹣3考点:等比数列的前n项和.专题:等差数列与等比数列.分析:首先根据等比数列的前n项和公式建立等量关系,解方程求的结果.解答:解:根据等比数列的前n项和公式:S n=∵S3+3S2=0∴+3=0(1﹣q)(q2+4q+4)=0解得:q=﹣2,q=1(舍去)故选:A点评:本题考查的知识点:等比数列的前n项和公式及相关的运算问题.9.有10件不同的电子产品,其中有2件产品运行不稳定.技术人员对它们进行一一测试,直到2件不稳定的产品全部找出后测试结束,则恰好3次就结束测试的方法种数是() A. 16 B. 24 C. 32 D. 48考点:排列、组合及简单计数问题.专题:计算题.分析:根据题意,分析可得若恰好3次就结束测试,必有前2次测试中测出1件次品,第3次测出第2件次品,先分析第3次测出次品情况数目,再分析前2次测试,即一次正品、1次次品的情况数目,由分步计数原理,计算可得答案.解答:解:根据题意,若恰好3次就结束测试,则前2次测试中测出1件次品,第3次测出第2件次品,第3次测试的是次品,而共有2件次品,则有C21=2种情况,前2次测试,即一次正品、1次次品,有C81×A22=16种情况,则恰好3次就结束测试共有2×16=32种情况,故选C.点评:本题考查排列、组合的应用,涉及分步计数原理的应用,易错点是对“恰好3次就结束测试”的理解.10.已知函数f(x)=,若对于任意x∈R,不等式f(x)≤﹣t+1恒成立,则实数t的取值范围是()A.(﹣∞,1]∪[2,+∞) B.(﹣∞,1]∪[3,+∞) C. [1,3] D.(﹣∞,2]∪[3,+∞)考点:函数恒成立问题.专题:函数的性质及应用.分析:这是一个不等式恒成立问题,只需即可,再求分段函数的最大值,解出关于t的不等式即为所求.解答:解:对于f(x),当x≤1时,y=﹣在(﹣∞,]递增,在(]上递减,故此时y max=f()=;当x>1时,y=log0.5x是减函数,此时y<log0.51=0,;综上原函数的最大值为,故不等式f(x)≤﹣t+1恒成立,只需﹣t+1即可,解得t≤1或t≥3.故选B.点评:本题考查了不等式恒成立的问题、分段函数的最值的求法等问题,一般是把不等式恒成立问题转化为函数的最值问题来解.11.点A,B,C,D均在同一球面上,且AB、AC、AD两两垂直,且AB=1,AC=2,AD=3,则该球的表面积为()A.7π B.14π C. D.考点:球的体积和表面积.专题:计算题;空间位置关系与距离.分析:三棱锥A﹣BCD的三条侧棱两两互相垂直,所以把它扩展为长方体,它也外接于球,对角线的长为球的直径,然后解答即可.解答:解:三棱锥A﹣BCD的三条侧棱两两互相垂直,所以把它扩展为长方体,它也外接于球,对角线的长为球的直径,d==,它的外接球半径是外接球的表面积是4π()2=14π故选:B.点评:本题考查球的表面积,考查学生空间想象能力,是基础题.12.已知函数y=f(x)是定义在R上的偶函数,对于任意x∈R都f(x+6)=f(x)+f(3)成立;当x1,x2∈[0,3],且x1≠x2时,都有>0.给出下列四个命题:①f(3)=0;②直线x=﹣6是函数y=f(x)图象的一条对称轴;③函数y=f(x)在[﹣9,﹣6]上为增函数;④函数y=f(x)在[0,2014]上有335个零点.其中正确命题的个数为()A. 1 B. 2 C. 3 D. 4考点:命题的真假判断与应用.专题:综合题;函数的性质及应用.分析:①在f(x+6)=f (x)+f (3)中,令x=﹣3,可得f(﹣3)=0,f(x)是R上的偶函数,从而可判断①;②由(1)知f(x+6)=f (x),所以f(x)的周期为6,再利用f(x)是R上的偶函数,可得f(﹣6﹣x)=f(﹣6+x),从而可判断②;③依题意知,函数y=f(x)在[0,3]上为增函数,利用f(x)的周期为6,且f(x)是R 上的偶函数,可判断函数y=f(x)在[﹣9,﹣6]上为减函数,从而可判断③;④由题意可知,y=f(x)在[0,6]上只有一个零点3,而2014=335×6+3,从而可判断④.解答:解:①:对于任意x∈R,都有f(x+6)=f (x)+f (3)成立,令x=﹣3,则f(﹣3+6)=f(﹣3)+f (3),即f(﹣3)=0,又因为f(x)是R上的偶函数,所以f(3)=0,即①正确;②:由(1)知f(x+6)=f (x),所以f(x)的周期为6,又因为f(x)是R上的偶函数,所以f(x+6)=f(﹣x),而f(x)的周期为6,所以f(x+6)=f(﹣6+x),f(﹣x)=f(﹣x﹣6),所以:f(﹣6﹣x)=f(﹣6+x),所以直线x=﹣6是函数y=f(x)的图象的一条对称轴,即②正确;③:当x1,x2∈[0,3],且x1≠x2时,都有>0,所以函数y=f(x)在[0,3]上为增函数,因为f(x)是R上的偶函数,所以函数y=f(x)在[﹣3,0]上为减函数而f(x)的周期为6,所以函数y=f(x)在[﹣9,﹣6]上为减函数,故③错误;④:f(3)=0,f(x)的周期为6,函数y=f(x)在[0,3]上为增函数,在[3,6]上为减函数,所以:y=f(x)在[0,6]上只有一个零点3,而2014=335×6+3,所以,函数y=f(x)在[0,2014]上有335+1=336个零点,故④错误.故正确命题的个数为2个,故选:B.点评:本题考查命题的真假判断与应用,着重考查函数的奇偶性、周期性、对称性及零点的确定的综合应用,属于难题.二、填空题(5×4=20分,把答案填在答题纸的相应位置上)13.已知⊥,||=2,||=3,且+2与λ﹣垂直,则实数λ的值为.考点:数量积判断两个平面向量的垂直关系.专题:平面向量及应用.分析:由已知得(+2)•(λ﹣)==4λ﹣18=0,由此能求出实数λ的值.解答:解:∵⊥,||=2,||=3,且+2与λ﹣垂直,∴(+2)•(λ﹣)==4λ﹣18=0,解得.故答案为:.点评:本题考查实数值的求法,是基础题,解题时要注意向量垂直的性质的合理运用.14.如图,矩形OABC内的阴影部分由曲线f(x)=sinx及直线x=a(a∈(0,2π)与x轴围成.向矩形OABC内随机掷一点,该点落在阴影部分的概率为,则a= π.考点:几何概型.专题:概率与统计.分析:根据几何概型的概率公式,以及利用积分求出阴影部分的面积即可得到结论.解答:解:根据题意,阴影部分的面积为==1﹣cosa,矩形的面积为,则由几何概型的概率公式可得,即cosa=﹣1,又a∈(0,2π),∴a=π,故答案为:π点评:本题主要考查几何概型的概率的计算,根据积分的几何意义求出阴影部分的面积是解决本题的关键.15.曲线在点M(,0)处的切线的斜率为.考点:利用导数研究曲线上某点切线方程.专题:导数的概念及应用.分析:先求出导函数,然后根据导数的几何意义求出函数f(x)在x=处的导数,从而求出切线的斜率.解答:解:∵∴y'==y'|x==|x==故答案为:.点评:本题主要考查了导数的几何意义,以及导数的计算,同时考查了计算能力,属于基础题.16.数列{a n}的前n项和记为S n,a1=1,a n+1=2S n+1(n≥1),则{a n}的通项公式为a n=3n﹣1.考点:数列的函数特性.专题:等差数列与等比数列.分析:当n≥2时,a n+1=2S n+1(n≥1),a n=2S n﹣1+1,两式相减可得a n+1=3a n.利用等比数列的通项公式即可得出.解答:解:当n≥2时,a n+1=2S n+1(n≥1),a n=2S n﹣1+1,∴a n+1﹣a n=2a n,∴a n+1=3a n.当n=1时,a2=2a1+1=3.∴数列{a n}为等比数列.∴a n=3n﹣1.故答案为:3n﹣1.点评:本题考查了递推式的意义、等比数列的通项公式,属于基础题.三、解答题(本大题6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.在△ABC中,角A,B,C的对边分别是a,b,c,其面积为S,且b2+c2﹣a2=S.(1)求A;(2)若a=5,cosB=,求c.考点:余弦定理.专题:解三角形.分析:(1)已知等式利用余弦定理及三角形面积公式化简,整理求出tanA的值,即可确定出A的度数;(2)由cosB的值求出sinB的值,进而求出sinC的值,由a,sinA,sinC的值,利用正弦定理即可求出c的值.解答:解:(1)∵b2+c2﹣a2=2bccosA,S=bcsinA,∴代入已知等式得:2bcosA=•bcsinA,整理得:tanA=,∵A是三角形内角,∴A=60°;(2)∵B为三角形内角,cosB=,∴sinB==,∴sinC=sin(B+A)=sin(B+60°)=sinB+cosB=,∵a=5,sinA=,sinC=,∴由正弦定理得:c==3+4.点评:此题考查了正弦、余弦定理,以及三角形面积公式,熟练掌握定理及公式是解本题的关键.18.如图五面体中,四边形CBB1C1为矩形,B1C1⊥平面ABB1N,四边形ABB1N为梯形,且AB⊥BB1,BC=AB=AN==4.(1)求证:BN⊥平面C1B1N;(2)求此五面体的体积.考点:棱柱、棱锥、棱台的体积;直线与平面垂直的判定.专题:空间位置关系与距离.分析:(1)利用直线与平面垂直的性质定理证明B1C1⊥BN,然后利用勾股定理证明BN⊥B1N,通过B1N∩B1C1=B1,利用直线与平面垂直的判定定理证明:BN⊥平面C1B1N;(2)连接CN,说明NM⊥平面B1C1CB,然后五面体的体积分别求解即可.解答:解:(1)证明:连4,过N作NM⊥B B1,垂足为M,∵B1C1⊥平面ABB1N,BN⊂平面ABB1N,∴B1C1⊥BN,…(2分)又,BC=4,AB=4,BM=AN=4,BA⊥AN,∴,=,∵,∴BN⊥B1N,…(4分)∵B1C1⊂平面B1C1N,B1N⊂平面B1C1N,B1N∩B1C1=B1∴BN⊥平面C1B1N…(6分)(2)连接CN,,…(8分)又B1C1⊥平面ABB1N,所以平面CBB1C1⊥平面ABB1N,且平面CBB1C1∩ABB1N=BB1,NM⊥BB1,NM⊂平面B1C1CB,∴NM⊥平面B1C1CB,…(9分)…(11分)此几何体的体积…(12分)点评:本题考查直线与平面垂直的判定定理以及性质定理的应用,几何体的体积的求法,考查转化思想以及空间想象能力.19.为迎接高一新生报到,学校向高三甲、乙、丙、丁四个实验班征召志愿者.统计如下:班级甲乙丙丁志愿者人数45 60 30 15为了更进一步了解志愿者的来源,采用分层抽样的方法从上述四个班的志愿者中随机抽取50名参加问卷调查.(1)从参加问卷调查的50名志愿者中随机抽取两名,求这两名来自同一个班级的概率;(2)在参加问卷调查的50名志愿者中,从来自甲、丙两个班级的志愿者中随机抽取两名,用X表示抽得甲班志愿者的人数,求X的分布列和数学期望.考点:离散型随机变量及其分布列;离散型随机变量的期望与方差.专题:概率与统计.分析:(1)由已知得问卷调查中,从四个班级中抽取的人数分别为15,20,10,5,从参加问卷调查的50名志愿者中随机抽取两名的取法共有种,这两名志愿者来自同一班级的取法共有+++,由此能求出这两名来自同一个班级的概率.(2)由(1)知,在参加问卷调查的50名志愿者中,来自甲、丙两班的人员人数分别为15,10.X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和数学期望.解答:解:(1)由已知得问卷调查中,从四个班级中抽取的人数分别为15,20,10,5…(2分)从参加问卷调查的50名志愿者中随机抽取两名的取法共有种,这两名志愿者来自同一班级的取法共有+++=350.…(5分)∴.…(6分)(2)由(1)知,在参加问卷调查的50名志愿者中,来自甲、丙两班的人员人数分别为15,10.X的可能取值为0,1,2,…(8分)P(X=0)=,,.∴X的分布列为:X 0 1 2P…(11分)EX=0×=1.2.…(12分)点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型.20.已知椭圆C的中心在原点,焦点在x轴上,左右焦点分别为F1,F2,且|F1F2|=2,点(1,)在椭圆C上.(1)求椭圆C的方程;(2)过F1的直线l与椭圆C相交于A,B两点,且△AF2B的面积为,求直线l的方程.考点:直线与圆锥曲线的关系;椭圆的标准方程.专题:圆锥曲线的定义、性质与方程.分析:(1)由题意可设椭圆的标准方程,并求出椭圆两个焦点的坐标,又点(1,)在椭圆C上,利用椭圆定义可求出长轴长,从而求出椭圆C的方程;(2)为避免讨论可设过F1的直线l的方程为x=ty﹣1,和椭圆方程联立后化为关于y的一元二次方程,利用根与系数的关系求出直线和椭圆两个交点纵坐标的和与积,△AF2B的面积就是=,由此求出t的值,则直线l的方程可求.解答:解:(1)由题意可设椭圆C的方程为(a>b>0),由|F1F2|=2得c=1,∴F1(﹣1,0),F2(1,0),又点(1,)在椭圆C上,∴,a=2.则b2=a2﹣c2=4﹣1=3.∴椭圆C的方程为;(2)如图,设直线l的方程为x=ty﹣1,A(x1,y1),B(x2,y2),把x=ty﹣1代入,得:(3t2+4)y2﹣6ty﹣9=0,∴==,∴,解得:(舍)或t2=1,t=±1.故所求直线方程为:x±y+1=0.点评:本题考查了利用定义求椭圆的标准方程,考查了直线与圆锥曲线的位置关系,采用了设而不求的数学方法,该题把直线l的方程设为x=ty﹣1,避免了讨论直线斜率存在和不存在的情况,此题属中档题.21.已知函数在点(﹣1,f(﹣1))的切线方程为x+y+3=0.(Ⅰ)求函数f(x)的解析式;(Ⅱ)设g(x)=lnx,求证:g(x)≥f(x)在x∈[1,+∞)上恒成立.考点:利用导数研究曲线上某点切线方程;函数恒成立问题.专题:计算题.分析:(I)首先求出f(1)的值,进而得出b﹣a=﹣4,然后求出函数的导数,求出f'(﹣1)==﹣1,就可以求出a、b的值,得出函数的解析式;(II)将不等式整理得出(x2+1)lnx≥2x﹣2,问题转化成x2lnx+lnx﹣2x+2≥0在[1,+∞)上恒成立,然后设h(x)=x2lnx+lnx﹣2x+2,并求出h'(x),得出x≥1时h'(x)≥0,可知h(x)在[1,+∞)上单调递增,从而求出h(x)的最小值,得出结果.解答:解:(Ⅰ)将x=﹣1代入切线方程得y=﹣2∴,化简得b﹣a=﹣4.…(2分).…(4分)解得:a=2,b=﹣2∴.…(6分)(Ⅱ)由已知得在[1,+∞)上恒成立化简得(x2+1)lnx≥2x﹣2即x2lnx+lnx﹣2x+2≥0在[1,+∞)上恒成立.…(8分)设h(x)=x2lnx+lnx﹣2x+2,∵x≥1∴,即h'(x)≥0.…(10分)∴h(x)在[1,+∞)上单调递增,h(x)≥h(1)=0∴g(x)≥f(x)在x∈[1,+∞)上恒成立.…(12分)点评:本题考查了利用导数研究某点的切线方程以及函数恒成立问题,关于函数恒成立问题一般转化成求函数的最值问题,属于中档题.四、解答题(共1小题,满分8分)22.已知直线L的参数方程:(t为参数)和圆C的极坐标方程:ρ=2sin(θ+)(θ为参数).(1)求圆C的直角坐标方程.(2)判断直线L和圆C的位置关系.考点:直线的参数方程;简单曲线的极坐标方程.专题:计算题;直线与圆;坐标系和参数方程.分析:(1)运用代入法,即可得到直线的普通方程,运用x=ρcosθ,y=ρsinθ,x2+y2=ρ2,即可化极坐标方程为直角坐标方程;(2)求出圆心到直线的距离你,再由d,r的大小,即可判断直线和圆的位置关系.解答:解:(1)消去参数t,得直线l的方程为y=2x+1;ρ=2sin(θ+),即ρ=2(sin θ+cos θ),两边同乘以ρ得ρ2=2(ρsin θ+ρcos θ),消去参数θ,得⊙C的直角坐标方程为:(x﹣1)2+(y﹣1)2=2;(2)由于圆心C(1,1)到直线l的距离,d==<r=,所以直线l和⊙C相交.点评:本题考查参数方程、极坐标方程与普通方程或直角坐标方程的互化,考查直线和圆的位置关系,属于基础题.五、解答题(共1小题,满分10分)【选修4-5:不等式选讲】23.已知函数f(x)=|x﹣2|﹣|x﹣5|(Ⅰ)证明:﹣3≤f(x)≤3;(Ⅱ)求不等式f(x)≥x2﹣8x+15的解集.考点:绝对值不等式的解法.专题:计算题;压轴题;分类讨论.分析:(Ⅰ)分x≤2、2<x<5、x≥5,化简f(x)=,然后即可证明﹣3≤f(x)≤3(Ⅱ)由(Ⅰ)可知当x≤2时,当2<x<5时,当x≥5时,分别求出f(x)≥x2﹣8x+15的解集.解答:解:(Ⅰ)f(x)=|x﹣2|﹣|x﹣5|=当2<x<5时,﹣3<2x﹣7<3,所以,﹣3≤f(x)≤3(Ⅱ)由(Ⅰ)可知当x≤2时,f(x)≥x2﹣8x+15的解集为空集;当2<x<5时,f(x)≥x2﹣8x+15的解集为{x|5﹣≤x<5}当x≥5时,f(x)≥x2﹣8x+15的解集为{x|5≤x≤6}综上:不等式f(x)≥x2﹣8x+15的解集:{x|5﹣≤x≤6}点评:本题是中档题,考查绝对值不等式的求法,考查分类讨论思想的应用,考查计算能力,常考题型.。
青海省西宁市第四高级中学2018-2019学年高一上学期月考数学试题Word版含答案

西宁市第四高级中学2018-19学年高一年级第一学期月考试卷数学 试卷一、选择题(本大题共12小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 设集合{}{}51,2A x x B x x =-≤<=≤,则A B ⋂等于( ) A .{}51x x -≤< B .{}52x x -≤≤ C .{}1x x < D .{}2x x ≤2.17cos 4π⎛⎫- ⎪⎝⎭的值是( ) A .12 B.2 C.2D.2 3.如果幂函数f (x )=x α的图象经过点(4,21),则f (8)的值等于( ) A.22 B.24 C.2 D.224.若sin θcos θ>0,则θ在 ( )A.第一、二象限 B.第二、四象限C.第一、三象限 D.第一、四象限5.设f(x)=3x +3x -8,用二分法求方程3x +3x -8=0在x ∈(1,2)内近似解的过程中,计算得到f(1)<0,f(1.5)>0,f(1.25)<0,则方程的根落在区间( )A .(1, 1.25)B .(1.25, 1.5)C .(1.5, 2)D .不能确定 6.函数1lg 4)(--=x x x f 的定义域是( ) A .),4[+∞ B .),10(+∞ C . ),10()10,4(+∞⋃ D .),10()10,4[+∞⋃7.下列角的终边位于第二象限的是( )A.420°B.860°C.1060°D.1260°8.已知函数()f x 是定义域为R 的奇函数,当0>x 时,1)(+-=x x f ,则)4(-f 等于A .5B .3C .3-D . 5-9.已知(8,6)P -是角终边上一点,则ααcos sin 2+ 的值等于( ) A10. 设函数()⎩⎨⎧>-=0,02x x x x f ,若()4=a f ,则实数a=( )A .-4或-2B .-2或4C . -4或2D .-2或211.设12log 3a =,0.21()3b =,132c =,则 A.a b c << B.c b a << C.c a b << D.b a c <<12.偶函数f(x)在(-∞,0)上单调递增,若f(-1)=0,则不等式f(x)<0的解集是( ).A .(-∞,-1)∪(0,1)B .(-∞,-1)∪(1,+∞)C .(-1,0)∪(0,1)D .(-1,0)∪(1,+∞)第II 卷二、填空题(本大题共4小题,每小题5分,共20分,将答案填在答题卷相应位置上)13. 已知()112-=+x x f ,则()=4f ________.14.已知扇形的圆心角为,弧长为,则该扇形的面积为 _________ 15.函数()()log 2301a y x a a =-+>≠且恒过定点为 _________16.若函数f(x)=|2x -2|-b 有两个零点,则实数b 的取值范围是____三、解答题(本大题共6小题,满分70分。
青海省西宁市第四高级中学高一数学下学期第一次月考试题

西宁市第四高级中学14—15学年第二学期第一次月考试卷高 一 数 学一、 选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1. 已知等比数列}{n a 的公比为正数,且25932a a a =,22=a ,则=q ( )A .21B .22 C .2D .2.已知{}n a 为等差数列,若π=++951a a a ,则28cos()a a +的值为( )A .21-B .23-C .21D .233. 自然数按照下表的规律排列,则上起第2013行,左起第2014列的数为( )A.320142013+⨯B.220142013+⨯C.120142013+⨯D.20142013⨯4.设等差数列{}n a 的前项和为n S ,若94=a ,116=a ,则9S 等于( )A. 180B. 90C. 72D.1005.S n =1-2+3-4+5-6+…+(-1)n+1·n ,则S 100+S 200+S 301=( ) A 1B -1C 51D 526.已知数列{}()*1101113n na a n N a a ==+∈=n+1中,,且,则a ( ) A .28B .33C .133 D .128 7.已知ABC ∆的内角C B A ,,的对边分别为c b a ,,且CB Aa cbc sin sin sin +=--,则B =( ) A.6π B.4π C.3π D.43π8.在ABC ∆中,内角C B A ,,所对的边分别是c b a ,,若3,6)(22π=+-=C b a c ,则ABC ∆的面积是( )A .3 B.239 C. 233 D .3 9.已知△ABC 的三边长6,5,3===c b a ,则△A BC 的面积为 ( )A 14B 142C 15D 15210.△ABC 的三内角A 、B 、C 的对边边长分别为a 、b 、c.若a =52b ,A =2B ,则cosB 等于( ) A.53 B.54 C.55 D.5611.在△ABC 中,A 、B 、C 的对边分别为a 、b 、c ,a∶b∶c=3∶3∶5,则2sinA -sinBsinC等于… ( )A .-15B .-23 C.35 D .不是常数12.在△ABC 中,AB =3,AC =2,BC =10,则AB →·AC →等于( )A .-32B .-23 C.23 D.32二.填空题:(本大题共4小题,每小题5分,共20分)13.在等比数列{a n }中, 若a 1,a 10是方程3x 2-2x -6=0的两根,则a 4·a 7= 。
青海省西宁市高一上学期数学第一次月考试卷
青海省西宁市高一上学期数学第一次月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分) (2019高一上·延安期中) 已知集合S={a,b,c,}中的三个元素可构成 ABC的三条边长,那么ABC一定不是()A . 锐角三角形B . 直角三角形C . 钝角三角形D . 等腰三角形2. (2分)(2020·攀枝花模拟) 已知全集为,集合,,则元素个数为()A . 1B . 2C . 3D . 43. (2分)若集合,,则等于()A .B .C .D .4. (2分) (2019高一上·永安月考) 已知集合,若,则集合A的子集个数为()A . 4B . 3C . 2D . 15. (2分)设集合A={a,b},B={0,1},则从A到B的映射共有()A . 2个B . 3个C . 4个D . 5个6. (2分) (2019高一上·通榆月考) 下列函数中,是同一函数的是()A . 与B . 与C . 与D . 与7. (2分) (2016高一下·浦东期末) 下列四个函数中,以π为最小正周期,且在区间(,π)上为减函数的是()A . y=cos2xB . y=2|sinx|C .D . y=﹣cotx8. (2分) (2019高一下·扶余期末) 若,则的大小关系为()A .B .C .D .9. (2分)若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是()A . m<a<b<nB . a<m<n<bC . a<m<b<nD . m<a<n<b10. (2分) (2016高一上·辽宁期中) 已知f(x)是一次函数,且3f(1)﹣2f(2)=﹣5,2f(0)﹣f(﹣1)=1,则f(x)的解析式为()A . f(x)=3x﹣2B . f(x)=3x+2C . f(x)=2x+3D . f(x)=2x﹣311. (2分) (2017高一上·葫芦岛期末) 函数f(x)= 的图象大致是()A .B .C .D .12. (2分)对于函数f(x)=-2x2+k,当实数k属于下列选项中的哪一个区间时,才能确保一定存在实数对a,b(a<b<0),使得当函数f(x)的定义域为[a,b]时,其值域也恰好是[a,b]A . [-2,0)B .C .D .二、填空题 (共4题;共4分)13. (1分) (2019高三上·上海期中) 方程的解是________14. (1分) (2016高一上·荆州期中) 已知函数f(x)=4x2﹣kx﹣8在(5,20)上既无最大值也无最小值,则实数k的取值范围是________.15. (1分)已知集合A={a,,1},B={a2 , a+b,0},若A⊆B且B⊆A,则a=________,b=________16. (1分) (2018高一上·新乡期中) 已知函数.若总是存在实数a,b.使得,则b的取值范围为________。
青海省西宁市第四高级中学2015届高三上学期第一次月考数学(理)试题
青海省西宁市第四高级中学2015届高三上学期第一次月考数学(理)试题考试时间:120分钟一、选择题(5×12=60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集为R ,集合}1log {},4{22≥=>=x x N x x M ,则=N MA .[-2,2]B .)2,(--∞C .),2(+∞D .),2(+∞-2.若复数z 满足(34)43i z i -=+,则z 的虚部为A .45-B .45C .4-D .4 3.执行如图所示的程序框图,当输出值为4时,输入x 的值为A .2B .2±C .-2或-3D .2或-3 4.实数y x ,满足⎪⎩⎪⎨⎧≤≥-+≤-+1033032y y x y x ,则y x z -=的最大值是A .-1B .0C .3D .45.二项式102)2(x x +展开式中的常数项是 A .180 B .90 C .45 D .360 6.三棱锥的三视图如图,正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形,则此三棱锥的体积为AC7.已知双曲线)0,0(12222>>=-b a by a x 的离心率为26,则此双曲线的渐近线方程为 A .x 2y ±= B .x y 2±= C .x y 22±= D .x y 21±= 8.等比数列}{n a 的前n 项和为n S ,若0323=+S S ,则公比q = A .-2 B .2 C .3 D .-39.有10件不同的电子产品,其中有2件产品运行不稳定。
技术人员对它们进行一一测试,直到2件不稳定的产品全部找出后测试结束,则恰好3次就结束测试的方法种数是A. 16B. 24C. 32D. 48侧视图 正视图 俯视图10.已知函数⎩⎨⎧>≤+-=1,log 1,)(5.02x x x x x x f , 若对于任意R x ∈,不等式14)(2+-≤t t x f 恒成立, 则实数t 的取值范围是A. (][)+∞∞-,21,B. (][)+∞∞-,31,C.[]3,1D. (][)+∞∞-,32,11.点D C B A ,,,均在同一球面上,且AB 、AC 、AD 两两垂直,且,1=AB ,2=AC 3=AD ,则该球的表面积为A .π7B .π14C .27π D .3147π 12.已知函数)(x f y =是定义在R 上的偶函数,对于任意R x ∈都)3()()6(f x f x f +=+成立;当]3,0[,21∈x x ,且21x x ≠时,都有0)()(2121>--x x x f x f .给出下列四个命题:①0)3(=f ;②直线6-=x 是函数)(x f y =图象的一条对称轴;③函数)(x f y =在]6,9[--上为增函数;④函数)(x f y =在]2014,0[上有335个零点.其中正确命题的个数为A .1B .2C .3D .4二、填空题(5×4=20分,把答案填在答题纸的相应位置上)13. 已知b a ⊥,2=a ,3=b ,且b a 2+与b a -λ垂直,则实数λ的值为 .14.如图,矩形OABC 内的阴影部分由曲线()x x f sin =及直线()],0(π∈=a a x 与x 轴围成的区域,向矩形OABC 内随机掷一点,该点落在阴影部分的概率为21,则=a .15处的切线的斜率为 . 16. 数列}{n a 的前n 项和记为n S ,11=a ,)1(121≥+=+n S a n n ,则}{n a 的通项公式为 .三、解答题(本大题6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.在ABC ∆中,角A ,B ,C 的对边分别是a ,b ,c ,其面积为S ,且S a c b 334222=-+. (1)求A ; (2)若35=a ,54cos =B ,求c .18.如图五面体中,四边形11C CBB 为矩形,N ABB C B 111平面⊥,四边形N ABB 1为梯形,且1BB AB ⊥,4211====BB AN AB BC . (1)求证:BN 11C B N ⊥平面;(2)求此五面体的体积.19.为迎接高一新生报到,学校向高三甲、乙、丙、丁四个实验班征召志愿者.统计如下:为了更进一步了解志愿者的,采用分层抽样的方法从上述四个班的志愿者中随机抽取50名参加问卷调查.(1)从参加问卷调查的50名志愿者中随机抽取两名,求这两名自同一个班级的概率;(2)在参加问卷调查的50名志愿者中,从自甲、丙两个班级的志愿者中随机抽取两名,用X 表示抽得甲班志愿者的人数,求X 的分布列和数学期望.20.已知椭圆C 的中心在原点,焦点在x 轴上,左右焦点分别为12,F F ,且12||2F F =,点(1,23)在椭圆C 上. (1)求椭圆C 的方程;(2)过1F 的直线l 与椭圆C 相交于,A B 两点,且2AF B ∆l 的方程.21.已知函数2()1ax b f x x -=+在点(1,(1))f 的切线方程为10x y --=. (1)求函数()f x 的解析式;(2)设x x g ln )(=,求证:)()(x f x g ≥在),1[+∞∈x 上恒成立.请考生在第22、23题中任选一题做答,如果多做,则按所做的第一题记分.22.《选修4-4:坐标系与参数方程》已知直线L 的参数方程:⎩⎨⎧ x =t ,y =1+2t ,(t 为参数)和圆C 的极坐标方程:ρ=22sin(θ+π4)(θ为参数). (1)求圆C 的直角坐标方程.(2)判断直线L 和圆C 的位置关系.23.《选修4-5:不等式选讲》 已知函数52)(---=x x x f .(1)证明:3)(3≤≤-x f ; (2)求不等式158)(2+-≥x x x f 的解集.M B 1C 1NC B A西宁市第四高级中学2015届高三数学答案(理科)三、解答题:17. (本小题满分12分)解:(1)由已知得:A bc A bc sin 21334cos 2⋅= ………4分 3tan =∴A ………5分由A 是内角,∴ 060=A ………6分(2)由54cos =B 得53in =B s ………7分 ∴10343c 23sin 21)3(si inC +=+=+=osB B B n s π………10分 由正弦定理得:343sin sin +==AC a c ………12分 18 .(本小题满分12分) 解:(1)证明:连BN ,过N 作1BB NM ⊥,垂足为M ,∵N ABB C B 111平面⊥,N ABB BN 1平面⊂,∴BN C B ⊥11, ………………………2分又,BC=4,AB=4,BM=AN=4,AN BA ⊥, ∴ 244422=+=BN ,22212144+=+=M B NM N B =24,∵643232,64822121=+=+==BN N B BB ,∴N B BN 1⊥,……………… 4分 ∵N C B N B N C B C B 1111111,平面平面⊂⊂,1111B C B N B =⋂∴BN 11C B N ⊥平面 ……………………… 6分(2)连接CN ,332442143131=⨯⨯⨯⨯=⋅⨯=∆-ABN ABN C S BC V ,…… 8分 又N ABB C B 111平面⊥,所以平面⊥11C CBB 平面N ABB 1,且平面11C CBB 11BB N ABB =,1BB NM ⊥,CB C B NM 11平面⊂,∴ CB C B NM 11平面⊥, ………9分312884431311111=⨯⨯⨯=⋅⨯=-CB C B CB C B N S NM V 矩形 ………11分 此几何体的体积3160312833211=+=+=--CB C B N ABN C V V V …12分 19. (本小题满分12分)解:(1)由已知得问卷调查中,从四个班级中抽取的人数分别为15,20,10,5…2分 从参加问卷调查的50名志愿者中随机抽取两名的取法共有2501225C =种,这两名志愿者自同一班级的取法共有215C +220C +210C +25C =350. ………5分 ∴721225350p ==. ………6分 (2)由(1)知,在参加问卷调查的50名志愿者中,自甲、丙两班的人员人数分别为15,10. X 的可能取值为0,1,2, ………8分==)0(X P 203225210=C C , 21)1(225110115===C C C X P , 207)2(225215===C C X P .………11分 ………12分22.(本小题满分10分)选修4-4:坐标系与参数方程(1)消去参数t,得直线l的方程为y=2x+1;ρ=22sin(θ+π4 ),即ρ=2(sin θ+cos θ),两边同乘以ρ得ρ2=2(ρsin θ+ρcos θ),消去参数θ,得⊙C的直角坐标方程为:(x-1)2+(y-1)2=2.(2)圆心C到直线l的距离d=|2-1+1|22+12=255<2,所以直线l和⊙C相交.(1)(x-1)2+(y-1)2=2 (2)相交23、(本小题满分10分)选修4-5:不等式选讲解:(1)3,2,()|2||5|27,25,3, 5.x f x x x x x x -≤⎧⎪=---=-<<⎨⎪≥⎩当25,327 3.x x <<-<-<时 所以3() 3.f x -≤≤ ………………5分(2)由(I )可知,当22,()815x f x x x ≤≥-+时的解集为空集;当225,()815{|55}x f x x x x x <<≥-+-≤<时的解集为;当25,()815{|56}x f x x x x x ≥≥-+≤≤时的解集为.综上,不等式2()815{|56}.f x x x x x ≥-+≤≤的解集为…………10分。
青海省高一上学期数学第一次月考试卷
青海省高一上学期数学第一次月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共11题;共22分)1. (2分) (2020高一上·开鲁期中) 把分解因式为()A .B .C .D .2. (2分) (2016高一下·厦门期中) 如图,矩形OABC′是水平放置的一个平面图形的直观图,其中OA′=6,OC′=2,则原图形OABC的面积为()A . 24B . 12C . 48D . 203. (2分) (2019高一上·双流月考) 若关于的不等式的解集为,其中,为常数,则不等式的解集是()A .C .D .4. (2分) (2018高三上·鹤岗月考) 函数的零点所在的区间为()A .B .C .D .5. (2分)如果函数对于任意实数t,都有,那么()A .B .C .D .6. (2分)已知集合,则()A . {0,x,1,2}B . {2,0,1,2}C . {0,1,2}D . 不能确定7. (2分)(2017·黑龙江模拟) 若集合A={x|1≤3x≤81},B={x|log2(x2﹣x)>1},则A∩B=()A . (2,4]C . (﹣∞,0)∪[0,4]D . (﹣∞,﹣1)∪[0,4]8. (2分) (2016高三上·石家庄期中) 已知集合A⊆{1,2,3,4,5},且A∩{1,2,3}={1,2},则满足条件的集合A的个数是()A . 2B . 4C . 8D . 169. (2分)已知U为全集,A,B,I都是U的子集,且,则=()A . {且}B . {或}C . {且}D . {或}10. (2分) (2020高一上·沧县月考) 已知全集,集合 ,,集合,则()A .B .C .D .11. (2分) (2019高一上·上海月考) 设集合,,,则()A .B .C .D .二、多选题 (共1题;共3分)12. (3分) (2020高一上·汕头月考) 若是方程的两个根,则下列式子正确的是()A .B .C .D .三、填空题 (共4题;共4分)13. (1分) (2019高一上·鸡泽月考) 设集合,且,则实数的取值范围是________.14. (1分) (2017高二上·集宁月考) 已知锐角三角形的三边长分别为 ,则的取值范围为________.15. (1分) (2019高一上·杭州期中) 已知,则实数的值是________.16. (1分) A={x|x2﹣5x+6=0},B={x|mx=1},若B⊆A,则实数m=________.四、解答题 (共6题;共50分)17. (5分) (2019高二下·吉林期末) 已知,,且是的充分条件,求实数a的取值范围.18. (10分) (2020高三上·怀宁月考) 设关于 x 的函数 f(x)=lg(x2﹣2x﹣3)的定义域为集合 A,函数 g(x)=x﹣a,(0≤x≤4)的值域为集合 B.(1)求集合 A,B;(2)若集合 A,B 满足A∩B=B,求实数 a 的取值范围.19. (5分) (2018高二上·齐齐哈尔期中) 2017年10月18日至10月24日,中国共产党第十九次全国代表大会简称党的“十九大” 在北京召开一段时间后,某单位就“十九大”精神的领会程度随机抽取100名员工进行问卷调查,调查问卷共有20个问题,每个问题5分,调查结束后,发现这100名员工的成绩都在内,按成绩分成5组:第1组,第2组,第3组,第4组,第5组,绘制成如图所示的频率分布直方图,已知甲、乙、丙分别在第3,4,5组,现在用分层抽样的方法在第3,4,5组共选取6人对“十九大”精神作深入学习.(1)求这100人的平均得分同一组数据用该区间的中点值作代表;(2)求第3,4,5组分别选取的作深入学习的人数;(3)若甲、乙、丙都被选取对“十九大”精神作深入学习,之后要从这6人随机选取2人再全面考查他们对“十九大”精神的领会程度,求甲、乙、丙这3人至多有一人被选取的概率.20. (5分) (2016高一上·蕲春期中) 某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.(1)当每辆车的月租金定为3600元时,能租出多少辆车?(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?21. (10分) (2019高二上·兰州期中) 设数列前项和为 , 满足.(1)求数列的通项公式;(2)令求数列的前项和;(3)若不等式对任意的恒成立,求实数的取值范围.22. (15分) (2020高一上·玉溪月考) 如图,圆的直径与弦相交于点,若,求圆的半径长.参考答案一、单选题 (共11题;共22分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:二、多选题 (共1题;共3分)答案:12-1、考点:解析:三、填空题 (共4题;共4分)答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:四、解答题 (共6题;共50分)答案:17-1、考点:解析:答案:18-1、答案:18-2、考点:解析:答案:19-1、答案:19-2、答案:19-3、考点:解析:答案:20-1、答案:20-2、考点:解析:答案:21-1、答案:21-2、答案:21-3、考点:解析:答案:22-1、考点:解析:。
青海省2021年高一上学期数学第一次月考试卷A卷(新版)
青海省2021年高一上学期数学第一次月考试卷A卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)如图,阴影部分表示的集合是()A .B .C .D .2. (2分) (2019高一上·拉萨期中) 考察下列每组对象,能组成一个集合的是()①某高中高一年级聪明的学生②直角坐标系中横、纵坐标相等的点③不小于3的正整数④ 的近似值.A .B .C .D .3. (2分)A . 2x-5B . -2x-1C . -1D . 5-2x4. (2分) (2017高一上·和平期中) 设函数,t=f(2)﹣6,则f(t)的值为()A . ﹣3B . 3C . ﹣4D . 45. (2分) (2019高一上·扬州月考) 已知函数,,则函数的最大值为()A .B .C .D . 16. (2分)函数的定义域是()A .B .C .D .7. (2分) (2016高一上·成都期中) 若函数y=f(x)为奇函数,则它的图象必经过点()A . (﹣a,﹣f(a))B . (0,0)C . (a,f(﹣a))D . (﹣a,﹣f(﹣a))8. (2分)已知a =ln,b=sin,c=,则a,b,c的大小关系为()A . a < b < cB . a <c <bC . b <a<cD . b <c < a9. (2分) (2016高一上·嘉峪关期中) 幂函数f(x)的图象过点,则f(8)=()A . 8B . 6C . 4D . 210. (2分)如图,长方形的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记BOP=x,将动点P到A,B两点距离之和表示为x的函数f(x),则图像大致为()A .B .C .D .11. (2分) (2020高一上·玉溪月考) 在平面直角坐标系中直线与反比例函数的图象有唯一公共点,若直线与反比例函数的图象有个公共点,则m的取值范围是()A .B .C .D . 或12. (2分)二次函数f(x)=ax2+bx+c(a>0)的图象与x轴交点的横坐标为﹣5和3,则这个二次函数的单调减区间为()A . (﹣∞,﹣1]B . [2,+∞)C . (﹣∞,2]D . [﹣1,+∞)二、填空题 (共4题;共4分)13. (1分) (2019高一上·大荔月考) ________.14. (1分) (2016高一上·运城期中) 若,则a,b,c大小关系是________(请用”<”号连接).15. (1分) (2019高二下·宁波期中) 已知函数是上的偶函数,其相邻对称轴之间的距离为,则 ________; ________.16. (1分) (2016高一上·南京期中) 函数y= 的值域为________三、解答题 (共6题;共60分)17. (10分) (2020高一上·苍南月考) 已知全集,集合或.(1)求;(2)求18. (10分) (2020高一下·邯郸期中) 已知函数.(1)若函数在上是单调函数,求实数a的取值范围;(2)当,时,不等式恒成立,求实数m的范围.19. (10分) (2019高一上·天津月考) 若集合,,且,求m的值20. (15分) (2019高一上·漯河月考) 已知定义域为R的函数是奇函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西宁市第四高级中学2017-18学年第一学期第一次月考试卷
高 一 数 学
一、选择题(本大题共12小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
)
1. 如果集合{}
1->=x x P ,那么 ( )
A .P ⊆0
B .{}P ∈0
C .P ∈∅
D .{}P ⊆0 2. 若全集{}{}0,1,2,32U U C A ==且,则集合A 的真子集共有( ) A . 3个 B .5个 C . 7个 D . 8个
3. 已知集合{}|1A x x =≤,{}
a x x B >=,且R B A =U ,则实数a 的取值范围是 A .()1,∞- B .(]1,∞- C .()∞,1 D .[)+∞,1
4. 已知函数f (x )的定义域为[a ,b ],函数y =f (x )的图象如图甲所示,则函数f (|x |)的图象是图乙中的( )
甲
乙
5. 下列各组函数中是同一函数的是 ( )
A .0
()()1f x x
g x == B .x x x g x x f ⋅==)(,)(2
C .1(0)||(),()(0)
x t f x g t x x t <⎧==⎨->⎩
D .()()2
,t t g x x f ==
6. 下列函数中, 既是奇函数又是增函数的为( )
A .y=x|x|
B .y= - x
C . y=
1
x
D . y=x+1 7. 已知M ={x|y =x 2
+1},N ={y|y =x 2
+1},则)(N C M R ⋂=( )
甲
A .∅
B .M
C .)1,(-∞
D .R
8.下列各图中,不可能是函数f(x)图象的是 ( ) 9. 设函数()⎩⎨
⎧>≤-=0
,0
,2
x x x x x f ,若()4=a f ,则实数a=( ) A .-4或-2 B .-4或2 C .-2或4 D .-2或2
10. 函数f (x )=ax 2
-x +a +1在 (-∞,2)上单调递减,则a 的取值范围是( )
A .[0,4]
B .[2,+∞)
C .[0,14]
D .(0,1
4]
11.函数1)(2++=
mx mx x f 的定义域为R ,则实数m 的取值范围是( )
A . [0,4]
B .[ 0,4)
C .[4,+∞)
D .(0,4)
12.设定义在R 上的奇函数f(x)满足,对任意12,x x ∈(0,+∞),且12x x ≠都有
0)()(1212<--x x x f x f ,且f(2)=0,则不等式x
x f x f 5)
(2)(3--≤0的解集为( )
A .(-∞,-2]∪(0,2]
B .[-2,0]∪[2,+∞)
C .(-∞,-2]∪[2,+∞)
D .[-2,0)∪(0,2]
第II 卷
二、填空题(本大题共4小题,每小题5分,共20分,将答案填在答题卷相应位置上)
13. 若函数()1,(0)
()(2),0x x f x f x x +≥⎧=⎨+<⎩
,则)3(-f =________
14. 已知()112
-=+x x f ,则()=x f ________.
15. 若函数y =(x +1)(x -a )为偶函数,则a 等于_______________
C A
D
B
16. 函数234y x x =--的增区间是 。
三、解答题(本大题共6小题,满分70分。
解答须写出文字说明、证明过程和演算步骤) 17.(本小题满分10分)判断下列函数的奇偶性:
(1)1
22)(2++=x x x x f (2)x x x f 2)(3
-=
18.(本小题满分12分) 设
{}{}25,121A x x B x m x m =-≤≤=+≤≤-,若A B B ⋂=,求实数m 的
取值范围
19.(本小题满分12分)
已知全集R U =,集合{}
0,,3≠∈-==x R x x y y A 且,集合B 是函数1
11++-=x x y 的定义域 (Ⅰ)求集合A 和B (结果用区间表示)
(Ⅱ)求()B C A U ⋂
20.(本小题满分12分) 已知函数y=2
x -ax-3 (55≤≤
-x )
(1)若a=2,求函数的最大、最小值
(2)若函数在定义域内是单调函数,求a 取值的范围
21.(本小题满分12分)
若函数()f x 为奇函数,当0x ≥时,
2()24f x x x =-(如图).
(1)求函数()f x 的表达式,并补齐函数()f x 的图象 (2)用定义证明:函数()y f x =在区间[)1,+∞上单调递增
22.(本小题满分12分)
若函数)(x f y =对于一切实数y x ,,都有)()()(y f x f y x f +=+, (1)求)0(f 并证明)(x f y =是奇函数 (2)若3)1(=f ,求)3(-f。
