数学物理方程1 电子科技大学李明奇

数学物理方程_谷超豪_第二章答案

数学物理方程谷超豪第二章答案1. 引言本文档是《数学物理方程》一书中第二章的答案。

该章节主要涵盖了偏微分方程的分类和解法。

在本文中，我们将解答课后习题和深入讨论相关概念，以帮助读者更好地理解和应用这些知识。

2. 偏微分方程的分类在第二章中，我们学习了偏微分方程的分类方法。

根据方程中未知函数的阶数和自变量的个数，偏微分方程可以分为以下几类：1.一阶偏微分方程：只涉及一阶导数的方程，如线性一阶波动方程和拟线性一阶方程等。

2.二阶偏微分方程：涉及二阶导数的方程，如线性二阶波动方程和拉普拉斯方程等。

3.高阶偏微分方程：涉及高阶导数的方程，如线性高阶波动方程和椭圆方程等。

根据自变量的个数，偏微分方程还可以分为以下两类：1.单自变量偏微分方程：只含有一个自变量的方程，如一维波动方程和一维热传导方程。

2.多自变量偏微分方程：含有多个自变量的方程，如二维波动方程和三维热传导方程。

3. 课后习题答案3.1 第一题题目：求解一维波动方程 $\\frac{\\partial^2 u}{\\partial t^2} = c^2 \\frac{\\partial^2 u}{\\partial x^2}$，其中c为常数。

解答：我们可以使用分离变量法求解这个一维波动方程。

首先，假设c=c(c)c(c)，代入原方程得到：$$\\frac{T''(t)}{c^2T(t)} = \\frac{X''(x)}{X(x)}$$两边同时等于一个常数 $-\\lambda^2$，即：$$\\begin{cases} T''(t) + \\lambda^2 c^2 T(t) = 0 \\\\ X''(x) + \\lambda^2 X(x) = 0 \\end{cases}$$解这个常微分方程得到：$$\\begin{cases} T(t) = A\\cos(\\lambda c t) +B\\sin(\\lambda c t) \\\\ X(x) = C\\cos(\\lambda x) +D\\sin(\\lambda x) \\end{cases}$$其中c,c,c,c都是常数。

第1章复数与复变函数数学物理方程

z平面
ω 平面
复变函数w =f(z)可以写成w =u(x,y)+iv(x,y)，其中z=x+iy
All Rights Reserved by CDUT.
复变函数论
第1章复数与复变函数

几类基本初等函数幂函数
n为正整数
z n n (cos i sin ) n n (cosn i sin n ) n e in
z1
z2 p
区域D连同它的边界一起构成闭区域，记为 D
All Rights Reserved by CDUT.
复变函数论
第1章复数与复变函数
定义5：单连通域与多连通域
若在区域D内作任意闭合曲线，曲线所包围的所有点都属于D，那么D称为单连通区域，否则，D称为复连通区域。规定：若观察者沿边界线走时，区域总保持在观察者的左边，那么观察者的走向为边界线的正向；反之，则称为边界线的负向。
两个复数相乘等于它们的模相乘，幅角相加
All Rights Reserved by CDUT.
复变函数论
第1章复数与复变函数
z1 x1 x2 y1 y2 x1 y2 x2 y1 i 2 2 2 2 z2 x2 y 2 x2 y 2 r1 cos(1 2 ) i sin(1 2 ) r2 r1 exp[i(1 2 )] r2
指数函数 e z e x cos y i sin y
e z e x , Arg e z y
z x iy
性质
周期性
y 0时, e z e x ; x 0时, eiy cosy isiny
exp(z i2 ) exp(z)

电子科技大学2011年研究生数学物理方程期末试题

电子科技大学研究生试卷（考试时间：至，共 2小时）课程名称数理方程与特殊函数教师学时60 学分 3 教学方式闭卷考核日期 2011年 12 月 28 日成绩考核方式：（学生填写）1．化方程2220xx xy yy x y x u xyu y u xu yu ++++=为标准形. (10分)2. 把定解问题：(10分)212(0)(0,)(),(,)()(,0)(),(,0)(),(0)tt xx x x t u a u x l u t h t u l t h t u x x u x x x l ϕψ⎧=<<⎪==⎨⎪==<<⎩的非齐次边界条件化为齐次边界条件.第 1页学号姓名学院教师座位号……………………密……………封……………线……………以……………内……………答……………题……………无……………效……………………3．有一带状的均匀薄板(0x a ≤≤,0y ≤<+∞), 边界0y =上的温度为0u ，其余边界上的温度保持零度，并且当y →+∞时，温度极限为零. 求解板的稳定温度分布. (用分离变量法求解).(20分)4．求下面的定解问题：（10分）090,(,0)0,sin tt xx t t t u u x R t u u x ==-=∈>⎧⎪⎨==⎪⎩.第2页5．求()21,1(),()0,1x x F f x f x x ⎧-≤⎪=⎨>⎪⎩，其中()F ⋅表示Fourior 变换.（10分）6．求()2(),()sin(),03L f t f t t t π=-≥，其中()L ⋅为Laplace 变换.（10分）第3页学号姓名学院教师座位号……………………密……………封……………线……………以……………内……………答……………题……………无……………效……………………7．写出球形域的Dirichlets 问题对应的Green 函数及其定解问题.（10分）8．证明：()10d()()d xJ x xJ x x=.（10分）9．（1）写出Legendre 方程和Legendre 多项式；（2）将函数()23,1f x x x =+≤用Legendre 多项式展开.（10分）第4页。

数学物理方程第一章典型方程和定解条件

x
sin ' tan ' u(x dx,t)
x
则
T T'
u
M'
ds
T'
'
M
gds
T
x
x dx x
T
u(
x dx, x
t)
u ( x, x
t
)
gds
ma
T
u(x dx,t) x
u ( x, x
t)
gds
ma
m ds
其中：
a 2u(x,t) t 2
ds dx
T
u(x dx,t) x
微小：振幅极小，张力与水平方向的夹角很小。
u
M'
ds
T'
'
M
gds
T
x
x dx x
牛顿运动定律：
横向：T cos T 'cos ' 0
纵向：T sin T 'sin ' gds ma 其中： cos 1 2 4 1
2! 4!
cos ' 1
sin tan u(x,t)
数学物理方程与特殊函数
☆ 数学与物理的关系
数理不分家
☆ 数学物理方程：用数学方程来描述一定的物理现象
数学物理方程（简称数理方程）是指自然科学和工程技术的各门分支学科中出现的一些偏微分方程(有时也包括积分方程、微分方程等)，它们反映了物理量关于时间的导数和关于空间变量的导数之间的制约关系。例如声学、流体力学、电磁学、量子力学等等方面的基本方程都属于数学物理方程的研究对象。
• 如图，取杆长方向为x轴方向，垂直于杆长方向的各截面均用平行位置x标记；在任一时刻t，此截面相对于平衡位置的位移为u( x, t )

电子科大2013-2014-1学期清水河校区课程表

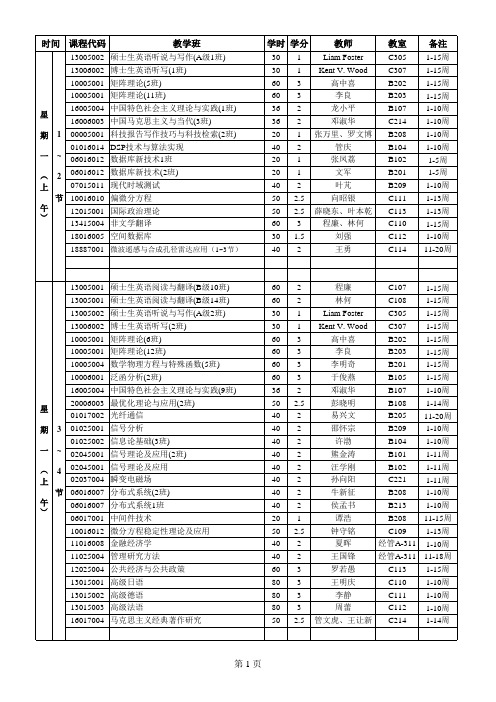
教室
C107 C108 C305 C307 B203 B208 B209 B107 B103 B204 B205 B104 B202 B213 B201
备注
1-15周 1-15周 1-15周 1-15周 1-15周 1-15周 1-15周 1-10周 1-15周 2-12周 1-11周 1-11周 1-10周 1-10周
08015001 有限元分析与建模方法星期一 7 ~ 8 节午） 10026016 非线性分析 11026006 经济理论 12415001 中外新闻传播史 13015004 语言学通论 16036002 中外政治思想史专题研究 18016001 遥感物理 19887001 学科前沿知识专题讲座（理工科）
教室
C305 C307 B202 B203 B107 C214 B208 B104 B102 B201 B209 C111 C113 C110 C112 C114
备注
1-15周 1-15周 1-15周 1-15周 1-10周 1-10周 1-10周 1-10周 1-5周 1-5周 1-10周 1-13周 1-13周 1-15周 1-10周 11-20周
（上
节 06016007 分布式系统(2班) 午 06016007 分布式系统1班） 06017001 中间件技术 10016012 微分方程稳定性理论及应用 11016008 金融经济学 11025004 管理研究方法 12025004 公共经济与公共政策 13015001 高级日语 13015002 高级德语 13015003 高级法语 16017004 马克思主义经典著作研究
60 60 30 30 60 60 60 60 36 50 40 40 40 40 40 40 40 40 20 50 40 40 60 80 80 80 50

数学物理方程(很好的学习教材)

方法：比较是分类的前提和基础，分类是比较的深化和结果
数学物理方程(很好的学习教材)
二、数学物理方程的一般分类
一般分类按自变量的个数，分为二元和多元方程；按未知函数及其导数的幂次，分为线性微分方程和非线性微分方程；按方程中未知函数导数的最高阶数，分为一阶、二阶和高阶微分方程。
由能量守恒定律 c ρdx du=dQ =[q(x,t)-q(x+dx,t)]dt =-qx(x,t)dxdt
于是有 c ρut = -qx 由热传导定律 q(x,t) = -k ux(x,t) 代入前面的式子，得到 c ρut = k uxx ut = a2 uxx
a2 = k/(cρ)
数学物理方程(很好的学习教材)
四、常见数学物理方程的定解条件
波动方程
方程形u式 tt ： a2u f 定解条初件边始界条条件件：：包第含一位初第类移始二或 ”“ 类者和或初者始第“三速
输运方程
方程形u式 t a： 2uf 定解条边件初界始条条件件：：第物一第理类始二量或时类在者刻或初的者值第
三类线性边界条件
第一类边界条 u(x件 ,y,： z,t)边界x0,y0,z0 f(x0,y0,z0,t)
第二类边界条件： u n边界x0,y0,z0
f(x0,y0,z0,t)
第三类边界条 u件 H： u
n边界x0,y0,z0
f(x0,y0,z0,t)
初始条件
定解条件
边界条件
数学物理方程(很好的学习教材)
u u 2u u u 2
2
yy
y数学物理方程(很好y的学y习教材) y
yyu
yy
于是，方程化为：

2014年“高教社杯”全国大学生数学建模竞赛四川赛区四川省获奖名单

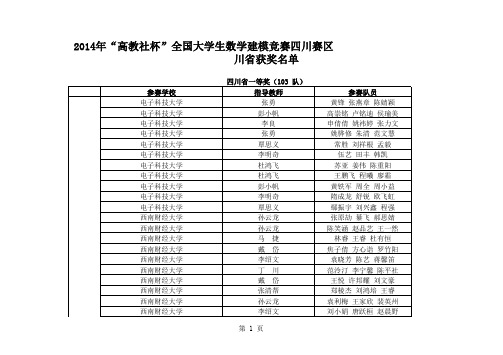
A题 64队
四川理工学院四川理工学院四川理工学院四川农业大学四川师范大学四川师范大学成都学院四川师范大学成都学院西华师范大学西南财经大学西南财经大学西南财经大学西南交通大学西南交通大学西南交通大学西南交通大学西南交通大学西南交通大学西南交通大学西南交通大学西南交通大学西南交通大学西南交通大学西南交通大学西南交通大学西南交通大学西南交通大学西南交通大学
西南交通大学西南交通大学西南交通大学西南交通大学峨眉校区西南交通大学峨眉校区西南交通大学峨眉校区西南交通大学峨眉校区西南交通大学峨眉校区西南交通大学峨眉校区西南交通大学峨眉校区西南交通大学希望学院西南科技大学西南民族大学西南民族大学西南石油大学西南石油大学电子科技大学电子科技大学电子科技大学电子科技大学电子科技大学电子科技大学电子科技大学四川理工学院四川师范大学四川师范大学
B题 30队
B题 30队
西南财经大学西南财经大学西南财经大学西南财经大学西南财经大学西南财经大学西南财经大学西南交通大学西南交通大学西南交通大学西南交通大学西南交通大学乐山职业技术学院四川工程职业技术学院四川建筑职业技术学院四川建筑职业技术学院四川水利职业技术学院四川职业技术学院四川职业技术学院西南石油大学成都纺织高等专科学校成都工业学院成都航空职业技术学院电子科技大学成都学院四川建筑职业技术学院
C题 8队
D题 9队
D题 9队四川交通职业技术学院四川水利职业技术学院四川文理学院四川文理学院指导教师组冷忠全数模组数模组四川省二等奖（118队）黄丽韩会磊郑茂波指导教师组指导教师组指导教师组吴建国程光辉杜鸿飞覃思义杜鸿飞李良李良张利凤张利凤张利凤刘好斌刘好斌牟廉明秦振涛马亮亮第 5 页李月姣高旭贾延元张凤宋远飞李佳美、陈强、郭孙渝何立、石鑫、张霞

数学物理方程数学物理第一章

偏分方程中所有最高阶偏导数都是线性的，而其系数
本课遇到一二阶线性偏微分方程的一般表达形式一阶线性偏微分方程的一般表达形式
u u a( x, y ) b( x, y ) c( x, y )u f ( x, y ) x y
二阶线性偏微分方程的一般表达形式
2u 2u 2u A( x, y ) 2 2 B( x, y ) C ( x, y ) 2 x xy y u u D( x, y ) E ( x, y ) F ( x, y )u G ( x, y ) 0 x y
在数学物理方程中，我们特别强调通过分析过程推测可能得到的结论！而对结论的严格论证则常给予略去。这种做法并不意味着可以取消综合过程，而是意味着分析过程从方法到结论都能给我们一些新的结论，而验证结论的正确性原则上没有什么困难。
正因为分析过程的任务在于探求新结论，而结论的确实成立与否还需另行证明，所以在分析过程的推理中，并不要求十分严格，特别的不要由于某些定理的条件限制而束缚自己的思路，这是本课程中应该注意的。
2
2u
二阶线性非齐次的
三阶非线性
2
3u x y
2
ln u 0
§2方程及定解问题的物理推导
2.1、弦振动方程 2.1.1、物理模型
设有长为 l一根拉紧的均匀柔软弦细，两端被固定在 O, A 两点，且在单位长度受上到垂直于 OA向上的力 F作用当它在平衡位置附近垂作直于 OA方向的微小横向振动
18世纪著名数学家、物理学家达朗贝尔（1717-1783欧拉（1707-1783））
弦振动的研究先驱