2017高考数学一轮复习第八章立体几何8.3平行的判定与性质课时练理
高考数学一轮复习 第八章 立体几何 8.4 直线、平面平行的判定与性质真题演练集训 理 新人教A版(

质真题演练集训理新人教A版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018版高考数学一轮复习第八章立体几何8.4 直线、平面平行的判定与性质真题演练集训理新人教A版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018版高考数学一轮复习第八章立体几何8.4 直线、平面平行的判定与性质真题演练集训理新人教A版的全部内容。
与性质真题演练集训理新人教A版1.[2016·山东卷节选]在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线.已知G,H分别为EC,FB的中点,求证:GH∥平面ABC.证明:设FC的中点为I,连接GI,HI,在△CEF中,因为点G是CE的中点,所以GI∥EF.又EF∥OB,所以GI∥OB.在△CFB中,因为H是FB的中点,所以HI∥BC。
又HI∩GI=I,OB∩BC=B,所以平面GHI∥平面ABC。
因为GH⊂平面GHI,所以GH∥平面ABC。
2.[2016·新课标全国卷Ⅲ节选]如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB =AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.证明:MN∥平面PAB。
证明:由已知得AM=错误!AD=2。
取BP的中点T,连接AT,TN。
由N为PC的中点知,TN∥BC,TN=错误!BC=2.又AD∥BC,故TN綊AM,四边形AMNT为平行四边形,于是MN∥AT.因为AT⊂平面PAB,MN⊄平面PAB,所以MN∥平面PAB。
3.[2015·江苏卷节选]如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.求证:DE∥平面AA1C1C。
高考数学一轮复习 第八章 立体几何8.4直线、平面平行的判定及其性质教学案 理 新人教A版

高考数学一轮复习第八章立体几何8.4直线、平面平行的判定及其性质教学案理新人教A版考纲要求1.以立体几何的定义、公理和定理为出发点,认识和理解空间中线面平行的有关性质与判定定理.2.能运用公理、定理和已获得的结论证明一些空间图形的平行关系的简单命题.1.直线和平面平行(1)定义:直线和平面没有公共点,则称直线平行于平面.(2)判定定理:如果平面外的一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.用符号表示为:________________.(3)性质定理:如果一条直线和一个平面平行,______________________________.用符号表示为:a∥α,a⊂β,α∩β=b⇒a∥b.2.两个平面平行(1)定义:两个平面没有公共点,称这两个平面平行.(2)判定定理:如果______________________________________,那么这两个平面平行.用符号表示:a⊂α,b⊂α,a∩b=M,a∥β,b∥β⇒α∥β.(3)性质定理:如果两平行平面同时和第三个平面相交,那么它们的交线平行.用符号表示为:__________________________.1.下列条件中,能判断两个平面平行的是( ).A.一个平面内的一条直线平行于另一个平面B.一个平面内的两条直线平行于另一个平面C.一个平面内有无数条直线平行于另一个平面D.一个平面内任何一条直线都平行于另一个平面2.若直线a平行于平面α,则下列结论错误的是( ).A.a平行于α内的所有直线B.α内有无数条直线与a平行C.直线a上的点到平面α的距离相等D.α内存在无数条直线与a垂直3.已知不重合的直线a,b和平面α,①若a∥α,b⊂α,则a∥b;②若a∥α,b∥α,则a∥b;③若a∥b,b⊂α,则a∥α;④若a∥b,a∥α,则b∥α或b⊂α,上面命题中正确的是__________(填序号).一、直线与平面平行的判定与性质【例1】如图所示,四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC 的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:AP∥GH.方法提炼1.判断或证明两直线平行的常用方法: (1)三角形中位线; (2)平行四边形; (3)分线段成比例;(4)利用公理4(a ∥b ,b ∥c ⇒a ∥c );(5)利用线面平行的性质定理(a ⊂α,a ∥β,α∩β=b ⇒a ∥b );(6)利用面面平行的性质定理(α∥β,γ∩α=a ,γ∩β=b ⇒a ∥b ); (7)利用线面垂直的性质定理(a ⊥α,b ⊥α⇒a ∥b ). 2.判断或证明线面平行的常用方法: (1)利用线面平行的定义(无公共点);(2)利用线面平行的判定定理(a α,b ⊂α,a ∥b ⇒a ∥α); (3)利用面面平行的性质定理(α∥β,a ⊂α⇒a ∥β);(4)利用面面平行的性质(α∥β,a α,a β,a ∥α⇒a ∥β). 请做演练巩固提升2二、平面与平面平行的判定与性质【例2-1】 如图,AB ,CD 是夹在两个平行平面α,β间的线段,且直线AB ,CD 是异面直线,M ,P 分别是AB ,CD 的中点.求证:直线MP ∥平面α.【例2-2】 (2012山东淄博模拟)如图,在三棱锥A BOC 中,AO ⊥平面COB ,∠OAB =∠OAC =π6,AB =AC =2,BC =2,D ,E 分别为AB ,OB 的中点.(1)求证:CO ⊥平面AOB ;(2)在线段CB 上是否存在一点F ,使得平面DEF ∥平面AOC ,若存在,试确定F 的位置,并证明此点满足要求;若不存在,请说明理由.方法提炼证明面面平行的方法: (1)面面平行的定义;(2)面面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行;(3)利用垂直于同一条直线的两个平面平行;(4)两个平面同时平行于第三个平面,那么这两个平面平行;(5)利用“线线平行”、“线面平行”、“面面平行”的相互转化.请做演练巩固提升3立体几何主观题的规范解答【典例】 (12分)(2012山东高考)如图,几何体EABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.(1)求证:BE=DE;(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.规范解答:(1)取BD的中点O,连接CO,EO.由于CB=CD,所以CO⊥BD.(2分)又EC⊥BD,EC∩CO=C,CO,EC⊂平面EOC,所以BD⊥平面EOC,(5分)因此BD⊥EO.又O为BD的中点,所以BE=DE.(6分)(2)证法一:取AB的中点N,连接DM,DN,MN.因为M是AE的中点,所以MN∥BE.又MN平面BEC,BE⊂平面BEC,所以MN∥平面BEC.(8分)又因为△ABD为正三角形,所以∠BDN=30°.又CB=CD,∠BCD=120°,因此∠CBD=30°,所以DN∥BC.又DN平面BEC,BC⊂平面BEC,所以DN∥平面BEC.(10分)又MN∩DN=N,故平面DMN∥平面BEC,又DM⊂平面DMN,所以DM∥平面BEC.(12分)证法二:延长AD,BC交于点F,连接EF.因为CB =CD ,∠BCD =120°,所以∠CBD =30°.(8分) 因为△ABD 为正三角形,所以∠BAD =60°,∠ABC =90°,因此∠AFB =30°,所以AB =12AF .(9分)又AB =AD ,所以D 为线段AF 的中点.(10分) 连接DM ,由点M 是线段AE 的中点, 因此DM ∥EF .又DM 平面BEC ,EF ⊂平面BEC , 所以DM ∥平面BEC .(12分)答题指导:从近几年的高考来看,对立体几何解答题的考查的难度逐步降低,一般以低中档题的形式考查,因此在备考时要高度关注基础知识,避免不必要的失分.以下几点还应注意:1.重视知识间的相互转化,如能熟练地将空间中的线线、线面、面面间的问题相互转化,以达到解决问题的目的;2.重视解题规范性的训练,强化解题步骤的完整性和严谨性,避免不必要的失分; 3.重视立体几何中通过构造模型解题的训练和计算能力的培养.1.对于平面α,β,γ和直线a ,b ,m ,n ,下列命题中是真命题的是( ). A .若a ⊥m ,a ⊥n ,m ⊂α,n ⊂α,则a ⊥α B .若a ∥b ,b ⊂α,则a ∥αC .若a ⊂β,b ⊂β,a ∥α,b ∥α,则β∥αD .若α∥β,α∩γ=a ,β∩γ=b ,则a ∥b2.(2012长沙模拟)已知m ,n 表示两条不同直线,α,β,γ表示不同平面,给出下列三个命题:(1)⎩⎪⎨⎪⎧ m ⊥αn ⊥α⇒m ∥n (2)⎩⎪⎨⎪⎧ m ⊥αm ⊥n ⇒n ∥α (3)⎩⎪⎨⎪⎧m ⊥αn ∥α⇒m ⊥n其中真命题的个数为( ).A .0B .1C .2D .3 3.(2012山东潍坊模拟)已知m ,n ,l 1,l 2表示直线,α,β表示平面.若m ⊂α,n ⊂α,l 1⊂β,l 2⊂β,l 1∩l 2=M ,则α∥β的一个充分条件是( ).A .m ∥β且l 1∥αB .m ∥β且n ∥βC .m ∥β且n ∥l 2D .m ∥l 1且n ∥l 24.如图,在正方体ABCD A 1B 1C 1D 1中,AB =2,点E 为AD 的中点,点F 在CD 上.若EF ∥平面AB 1C ,则线段EF 的长度等于________.5.如图,在直四棱柱ABCDA1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1,F分别为棱AD,AA1,AB的中点,求证:直线EE1∥平面FCC1.参考答案基础梳理自测知识梳理1.(2)a ⊄α,b ⊂α,a ∥b ⇒a ∥α (3)那么过这条直线的任一平面与此平面的交线与该直线平行2.(2)一个平面内的两条相交直线与另一个平面平行 (3)α∥β,α∩γ=a ,β∩γ=b ⇒a ∥b基础自测 1.D2.A 解析:A 错误,a 与α内的直线平行或异面.3.④ 解析:①中a 与b 可能异面;②中a 与b 可能相交、平行或异面;③中a 可能在平面α内,④正确. 考点探究突破【例1】 证明:如图所示,连接AC 交BD 于点O ,连接MO .∵四边形ABCD 是平行四边形. ∴O 是AC 的中点. 又M 是PC 的中点, ∴AP ∥OM .又AP ⊄平面BMD ,OM ⊂平面BMD , ∴AP ∥平面BMD .又AP ⊂平面PAHG ,平面PAHG ∩平面BMD =GH , ∴AP ∥GH .【例2-1】 证明:经过A ,C ,D 三点可确定一个平面γ,并且分别与平面β,平面α交于AC ,FD ,根据两个平面平行的性质,可知AC ∥DF .过A 作AE ∥CD ,交DF 于点E ,取AE 的中点N ,连接MN ,根据三角形中位线定理,MN ∥BE ,又NP ∥ED .根据平行平面判定定理,知平面MNP ∥平面α. 因为MP ⊂平面MNP , 所以直线MP ∥平面α.【例2-2】 解:(1)因为AO ⊥平面COB , 所以AO ⊥CO ,AO ⊥BO ,即△AOC 与△AOB 为直角三角形.又因为∠OAB =∠OAC =π6,AB =AC =2,所以OB =OC =1.由OB 2+OC 2=1+1=2=BC 2,可知△BOC 为直角三角形. 所以CO ⊥BO ,又因为AO ∩BO =O ,所以CO ⊥平面AOB .(2)在线段CB 上存在一点F ,使得平面DEF ∥平面AOC ,此时F 为线段CB 的中点. 证明过程:如图,连接DF ,EF ,因为D ,E 分别为AB ,OB 的中点,所以DE ∥OA .又DE ⊄平面AOC 上,所以DE ∥平面AOC . 因为E ,F 分别为OB ,BC 的中点, 所以EF ∥OC .又EF ⊄平面AOC ,所以EF ∥平面AOC ,又EF ∩DE =E ,EF ⊂平面DEF ,DE ⊂平面DEF , 所以平面DEF ∥平面AOC . 演练巩固提升1.D 解析:A 中只有当m 与n 相交时才有a ⊥α;B 中若a ⊂α,则结论不成立;C 中a 与b 平行时结论不成立;故D 正确.2.C 解析:若⎩⎪⎨⎪⎧m ⊥α,n ⊥α,则m ∥n ,即命题(1)正确;若⎩⎪⎨⎪⎧ m ⊥α,m ⊥n ,则n ∥α或n ⊂α,即命题(2)不正确; 若⎩⎪⎨⎪⎧m ⊥α,n ∥α,则m ⊥n ,即命题(3)正确;综上可得,真命题共有2个.3.D 解析:由定理“如果一个平面内有两条相交直线分别与另一个平面平行,那么这两个平面平行”可得,由选项D 可推知α∥β.4. 2 解析:由EF ∥平面AB 1C ,可知EF ∥AC .所以EF =12AC =12×22= 2.5.证明:方法一:取A 1B 1的中点为F 1,连接FF 1,C 1F 1,由于FF 1∥BB 1∥CC 1,所以F 1∈平面FCC 1,因此平面FCC 1即为平面C 1CFF 1.连接A 1D ,F 1C ,由于A 1F 1D 1C 1CD , 所以四边形A 1DCF 1为平行四边形, 因此A 1D ∥F 1C .又EE 1∥A 1D ,得EE 1∥F 1C ,而EE 1⊄平面FCC 1,F 1C ⊂平面FCC 1,故EE 1∥平面FCC 1. 方法二:因为F 为AB 的中点,CD =2,AB =4,AB ∥CD ,所以CD AF . 因此四边形AFCD 为平行四边形, 所以AD ∥FC .又CC 1∥DD 1,FC ∩CC 1=C ,FC ⊂平面FCC 1,CC 1⊂平面FCC 1, 所以平面ADD 1A 1∥平面FCC 1,又EE1 平面ADD1A1,所以EE1∥平面FCC1.。
新人教A版版高考数学一轮复习第八章立体几何直线平面平行的判定及性质教案理解析版

基础知识整合1.直线与平面平行(1)判定定理(2)性质定理2.平面与平面平行(1)判定定理(2)性质定理1.垂直于同一条直线的两个平面平行,即若a⊥α,a⊥β,则α∥β.2.垂直于同一个平面的两条直线平行,即若a⊥α,b⊥α,则a∥B.3.平行于同一个平面的两个平面平行,即若α∥β,β∥γ,则α∥γ.1.已知直线l和平面α,若l∥α,P∈α,则过点P且平行于l的直线()A.只有一条,不在平面α内B.只有一条,且在平面α内C.有无数条,一定在平面α内D.有无数条,不一定在平面α内答案B解析过直线外一点作该直线的平行线有且只有一条,因为点P在平面α内,所以这条直线也应该在平面α内.2.(2019·吉林普通中学模拟)已知α,β表示两个不同的平面,直线m是α内一条直线,则“α∥β ”是“m∥β ”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案A解析由α∥β,m⊂α,可得m∥β;反过来,由m∥β,m⊂α,不能推出α∥β.综上,“α∥β ”是“m∥β ”的充分不必要条件.3.若空间四边形ABCD的两条对角线AC,BD的长分别是8,12,过AB的中点E且平行于BD,AC 的截面四边形的周长为()A.10 B.20C.8 D.4答案B解析设截面四边形为EFGH,F,G,H分别是BC,CD,DA的中点,∴EF=GH=4,FG=HE=6.∴周长为2×(4+6)=20.4.如图所示,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出下列五个结论:1PD∥平面AMC;2OM∥平面PCD;3OM∥平面PDA;4OM∥平面PBA;5OM∥平面PBC.其中正确的个数是()A.1B.2C.3D.4答案C解析矩形ABCD的对角线AC与BD交于点O,所以O为BD的中点.在△PBD中,M是PB的中点,所以OM是△PBD的中位线,OM∥PD,则PD∥平面AMC,OM∥平面PCD,且OM∥平面PDA.因为M∈PB,所以OM与平面PBA,平面PBC相交.5.(2019·南通模拟)如图,四棱锥P—ABCD的底面是一直角梯形,AB∥CD,BA⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,则BE与平面PAD的位置关系为________.答案平行解析取PD的中点F,连接EF,AF,在△PCD中,EF綊错误!CD.又∵AB∥CD且CD=2AB,∴EF綊AB,∴四边形ABEF是平行四边形,∴EB∥AF.又∵EB⊄平面PAD,AF⊂平面PAD,∴BE∥平面PAD.6.如图所示,ABCD—A1B1C1D1是棱长为a的正方体,M,N分别是下底面的棱A1B1,B1C1的中点,P是上底面的棱AD上的一点,AP=错误!,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=________.答案错误!a解析如图所示,连接AC,易知MN∥平面ABCD.∴MN∥PQ.又∵MN∥AC,∴PQ∥AC.又∵AP=错误!,∴错误!=错误!=错误!=错误!.∴PQ=错误!AC=错误!×错误!a=错误!A.核心考向突破考向一有关平行关系的判断例1(1)(2019·湖南联考)已知m,n是两条不同的直线,α,β,γ是三个不同的平面,下列命题中正确的是()A.若m∥α,n∥α,则m∥nB.若m∥α,m∥β,则α∥βC.若α⊥γ,β⊥γ,则α∥βD.若m⊥α,n⊥α,则m∥n答案D解析A中,两直线可能平行、相交或异面;B中,两平面可能平行或相交;C中,两平面可能平行或相交;D中,由线面垂直的性质定理可知结论正确,故选D.(2)(2019·四川成都模拟)已知直线a,b和平面α,下列说法中正确的是()A.若a∥α,b⊂α,则a∥bB.若a⊥α,b⊂α,则a⊥bC.若a,b与α所成的角相等,则a∥bD.若a∥α,b∥α,则a∥b答案B解析对于A,若a∥α,b⊂α,则a∥b或a与b异面,故A错误;对于B,利用线面垂直的性质,可知若a⊥α,b⊂α,则a⊥b,故B正确;对于C,若a,b与α所成的角相等,则a与b相交、平行或异面,故C错误;对于D,由a∥α,b∥α,得a,b之间的位置关系可以是相交、平行或异面,故D错误.触类旁通解决有关线面平行、面面平行的基本问题的注意点(1)判定定理与性质定理中易忽视的条件,如线面平行的判定定理中,条件“线在面外”易忽视.(2)结合题意构造或绘制图形,结合图形作出判断.(3)举反例否定结论或用反证法推断命题是否正确.即时训练1.(2019·潍坊模拟)已知m,n,l1,l2表示直线,α,β表示平面.若m⊂α,n⊂α,l1⊂β,l2⊂β,l1∩l2=M,则α∥β的一个充分条件是()A.m∥β且l1∥α B.m∥β且n∥βC.m∥β且n∥l2D.m∥l1且n∥l2答案D解析由定理“如果一个平面内有两条相交直线分别与另一个平面平行,那么这两个平面平行”可得,由选项D可推知α∥β.故选D.2.已知m,n表示两条不同的直线,α表示平面,则下列说法正确的是()A.若m∥α,n∥α,则m∥nB.若m⊥α,n⊂α,则m⊥nC.若m⊥α,m⊥n,则n∥αD.若m∥α,m⊥n,则n⊥α答案B解析由题可知,若m∥α,n∥α,则m与n平行、相交或异面,所以A错误;若m⊥α,n⊂α,则m ⊥n,故B正确;若m⊥α,m⊥n,则n∥α或n⊂α,故C错误;若m∥α,m⊥n,则n∥α或n⊥α或n 与α相交,故D错误.考向二直线与平面平行的判定与性质角度错误!用线线平行证明线面平行例2(1)在四棱锥O—ABCD中,底面ABCD是平行四边形,M为OA的中点,N为BC的中点,证明:直线MN∥平面OCD.证明证法一:取OB的中点E,连接ME,NE,如图1,则ME∥AB,又AB∥CD,所以ME∥CD,又NE∥OC,且ME∩NE=E,OC∩CD=C,所以平面MNE∥平面OCD,所以MN∥平面OCD.证法二:取OD的中点F,连接MF,CF,如图2,则MF綊错误!AD,又底面ABCD是平行四边形,则NC綊错误!AD,所以MF綊NC,所以四边形MNCF是平行四边形,所以MN∥FC,又MN⊄平面OCD,FC⊂平面OCD,根据直线与平面平行的判定定理可知,直线MN∥平面OCD.(2)(2019·山东模拟)如图,在三棱台DEF—ABC中,AB=2DE,G,H分别为AC,BC的中点.求证:BD∥平面FGH.证明证法一:连接DG,CD,设CD∩GF=M,连接MH.在三棱台DEF—ABC中,AB=2DE,G为AC的中点,可得DF∥GC,DF=GC,所以四边形DFCG为平行四边形,则M为CD的中点,又H为BC的中点,所以HM∥BD.又HM⊂平面FGH,BD⊄平面FGH,所以BD∥平面FGH.证法二:在三棱台DEF—ABC中,由BC=2EF,H为BC的中点,可得BH∥EF,BH=EF,所以四边形HBEF为平行四边形,BE∥HF.在△ABC中,G为AC的中点,H为BC的中点,所以GH∥AB.又GH∩HF=H,所以平面FGH∥平面ABED.因为BD⊂平面ABED,所以BD∥平面FGH.角度错误!用线面平行证明线线平行例3如图,在多面体ABCDEF中,DE⊥平面ABCD,AD∥BC,平面BCEF∩平面ADEF=EF,∠BAD=60°,AB=2,DE=EF=1.(1)求证:BC∥EF;(2)求三棱锥B—DEF的体积.解(1)证明:∵AD∥BC,AD⊂平面ADEF,BC⊄平面ADEF,∴BC∥平面ADEF.又BC⊂平面BCEF,平面BCEF∩平面ADEF=EF,∴BC∥EF.(2)过点B作BH⊥AD于点H.∵DE⊥平面ABCD,BH⊂平面ABCD,∴DE⊥BH.∵AD⊂平面ADEF,DE⊂平面ADEF,AD∩DE=D,∴BH⊥平面ADEF.∴BH是三棱锥B—DEF的高.在Rt△ABH中,∠BAD=60°,AB=2,故BH=错误!.∵DE⊥平面ABCD,AD⊂平面ABCD,∴DE⊥AD.由(1)知BC∥EF,且AD∥BC,∴AD∥EF,∴DE⊥EF.∴三棱锥B—DEF的体积V=错误!×S△DEF×BH=错误!×错误!×1×1×错误!=错误!.触类旁通判断或证明线面平行的常用方法(1)利用线面平行的定义(无公共点).(2)利用线面平行的判定定理(a⊄α,b⊂α,a∥b⇒a∥α).错误!(4)利用面面平行的性质(α∥β,a⊄α,a⊄β,a∥α⇒a∥β).即时训练3.(2019·长春一调)如图所示,E是以AB为直径的半圆弧上异于A,B的点,矩形ABCD 所在平面垂直于该半圆所在的平面.(1)求证:EA⊥EC;(2)设平面ECD与半圆弧的另一个交点为F.求证:EF∥AB.证明(1)∵E是半圆上异于A,B的点,∴AE⊥EB.又∵平面ABCD⊥平面ABE,平面ABCD∩平面ABE=AB,CB⊥AB,∴CB⊥平面ABE.又∵AE⊂平面ABE,∴CB⊥AE.∵BC∩BE=B,∴AE⊥平面CBE.又∵EC⊂平面CBE.∴AE⊥EC.(2)∵CD∥AB,AB⊂平面ABE,CD⊄平面ABE,∴CD∥平面ABE.又∵平面CDE∩平面ABE=EF.∴CD∥EF.又∵CD∥AB.∴EF∥AB.考向三面面平行的判定与性质例4(2018·云南模拟)如图所示的几何体ABCDFE中,△ABC,△DFE都是等边三角形,且所在平面平行,四边形BCED是边长为2的正方形,且所在平面垂直于平面ABC.(1)求几何体ABCDFE的体积;(2)证明:平面ADE∥平面BCF.解(1)取BC的中点O,ED的中点G,连接AO,OF,FG,AG.∵AO⊥BC,AO⊂平面ABC,平面BCED⊥平面ABC,∴AO⊥平面BCED.同理FG⊥平面BCED.∵AO=FG=错误!,∴VABCDFE=错误!×4×错误!×2=错误!.(2)证明:由(1)知AO∥FG,AO=FG,∴四边形AOFG为平行四边形,∴AG∥OF,又∵DE∥BC,DE∩AG=G,DE⊂平面ADE,AG⊂平面ADE,FO∩BC=O,FO⊂平面BCF,BC⊂平面BCF,∴平面ADE∥平面BCF.触类旁通判定面面平行的方法(1)利用定义:即证两个平面没有公共点(不常用).错误!错误!4利用平面平行的传递性,即两个平面同时平行于第三个平面,则这两个平面平行客观题可用.即时训练4.如图,在四棱锥P—ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,PA=2,AB=1.设M,N分别为PD,AD的中点.(1)求证:平面CMN∥平面PAB;(2)求三棱锥P—ABM的体积.解(1)证明:∵M,N分别为PD,AD的中点,∴MN∥PA,又MN⊄平面PAB,PA⊂平面PAB,∴MN∥平面PAB.在Rt△ACD中,∠CAD=60°,CN=AN,∴∠ACN=60°.又∠BAC=60°,∴CN∥AB.∵CN⊄平面PAB,AB⊂平面PAB,∴CN∥平面PAB.又CN∩MN=N,∴平面CMN∥平面PAB.(2)由(1)知,平面CMN∥平面PAB,∴点M到平面PAB的距离等于点C到平面PAB的距离.∵AB=1,∠ABC=90°,∠BAC=60°,∴BC=错误!,∴三棱锥P—ABM的体积V=VM—PAB=VC—PAB=VP—ABC=错误!×错误!×1×错误!×2=错误!.。
(浙江专版)高考数学一轮复习 第八章 立体几何 8.3直线 平面平行的判定和性质学案-人教版高三全册

§8.3直线、平面平行的判定和性质考纲解读考点考纲内容要求浙江省五年高考统计2013 2014 2015 2016 2017平行的判定和性质1.理解以下判定定理:①如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.②如果一个平面内的两条相交直线与另一个平面都平行,那么这两个平面平行.2.理解以下性质定理,并能够证明:①如果一条直线与一个平面平行,经过该直线的任一个平面与此平面相交,那么这条直线就和交线平行.②如果两个平行平面同时和第三个平面相交,那么它们的交线相互平行.3.能证明一些空间位置关系的简单命题.理解18(1),6分4(文),5分4(文),5分2,5分2(文),5分19,约7分分析解读 1.平行关系是立体几何中的一种重要关系.判断命题及位置关系常以选择题、填空题形式出现.2.直线与平面、平面与平面平行的判定与性质是高考考查的重点和热点,常以棱锥、棱柱及不规则几何体为背景,以解答题的形式出现.3.预计2019年高考中,直线与平面、平面与平面平行的判定与性质的应用,证明线面、面面的平行关系,仍是高考的考查重点.五年高考考点平行的判定和性质1.(2017课标全国Ⅰ,6,5分)如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( )答案 A2.(2016课标全国Ⅱ,14,5分)α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有.(填写所有正确命题的编号)答案②③④3.(2017江苏,15,14分)如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.求证:(1)EF∥平面ABC;(2)AD⊥AC.证明(1)在平面ABD内,因为AB⊥AD,EF⊥AD,所以EF∥AB.又因为EF⊄平面ABC,AB⊂平面ABC,所以EF∥平面ABC.(2)因为平面ABD⊥平面BCD,平面A BD∩平面BCD=BD,BC⊂平面BCD,BC⊥BD,所以BC⊥平面ABD.因为AD⊂平面ABD,所以BC⊥AD.又AB⊥AD,BC∩AB=B,AB⊂平面ABC,BC⊂平面ABC,所以AD⊥平面ABC.又因为AC⊂平面ABC,所以AD⊥AC.4.(2016山东,17,12分)在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O'的直径,FB是圆台的一条母线.(1)已知G,H分别为EC,FB的中点.求证:GH∥平面ABC;(2)已知EF=FB=AC=2,AB=BC.求二面角F-BC-A的余弦值.解析(1)证明:设FC中点为I,连接GI,HI.在△CEF中,因为点G是CE的中点,所以GI∥EF.又EF∥OB,所以GI∥OB.在△CFB中,因为H是FB的中点,所以HI∥BC.又HI∩GI=I,所以平面GHI∥平面ABC.因为GH⊂平面GHI,所以GH∥平面ABC.(2)解法一:连接OO',则OO'⊥平面ABC.又AB=BC,且AC是圆O的直径,所以BO⊥AC.以O为坐标原点,建立如图所示的空间直角坐标系O-xyz.由题意得B(0,2,0),C(-2,0,0),所以=(-2,-2,0),过点F作FM垂直OB于点M.所以FM==3,可得F(0,,3).故=(0,-,3).设m=(x,y,z)是平面BCF的法向量.由可得可得平面BCF的一个法向量m=.因为平面ABC的一个法向量n=(0,0,1),所以cos<m,n>==.所以二面角F-BC-A的余弦值为.解法二:连接OO'.过点F作FM垂直OB于点M.则有FM∥OO'.又OO'⊥平面ABC,所以FM⊥平面ABC.可得FM==3.过点M作MN垂直BC于点N,连接FN.可得FN⊥BC,从而∠FNM为二面角F-BC-A的平面角.又AB=BC,AC是圆O的直径,所以MN=BMsin 45°=.从而FN=,可得cos∠FNM=.所以二面角F-BC-A的余弦值为.5.(2016江苏,16,14分)如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:(1)直线DE∥平面A1C1F;(2)平面B1DE⊥平面A1C1F.证明(1)在直三棱柱ABC-A1B1C1中,A1C1∥AC.在△ABC中,因为D,E分别为AB,BC的中点,所以DE∥AC,于是DE∥A1C1.又因为DE⊄平面A1C1F,A1C1⊂平面A1C1F,所以直线DE∥平面A1C1F.(2)在直三棱柱ABC-A1B1C1中,A1A⊥平面A1B1C1.因为A1C1⊂平面A1B1C1,所以A1A⊥A1C1.又因为A1C1⊥A1B1,A1A⊂平面ABB1A1,A1B1⊂平面ABB1A1,A1A∩A1B1=A1,所以A1C1⊥平面ABB1A1.因为B1D⊂平面ABB1A1,所以A1C1⊥B1D.又因为B1D⊥A1F,A1C1⊂平面A1C1F,A1F⊂平面A1C1F,A1C1∩A1F=A1,所以B1D⊥平面A1C1F.因为直线B1D⊂平面B1DE,所以平面B1DE⊥平面A1C1F.6.(2016四川,18,12分)如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=AD,E为棱AD的中点,异面直线PA与CD所成的角为90°.(1)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;(2)若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.解析(1)在梯形ABCD中,AB与CD不平行.延长AB,DC,相交于点M(M∈平面PAB),点M即为所求的一个点.理由如下:由已知,BC∥ED,且BC=ED.所以四边形BCDE是平行四边形.从而CM∥EB.又EB⊂平面PBE,CM⊄平面PBE,所以CM∥平面PBE.(说明:延长AP至点N,使得AP=PN,则所找的点可以是直线MN上任意一点) (2)解法一:由已知,CD⊥PA,CD⊥AD,PA∩AD=A,所以CD⊥平面PAD.从而CD⊥PD.所以∠PDA是二面角P-CD-A的平面角.所以∠PDA=45°.设BC=1,则在Rt△PAD中,PA=AD=2.过点A作AH⊥CE,交CE的延长线于点H,连接PH.易知PA⊥平面ABCD,又CE⊂平面ABCD,从而PA⊥CE.于是CE⊥平面PAH.所以平面PCE⊥平面PAH.过A作AQ⊥PH于Q,则AQ⊥平面PCE.所以∠APH是PA与平面PCE所成的角.在Rt△AEH中,∠AEH=45°,AE=1,所以AH=.在Rt△PAH中,PH==,所以sin∠APH==.解法二:由已知,CD⊥PA,CD⊥AD,PA∩AD=A,所以CD⊥平面PAD.于是CD⊥PD.从而∠PDA是二面角P-CD-A的平面角.所以∠PDA=45°.由PA⊥AB,可得PA⊥平面ABCD.设BC=1,则在Rt△PAD中,PA=AD=2.作Ay⊥AD,以A为原点,以,的方向分别为x轴,z轴的正方向,建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),P(0,0,2),C(2,1,0),E(1,0,0),所以=(1,0,-2),=(1,1,0),=(0,0,2).设平面PCE的法向量为n=(x,y,z),由得设x=2,则可得n=(2,-2,1).设直线PA与平面PCE所成角为α,则sin α===.所以直线PA与平面PCE所成角的正弦值为.7.(2015江苏,16,14分)如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.求证:(1)DE∥平面AA1C1C;(2)BC1⊥AB1.证明(1)由题意知,E为B1C的中点,又D为AB1的中点,因此DE∥AC.又因为DE⊄平面AA1C1C,AC⊂平面AA1C1C,所以DE∥平面AA1C1C.(2)因为棱柱ABC-A1B1C1是直三棱柱,所以CC1⊥平面ABC.因为AC⊂平面ABC,所以AC⊥CC1.又因为AC⊥BC,CC1⊂平面BCC1B1,BC⊂平面BCC1B1,BC∩CC1=C,所以AC⊥平面BCC1B1.又因为BC1⊂平面BCC1B1,所以BC1⊥AC.因为BC=CC1,所以矩形BCC1B1是正方形,因此BC1⊥B1C.因为AC,B1C⊂平面B1AC,AC∩B1C=C,所以BC1⊥平面B1AC.又因为AB1⊂平面B1AC,所以BC1⊥AB1.8.(2015安徽,19,13分)如图所示,在多面体A1B1D1DCBA中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F.(1)证明:EF∥B1C;(2)求二面角E-A1D-B1的余弦值.解析(1)证明:由正方形的性质可知A1B1∥AB∥DC,且A1B1=AB=DC,所以四边形A1B1CD为平行四边形,从而B1C∥A1D,又A1D⊂面A1DE,B1C⊄面A1DE,于是B1C∥面A1DE.又B1C⊂面B1CD1,面A1DE∩面B1CD1=EF,所以EF∥B1C.(2)因为四边形AA1B1B,ADD1A1,ABCD均为正方形,所以AA1⊥AB,AA1⊥AD,AB⊥AD且AA1=AB=AD,以A为原点,分别以,,为x轴,y轴和z轴单位正向量建立如图所示的空间直角坐标系,可得点的坐标A(0,0,0),B(1,0,0),D(0,1,0),A1(0,0,1),B1(1,0,1),D1(0,1,1),而E点为B1D1的中点,所以E点的坐标为(0.5,0.5,1).设面A1DE的法向量n1=(r1,s1,t1),而该面上向量=(0.5,0.5,0),=(0,1,-1),由n1⊥,n1⊥得r1,s1,t1应满足的方程组(-1,1,1)为其一组解,所以可取n1=(-1,1,1).设面A1B1CD的法向量n2=(r2,s2,t2),而该面上向量=(1,0,0),=(0,1,-1),由此同理可得n2=(0,1,1).所以结合图形知二面角E-A1D-B1的余弦值为==.教师用书专用(9—15)9.(2015福建,17,13分)如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BE C,BE⊥EC,AB=BE=EC=2,G,F 分别是线段BE,DC的中点.(1)求证:GF∥平面ADE;(2)求平面AEF与平面BEC所成锐二面角的余弦值.解析解法一:(1)证明:如图,取AE的中点H,连接HG,HD,又G是BE的中点,所以GH∥AB,且GH=AB.又F是CD的中点,所以DF=CD.由四边形ABCD是矩形得,AB∥CD,AB=CD,所以GH∥DF,且GH=DF,从而四边形HGFD是平行四边形,所以GF∥DH.又DH⊂平面ADE,GF⊄平面ADE,所以GF∥平面ADE.(2)如图,在平面BEC内,过B点作BQ∥EC.因为BE⊥CE,所以BQ⊥BE.又因为AB⊥平面BEC,所以AB⊥BE,AB⊥BQ.以B为原点,分别以,,的方向为x轴,y轴,z轴的正方向建立空间直角坐标系,则A(0,0,2),B(0,0,0),E(2,0,0),F(2,2,1).因为AB⊥平面BEC,所以=(0,0,2)为平面BEC的法向量.设n=(x,y,z)为平面AEF的法向量.又=(2,0,-2),=(2,2,-1),由得取z=2,得n=(2,-1,2).从而cos<n,>===,所以平面AEF与平面BEC所成锐二面角的余弦值为.10.(2015山东,17,12分)如图,在三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.(1)求证:BD∥平面FGH;(2)若CF⊥平面ABC,AB⊥BC,CF=DE,∠BAC=45°,求平面FGH与平面ACFD所成的角(锐角)的大小.解析(1)连接DG,CD,设CD∩GF=O,连接OH.在三棱台DEF-ABC中,AB=2DE,G为AC的中点,可得DF∥GC,DF=GC,所以四边形DFCG为平行四边形. 则O为CD的中点,又H为BC的中点,所以OH∥BD,又OH⊂平面FGH,BD⊄平面FGH,所以BD∥平面FGH.(2)设AB=2,则CF=1.在三棱台DEF-ABC中,G为AC的中点,由DF=AC=GC,可得四边形DGCF为平行四边形,因此DG∥FC.又FC⊥平面ABC,所以DG⊥平面ABC.在△ABC中,由AB⊥BC,∠BAC=45°,G是AC中点,所以AB=BC,GB⊥GC,因此GB,GC,GD两两垂直.以G为坐标原点,建立如图所示的空间直角坐标系G-xyz.所以G(0,0,0),B(,0,0),C(0,,0),D(0,0,1).可得H,F(0,,1),故=,=(0,,1).设n=(x,y,z)是平面FGH的法向量,则由可得可得平面FGH的一个法向量n=(1,-1,).因为是平面ACFD的一个法向量,=(,0,0),所以cos<,n>===.所以平面FGH与平面ACFD所成角(锐角)的大小为60°.11.(2015四川,18,12分)一个正方体的平面展开图及该正方体的直观图的示意图如图所示.在正方体中,设BC 的中点为M,GH的中点为N.(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);(2)证明:直线MN∥平面BDH;(3)求二面角A-EG-M的余弦值.解析(1)点F,G,H的位置如图所示.(2)证明:连接BD,设O为BD的中点.因为M,N分别是BC,GH的中点,所以OM∥CD,且OM=CD,HN∥CD,且HN=CD.所以OM∥HN,OM=HN.所以MNHO是平行四边形,从而MN∥OH.又MN⊄平面BDH,OH⊂平面BDH,所以MN∥平面BDH.(3)解法一:连接AC,过M作MP⊥AC于P.在正方体ABCD-EFGH中,AC∥EG,所以MP⊥EG.过P作PK⊥EG于K,连接KM,所以EG⊥平面PKM,从而KM⊥EG.所以∠PKM是二面角A-EG-M的平面角.设AD=2,则CM=1,PK=2.在Rt△CMP中,PM=CMsin 45°=.在Rt△PKM中,KM==.所以cos∠PKM==.即二面角A-EG-M的余弦值为.解法二:如图,以D为坐标原点,分别以,,方向为x,y,z轴的正方向,建立空间直角坐标系D-xyz.设AD=2,则M(1,2,0),G(0,2,2),E(2,0,2),O(1,1,0),所以,=(2,-2,0),=(-1,0,2).设平面EGM的法向量为n1=(x,y,z),由得取x=2,得n1=(2,2,1).在正方体ABCD-EFGH中,DO⊥平面AEGC,则可取平面AEG的一个法向量为n2==(1,1,0),所以cos<n1,n2>===,故二面角A-EG-M的余弦值为.12.(2014课标Ⅱ,18,12分)如图,四棱锥P-ABCD中,底面ABCD为矩形,P A⊥平面ABCD,E为PD的中点.(1)证明:PB∥平面AEC;(2)设二面角D-AE-C为60°,AP=1,AD=,求三棱锥E-ACD的体积.解析(1)证明:连接BD交AC于点O,连接EO.因为ABCD为矩形,所以O为BD的中点.又E为PD的中点,所以EO∥PB.又EO⊂平面AEC,PB⊄平面AEC,所以PB∥平面AEC.(2)因为PA⊥平面ABCD,ABCD为矩形,所以AB,AD,AP两两垂直.如图,以A为坐标原点,的方向为x轴的正方向,||为单位长,建立空间直角坐标系A-xyz,则D(0,,0),E,=.设B(m,0,0)(m>0),则C(m,,0),=(m,,0).设n1=(x,y,z)为平面ACE的法向量,则即可取n1=.又n2=(1,0,0)为平面DAE的法向量,由题设得|cos<n1,n2>|=,即=,解得m=.因为E为PD的中点,所以三棱锥E-ACD的高为.三棱锥E-ACD的体积V=××××=.13.(2014江苏,16,14分)如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.求证:(1)直线PA∥平面DEF;(2)平面BDE⊥平面ABC.证明(1)因为D,E分别为棱PC,AC的中点,所以DE∥PA.又因为PA⊄平面DEF,DE⊂平面DEF,所以直线PA∥平面DEF.(2)因为D,E,F分别为棱PC,AC,AB的中点,PA=6,BC=8,所以DE∥PA,DE=PA=3,EF=BC=4.又因为DF=5,故DF2=DE2+EF2,所以∠DEF=90°,即DE⊥EF.又PA⊥AC,DE∥PA,所以DE⊥AC.因为A C∩EF=E,AC⊂平面ABC,EF⊂平面ABC,所以DE⊥平面ABC.又DE⊂平面BDE,所以平面BDE⊥平面ABC.14.(2013江苏,16,14分)如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.求证:(1)平面EFG∥平面ABC;(2)BC⊥SA.证明(1)因为AS=AB,AF⊥SB,垂足为F,所以F是SB的中点.又因为E是SA的中点,所以EF∥AB.因为EF⊄平面ABC,AB⊂平面ABC,所以EF∥平面ABC.同理,EG∥平面ABC.又EF∩EG=E,所以平面EFG∥平面ABC.(2)因为平面SAB⊥平面SBC,且交线为SB,又AF⊂平面SAB,AF⊥SB,所以AF⊥平面SBC,因为BC⊂平面SBC,所以AF⊥BC.又因为AB⊥BC,AF∩AB=A,AF,AB⊂平面SAB,所以BC⊥平面SAB.因为SA⊂平面SAB,所以BC⊥SA.15.(2013安徽,19,13分)如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°.(1)证明:平面PAB与平面PCD的交线平行于底面;(2)求cos∠COD.解析(1)证明:设面PAB与面PCD的交线为l.因为AB∥CD,AB不在面PCD内,所以AB∥面PCD.又因为AB⊂面PAB,面PAB与面PCD的交线为l,所以AB∥l.由直线AB在底面上而l在底面外可知,l与底面平行.(2)设CD的中点为F.连接OF,PF.由圆的性质,得∠COD=2∠COF,OF⊥CD.因为OP⊥底面,CD⊂底面,所以OP⊥CD,又OP∩OF=O,故CD⊥面OPF.又CD⊂面PCD,因此面OPF⊥面PCD,从而直线OP在面PCD上的射影为直线PF,故∠OPF为OP与面PCD所成的角.由题设,得∠OPF=60°.设OP=h,则OF=OP·tan∠OPF=h·tan 60°=h.根据题设有∠OCP=22.5°,得OC==.由1=tan 45°=和tan 22.5°>0,可解得tan 22.5°=-1,因此OC==(+1)h.在Rt△OCF中,cos∠COF===-,故cos∠COD=cos 2∠COF=2cos2∠COF-1=2(-)2-1=17-12.三年模拟A组2016—2018年模拟·基础题组考点平行的判定和性质1.(2018浙江镇海中学模拟,5)已知两条不相交的空间直线a和b,则( )A.必定存在平面α,使得a⊂α,b⊂αB.必定存在平面α,使得a⊂α,b∥αC.必定存在直线c,使得a∥c,b∥cD.必定存在直线c,使得a∥c,b⊥c答案 B2.(2017浙江湖州期末,4)已知m,n是两条不同的直线,α,β是两个不同的平面,则下列说法正确的是( )A.若m∥α,m∥β,则α∥βB.若m⊥α,m∥β,则α∥βC.若m⊥α,n∥α,则m∥nD.若m⊥α,n⊥α,则m∥n答案 D3.(2018浙江“七彩阳光”联盟期中,15)已知m,n,l是互不相同的直线,α,β是两个不重合的平面,给出以下四个命题:①m,n是两条异面直线,m⊂α,n⊂β,且m∥β,n∥α,则α∥β;②若m⊂α,n∩α=A,且点A∉m,则m,n是两条异面直线;③若m,n是异面直线,m∥α,n∥α,且l⊥m,l⊥n,则l⊥α;④已知直线m⊥平面α,直线n⊂平面β,α⊥β⇒m∥n.其中为真命题的序号是.(把所有真命题的序号都填上)答案①②③4.(2018浙江“七彩阳光”联盟期初联考,19)如图,四边形ABCD为正方形,PDCE为直角梯形,∠PDC=90°,平面ABCD⊥平面PDCE,且PD=AD=2EC=2.(1)若PE和DC延长线交于点F,求证:BF∥平面PAC.(2)若Q为EC边上的动点,求直线BQ与平面PDB所成角正弦值的最小值.解析(1)证明:在△PDF中,∵∠PDC=∠ECF=90°,PD=2EC,∴C为DF中点,∴CF=CD=AB,且AB∥CF,∴四边形ABFC为平行四边形,∴BF∥AC,又AC⊂面PAC,BF⊄面PAC,∴BF∥平面PAC.(7分)(2)解法一:设点Q在面PBD上的射影为O,则∠QBO为直线BQ与平面PDB所成角.(9分)∵EC∥PD,所以EC平行于平面PBD,因为四边形ABCD为正方形,所以AC⊥BD,又易知PD⊥平面ABCD,所以PD⊥AC,所以AC⊥平面PBD,所以点C到面PBD的距离为,因为EC平行于平面PBD,所以点Q到PBD的距离OQ=,(12分)设CQ=k(0≤k≤1),所以BQ=,所以sin∠QBO==≥=.(15分)解法二:建立如图所示的空间直角坐标系D-xyz,可知平面PDB的一个法向量为=(-2,2,0),B(2,2,0),设Q(0,2,t)(0≤t≤1),(12分)∴=(-2,0,t),设直线BQ与平面PDB所成角为α,∴sin α==≥=.(15分)5. (2017浙江宁波十校适应性考试(5月),19)如图,在四棱锥P-ABCD中,∠BAD=120°,AB=AD=2,△BCD是等边三角形,E是BP的中点,AC与BD交于点O,且O P⊥平面ABCD.(1)求证:PD∥平面ACE;(2)当OP=1时,求直线PA与平面ACE所成角的正弦值.解析(1)连接OE,因为O为BD的中点,E为PB的中点,所以OE∥PD.因为PD⊄平面ACE,OE⊂平面ACE,所以PD∥平面ACE.(2)因为BD⊥AC,PO⊥平面ABCD,所以AC,BD,PO两两垂直.以O为坐标原点,OB,OC,OP分别为x,y,z轴建立空间直角坐标系(图略),则P(0,0,1),A(0,-1,0),B(,0,0),C(0,3,0),E,=,=,=(0,-1,-1).设平面ACE的法向量为n=(x,y,z).由即得取x=1,则n=(1,0,-),所以平面ACE的一个法向量为n=(1,0,-).设直线PA与平面ACE所成的角为θ,则sin θ===.所以直线PA与平面ACE所成角的正弦值为.6.(2017浙江名校协作体,19)如图,在四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC,AB=BC=CD=1,DA=2,DP⊥平面ABP,O,M分别是AD,PB的中点.(1)求证:PD∥平面OCM;(2)若AP与平面PBD所成的角为60°,求线段PB的长.解析(1)连接OB,设BD与OC的交点为N,连接MN.因为O为AD的中点,AD=2,所以OA=OD=1=BC.又因为AD∥BC,所以四边形OBCD为平行四边形,(2分)所以N为BD的中点,又因为M为PB的中点,所以MN∥PD.(4分)又因为MN⊂平面OCM,PD⊄平面OCM,所以PD∥平面OCM.(6分)(2)由四边形OBCD为平行四边形,知OB=CD=1,所以△AOB为等边三角形,所以∠BAD=60°,(8分)所以BD==,则AB2+BD2=AD2,即AB⊥BD.因为DP⊥平面ABP,所以AB⊥PD.又因为BD∩PD=D,所以AB⊥平面BDP,(11分)所以∠APB为AP与平面PBD所成的角,则∠APB=60°,(13分)所以PB=.(15分)B组2016—2018年模拟·提升题组一、选择题1.(2017浙江镇海中学模拟训练(一),3)若有直线m、n和平面α、β,下列四个命题中,为真的是( )A.若m∥α,n∥α,则m∥nB.若m⊂α,n⊂α,m∥β,n∥β则α∥βC.若α⊥β,m⊂α,则m⊥βD.若α⊥β,m⊥β,m⊄α,则m∥α答案 D2.(2017浙江湖州期末,4)已知m,n是两条不同的直线,α,β是两个不同的平面,则下列说法正确的是( )A.若m∥α,m∥β,则α∥βB.若m⊥α,m∥β,则α∥βC.若m⊥α,n∥α,则m∥nD.若m⊥α,n⊥α,则m∥n答案 D二、解答题3.(2018浙江重点中学12月联考,19)已知等腰梯形ABCD中(如图1),AB=4,BC=CD=DA=2,F为线段CD的中点,E、M为线段AB上的点,AE=EM=1,现将四边形AEFD沿EF折起(如图2).图1图2(1)求证:AM∥平面BCD;(2)若BD=,求直线CD与平面BCFE所成角的正弦值.解析(1)证明:连接CM,∵EM∥FC且EM=FC=1,∴四边形EFCM为平行四边形,(2分)∴EF∥CM且EF=CM.又EF∥AD且EF=AD,∴CM∥AD且CM=AD,(4分)∴四边形ADCM为平行四边形,∴AM∥DC,又∵DC⊂面BCD,AM⊄面BCD,∴AM∥面BCD.(6分)(2)过点D作DH⊥EF于H,连接BH,CH,在Rt△DFH中,易知∠DFH=60°,又DF=1,∴DH=,FH=,在△BEH中,EH=EF-FH=,(10分)∠HEB=60°,EB=3,∴HB2=+32-2××3cos 60°=.在△BDH中,DH=,BH=,BD=,∴DH2+BH2=BD2,∴DH⊥HB,又DH⊥EF,∴DH⊥平面BCFE.(13分)∴CH为CD在平面BCFE内的射影,∴∠DCH为CD与平面BCFE所成的角,在△FCH中,易知∠CFH=120°,∴CH==,在Rt△CDH中,CD==,∴sin∠DCH==,∴CD与平面BCFE所成的角的正弦值为.(15分)4.(2018浙江9+1高中联盟期中,19)如图,在三棱锥P-ABC中,△ABC是正三角形,面PAB⊥面ABC,∠PAB=30°,AB=PB=2,△ABC和△PBC的重心分别为D,E.(1)证明:DE∥面PAB;(2)求AB与面PDE所成角的正弦值.解析(1)证明:取BC中点F,连接AF,PF,由重心性质可知D,E分别在AF,PF上且AD=2DF,PE=2EF,所以在△AFP 中有=,所以DE∥AP,又DE⊄平面PAB,AP⊂平面PAB,所以DE∥平面PAB.(7分)(2)以AB中点O为原点,建立如图所示的空间直角坐标系.∵AB=PB=2,∠PAB=30°,∴∠PBA=120°,∴P(0,2,),又由已知条件知A(0,-1,0),B(0,1,0),F,∴=,=,=(0,2,0).设面PDE的法向量为n=(x,y,z),则取x=,则∴n=(,-1,),设AB与面PDE所成角为θ,则sin θ=|cos<n,>|=,所以AB与面PDE所成角的正弦值为.(15分)5.(2016浙江名校(衢州二中)交流卷五,18)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,且B1C1=BC.(1)求证:AB1∥面A1C1C;(2)求二面角C-A1C1-B的余弦值.解析(1)证明:取BC的中点E,连接AE,C1E,B1E,如图.∵B1C1∥BC,B1C1=BC,∴B1C1∥EC,B1C1=EC,∴四边形CEB1C1为平行四边形,从而B1E∥C1C,∵C1C⊂面A1C1C,B1E⊄面A1C1C,∴B1E∥面A1C1C.(2分)∵B1C1∥BC,B1C1=BC,∴B1C1∥BE,B1C1=BE,∴四边形BB1C1E为平行四边形,∴B1B∥C1E,且B1B=C1E.又∵ABB1A1是正方形,∴A1A∥B1B,A1A=B1B,∴A1A∥C1E,且A1A=C1E,故AEC1A1为平行四边形,∴AE∥A1C1.∵A1C1⊂面A1C1C,AE⊄面A1C1C,∴AE∥面A1C1C.(4分)∵AE∩B1E=E,∴面B1AE∥面A1C1C.∵AB1⊂面B1AE,∴AB1∥面A1C1C.(6分)(2)∵四边形ABB1A1为正方形,∴A1A=AB=AC=1,又A1A⊥AB,∴A1B=.∵A1C=A1B,∴A1C=,∴A1C2=AC2+A,∴∠A1AC=90°,∴A1A⊥AC.∵AB∩AC=A,∴A1A⊥面ABC,∵A1C=A1B=BC,∴BC=.∴AC2+AB2=BC2,∴∠BAC=90°,∴AB⊥AC.(8分)以A为原点,AC,AB,AA1所在直线为x轴,y轴,z轴建立空间直角坐标系,如图,则C(1,0,0),A1(0,0,1),C1,B(0,1,0),所以=(-1,0,1),=,=(0,-1,1),=.设面A1C1C的法向量为n1=(x,y,z),由n1·=0,n1·=0,得令z=1,得n1=(1,-1,1).设面A1C1B的法向量为n2=(m,n,k),由n2·=0,n2·=0,得令k=1,得n2=(-1,1,1),(12分) 所以cos<n1,n2>===-.设二面角C-A1C1-B的平面角为α,<n1,n2>=θ,所以cos α=cos(π-θ)=.(15分)C组2016—2018年模拟·方法题组方法1 线面、面面平行的判定的解题策略1.(2017浙江测试卷,19)如图,已知四棱柱ABCD-A1B1C1D1的底面是菱形,侧棱AA1⊥底面ABCD,M是AC的中点,∠BAD=120°,AA1=AB.(1)证明:MD1∥平面A1BC1;(2)求直线MA1与平面A1BC1所成的角的正弦值.解析(1)连接B1D1交A1C1于点E,连接BE,BD,则BD与AC交于点M,连接ME,由ED1∥BM,ED1=BM,知四边形ED1MB 是平行四边形,∴MD1∥BE,又MD1⊄平面A1BC1,BE⊂平面A1BC1,∴MD1∥平面A1BC1.(2)由A1B1C1D1为菱形,得A1C1⊥B1D1,又ABCD-A1B1C1D1是直四棱柱,∴BB1⊥A1C1,又B1D1∩BB1=B1,∴A1C1⊥平面BB1D1D,又A1C1⊂平面A1BC1,∴平面BB1D1D⊥平面A1BC1.过点M作BE的垂线,垂足为H,则MH⊥平面A1BC1,连接HA1,则∠MA1H即为直线MA1与平面A1BC1所成的角,设AA1=1,∵ABCD是菱形且∠BAD=120°,∴AM=,MB=.在Rt△MAA1中,由AM=,AA1=1,得MA1=,在Rt△EMB中,由MB=,ME=1,得MH=,∴sin∠MA1H==.方法2 线面、面面平行的性质的解题策略2.(2017浙江镇海中学第一学期期中,2)已知平面α和不同在平面α内但共面的两条不同的直线m,n,下列命题是真命题的是( )A.若m,n与α所成的角相等,则m∥nB.若m∥α,n∥α,则m∥nC.若m⊥α,m⊥n,则n∥αD.若m⊂α,n∥α,则m∥n答案 D。
高考数学一轮复习 第八章 立体几何 第3讲 直线、平面平行的判定与性质教学案 理
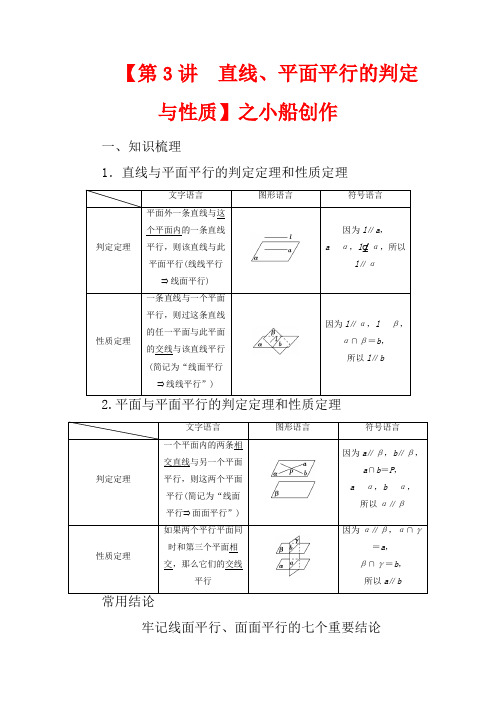
【第3讲直线、平面平行的判定与性质】之小船创作一、知识梳理1.直线与平面平行的判定定理和性质定理文字语言图形语言符号语言判定定理平面外一条直线与这个平面内的一条直线平行,则该直线与此平面平行(线线平行⇒线面平行)因为l∥a,aα,l⊆/α,所以l∥α性质定理一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行(简记为“线面平行⇒线线平行”)因为l∥α,lβ,α∩β=b,所以l∥b2.平面与平面平行的判定定理和性质定理文字语言图形语言符号语言判定定理一个平面内的两条相交直线与另一个平面平行,则这两个平面平行(简记为“线面平行⇒面面平行”)因为a∥β,b∥β,a∩b=P,aα,bα,所以α∥β性质定理如果两个平行平面同时和第三个平面相交,那么它们的交线平行因为α∥β,α∩γ=a,β∩γ=b,所以a∥b牢记线面平行、面面平行的七个重要结论(1)垂直于同一条直线的两个平面平行,即若a⊥α,a ⊥β,则α∥β.(2)垂直于同一个平面的两条直线平行,即若a⊥α,b ⊥α,则a∥b.(3)夹在两个平行平面之间的平行线段长度相等.(4)经过平面外一点有且只有一个平面与已知平面平行.(5)两条直线被三个平行平面所截,截得的对应线段成比例.(6)如果两个平面分别平行于第三个平面,那么这两个平面互相平行.(7)如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,那么这两个平面平行.二、教材衍化1.下列命题中正确的是( )A.若a,b是两条直线,且a∥b,那么a平行于经过b 的任何平面B.若直线a和平面α满足a∥α,那么a与α内的任何直线平行C.平行于同一条直线的两个平面平行D.若直线a,b和平面α满足a∥b,a∥α,b⊆/α,则b∥α解析:选D.A错误,a可能在经过b的平面内;B错误,a与α内的直线平行或异面;C错误,两个平面可能相交;D正确,由a∥α,可得a平行于经过直线a的平面与α的交线c,即a∥c,又a∥b,所以b∥c,b⃘α,cα,所以b∥α.2.平面α∥平面β的一个充分条件是( )A.存在一条直线a,a∥α,a∥βB.存在一条直线a,aα,a∥βC.存在两条平行直线a,b,aα,bβ,a∥β,b ∥αD.存在两条异面直线a,b,aα,bβ,a∥β,b ∥α解析:选D.若α∩β=l,a∥l,a⃘α,a⃘β,a∥α,a∥β,故排除A.若α∩β=l,aα,a∥l,则a∥β,故排除B.若α∩β=l,aα,a∥l,bβ,b∥l,则a∥β,b∥α,故排除C.3.如图,在正方体ABCDA1B1C1D1中,E为DD1的中点,则BD1与平面AEC的位置关系为________.解析:连接BD,设BD∩AC=O,连接EO,在△BDD1中,E为DD1的中点,O为BD的中点,所以EO为△BDD1的中位线,则BD1∥EO,而BD1⊆/平面ACE,EO平面ACE,所以BD1∥平面ACE.答案:平行一、思考辨析判断正误(正确的打“√”,错误的打“×”)(1)若一条直线平行于一个平面内的一条直线,则这条直线平行于这个平面.( )(2)若一条直线平行于一个平面,则这条直线平行于这个平面内的任一条直线.( )(3)如果一个平面内的两条直线平行于另一个平面,那么这两个平面平行.( )(4)如果两个平面平行,那么分别在这两个平面内的两条直线平行或异面.( )(5)若直线a与平面α内无数条直线平行,则a∥α.( )(6)若α∥β,直线a∥α,则a∥β.( )答案:(1)×(2)×(3)×(4)√(5)×(6)×二、易错纠偏常见误区|K(1)对空间平行关系的转化条件理解不够致误;(2)对面面平行判定定理的条件“平面内两相交直线”认识不清致误;(3)对面面平行性质定理理解不深致误.1.若平面α∥平面β,直线a∥平面α,点B∈β,则在平面β内且过B点的所有直线中( )A.不一定存在与a平行的直线B.只有两条与a平行的直线C.存在无数条与a平行的直线D.存在唯一的与a平行的直线解析:选A.当直线a在平面β内且过B点时,不存在与a平行的直线.故选A.2.下列条件中,能判断两个平面平行的是________.①一个平面内的一条直线平行于另一个平面;②一个平面内的两条直线平行于另一个平面;③一个平面内有无数条直线平行于另一个平面;④一个平面内任何一条直线都平行于另一个平面.解析:由两个平面平行的判定定理可知,如果一个平面内的两条相交直线与另外一个平面平行,那么这两个平面平行.显然只有④符合条件.答案:④3.如图是长方体被一平面所截得的几何体,四边形EFGH 为截面,则四边形EFGH的形状为________.解析:因为平面ABFE∥平面DCGH,又平面EFGH∩平面ABFE=EF,平面EFGH∩平面DCGH=HG,所以EF∥HG.同理EH∥FG,所以四边形EFGH是平行四边形.答案:平行四边形线面平行的判定与性质(多维探究)角度一直线与平面平行的判定如图所示,斜三棱柱ABCA1B1C1中,点D,D1分别为AC,A1C1的中点.(1)证明:AD1∥平面BDC1;(2)证明:BD∥平面AB1D1.【证明】(1)因为D1,D分别为A1C1,AC的中点,四边形ACC1A1为平行四边形,所以C1D1綊DA,所以四边形ADC1D1为平行四边形,所以AD1∥C1D,又AD1⊆/平面BDC1,C1D平面BDC1,所以AD1∥平面BDC1.(2)连接D1D,因为BB1∥平面ACC1A1,BB1平面BB1D1D,平面ACC1A1∩平面BB1D1D=D1D,所以BB1∥D1D,又因为D1,D分别为A1C1,AC的中点,所以DD1綊AA1,所以BB1=AA1=DD1,故四边形BDD1B1为平行四边形,所以BD∥B1D1,又BD⊆/平面AB1D1,B1D1平面AB1D1,所以BD∥平面AB1D1.角度二直线与平面平行的性质如图,四棱锥PABCD的底面是边长为8的正方形,四条侧棱长均为217,点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.(1)证明:GH∥EF;(2)若EB=2,求四边形GEFH的面积.【解】(1)证明:因为BC∥平面GEFH,BC平面PBC,且平面PBC∩平面GEFH=GH,所以GH∥BC.同理可证EF∥BC,因此GH∥EF.(2)连接AC,BD交于点O,BD交EF于点K,连接OP,GK.因为PA=PC,O是AC的中点,所以PO⊥AC,同理可得PO⊥BD.又BD∩AC=O,且AC,BD都在底面ABCD内,所以PO⊥底面ABCD.又因为平面GEFH⊥平面ABCD,且PO⊆/平面GEFH,所以PO∥平面GEFH.因为平面PBD∩平面GEFH=GK,所以PO∥GK,所以GK⊥底面ABCD,从而GK⊥EF.所以GK是梯形GEFH的高.由AB=8,EB=2得EB∶AB=KB∶DB=1∶4,从而KB=14DB=12OB,即K为OB的中点.再由PO∥GK得GK=12PO,且G是PB的中点,所以GH=12BC=4.由已知可得OB=42,PO=PB2-OB2=68-32=6,所以GK=3.易得EF=BC=8,故四边形GEFH的面积S=GH+EF2·GK=4+82×3=18.判断或证明线面平行的常用方法(1)利用线面平行的定义(无公共点).(2)利用线面平行的判定定理(a⊆/α,bα,a∥b⇒a ∥α).(3)利用面面平行的性质定理(α∥β,aα⇒a∥β).(4)利用面面平行的性质(α∥β,a⊆/α,a⊆/β,a∥α⇒a∥β).1.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( )解析:选A.对于选项B,如图所示,连接CD,因为AB∥CD,M,Q分别是所在棱的中点,所以MQ∥CD,所以AB∥MQ,又AB ⊆/平面MNQ ,MQ 平面MNQ ,所以AB ∥平面MNQ .同理可证选项C ,D 中均有AB ∥平面MNQ .故选A.2.如图,四棱锥P ABCD 中AD ∥BC ,AB =BC =12AD ,E ,F ,H 分别为线段AD ,PC ,CD的中点,AC 与BE 交于O 点,G 是线段OF 上一点.(1)求证:AP ∥平面BEF ; (2)求证:GH ∥平面PAD .证明:(1)连接EC ,因为AD ∥BC ,BC =12AD ,所以BC 綊AE ,所以四边形ABCE 是平行四边形,所以O 为AC 的中点. 又因为F 是PC 的中点, 所以FO ∥AP ,FO 平面BEF ,AP ⊆/平面BEF ,所以AP ∥平面BEF .(2)连接FH ,OH ,因为F ,H 分别是PC ,CD 的中点, 所以FH ∥PD ,所以FH ∥平面PAD .又因为O 是BE 的中点,H 是CD 的中点, 所以OH ∥AD ,所以OH ∥平面PAD . 又FH ∩OH =H ,所以平面OHF ∥平面PAD . 又因为GH平面OHF ,所以GH∥平面PAD.面面平行的判定与性质(典例迁移)如图所示,在三棱柱ABCA1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:(1)B,C,H,G四点共面;(2)平面EFA1∥平面BCHG.【证明】(1)因为G,H分别是A1B1,A1C1的中点,所以GH∥B1C1,又B1C1∥BC,所以GH∥BC,所以B,C,H,G四点共面.(2)在△ABC中,E,F分别为AB,AC的中点,所以EF∥BC,因为EF⊆/平面BCHG,BC平面BCHG,所以EF∥平面BCHG.又因为G,E分别为A1B1,AB的中点,所以A1G綊EB,所以四边形A1EBG是平行四边形,所以A1E∥GB.因为A1E⊆/平面BCHG,GB平面BCHG,所以A1E∥平面BCHG.又因为A1E∩EF=E,所以平面EFA1∥平面BCHG.【迁移探究1】(变条件)在本例条件下,若D为BC1的中点,求证:HD∥平面A1B1BA.证明:如图所示,连接HD,A1B,因为D为BC1的中点,H为A1C1的中点,所以HD∥A1B,又HD⊆/平面A1B1BA,A1B平面A1B1BA,所以HD∥平面A1B1BA.【迁移探究2】(变条件)在本例条件下,若D1,D分别为B1C1,BC的中点,求证:平面A1BD1∥平面AC1D.证明:如图所示,连接A1C交AC1于点M,因为四边形A1ACC1是平行四边形,所以M是A1C的中点,连接MD,因为D为BC的中点,所以A1B∥DM.因为A1B平面A1BD1,DM⊆/平面A1BD1,所以DM∥平面A1BD1.又由三棱柱的性质知,D1C1綊BD,所以四边形BDC1D1为平行四边形,所以DC1∥BD1.又DC1⊆/平面A1BD1,BD1平面A1BD1,所以DC1∥平面A1BD1,又因为DC 1∩DM =D ,DC 1,DM 平面AC 1D ,所以平面A 1BD 1∥平面AC 1D .证明面面平行的常用方法(1)面面平行的定义.(2)面面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.(3)利用垂直于同一条直线的两个平面平行.(4)如果两个平面同时平行于第三个平面,那么这两个平面平行.(5)利用“线线平行”“线面平行”“面面平行”的相互转化进行证明.1.如图,AB ∥平面α∥平面β,过A ,B 的直线m ,n 分别交α,β于C ,E 和D ,F ,若AC =2,CE =3,BF =4,则BD 的长为( )A.65 B .75C.85D .95解析:选C.由AB ∥α∥β,易证 AC CE =BD DF .即AC AE =BDBF ,所以BD =AC ·BF AE =2×45=85.2.如图,在正方体ABCD A 1B 1C 1D 1中,S 是B 1D 1的中点,E ,F ,G 分别是BC ,DC ,SC 的中点,求证:(1)直线EG ∥平面BDD 1B 1; (2)平面EFG ∥平面BDD 1B 1. 证明:(1)如图,连接SB ,因为E ,G 分别是BC ,SC 的中点, 所以EG ∥SB . 又因为SB平面BDD 1B 1,EG ⊆/平面BDD 1B 1,所以直线EG ∥平面BDD 1B 1. (2)连接SD ,因为F ,G 分别是DC ,SC 的中点, 所以FG ∥SD . 又因为SD平面BDD 1B 1,FG ⊆/平面BDD 1B 1,所以FG ∥平面BDD 1B 1,又EG平面EFG ,FG 平面EFG ,EG ∩FG =G ,所以平面EFG ∥平面BDD 1B 1.平行关系中的探索性问题(师生共研) 如图,已知斜三棱柱ABC A 1B 1C 1中,点D ,D 1分别为AC ,A 1C 1上的点.(1)当A 1D 1D 1C 1等于何值时,BC 1∥平面AB 1D 1?(2)若平面BC 1D ∥平面AB 1D 1,求ADDC的值.【解】(1)如图,取D1为线段A1C1的中点,此时A1D1D1C1=1,连接A1B交AB1于点O,连接OD1.由棱柱的性质,知四边形A1ABB1为平行四边形,所以点O为A1B的中点.在△A1BC1中,点O,D1分别为A1B,A1C1的中点,所以OD1∥BC1.又因为OD1平面AB1D1,BC1⊆/平面AB1D1,所以BC1∥平面AB1D1.所以当A1D1D1C1=1时,BC1∥平面AB1D1.(2)由已知,平面BC1D∥平面AB1D1,且平面A1BC1∩平面BDC1=BC1,平面A1BC1∩平面AB1D1=D1O.因此BC1∥D1O,同理AD1∥DC1.因为A1D1D1C1=A1OOB,A1D1D1C1=DCAD.又因为A1OOB=1,所以DCAD=1,即ADDC=1.解决探索性问题的方法(1)根据探索性问题的设问,假设其存在并探索出结论,然后在这个假设下进行推理论证,若得到合乎情理的结论就肯定假设,若得到矛盾就否定假设.(2)按类似于分析法的格式书写步骤:从结论出发“要使……成立”“只需使……成立”.(一题多解)如图,四棱锥EABCD,平面ABCD⊥平面ABE,四边形ABCD为矩形,AD=6,AB=5,BE=3,F 为CE上的点,且BF⊥平面ACE.(1)求证:AE⊥BE;(2)设M在线段DE上,且满足EM=2MD,试在线段AB上确定一点N,使得MN∥平面BCE,并求MN的长.解:(1)证明:因为四边形ABCD为矩形,所以BC⊥AB.因为平面ABCD⊥平面ABE,平面ABCD∩平面ABE=AB,且BC平面ABCD,所以BC⊥平面ABE.又AE平面ABE,所以BC⊥AE.因为BF⊥平面ACE,AE平面ACE,所以BF⊥AE.又因为BC∩BF=B,BC平面BCE,BF平面BCE,所以AE⊥平面BCE,因为BE平面BCE,所以AE⊥BE.(2)法一:如图,在△ADE中过M点作MG∥AD交AE于G 点,在△ABE中过G点作GN∥BE交AB于N点,连接MN,因为NG∥BE,NG⊆/平面BCE,BE平面BCE,所以NG∥平面BCE.同理可证,GM∥平面BCE.因为MG∩GN=G,所以平面MGN∥平面BCE,又因为MN平面MGN,所以MN∥平面BCE,因为N点为线段AB上靠近A点的一个三等分点,AD=6,AB=5,BE=3,所以MG=23AD=4,NG=13BE=1,所以MN=MG2+NG2=42+12=17.法二:如图,过M点作MG∥CD交CE于G点,连接BG,在AB上取N点,使得BN=MG,连接MN,因为MG∥CD,EM=2MD,所以MG=23 CD,因为AB∥CD,BN=MG,所以四边形MGBN是平行四边形,所以MN∥BG,又因为MN⊆/平面BCE,BG平面BCE,所以MN∥平面BCE,又MG=23CD,MG=BN,所以BN=23AB,所以N点为线段AB上靠近A点的一个三等分点.在△CBG中,因为BC=AD=6,CG=13CE=1362+32=5,cos∠BCG=255,所以BG2=36+5-2×6×5×255=17,所以MN=BG=17.[基础题组练]1.(2020·河北衡水模拟一)已知m,n为两条不重合直线,α,β为两个不重合平面,下列条件中,α∥β的充分条件是( )A.m∥n,mα,nβB.m∥n,m⊥α,n⊥βC.m⊥n,m∥α,n∥βD.m⊥n,m⊥α,n⊥β解析:选B.对于A,两个平面内分别有一条直线,这两条直线互相平行,这两个平面可能平行,也可能相交,因此A中条件不是α∥β的充分条件;对于B,因为m∥n,m ⊥α,所以n⊥α,结合n⊥β,知α∥β,因此B中条件是α∥β的充分条件;对于C,由m⊥n,m∥α知nα,或n∥α,或n与α相交,结合n∥β,知α,β可能平行,也可能相交,所以C中条件不是α∥β的充分条件;对于D,由m⊥n,m⊥α知nα,或n∥α,结合n⊥β,知α⊥β,所以D中条件不是α∥β的充分条件.综上可知.选B.2.(2020·江西红色七校联考)设m,n是空间中两条不同的直线,α,β是两个不同的平面,则下列说法正确的是( )A.若m∥n,nα,则m∥αB.若mα,nβ,α∥β,则m∥nC.若α∥β,m⊥α,则m⊥βD.若mα,nβ,m∥β,n∥α,则α∥β解析:选C.若m∥n,nα,则m∥α或mα,所以选项A不正确;若mα,nβ,α∥β,则m∥n或m与n异面,所以选项B不正确;若mα,nβ,m∥β,n∥α,则α∥β或α与β相交,所以选项D不正确.故选C.3.(2020·湖南长沙模拟)设a,b,c表示不同直线,α,β表示不同平面,下列命题:①若a∥c,b∥c,则a∥b;②若a∥b,b∥α,则a∥α;③若a∥α,b∥α,则a∥b;④若aα,bβ,α∥β,则a∥b.其中真命题的个数是( )A.1 B.2C.3 D.4解析:选A.由题意,对于①,根据线线平行的传递性可知①是真命题;对于②,根据a∥b,b∥α,可以推出a∥α或aα,故②是假命题;对于③,根据a∥α,b∥α,可以推出a与b平行,相交或异面,故③是假命题;对于④,根据aα,bβ,α∥β,可以推出a∥b或a与b异面,故④是假命题.所以真命题的个数是1.故选A.4.如图所示,在空间四边形ABCD中,E,F分别为边AB,AD上的点,且AE∶EB=AF∶FD=1∶4,又H,G分别为BC,CD的中点,则( )A.BD∥平面EFGH,且四边形EFGH是矩形B.EF∥平面BCD,且四边形EFGH是梯形C.HG∥平面ABD,且四边形EFGH是菱形D.EH∥平面ADC,且四边形EFGH是平行四边形解析:选B.由AE∶EB=AF∶FD=1∶4知EF綊15BD,又EF⊆/平面BCD,所以EF∥平面BCD.又H,G分别为BC,CD的中点,所以HG綊12BD,所以EF∥HG且EF≠HG.所以四边形EFGH是梯形.5.在正方体ABCDA1B1C1D1中,E,F,G分别是A1B1,B1C1,BB1的中点,给出下列四个推断:①FG∥平面AA1D1D;②EF∥平面BC1D1;③FG∥平面BC1D1;④平面EFG∥平面BC1D1.其中推断正确的序号是( )A.①③B.①④C.②③D.②④解析:选A.因为在正方体ABCDA1B1C1D1中,E,F,G分别是A1B1,B1C1,BB1的中点,所以FG∥BC1,因为BC1∥AD1,所以FG∥AD1,因为FG⊄平面AA1D1D,AD1⊂平面AA1D1D,所以FG∥平面AA1D1D,故①正确;因为EF∥A1C1,A1C1与平面BC1D1相交,所以EF与平面BC1D1相交,故②错误;因为E,F,G分别是A1B1,B1C1,BB1的中点,所以FG∥BC1,因为FG⊆/平面BC1D1,BC1平面BC1D1,所以FG∥平面BC1D1,故③正确;因为EF与平面BC1D1相交,所以平面EFG与平面BC1D1相交,故④错误.故选A.6.在四面体ABCD中,M,N分别是△ACD,△BCD的重心,则四面体的四个面中与MN平行的是________.解析:如图,取CD的中点E,连接AE,BE,则EM∶MA=1∶2,EN∶BN=1∶2,所以MN∥AB.因为AB平面ABD,MN⊆/平面ABD,AB平面ABC,MN⊆/平面ABC,所以MN∥平面ABD,MN∥平面ABC.答案:平面ABD与平面ABC7.如图,正方体ABCDA1B1C1D1中,AB=2,点E为AD 的中点,点F在CD上.若EF∥平面AB1C,则线段EF的长度等于________.解析:因为EF∥平面AB1C,EF平面ABCD,平面ABCD ∩平面AB1C=AC,所以EF∥AC,所以点F为DC的中点.故EF=12AC= 2.答案:28.如图所示,在正四棱柱ABCDA1B1C1D1中,E,F,G,H 分别是棱CC1,C1D1,D1D,DC的中点,N是BC的中点,点M 在四边形EFGH及其内部运动,则M只需满足条件________时,就有MN∥平面B1BDD1.(注:请填上你认为正确的一个条件即可,不必考虑全部可能情况)解析:连接HN,FH,FN,则FH∥DD1,HN∥BD,FH∩HN=H,DD1∩BD=D,所以平面FHN∥平面B1BDD1,只需M∈FH,则MN平面FHN,所以MN∥平面B1BDD1.答案:点M在线段FH上(或点M与点H重合)9.在如图所示的一块木料中,棱BC平行于平面A′B′C′D′.(1)要经过平面A′B′C′D′内的一点P和棱BC将木料锯开,应怎样画线?(2)所画的线与平面ABCD是什么位置关系?并证明你的结论.解:(1)过点P作B′C′的平行线,交A′B′,C′D′于点E,F,连接BE,CF.作图如下:(2)EF∥平面ABCD.理由如下:因为BC∥平面A′B′C′D′,又因为平面B′C′CB∩平面A′B′C′D′=B′C′,所以BC∥B′C′,因为EF∥B′C′,所以EF∥BC,又因为EF⊆/平面ABCD,BC平面ABCD,所以EF∥平面ABCD.10.如图所示,四边形ABCD与四边形ADEF都为平行四边形,M,N,G分别是AB,AD,EF的中点.求证:(1)BE∥平面DMF;(2)平面BDE∥平面MNG.证明:(1)如图所示,设DF与GN交于点O,连接AE,则AE必过点O,连接MO,则MO为△ABE的中位线,所以BE∥MO.因为BE⊆/平面DMF,MO平面DMF,所以BE∥平面DMF.(2)因为N,G分别为平行四边形ADEF的边AD,EF的中点,所以DE∥GN.因为DE⊆/平面MNG,GN平面MNG,所以DE∥平面MNG.因为M为AB的中点,所以MN为△ABD的中位线,所以BD∥MN.因为BD⊆/平面MNG,MN平面MNG,所以BD∥平面MNG.因为DE与BD为平面BDE内的两条相交直线,所以平面BDE∥平面MNG.[综合题组练]1.如图,透明塑料制成的长方体容器ABCDA1B1C1D1内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜度的不同,有下面四个命题:①没有水的部分始终呈棱柱形;②水面EFGH所在四边形的面积为定值;③棱A1D1始终与水面所在的平面平行;④当容器倾斜如图所示时,BE·BF是定值.其中正确的个数是( )A.1 B.2C.3 D.4解析:选C.由题图,显然①是正确的,②是错的;对于③因为A1D1∥BC,BC∥FG,所以A1D1∥FG且A1D1⊆/平面EFGH,所以A1D1∥平面EFGH(水面).所以③是正确的;因为水是定量的(定体积V).所以S△BEF·BC=V,即12BE·BF·BC=V.所以BE·BF=2VBC(定值),即④是正确的,故选C.2.(2020·江西吉安一模)如图,在棱长为1的正方体ABCDA1B1C1D1中,M,N分别是A1D1,A1B1的中点,过直线BD 的平面α∥平面AMN,则平面α截该正方体所得截面的面积为( )A. 2 B .98C. 3D .62解析:选B.如图1,取B 1C 1的中点E ,C 1D 1的中点F ,连接EF ,BE ,DF ,B 1D 1,则EF ∥B 1D 1,B 1D 1∥BD ,所以EF ∥BD ,故EF ,BD 在同一平面内,连接ME ,因为M ,E 分别为A 1D 1,B 1C 1的中点,所以ME ∥AB ,且ME =AB ,所以四边形ABEM 是平行四边形,所以AM ∥BE ,又因为BE平面BDFE ,AM ⊆/平面BDFE ,所以AM ∥平面BDFE ,同理AN ∥平面BDFE ,因为AM ∩AN =A ,所以平面AMN ∥平面BDFE ,BD =2,EF =12B 1D 1=22,DF =BE =52,等腰梯形BDFE如图2,过E ,F 作BD 的垂线,垂足分别为G ,H ,则四边形EFGH 为矩形,所以FG =DF 2-DG 2=54-18=324, 故所得截面的面积为12×⎝ ⎛⎭⎪⎪⎫22+2×324=98,故选B.3.在正方体ABCD A 1B 1C 1D 1中,M ,N ,Q 分别是棱D 1C 1,A1D1,BC的中点,点P在BD1上且BP=23BD1.则以下四个说法:①MN∥平面APC;②C1Q∥平面APC;③A,P,M三点共线;④平面MNQ∥平面APC.其中说法正确的是________(填序号).解析:①连接MN,AC,则MN∥AC,连接AM,CN,易得AM,CN交于点P,即MN平面APC,所以MN∥平面APC是错误的;②由①知M,N在平面APC上,由题易知AN∥C1Q,AN平面APC,所以C1Q∥平面APC是正确的;③由①知A,P,M三点共线是正确的;④由①知MN平面APC,又MN平面MNQ,所以平面MNQ∥平面APC是错误的.答案:②③4.如图所示,正方体ABCDA1B1C1D1的棱长为a,点P是棱AD上一点,且AP=a3,过B1,D1,P的平面交底面ABCD于PQ,Q在直线CD上,则PQ=________.解析:因为平面A1B1C1D1∥平面ABCD,而平面B1D1P∩平面ABCD=PQ,平面B1D1P∩平面A1B1C1D1=B1D1,所以B1D1∥PQ.又因为B1D1∥BD,所以BD∥PQ,设PQ∩AB=M,因为AB∥CD,所以△APM∽△DPQ.所以PQPM=PDAP=2,即PQ=2PM.又知△APM∽△ADB,所以PMBD=APAD=13,所以PM=13BD,又BD=2a,所以PQ=223a.答案:22 3a5.如图,在四棱锥PABCD的底面ABCD中,BC∥AD,且AD=2BC,O,E分别为AD,PD的中点.(1)设平面PAB∩平面PCD=l,请作图确定l的位置并说明你的理由;(2)若Q为直线CE上任意一点,证明:OQ∥平面PAB.解:(1)分别延长AB和DC交于点R,连接PR,则直线PR就是l的位置;R∈AB平面PAB,R∈CD平面PCD,所以P、R是平面PAB和平面PCD的两个公共点,由公理1可知,过P、R的直线就是两个平面的交线l.(2)证明:连接OE、OC,因为BC∥AD,且BC=12 AD,又AO=12AD,所以BC∥AO,且BC=AO,所以四边形ABCO为平行四边形,所以OC∥AB,则OC∥平面PAB;又OE为△PAD的中位线,则OE∥AP,所以OE∥平面PAB,又OE平面OEC,OC平面OEC,且OE∩OC=O,所以平面PAB∥平面OEC,又OQ平面OEC,所以OQ∥平面PAB.6.如图,四棱柱ABCDA1B1C1D1的底面ABCD是正方形.(1)证明:平面A1BD∥平面CD1B1;(2)若平面ABCD∩平面B1D1C=直线l,证明B1D1∥l.证明:(1)由题设知BB1綊DD1,所以四边形BB1D1D是平行四边形,所以BD∥B1D1.又BD⊆/平面CD1B1,B1D1平面CD1B1,所以BD∥平面CD1B1.因为A1D1綊B1C1綊BC,所以四边形A1BCD1是平行四边形,所以A1B∥D1C.又A1B⊆/平面CD1B1,D1C平面CD1B1,所以A1B∥平面CD1B1.又因为BD∩A1B=B,所以平面A1BD∥平面CD1B1.(2)由(1)知平面A1BD∥平面CD1B1,又平面ABCD∩平面B1D1C=直线l,平面ABCD∩平面A1BD=直线BD,所以直线l∥直线BD,在四棱柱ABCDA1B1C1D1中,四边形BDD1B1为平行四边形,所以B1D1∥BD,所以B1D1∥l.。
高中数学高考45第八章 立体几何 8 3 空间点、直线、平面之间的位置关系

例2 (1)若直线l1和l2是异面直线,l1在平面α内,l2在平面β内,l是平面α与平 面β的交线,则下列命题正确的是 A.l与l1,l2都不相交 B.l与l1,l2都相交 C.l至多与l1,l2中的一条相交
√D.l至少与l1,l2中的一条相交
解析 由直线l1和l2是异面直线可知l1与l2不平行,故l1,l2中至少有一条与l相 交.故选D.
的公共直线. 公理4:平行于同一条直线的两条直线互相 平行 .
2.直线与直线的位置关系 (1)位置关系的分类
平行 直线 共面直线
相交直线 异面直线:不同在 任何 一个平面内,没有公共点
(2)异面直线所成的角 ①定义:设a,b是两条异面直线,经过空间任一点O作直线a′∥a,b′∥b, 把a′与b′所成的 锐角(或直角) 叫做异面直线a与b所成的角(或夹角). ②范围: 0,π2. .
√D.点C和点M
解析 ∵AB⊂γ,M∈AB,∴M∈γ. 又α∩β=l,M∈l,∴M∈β. 根据公理3可知,M在γ与β的交线上. 同理可知,点C也在γ与β的交线上.
123456
6.如图为正方体表面的一种展开图,则图中的四条线段AB,CD,EF,GH 在原正方体中互为异面的对数为_3_.
解析 平面图形的翻折应注意翻折前后相对位置的变化, 则AB,CD,EF和GH在原正方体中, 显然AB与CD,EF与GH,AB与GH都是异面直线, 而AB与EF相交,CD与GH相交,CD与EF平行. 故互为异面的直线有且只有3对.
解 ∵BE∥AF 且 BE=12AF,G 为 FA 的中点, ∴BE∥FG且BE=FG, ∴四边形BEFG为平行四边形,∴EF∥BG. 由(1)知BG∥CH. ∴EF∥CH,∴EF与CH共面. 又D∈FH,∴C,D,F,E四点共面.
高考数学一轮复习 第八章立体几何8.4直线、平面平行的判定及其性质课时作业 理

课时作业38 直线、平面平行的判定及其性质一、选择题1.已知直线a∥平面α,P∈α,那么过点P且平行于直线a的直线( ).A.只有一条,不在平面α内B.有无数条,不一定在平面α内C.只有一条,在平面α内D.有无数条,一定在平面α内2.空间中,下列命题正确的是( ).A.若a∥α,b∥a,则b∥αB.若a∥α,b∥α,a⊂β,b⊂β,则β∥αC.若α∥β,b∥α,则b∥βD.若α∥β,a⊂α,则a∥β3.下列命题中正确的个数是( ).①若直线a不在α内,则a∥α;②若直线l上有无数个点不在平面α内,则l∥α;③若直线l与平面α平行,则l与α内的任意一条直线都平行;④若l与平面α平行,则l与α内任何一条直线都没有公共点;⑤平行于同一平面的两直线可以相交.A.1 B.2 C.3 D.44.下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是( ).A.①③B.①④C.②③D.②④5.(2012天津模拟)如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是( ).①动点A′在平面ABC上的射影在线段AF上;②BC∥平面A′DE;③三棱锥A′FED的体积有最大值.A.①B.①②C.①②③D.②③6.(2013届湖南永州三校高三摸底)如图所示,在四面体ABCD中,截面PQMN是正方形,则在下列命题中,错误的为( ).A.AC⊥BDB.AC∥截面PQMNC.AC=BDD.异面直线PM与BD所成的角为45°7.“直线a∥平面β”是“直线a至少平行于平面β内的一条直线”的( ).A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件二、填空题8.(2012山西晋城模拟)已知l,m,n是互不相同的直线,α,β,γ是三个不同的平面,给出下列命题:①若l与m为异面直线,l⊂α,m⊂β,则α∥β;②若α∥β,l⊂α,m⊂β,则l∥m;③若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.其中所有真命题的序号为__________.9.如图所示,ABCD A 1B 1C 1D 1是棱长为a 的正方体,M ,N 分别是下底面的棱A 1B 1,B 1C 1的中点,P 是上底面的棱AD 上的一点,AP =a3,过P ,M ,N 的平面交上底面于PQ ,Q 在CD 上,则PQ =__________.10.设x ,y ,z 是空间的不同直线或不同平面,且直线不在平面内,下列条件中能保证“若x ⊥z ,且y ⊥z ,则x ∥y ”为真命题的是__________.(填所有正确条件的代号)①x 为直线,y ,z 为平面;②x ,y ,z 为平面;③x ,y 为直线,z 为平面;④x ,y 为平面,z 为直线;⑤x ,y ,z 为直线.三、解答题11.如图,在三棱柱ABC A 1B 1C 1中,E ,F ,G ,H 分别是AB ,AC ,A 1B 1,A 1C 1的中点,求证:(1)B ,C ,H ,G 四点共面;(2)平面EFA 1∥平面BCHG .12.如图,在四棱锥P ABCD 中,底面ABCD 是矩形,PA ⊥平面ABCD ,AP =AB ,BP =BC =2,E ,F 分别是PB ,PC 的中点.(1)证明:EF∥平面PAD;(2)求三棱锥EABC的体积V.参考答案一、选择题1.C 解析:过直线外一点作已知直线的平行线有且只有一条.2.D 解析:A项,若a∥α,b∥a,则b∥α或b⊂α;B项,只有在a和b是相交直线时才成立;C项,若α∥β,b∥α,则b∥β或b⊂β.3.B 解析:a∩α=A时,a⊄α,故①错;直线l与α相交时,l上有无数个点不在α内,故②错;l∥α时,α内的直线与l平行或异面,故③错;l∥α,l与α无公共点,所以l与α内任一条直线都无公共点,④正确;长方体中的相交直线A1C1与B1D1都与面ABCD平行,所以⑤正确.4.B 解析:①由平面ABC∥平面MNP,可得AB∥平面MNP.④由AB∥CD,CD∥NP,得AB∥NP,所以AB∥平面MNP.5.C 解析:①中由已知可得平面A′FG⊥平面ABC,∴点A′在平面ABC上的射影在线段AF上.②∵BC∥DE,∴BC∥平面A′DE.③当平面A′DE⊥平面ABC时,三棱锥A′FED的体积取最大值.6.C 解析:由PQ∥MN∥AC,QM∥PN∥BD,PQ⊥QM,可得AC⊥BD,故A正确;由PQ∥AC 可得AC∥截面PQMN,故B正确;异面直线PM与BD所成的角等于PM与PN所成的角,故D正确,排除法选C.7.B 解析:直线a ∥平面β,则“直线a 至少平行于平面β内的一条直线”一定成立.反之不能成立.二、填空题8.③ 解析:①中α可能与β相交;②中直线l 与m 可能异面;③中结合线面平行的判定和性质可以证明,m ∥n . 9.223a 解析:如图所示,连接AC ,易知MN ∥平面ABCD ,∴MN ∥PQ .又∵MN ∥AC ,∴PQ ∥AC .又∵AP =a3,∴PD AD =DQCD =PQAC =23.∴PQ =23AC =223a .10.①③④三、解答题 11.证明:(1)∵GH 是△A 1B 1C 1的中位线,∴GH ∥B 1C 1.又∵B 1C 1∥BC ,∴GH ∥BC .∴B ,C ,H ,G 四点共面. (2)∵E ,F 分别为AB ,AC 的中点,∴EF ∥BC .∵EF ⊄平面BCHG ,BC ⊂平面BCHG ,∴EF ∥平面BCHG .∵A 1G EB ,∴四边形A 1EBG 是平行四边形.∴A 1E ∥GB .∵A 1E ⊄平面BCHG ,GB ⊂平面BCHG .∴A 1E ∥平面BCHG .∵A 1E ∩EF =E ,∴平面EFA 1∥平面BCHG .12.(1)证明:在△PBC 中,E ,F 分别是PB ,PC 的中点,∴EF ∥BC .又BC ∥AD ,∴EF ∥AD .又∵AD ⊂平面PAD ,EF ⊄平面PAD ,∴EF ∥平面PAD .(2)解:连接AE ,AC ,EC ,过E 作EG ∥PA 交AB 于点G , 则EG ⊥平面ABCD ,且EG =12PA .在△PAB 中,AP =AB ,∠PAB =90°,BP =2, ∴AP =AB =2,EG =22.∴S △ABC =12AB ·BC =12×2×2= 2.∴V E ABC =13S △ABC ·EG =13×2×22=13.。
高考数学一轮复习第八章立体几何第3讲直线、平面平行

【创新设计】(江苏专用)2017版高考数学一轮复习第八章立体几何第3讲直线、平面平行的判定与性质练习理基础巩固题组(建议用时:40分钟)一、填空题1.若直线ɑ平行于平面α,给出以下结论:①ɑ平行于α内的所有直线;②α内有无数条直线与ɑ平行;③直线ɑ上的点到平面α的距离相等;④α内存在无数条直线与ɑ成90°角.其中错误的结论是________(填序号).解析若直线ɑ平行于平面α,则α内既存在无数条直线与ɑ平行,也存在无数条直线与ɑ异面且垂直,所以①不正确,②,④正确,又夹在相互平行的线与平面间的平行线段相等,所以③正确.答案①2.平面α∥平面β,点A,C∈α,B,D∈β,则直线AC∥直线BD的充要条件是________(填序号).①AB∥CD;②AD∥CB;③AB与CD相交;④A,B,C,D四点共面.解析充分性:A,B,C,D四点共面,由平面与平面平行的性质知AC∥BD.必要性显然成立.答案④3.(2015·常州监测)给出下列命题:①若两个平面平行,那么其中一个平面内的直线一定平行于另一个平面;②若两个平面平行,那么垂直于其中一个平面的直线一定垂直于另一个平面;③若两个平面垂直,那么垂直于其中一个平面的直线一定平行于另一个平面;④若两个平面垂直,那么其中一个平面内的直线一定垂直于另一个平面.则其中所有真命题的序号为________.解析利用相关定理逐一判断.由面面平行的性质可知①正确;由线面垂直的性质可知②正确;若两个平面垂直,那么垂直于其中一个平面的直线可能与另一个平面平行,也可能在另一个平面内,所以③错误;若两个平面垂直,那么其中一个平面内垂直于它们交线的直线一定垂直于另一个平面,所以④错误.故真命题序号是①②.答案①②4.(2015·苏州月考)有下列命题:①若直线l平行于平面α内的无数条直线,则直线l∥α;②若直线a在平面α外,则a∥α;③若直线a∥b,b∥α,则a∥α;④若直线a ∥b ,b ∥α,则a 平行于平面α内的无数条直线.其中真命题的个数有________.解析 命题①直线l 可以在平面α内,不正确;命题②直线a 与平面α可以是相交关系,不正确;命题③直线a 可以在平面α内,不正确;命题④正确.答案 15.(2016·淮安调研)已知m ,n 是两条不同的直线,α,β,γ是三个不同的平面,下列命题中错误的有________.①若m ⊥α,m ⊥β,则α∥β;②若α∥γ,β∥γ,则α∥β;③若m ⊂α,n ⊂β,m ∥n ,则α∥β;④若m ,n 是异面直线,m ⊂α,m ∥β,n ⊂β,n ∥α,则α∥β.解析 由线面垂直的性质可知①正确;由两个平面平行的性质可知②正确;由异面直线的性质及面面平行的判定易知④也是正确的;对于③,α,β可以相交、可以平行,故③错误.答案 ③6.(2016·连云港调研)如图所示,在四面体ABCD 中,M ,N 分别是△ACD ,△BCD 的重心,则四面体的四个面中与MN 平行的是________.解析 连接AM 并延长,交CD 与E ,连接BN ,并延长交CD 于F ,由重心性质可知,E ,F 重合为一点,且该点为CD 的中点E ,由EM MA =EN NB =12,得MN ∥AB .因此,MN ∥平面ABC ,且MN ∥平面ABD .答案 平面ABC 、平面ABD7.(2015·盐城二模)已知α,β是两个不同的平面,下列四个条件:①存在一条直线a ,a ⊥α,a ⊥β;②存在一个平面γ,γ⊥α,γ⊥β;③存在两条平行直线a ,b ,a ⊂α,b ⊂β,a ∥β,b ∥α;④存在两条异面直线a ,b ,a ⊂α,b ⊂β,a ∥β,b ∥α.其中是平面α∥平面β的充分条件的为________(填上所有符合要求的序号).解析 对于①,垂直于同一直线的两平面平行,可知①正确;对于②,垂直于同一平面的两平面不一定平行,如三个平面两两垂直,②不正确;对于③,有可能直线a ,b 都与两平面的交线平行,故③不正确;对于④,在平面β内一定存在直线a ′,使得a ′∥a ,从而a ′∥α,这样平面β内两条相交直线都和平面α平行,则平面α∥平面β,④正确.答案 ①④8.(2016·泉州一模)如图,四棱锥P -ABCD 的底面是一直角梯形,AB ∥CD ,BA ⊥AD ,CD =2AB ,PA ⊥底面ABCD ,E 为PC 的中点,则BE 与平面PAD 的位置关系为________.解析 取PD 的中点F ,连接EF ,AF ,在△PCD 中,EF 綊12CD .又∵AB ∥CD 且CD =2AB ,∴EF 綊AB ,∴四边形ABEF 是平行四边形,∴EB ∥AF .又∵EB ⊄平面PAD ,AF ⊂平面PAD ,∴BE ∥平面PAD .答案 平行二、解答题9.如图,在三棱柱ABC -A 1B 1C 1中,D 是BC 上一点,且A 1B ∥平面AC 1D ,D 1是B 1C 1的中点,求证:平面A 1BD 1∥平面AC 1D .证明 如图,连接A 1C 交AC 1于点E ,连接ED .∵四边形A 1ACC 1是平行四边形,∴E 是A 1C 的中点.∵A 1B ∥平面AC 1D ,平面A 1BC ∩平面AC 1D =ED ,∴A 1B ∥ED .∵E 是A 1C 的中点,∴D 是BC 的中点.又D 1是B 1C 1的中点,∴D 1C 1綊BD ,∴四边形BDC 1D 1为平行四边形,∴BD 1∥C 1D .又A 1B ∩BD 1=B ,DE ∩DC 1=D ,∴平面A1BD1∥平面AC1D.10.(2016·苏、锡、常、镇模拟)如图,ABCD与ADEF为平行四边形,M,N,G分别是AB,AD,EF的中点.求证:(1)BE∥平面DMF;(2)平面BDE∥平面MNG.证明(1)如图,连接AE,则AE必过DF与GN的交点O,连接MO,则MO为△ABE的中位线,所以BE∥MO,又BE⊄平面DMF,MO⊂平面DMF,所以BE∥平面DMF.(2)因为N,G分别为平行四边形ADEF的边AD,EF的中点,所以DE∥GN,又DE⊄平面MNG,GN⊂平面MNG,所以DE∥平面MNG.又M为AB中点,所以MN为△ABD的中位线,所以BD∥MN,又BD⊄平面MNG,MN⊂平面MNG,所以BD∥平面MNG,又DE与BD为平面BDE内的两条相交直线,所以平面BDE∥平面MNG.能力提升题组(建议用时:20分钟)11.(2016·泰州调研)若α,β是两个相交平面,则在下列命题中,真命题的序号为________(写出所有真命题的序号).①若直线m⊥α,则在平面β内,一定不存在与直线m平行的直线;②若直线m⊥α,则在平面β内,一定存在无数条直线与直线m垂直;③若直线m⊂α,则在平面β内,一定不存在与直线m垂直的直线;④若直线m⊂α,则在平面β内,一定存在与直线m垂直的直线.解析如图(1),α⊥β,α∩β=l,则β内垂直于l的直线都平行于m,平行于l的直线都垂直于m,①错误,②正确.如图(2),设α∩β=l,若m∥l,则在平面β内一定存在l的垂线,也是m的垂线.若m ∩l =A ,过m 上异于A 的任一点B 作BH ⊥β,垂足为H ,则AH 为AB 在平面β内的射影,平面β内与AH 垂直的直线都垂直于AB .故③错误,④正确.答案 ②④12.在棱长为2的正方体ABCD -A 1B 1C 1D 1中,M 是棱AA 1的中点,过C ,M ,D 1作正方体的截面,则截面的面积是________.解析 由面面平行的性质知截面与面AB 1的交线MN 是△AA 1B 的中位线,所以截面是梯形CD 1MN ,易求其面积为92.答案 9213.如图,在长方体ABCDA 1B 1C 1D 1中,E ,F ,G ,H 分别是棱CC 1,C 1D 1,D 1D ,DC 的中点,N 是BC 的中点,点M 在四边形EFGH 及其内部运动,则M满足条件________时,有MN ∥平面B 1BDD 1.解析 如图,连接FH ,HN ,FN ,由题意知HN ∥面B 1BDD 1,FH ∥面B 1BDD 1.且HN ∩FH =H ,∴面NHF ∥面B 1BDD 1.∴当M 在线段HF 上运动时,有MN ∥面B 1BDD 1.答案 M ∈线段HF14.如图,四棱锥P -ABCD 中,PD ⊥平面ABCD ,底面ABCD 为矩形,PD =DC =4,AD =2,E 为PC 的中点.(1)求三棱锥A -PDE 的体积;(2)AC 边上是否存在一点M ,使得PA ∥平面EDM ?若存在,求出AM 的长;若不存在,请说明理由.解 (1)因为PD ⊥平面ABCD ,所以PD ⊥AD .又因ABCD 是矩形,所以AD ⊥CD .因PD ∩CD =D ,所以AD ⊥平面PCD ,所以AD 是三棱锥A -PDE 的高.因为E 为PC 的中点,且PD =DC =4,所以S △PDE =12S △PDC =12×⎝ ⎛⎭⎪⎫12×4×4=4. 又AD =2,所以V A -PDE =13AD ·S △PDE =13×2×4=83.(2) 取AC 中点M ,连接EM ,DM ,因为E 为PC 的中点,M 是AC 的中点,所以EM ∥PA .又因为EM ⊂平面EDM ,PA ⊄平面EDM ,所以PA ∥平面EDM .所以AM =12AC = 5.即在AC 边上存在一点M ,使得PA ∥平面EDM ,AM 的长为 5.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017高考数学一轮复习 第八章 立体几何 8.3 平行的判定与性质课时练 理 时间:45分钟基础组1.[2016·武邑中学预测]已知m,n为两条不同的直线,α,β为两个不同的平面,则下列为真命题的是( )A.m∥n,m⊥α⇒n⊥αB.α∥β,m⊂α,n⊂β⇒m∥nC.m⊥α,m⊥n⇒n∥αD.m⊂α,n⊂α,m∥β,n∥β⇒α∥β答案 A解析 选项A中,如图①,n∥m,m⊥α⇒n⊥α一定成立,选项A正确.选项B中,如图②,α∥β,m⊂α,n⊂β,m与n互为异面直线,∴选项B不正确.选项C中,如图③,m⊥α,m⊥n,n⊂α,∴选项C不正确.选项D中,如图④,m⊂α,n⊂α,m∥β,n∥β,但α与β相交,∴选项D不正确.2.[2016·衡水二中模拟]直线m,n均不在平面α,β内,给出下列命题:①若m∥n,n∥α,则m∥α;②若m∥β,α∥β,则m∥α;③若m⊥n,n⊥α,则m∥α;④若m⊥β,α⊥β,则m∥α.其中正确命题的个数是( )A.1 B.2C.3 D.4答案 D解析 对命题①,根据线面平行的判定定理知,m∥α;对命题②,如果直线m与平面α相交,则必与平面β相交,而这与α∥β矛盾,故m∥α;对命题③,在平面α内取一点A,设过A,m的平面γ与平面α相交于直线b.因为n⊥α,所以n⊥b,又m⊥n,所以m∥b,则m∥α;对命题④,设α∩β=l,在α内作m′⊥β,因为m⊥β,所以m∥m′,从而m∥α.故四个命题都正确.3.[2016·枣强中学期末]已知m,n是两条不同的直线,α,β,γ是三个不同的平面,下列命题中错误的是( )A.若m⊥α,m⊥β,则α∥βB.若α∥γ,β∥γ,则α∥βC.若m⊂α,n⊂β,m∥n,则α∥βD.若m,n是异面直线,m⊂α,m∥β,n⊂β,n∥α,则α∥β答案 C解析 由线面垂直的性质可知A正确;由两个平面平行的性质可知B正确;由异面直线的性质易知D也是正确的;对于选项C,α,β可以相交、可以平行,故C错误,选C.4.[2016·衡水二中仿真]平面α∥平面β,点A,C∈α,B,D∈β,则直线AC∥直线BD的充要条件是( )A.AB∥CD B.AD∥CBC.AB与CD相交 D.A,B,C,D四点共面答案 D解析 充分性:A,B,C,D四点共面,由平面与平面平行的性质知AC∥BD.必要性显然成立.5.[2016·枣强中学期中]如图,在正四棱柱A1C中,E,F,G,H分别是棱CC1,C1D1,D1D,DC的中点,N是BC的中点,点M在四边形EFGH及其内部运动,则M只需满足条件________时,就有MN∥平面B1BDD1.(注:请填上你认为正确的一个条件即可,不必考虑全部可能情况)答案 M位于线段FH上解析 连接HN,FH,FN,则FH∥DD1,HN∥BD,∴平面FHN∥平面B1BDD1,只要M∈FH,则MN⊂平面FHN,∴MN∥平面B1BDD1. (答案不唯一)6.[2016·冀州中学期末]给出下列关于互不相同的直线l、m、n和平面α、β、γ的三个命题:①若l与m为异面直线,l⊂α,m⊂β,则α∥β;②若α∥β,l⊂α,m⊂β,则l∥m;③若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.其中真命题为________.答案 ③解析 ①中当α与β不平行时,也能存在符合题意的l、m.②中l与m也可能异面.③中⇒l∥m,同理l∥n,则m∥n,正确.7.[2016·衡水中学预测]如图所示,四棱锥P-ABCD的底面是一个直角梯形,AB∥CD,BA⊥AD,CD=2AB,PA⊥底面ABCD.若E为PC 的中点,则BE与平面PAD的位置关系是________.答案 平行解析 取PD的中点F,连接EF,AF.在△PCD中,EF∥CD,且EF =CD.∵AB∥CD,且CD=2AB,∴EF∥AB,且EF=AB,∴四边形ABEF为平行四边形,∴EB∥AF.又∵EB⊄平面PAD,AF⊂平面PAD,∴BE∥平面PAD.8.[2016·枣强中学热身]如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA上的中点.(1)求证:PC∥平面BDE;(2)求四棱锥P-ABCD的体积.解 (1)证明:连接AC交BD于点O,连接OE,如图:∵四边形ABCD是正方形,∴O是AC的中点.又E是PA的中点,∴PC∥OE.∵PC⊄平面BDE,OE⊂平面BDE,∴PC∥平面BDE.(2)∵PA⊥平面ABCD,∴V P-ABCD=S正方形ABCD·PA=×12×2=,∴四棱锥P-ABCD的体积为.9.[2016·衡水中学猜题]已知三棱柱ABC-A′B′C′中,平面BCC′B′⊥底面ABC,BB′⊥AC,底面ABC是边长为2的等边三角形,AA′=3,E,F 分别在棱AA′,CC′上,且AE=C′F=2.(1)求证:BB′⊥底面ABC;(2)在棱A′B′上找一点M,使得C′M∥平面BEF,并给出证明.证明 (1)如图,取BC中点O,连接AO,因为三角形ABC是等边三角形,所以AO⊥BC,又平面BCC′B′⊥底面ABC,AO⊂平面ABC,平面BCC′B′∩平面ABC =BC,所以AO⊥平面BCC′B′,又BB′⊂平面BCC′B′,所以AO⊥BB′.又BB′⊥AC,AO∩AC=A,AO⊂平面ABC,AC⊂平面ABC,所以BB′⊥底面ABC.(2)如图,显然M不是A′,B′,棱A′B′上若存在一点M,使得C′M∥平面BEF,过M作MN∥AA′交BE于N,连接FN,MC′,所以MN∥C′F,即C ′M和FN共面,所以C′M∥FN,所以四边形C′MNF为平行四边形,所以MN=2,所以MN是梯形A′B′BE的中位线,M为A′B′的中点.10.[2016·衡水中学一轮检测]如图所示,在棱长均为4的三棱柱ABC-A1B1C1中,D,D1分别是BC和B1C1的中点.(1)求证:A1D1∥平面AB1D;(2)若平面ABC⊥平面BCC1B1,∠B1BC=60°,求三棱锥B1-ABC 的体积.解 (1)证明:如图所示,连接DD1,在三棱柱ABC-A1B1C1中,因为D,D1分别是BC与B1C1的中点,所以B1D1∥BD,且B1D1=BD.所以四边形B1BDD1为平行四边形,所以BB1∥DD1,且BB1=DD1.又因为AA1∥BB1,AA1=BB1,所以AA1∥DD1,AA1=DD1,所以四边形AA1D1D为平行四边形,所以A1D1∥AD.又A1D1⊄平面AB1D,AD⊂平面AB1D,故A1D1∥平面AB1D.(2)在△ABC中,因为AB=AC,D为BC的中点,所以AD⊥BC.因为平面ABC⊥平面B1C1CB,交线为BC,AD⊂平面ABC,所以AD⊥平面B1C1CB,即AD是三棱锥A-B1BC的高.在△ABC中,因为AB=AC=BC=4,得AD=2.在△B1BC中,B1B=BC=4,∠B1BC=60°,所以△B1BC的面积S△B1BC=×4×4×=4,所以三棱锥B1-ABC的体积即三棱锥A-B1BC的体积,V=S△B1BC·AD=×4×2=8.11.[2016·冀州中学模拟]如图,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E、F、G分别是BC、DC、SC的中点,求证:(1)直线EG∥平面BDD1B1;(2)平面EFG∥平面BDD1B1.证明 (1)如图,连接SB,∵E、G分别是BC、SC的中点,∴EG∥SB.又∵SB⊂平面BDD1B1,EG⊄平面BDD1B1,∴直线EG∥平面BDD1B1.(2)连接SD,∵F、G分别是DC、SC的中点,∴FG∥SD.又∵SD⊂平面BDD1B1,FG⊄平面BDD1B1,∴FG∥平面BDD1B1,又EG⊂平面EFG,FG⊂平面EFG,EG∩FG=G,∴平面EFG∥平面BDD1B1.12.[2016·衡水二中周测]如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥平面ABCD,∠BAD=,AD=2.(1)求证:平面FCB∥平面AED;(2)若二面角A-EF-C为直二面角,求直线BC与平面AEF所成的角θ的正弦值.解 (1)证明:在矩形BDEF中,FB∥ED,∵FB⊄平面AED,ED⊂平面AED,∴FB∥平面AED,同理BC∥平面AED,又FB∩BC=B,∴平面FBC∥平面EDA.(2)取EF的中点M.连接AM,CM.连接AC交BD于点N.由于ED⊥平面ABCD,ED∥FB,∴ED⊥AD,ED⊥DC,FB⊥BC,FB⊥AB.又ABCD是菱形,BDEF是矩形,∴△ADE,△EDC,△ABF,△BCF是全等三角形,∴AE=AF,CE=CF,∴AM⊥EF,CM⊥EF,∠AMC就是二面角A-EF-C的平面角.解法一:(几何法)延长CB到G,使BC=BG,由已知可得,ADBG是平行四边形,又BDEF是矩形,∴AEFG是平行四边形,即A,E,F,G共面,由此可知,AM⊥MC,CM⊥EF,EF,AM相交于M,∴CM⊥平面AEFG,∠CGM为所求.由AD=2,∠DAB=60°,得AC=2,等腰Rt△AMC中,AC=2,可得MC=,Rt△GMC中,sin∠CGM==.解法二:(向量法)以D为原点,DC为y轴,DE为z轴,建立如图的直角坐标系,由AD =2,则M,C(0,2,0),平面AEF的法向量n==.==(,-1,0),cos〈n,〉==-.∴sinθ=.能力组13.[2016·枣强中学仿真]已知m,n,l1,l2表示直线,α,β表示平面.若m⊂α,n⊂α,l1⊂β,l2⊂β,l1∩l2=M,则α∥β的一个充分条件是( )A.m∥β且l1∥α B.m∥β且n∥βC.m∥β且n∥l2 D.m∥l1且n∥l2答案 D解析 由定理“如果一个平面内有两条相交直线分别与另一个平面平行,那么这两个平面平行”可知,选项D可推知α∥β.14.[2016·衡水二中月考]平面α∥平面β的一个充分条件是________(填写正确的序号).①存在一条直线a,a∥α,a∥β;②存在一条直线a,a⊂α,a∥β;③存在两条平行直线a,b,a⊂α,b⊂βa∥β,b∥α;④存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α.答案 ④解析 根据两平面平行的条件,只有④符合.15. [2016·武邑中学热身]在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.(1)若AC⊥BC,证明:直线BC⊥平面ACC1A1;(2)设D,E分别是线段BC,CC1的中点,在线段AB上是否存在一点M,使直线DE∥平面A1MC?请证明你的结论.解 (1)证明:因为四边形ABB1A1和ACC1A1都是矩形,所以AA1⊥AB,AA1⊥AC.因为AB,AC为平面ABC内两条相交直线,所以AA1⊥平面ABC.因为直线BC⊂平面ABC,所以AA1⊥BC.又AC⊥BC,AA1,AC为平面ACC1A1内两条相交直线,所以BC⊥平面ACC1A1.(2)取线段AB的中点M,连接A1M,MC,A1C,AC1,设O为A1C,AC1的交点.由已知可知O为AC1的中点.连接MD,OE,则MD,OE分别为△ABC,△ACC1的中位线,所以MD綊AC,OE綊AC,因此MD綊OE.连接OM,从而四边形MDEO为平行四边形,则DE∥MO.因为直线DE⊄平面A1MC,MO⊂平面A1MC,所以直线DE∥平面A1MC,即线段AB上存在一点M(线段AB的中点),使直线DE∥平面A1MC.。
