材料力学第10章 强度理论
材料力学性能-第2版课后习题答案

第一章 单向静拉伸力学性能1、 解释下列名词。
2.滞弹性:金属材料在弹性范围内快速加载或卸载后,随时间延长产生附加弹性应变的现象称为滞弹性,也就是应变落后于应力的现象。
3.循环韧性:金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。
4.包申格效应:金属材料经过预先加载产生少量塑性变形,卸载后再同向加载,规定残余伸长应力增加;反向加载,规定残余伸长应力降低的现象。
11.韧脆转变:具有一定韧性的金属材料当低于某一温度点时,冲击吸收功明显下降,断裂方式由原来的韧性断裂变为脆性断裂,这种现象称为韧脆转变2、 说明下列力学性能指标的意义。
答:E 弹性模量 G 切变模量 r σ规定残余伸长应力 2.0σ屈服强度 gt δ金属材料拉伸时最大应力下的总伸长率 n 应变硬化指数 【P15】3、 金属的弹性模量主要取决于什么因素?为什么说它是一个对组织不敏感的力学性能指标?答:主要决定于原子本性和晶格类型。
合金化、热处理、冷塑性变形等能够改变金属材料的组织形态和晶粒大小,但是不改变金属原子的本性和晶格类型。
组织虽然改变了,原子的本性和晶格类型未发生改变,故弹性模量对组织不敏感。
【P4】4、 现有45、40Cr 、35 CrMo 钢和灰铸铁几种材料,你选择哪种材料作为机床起身,为什么?选灰铸铁,因为其含碳量搞,有良好的吸震减震作用,并且机床床身一般结构简单,对精度要求不高,使用灰铸铁可降低成本,提高生产效率。
5、 试述韧性断裂与脆性断裂的区别。
为什么脆性断裂最危险?【P21】答:韧性断裂是金属材料断裂前产生明显的宏观塑性变形的断裂,这种断裂有一个缓慢的撕裂过程,在裂纹扩展过程中不断地消耗能量;而脆性断裂是突然发生的断裂,断裂前基本上不发生塑性变形,没有明显征兆,因而危害性很大。
6、 何谓拉伸断口三要素?影响宏观拉伸断口性态的因素有哪些?答:宏观断口呈杯锥形,由纤维区、放射区和剪切唇三个区域组成,即所谓的断口特征三要素。
材料力学强度理论

材料力学强度理论
材料力学强度理论是材料力学的一个重要分支,它研究材料在外力作用下的强
度和变形特性。
材料的强度是指材料抵抗破坏的能力,而变形特性则是指材料在外力作用下的形变行为。
强度理论的研究对于材料的设计、制备和应用具有重要意义。
首先,强度理论可以帮助我们了解材料的破坏机制。
材料在外力作用下会发生
破坏,而不同的材料在受力时表现出不同的破坏模式,比如拉伸、压缩、剪切等。
强度理论可以通过实验和理论分析,揭示材料在受力时的破坏机制,为材料的设计和选用提供依据。
其次,强度理论可以指导材料的合理使用。
在工程实践中,我们需要根据材料
的强度特性来选择合适的材料,并确定合理的使用条件。
强度理论可以帮助我们评估材料在特定工况下的承载能力,从而保证材料的安全可靠使用。
此外,强度理论还可以为材料的改进和优化提供指导。
通过对材料强度特性的
研究,我们可以发现材料的强度局限性,并提出改进的方案。
比如,可以通过合金化、热处理等手段来提高材料的强度,或者通过结构设计来减小应力集中,提高材料的抗破坏能力。
综上所述,材料力学强度理论是材料科学中的重要内容,它不仅可以帮助我们
了解材料的破坏机制,指导材料的合理使用,还可以为材料的改进和优化提供指导。
在未来的研究和工程实践中,我们需要进一步深入研究强度理论,不断提高材料的强度和可靠性,为社会发展和科技进步做出贡献。
材料力学练习-知识归纳整理
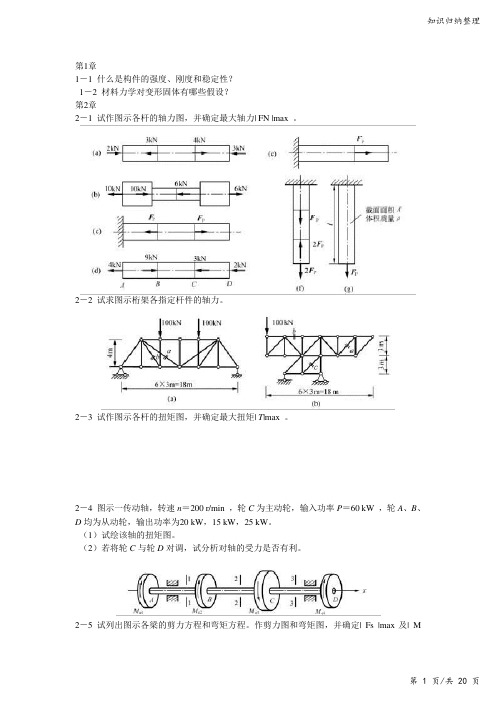
知识归纳整理第1章1-1 什么是构件的强度、刚度和稳定性?1-2 材料力学对变形固体有哪些假设?第2章2-1 试作图示各杆的轴力图,并确定最大轴力| FN |max 。
2-2 试求图示桁架各指定杆件的轴力。
2-3 试作图示各杆的扭矩图,并确定最大扭矩| T|max 。
2-4 图示一传动轴,转速n=200 r/min ,轮C为主动轮,输入功率P=60 kW ,轮A、B、D均为从动轮,输出功率为20 kW,15 kW,25 kW。
(1)试绘该轴的扭矩图。
(2)若将轮C与轮D 对调,试分析对轴的受力是否有利。
2-5 试列出图示各梁的剪力方程和弯矩方程。
作剪力图和弯矩图,并确定| Fs |max及| M求知若饥,虚心若愚。
|max 值。
2-6 试用简易法作图示各梁的剪力图和弯矩图,并确定| F s |max及| M|max值,并用微分关系对图形举行校核。
2-7 图示起重机横梁AB承受的最大吊重F P=12kN,试绘出横梁A B 的内力图。
2-8 图示处于水平位置的控制手柄,在自由端C处受到一铅垂向下的集中力F p作用。
试画出AB段的内力图。
千里之行,始于足下。
第3章3-1图示圆截面阶梯杆,承受轴向荷载F1=50kN与F2的作用,AB与BC段的直径分别为d1=20mm与d2=30mm,如欲使AB与BC段横截面上的正应力相同,试求荷载F2之值。
3-2变截面直杆如图所示。
已知A1=8cm2,A2=4cm2,E=200GPa 。
求杆的总伸长量。
3-3 在图示结构中,AB为刚性杆,CD为钢斜拉杆。
已知F P1=5kN ,F P2=10kN ,l=1m ,杆CD的截面积A=100mm2 ,钢的弹性模量E=200GPa 。
试求杆CD的轴向变形和刚性杆AB在端点B 的铅垂位移。
3-4 一木柱受力如图所示。
柱的横截面为边长200mm的正方形,材料可以为符合胡克定律,其弹性模量E=10GPa。
如不计柱的自重,试求:求知若饥,虚心若愚。
09材料力学强度理论

2016/11/20单向拉伸时材料的破坏准则可通过试验很容易地建立起来・9.1强度理论的概念 问题的提一出 强度:保证构件不发生破坏.也即保证构件中每一点 不发生破坏.如何保证? 建立强度条件:I 计算应力卡许用值I 于向力态 对单应状 单向拉伸(压缩)纯剪 2016/11/20 塑性材料屈服破坏 腌性材料斷裂破坏ma % 是否强度就没有问题了? 2016/11/20 9.1强度理论的概念 建立送应条件:肚算应力K 胖用值] 于杂力态 对复应状 构件强度安生_ 、:]结构计算 确定危险点及其 应力状态 计算应力 通过实验或规范 建立复杂应力状态下的强度条件的问题: 选取何值作为计算应力? 这就是强度理论的内容. 即强度理论的选取问題.强40^选取与材料的破坏形式有关・2016/11/208复杂应力状态(二向应力状态或三向应力状态),材料的破坏与三个主应力的大小、正负的排列,及主应力间的比 例有关.各种组合很多,无法通过试验一一对应地建立破坏 准則.于是,人们比着单向拉伸提出一些假说,这些假说通 常称为怎度理论,并根据这些理论建立相应的强度条件2016/11/20利用单向应力状态的实验结果,分 建立复杂应力状态的强度条件.o 69.1强度理论的概念强度理论研究途径7-2 v经典强度理论强度理论:人们根据大量的破坏现象,通过判断推理、概括,提出了种种关于破坏原因的假说,找出引起破坏的主要因素,经过实践检验,不断完善,在一定范围与实际相符合,上升为理论。
为了建立复杂应力状态下的强度条件,而提出的关于材料破坏原因的假设及计算方法。
2016/11/207-2 v经典强度理论旃件由于强度不足将引发两种失效形式(D 脆性断裂:材料无明显的塑性变形即发生断裂, 断面较粗糙,且多发生在垂直于最大正应力的截面上, 如铸铁受拉、扭,低温脆断等。
关于断裂的强度理论:最大拉应力理论和最大伸长线应变理论(2)塑性屈服(流动):材料破坏前发生显著的塑性变形,破坏断面粒子较光滑,且多发生在最大剪应力面上,例如低碳钢拉、扭,铸铁压。
材料力学应力状态和强度理论

x 122.5MPa x 64.6MPa
σy 0
τ y 64.6
(122.5 , 64.6)
D1
B2
o
C
B1
(0 , - 64.6)
由 x , x 定出 D1 点 由 y , y 定出 D2 点 以 D1D2 为直径作应力圆。
D2
A1,A2 两点的横坐标分别代表 a 点的两个主应力
1 oA1 150MPa
1 x 136.5MPa
σ x 136.5MPa σy 0
τx0 τy0
2 3 0
D2 (0,0)
D1(136.5,0)
x 136.5MPa
b
σ1
σ x 136.5MPa τ x 0
σy 0
τy0
1 所在的主平面就是 x 平面 , 即梁的横截面 C 。
解析法求 a 点的主平面和主应力
解: x 100MPa, y 20MPa, x 40MPa, 300
20
300
100 40
x 100MPa, y 20MPa, x 40MPa, 300
x
2
y
x
2
y
cos
2
x
sin
2
x
2
y
sin
2
x
cos
2
300
100
(20) 2
100
(20) 2
cos( 600)
m
F
A
F
m
A
F
F
A
A 点 横截面 m—m 上的应力为: F
A
n
m
F
A
F
m
n
F
A
2
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第10章 组合受力与变形杆件的强度计算

解:危险截面在 A 处,其上之内力分量为: 弯矩: M y = FP1 a , M z = FP2 H 扭矩: M x = FP2 a 轴力: FNx = FP1 在截面上垂直与 M 方向的垂直线 ab 与圆环截 求得 M y 与 M z 的矢量和 M 过截面中心, 面边界交于 a、b 两点,这两点分别受最大拉应力和最大压应力。但由于轴向压力的作用,最 大压应力值大于最大拉应力值,故 b 点为危险点,其应力状态如图所示。 10-7 试求图 a 和 b 中所示之二杆横截面上最大正应力及其比值。 解: (a)为拉弯组合
7
y
y
A
O
0.795
B
14.526
+13.73MPa
z
(a)
O O
+14.43MPa
(b)
C
y
A
C
B B
y
A
O O
B
z
12.6mm
14.1mm
zC
−15.32MPa
16.55MPa
zC
z
(c)
(d)
习题 10-9 解图
∴
+ σ max
= 14.526 − 0.795 = 13.73 MPa
− σ max = −14.526 − 0.795 = −15.32 MPa
Ebh
由此得
2 FP 6e
e=
10-9
ε1 − ε 2 h × ε1 + ε 2 6
图中所示为承受纵向荷载的人骨受力简图。试:
1.假定骨骼为实心圆截面,确定横截面 B-B 上的应力分布; 2.假定骨骼中心部分(其直径为骨骼外直径的一半)由海绵状骨质所组成,忽略海绵状承受 应力的能力,确定横截面 B-B 上的应力分布;
13-3四个强度理论-材料力学

强度计算。
例1 图示几种单元体,分别按第三和第四强度理论 求相当应力(单位MPa)
60
100
(1)
40 100
40
(2)
10
60
30 (3)
例2 直径为d=0.1m的圆杆受力如图,T=7kNm,P=50kN, 为铸铁构
件,[]=40MPa,试用第一强度理论校核杆的强度。
7.7
0
0
所以,此容器不满足第三强度理论。不安全。
第三强度理论(第三相当应力) xd3 1 3
第四强度理论(第四相当应力)
xd 4
1 2
1
2
2
2
3
2
3
1
2
三、强度计算的步骤:
1、外力分析:确定所需的外力。 2、内力分析:画内力图,确定可能的危险面。 3、应力分析:画危险截面应力分布图,确定危险点并画出单元
2
1
2 2
2
3 2
3
1 2
3、实用范围:实用于破坏形式为屈服的构件。
第一、第二强度理论适合于脆性材料; 第三、第四强度理论适合于塑性材料。 1、伽利略1638年提出了第一强度理论; 2、马里奥特1682年提出了第二强度理论;
3、杜奎特(C.Duguet)提出了最大剪应力理论;也有一说是库 伦1773年提出,特雷斯卡1868完善的。
到单向拉伸的强度极限时,构件就发生断裂。
1、破坏判据: 1 b ;( 1 0)
2、强度准则: 1 ; ( 1 0)
3、实用范围:实用于破坏形式为脆断的构件。
[工学]材料力学中强度理论
![[工学]材料力学中强度理论](https://img.taocdn.com/s3/m/157e146fe518964bcf847cbb.png)
强度理论中直接与 [σ ] 比 1 b 较的量,称为相当应力σri b 1
nb
r1
1
15
r1 1
实验表明:该理论对于大部分脆性材料受拉应力作
用,结果与实验相符合,如铸铁受拉伸、扭转。
局限性: (1)没有考虑另外二个主应力的影响;
s
ns
实验表明:该理论对于塑性材料的屈服破坏能够得到
较为满意的解释,并能解释材料在三向均压下不发生
(2)无法应用于没有拉应力的应力状态; (3)无法解释塑性材料的破坏;
(4)无法解释三向均压时,既不屈服、也不破坏
的现象。
2018/11/20 16
(一)关于断裂的强度理论
2、最大拉应变理论(第二强度理论) (Maximum Tensile-Strain Criterion)
无论材料处于什么应力状态,只要发生脆性断裂, 都是由于单元体内的最大拉应变(线变形)达到简单 拉伸时的破坏伸长应变值。
无论材料处于什么应力状态 ,只要发生脆性断裂,
都是由于单元体内的最大拉应力达到了一个共同的
极限值。
2018/11/20
t max
o max
14
1、最大拉应力理论
t max
o max
2
1 3
= b
t max
1 (1 0)
o max
b
断裂条件
强度条件
2018/11/20
18
2018/11/20
r 2 1 ( 2 3 ) [ ]
实验表明:该理论对于一拉一压的二向应力状态的 脆性材料的断裂较符合,如铸铁受拉压比第一强度 理论更接近实际情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
0.42m
C
解: 1、作内力图,确定危险截面 FQmax 200kN,M max 84kN m
t 1 3 t c
材料力学
第10章 强度理论
§10-4 强度理论的应用 一、强度条件的统一式
r [ ]
第一强度理论
r 称为相当应力
r1 1
r 3 1 3
(Tresca应力)
第二强度理论 r 2 1 ( 2 3 ) 第三强度理论
历史点滴:
贝尔特拉密(E.Beltrami,1885)首先提出能量理论,后经 胡贝尔(F.Huber,1904)、米塞斯(R.Mises,1913)和汉 基(H.Hencky,1924)分别提出建议,认为不是以全部比能, 而是以改变材料形状的那一部分比能作为引起材料屈服的主要 因素。这一理论是在20世纪初期形成并在第三强度理论之后提 出与应用的,通常称第四强度理论。
26
材料力学
第10章 强度理论
§10-4 强度理论的应用 一、强度条件的统一式 r [ ] 二、强度计算的步骤: 三、强度理论选用一般规则: 常温、静载荷
对脆性材料:
在三向压缩应力状态下材料的破坏为屈服失效,应采用第三 或第四强度理论。 在复杂应力状态下的最大和最小主应力分别为拉应力和压应 力的情况下,宜采用莫尔强度理论。 在其他应力状态下材料的破坏为脆断,采用第一强度理论。
E
u
E
材料直到破坏时
1
3 = b
E
1 2 3 u 主应力表示的破坏条件
强度条件:
1 2 3 ≤[ ]=
u
n
材料力学
第10章 强度理论Fra bibliotek§10-2 四种常用的强度理论
一、关于断裂的强度理论
2.最大拉应变理论(第二强度理论、最大伸长线应变理论)
§10-2 四种常用的强度理论
一、关于断裂的强度理论
1.最大拉应力理论(第一强度理论) 优缺点: 实验证明,对于脆性材料,如铸铁、砖、岩石、混凝土、 陶瓷等脆性材料,不论在何种复杂应力状态下,其脆性脆性 断裂破坏,均发生在最大拉应力所在的截面上。此理论计算 简单,应用广泛,但没有考虑σ2、σ3对破坏的影响,在三轴 压缩应力状态下,显然此理论不适合。
第四强度理论
r4
1 [( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 ] 2
(Mises应力)
莫尔强度理论
rM
[ t ] 1 3 [ c ]
材料力学
第10章 强度理论
§10-4 强度理论的应用 一、强度条件的统一式 r [ ] 二、强度计算的步骤: 1、外力分析:确定所需的外力值。 2、内力分析:画内力图,确定可能的危险面。 3、应力分析:画危面应力分布图,确定危险点并画出单元体, 求主应力。 4、强度分析:选择适当的强度理论,计算相当应力,然后进行 强度计算。 在工程实际中,解决具体问题时,选用哪一种强度理论是一个 比较复杂的问题,需根据材料种类,受力情况,荷载的性质(静 、动)以及环境温度等因素决定。
2、按正应力条件选择截面 M max M max 84 103 6 3 ≤[ ] Wz≥ 494 10 m Wz [ ] 170 106 查型钢表选择28a工字钢。 4 I 3、切应力强度校核 I z 7114cm , z* =24.62,d =8.5cm Sz FQmax 200 103 max 2 3 Iz 24.62 10 8.5 10 d * Sz
强度条件:
1 [(1 2 )2 ( 2 3 )2 ( 3 1 )2 ]≤[ ] 2
材料力学
第10章 强度理论
§10-2 四种常用的强度理论 二、关于屈服的强度理论 2.形状改能密度理论(第四强度理论)
优缺点:
同时考虑了三个主应力的影响,同许多塑性材料的试验结果 相符合,相对于第三强度理论更精确,偏向于经济。
材料力学
第10章 强度理论
第十章 强度理论
材料力学
第10章 强度理论
• • • •
本章主要内容 强度理论的概念 四种常用的强度理论 强度理论的应用
材料力学
第10章 强度理论
§10-1 强度理论的概念
一、强度条件回顾
①正应力强度条件 轴向拉压 梁截面上下边缘
单向应力状态
σ σ
纯切应力状态
max ≤
280
z
a y
τ
σa
a
95.5MPa≤[ ]=100MPa
满足切应力强度要求。 4、主应力强度校核
材料力学
第10章 强度理论
例题1 两端简支的工字钢承受荷载如图所示,已知[ ]=170MPa, [ ]=100MPa,试按强度条件选择工字钢的型号。
200kN
200kN B D
1.66m 0.42m
提出的假说:
2 3
1
形状改变能密度是引起材料屈服破坏的原因。
屈服条件:
vd vdu
1 vdu .2 s2 6E
1 s , 2 3 0
代入上式
= s
三向应力状态 vd 1 [( 1 2 )2 ( 2 3 ) 2 ( 3 1 ) 2 ] 6E 单向应力状态
材料力学
第10章 强度理论
§10-3 莫尔强度理论 一、莫尔(Mohr)强度理论 莫尔认为:最大剪应力是使物体破坏的主要因素,但滑移面上的 摩擦力也不可忽略(莫尔摩擦定律)。综合最大剪应力及最大正应 力的因素,莫尔得出了他自己的强度理论。 莫尔强度理论是以几种典型应力状态下材料的破坏试验结果 为依据,而建立的带有一定经验性的强度理论。 强度条件:
材料力学
第10章 强度理论
§10-3 莫尔强度理论 二、 莫尔强度理论简介与推导
任何复杂应力状态下,以主应力1, 3作出的应力圆都不得与许用包络线 相交,而强度条件则以该应力圆与许 用包络线相切的条件来建立。
O3 N O3O1 O2 P O2O1
(a)
1 1 其中: O3 N O3 K O1 L 1 3 t
对塑性材料:
在三向等拉应力状态(或接近)下材料的破坏为脆断,应采用 第一强度理论。 在其他应力状态下材料的破坏为屈服失效,采用第三或第 四强度理论。
26
材料力学
第10章 强度理论
例题1 两端简支的工字钢承受荷载如图所示,已知[ ]=170MPa, [ ]=100MPa,试按强度条件选择工字钢的型号。
1
[ t ] 3 [ t ] [ c ]
当 [ t ] [ c ] [ ] 时,有
1 3 [ ]
莫尔强度理论可以看作是最大切应力理论的发展,考虑 了材料拉压强度不等的因素。
材料力学
第10章 强度理论
§10-3 莫尔强度理论 二、 莫尔强度理论简介与推导 按照材料在某些应力状态下破 坏时的主应力1,3可作出一组应力 圆——极限应力圆(如图),这组极限 应力圆有一条公共包络线(即极限包 络线,一般情况下为曲线,如图中 的曲线ABC和与它对称的另一曲线)。 莫尔强度理论认为,对于某一给 定的应力状态(1,2,3 )如果由1与 3所作应力圆与上述极限包络线相切 或相交,则表示材料要发生强度破坏。 在工程应用中,往往根据单轴拉伸和单轴压缩的强度试 验结果作两个极限应力圆定出公切线(直线)作为极限包络线。
材料力学
第10章 强度理论
§10-2 四种常用的强度理论 二、关于屈服的强度理论 1.最大切应力理论(第三强度理论)
提出的假说:
2 3
最大切应力是引起材料屈服破坏的原因 。
屈服条件:
1
max u
u s
2
三向应力状态
max
1 3
2
单向应力状态
= s
用主应力表示
历史点滴:
远在17世纪,伽利略(G. Galileo,1638)首先提出最大 正应力理论,后来又经过拉梅(me,1833)和兰金 (W.J.Rankine,1859)的修正而成为最大拉应力理论,由于 该理论是最早提出的强度理论,所以也称最大拉应力理论为第 一强度理论。
材料力学
第10章 强度理论
历史点滴:
库仑(C.A.Coulomb,1773)首先提出这个理论,后经屈雷斯加 (H.Tresca,1868)、格斯特(J.J.Guest,1900)和其他学者的 试验所验证。由于最大剪应力理论是在最大伸长线应变理论之后 提出的,因此,也将这一理论称为第三强度理论。
材料力学
第10章 强度理论
§10-2 四种常用的强度理论 二、关于屈服的强度理论 2.形状改能密度理论(第四强度理论)
材料力学
第10章 强度理论
§10-2 四种常用的强度理论
一、关于断裂的强度理论
1.最大拉应力理论(第一强度理论)
提出的假说:
2
1
3 = b
最大拉应力是引起材料断裂破坏的原因。
脆性断裂破坏的条件:
1 u
强度条件:
u材料的极限应力
1≤[ ]=
u
n
材料力学
第10章 强度理论
200kN
200kN B D
1.66m 0.42m
解: 1、作内力图,确定危险截面
C、D截面
A
0.42m
C
FQmax 200kN,M max 84kN m
200 FQ
(kN)
M (kN .m) 84
122
200
126.3 126.3 13.7 13.7
8.5
σ max τ σa τ
