中考数学专题训练---一题多变
初中平面几何一题多变

平面几何一题多变在完成一个数学题的解答时,有必要对该题的容、形式、条件、结论,做进一步的探讨, 真正掌握该题所反映的问题的实质。
如果能对一个普通的数学题进行一题多变,解题方法;从变中发现解题规律,从变中发现“不变”,必将使人受益匪浅。
“一题多变”的常用方法有:1、 变换命题的条件与结论;2、 保留条件,深化结论;3、 减弱条件,加强结论;4、 探讨命题的推广;5、 考查命题的特例;6、 生根伸枝,图形变换;7、 接力赛,一变再变;8、 解法的多变等。
题1、已知,ZkREC 中,ZACB70度,D 为垂是=求证,01,图中有几条线段?监 图中有几个角,是哪几个角?03.图中有哪几个三角形,请你写出来.04.图中和ZCAB 相等的是嘱些角?和ZCAB 互余的角是哪些角?05. AAEC 中,BC 也上的高是哪条线段? AABR 的垂心是()点-0^ 求证:AC - - CD07.求证;SAADC : SACDB-^D : DB08、求证;AABC ^AACD ^ACBDm 月芒==AD 奶0L 求证;BC- = BDAB1 卜求证! AC- + BC- - AB''1U 如 S AC=3B,C,那么 5CD-2AB12、 如果 AE =2BD-那么 A 咨=53。
'13、求证;IWD3 蜷址14、 求证:二 以 从变中总结CD 2 孙15、设AB 的中点.为M,求证!AC- ^BC-I日噌加题!的条件)DE_LA C于E, DF_LBC于F,(2) 、CD^CECF AB《3)、职AE = BC\必17」增加题1的条件)CE平分曷CD求证:^AD AB低(增加题1的条件)在麋图中.作匕BCE=《BCD木证;BDt DA^CE\ AE:19、(增加题1的条件)AE平分Z BAC交BC于E,求证:CE: EB=CD: CB 20、(增加题1的条件)CE平分Z BCD, AF平分Z BAC交BC于F 求证:(1) BF CE= BE DF(2)AE±CF(3)设AE与CD交于Q,贝U FQ IBC21、已知,△ ABC中,/ ACB=90度,CD± AB, D为垂足,以CD为直径的圆交AC、BC 于E、F,求证:CE: BC=CF: AC (注意本题和16题有无联系)22、已知,△ ABC中,Z ACB=90度,CD± AB, D为垂足,以AD为直径的圆交AC于E, 以BD为直径的圆交BC于F,求证:EF是③O1和③O2的一条外公切线23、已知,△ ABC中,Z ACB=90度,CD± AB, D为垂足,作以AC为直径的圆O1 ,和以CD为弦的圆O2,求证:点A到圆O2的切线长和AC相等(AT=AC)24、已知,△ ABC 中,Z ACB=90 度,CD± AB, D 为垂足,E为ACD的中点,连ED并延长交CB的延长线于F,求证:DF: CF=BC: AC 25、如图,O O1与OO2外切与点D, 公切线DO交外公切线EF于点O, 求证:OD是两圆半径的比例中项。
湘教版九年级数学中考复习:一题多解专项练习(含解析)

初中数学一题多解(试题)1、若()16x 3-m 2x 2++ 是关于x 的完全平方公式(或完全平方数),则m=2、4的平方根为 ,16的平方根为 3、若2a =时, a 为 。
在数轴上,到原点的距离为3个单位的数有 。
4、若64x 1x 2=⎪⎭⎫ ⎝⎛+ ,则代数式=+x 1x 5、若关于x 的方程16-x 3m 4x m 4-x 12+=++无解,则m 的值为 6、在平面直角坐标系xoy 中,已知点A (3,4),点P 在x 轴上,若△AOP 为等腰三角形,则点P 的坐标是7、在一个等腰三角形中,有一个角为70°,则另两个角分别为8、已知直角三角形的两边长分别为5和12,那么以这个直角三角形的斜边为边长的正方形的面积为9、 在△ABC 中,AB=15,AC=13,BC 边上的高为12,求BC 边的边长为10、在平行四边形ABCD 中,∠A 的角平分线把BC 边分为3和4的两条线段,则此平行四边形ABCD 的周长为11、若⊙O 的半径为5cm ,某个点A 到圆上的距离为2cm ,则圆心到点A 的距离为12、 若⊙O 中的某条弦AB 所对的圆心角为120°,则弦AB 所对的圆周角为13、已知x满足62x1x22=+,则x1x+的值是14、当-2≤x≤1时,二次函数()1mm-x-y22++=有最大值4,则实数m 的值为15、在平面直角坐标系中有一点M,点M到x轴的距离为3,到y轴的距离为4,则点M的坐标为16、若某条线段AB长为2,则该线段AB的黄金分割点离A点的距离为17、若△OAB与△OCD是以坐标原点O为位似中心的位似图形,相似比为3:4,∠OCD=90°,∠AOB=60°,若点B的坐标为(6,0),则点A的对应点C的坐标为18、如下图在△ABC中,AB=5,AC=4,点Q从点A出发向点B以2个单位/s的速度出发,点P从点C向点A以1个单位/s的速度出发,若要使△ABC 与△AQP相似,则运动的时间为s。
——“多题归一,一题多变”例图解析
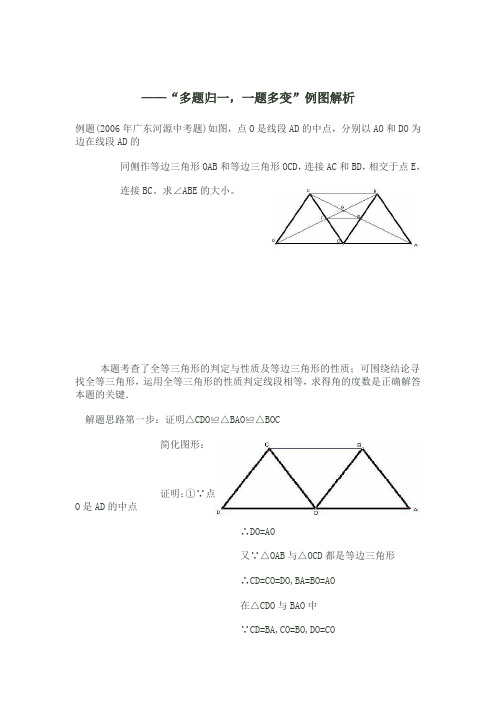
——“多题归一,一题多变”例图解析例题(2006年广东河源中考题)如图,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC。
求∠ABE的大小。
本题考查了全等三角形的判定与性质及等边三角形的性质;可围绕结论寻找全等三角形,运用全等三角形的性质判定线段相等,求得角的度数是正确解答本题的关键.解题思路第一步:证明△CDO≌△BAO≌△BOC简化图形:证明:①∵点O是AD的中点∴DO=AO又∵△OAB与△OCD都是等边三角形∴CD=CO=DO,BA=BO=AO在△CDO与BAO中∵CD=BA,CO=BO,DO=CO∴△CDO≌△BAO∴∠COD=∠BOA=60º∵∠COD+∠COB+∠BOA=180º∴∠COB=180º-∠COD-∠COB=180º-60º-60º=60º在四边形CDAB中∵∠BCD+∠CDA+∠DAB+∠CBA=360º∴∠DCB+∠ABC=360º-∠CDA-∠BAD=360º-60º-60º=240º∵∠1+∠2+∠OBC+∠OCB=240º且∠1=∠2=60º∴∠OBC+∠OCB=240º-60º-60º=120º又∵OC=OB∴∠OCB=∠OBC∴∠OCB=∠OBC=1\2×120º=60º∴△COB是等边三角形且全等于△CDO和△BAO②∵∠COD=∠BOA∴∠COD+∠COB=∠BOA+∠COB即∠DOB=∠AOB在△BOD与△COA中∵OB=OC,∠DOB=∠AOC,OD=OA∴△BOD≌△COA∵OD=OB∴∠BDO=∠DBO∵∠DOB=∠COD+∠COB=60º+60º=120º且∠BDO+∠DBO+∠DOB=180º∴∠BDO=∠DBO=(180º-120º) ÷2=30º∵△BOD≌△COA∴∠CAD=∠DBO在△BEG与△AOG中∵∠CAD=∠DBO,∠EGB=∠OGA∴△BEG∽△AOG∴∠GOA=∠AEB=60º由此图经证明得到的更多结论:Ⅰ.△AOC≌△DOBⅡ.∠BEA=60ºⅢ.AC=BD.Ⅳ. △AOG≌△BOFⅤ.FG∥ADⅥ.1\OA+1\OD=1\FG当图形如下图,结论同理,与第一幅图一致。
初中数学“一题多变”的训练策略

初中数学“一题多变”的训练策略
初中数学的一题多变是指一个问题可以根据不同的情境和条件进行变换,从而得到不同的题目。
这种训练策略有助于学生掌握数学的基本概念和解题方法,提高解题能力和思维灵活性。
以下是初中数学“一题多变”的训练策略。
通过改变题目的条件来变换问题。
对于一个求两数之和的问题,可以改变题目条件为求两数之差或者两数之积。
这样可以让学生从不同的角度思考问题,加深对数学概念和运算方法的理解。
可以通过改变题目的情境来变换问题。
一个问题是求两个人同时从不同地点出发到达相同地点的时间,可以通过改变题目情境为两个车同时从不同地点出发到达相同地点的时间。
这样可以让学生将抽象的数学概念与实际情境结合起来,提高解题能力。
可以通过改变题目的形式来变换问题。
一个问题是求一个几何图形的面积,可以通过改变题目形式为求图形的周长或者体积。
这样可以让学生在解题过程中充分运用数学概念和运算方法,提高解题能力和学习成效。
最新初中数学一题多变、一题多解
CBAS 2S 3S 1CBAS 3S 2S 1S 3S 2S 1CBA一题多解、一题多变原题条件或结论的变化所谓条件或结论的变化,就是对某一问题的条件或结论进行变化探讨,并针对问题的内涵与外延进行深入与拓展,从而得到一类变式题组。
通过对问题的分析解决,使我们掌握某类问题的题型结构,深入认识问题的本质,提高解题能力。
例1 求证:顺次连接平行四边形各边中点所得的四边形是平行四边形。
变式1 求证:顺次连接矩形各边中点所得的四边形是菱形。
变式2 求证:顺次连接菱形各边中点所得的四边形是矩形。
变式3 求证:顺次连接正方形各边中点所得的四边形是正方形。
变式4 顺次连接什么四边形各边中点可以得到平行四边形? 变式5 顺次连接什么四边形各边中点可以得到矩形? 变式6 顺次连接什么四边形各边中点可以得到菱形? ……通过这样一系列变式训练,使学生充分掌握了四边形这一章节所有基础知识和基本概念,强化沟通了常见特殊四边形的性质定理、判定定理、三角形中位线定理等,极大地拓展了学生的解题思路,活跃了思维,激发了兴趣。
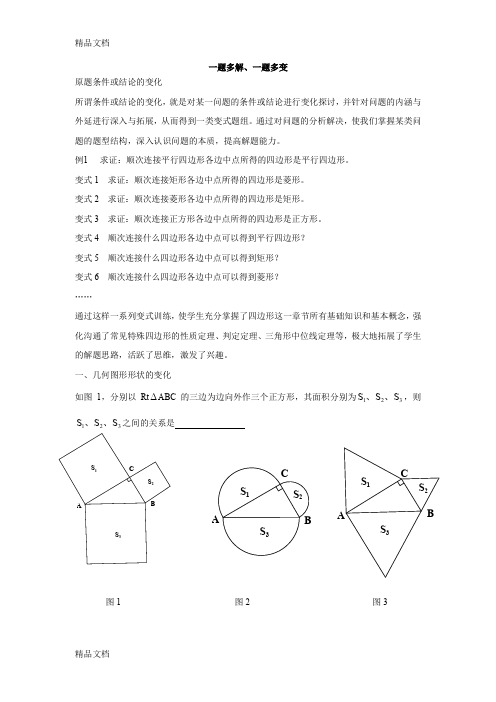
一、几何图形形状的变化如图1,分别以Rt ABC 的三边为边向外作三个正方形,其面积分别为321S S S 、、,则321S S S 、、之间的关系是图1 图2 图3E S 3S 2S 1DCBAS 3S 2S 1ABCDABCD S 3S 2S 1变式1:如图2,如果以Rt ∆ABC 的三边为直径向外作三个半圆,其面积分别为321S S S 、、,则321S S S 、、之间的关系是变式2:如图3,如果以Rt ∆ABC 的三边为边向外作三个正三角形,其面积分别为321S S S 、、,则321S S S 、、之间的关系是变式3:如果以Rt ∆ABC 的三边为边向外作三个一般三角形,其面积分别为321S S S 、、,为使321S S S 、、之间仍具有上述这种关系,所作三角形应满足什么条件?证明你的结论。
中考数学专题复习一题多变与多解试题

无棣县埕口中学中考数学专题复习 一题多变与多解 新人教版制卷人:打自企; 成别使; 而都那。
审核人:众闪壹; 春壹阑; 各厅…… 日期:2022年二月八日。
一、一题多解,拓宽思路,培养思维的多向性,发散性,采用一题多解的方法可以训练同学们应用多种方法,以多种角度去认识、解决问题. 例 :如图1,直线AB ∥CD ,P 是AB 和CD 之间的一点.试说明∠ABP +∠PDC =∠BPD .该题证明思路较多,主要有以下几种:证法一:如图1,过点P 向右作PE ∥AB ,那么有∠ABP =∠BPE .又∵ AB ∥CD ,∴ PE ∥CD ,∴ ∠EPD =∠PDC .因此,∠ABP +∠PDC =∠BPE +∠EPD =∠BPD .证法二:如图2,过点P 向左作PE ∥AB ,那么有∠ABP +∠BPE =180°. 易得PE ∥CD ,∴∠EPD +∠PDC =180°. 故有∠ABP +∠BPE +∠EPD +∠PDC =360°.又∵ ∠BPE +∠EPD +∠BPD =360°,∴ ∠ABP +∠PDC =∠BPD . 证法三:如图3,延长BP ,交CD 于点E ,那么∠BPD =∠PED +∠PDC . ∵ AB ∥CD ,∴ ∠ABP =∠PED . ∴ ∠ABP +∠PDC =∠BPD . 证法四:如图4,过点P 作直线EF ,分别交AB 、CD 于点E 、F . 那么∠EPB +∠BPD =∠EPD =∠PFD +∠PDC .又∵ AB ∥CD ,∴ ∠PFD =∠AEF =∠ABP +∠EPB , ∴ ∠EPB +∠BPD =∠ABP +∠EPB +∠PDC . ∴ ∠ABP +∠PDC =∠BPD .二、题多变,同中求异,培养思维的敏捷性、深入性.ACDP图1 E B ACD 图2E BP图3C D E AP BP E 图4A CD F B一题多变指改变同一问题中的条件或者题目改变求解目的,或者加深题目难度,从而训练同学生举一反三,以不变应万变的才能。
初中数学一题多变一题多解(六)

一题多解,一题多变(六)中考几何母题的一题多解(多变)一、三角形一题多解如图:已知AB=AC,E是AC延长线上一点,且有BF=CE,连接FE交BC于D。
求证:FD=DE。
证法一证明:过E点作EM ∥AB交DC延长线于M点,则∠M=∠B,又因为∠ACB=∠B∠ACB=∠ECM=∠M,所以CE=EM,又EC=BF 从而EM=BF,∠BFD=∠DEM则△DBF≌△DME,故FD=DE;证法二证明:过E点作EM ∥AB交DC延长线于M点,则∠M=∠B,又因为∠ACB=∠B∠ACB=∠ECM=∠M,所以CE=EM,又EC=BF 从而EM=BF,∠BFD=∠DEM则△DBF≌△DME,故 FD=DE;证法二证明:过F点作FM∥AE,交BD于点M,则∠1=∠2 = ∠B 所以BF=FM,又∠4=∠3 ∠5=∠E所以△DMF≌△DCE,故 FD=DE。
二、平行四边形一题多解如图4,平行四边形ABCD中AD=2AB,E、F在直线AB上,且AE=BF=AB,求证:DF⊥CE.证法一、易知ΔADF、ΔBCE为等腰三角形,故∠1=∠F, ∠2=∠E,又CD∥AB,故∠3=∠F, ∠4=∠E,从而∠1=∠3,∠2=∠4,而∠1+∠2+∠3+∠4=1800,故∠3+∠4=900,表明∠COD=900,所以DF⊥CE。
证法二、如图5,连接MN,则CD=BF,且CD∥BF,故BFCD为平行四边形,则CN=BN=AB,同理,DM=MA=AB,故CN=DM且CN∥DM,得平行四边形CDMN,易见CD=DM,故CDMN也是菱形,根据菱形的对角线互相垂直,结论成立。
证法三、如图6,连接BM、AN, 可证ΔAFN中,BN=BF=BA,则ΔAFN为直角三角形,即DF⊥AN,利用中位线定理可知AN∥CE,故DF⊥CE。
证法四、如图7,作DG∥CE交AE延长线于G,则EG=CD=AB=AE,故AD=AG=AF,从而DF⊥DG,而DGCE,故DF⊥CE四\一题多解、多变《四边形面积》1.如图所示,一个长为a,宽为b的矩形,两个阴影都是长为c的矩形与平行四边形,则阴影部分面积是多少。
初中数学一题多变一题多解(一)

“一题多变”(一)一、“一题多变”的作用:在平时的数学教学过程中实施一题多变的训练,可以提高学生学习数学的积极性,增强学习数学的兴趣:1、新课中,实施一题多变,以简单题入手由浅入深,可使大部分学生对当堂课内容产生兴趣。
2、习题课中,把较难题改成多变题目,让学生找到突破口,对难题也产生兴趣。
3、学生自己能够将题目中的问题或某一条件改变,对知识进行重组,自己将题目中的问题或某一条件进行改变,对已学知识进行重组,探索出新知识,解决新问题。
不就题论题,能多思多变。
在完成一个数学题的解答时,有必要对该题的内容、形式、条件、结论,做进一步的探讨,以真正掌握该题所反映的问题的实质。
如果能对一个普通的数学题进行一题多变,从变中总结解题方法;从变中发现解题规律,从变中发现“不变”,必将使人受益匪浅。
二、“一题多变”的常用方法有:1、变换命题的条件与结论;2、变换题型;3、深化条件,保留结论;4、减弱条件,加强结论;5、探讨命题的推广;6、考查命题的特例;7、生根伸枝,图形变换;8、接力赛,一变再变等等。
三、一题多变,挖掘习题涵量:1、变换命题的条件与结论即通过对习题的条件或结论进行变换,而对同一个问题从多个角度来研究。
这种训练可以增强学生解题的应变能力,培养思维的广阔性和深刻性,从而培养创新思维的品质。
例1、如图,在梯形ABCD中,AB∥CD,BC=AB+CD,E是AD中点。
求证:∠BEC=90°.变换1:如图,在梯形ABCD中,AB∥CD,BC=AB+CD,E是AD中点。
求证:CE⊥BE.变换2:如图,在梯形ABCD中,AB∥CD,CE⊥BE., E是AD中点.求证:BC=AB+CD.变换3:如图,在梯形ABCD中,AB∥CD,BC=AB+CD, CE⊥BE.判断E是AD中点吗?为什么?变换4:如图,在梯形ABCD中,AB∥CD,BC=AB+CD,CE⊥BE.求证:AE=ED.2、变换题型即将原题重新包装成新的题型,改变单调的习题模式,从而训练学生解各种题型的综合能力,培养学生思维的适应性和灵活性,有助于学生创新思维品质的养成。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学专题训练-------一题多变
1、已知如图:在四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 边上的中点,求证:四边形EFGH 是平行四边形。
分析:欲证四边形EFGH 是平行四边形,根据条件需从边上着手分析,由E 、F 、G 、H 分别是各边上的中点,可联想到三角形的中位线定理,连结AC
后,EF 和GH 的关系就明确了,此题也便得证。
(证明略) 变式1:顺次连结矩形四边中点所得的四边形是菱形。
变式2:顺次连结菱形四边中点所得的四边形是矩形。
变式3:顺次连结正方形四边中点所得的四边形是正方形。
变式4:顺次连结等腰梯形四边中点所得的四边形是菱形。
变式5:若AC =BD ,AC ⊥BD ,则四边形EFGH 是正方形。
变式6:在四边形ABCD 中,若AB =CD ,E 、F 、G 、H 分别为AD 、BC 、BD 、AC 的中点,求证:EFGH 是菱形。
娈式6图
娈式7图
变式7:如图:在四边形ABCD 中,E 为边AB 上的一点,△ADE 和△BCE 都是等边三角形,P 、Q 、M 、N 分别是AB 、BC 、CD 、DA 边上的中点,求证:四边形PQMN 是菱形。
2、在正方形ABCD 的CD 边上取一点G ,在CG 上向原正方形外作正方形GCEF , 求证:DE ⊥BG ,DE=BG 。
变式:如图,ABCD 、CEFG 是正方形,E 在CD 上,直线BE 、DG 交于H ,且HE ·HB
=4-BD 、AH 交于M ,当E 在线段CD (不与C 、D 重合)上运动时,下列四个结论:① BE ⊥GD ;② AH 、GD 所夹的锐角为45°;③
;④ 若BE 平分∠DBC ,则正方形ABCD 的面积为4。
其中正确的结论个数有(D )
A. 1个
B. 2个
C. 3个
D. 4个
由①对,知∠BHD=90,由∠BAD=90知:A 、B 、H 、D 四点共圆,∴∠AHD=∠ABD=45.∴②对。
由△DBE ∽△DAM ∴
AM BE AD
BD
AM BE 22=∴==∵DG=BE ∴AM DG 2=∴③对。
由BE 平分∠DBC 知:∠HDE=∠DBH ,∴△HDE ∽△HBD ∴2242
-=⨯=HB HE DH .∴
DH=28162
12
-=∴DG DG ()
CG BC CG BC BG BD DG CG DC =-∴+===+12222 ,
例2图
(
)[]
4281612222
2=∴-==-+
∴BC DG BC BC ∴④对。
故选D
3、有这样一道习题:如图1,已知OA 和OB 是⊙O 的半径,并且OA ⊥OB ,P 是OA 上任一点(不与O 、
A 重合),BP 的延长线交⊙O 于Q ,过Q 点作⊙O 的切线交OA 的延长线于R .说明:RP =RQ . 请探究下列变化:
变化一:交换题设与结论.
已知:如图1,OA 和OB 是⊙O 的半径,并且OA ⊥OB ,P 是OA 上任一点(不与O 、A 重合),BP 的延长线交⊙O 于Q ,R 是OA 的延长线上一点,且RP =RQ . . 说明:RQ 为⊙O 的切线. .
变化二:运动探求.
1.如图2,若OA 向上平移,变化一中的结论还成立吗?(只需交待判断) 答: . 2.如图3,如果P 在OA 的延长线上时,BP 交⊙O 于Q , 过点Q 作⊙O 的切线交OA 的延长线于R ,原题中的结论 还成立吗?为什么?
4.如图,在正方形ABCD 中,P 、Q 分别是BC 、CD 上的点,若∠PAQ =450,求证:PB +DQ =PQ 。
分析:利用正方形的性质,通过构造全等三角形来证明。
变式:若条件改为PQ =PB +DQ ,那么∠PAQ =?你还能得到哪些结论?
5. 如图,已知正方形ABCD 的对角线AC 、BD 相交于点O ,E 是AC
上一点,过A 作AG ⊥EB 于G ,AG 交BD 于点F ,则OE =OF ,对上述命题,若点E 在AC 的延长线上,AG ⊥EB ,交EB 的延长线于点G ,AG 的延长线交DB 的延长线于点F ,其它条件不变,则结论“OE =OF ”还成立吗?如果成立,请给出证明;如果不成立,说明理由。
问题一图1 O F G E
D
C B
A 问题一图
2
分析:对于图1通过全等三角形证明OE =OF ,这种证法是否能应用到图2的情境中去,从而作出正
O
R
B Q
A
P
图1
图2
O
B Q
A
P
O
P
B
Q
A R
图3
例2
图
确的判断。
结论:(2)的结论“OE =OF ”仍然成立。
提示:只须证明△AOF ≌△BOE 即可。
评注:本题以正方形为背景,突破了单纯的计算与证明,着重考查了学生观察、分析、判断等多种能力。
6、原题:
(1)如图:△ABC 中,以AB 为直径的⊙O 交BC 于点D ,过点D 作EF ⊥AC 于点E ,交AB 的延长线于点F 。
⑴求证:EF 是⊙O 的切线。
⑵如果∠A=60,则DE 与DF 有何数量关系。
请说明理由。
⑶如果AB=5,BC=6,求tam ∠BAC 的值。
变式:
2、如图,在锐角△ABC 中,AB 是最短的边,以AB 为直径作⊙O ,交BC 于E ,过O 作OD ∥BC 交⊙O 于D ,连结AE 、AD 、DB 。
⑴求证:D 是⋂
AE 的中点, ⑵求证:∠DAO=∠C+∠CAD ,
⑶若2
1
=∆∆OBD BEF S s 且AB=4,求BF 的长。
变式:3、如图,在锐角△ABC 中,AB=4是最短的边,以AB 为直径作⊙O ,交BC 于E ,H 是直线BC 上一动点,AH 交⊙O 于D 点。
⑴当OD ∥BC 时,D 是⋂
AE 的中点。
当⋂
AE 的中点时,OD ∥BC 。
⑵若BD 交AE 于F 点,是否存在一点H ,当BF =2,使2
1
=∆∆OBD BEF S s 。
C
C
C。
