数学常用符号中英文
常用数学符号读法大全以及主要数学符号含义

常⽤数学符号读法⼤全以及主要数学符号含义常⽤数学符号读法⼤全以及主要数学符号含义⼤写⼩写英⽂注⾳国际⾳标注⾳中⽂注⾳Ααalpha alfa 阿⽿法Ββbeta beta 贝塔Γγgamma gamma 伽马Δδdeta delta 德⽿塔Εεepsilon epsilon 艾普西隆Ζζzeta zeta 截塔Ηηeta eta 艾塔Θθtheta θita 西塔Ιιiota iota 约塔Κκkappa kappa 卡帕∧λlambda lambda 兰姆达Μµmu miu 缪Ννnu niu 纽Ξξxi ksi 可塞Οοomicron omi kron 奥密可戎∏πpi pai 派Ρρrho rou 柔∑σsigma sigma 西格马Ττtau tau 套Υυupsilon jupsilon ⾐普西隆Φφphi fai 斐Χχchi khai 喜Ψψpsi psai 普西Ωωomega omiga 欧⽶伽数学符号:(1)数量符号:如:i,2+i,a,x,⾃然对数底e,圆周率π.(2)运算符号:如加号(+),减号(-),乘号(×或·),除号(÷或/),两个集合的并集(∪),交集(∩),根号(√),对数(log,lg,ln),⽐(:),微分(dx),积分(∫)等.(3)关系符号:如“=”是等号,“≈”是近似符号,“≠”是不等号,“>”是⼤于符号,“<”是⼩于符号,“→”表⽰变量变化的趋势,“∽”是相似符号,“≌”是全等号,“∥”是平⾏符号,“⊥”是垂直符号,“∝”是反⽐例符号,“∈”是属于符号,“C”或“C下⾯加⼀横”是“包含”符号等.(4)结合符号:如圆括号“()”⽅括号“[]”,花括号“{}”括线“—”(5)性质符号:如正号“+”,负号“-”,绝对值符号“‖”(6)省略符号:如三⾓形(△),正弦(sin),余弦(cos),x的函数(f(x)),极限(lim),因为(∵),所以(∴),总和(∑),连乘(∏),从n个元素中每次取出r个元素所有不同的组合数(C(r)(n) ),幂(A,Ac,Aq,x^n),阶乘(!)等.数学符号的意义符号意义∞⽆穷⼤π圆周率|x|绝对值∪并集∩交集≥⼤于等于≤⼩于等于≡恒等于或同余ln(x)以e为底的对数lg(x)以10为底的对数floor(x)上取整函数ceil(x)下取整函数x mod y求余数x - floor(x) ⼩数部分∫f(x)dx不定积分∫[a:b]f(x)dx a到b的定积分→等价于趋向于数学符号的应⽤P为真等于1否则等于0∑[1≤k≤n]f(k) 对n进⾏求和,可以拓⼴⾄很多情况如:∑[n is prime][n < 10]f(n)∑∑[1≤i≤j≤n]n^2lim f(x) (x->?) 求极限f(z) f关于z的m阶导函数C(n:m) 组合数,n中取mP(n:m) 排列数m|n m整除nm⊥n m与n互质a ∈A a属于集合A#A 集合A 中的元素个数“∑”数学⾥的连加符号,叫西格马,求和的意思要给出上下界限(⽐如k是⾃然数∑k(上界限⾄n,下界限从k=0开始) ∑k=0+1+2+……+n {⼤括号(bracket)是⽤来规定运算次序的符号。
常用数学符号大全
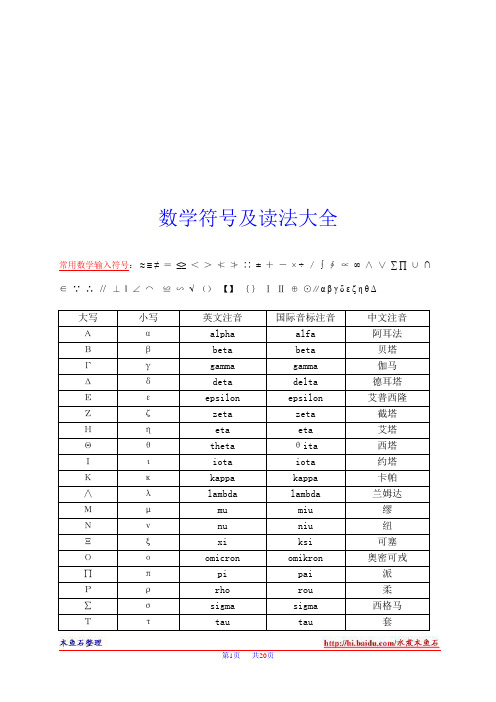
数学符号及读法大全常用数学输入符号:≈≡≠=≤≥<>↉↊ↁ±+-× ÷/∫ⅽⅴ∞ⅸⅹ∑∏ⅻ∩ⅰⅿⅾ//‖ⅶↄↂ√()【】{}ⅠⅡ▝↋ⅷαβγδεδεζΓ符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值,常被写作e x a^x a的x次方;有理数x由反函数定义ln x exp x 的反函数a x同 a^xlogb a 以b为底a的对数; b logba = acos x 在自变量x处余弦函数的值tan x 其值等于 sin x/cos xcot x 余切函数的值或 cos x/sin xsec x 正割含数的值,其值等于 1/cos xcsc x 余割函数的值,其值等于 1/sin xasin x y,正弦函数反函数在x处的值,即 x = sin y acos x y,余弦函数反函数在x处的值,即 x = cos y atan x y,正切函数反函数在x处的值,即 x = tan y acot x y,余切函数反函数在x处的值,即 x = cot y asec x y,正割函数反函数在x处的值,即 x = sec y acsc x y,余割函数反函数在x处的值,即 x = csc yζ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a•b a、b向量的点积(a•b)a、b向量的点积|v| 向量v的模|x| 数x的绝对值表示求和,通常是某项指数。
下边界值写在其下部,上边界值写在其上部。
如j从1到100 的和可以表示成:。
这表示 1 + 2 + … + nM 表示一个矩阵或数列或其它|v> 列向量,即元素被写成列或可被看成k×1阶矩阵的向量<v| 被写成行或可被看成从1×k阶矩阵的向量dx 变量x的一个无穷小变化,dy, dz, dr等类似ds 长度的微小变化ξ变量 (x2 + y2 + z2)1/2或球面坐标系中到原点的距离r 变量 (x2 + y2)1/2或三维空间或极坐标中到z轴的距离|M| 矩阵M的行列式,其值是矩阵的行和列决定的平行区域的面积或体积||M|| 矩阵M的行列式的值,为一个面积、体积或超体积det M M的行列式M-1矩阵M的逆矩阵v×w向量v和w的向量积或叉积ζvw向量v和w之间的夹角A•B×C标量三重积,以A、B、C为列的矩阵的行列式uw在向量w方向上的单位向量,即 w/|w|df 函数f的微小变化,足够小以至适合于所有相关函数的线性近似df/dx f关于x的导数,同时也是f的线性近似斜率f ' 函数f关于相应自变量的导数,自变量通常为x∂f/∂x y、z固定时f关于x的偏导数。
常用数学符号读法大全以及主要数学符号含义

x mod y 求余数 x - floor(x 小数部分 ∫ f(xdx不定积分
∫ [a:b]f(xdx a到 b 的定积分
数学符号的应用
P 为真等于 1 否则等于 0 ∑ [1 ≤ k≤ n对]f(kn 进行求和 , 可以拓广至很多情况
如: ∑[n is prime][n < 10]f(n
∑∑ [ (x
∑ ζ sigma sigm西a格马 Τ η tau t套au Υ υ upsilon jupsilo衣n 普西隆 Φ θ phi f斐ai Φ χ chi kh喜ai Χ ψ psi ps普ai西 Ψ ω omega omig欧a米伽 数学符号: (1)数量符号:如: i ,2+i,a , x ,自然对数底 e ,圆周率 π。 (2)运算符号:如加号(+),减号(-),乘号( ×或 ·),除号( ÷或 /),两个集合的并集(∪),交集( ∩),根号( √),对数( log , lg ,ln ), 比(:),微分( dx ),积分( ∫)等。 (3)关系符号:如 “=”是等号, “≈是”近似符号, “≠是”不等号, “>”是大于 符号, “<”是小于符号, “→ 表”示变量变化的趋势, “∽”是相似符号, “≌ ”是全等 号, “∥ ”是平行符号, “⊥”是垂直符号, “∝ ”是反比例符号, “∈”是属于符号, “ C或”“C下面加一横 ”是 “包含 ”符号等。 (4)结合符号:如圆括号 “() ”方括号 “[] ”,花括号 “{} ”括线 “—” (5)性质符号:如正号 “+ ”,负号 “- ”,绝对值符号 “‖” (6)省略符号:如三角形( △ ),正弦( sin ),余弦( cos ), x 的函数 ( f(x ),极限( lim ),因为(∵),所以(∴),总和( ∑),连乘( ∏),从
常用数学符号英文对照

常⽤数学符号英⽂对照常⽤数学符号英⽂对照Basic math symbolsSymbol Symbol Name Meaning / definition Example = equals sign equality 5 = 2+35 is equal to 2+3≠not equal sign inequality 5 ≠ 45 is not equal to 4≈approximatelyequal approximationsin(0.01) ≈ 0.01,x≈y means x isapproximately equal to y> strict inequality greater than 5 > 45 is greater than 4< strict inequality less than 4 < 54 is less than 5≥inequality greater than or equal to 5 ≥ 4,x≥y means x is greater than or equal to y≤inequality less than or equal to 4 ≤ 5,x ≤ y means x is greater than or equal to y( ) parentheses calculate expressioninside first2 × (3+5) = 16[ ] brackets calculate expressioninside first[(1+2)×(1+5)] = 18 + plus sign addition 1 + 1 = 2 minus sign subtraction 2 1 = 1±plus - minus both plus and minusoperations3 ± 5 = 8 and -2±minus - plus both minus and plusoperations3 ± 5 = -2 and 8* asterisk multiplication 2 * 3 = 6×times sign multiplication 2 × 3 = 6 ·multiplicationmultiplication 2 · 3 = 6dot÷division sign /division 6 ÷ 2 = 3 obelus/ division slash division 6 / 2 = 3–horizontal line division / fractionmod modulo remainder calculation 7 mod 2 = 1. period decimal point, decimal2.56 = 2+56/100separatora b power exponent 23= 8a^b caret exponent 2 ^ 3= 8√a square root √a ·√a= a√9= ±33√a cube root 3√a ·3√a ·3√a= a3√8= 24√a fourth root 4√a ·4√a ·4√a ·4√a= a4√16= ±2n√a n-th rootfor n=3,n√8= 2 (radical)% percent 1% = 1/100 10% × 30 = 3‰per-mille 1‰ = 1/1000 = 0.1% 10‰× 30 = 0.3 ppm per-million 1ppm = 1/1000000 10ppm × 30 = 0.0003 ppb per-billion 1ppb = 1/1000000000 10ppb × 30 = 3×10-7 ppt per-trillion 1ppt = 10-1210ppt × 30 = 3×10-10 Geometry symbols Symbol Symbol Name Meaning / definition Example∠angle formed by two rays ∠ABC = 30°measured angle ABC = 30°sphericalangle AOB = 30° ∟ right angle = 90°α = 90° °degree 1 turn = 360° α = 60° degdegree 1 turn = 360degα = 60deg ′ prime arcminute, 1° = 60′α = 60°59′″ double primearcsecond, 1′ = 60″α = 60°59′59″line infinite lineABline segment line from point A to point Bray line that start from point Aarc arc from point A to point B= 60° ⊥ perpendicular perpendicular lines (90° angle)AC ⊥ BC| | parallel parallel lines AB | | CDcongruent to equivalence of geometric shapes and size ABC XYZ ~ similarity same shapes, not same size ?ABC~ ?XYZ Δtriangle triangle shapeΔABC ? ΔBCD |x -y | distancedistance between points x and y| x -y | = 5πpi constantπ = 3.141592654...is the ratio between the circumference and diameter of a circlec = π·d = 2·π·rAlgebra symbolsSymbol Symbol NameMeaning /definitionExamplex x variable unknown value tofindwhen 2x= 4, then x= 2≡equivalence identical toequal by definition equal bydefinition:= equal by definition equal bydefinition~ approximately equal weakapproximation11 ~ 10≈approximately equal approximation sin(0.01) ≈ 0.01∝proportional to proportional to y∝x when y=kx, k constant ∞lemniscate infinity symbol much less than much less than 1 1000000much greater than much greater than 1000000 1( ) parentheses calculateexpressioninside first2 * (3+5) = 16[ ] brackets calculateexpressioninside first[(1+2)*(1+5)] = 18{ } braces setxfloor brackets rounds number tolower integer4.3 = 4xceiling brackets rounds number toupper integer4.3 = 5x! exclamation mark factorial 4! = 1*2*3*4 = 24 |x| single vertical bar absolute value | -5 | = 5 f(x) function of x maps values of xto f(x)f(x) = 3x+5(f°g) function composition (f°g) (x) =f(g(x))f(x)=3x,g(x)=x-1 ?(f°g)(x)=3(x-1)(a,b) open interval (a,b) ={x|ax∈ (2,6)[a,b] closed interval [a,b] ={x|a≤x≤b}x∈ [2,6]delta change /differencet=t1-t0discriminant Δ =b2- 4ac∑sigma summation - sumof all values inrange of series∑x i= x1+x2+...+x n∑∑sigma double summation∏capital pi product - productof all values inrange of series∏x i=x1?x2?...?x ne e constant/ Euler's number e=2.718281828...e= lim (1+1/x)x,x→∞γEuler-Mascheroni constant γ = 0.527721566...φgolden ratio golden ratio constantπpi constant π=3.141592654...is the ratioLinear Algebra SymbolsSymbol Symbol Name Meaning / definition Example·dot scalar product a·b×cross vector product a×bA?B tensor product tensor product of A and B A?Binner product[ ] brackets matrix of numbers( ) parentheses matrix of numbers|A| determinant determinant of matrix Adet(A) determinant determinant of matrix A||x|| double vertical bars normA T transpose matrix transpose (A T)ij= (A)jiA?Hermitian matrix matrix conjugate transpose (A?)ij= (A)ji A*Hermitian matrix matrix conjugate transpose (A*)ij= (A)ji A-1inverse matrix A A-1=Irank(A) matrix rank rank of matrix A rank(A) = 3Probability and statistics symbols Symbol Symbol Name Meaning / definition ExampleP(A) probabilityfunction probability of eventAP(A) = 0.5P(A∩B) probability ofeventsintersectionprobability that ofevents A and BP(A∩B) = 0.5P(A∪B) probability ofevents union probability that ofevents A or BP(A|B) conditionalprobabilityfunctionprobability of eventA given event BoccuredP(A | B) = 0.3f(x) probabilitydensityfunction (pdf)P(a≤x≤b) =∫f(x)dxF(x) cumulativedistributionfunction (cdf)F(x) =P(X≤x)µpopulation mean mean of population valuesµ= 10E(X) expectationvalue expected value ofrandom variable XE(X) = 10E(X | Y) conditionalexpectation expected value of random variable Xgiven YE(X | Y=2) = 5var(X) variance variance of random variable Xvar(X) = 4σ2variance variance ofpopulation valuesσ2= 4deviation standard deviation ofrandom variable Xstd(X) = 2σXstandard deviationstandard deviation value of random variable X σX = 2 medianmiddle value of random variable xcov (X ,Y )covariancecovariance of random variables X and Y cov (X,Y ) = 4 corr (X ,Y ) correlationcorrelation of random variables X and Y corr (X,Y ) = 0.6ρX ,Y correlationcorrelation of random variables X and Y ρX ,Y = 0.6∑summation summation - sum of allvalues in range of series∑∑double summationdouble summationMo mode value that occursmost frequently in populationMR mid-rangeMR = (x max +x min )/2Mdsample median half the population is below this value Q 1lower / first quartile25% of population are below this valueQ 2median / second quartile50% of population are below this value = median of samples Q 3upper / third quartile75% of population are below this valuex sample meanaverage / arithmetic meanx = (2+5+9) / 3 = 5.333s 2sample variancepopulation samples variance estimators 2 = 4s sample standard deviationpopulation samples standard deviation estimators = 2z x standard scorez x = (x -x ) / s xX ~distributionof X distribution of random variable X X ~ N (0,3)N (µ,σ2)normal distribution gaussian distribution X ~ N (0,3)U (a ,b ) uniform distribution equal probability in range a,bX ~ U (0,3)exp (λ)exponential distribution f (x ) = λe -λx , x ≥0 gamma (c , λ) gamma distribution f (x ) = λ c x c-1e -λx /Γ(c ), x ≥0χ 2(k )chi-square distributionf (x ) = x k /2-1e -x /2 /( 2k/2Γ(k /2) )F (k 1, k 2)F distributionBin (n ,p ) binomial distribution f (k ) = n C k p k (1-p )n-k Poisson (λ)Poisson distribution f (k ) = λk e -λ / k !Geom (p )geometric distribution f (k ) = p (1-p ) kHG (N ,K ,n )hyper-geometric distributionBern (p )Bernoulli distributionSet theory symbolsSymbolSymbol NameMeaning / definitionExample{ }set a collection of elementsA = {3,7,9,14},B = {9,14,28} A ∩ B intersectionobjects that belong to set A and set BA ∩B = {9,14}A ∪B unionobjects that belong to set A or set BA ∪B = {3,7,9,14,28}A ?B subsetsubset has fewer elements or equal to the set{9,14,28} ? {9,14,28}A ? Bproper subset / strict subsetsubset has fewer elements than the set{9,14} ? {9,14,28} A ? B not subset left set not a subset of right set {9,66} ? {9,14,28}A ?B supersetset A has more elements or equal to the set B{9,14,28} ? {9,14,28} A ? B proper superset / strict supersetset A has more elements than set B{9,14,28} ? {9,14} A ? B not superset set A is not a superset of set B {9,14,28} ? {9,66}2Apower set all subsets of Apower set all subsets of AA =B equality both sets have the same membersA={3,9,14}, B={3,9,14},。
常用数学符号的汉英读法

常用数学符号的汉英读法1. 逻辑:Logic∃存在:there exists∀任意:for allp q⇒由p推出q :p implies q / if p, then q⇔p、q相互推出:p if and only if q /p is equivalent to q / p and q are equivalentp q2.集合:Sets∈x 属于A:x belongs to A / x is an element (or a member) of Ax A∉x 不属于A:x does not belong to A / x is not an element (or a member) of Ax A⊂A真包含B:A is contained in B / A is a subset of BA B⊃A真包含于B:A contains B / B is a subset of AA BA B A 与B的交集:A cap B / A meet B / A intersection BA B A 与B的并集:A cup B / A join B / A union B3. 实数:Real numbersx+x加1:x plus one1x-x减1:x minus one1x±x加或减1:x plus or minus one1xy x乘y:xy / x multiplied by yxx除以y:x over yy=等于:the equals sign5x=x等于5 :x equals 5 / x is equal to 5≡x恒等于y:x is equivalent to (or identical with) yx y≠x不等于y :x is not equivalent to (or identical with) yx y>x 大于y:x is greater than yx y≥x 大于或等于y:x is greater than or equal to yx y<x 小于y:x is less than yx y≤x 小于或等于y;x is less than or equal to yx y<<0小于x小于1:zero is less than x is less than 1x01≤≤0小于或等于x小于或等于1:zero is less than or equal to x is less than or equal to 1 01x||x x的模(x的绝对值):mod x / modulus x2x x的2次方:x squared / x (raised) to the power 23x x的3次方:x cubed4x x的4次方:x to the fourth / x to the power fournx x的n次方:x to the nth / x to the power nnx-x的负n次方:x to the (power) minus nx的2次根式:(square) root x / the square root of xx的3次根式:cube root (of) xx的4次根式:fourth root (of) xx的n次根式:nth root (of) x2+x与y的和的平方:x plus y all squared()x y2()x yx 与y 的商的平方:x over y all squared !n n 的阶乘:n factorialx x 拔:x bari x i x :i x / x subscript i / x suffix i/ x sub i1n i i a =∑ i a 从1到n 求和:the sum from i equals one to n i a / the sum as i runs from 1 to n of the i a 4.线性代数:Linear algebra OA 向量OA :OA / vector OAOA 有向线段OA :OA / the length of the segment OA a b 向量a 与b 平行:vector a parallel to vector ba ⊥b 向量a 与b 垂直:vector a is perpendicular to vector b5. 函数:Functions()f x 函数()f x : fx / f of x / the function f of x:f S T → f 是从集合S 到T 的函数:a function f from S to Tx y → 从x 到y :x maps to y / x is sent (or mapped) to y'()f x ()f x 的导数:f prime x / f dash x / the (first) derivative of f with respect to x ''()f x ()f x 的二阶导数:f double-prime x / f double-dash x /the second derivative of f with respect to x'''()f x ()f x 的三阶导数:f triple-prime x / f triple-dash x /the third derivative of f with respect to x()()n f x ()f x 的四阶导数: the nth derivative of f with respect to x1f x ∂∂ f 关于1x 的偏导数:the partial (derivative) of f with respect to 1x 221f x ∂∂ f 关于1x 的二阶偏导数:the second partial (derivative) of f with respect to 1x 0∞⎰ 从0到∞求积分:the integral from zero to infinitylim x → x 趋于0求极限:the limit as x approaches zero 0lim x →+ x 右趋于0求极限:the limit as x approaches zero from above 0lim x →- x 左趋于0求极限:the limit as x approaches zero from belowlog e y 以e 为底数的y 的对数:log y to the base e / log to the base e of y / natural log (of) y ln y y 的自然对数:log y to the base e / log to the base e of y / natural log (of) y。
常用数学符号英文对照
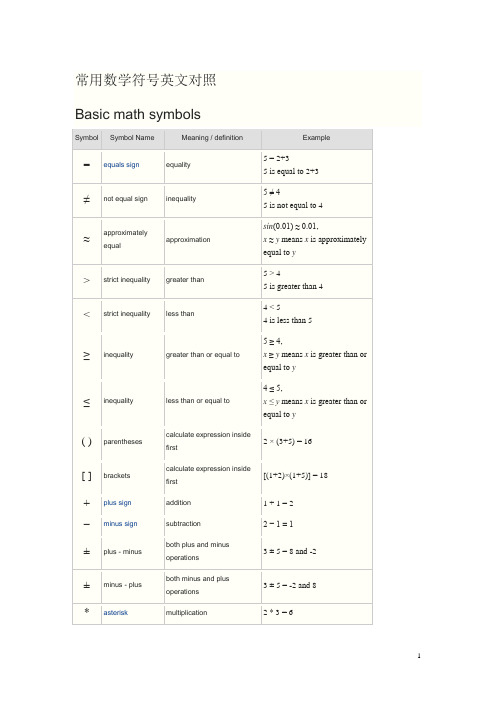
×times sign multiplication 2 × 3 = 6 ·multiplication dot multiplication 2 · 3 = 6÷division sign /division 6 ÷ 2 = 3obelus/ division slash division 6 / 2 = 3–horizontal line division / fractionmod modulo remainder calculation 7 mod 2 = 1. period decimal point, decimal2.56 = 2+56/100separatora b power exponent 23= 8a^b caret exponent 2 ^ 3= 8√a square root √a ·√a = a√9 = ±33√a cube root 3√a ·3√a ·3√a = a3√8 = 24√a fourth root 4√a ·4√a ·4√a ·4√a = a4√16 = ±2n√a n-th root (radical) for n=3, n√8 = 2% percent1% = 1/100 10% × 30 = 3‰per-mille1‰ = 1/1000 = 0.1%10‰ × 30 = 0.3ppm per-million1ppm = 1/1000000 10ppm × 30 = 0.0003ppb per-billion 1ppb = 1/1000000000 10ppb × 30 = 3×10-7ppt per-trillion 1ppt = 10-1210ppt × 30 = 3×10-10Geometry symbolsSymbol Symbol Name Meaning / definition Example ∠angle formed by two rays ∠ABC = 30°measuredABC = 30°anglespherical angle AOB = 30°∟right angle = 90°α = 90°°degree 1 turn = 360°α = 60°deg degree 1 turn = 360deg α = 60deg′prime arcminute, 1° = 60′α = 60°59′″double prime arcsecond, 1′ = 60″α = 60°59′59″line infinite lineAB line segment line from point A to point Bray line that start from point Aarc arc from point A to point B= 60°⊥perpendicular perpendicular lines (90° angle) AC ⊥ BC| | parallel parallel lines AB | | CD≅congruent to equivalence of geometric shapes and size ∆ABC≅∆XYZ ~ similarity same shapes, not same size ∆ABC~ ∆XYZ Δtriangle triangle shape ΔABC≅ΔBCD |x-y| distance distance between points x and y | x-y | = 5πpi constant π = 3.141592654...is the ratio between the circumference and diameter of acirclec = π·d = 2·π·rrad radians radians angle unit 360° = 2π rad c radians radians angle unit 360° = 2πcgrad gradians / gons grads angle unit 360° = 400 gradg gradians / gons grads angle unit 360° = 400 g Algebra symbolsSymbol Symbol Name Meaning /definitionExample[a,b] closed interval [a,b] ={x | a≤x≤b}x∈[2,6]∆delta change /difference∆t = t1 - t0∆discriminant Δ =b2 - 4ac∑sigma summation -sum of allvalues in rangeof series∑ x i= x1+x2+...+x n∑∑sigma doublesummation∏capital pi product -product of allvalues in rangeof series∏ x i=x1∙x2∙...∙x ne e constant / Euler's number e =2.718281828...e = lim (1+1/x)x , x→∞γEuler-Mascheroni constantγ =0.527721566...φgolden ratio golden ratioconstantπpi constant π =3.141592654...is the ratiobetween thecircumference anddiameter of acirclec = π·d = 2·π·rLinear Algebra SymbolsSymbol Symbol Name Meaning / definition Example ·dot scalar product a · b×cross vector product a × bA⊗B tensor product tensor product of A and B A⊗B inner product[ ] brackets matrix of numbers( ) parentheses matrix of numbers| A | determinant determinant of matrix Adet(A) determinant determinant of matrix A|| x || double vertical bars normA T transpose matrix transpose (A T)ij = (A)jiA†Hermitian matrix matrix conjugate transpose (A†)ij = (A)ji A*Hermitian matrix matrix conjugate transpose (A*)ij = (A)ji A-1inverse matrix A A-1 = Irank(A) matrix rank rank of matrix A rank(A) = 3 dim(U) dimension dimension of matrix A rank(U) = 3 Probability and statistics symbolsSymbol Symbol Name Meaning / definition ExampleP(A) probabilityfunctionprobability of event A P(A) = 0.5P(A∩B) probability ofeventsintersectionprobability that ofevents A and BP(A∩B) = 0.5P(A∪B) probability ofevents union probability that ofevents A or BP(A∪B) = 0.5P(A | B) conditionalprobabilityfunctionprobability of event Agiven event BoccuredP(A | B) = 0.3f (x) probabilitydensity function(pdf)P(a ≤ x ≤ b) = ∫f (x) dxF(x) cumulative F(x) = P(X≤ x)distribution function (cdf)μpopulationmean mean of populationvaluesμ = 10E(X) expectationvalue expected value ofrandom variable XE(X) = 10E(X | Y) conditionalexpectation expected value ofrandom variable Xgiven YE(X | Y=2) = 5var(X) variance variance of randomvariable Xvar(X) = 4σ2variance variance ofpopulation valuesσ2 = 4std(X) standarddeviation standard deviation ofrandom variable Xstd(X) = 2σX standarddeviation standard deviationvalue of randomvariable XσX=2median middle value of random variable xcov(X,Y) covariance covariance ofrandom variables Xand Ycov(X,Y) = 4corr(X,Y) correlation correlation ofrandom variables Xand Ycorr(X,Y) = 0.6ρX,Y correlation correlation ofrandom variables Xand YρX,Y = 0.6∑summation summation - sum of all values in range of series∑∑doublesummationdouble summationBin(n,p) binomialdistributionf (k) = n C k p k(1-p)n-kPoisson(λ)Poissondistributionf (k)= λk e-λ / k!Geom(p) geometricdistributionf (k) = p(1-p) kHG(N,K,n) hyper-geometric distributionBern(p) Bernoulli distributionCombinatorics SymbolsSymbol Symbol Name Meaning / definition Examplen! factorial n! = 1·2·3·...·n5! = 1·2·3·4·5 = 120 n P k permutation 5P3 = 5! / (5-3)! = 60 n C kcombination 5C3 = 5!/[3!(5-3)!]=10Set theory symbolsSymbol Symbol Name Meaning / definition Example{ } set a collection of elements A = {3,7,9,14},B = {9,14,28}A ∩B intersection objects that belong to set A and setBA ∩B = {9,14}A ∪B union objects that belong to set A or setBA ∪B ={3,7,9,14,28}A ⊆B subset subset has fewer elements orequal to the set{9,14,28} ⊆{9,14,28}A ⊂B proper subset / strict subset has fewer elements than {9,14} ⊂subset the set {9,14,28}A ⊄B not subset left set not a subset of right set {9,66} ⊄{9,14,28}A ⊇B superset set A has more elements or equalto the set B{9,14,28} ⊇{9,14,28}A ⊃B proper superset / strictsupersetset A has more elements than setB{9,14,28} ⊃{9,14}A ⊅B not superset set A is not a superset of set B {9,14,28} ⊅{9,66}2A power set all subsets of A power set all subsets of AA =B equality both sets have the same members A={3,9,14}, B={3,9,14}, A=BA c complement all the objects that do not belong to set AA \B relative complement objects that belong to A and not toBA = {3,9,14},B = {1,2,3},A-B = {9,14}A -B relative complement objects that belong to A and not toBA = {3,9,14},B = {1,2,3},A-B = {9,14}A ∆B symmetric difference objects that belong to A or B butnot to their intersectionA = {3,9,14},B = {1,2,3},A ∆B ={1,2,9,14}A ⊖B symmetric difference objects that belong to A or B butnot to their intersectionA = {3,9,14},B = {1,2,3},A ⊖B ={1,2,9,14}a∈A element of set membership A={3,9,14}, 3 ∈Ax∉A not element of no set membership A={3,9,14}, 1 ∉A(a,b) ordered pair collection of 2 elementsA×B cartesian product set of all ordered pairs from A andB|A| cardinality the number of elements of set A A={3,9,14},|A|=3#A cardinality the number of elements of set A A={3,9,14},#A=3aleph-null infinite cardinality of natural numbers setaleph-one cardinality of countable ordinal numbers setØ empty set Ø = { } C = {Ø} universal set set of all possible values0natural numbers / wholenumbers set (with zero) 0= {0,1,2,3,4,...} 0 ∈01natural numbers / wholenumbers set (withoutzero)1= {1,2,3,4,5,...} 6 ∈1 integer numbers set = {...-3,-2,-1,0,1,2,3,...} -6 ∈rational numbers set = {x | x=a/b, a,b∈} 2/6 ∈real numbers set = {x | -∞ < x <∞} 6.343434∈complex numbers set= {z | z=a+bi,-∞<a<∞,-∞<b<∞}6+2i∈Logic symbolsSymbol Symbol Name Meaning / definition Example ·and and x·y^ caret / circumflex and x ^ y& ampersand and x & y+ plus or x + y∨reversed caret or x∨y | vertical line or x | yx' single quote not - negation x'x bar not - negation x¬not not - negation ¬x! exclamation mark not - negation ! x⊕circled plus / oplus exclusive or - xor x⊕y ~ tilde negation ~ x⇒implies⇔equivalent if and only if (iff)↔equivalent if and only if (iff)∀for all∃there exists∄there does not exists∴therefore∵because / sinceCalculus & analysis symbolsSymbol Symbol Name Meaning / definition Example limit limit value of a functionεepsilon represents a very small number,ε→0near zeroe e constant / Euler'snumber e = 2.718281828...e = lim(1+1/x)x ,x→∞y ' derivative derivative - Lagrange's notation (3x3)' = 9x2y '' second derivative derivative of derivative (3x3)'' = 18xy(n)nth derivative n times derivation (3x3)(3) = 18 derivative derivative - Leibniz's notation d(3x3)/dx = 9x2second derivative derivative of derivative d2(3x3)/dx2 = 18xnth derivative n times derivationtime derivative derivative by time - Newton's notationtime secondderivativederivative of derivativeD x y derivative derivative - Euler's notationD x2y second derivative derivative of derivativepartial derivative ∂(x2+y2)/∂x = 2x ∫integral opposite to derivation ∫f(x)dx∫∫double integral integration of function of 2variables∫∫f(x,y)dxdy∫∫∫triple integral integration of function of 3variables∫∫∫f(x,y,z)dxdydz∮closed contour / lineintegral∯closed surfaceintegral∰closed volumeintegral[a,b] closed interval [a,b] = {x | a ≤ x ≤ b}(a,b) open interval (a,b) = {x | a < x < b}i imaginary unit i≡ √-1 z = 3 + 2i z* complex conjugate z = a+bi→z*=a-bi z* = 3 - 2i z complex conjugate z = a+bi→z = a-bi z = 3 - 2i ∇nabla / del gradient / divergence operator ∇f (x,y,z) vectorunit vectorx * y convolution y(t) = x(t) * h(t)Laplace transform F(s) = {f (t)}Fourier transform X(ω) = {f (t)}δdelta function∞lemniscate infinity symbol。
常用英文数学式符号的读法

⼀、⼀般符号对应的英⽂单词 . period 句号 , comma 逗号 : colon 冒号 ; semicolon 分号 ! exclamation 惊叹号 ? question mark 问号 ─ hyphen 连字符 ’ apostrophe 省略号;所有格符号 — dash 破折号 ‘’single quotation marks 单引号 “”double quotation marks 双引号 ( ) parentheses 圆括号 [ ] square brackets ⽅括号 《》French quotes 法⽂引号;书名号 ... ellipsis 省略号 ¨ tandem colon 双点号 " ditto 同上 ‖ parallel 平⾏ / virgule 斜线号 & ampersand = and ~ swung dash 代字号 § section; division 分节号 → arrow 箭号;参见号 + plus 加号;正号 - minus 减号;负号 ± plus or minus 正负号 × is multiplied by or cross 叉乘 ÷ is divided by 除号 = is equal to 等于号 ≠ is not equal to 不等于号 ≡ is equivalent to 全等于号 ≌ is equal to or approximately equal to 等于或约等于号 ≈ is approximately equal to 约等于号 < is less than ⼩于号 > is more than (is greater than在数学中更常⽤)⼤于号 ≮ is not less than 不⼩于号 ≯ is not more than 不⼤于号 ≤ is less than or equal to ⼩于或等于号 ≥ is more than or equal to ⼤于或等于号 % per cent 百分之… ‰ per mill 千分之… ∞ infinity ⽆限⼤号 ∝ varies as 与…成⽐例 √ (square) root 平⽅根 ∵ since; because 因为 ∴ hence 所以 ∷ equals, as (proportion) 等于,成⽐例 ∠ angle ⾓ ⌒ semicircle 半圆 ⊙ circle 圆 ○ circumference 圆周 π pi 圆周率 △ triangle 三⾓形 ⊥ perpendicular to 垂直于;另外normal to,right to也都有垂直的意思。
数学符号

、希腊字母:α——阿尔法β——贝塔γ——伽马Δ——德尔塔ξ——可sei ψ——可赛ω——奥秘噶μ——米哟λ——南木打σ——西格玛τ——套φ——fai2、数学运算符:∑—连加号∏—连乘号∪—并∩—补∈—属于∵—因为∴—所以√—根号‖—平行⊥—垂直∠—角⌒—弧⊙—圆∝—正比于∞—无穷∫—积分≈—约等≡—恒等3、三角函数:sin—赛因cos—考赛因tan—叹近体cot—考叹近体sec—赛看近体csc —考赛看近体序号大写小写英文注音国际音标注音中文注音1 Α α alpha a:lf 阿尔法2 Β β beta bet 贝塔3 Γ γ gamma ga:m 伽马4 Δ δ delta delt 德尔塔5 Ε ε epsilon ep`silon 伊普西龙6 Ζ ζ zeta zat 截塔7 Η η eta eit 艾塔8 Θ θ thet θit 西塔9 Ι ι iot aiot 约塔10 Κ κ k appa kap 卡帕11 Λ λ lambda lambd 兰布达12 Μ μ mu mju 缪13 Ν ν nu nju 纽14 Ξ ξ xi ksi 克西15 Ο ο omicron omik`ron 奥密克戎16 Π π pi pai 派17 Ρ ρ rho rou 肉18 Σ σ sigma `sigma 西格马19 Τ τ tau tau 套20 Υ υ upsilon jup`silon 宇普西龙21 Φ φ phi fai 佛爱22 Χ χ c hi phai 西23 Ψ ψ psi psai 普西24 Ω ω omega o`miga 欧米伽希腊字母的正确读法是什么?1 Α α alpha a:lf 阿尔法2 Β β beta bet 贝塔3 Γ γ gamma ga:m 伽马4 Δ δ delta delt 德尔塔5 Ε ε epsilon ep`silon 伊普西龙6 Ζ ζ zeta zat 截塔7 Η η eta eit 艾塔8 Θ θ thet θit 西塔9 Ι ι iot aiot 约塔10 Κ κ kappa kap 卡帕11 ∧λ lambda lambd 兰布达12 Μ μ mu mju 缪13 Ν ν nu nju 纽磁阻系数14 Ξ ξ xi ksi 克西15 Ο ο omicron omik`ron 奥密克戎16 ∏ π pi pai 派17 Ρ ρ rho rou 肉18 ∑ σ sigma `sigma 西格马19 Τ τ tau tau 套20 Υ υ upsilon jup`silon 宇普西龙21 Φ φ phi f ai 佛爱22 Χ χ chi phai 西23 Ψ ψ psi psai 普西角速;24 Ω ω omega o`miga 欧米伽希腊字母读法Αα:阿尔法AlphaΒβ:贝塔BetaΓγ:伽玛GammaΔδ:德尔塔DelteΕε:艾普西龙Epsilonζ :捷塔ZetaΖη:依塔EtaΘθ:西塔ThetaΙι:艾欧塔IotaΚκ:喀帕Kappa∧λ:拉姆达LambdaΜμ:缪MuΝν:拗NuΞξ:克西XiΟο:欧麦克轮Omicron∏π:派PiΡρ:柔Rho∑σ:西格玛SigmaΤτ:套TauΥυ:宇普西龙UpsilonΦφ:fai PhiΧχ:器ChiΨψ:普赛PsiΩω:欧米伽Omega数学符号大全2008年01月29日星期二 15:25因为自然科学的讨论经常要用到数学,但用文本方式只能表达L!t d5w x r ^ |$s Y 左右结构的数学公式,上下结构、根式、指数等都很难表达。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
+ plus 加号;正号
- minus 减号;负号
± plus or minus 正负号
× is multiplied by 乘号
÷ is divided by 除号
=is equal to 等于号
≠ is not equal to 不等于号
≡ is equivalent to 全等于号
≌is equal to or approximately equal to 等于或约等于≈ is approximately equal to 约等于号
<is less than 小于号
>is more than 大于号
≮is not less than 不小于号
≯is not more than 不大于号
≤ is less than or equal to 小于或等于号
≥ is more than or equal to 大于或等于号
% per cent 百分之…
‰ per mill 千分之…
∞ infinity 无限大号
∝varies as 与…成比例
√ (square) root 平方根
∵since; because 因为
∴hence 所以
∷equals, as (proportion) 等于,成比例
∠angle 角
⌒semicircle 半圆
⊙circle 圆
○ circumference 圆周
π pi 圆周率
△ triangle 三角形
⊥perpendicular to 垂直于
∪union of 并,合集
∩ intersection of 交,通集∫ the integral of …的积分
∑ (sigma) summation of 总和
° degree 度
′ minute 分
〃second 秒
℃Celsius system 摄氏度
{ open brace, open curly 左花括号
} close brace, close curly 右花括号
( open parenthesis, open paren 左圆括号
) close parenthesis, close paren 右圆括号
() brakets/ parentheses 括号
[ open bracket 左方括号
] close bracket 右方括号
[] square brackets 方括号
. period, dot 句号,点
| vertical bar, vertical virgule 竖线
& ampersand, and, reference, ref 和,引用
* asterisk, multiply, star, pointer 星号,乘号,星,指针
/ slash, divide, oblique 斜线,斜杠,除号
// slash-slash, comment 双斜线,注释符
# pound 井号
\ backslash, sometimes escape 反斜线转义符,有时表示
转义符或续行符
~ tilde 波浪符
. full stop 句号
, comma 逗号
: colon 冒号
; semicolon 分号
? question mark 问号
! exclamation mark (英式) exclamation point (美式)
' apostrophe 撇号
- hyphen 连字号
-- dash 破折号
... dots/ ellipsis 省略号
" single quotation marks 单引号
"" double quotation marks 双引号
‖ par allel 双线号
& ampersand = and
~swung dash 代字号
§ section; division 分节号
→ arrow 箭号;参见号。
