统计学(第4章)
统计学第4章学习指导
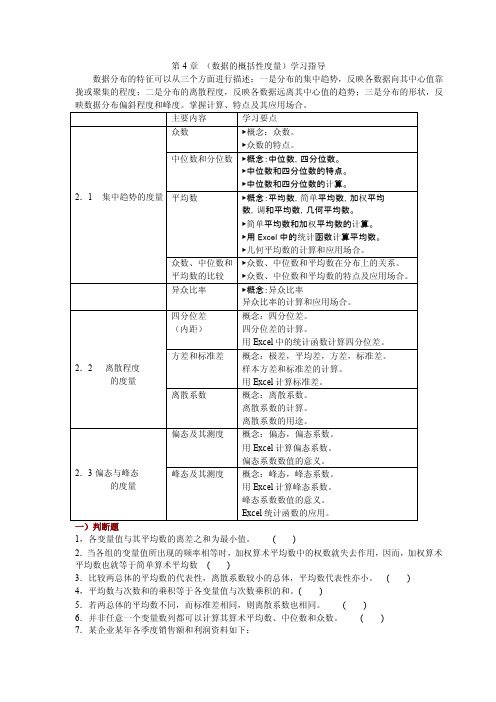
第4章(数据的概括性度量)学习指导数据分布的特征可以从三个方面进行描述:一是分布的集中趋势,反映各数据向其中心值靠拢或聚集的程度;二是分布的离散程度,反映各数据远离其中心值的趋势;三是分布的形状,反映数据分布偏斜程度和峰度。
掌握计算、特点及其应用场合。
主要内容学习要点2.1 集中趋势的度量众数▶概念:众数。
▶众数的特点。
中位数和分位数▶概念:中位数,四分位数。
▶中位数和四分位数的特点。
▶中位数和四分位数的计算。
平均数▶概念:平均数,简单平均数,加权平均数,调和平均数,几何平均数。
▶简单平均数和加权平均数的计算。
▶用Excel中的统计函数计算平均数。
▶几何平均数的计算和应用场合。
众数、中位数和平均数的比较▶众数、中位数和平均数在分布上的关系。
▶众数、中位数和平均数的特点及应用场合。
异众比率▶概念:异众比率异众比率的计算和应用场合。
2.2离散程度的度量四分位差(内距)概念:四分位差。
四分位差的计算。
用Excel中的统计函数计算四分位差。
方差和标准差概念:极差,平均差,方差,标准差。
样本方差和标准差的计算。
用Excel计算标准差。
离散系数概念:离散系数。
离散系数的计算。
离散系数的用途。
2.3偏态与峰态的度量偏态及其测度概念:偏态,偏态系数。
用Excel计算偏态系数。
偏态系数数值的意义。
峰态及其测度概念:峰态,峰态系数。
用Excel计算峰态系数。
峰态系数数值的意义。
Excel统计函数的应用。
一)判断题1,各变量值与其平均数的离差之和为最小值。
( )2.当各组的变量值所出现的频率相等时,加权算术平均数中的权数就失去作用,因而,加权算术平均数也就等于简单算术平均数( )3.比较两总体的平均数的代表性,离散系数较小的总体,平均数代表性亦小。
( )4,平均数与次数和的乘积等于各变量值与次数乘积的和。
( )5.若两总体的平均数不同,而标准差相同,则离散系数也相同。
( )6.并非任意一个变量数列都可以计算其算术平均数、中位数和众数。
统计学第四章

第四章 差异量教学目的:1.理解全距、四分位距、百分位距、平均差、方差、标准差和差异系数等概念;2.掌握各种差异量指标的计算方法。
数据的分布特征不仅有集中趋势,还有离中趋势。
以动态的眼光,从不同的角度看,数据是向中间变动的,也是向两端变动的。
两组数据可能平均水平相同,但两组数据的分布特征并不完全相同。
【如】:比较下列两组数据 A 组:88、82、73、76、81 B 组:92、86、70、72、80两组平均数,80==B A X X 但R A =88-73=15,R B=92-70=22。
即A 组较集中,B 组较分散。
因此,我们描述一组数据的分布特征,既要描述其集中趋势,也要描述其离中趋势。
差异量:表示一组数据的离中趋势或变异程度的量称为差异量。
常用的差异量指标有全距、四分位距、百分位距、平均差、方差、标准差和差异系数。
第一节全距、四分位距、百分位距一、全距全距:是一组数距中最大值与最小值之差。
优点:意义明确,计算方便。
缺点:反应不灵敏,易受极端值影响。
二、四分位距(一)四分位距的的概念四分位距:是指一组按大小顺序排列的数据中间部位50%个频数距离的一半。
)(1.4213Q Q QD -=QD :表示四分位距; Q 3:表示第三四分位数;Q 1:表示第一四分位数。
所以:四分位距的公式又为:22575P P QD -=(二)四分位数的计算方法 1、原始数据计算法(1)将数据由小到大进行排列; (2)分别求出三位四分位数(点); (3)代入公式计算。
【例如】:有以下16个数据25、22、29、12、40、15、14、39、37、31、33、19、17、20、35、30,其中四分位距的计算方法如下:(1)先将原始数据从小到大排列好;12、14、15、17、*19、20、22、25、*29、30、31、33、*35、37、39、40Q 1=18 Md =27 Q 3=34(2)求出Q 1、Md 、Q 3;(3)将Q 1、Md 、Q 3的得数代入公式(4.1)。
统计学-第四章 总量指标和相对指标

统计工作的第四个阶段——统计分析的基础
2020/1/10
引例
统计指标,无处不在。如≪中华人民共和国 2017年国民经济和社会发展统计公报≫中所说: “初步核算,全年国内生产总值827122亿元,比 上年增长6.9%。其中,第一产业增加值65468亿 元,增长3.9%;第二产业增加值334623亿元, 增长6.1%;第三产业增加值427032亿元,增长 8.0%。第一产业增加值占国内生产总值的比重为 7.9%,第二产业增加值比重为40.5%,第三产业 增加值比重为51.6%。如图4-1、图4-2所示。
50
第五年第3季至第四年第4季:52;
第五年第2季至第四年第3季:51;
第五年第1季至第四年第2季:50。
提前三个季度完成五年计划。
2(重点)
3.中长期计划任务的检查
累计法:计划任务数以累计数形式出现。可用于检查计 划执行情况。计算公式为:
计划完成相对指标
A.总产量520万元
B.净产值320万元
C.职工人数160万人
D.工人占职工人数的80%
5.2001年我国发行长期建设国债1500亿元;2001年末,居民个 人储蓄存款 余额突破75000亿元。这两个指标()
A.都是时期数 B.都是时点数 C.都是绝对数
D.前者是时点数,后者是时期数 E.前者是时期数,后者是 时点数
这些指标数据说明了2017年我国经济总量及增长速度、 价格情况、粮食产量、人口及就业等构成的发展状况。而这 些指标的涵义就是我们本章要学习的总量指标和相对指标所 涉及的内容。
2020/1/10
学习内容
1.总量指标 2.相对指标
学习重点
1.掌握绝对数和相对数的 特点及相应的计算方法
统计学第四章分组和次数分布

重点、难点
1、统计分组的概念和作用 2、统计分组的原则 3、 分组标志选择及界限的确定(统计分组的
关键)(单选、判断) 4、统计分组的方法(单选、判断) 5、变量数列的编制(计算)(难点)
第一节 统计分组(统计整理的关键)
五、 统计分组的方法
1、品质标志分组 组数的确定取决于事物的特
点和统计研究的任务 2、数量标志分组(补充)
单项式分组(变动范围不大 的离散变量)
组距式分组(连续性变量和 变动范围较大的离散变量)
数量标志分组,不是简单的确 定各组间的数量差异,而是通过 分组体现数量变化来确定现象的 不同性质和类型。
(对总体而言是分,对个体而言是合) ● 统计分组的作用主要体现在以下三个方面:
1.划分事物的类型 2.反映现象总体的内部结构 3.分析现象之间的依存关系
二、统计分组的种类(p90—94)
1.按分组的作用或目的不同,分为类型分组、结构 分组和分析分组。 (补充)
2.按分组标志的多少及其排列形式,可分为简单分组、 复合分组和分组体系 平行分组体系(p93)
体是次数分布图的直方图。 连接各矩形顶边的中点(即各组的组中值),形成一
条折线,并在直方图的左右两边各假设有一个组,将折 线与两个假设组的中点连接,就形成次数分布曲线(次 数分布图)
标准组距次数=该组次数密度*标准组距(书55页实例3.3) 次数密度=各组的次数/各组的组距 标准组距是异距变量数列组距中最小的组距
(3)按其分组方法的不同,可以分为单项式变量数列和 组距式变量数列。 (p100,表4-9和表4-10)
三、累计次数(频数)分布(书100—101)
(1)向上累计 (上限以下) (2)向下累计(下限以上)
统计学基础第四章

4.2.4 比较相对指标
(一)概念 (二)计算公式
(一)概念
比较相对指标是将不同空间条件下同类 指标数值进行对比,反映同类事物在同 一时期不同空间条件下数量对比关系, 一般用百分数表示。也可以用倍数。
(二)计算公式
比较相对指标=某地区某一指标数值另一地区 同类指标数值×100%
随着研究目的的改变,比较指标的分子和分母 的数值可以对换。在经济管理工作中,将各单 位的技术经济指标与同类的先进水平对比,或 与规定的标准水平对比,便可找出差距。比较 相对指标的特点有:对比的分子与分母必须是 同质现象;分子、分母可互换。
2.时点指标(又称存量指标) 是反映现象处于某一时点上(某一时刻或某一瞬间)的数量水平。
例如,人口数、学校数、企业数、商店数、物资库存数量、银行 储蓄余额、牲畜存栏数等。时点指标有以下特点: (1)时点指标不能累计相加。因为,这种累计总量的重复计算没有 实际意义。例如,某班有学生45人。第一天统计实有45人,第二 天统计实有45人,但不能把两天实有人数加在一起说该班实有人 数为90人。 (2)时点指标数值的大小与时点的间隔长短没有直接关系。虽然时 点指标数值也会随着时间的变化而出现增减变动,但它与相邻时 点的间隔长短无关。例如,某种原材料的库存量多少只与原材料 的购进、拨出、消费等有关而与时间间隔无直接关系。 (3)时点指标是通过专门组织的一次性的全面调查所取得的标准时 点上的数值。
4.2 相对分析
4.2.1 相对指标 4.2.2 结构相对指标 4.2.3 比例相对指标 4.2.4 比较相对指标 4.2.5 强度相对指标 4.2.6 动态相对指标 4.2.7 计划完成相对指标
4.2.1 相对指标
(一)概念 (二)表现形式
(一)概念
《统计学》-第四章-统计综合指标

《统计学》-第四章-统计综合指标第四章统计综合指标(⼀)(⼀)填空题1、总量指标是反映社会经济现象的统计指标,其表现形式为绝对数。
2、总量指标按其反映总体的内容不同,分为总体的标志总量和总体单位总量;按其反映的时间状况不同,分为时期结构和时点结构。
反映总体在某⼀时刻(瞬间)上状况的总量指标称为时点结构,反映总体在⼀段时期内活动过程的总量指标称为时期结构。
3、相对指标的数值有两种表现形式,⼀是有名数,⼆是⽆名数。
4、某企业中,⼥职⼯⼈数与男职⼯⼈数之⽐为1:3,即⼥职⼯占25%,则1:3属于⽐例相对数,25%属于结构相对数。
(⼆)单项选择题(在每⼩题备选答案中,选出⼀个正确答案)1、银⾏系统的年末储蓄存款余额是( D )A. 时期指标并且是实物指标B. 时点指标并且是实物指标C. 时期指标并且是价值指标D. 时点指标并且是价值指标2、某企业计划规定本年产值⽐上年增长4%,实际增长6%,则该企业产值计划完成程度为( B )A、150%B、101.9%C、66.7%D、⽆法计算3、总量指标具有的⼀个显著特点是( A )A. 指标数值的⼤⼩随总体范围的扩⼤⽽增加B. 指标数值的⼤⼩随总体范围的扩⼤⽽减少C. 指标数值的⼤⼩随总体范围的减少⽽增加D. 指标数值的⼤⼩随总体范围的⼤⼩没有直接联系4、在出⽣婴⼉中,男性占53%,⼥性占47%,这是( D )A、⽐例相对指标B、强度相对指标C、⽐较相对指标D、结构相对指标5、我国1998年国民经济增长(即国内⽣产总值为)7.8% ,该指标是( C )A. 结构相对指标B. ⽐例相对指标C. 动态相对指标D. ⽐较相对指标6、某商店某年第⼀季度的商品销售额计划为去年同期的110%,实际执⾏的结果,销售额⽐去年同期增长24.3%,则该商店的商品销售计划完成程度的算式为( B )A. 124.3%÷210%B. 124.3%÷110%C. 210%÷124.3D. 条件不够,⽆法计算7、下⾯属于时点指标的是( A )A. 商品库存量B. 商品销售量C. 婴⼉出⽣数D. 平均⼯资8、将粮⾷产量与⼈⼝数相⽐得到的⼈均粮⾷产量指标是( D )A、统计平均数B、结构相对数C、⽐较相对数D、强度相对数9、某⼯业企业总产值计划⽐去年提⾼8%,实际⽐去年提⾼10%,则实际总产值⽐计划的任务数提⾼( B )A. 2%B. 1.85%C. 25%D. 101.85%10、某企业产值计划完成程度为102%,实际⽐基期增长12%,则计划规定⽐基期增长( A )A. 9.8%B. 10%C. 8.5%D. 6%11、已知某市有各种经济类型的⼯业企业3128个,⼯业总产值为210亿元,则在该资料中总体标志总量是( C )A. 各种经济类型的⼯业企业共3128个B. 其中国有⼯业企业所占的百分⽐C. ⼯业总产值210亿元D. 平均每个⼯⼚的产值为671万元12、⽐较相对指标是( A )A、同类现象在不同空间上对⽐B、同类现象在不同时间上对⽐C、同⼀现象的部分与总体的对⽐D、有联系的不同现象的相互对⽐13、正确计算和应⽤相对指标的前提条件是( B )A、正确选择对⽐基础B、严格保持分⼦、分母的可⽐性C、相对指标应与总量指标结合应⽤D、分⼦、分母必须同类(三)多项选择题(在每⼩题备选答案中,⾄少有两个答案是正确的)1、强度相对数是两个不同但有⼀定联系的总体的总量指标相对⽐⽽计算的统计指标,所以( BE )A. 强度相对数的分⼦、分母都是可以互换的B. 强度相对数的分⼦、分母有的是可以互换的C. 在各种相对指标中,只有强度相对指标的分⼦、分母都是可以互换的D. 强度相对指标都是有名数E. 强度相对指标也有的是⽤⽆名数来表⽰2、下列指标中属于时期指标的有( ABCD )A、全年出⽣⼈数B、国民⽣产总值C、粮⾷总产量D、商品销售额E、产品合格率3、下列各项指标中,属于时点指标的是( ABD )A. 在册职⼯⼈数B. 企业数C. 某种商品的销售量D. 某地区1998年年末的⼈⼝数E. 企业某年所⽣产的产品产量4、下列指标中属于时点指标的有( AB )A、年末⼈⼝数B、钢材库存量C、粮⾷产量D、⼯业总产值E、经济增长率5、⽆名数是⼀种抽象化的数值,常⽤的表⽰⽅法有( ABC )A. 系数或倍数B. 成数C. 百分⽐或千分数D. ⼈均指标6、总量指标的计量单位有( ABCDE )A、货币单位B、劳动量单位C、⾃然单位D、度量衡单位E、标准实物单位7、分⼦与分母可以互换的相对指标有( BCD )A. 结构相对指标B. ⽐例相对指标C. 强度相对指标D. ⽐较相对指标E. 计划完成程度相对指标8、相对指标中分⼦与分母可以互换位置的有( CD )A、计划完成程度许多相对指标B、结构相对指标C、⽐较相对指标D、强度相对指标E、动态相对指标9、在以下各项指标中,属于强度相对指标的有( BD )A. 平均⼯资B. ⼈⼝⾃然增长率C. 商品流转次数D. ⼀个国家的⼈均粮⾷产量E. 平均每⼈的主要产品的产量10、加权算术平均数的⼤⼩( ABCD )A、受各组变量值⼤⼩的影响B、受各组次数多少的影响C、随X的增⼤⽽增⼤D、随X的减少⽽减少E、与次数多少成反⽐关系11、⽐较相对指标的计算,可以是( ABCE )A. 不同国家、不同地区和不同单位之间的⽐较B. 先进⽔平与落后⽔平的⽐较C. 有联系的两个不同总体的总量指标的⽐较D. 同⼀总体内部部分与整体的⽐较E. 实际达到的⽔平与标准⽔平或平均⽔平的⽐较12、总量指标与相对指标的关系表现为( ABCDE )A、总量指标是计算相对指标的基础B、相对指标能补充总量指标的不⾜C、相对指标可表明总量指标之间的关系D、相对指标要与总量指标结合应⽤E、总量指标和相对指标都是综合指标13、相对指标的计量形式可以是( ABCDE )A、系数B、倍数C、成数D、百分数E、复名数第四章统计综合指标(⼆)(⼀)填空题1、平均指标是指同类社会经济现象在⼀定时间、地点和条件下将总体内单位的数量差异抽象化的代表性⽔平指标。
统计学(第4章)

连续变动结果的总量指标,时期指标是
一个流量。
时间维度上
时期指标的三个特点 具有可加性
时期指标可以累计
时期指标数值大小与时期长短有直接关系
时期指标的数值一般为连续登记
2019/6/15
第四章 描述统计
5
统计学
2、时点指标
时点指标又叫存量指标,是指反映社 会经济现象在某一时点上的总量指标,
四 季度
1 500
计划完成百分数=
1400+1420+1470+1500 5000
=115.8%
注:2010年第一季度前的四个季度的累计量已达5000,说明五年计 划提前三个季度完成。
2019/6/15
第四章 描述统计
33
统计学
(2)累计法
如何确定提前 完成时间?
计算公式:
计划完成相对指标 长期计划期间实际累计完成数 长期计划规定的累计数
时点指标是一个存量。
时间维度上
时点指标的三个特点
不具可加性
不同时点指标数值是不能累加
时点指标数值大小与时点间隔长短无直 接关系
时点指标一般为间断统计
2019/6/15
第四章 描述统计
6
统计学
三、总量指标的计量单位
1、实物量单位(包括度量衡单位) 2、价值量单位 3、劳动量单位(工时和工日)
5 000 1 250 1 340 1 280
102.4
52.4
4 000 1 000 1 030 1 215
121.5
56.1
2 000 500 600 400
80.0
50.0
11 000 2 750 2 970 2 895 105.33
统计学基础(第4章总量指标与相对指标)

2020/6/8
.
8
第二,时期指标的大小与现象活动时期的长短有直 接关系。一般情况下,现象活动时期越长、指标数 值就越大,反之则越小。因此,对时期指标进行比 较,必须注意时期长短上的可比性。
第三,时期指标数值是连续登记、累计的结果。
2020/6/8
.
9
时点指标是反映社会经济现象在某一时点(瞬间) 上所处状况的总量指标。如某一时点上的人口数、 商品库存数 相对指标
2020/6/8
.
3
第一节 总量指标 总量指标是表明社会经济现象在一定时
间、地点条件下的规模或水平的统计指 标,又称为绝对指标或绝对数。
总量指标可以表现为总量指标之间相比 较,得到的增加量或减少量。例如:某 地区社会商品零售额2001年比2000年增 加120万元,也是总量指标。
(3)总量指标是计算相对指标和平均指标的基础,相对
202指0/6标/8和平均指标都是在总量指标. 的基础上派生出来的。
5
总量指标的种类
(一)按反映总体内容不同,分为总体单位总量 和总体标志总量。
1、总体单位总量
是总体中的单位总数,比如以全国普通高校为总体, 2000年全国共有普通高校1041所,“1041”就是反 映总体的单位数。它是数个单位相加汇总而得到的
2020/6/8
.
14
第二节 相对指标
总量指标只表明现象所达到的总规模、总水平和 工作量,但要深入了解事物的状况,仅了解总量指 标还是远远不够的,还要在总量指标数值的基础上 进行对比分析,计算相对指标和平均指标,这是统 计分析方法的主要内容之一。
2020/6/8
.
15
一、相对指标及其表现形式
(一)相对指标的定义
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相对指标按所反映的时空关系不 同可分为三类:
静态相对指标 动态相对指标 计划完成程度相对指标
2013-9-13
第四章 总量指标
16
统计学
(一)静态相对指标
1.结构相对指标
结构相对指标表明总体内部各个组成部 分在总体中占的比重。俗称比重 。 计算公式
总体中某一部分的总量 结构相对指标 总体全部总量
11 000
(2) (3) (4) 1 250 1 000 500 2 750 1 340 1 280 1 030 1 215 600 400 2 970 2 895
102.4 121.5 80.0 105.33
52.4 56.1 50.0 53.3
2013-9-13
第四章 总量指标
34
统计学
2.计划任务采用相对数形式表现
2008年A城市的GDP为1250亿元,B城市 的GDP为980亿元。 比较相对指标:1250÷980 = 1.28 或 980÷1250 = 0.784 A城市GDP为B城市GDP的1.28倍或128%。 或B城市GDP是A城市GDP的78.4%。
2013-9-13
第四章 总量指标
24
统计学
2013-9-13
第四章 总量指标
9
统计学
四、总量指标的计算方法
1、直接计量法 2、推算法 3、专家估算法
2013-9-13
第四章 总量指标
10
统计学
五、计算和应用总量指标应注意的问题
1、要明确指标涵义,界定统计范围。
2、要注意现象的同质性,正确使用计 量单位。 3、计算总量指标必须注意计量单位的 统一性,特别是实物指标。
统计学
例.强度相对指标计算
251.9 亿元,钢产 量为22 233.6万吨,人口平均数为128 840 万人。 不是平均数。 则: 为什么?
2003年我国的GDP为117
人均GDP:910 0.5 元 人均钢铁产量:172.6 千克
2013-9-13
第四章 总量指标
27
统计学
(二)动态相对指标
统计学
例.计划任务用相对数表示
例1:某企业2010年的计划产量是2009年的 105%,2010年实际产值是2009年的110%。 则:
2010年计划完成程度=110% ÷ 105% = 104.8% 即超额4.8%完成。
例2:某企业2010年的计划劳动生产率比2009年提 高10%,而2010年实际比2009年提高的16%。
两个同类指标的指标涵义、口径范围、计 算方法、计量单位、所属时间应一致。 比较相对指标可以用用百分比来表示;也 可以用倍数来表示。 计算比较相对指标,可以用绝对数对比, 也可以用相对数、平均数对比。比较相对 指标的分子与分母可以互换。
23
2013-9-13
第四章 总量指标
统计学
例.比较相对指标计算
2013-ห้องสมุดไป่ตู้-13
第四章 总量指标
32
统计学
1.计划任务采用绝对数形式表现
用来进行短期计划执行情况检查分析 第一种情况:计划任务已经完成,即实际完成 数与计划数属于同一时期且长度相等。则直接 采用以上所列的基本公式计算。 第二种情况:计划任务还未完成,则采用以下 公式计算: 报告期累计完成数 计划完成程度相对指标 全期计划数
统计学
2、总量指标的作用
总量指标是对社会经济现象总体认 识的起点。 总量指标是国家编制发展规划、实 施宏观经济调控,企业进行经营决 策的主要依据。 总量指标是用来计算相对指标和平 均指标的基础。
第四章 总量指标 3
2013-9-13
统计学
二、总量指标的种类
(一)按总量指标反映总体内容的不同分 总体单位总量:是指总体内所有单位 的数量。 总体标志总量:总体中各单位标志值 的总和。在一个特定的总体内,只能 存在一个单位总量,而可以同时并存 多个标志总量,构成一个总量指标体 系。
第四章 总量指标
7
统计学
2.价值单位
是以货币单位计量的单位标。
价值指标的最大特点在于它的综合性。
价值指标也有一定的局限性,它脱离
了物质内容,具有抽象性。 价值指标也容易受价格的影响。
2013-9-13
第四章 总量指标
8
统计学
3.劳动量单位
劳动量单位是以劳动时间表示的单位 计量。 常用的劳动时间单位有工时、工日等。 一个工人做一小时工叫做一个工时, 八个工时等于一个工日。
2013-9-13 第四章 总量指标 4
统计学
(二)按反映时间性质不同分
1、时期指标
指反映某种社会经济现象在一段时间内
连续变动结果的总量指标,时期指标是 一个流量。 具有可加性 时期指标的三个特点
时期指标可以累计 时期指标数值大小与时期长短有直接关系 时期指标的数值一般为连续登记
统计学
第四章 综合指标
(描述统计)
统计学
第一节 总量指标
一、总量(Amounts)指标的意义
1. 总量指标的含义: 总量指标又称统计绝对数,它是反映 社会经济现象发展的总规模、总水平 和工作总量的综合指标。 总量指标的数值大小与统计范围的大 小成正比。 是最基本的统计指标。
2013-9-13 第四章 总量指标 2
动态相对指标又称发展速度,它是某现象
在两个不同时期或不同时点的指标数值之 比,反映现象在不同时间的发展变化情况。 计算公式:
动态相对指标(发展速度)=
报告期水平(a1) 基期水平(a0)
2013-9-13
第四章 总量指标
28
统计学
注意点:
作为比较基础的时期,称为“基期”。 可以是前期,也可以是报告期前的任 何一期。 研究的时期,称为“报告期”。 动态相对指标一般用百分数、倍数表 示。
2013-9-13 第四章 总量指标 33
统计学
例.计划完成程度的计算
某公司某年一二季度产资料
计划总产值 实际总产值
(万元)
企业
(万元)
全年
第二 季度
第一 季度
第二季度产值 第二 计划完成(%)
季度
(5)=(4)÷(2)
截止第二季度完 成全年产值的 (%)
(6)=(3 + 4) ÷(1)
(1) 甲 乙 丙 合计 5 000 4 000 2 000
39.4 60.6
2001 1: 1.54
39.1 60.9
2002 1: 1.56
35.5 64.5
2003 1: 1.82
年 份
轻工业产值与 重工业产值的 比例
2013-9-13
第四章 总量指标
20
统计学
结构相对指标与比例相对指标的关系
1 乙的比重 1 甲与乙之比
甲的比重 甲与乙之比 乙的比重
4.强度相对指标
不一定是同 一总体的
强度相对指标是两个性质不同但有一定联 系的总量指标对比计算的相对数,用来表 明一种现象在另一种现象中的发展强度、 密度和普遍程度。 注意与平均 计算公式: 数的区别
某一总量指标 强度相对指标 另一不同类的但有联系 的总体的总量指标
2013-9-13
第四章 总量指标
第四章 总量指标 29
2013-9-13
统计学
例.动态相对指标计算
某市2003年末职工人数为141.94万人,
2004年末职工人数为142.86万人。 则:
2004年末是2003年末的:100.65% 或1.006 5倍
2013-9-13
第四章 总量指标
30
统计学
(三)计划完成程度相对指标
则:计划完成程度=(100%+16%)÷(100%+10%) =105.5%
2013-9-13 第四章 总量指标 19
统计学
例:比例相对指标计算
1998~2003年我国轻重工业结构
年 份
轻工业产值% 重工业产值%
1998
1999
2000
2001
2002
2003
42.9 57.1
1998 1: 1.33
41.9 58.1
1999 1: 1.39
39.8 60.2
2000 1: 1.51
第四章 总量指标
18
统计学
2.比例相对指标
比例相对指标是总体内不同部分数量对比计算 的相对数,用以分析总体内各个组成部分之间 的比例关系和协调平衡状况。比例相对指标简 称比例。 比例相对指标可以用绝对数对比,也可以用相 分子与分母 对数、平均数对比。 可以互换 计算公式 总体中某一部分的数值 比例相对指标 总体中另一部分的数值
25
统计学
注意点:
一是两个对比的指标一般是总量指标 二是这两个不同类的指标是有一定社会经 济联系的。 强度相对指标一般以有名数表示。 有些强度相对指标的分子与分母可以互换, 这时,强度相对指标有正指标、逆指标之 分。如:用水量/万元产值 与平均数不同。
第四章 总量指标 26
2013-9-13
2013-9-13
第四章 总量指标
14
统计学
二、相对指标的表现形式
相对指标的表现形式:主要包括无名数和 有名数。 无名数:多以系数、倍数、成数、百分数 和千分数等表示 有名数:如公斤/人,元/人,人/平方公里 等。有名数主要是相对强度指标。
2013-9-13
第四章 总量指标
