2011年全国初中数学联合竞赛试题及参考答案_
2011年全国初中数学竞赛试题参考答案及解析

2011年全国初中数学竞赛试题参考答案及解析一、选择题 1.A 解:因为1a =,1a += 262a a =-, 所以322312612362126261261260662126024.a a a a a a a a a a a +--=-+---=--+=---+=()()()2. B3. D 4.C解:由已知得2310x x ++=, 于是 2222(1)(2)(3)(3)(32)(31)1 1.x x x x x x x x x x +++=+++=++-=-5.B解:依定义的运算法则,有ux vy u vx uy v +=⎧⎨+=⎩,,即(1)0(1)0u x vy v x uy -+=⎧⎨-+=⎩,对任何实数u v ,都成立. 由于实数u v ,的任意性,得(x y ,)=(1,0).6.D解:由 25325x y z x y z +-=⎧⎨--=-⎩,,可得 312.x z y z =-⎧⎨=+⎩,于是 22221125x y z z z ++=-+.因此,当111z =时,222x y z ++的最小值为5411.7.C解:由题设可知1y y x -=,于是341yy x yxx-==,所以 411y -=, 故12y =,从而4x =.于是92x y +=.8.C解:两式相加,得2358t t +=,解得1t =,或83t =-(舍去).当1t =时,4530A B =︒=︒,满足等式,故1t =. 所以,实数t 的所有可能值的和为1. 9.C解:如图,连接D E ,设1D E F S S ∆'=,则1423S S EF S BFS '==,从而有1324S S S S '=.因为11S S '>,所以1324S S S S >.10.A解:当2 3 2011k = ,,,,因为 ()()()32111112111kk k k k k k ⎡⎤<=-⎢⎥-+-⎣⎦,所以 333111111511123201122201120124S ⎛⎫<=++++<+-< ⎪⨯⎝⎭ , 于是有445S <<,故4S 的整数部分等于4.二、填空题 11.3<m ≤4解:易知2x =是方程的一个根,设方程的另外两个根为12 x x ,,则124x x +=,12x x m=.显然1242x x +=>,所以122x x -<, 164m∆=-≥0,即2,164m∆=-≥0,所以2, 164m∆=-≥0,解之得 3<m ≤4.12.19解: 在36对可能出现的结果中,有4对:(1,4),(2,3),(2,3),(4,1)的和为5,所以朝上的面两数字之和为5的概率是41369=.13.6解:如图,设点C 的坐标为a b (,),点D 的坐标为c d (,),则点A 的坐标为a a (,),点B 的坐标为.c c (,) 因为点C D ,在双曲线1y x=上,所以11ab cd ==,.由于AC a b =-,BD c d =-, 又因为2B D A C =,于是22222242c d a b c cd d a ab b -=--+=-+,(),所以 22224826a b c d ab cd +-+=-=()(),即224OC OD -=6.14.32解:由1x -≥0,且12x -≥0,得12≤x ≤1.21122y =+=+由于13124<<,所以当34x =时,2y 取到最大值1,故1a =.当12x =或1时,2y 取到最小值12,故2b =.所以,2232a b +=.15.84解:如图,设BC =a ,AC =b ,则22235a b +==1225. ①又Rt △AFE ∽Rt △ACB ,所以F E A F C BA C=,即1212b a b-=,故12()a b ab +=. ②由①②得2222122524a b a b a b a b+=++=++()(), 解得a +b =49(另一个解-25舍去),所以493584a b c ++=+=.三、解答题16.解:设方程20x a x b ++=的两个根为αβ,,其中αβ,为整数,且α≤β,则方程20x cx a ++=的两根为11αβ++,,由题意得()()11a a αβαβ+=-++=,,两式相加得 2210αβαβ+++=, 即 (2)(2)3αβ++=, 所以 2123αβ+=⎧⎨+=⎩,;或232 1.αβ+=-⎧⎨+=-⎩,解得 11αβ=-⎧⎨=⎩,;或53.αβ=-⎧⎨=-⎩,又因为[11]a b c αβαβαβ=-+==-+++(),,()(),所以 012a b c ==-=-,,;或者8156a b c ===,,,故3a b c ++=-,或29.17.证明:如图,延长A P 交⊙2O 于点Q , 连接 AH BD QB QC QH ,,,,.因为A B 为⊙1O 的直径, 所以∠A D B =∠BDQ =90°, 故BQ 为⊙2O 的直径. 于是CQ BC BH HQ ⊥⊥,.又因为点H 为△ABC 的垂心,所以.AH BC BH AC ⊥⊥,所以A H ∥CQ ,A C ∥HQ ,四边形ACQH 为平行四边形.所以点P 为C H 的中点.18.解:(1)如图,分别过点P Q , 作y 轴的垂线,垂足分别为C D , . 设点A 的坐标为(0,t ),则点B 的坐标为(0,-t ). 设直线PQ 的函数解析式为y kx t =+,并设P Q ,的坐标分别为 P P x y (,),Q Q x y (,).由 223y kx t y x =+⎧⎪⎨=⎪⎩,, 得 2203x kx t --=,于是 32P Qx x t=-,即 23P Q t x x =-.于是222323P P Q Q x t y tBCBD y tx t++==++22222()333.222()333P P Q P P Q P QQ P QQ Q P x x x x x x x x x x x x x x --===---又因为P Qx PC Q Dx =-,所以BC PC BDQD=.因为∠B C P =∠90BDQ =︒,所以△B C P ∽△BDQ , 故∠A B P =∠ABQ .(2)解法一 设P C a =,DQ b =,不妨设a ≥b >0,由(1)可知∠A B P =∠30ABQ =︒,B C,B D,所以 A C=2-,A D=2-.因为P C ∥DQ ,所以△AC P ∽△ADQ . 于是PC AC D QAD=,即a b=所以a b +=.由(1)中32P Qx x t=-,即32ab -=-,所以322ab a b =+=,于是可求得2a b ==将2b =代入223y x=,得到点Q 2,12).再将点Q 的坐标代入1y kx =+,求得3k =-所以直线PQ 的函数解析式为13y =-+.根据对称性知,所求直线PQ 的函数解析式为13y =-+,或13y x =+.解法二 设直线PQ 的函数解析式为y kx t =+,其中1t =. 由(1)可知,∠A B P =∠30ABQ =︒,所以2BQ DQ =.故 2Q x =将223Q Qy x =代入上式,平方并整理得4241590Q Q x x -+=,即22(43)(3)0Q Q x x --=.所以 2Q x =又由 (1)得3322P Q x x t =-=-,32PQ x x k+=.若2Q x =代入上式得 P x = 从而 2()33P Q k x x =+=.同理,若Q x = 可得2P x =-从而 2()33P Q k x x =+=.所以,直线PQ 的函数解析式为13y =-+,或13y x =+.19.解:如图,作△ABQ ,使得QAB PAC ABQ ACP ∠=∠∠=∠,,则△ABQ ∽△ACP .由于2A B A C =,所以相似比为2. 于是224A Q A P B Q C P ====.60QAP QAB BAP PAC BAP BAC ∠=∠+∠=∠+∠=∠=︒.由:2:1AQ AP =知,90APQ ∠=︒,于是3PQ ==.所以 22225BP BQ PQ ==+,从而90BQP ∠=︒. 于是222()28AB PQ AP BQ =++=+.故 213s i n 60282ABC S AB AC AB ∆=⋅︒==.不同见解,敬请海涵。
数学周报杯2011年全国初中数学竞赛试题及答案

中国教育学会中学数学教学专业委员会“《数学周报》杯”2011年全国初中数学竞赛试题及答案一、选择题(每小题7分,共35分,每小题只有一个正确选项)1、设17-=a ,则代数式12612323--+a a a 的值为( )(A )24 (B )25 (C )1074+ (D )1274+2、对于任意实数a ,b ,c ,d ,定义有序实数对(a ,b )与(c ,d )之间的运算“△”为:(a ,b )△(c ,d )=(ac+bd ,ad+bc )。
如果对于任意实数u ,v ,都有(u ,v )△(x ,y )=(u ,v ),那么(x ,y )为( )(A )(0,1) (B )(1,0) (C )(-1,0) (D )(0,-1)3、若x>1,y>0,且满足xy=x y ,y x yx 3=,则x+y 的值为( ) (A )1 (B )2 (C )29 (D )211 4、点D ,E 分别在△ABC 的边AB ,AC 上,BE ,CD 相交于点F ,设S 四边形EADF =S 1,S △BDF =S 2, S △BCF =S 3,S △CEF =S 4,则S 1S 3与S 2S 4的大小关系为( )(A )S 1S 3< S 2S 4 (B )S 1S 3=S 2S 4 (C )S 1S 3>S 2S 4 (D )不能确定5、设3333991312111+⋅⋅⋅+++=S ,则4S 的整数部分等于( ) (A )4 (B )5 (C )6 (D )7二、填空题(每小题7分,共35分)6、若关于x 的方程(x-2)(x 2-4x+m )=0有三个根,且这三个根恰好可以作为一个三角形的三条边的长,则m 的取值范围是___________。
7、一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,2,3,3,4;另一枚质地均匀的正方体骰子的六个面上的数字分别是1,3,4,5,6,8。
2011年全国初中数学联合竞赛试题及参考答案

D, F, M 为 AB 的平 分 线 , P 的延 长 线 交 A £, B C M B
C
于 点 N. 果 PD—PE+ PF, 证 : 如 求 CN 是 ACB 的 平分线.
直 径 , C 与 A 交 于 点 E, 弦 D B 过 点 A 作 圆 的切 线 与 C 的 延 长 D
AE 的 延 长 线 于 点 H . 由 D 为 AC 的 中 点 , CH =2 知 FD. 由分 析 2, BF= 4 FD.
由 :B _ ③ 圈2 A
、
SnA F  ̄
④ 得 BE一2 EC.
@ 芝
注 该证法灵活运用三角形面积比 及三 罐
角 形 相 似 的 性 质 , 开 生 面 , 截 了 当. 别 直 继 续 探 究 , 有 其 它 的 证 法 , 用 梅 涅 劳 还 如
一
2 二 次 函数 一2 +6 . 1 7 z+C的 图像 的 顶 点 为 D, 与
2轴 正 方 向 从 左 至 右依 次 交 于 A , 2 B两 点 , Y轴 正 方 与
向 交 于 c点 , △ ABD 和 △ OBC 均 为 等腰 直 角 三 角 若 形 ()为坐 标 原 点 ) 则 6 c ( , +2 = .
二 、 空 题 :本 题 满 分 2 填 ( 8分 , 每小 题 7分 )
1 在 △ ABC 中 , 知 B 一 2 A , . 已 BC一 2, AB一 2 +2 , 则 A 一 .
三 、 本 题 满 分 2 分 ) 知 m, 为 正 整 数 , ( 5 已 , m<
一6 。 EFG=I 。FG上BC, AE= ( 0 5, 则 )
2 已 知 △ ABC 的两 条 高 线 的 长 分 别 为 5和 2 , . O
初中数学竞赛试题及答案解析

初中数学竞赛试题二、填空题1、 41-的负倒数与4-的倒数之和等于 . 2、 甲、乙、丙、丁四个数之和等于90-.甲数减4-,乙数加4-,丙数乘4-,丁数除以4-彼此相等.则四个数中的最大的一个数比最小的一个数大 .3、 已知a 1999=,则=-+---+-200133314232323a a a a a a .4、 填数计算:〇中填入的最小的自然数.△中填入最小的非负数.□中填入不小于5-且小于3的整数的个数.将下式的计算结果写在等号右边的横线上.(〇+□)⨯△= .5、 从集合}5,4,1,2,3{---中取出三个不同的数,可能得到的最大乘积填在□中,可能得到的最小乘积填在〇中,并将下式计算的结果写在等号右边的横线上.-(-□)÷〇= .6、 计算:=------------)4151()3141()2131(1)4151()3141()2131(1 . 7、 x 是有理数,则22195221100++-x x 的最小值是 . 8、 如图,C 是线段AB 的中点,D 是线段AC 的中点.已知图中所有线段的长度之和为23,则线段AC 的长度为.9、 在1000到5000之间同时被24,36,30整除的最小整数是_________,最大整数是__________.10、 一个有理数的倒数的相反数的3倍是31,那么这个有理数是 . 11、 一个有理数的二次幂大于这个有理数,那么这样的有理数的取值范围是 .12、 若8919+=+=+c b a ,则=-+-+-222)()()(a c c b b a .13、 a 1的倒数是51-,那么=a _____. 14、 小丽写出三个有理数,其中每两个有理数的平均值分别是326,217,7,那么这三个有理数的平均值是 .15、 计算:=--+-)36173)(72.0()722(125.11.16、 m ,y 互为相反数,n 和y 互为倒数,则5)(y my n -的值是_____.17、 已知1171=x ,则3)114(3)711)(1(2++--x x x 的值是 . 18、 已知52,32<-<-b a a b .则化简98272-+++-----b a a b a b 所得的结果是 .19、 m ,n 是正整数,mn =120,则m +n 可能取到的最小值是_____.20、 若a=1997,则7122----+a a a a 的值是 .21、 若x = -0.239,则199********-------++-+-x x x x x x 的值等于_____.参考答案二、填空题1、 417- 解:41-的负倒数为411--,4-的倒数为41-, 二者之和为:411--+41-417414-=--=.2、 204解:设等数为a ,则 90)4()4()]4([)]4([-=-⨯+-+--+-+a a a a 即90412-=-a ,∴ a =40, 因此,甲数为36,乙数为44,丙数为-10,丁数为-160,其中,最大数-最小数=44-(-160)=204.3、 4000000 解:当a 1999=时,142314232323-+-=-+-a a a a a a=-+-200133323a a a 200133323-+-a a a ,所以,原式=142323-+-a a a )2001333(23-+--a a a2000200019992000)1(20002+⨯=++=++=a a a a400000020002000=⨯=.4、 0解:〇中填1,△中0,□填8. []⎣⎦⎡⎤00)81(=⨯+.5、 ⎣⎦⎡⎤2160)30(-=÷-- 解:由-3,-2,-1,4,5中任取三个相乘可得10种不同的乘积,它们是:124)1)(3(,205)2)(3(,244)2)(3(,6)1)(2)(3(=⋅--=⋅--=⋅--=---,105)1)(2(,84)1)(2(,6054)3(,155)1)(3(=⋅--=⋅---=⋅⋅-=⋅--,2054)1(,4054)2(-=⋅⋅--=⋅⋅-,最大乘积是30,最小的乘积是-60.∴ ⎣⎦⎡⎤2160)30(-=÷--.6、 137 解:)4151()3141()2131(1)4151()3141()2131(1------------ )4151()3141()2131(1)]4151([)]3141([)]2131([1---------------= )4151()3141()2131(1)4151()3141()2131(1-------+-+-+= 41513141213114151314121311+-+-+--+-+-+= 13710131075121151211==-++-=.7、 1715 解:一般解法是分三种情况讨论:(1)当22195-<x 时 ,,(2)当22110022195≤≤-x 时 ,,(3)当221100>x 时 ,.综合(1),(2),(3)可得,最小值是1715.最简单的解法是:根据绝对值的几何意义,22195221100++-x x 表示数轴上x 对应的点P 到22195-对应的点A 和221100对应的点B 的距离之和,易知当P 在线段AB 上时,P A +PB 最小值为2211001715)22195(=--.8、 1373 解:设线段AC 的长度为x ,则AD =2x ,则AB =2x ,DC =2x ,DB =x 23,CB =x ,所以 232321221=+++++x x x x x x ,即23213=x .∴13731346==x .即AB 长度为1373.9、 4680解:24,30,36三个数的最小公倍数是360,10803360=⨯,∴大于10000且能被24,30,36整除的最小整数是1080,又36010805000⋅+>n ,其中n 为自然数,解得9810<n .∴取10=n ,得4680360101080=⋅+.∴具有这种性质的最大整数是4680.10、 -9解:利用还原算法:某数a 的3倍是31,显然91=a ,而91应是一个有理数倒数的相反数,所以这个有理数的倒数为91-,故这个有理数是-9.11、 大于1的有理数和负有理数解:画出数轴如图.大于1的有理数的二次幂大于它自身;1的二次幂等于1;大于0且小于1的有理数的二次幂小于它本身;0的二次幂是0;负有理数的二次幂是正数,大于它自身.综上可知,二次幂大于其自身的有理数的范围,是大于1的有理数和负有理数.12、 222解:由8919+=+=+c b a 得:11,1,10=--=--=-a c c b b a .∴+-+-22)()(c b b a =-2)(a c 222121110011)1()10(222=++=+-+-.13、 51- 解:a 1的倒数是51-,那么a 1=-5,51-=a .14、 1817 解:设小丽写出的三个有理数为x ,y ,z ,则3262,2172,72=+=+=+z y z x y x , 所以15,340,14=+=+=+x z z y y x ,三式相加,3127)(2=++z y x , 则1817181273==++z y x .15、 -14 解:因为2179167212518511.125(2)(0.72)(3)73687100367214-+--=-+=-+=-. 所以原分式的值为-14.16、 0解:由m 和y 互为相反数,知m = -y ,由n 和y 互为倒数,知道0,0≠≠y n 且yn 1= ∴0=-=-y y y y y m y n ,故5)(ym y n -=0. ∴17、 38 解:由1171=x ,可知2114,1171=+=-x x ,所以原式= 37772(1117)322113838111111-+=+=.18、 -6解:由32<-a b ,得03272<--<--a b a b .由52<-b a ,得052>+-a b ,得 05282>+->+-a b a b .而853)2()2(=+<-+-=+b a a b a b . 089<-+<-+∴a b b a98272-+++-----b a a b a b9)()82()72(-+-+----=b a a b a b987+--=6-=.19、 22解:由222)(1204)(4)(n m n m mn n m -+⋅=-+=+当2)(n m -愈小时,2)(n m +越小,从而m +n 也愈小,m 、n 为120的约数,且n m -要最小,由53222120⋅⋅⋅⋅==mn所以,当m =12,n =10时,m +n =22为最小值.20、 4000解:当a =1997时,0719971997,011997199722>-->-+7122----+a a a a)7()1(22----+=a a a a7122++--+=a a a a62+=a4000619972=+⋅=.21、 999解:由b a x <≤,可得a b a x b x -=---,则原式)19961997()23()1(---++---+--=x x x x x x)19961997()23()01(-++-+-=个99921998111=÷+++= 999=.。
2011年《数学周报》杯全国初中数学竞赛试题及评分标准

中国教育学会中学数学教学专业委员会 “《数学周报》杯”2011年全国初中数学竞赛试题题 号 一 二 三总 分1~5 6~10 11 12 13 14 得 分 评卷人 复查人答题时注意.1.用圆珠笔或钢笔作答; 2.解答书写时不要超过装订线;一、选择题(共5小题,每小题7分,共35分. 每道小题均给出了代号为A,B,C,D 的四个选项,其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.设71a =-,则代数式2212a a +-的值为( ).(A )-6 (B )24 (C )4710+ (D )4712+2.在同一直角坐标系中,函数x ky =(0≠k )与k kx y +=(0≠k )的图象大致是(A ) (B ) (C ) (D ) 3、在等边三角形ABC 所在的平面内存在点P,使⊿PAB 、⊿PBC 、⊿PAC 都是等腰三角形.请指出具有这种性质的点P 的个数( )(A )1 (B )7 (C )10 (D )154.若1x >,0y >,且满足3y y xxy x x y==,,则x y +的值为( ).(A )1 (B )2 (C )92(D )1125.设3333111112399S =++++,则4S 的整数部分等于( ). (A )4 (B )5 (C )6 (D )7 二、填空题(共5小题,每小题7分,共35分)6.若a 是一个完全平方数,则比a 大的最小完全平方数是 . 。
7.若关于x 的方程2(2)(4)0x x x m --+=有三个根,且这三个根恰好可 以作为一个三角形的三条边的长,则m 的取值范围是 .8.一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,2,3,3,4;另一枚质地均匀的正方体骰子的六个面上的数字分别是1,3,4,5,6,8. 同时掷这两枚骰子,则其朝上的面两数字之和为奇数5的概率是 .9.如图,点A B ,为直线y x =上的两点,过A B ,两点分别作y 轴的平行线交双曲线1y x=(x >0)于C D ,两点. 若2BD AC =,则224OC OD - 的值为 .10.如图,在Rt △ABC 中,斜边AB 的长为35,正方形CDEF 内接于△ABC ,且其边长为12,则△ABC 的周长为 .三、解答题(共4题,每题20分,共80分)11.已知.不论k 取什么实数,关于x 的方程1632=--+bkx a kx (a 、b 是常数)的根总是x =1,试求a 、b 的值。
全国初中数学竞赛历年竞赛试题及参考答案

初中数学竞赛试题答题时注意:1.用圆珠笔或钢笔作答; 2.解答书写时不要超过装订线; 3.草稿纸不上交.一、选择题(共5小题,每小题7分,共35分. 每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是准确的. 请将准确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.设1a =,则代数式32312612a a a +--的值为( ).(A )24 (B )25 (C )10 (D )12 2.对于任意实数a b c d ,,,,定义有序实数对a b (,)与c d (,)之间的运算“△”为:(a b ,)△(c d ,)=(ac bd ad bc ++,).如果对于任意实数u v ,, 都有(u v ,)△(x y ,)=(u v ,),那么(x y ,)为( ).(A )(0,1) (B )(1,0) (C )(﹣1,0) (D )(0,-1)3.若1x >,0y >,且满足3y y xxy x x y==,,则x y +的值为( ).(A )1 (B )2 (C )92(D )1124.点D E ,分别在△ABC 的边AB AC ,上,BE CD ,相交于点F ,设1234BDF BCF CEF EADF S S S S S S S S ∆∆∆====四边形,,,,则13S S 与24S S 的大小关系为( ).(A )1324S S S S < (B )1324S S S S = (C )1324S S S S > (D )不能确定 5.设3333111112399S =++++,则4S 的整数部分等于( ).(A )4 (B )5 (C )6 (D )7二、填空题(共5小题,每小题7分,共35分)6.若关于x 的方程2(2)(4)0x x x m --+=有三个根,且这三个根恰好可 以作为一个三角形的三条边的长,则m的取值范围是 .7.一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,2,3,3,4;另一枚质地均匀的正方体骰子的六个面上的数字分别是1,3,4,5,6,8. 同时掷这两枚骰子,则其朝上的面两数字之和为奇数的概率是 .8.如图,点A B ,为直线y x =上的两点,过A B ,两点分别作y 轴的平行线交双曲线1y x=(x >0)于C D ,两点. 若2BD AC =,则224OC OD - 的值为 .9.若112y x x =-+-的最大值为a ,最小值为b ,则22a b +的值为 .10.如图,在Rt △ABC 中,斜边AB 的长为35,正方形CDEF 内接于△ABC ,且其边长为12,则△ABC 的周长为 .三、解答题(共4题,每题20分,共80分)11.已知关于x 的一元二次方程20x cx a ++=的两个整数根恰好比方程20x ax b ++=的两个根都大1,求a b c ++的值.12.如图,点H 为△ABC 的垂心,以AB 为直径的⊙(第8题)(第10题)1O 和△BCH 的外接圆⊙2O 相交于点D ,延长AD 交CH 于点P ,求证:点P 为CH 的中点.13.如图,点A 为y 轴正半轴上一点,A B ,两点关于x 轴对称,过点A 任作直线交抛物线223y x=于P ,Q 两点. (1)求证:∠ABP =∠ABQ ;(2)若点A 的坐标为(0,1),且∠PBQ =60º,试求所有满足条件的直线PQ 的函数解析式.14.如图,△ABC 中,60BAC ∠=︒,2AB AC =.点P 在△ABC 内,且352PA PB PC ===,,,求△ABC 的面积.(第13题)(第12题)(第14题)初中数学竞赛试题参考答案一、选择题 1.A解:因为71a =-, 17a +=, 262a a =-, 所以322312612362126261261260662126024.a a a a a a a a a a a +--=-+---=--+=---+=()()()2.B解:依定义的运算法则,有ux vy u vx uy v +=⎧⎨+=⎩,,即(1)0(1)0u x vy v x uy -+=⎧⎨-+=⎩,对任何实数u v ,都成立. 因为实数u v ,的任意性,得(x y ,)=(1,0).3.C解:由题设可知1y y x -=,于是341y y x yx x -==,所以 411y -=, 故12y =,从而4x =.于是92x y +=.4.C解:如图,连接DE ,设1DEFS S ∆'=,则1423S S EF S BF S '==,从而有1324S S S S '=.因为11S S '>,所以1324S S S S >.5.A解:当2 3 99k =,,,时,因为()()()32111112111k k k k k k k ⎡⎤<=-⎢⎥-+-⎣⎦, 所以 3331111115111239922991004S ⎛⎫<=++++<+-< ⎪⨯⎝⎭. (第4题)于是有445S <<,故4S 的整数部分等于4.二、填空题 6.3<m ≤4解:易知2x =是方程的一个根,设方程的另外两个根为12 x x ,,则124x x +=,12x x m =.显然1242x x +=>,所以122x x -<, 164m ∆=-≥0,即()2121242x x x x +-<,164m ∆=-≥0,所以1642m -<, 164m ∆=-≥0,解之得 3<m ≤4.7.19解: 在36对可能出现的结果中,有4对:(1,4),(2,3),(2,3),(4,1)的和为5,所以朝上的面两数字之和为5的概率是41369=. 8.6解:如图,设点C 的坐标为a b (,),点D 的坐标为c d (,),则点A 的坐标为a a (,),点B 的坐标为.c c (,) 因为点C D ,在双曲线1y x=上,所以11ab cd ==,. 因为AC a b =-,BD c d =-, 又因为2BD AC =,于是22222242c d a b c cd d a ab b -=--+=-+,(),所以 22224826a b c d ab cd +-+=-=()(),即224OC OD -=6.9.32解:由1x -≥0,且12x -≥0,得12≤x ≤1.22213113122()2222416y x x x =+-+-=+--+. 因为13124<<,所以当34x =时,2y 取到最大值1,故1a =. (第8题)当12x =或1时,2y 取到最小值12,故2b =.所以,2232a b +=. 10.84解:如图,设BC =a ,AC =b ,则22235a b +==1225. ①又Rt △AFE ∽Rt △ACB ,所以FE AFCB AC=,即1212b a b-=,故 12()a b ab +=. ② 由①②得2222122524a b a b ab a b +=++=++()(), 解得a +b =49(另一个解-25舍去),所以493584a b c ++=+=.三、解答题11.解:设方程20x ax b ++=的两个根为αβ,,其中αβ,为整数,且α≤β,则方程20x cx a ++=的两根为11αβ++,,由题意得()()11a a αβαβ+=-++=,,两式相加得 2210αβαβ+++=, 即 (2)(2)3αβ++=,所以 2123αβ+=⎧⎨+=⎩,; 或232 1.αβ+=-⎧⎨+=-⎩,解得 11αβ=-⎧⎨=⎩,; 或53.αβ=-⎧⎨=-⎩,又因为[11]a b c αβαβαβ=-+==-+++(),,()(),所以 012a b c ==-=-,,;或者8156a b c ===,,,(第10题)故3a b c ++=-,或29.12.证明:如图,延长AP 交⊙2O 于点Q , 连接 AH BD QB QC QH ,,,,.因为AB 为⊙1O 的直径, 所以∠ADB =∠BDQ =90°, 故BQ 为⊙2O 的直径. 于是CQ BC BH HQ ⊥⊥,.又因为点H 为△ABC 的垂心,所以.AH BC BH AC ⊥⊥,所以AH ∥CQ ,AC ∥HQ ,四边形ACQH 为平行四边形. 所以点P 为CH 的中点.13.解:(1)如图,分别过点P Q , 作y 轴的垂线,垂足分别为C D , . 设点A 的坐标为(0,t ),则点B 的坐标为(0,-t ). 设直线PQ 的函数解析式为y kx t =+,并设P Q ,的坐标分别为 P P x y (,),Q Q x y (,).由223y kx t y x =+⎧⎪⎨=⎪⎩,, 得 2203x kx t --=, 于是 32P Q x x t =-,即 23P Q t x x =-.于是222323P P Q Qx t y t BC BD y t x t ++==++22222()333.222()333P P Q P P Q P Q Q P Q Q Q P x x x x x x x x x x x x x x --===--- 又因为P Q x PC QD x =-,所以BC PCBD QD=. 因为∠BCP =∠90BDQ =︒,所以△BCP ∽△BDQ ,(第12题)(第13题)故∠ABP =∠ABQ .(2)解法一 设PC a =,DQ b =,不妨设a ≥b >0,由(1)可知∠ABP =∠30ABQ =︒,BC ,BD ,所以 AC 2-,AD =2.因为PC ∥DQ ,所以△ACP ∽△ADQ .于是PC ACDQ AD=,即a b ,所以a b +=.由(1)中32P Q x x t =-,即32ab -=-,所以322ab a b =+=,于是可求得2a b ==将2b =代入223y x =,得到点Q ,12).再将点Q 的坐标代入1y kx =+,求得3k =-所以直线PQ 的函数解析式为1y =+.根据对称性知,所求直线PQ 的函数解析式为1y =+,或1y +. 解法二 设直线PQ 的函数解析式为y kx t =+,其中1t =. 由(1)可知,∠ABP =∠30ABQ =︒,所以2BQ DQ =.故 2Q x =.将223Q Q y x =代入上式,平方并整理得 4241590Q Q x x -+=,即22(43)(3)0Q Q x x --=.所以 2Q x =又由 (1)得3322P Q x x t =-=-,32P Q x x k +=. 若3Q x =,代入上式得 3P x =-, 从而 23()3P Q k x x =+=-.同理,若3Q x =, 可得32P x =-, 从而 23()3P Q k x x =+=.所以,直线PQ 的函数解析式为31y x =-+,或31y x =+. 14.解:如图,作△ABQ ,使得QAB PAC ABQ ACP ∠=∠∠=∠,,则△ABQ ∽△ACP . 因为2AB AC =,所以相似比为2. 于是22324AQ AP BQ CP ====,.60QAP QAB BAP PAC BAP BAC ∠=∠+∠=∠+∠=∠=︒.由:2:1AQ AP =知,90APQ ∠=︒,于是33PQ AP ==.所以 22225BP BQ PQ ==+,从而90BQP ∠=︒. 于是222()2883AB PQ AP BQ =++=+ .故 213673sin 60282ABC S AB AC AB ∆+=⋅︒==.(第14题)。
历年初中数学竞赛真题库含答案
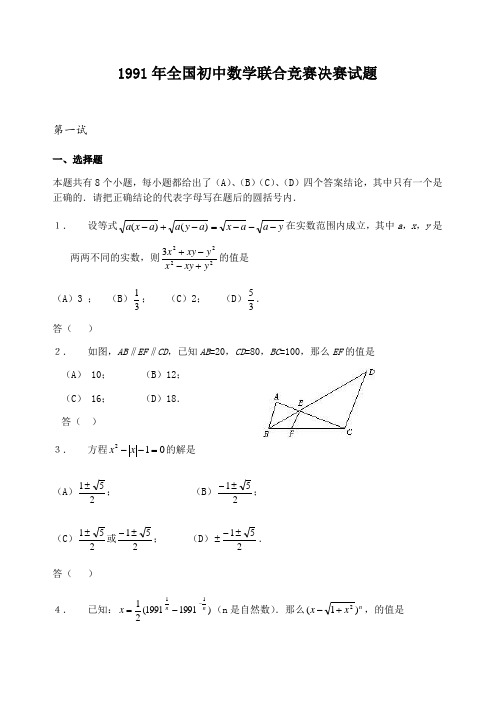
1991年全国初中数学联合竞赛决赛试题第一试一、选择题本题共有8个小题,每小题都给出了(A )、(B )(C )、(D )四个答案结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1. 设等式y a a x a y a a x a ---=-+-)()(在实数范围内成立,其中a ,x ,y 是两两不同的实数,则22223yxy x y xy x +--+的值是 (A )3 ; (B )31; (C )2; (D )35. 答( )2. 如图,AB ‖EF ‖CD ,已知AB =20,CD =80,BC =100,那么EF 的值是(A ) 10; (B )12;(C ) 16; (D )18.答( )3. 方程012=--x x 的解是(A )251±; (B )251±-; (C )251±或251±-; (D )251±-±. 答( )4.已知:)19911991(2111n n x --=(n 是自然数).那么n x x )1(2+-,的值是(A)11991-; (B)11991--;(C)1991)1(n -; (D)11991)1(--n .答( )5. 若M n 1210099321=⨯⨯⨯⨯⨯ ,其中M为自然数,n 为使得等式成立的最大的自然数,则M(A)能被2整除,但不能被3整除;(B)能被3整除,但不能被2整除;(C)能被4整除,但不能被3整除;(D)不能被3整除,也不能被2整除.答( )6. 若a ,c ,d 是整数,b 是正整数,且满足c b a =+,d c b =+,a d c =+,那么 d c b a +++的最大值是(A)1-;(B)5-;(C)0;(D)1.答( )7. 如图,正方形OPQR 内接于ΔABC .已知ΔAOR 、ΔBOP 和ΔCRQ 的面积分别是11=S ,32=S 和13=S ,那么,正方形OPQR 的边长是 (A)2;(B)3;(C)2 ;(D)3.答( )8. 在锐角ΔABC 中,1=AC ,c AB =, 60=∠A ,ΔABC 的外接圆半径R ≤1,则 (A)21< c < 2 ; (B)0< c ≤21; 答( )(C )c > 2; (D )c = 2.答( )二、填空题1.E是平行四边形ABCD 中BC 边的中点,AE 交对角线BD 于G ,如果ΔBEG 的面积是1,则平行四边形ABCD 的面积是 . 2.已知关于x 的一元二次方程02=++c bx ax 没有实数解.甲由于看错了二次项系数,误求得两根为2和4;乙由于看错了某一项系数的符号,误求得两根为-1和4,那么,=+ac b 32 .3.设m ,n ,p ,q 为非负数,且对一切x >0,qpn m x x x x )1(1)1(+=-+恒成立,则 =++q p n m 22)2( .4.四边形ABCD 中,∠ ABC 135=,∠BCD 120=,AB 6=,BC 35-=,CD = 6,则AD = .第二试x + y , x - y , x y , yx 四个数中的三个又相同的数值,求出所有具有这样性质的数对(x , y ).二、ΔABC中,AB<AC<BC,D点在BC上,E点在BA的延长线上,且BD=BE=AC,ΔBDE的外接圆与ΔABC的外接圆交于F点(如图).求证:BF=AF+CF三、将正方形ABCD分割为2n个相等的小方格(n是自然数),把相对的顶点A,C染成红色,把B,D染成蓝色,其他交点任意染成红、蓝两色中的一种颜色.证明:恰有三个顶点同色的小方格的数目必是偶数.1992年全国初中数学联合竞赛决赛试题第一试一.选择题本题共有8个题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.满足1=+-ab b a 的非负整数),(b a 的个数是(A)1; (B)2; (C)3; (D)4.2.若0x 是一元二次方程)0(02≠=++a c bx ax 的根,则判别式ac b 42-=∆与平方式20)2(b ax M +=的关系是(A)∆>M (B)∆=M (C)∆>M ; (D)不确定.3.若01132=+-x x ,则44-+x x 的个位数字是(A)1; (B)3; (C)5; (D)7.答( )4.在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于2,则这个多边形的边数必为(A)7; (B)6; (C)5; (D)4.答( )5.如图,正比例函数)0(>==a ax y x y 和的图像与反比例函数)0(>=k xk y 的图像分别相交于A 点和C 点.若AOB Rt ∆和COD ∆的面积分别为S 1和S 2,则S 1与S 2的关系是 (A)21S S > (B)21S S =(C)21S S < (D)不确定 答( )6.在一个由88⨯个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆周经过的所有小方格的圆内部分的面积之和记为1S ,把圆周经过的所有小方格的圆内部分的面积之和记为2S ,则21S S 的整数部分是 (A)0; (B)1; (C)2; (D)3.答( )7.如图,在等腰梯形ABCD 中, AB //CD , AB=2CD ,︒=∠60A ,又E 是底边AB 上一点,且FE=FB=AC , FA=AB .则AE :EB 等于(A)1:2 (B)1:3(C)2:5 (D)3:10答( )8.设9321,,,,x x x x ⋅⋅⋅均为正整数,且921x x x <⋅⋅⋅<<,220921=+⋅⋅⋅++x x x ,则当54321x x x x x ++++的值最大时,19x x -的最小值是(A)8; (B)9; (C)10; (D)11.答( )二.填空题1.若一等腰三角形的底边上的高等于18cm ,腰上的中线等15cm ,则这个等腰三角形的面积等于________________.2.若0≠x ,则x x x x 44211+-++的最大值是__________.3.在ABC ∆中,B A C ∠∠=∠和,90 的平分线相交于P 点,又AB PE ⊥于E 点,若3,2==AC BC ,则=⋅EB AE .4.若b a ,都是正实数,且0111=+--b a b a ,则=+33)()(ba ab . 第二试一、设等腰三角形的一腰与底边的长分别是方程062=+-a x x 的两根,当这样的三角形只有一个时,求a 的取值范围.二、如图,在ABC ∆中,D AC AB ,=是底边BC 上一点,E 是线段AD 上一点,且A CED BED ∠=∠=∠2.求证:CD BD 2=.三、某个信封上的两个邮政编码M 和N 均由0,1,2,3,5,6这六个不同数字组成,现有四个编码如下:A :320651B :105263C :612305D :316250已知编码A 、B 、C 、D 各恰有两个数字的位置与M 和N 相同.D 恰有三个数字的位置与M 和N 相同.试求:M 和N.1993年全国初中数学联合竞赛决赛试题第一试一.选择题本题共有8个小题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.多项式1612+-x x 除以12-x 的余式是(A)1; (B)-1; (C)1-x ; (D)1+x ;2.对于命题Ⅰ.内角相等的圆内接五边形是正五边形.Ⅱ.内角相等的圆内接四边形是正四边形,以下四个结论中正确的是(A )Ⅰ,Ⅱ都对 (B )Ⅰ对,Ⅱ错 (C )Ⅰ错,Ⅱ对. (D )Ⅰ,Ⅱ都错.3.设x 是实数,11++-=x x y .下列四个结论:Ⅰ.y 没有最小值;Ⅱ.只有一个x 使y 取到最小值;Ⅲ.有有限多个x (不止一个)使y 取到最大值;Ⅳ.有无穷多个x 使y 取到最小值.其中正确的是(A )Ⅰ (B )Ⅱ (C )Ⅲ (D )Ⅳ4.实数54321,,,,x x x x x 满足方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=++=++=++=++.;;;;52154154354324321321a x x x a x x x a x x x a x x x a x x x其中54321,,,,a a a a a 是实常数,且54321a a a a a >>>>,则54321,,,,x x x x x 的大小顺序是(A)54321x x x x x >>>>; (B )53124x x x x x >>>>;(C )52413x x x x x >>>>; (D )24135x x x x x >>>>.5.不等式73)1(12+<-<-x x x 的整数解的个解(A )等于4 (B )小于4 (C )大于5 (D )等于56.在ABC ∆中,BC AO O A =∠,,是垂心是钝角,则)cos(OCB OBC ∠+∠的值是 (A)22- (B)22 (C)23 (D)21-. 答( )7.锐角三角ABC 的三边是a , b , c ,它的外心到三边的距离分别为m , n ,p ,那么m :n :p 等于 (A)c b a 1:1:1; (B)c b a :: (C)C B A cos :cos :cos (D)C B A sin :sin :sin .答( )8.13333)919294(3-+-可以化简成 (A))12(333+; (B))12(333- (C)123- (D)123+答( )二.填空题1. 当x 变化时,分式15632212++++x x x x 的最小值是___________. 2.放有小球的1993个盒子从左到右排成一行,如果最左面的盒里有7个小球,且每四个相邻的盒里共有30个小球,那么最右面的盒里有__________个小球.3.若方程k x x =--)4)(1(22有四个非零实根,且它们在数轴上对应的四个点等距排列,则k =____________.4.锐角三角形ABC 中,︒=∠30A .以BC 边为直径作圆,与AB , AC分别交于D , E ,连接DE , 把三角形ABC 分成三角形ADE 与四边形BDEC ,设它们的面积分别为S 1, S 2,则S 1:S 2=___________. 第二试一.设H 是等腰三角形ABC 垂心,在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小,这时乘积HBC ABC S S ∆∆⋅的值变小,变大,还是不变?证明你的结论.二.ABC ∆中, BC =5, AC =12, AB =13, 在边AB ,AC 上分别取点D , E , 使线段DE 将ABC ∆分成面积相等的两部分.试求这样的线段DE 的最小长度.三.已知方程0022=++=++b cx x c bx x 及分别各有两个整数根21,x x 及21,x x '',且,021>x x 021>''x x . (1)求证:;0,0,0,02121<'<'<<x x x x (2)求证:1-b ≤c ≤1+b ; (3)求c b ,所有可能的值.1994年全国初中数学联赛试题第一试(4月3日上午8:30—9:30)考生注意:本试共两道大题,满分80分.一、选择题(本题满分48分,每小题6分)本题共有8个小题都给出了A,B、C,D,四个结论,其中只有一个是正确的,请把你认为正确结论的代表字母写在题后答案中的圆括号内,每小题选对得6分;不选、选错或选出的代表字母超过一个(不论是否写在圆括号内),一律得0分.〔答〕( )2.设a,b,c是不全相等的任意实数,若x=a2-bc,y=b2-ca,z=c2-ab,则x,y,zA.都不小于0B.都不大于0C.至少有一个小0于D.至少有一个大于0〔答〕( )3.如图1所示,半圆O的直径在梯形ABCD的底边AB上,且与其余三边BC,CD,DA相切,若BC=2,DA=3,则AB的长A.等于4B.等于5C.等于6D.不能确定〔答〕( )A.1 B.-1 C.22001D.-22001〔答〕( )5.若平行直线EF,MN与相交直线AB,CD相交成如图2所示的图形,则共得同旁内角A.4对B.8对C.12对D.16对〔答〕( )〔答〕( )7.设锐角三角形ABC的三条高AD,BE,CF相交于H。
全国初中数学竞赛试题及答案

中国教育学会中学数学教学专业委员会全国初中数学竞赛试题一、选择题(共5小题,每小题6分,共30分。
)1(甲).如果实数a ,b ,c 22||()||a a b c a b c -++-++可以化简为( ).(A )2c a - (B )22a b - (C )a - (D)a 1(乙).如果22a =-11123a+++的值为( ).(A)2- (B 2 (C )2 (D )222(甲).如果正比例函数y = ax (a ≠ 0)与反比例函数y =xb(b ≠0 )的图象有两个交点,其中一个交点的坐标为(-3,-2),那么另一个交点的坐标为( ). (A )(2,3) (B )(3,-2) (C )(-2,3) (D )(3,2)2(乙). 在平面直角坐标系xOy 中,满足不等式x 2+y 2≤2x +2y 的整数点坐标(x ,y )的个数为( ). (A )10 (B )9 (C )7 (D )53(甲).如果a b ,为给定的实数,且1a b <<,那么1121a a b a b ++++,, ,这四个数据的平均数与中位数之差的绝对值是( ). (A )1 (B )214a - (C )12 (D)143(乙).如图,四边形ABCD 中,AC ,BD 是对角线, △ABC 是等边三角形.30ADC ∠=︒,AD = 3,BD = 5, 则CD 的长为( ). (A)23 (B)4 (C )52 (D)4。
54(甲).小倩和小玲每人都有若干面值为整数元的人民币.小倩对小玲说:“你若给我2元,我的钱数将是你的n 倍”;小玲对小倩说:“你若给我n 元,我的钱数将是你的2倍”,其中n 为正整数,则n 的可能值的个数是( ).OAB CED(A )1 (B )2 (C )3 (D )44(乙).如果关于x 的方程 20x px q p q --=(,是正整数)的正根小于3, 那么这样的方程的个数是( ).(A ) 5 (B ) 6 (C ) 7 (D) 85(甲).一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,3,4,5,6.掷两次骰子,设其朝上的面上的两个数字之和除以4的余数分别是0,1,2,3的概率为0123p p p p ,,,,则0123p p p p ,,,中最大的是( ). (A )0p (B )1p (C )2p (D )3p 5(乙).黑板上写有111123100, , ,, 共100个数字.每次操作先从黑板上的数中选取2个数a b ,,然后删去a b ,,并在黑板上写上数a b ab ++,则经过99次操作后,黑板上剩下的数是( ).(A )2012 (B )101 (C )100 (D )99二、填空题(共5小题,每小题6分,共30分)6(甲).按如图的程序进行操作,规定:程序运行从“输入一个值x "到“结果是否>487?"为一次操作。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.已 知 △ABC 的 两 条 高 线 的 长 分 别 为 5 和 20, 若第三条高线的长也是 整 数,则 第 三 条 高 线 长 的 最 大
值 为 ( ). (A)5 (C)7
(B)6 (D)8
3.方程|x2-1|=(4-2槡3)(x+2)的解的 个 数 为
( ).
(A)1 个
(C)9 组
(D)11 组 .
5.如图,菱 形 ABCD 中,AB=3,DF=1,∠DAB =60°∠EFG=15°,FG⊥BC,则 AE=( )
(A)1+槡2.
(B)槡6.
(C)2槡3-1.
(D)1+槡3.
6.已 知
1 x
+y1+z=
1 ,1 2y
+z+1x =
1 ,1 3z
+
x1+y=
1 4
,则
线交于点 F,如 果 DE= 34CE,
AC=8 槡5,D 为 EF 的 中 点,则
AB=
.
第 二 试 (A)
一、(本题满分20分)已知 三 个 不 同 的 实 数a,b,c
满足a-b+c=3,方程 x2+ax+1=0和 x2+bx+c=
0 有 一 个 相 同 的 实 根 ,方 程x2 +x+a=0 和x2 +cx+b
AE 的延长线于点 H .
由 D 为AC 的中点,知 CH=2FD.
由 分 析 2,BF=4FD.
故 EBCE=CBHF=2.
由 EBCE=SS△△AACBFF =2SS△△AABDFF .
③
由 分 析 2,△ABF∽ △DAF.
得
S△ABF S△ADF
=
(AB AD
)2=4.
④
由③、④得 BE=2EC.
注 该证法灵活运用三角形面积比及三
角 形 相 似 的 性 质 ,别 开 生 面 ,直 截 了 当 .
继续 探 究,还 有 其 它 的 证 法,如 用 梅 涅 劳
斯 定 理 等 ,限 于 篇 幅 ,此 不 赘 述 .
(责 审 韩 乐 琴 )
· 31 · 网址:zxss.chinajournal.net.cn
第 二 试 (C) 一、(本题满分20分)题目和解答 与(A)卷 第 一 题 相同. 二、(本题满分25 分)如 图,已 知 P 为 锐 角 △ABC 内一 点,过 P 分 别 BC,AC,AB 的 垂 线,垂 足 分 别 为 D,E,F,BM 为∠ABC 的平分 线,MP 的 延 长 线 交 AB 于点 N .如 果 PD=PE+PF,求 证:CN 是 ∠ACB 的 平分线. 三、(本题满分25分)题 目 和 解 答 与 (B)卷 第 三 题 相同.
电 子 信 箱 :zxss@chinajournal.net.cn
(上 接 第 31 页 )
二 、填 空 题 :(本 题 满 分 28 分 ,每 小 题 7 分 ) 1.在△ABC 中,已 知 ∠B=2∠A,BC=2,AB=2
+2槡3,则 ∠A=
.
2.二 次 函 数y=x2 +bx+c 的 图 像 的 顶 点 为 D ,与
BD 的延长线于点 N .
助三角形中点的性质,沟通、转化,使 问 题 迎 刃
由 D 为AC 的中点,知 DN=FD.
而解.
由 分 析 2,BF=4FD.
分析5 如图3,连结 CF.
得 FN=2FD= 12BF.
故 EBCE=FBNF=2.
即 BE=2EC.
图3
分析4 如 图 3,过 点 C 作 CH ∥BD,交
=0 也 有 一 个 相 同 的 实 根 .求 a,b,c 的 值 .
二、(本 题 满 分 25 分 )如
图,在四边形 ABCD 中,已 知
∠BAD=60°,∠ABC=90°,
∠BCD=120°,对 角 线 AC,
BD 交于点S,且 DS=2SB,P 为 AC 的 中 点.求 证:
(1)∠PBD=30°;(2)AD=DC.
三、(本题满分25分)已 知 m,n,p 为 正 整 数,m<
n.设 A(-m,0),B(n,0),C(0,p),O 为 坐 标 原 点.若
∠ACB=90°,且 OA2 +OB2 +OC2 =3(OA +OB +
OC).
(1)证 明 :m+n=p+3;
(2)求图像经过 A,B,C 三点的二次函数的解析式.
(B)2 个
(C)3 个
(D)4 个
4.今有长度 分 别 为 1,2,…,9 的 线 段 各 一 条,现
从 中 选 出 若 干 条 线 段 组 成 “线 段 组 ”,由 这 一 组 线 段 恰
好可以拼接成一个正方形,则 这 样 的 “线 段 组”的 组 数
有 ( ).
(A)5 组 (B)7 组
x 轴正方向从左至右依次交于A,B 两点,与 y 轴 正 方
向交于C 点,若 △ABD 和 △OBC 均 为 等 腰 直 角 三 角
形(O 为坐标原点),则b+2c=
.
3.能使2n+256是完全平方数的正整数n 的值为
. 4.如 图,已 知 AB 是 ⊙O 的 直 径,弦CD 与AB 交于点E,过
点 A 作 圆 的 切 线 与CD 的 延 长
第 二 试 (B)
一、(本题满分20分)题目和解答与(A)卷 第 一 题
相同. 二、(本 题 满 分 25 分 )如
图,在四边形 ABCD 中,已 知 ∠BAD=60°,∠ABC=90°, ∠BCD=120°,对 角 线 AC, BD 交于点S,且 DS=2SB.求证:AD=DC.
三、(本题满分25分)已 知 m,n,p 为 正 整 数,m< n.设 A(-m,0),B(n,0),C(0,p),O 为 坐 标 原 点.若 ∠ACB=90°,且 OA2 +OB2 +OC2 =3(OA +OB + OC).求图像经过 A,B,C 三点的二次函数的解析式.
数学竞赛之窗
2011年全国初中数学联合 竞赛试题及参考答案
第一试
一 、选 择 题 :(本 题 满 分 42 分 ,每 小 题 7 分 )
1.已
知
a+b=2,(1-ba)2
+
(1-b)2 a
=
-4,则
ab
的 值 为 ( ). (A)1 (B)-1
(C)-
1 2
(D)12 .
2 x
+
3 y
+
4 z
的
值B)32
(C)2
(D)52
(下 转 第 32 页 )
檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪
(上 接 第 30 页 )
即 BE=2EC.
分析 3 如 图 3,过 点 C 作 CN ∥AE,交
注 上述三种证法都是通过 引 平 行 线,借
