第8章 梁的位移分析与刚度设计资料
合集下载
《梁的刚度分析》课件

截面形状的影响
矩形截面
矩形截面的梁在垂直于长边方向上刚 度较低,容易发生弯曲变形。
工字形截面
工字形截面的梁在垂直于腹板方向上 刚度较高,抗弯能力较强。
梁的跨度与支撑的影响
跨度大小
梁的跨度越大,其自由端处的转角和 挠度越大,刚度越小。
支撑条件
支撑条件如简支、固支等对梁的刚度 也有影响。例如,简支梁在跨中受到 集中载荷时,跨中挠度较大,刚度较 小。
案例三:实际工程中的梁刚度问题解决
总结词:实际应用
详细描述:在实际工程中,梁的刚度问题可能涉及到多种因素,如载荷、支撑条件、材料特性等。解决实际工程中的梁刚度 问题需要综合考虑多种因素,采用理论分析和实验验证相结合的方法。
外部载荷的影响
载荷大小
随着外部载荷的增大,梁的变形量增加,刚度减小。
载荷分布
集中载荷或分布载荷对梁的刚度有不同影响。例如,集中载荷可能导致梁在载 荷作用点处产生较大的局部变形。
03
梁的刚度分析方法
弹性分析
弹性分析方法基于弹性力学理论,通过求解弹性 方程得到梁的变形和应力分布。
弹性分析适用于材料处于弹性阶段的情形,能够 给出梁在受力过程中的变形和应力分布。
VS
详细描述
在梁的刚度设计中,应优先选择具有高弹 性模量和强度的材料,如钢铁、合金钢和 优质木材等。这些材料能够提供更好的抗 弯和抗剪切性能,从而提高梁的刚度。
截面形状优化建议
总结词
合理的截面形状可以有效地提高梁的刚度,常见的优化截面形状包括矩形、工字形和圆形等。
详细描述
根据梁所承受的载荷和跨度大小,可以选择不同的截面形状进行优化。例如,对于承受较大载荷的梁 ,可以选择工字形截面以提高抗弯刚度;对于跨度较大的梁,可以选择圆形截面以增强抗扭刚度。
《梁的刚度分析》课件

梁的刚度分析方法
1 弯矩-曲率法
通过分析梁的弯矩和曲率 关系来确定梁的刚度。
2 力-位移法
根据外力作用下梁的位移 和反力关系,计算梁的刚 度。
3 复合梁法
将梁视为由不同材料组成 的梁体,通过刚度的合成 计算梁的整体刚度。
弯矩-曲率法
弯矩-曲率方程
弯矩-曲率方程描述了梁的受力 和形变关系,是分析梁的刚度 的重要工具。
《梁的刚度分析》PPT课 件
本课件旨在介绍梁的刚度分析,让您了解梁的基本概念及其在工程中的应用。 通过弯矩-曲率法、力-位移法和复合梁法的讲解,帮助您掌握梁的刚度分析方 法。
概述
什么是梁的刚度
梁的刚度是指梁在受力作用下不产生过大的变 形,能够保持结构的稳定性。
梁在工程中的应用
梁广泛应用于桥梁、建筑物和机械设备等领域, 承受和传递荷载。
结论
1 梁的刚度分析方法选择
根据实际情况选择适合的梁的刚度分析方法。
2 工程实践中的应用
梁的刚度分析在工程实践中具有重要意义,可以保证结构的安全性和稳定性。
参考文献
[1] 参考文献1 [2] 参考文献2
弯矩-曲率图
绘制弯矩-曲率图以可视化梁在 不同位置的弯矩和曲率。
荷载作用下的梁的曲线
荷载作用下,梁会发生弯曲, 掌握梁在不同荷载情况下的曲 线变化很重要。
力-位移法
什么是刚度系数
刚度系数是梁的刚度指标,代 表单位力作用下梁的变形程度。
刚度系数的计算方法
通过力的大小和相应位移的比 值计算得到刚度系数。
常用的刚度系数表格
根据不同材料和截面形状,可 以找到常用的刚度系数表格进 行计算。
复合梁法
什么是复合梁
结构位移和刚度—梁的刚度计算(建筑力学)

二、用积分法求梁的变形
1.挠曲线近似微分方程
y( x)
M (x) EI
2.用积分法求变形 EI (x) M (x)dx C1
三、用叠加法求梁的变形
EIy(x) [ M (x)dx C1]dx C2
叠加法—梁截面的总变形,就等于各个荷载单独作用时产生变形的代数和。
四、梁的刚度计算 ymax [ f ]
梁的刚度计算
主要内容
梁的刚度条件和设计准则 梁的刚度计算 梁的刚度计算工程实例
梁的刚度计算
➢ 如果梁的弯曲变形过大,即使强度满足要求,也不能正常工作。例如:房 屋的楼面板或者梁长时间受较大荷载作用,导致变形过大,会造成抹灰面 出现裂缝,工业厂房的吊车梁变形过大,会影响吊车梁的正常使用等。设 计梁时,除了进行强度计算外,还应考虑进行刚度计算,需要把梁的最大 挠度和最大转角限制在一定的允许范围内。
l
l
课后作业:《建筑力学练习册》 练习二十五
3.6 4 4
3.6kN m
2、按正应力强度设计。查强度准则
3.6kNm
max
M max Wz
M max 0.1d 3
[ ]
得:
d3
M max
3
3.6 106 mm 153.3mm
0.1[ ] 0.110
取d=160mm
梁的刚度计算
3、按梁的刚度准则校核。
查变形表得
ymax
Fl 3 48EI
为:
ymax [ f ]
l
l
式中 ymax 为最大相对挠度,[ f ] 为许用相对挠度,其值可
l
l
根据梁的工作情况及要求查阅有关设计手册。土建工程中的许
用相对挠度值 [ f ] 常限制在
粱的位移分析-工程力学-课件-09
y1 0 0 y2 0 0
M1 x y1 x
M2 x
1 x
q B A y l
2 x
y2 x
x=a, y1 a y2 a
1 a 2 a
建立坐标系xy, 根据外力,梁分两段。
C x
a
M1 x y1 x
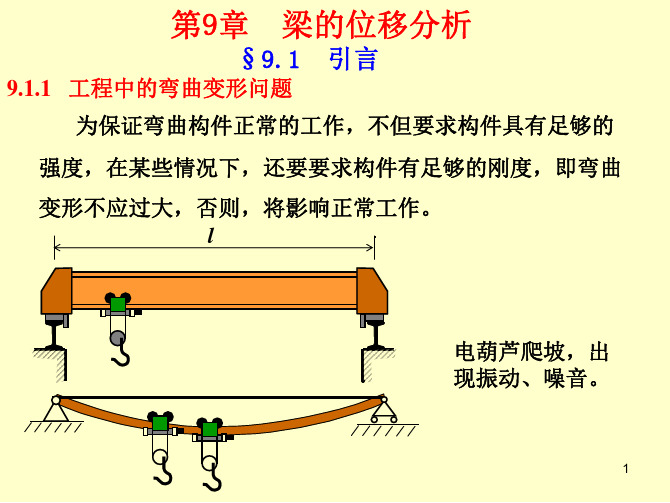
电葫芦爬坡,出 现振动、噪音。
1
齿轮轴
轧钢
轧辊 P2 P1
钢板
齿轮轴变形将导致齿轮不能正常 啮合、齿面磨损、轴与轴承配合 不好,出现噪音。
轧辊变形,钢板沿宽度 方向的厚度不均。
2
利用弯曲变形 汽车叠板弹簧 缓冲、减震
测力矩扳手
O
F
刻度
求解静不定梁则必须考虑梁的变形。
3
9.1.2 挠度、转角及相互关系
A x
b RA P l y
a x l
P C
b
B
RB
x
a P l
(2)列出挠曲线微分方程并积分 bP CB 段 EI y x P( x a) bP 2 AC段 EIy1 l x
l bP 2 EIy1 x C1 2l bP 3 EIy1 x C1 x D1 6l EIy 2
B点位移有影响。 yC yB1 yB2
yC
C
B
B= C
C
由于变形微小,由C引起的变形: yB2= C ×a
a
查表:
A a C
qa 4 yC y B1 8 EI
qa 3 C 6 EI
叠加:
qa 3 而: B C 6 EI
7qa 4 y B yB1 C a 24 EI
工程力学第8章 变形及刚度计算

第8章 变形及刚度计算
结构构件在满足强度要求条件下,若其变形过大, 会影响正常使用。本章将学习杆件的变 形及刚度计算。
1
8.1 轴向拉压杆的变形
杆件在发生轴向拉伸或轴向压缩变形时,其纵向尺 寸和横向尺寸一般都会发生改变,现分别予以讨论。 8.1.1 轴向变形 图8.1所示一等直圆杆,变形前原长为l,横向直径 为d;变形后长度为l′,横向直径为d′,则称
8.8 题8.8图所示一直径为d的圆轴,长度为l,A端 固定,B端自由,在长度方向受分布力偶m 作用发生扭 转变形。已知材料的切变模量为G,试求B端的转角。
56
8.9 某传动轴,转速 n=150 r/min,传递的功率 P =60 kW,材料的切变模量为 G =80GPa,轴的单位长度 许用扭转角[θ]=0.5(°)/m,试设计轴的直径。
30
例 8.9 简支梁受力如图 8.11所示
31
8.4 简单超静定问题
8.4.1 超静定问题的概念 前面几章所研究的杆或杆系结构,其支座反力和内 力仅仅用静力平衡条件即可全部求解出来,这类问题称 为静定问题(staticallydeterminateproblem)。例如,图 8.12所示各结构皆为静定问题。在工程实际中,有时为 了提高强度或控制位移,常常采取增加约束的方式,使 静定问题变成了超静定问题或静不定问题 (staticallyindeterminateproblem)。超静定问题的特点 是,独立未知力的数目大于有效静力平衡方程式的数目, 仅仅利用静力平衡条件不能求出全部的支座反力和内力。
52
8.5 高为l的圆截面锥形杆直立于地面上,如题8.5图 所示。已知材料的重度γ和弹性模量E,试求杆在自重作 用下的轴向变形Δl。
53
54
结构构件在满足强度要求条件下,若其变形过大, 会影响正常使用。本章将学习杆件的变 形及刚度计算。
1
8.1 轴向拉压杆的变形
杆件在发生轴向拉伸或轴向压缩变形时,其纵向尺 寸和横向尺寸一般都会发生改变,现分别予以讨论。 8.1.1 轴向变形 图8.1所示一等直圆杆,变形前原长为l,横向直径 为d;变形后长度为l′,横向直径为d′,则称
8.8 题8.8图所示一直径为d的圆轴,长度为l,A端 固定,B端自由,在长度方向受分布力偶m 作用发生扭 转变形。已知材料的切变模量为G,试求B端的转角。
56
8.9 某传动轴,转速 n=150 r/min,传递的功率 P =60 kW,材料的切变模量为 G =80GPa,轴的单位长度 许用扭转角[θ]=0.5(°)/m,试设计轴的直径。
30
例 8.9 简支梁受力如图 8.11所示
31
8.4 简单超静定问题
8.4.1 超静定问题的概念 前面几章所研究的杆或杆系结构,其支座反力和内 力仅仅用静力平衡条件即可全部求解出来,这类问题称 为静定问题(staticallydeterminateproblem)。例如,图 8.12所示各结构皆为静定问题。在工程实际中,有时为 了提高强度或控制位移,常常采取增加约束的方式,使 静定问题变成了超静定问题或静不定问题 (staticallyindeterminateproblem)。超静定问题的特点 是,独立未知力的数目大于有效静力平衡方程式的数目, 仅仅利用静力平衡条件不能求出全部的支座反力和内力。
52
8.5 高为l的圆截面锥形杆直立于地面上,如题8.5图 所示。已知材料的重度γ和弹性模量E,试求杆在自重作 用下的轴向变形Δl。
53
54
第8章 梁的弯曲问题(4)-位移分析与刚度计算

8—7 轴受力如图所示,已知 FP=1.6 kN,d=32 mm,E=200 GPa。若要求加力点的挠度 不大于许用挠度 [w]=0.05 mm,试校核该轴是否满足刚度要求。 解:由挠度表查得
wC = =
FPba 2 l − a 2 − b2 6lEI
(
)
−3
1.6 ×103 × 0.246 × 0.048 × 2942 − 482 − 2462 ×10−6 × 64 6 ( 246 + 48) ×10 × 200 ×10 × π × 32 ×10−12
d4w =q dx 4
对 x 求 4 次导数,有
这一结果表明,梁上作用有连续均布载荷。图(a)中的弯矩图就是对应连续均布载荷的弯 矩图,所以正确答案是: ( a)
8—6 图示承受集中力的细长简支梁,在弯矩最大截面上沿加载方向开一小孔,若不考 虑应力集中影响时, 关于小孔对梁强度和刚度的影响, 有如下论述, 试判断哪一种是正确的: (A) 大大降低梁的强度和刚度; (B) 对强度有较大影响,对刚度的影响很 小可以忽略不计. ; (C) 对刚度有较大影响,对强度的形响很 小可以忽略不计; (D) 对强度和刚度的影响都很小,都可以 忽略不计。 解:强度取决于危险截面上危险点的应力,
5ql 4 l ≤ 384 EI z 1000
Iz ≥
I z1 =
5 ×10000 × 4 3 × 1000 384 × 200 × 10 9
Iz 4 = 2083.3 cm 2
后 答
M max 10000 × 4 2 3 = = 2 × 10 − 4 m [σ ] 8 × 100 × 10 6 W 每根槽钢 W z1 = z ≥ 100 cm3 2 Wz ≥
wC − w B = δ 0 = 1.2
第八章__变形及刚度计算

8×103 ×180 o = 0.40 / m < [θ ] 4 9 π × 0.110 80×10 × ×π 32
满足刚度条件
例:实心圆轴受扭,若将轴的直径减小一半 实心圆轴受扭, 时,横截面的最大切应力是原来的 8 倍? 圆轴的扭转角是原来的 16 倍?
τ max MT MT = = W p πd 3 16
又因为BD段内虽然轴力 又因为 段内虽然轴力 为常数, 为常数,但截面面积又分两 所以要分4段求变形 段求变形。 段,所以要分 段求变形。
∆L AE =
∑ ∆L
i
= ∆L AB + ∆L BC
FN图
+ ∆L CD + ∆L DE =
∑
FN l EA
§ 8-1 轴向拉压杆的变形
已知杆的长度、 受力如图。 例 已知杆的长度、截面面 积,受力如图。 材料的 弹性模量 E = 2.1 × 10 5 MPa。求杆的总变形 。
A1 = 250mm
50kN
2
A 2 = 200mm
30kN E
∆L AB
2
解:用直接法画轴力图 用直接法画轴力图
20kN
∆L AE =
∑ ∆L
i
= ∆L AB + ∆L BC
A B C D 1m 2m 1m 3m 10KN + – – 40KN 20KN
+ ∆L CD + ∆L DE =
∑
3
FN l EA
§8—2
圆杆扭转时的变形和刚度计算
一、扭转变形——扭转角 扭转变形 扭转角
MT 扭转角: 扭转角: ϕ = θdx = dx ∫ ∫0 GI p l
l
单位: 单位:rad
第八章 位移法

当单跨梁除支座位移外,还有荷载作用及温度变化时, 其杆端弯矩为
6i F ΔAB M AB l 6i F M BA 4i B 2i A ΔAB M BA l M AB 4i A 2i B
转角位移方程
第8章 位移法
三、一端固定、另一端铰支梁的转角位移方程
EI FP B
FP
EI EI
EI
EI
3、图示结构,各杆长为l, 用位移法求解时, 典型方程的系数r11= ,自由项R1P= 。
FPl FP
4、已知刚架的弯矩图如图所示,各杆 EI为常数,杆长l=4m,则结点B的转角 ΦB= 。 30
30
l
l/2
l/2
第8章 位移法
例8-2 求图a所示刚架的支座A产生转角 ,支座B产生竖向位移 3 Δ l 。试用位移法绘其弯矩图,E为常数。
由
M M1Z1 M
第8章 位移法
§8-5 直接由平衡条件建立位移法基本方程
图a所示刚架用位移法求解时有两个基本未知量:刚结点1 的转角Z1,结点1、2的水平位移Z2。
如图b,由结点1的力矩平衡条件∑M1=0
M12 M13 0
如图c,由隔离体的投影平衡条件∑Fx=0
FS13 FS24 0
φA P q βAB φA FSAB FSBA l EI t1˚C t2˚C
MAB
A
B ΔAB
B'
EI EI F M 3 3 Δ M AB A AB l l2 M BA 0
EI 令:i 称为“线刚度”、 AB 称 为 “ 旋 转 角 ” , 则 : l l
一、杆端力的表示方法和正负号的规定
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
位移是各部分变形累加的结果。位移与变形有着
密切联系,但又有严格区别。有变形不一定处处 有位移;有位移也不一定有变形。
这是因为,杆件横截面的位移不仅与变形有关,
而且还与杆件所受的约束有关。
2020/9/10
5
在数学上,确定杆件横截面位移的过程主要是积分运
算,积分限或积分常数则与约束条件和连续条件有关。
若材料的应力-应变关系满足胡克定律,且在弹性范围
内加载,则位移与力(均为广义的)之间均存在线性关 系。因此,不同的力在同一处引起的同一种位移可以 相互叠加。
本章将在分析变形与位移关系的基础上,建立确定梁
位移的小挠度微分方程及其积分的概念,重点介绍工 程上应用的叠加法以及梁的刚度设计准则。
2020/9/10
弯矩的符号与前面第五章的规定一致,与坐标选取无关。
即M(x)为+,则梁的曲线向下凸。
M(x)为-,则梁的曲线向上凸。
M
M
1 M (x)
(x) EI
2020/9/10
17
ω
ω
M 0
x
d
2 w( x) dx2
w'' (x)
0
x
M 0
x
d 2w(x) 0
dx2
x
ω
M 0
2020/9/10
d 2w(x) 0
1M
EI
其中,ρ和M都是横截面位置x的函数,EI为横截面的 弯曲刚度。
(x) M M (x)
2020/9/10
8
8.1.2 梁的挠度与转角
梁在弯曲变形后,横截面的位置将发生改变,这种位置的改 变称为位移 (Displacement)。梁的位移包括三部分:
横截面形心处的铅垂位移,称为挠度(deflection),用ω表示
2020/9/10
2
失效(failure)或破坏
工程构件在外力作用下丧失正常功能的现象。 失效类型:
(1) 强度失效(failure by lost strength) 指构件在外力作用下发生不可恢复的塑性变形或发生断裂。
(2) 刚度失效(failure by lost rigidity) 指构件在外力作用下产生过量的弹性变形。
应用挠度曲线的曲率与弯矩和弯曲刚度之间的关系 式,以及数学中关于曲线的曲率公式有
1M
EI
1
1
w'' w'
2
3 2
在小变形条件下,由于w' 2 1,故被忽略。
d 2w(x) M (x)
dx2
EI
梁的挠曲线近似微分方程,又 称为Euler-Bernoulli方程。
2020/9/10
12
2020/9/10
9
dw tan
dx
tan
+
所以我们得到了挠度ω和转角θ之间的微分关系
dw(x)
y
dx
挠度方程(deflection equation) Z
2020/9/10
10
8.1.3 梁的位移与约束密切相关
2020/9/10
约束不同导 致梁的位移 不相同。
11
8.2 小挠度微分方程及其积分
dx2
ω
M 0
d 2w(x) w'' (x) 0 dx2
18
通常选取的坐标:
x
ω
M 0
d
2 w( x) dx2
0
根据弯矩的正负号规则和上面所选取的坐标系,弯 矩和挠度二阶导数总是不一致的,所以在公式右边应该 取负号。
d
2 w( x) dx2
M (x) EI
2020/9/10
19
对于等截面梁,应用确定弯矩方程的方法,写出弯矩方 程M(x),分别对x作不定积分,得到包含积分常数的挠 度方程与转角方程为:
(x) 1
f '' (x)
f
' ( x)
2
3 2
1
w'' (x) w'(x) 2
3 2
''
1
d 2w(x)
(x)
dx2
2020/9/10
1 M (x)
(x) EI
d 2w(x) M (x)
dx2
EI
14
2020/9/10
15
2020/9/10
16
1 d 2w(x)
(x)
dx2
挠度符号按照数学中的符号规定,与坐标系的选取有关。
第八章 梁的位移分析与刚度设计
主讲教师:毛卫国 单 位:材料与光电物理学院
2020/9/10
1
在第7章,我们主要学习了梁的纯弯曲、横向弯曲和 斜弯曲中正应力与外加力偶的关系,分析了正应力的分 布情况,如何判别最大正应力的位置,进而如何判断梁 的强度问题。
x
Mz Iz
y
max
另外,我们知道,当梁受到横向载荷或外加力偶时,其 中不仅产生正应力,而且在梁的不同位置处其变形情况 也不同。
(3) 稳定失效(failure by lost stability) 指构件在某种外力作用下,其平衡形式发生突然转变。
2020/9/10
3
研究的意义
位移分析中所涉及的梁的变形和位移,都是弹性的。尽管变形
和位移都是弹性的,工程设计中,对于结构或构件的弹性位移都 有一定的限制。弹性位移过大,也会使结构或构件丧失正常功能, 即发生刚度失效。 尤其是在高精密的仪器、器械中对于材料的弹性变形控制尤为重要。
变形后的横截面相对于变形前位置绕中性轴转过的角度
(slope),用θ表示。
横截面形心沿水平方向的位移,称为轴向位移或水平位移
(horizontal displacement),用u表示。
在小变形情形下,上述位移中,水平位移u与挠度ω相比为高
阶小量,故通常不予考虑水平位移u 。
所以我们主要关注挠度ω和转角θ之间的关系
符号问题:
挠度ω和转角θ的正负号由所选坐标系的正方向来确定。
沿y轴正向的挠度ω为正+,反之为负; 将x轴绕坐标原点旋转90o与y轴重合,转角θ和它的转向
相同为正,反之为负。 弯矩M(x)的正负号确定依旧与第5章的符号规则一样。
2020/9/10
13
补充知识
曲率的定义:
w (x) 1
我们要研究材料的变形和位移之间的关系。 位移分析也是解决超静定问题与振动问题的基础。
2020/9/10
4
上一章中已经提到,如果忽略剪力FQ的影响,在平面弯 曲的情形下,梁的轴线将弯曲成平面曲线,梁的横截面 变形后依然保持平面,且仍与梁变形后的轴线垂直。由 于发生弯曲变形,梁横截面的位置发生改变, 这种改变 称为位移(Displacement)。
6
8.1 基本概念
8.1.1 梁弯曲后的挠度曲线
若在弹性范围内加载,梁的轴线在梁弯曲后变成一条连续
光滑曲线。这一连续光滑曲线称为弹性曲线(elastic curve)
或挠度曲线(deflection curve),简称弹性线或挠曲线。
2020,弹性范围内的挠度曲线在 一点的曲率与这一点处横截面上的弯矩、弯曲刚度之间存 在下列关系
