高中数学:一元二次方程实根的分布
一元二次方程根的分布

3 m 1 时,根 x 2 3,0 ,即 m 1 满足题意;当 m 时, 得出 m 1或 m 3 ,当 2 2
15 3 m 或 m 1 根 x 33,0 ,故 m 3 不满足题意;综上分析,得出 14 2
3.一根在(m,n)内,另一根在(p,q)内
0 f m 0 f n 0 b m n 2a
0 f m 0 f n 0 b m n 2a
2.两根有且仅有一根在(m,n)内
f m f n 0
综合结论 (不讨论 a)
一.一元二次方程根的基本分布——零分布
所谓一元二次方程根的零分布,指的是方程的 根相对于零的关系。比如二次方程有一正根, 有一负根,其实就是指这个二次方程一个根比 零大,一个根比零小,或者说,这两个根分布 在零的两侧。 设一元二次方程ax2+bx+c=0(a≠0)的两个 实根为x1,x2,且x1<x2。
f m 0 f n 0
已知关于 x 的方程 x2 (2m 1) x 4 2m 0 ,求满足下列条件的 m 的取值范围. (1) 两个正根 (2)有两个负根 (3) 两个根都小于 1 (4) 两个根都大于 1 2 (5)一个根大于 2,一个根小于 2 (6) 两个根都在 (0, 2) 内 (7) 两个根有且仅有一个在 (0, 2) 内 (8)一个根在 (2,0) 内,另一个根在 (1,3) 内 (9) 一个正根,一个负根且正根绝对值较大 (10)一个根小于 2,一个根大于 4
一元二次方程根的分布
知识要点
一元二次方程ax2+bx+c=0 (a≠0)的根从几 何意义上来说就是抛物线y=ax2+bx+c (a≠0)与 轴交点的横坐标,所以研究方程 ax2+bx+c=0 (a≠0)的实根的情况,可借助二次函数图象来研 究求解.(几何法) 若在 (- ∞ ,+ ∞)内研究方程ax2+bx+c=0 (a≠0)的实根情况,只需考察函数 y=ax2+bx+c (a≠0)与 x轴交点个数及交点横坐标的符号,利 用韦达定理和判别式来解,由 y=ax2+bx+c (a≠0) 的系数可判断出 △,x1+x2,x1x2的符号,从而判断 出实根的情况.(代数法)
高中数学专题一元二次方程实数根的分布

一元二次方程实数根的分布教学目标:使学生掌握一元二次方程实根分布问题的处理,加强求解一元二次不等式及不等式组,初步训练学生的数形结合能力。
教学重点:利用二次函数的图象,把一元二次方程根的分布−−→−转化图形问题−−→−转化代数表达式(不等式组)−−→−计算参数取值范围。
教学难点:图形问题转化成代数表达式(不等式组)并求解。
一.一元二次方程根的基本分布——零分布所谓一元二次方程根的零分布,指的是方程的根相对于零的关系。
比如二次方程有一正根,有一负根,其实就是指这个二次方程一个根比零大,一个根比零小,或者说,这两个根分布在零的两侧。
设一元二次方程02=++c bx ax (0≠a )的两个实根为1x ,2x ,且21x x ≤。
1、两个正根⇔212124000b ac b x x a c x x a ⎧∆=-≥⎪⎪⎪+=->⎨⎪⎪=>⎪⎩, 2、两负根⇔⎪⎪⎪⎩⎪⎪⎪⎨⎧>=<-=+≥-=∆000421212a c x x a b x x ac b 3、一正根一负根 021<=acx x 4、一正根一负根,负根绝对值大⎪⎪⎩⎪⎪⎨⎧<=<-=+002121a c x x a b x x 5、一正根一负根,正根绝对值大⎪⎪⎩⎪⎪⎨⎧<=>-=+002121a c x x a b x x 6、有一根为0 0,0,021=>-==c abx x 例1:若方程0)5()2(2=++++m x m x有两正根,求实数m 的取值范围.变式1:两根两负? 变式2: 两根一正一负?变式3: 两根一正一负,且正根绝对值大? 变式4: 两根一正一负,且负根绝对值大?例2:若一元二次方程03)12(2=-+-+k x k kx 有一根为零,则另一根是正根还是负根?分析:由已知k -3=0,∴k =3,代入原方程得32x +5x =0,另一根为负。
二.一元二次方程的非零分布——k 分布设一元二次方程02=++c bx ax (0≠a )的两实根为1x ,2x ,且21x x ≤。
高一数学一元二次方程根的分布
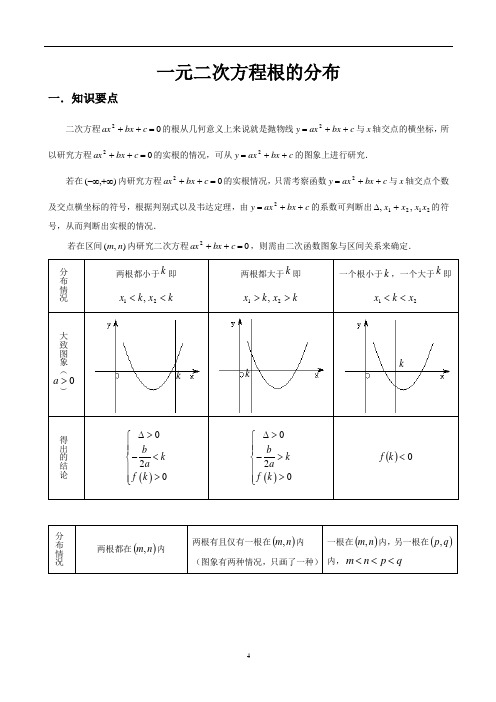
一元二次方程根的分布一.知识要点二次方程02=++c bx ax 的根从几何意义上来说就是抛物线c bx ax y ++=2与x 轴交点的横坐标,所以研究方程02=++c bx ax 的实根的情况,可从c bx ax y ++=2的图象上进行研究.若在),(+∞-∞内研究方程02=++c bx ax 的实根情况,只需考察函数c bx ax y ++=2与x 轴交点个数及交点横坐标的符号,根据判别式以及韦达定理,由c bx ax y ++=2的系数可判断出2121,,x x x x +∆的符号,从而判断出实根的情况.若在区间),(n m 内研究二次方程02=++c bx ax ,则需由二次函数图象与区间关系来确定.分布情况 两根都小于k 即 k x k x <<21, 两根都大于k 即 k x k x >>21, 一个根小于k ,一个大于k 即 21x k x <<大致图象(0>a )得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()0<k f分布情况两根都在()n m ,内 两根有且仅有一根在()n m ,内 (图象有两种情况,只画了一种) 一根在()n m ,内,另一根在()q p ,内,q p n m <<<kk k大致图象(>a )得出的结论 ()()0002f m f n b m n a ∆>⎧⎪>⎪⎪>⎨⎪⎪<-<⎪⎩ ()()0<⋅n f m f ()()()()0000f m f n f p f q ⎧>⎪<⎪⎨<⎪⎪>⎩或()()()()00f m f n f p f q <⎧⎪⎨<⎪⎩ 根在区间上的分布还有一种情况:两根分别在区间()n m ,外,即在区间两侧12,x m x n <>,(图形分别如下)需满足的条件是 (1)0a >时,()()00f m f n <⎧⎪⎨<⎪⎩; (2)0a <时,()()00f m f n >⎧⎪⎨>⎪⎩ 对以上的根的分布表中一些特殊情况作说明: (1)两根有且仅有一根在()n m ,内有以下特殊情况:1︒ 若()0f m =或()0f n =,则此时()()0f m f n <不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间()n m ,内,从而可以求出参数的值。
浅析一元二次方程根的分布问题
() 1若 m) =0或 n = , ) 0 则此 时 m)- n ・( ) 厂 < 0不成立 , 但对 于这 种 情况 是知 道 了方 程有 一根 为 m 或 n 可 以 求 出另 外 一 根 , 后 可 以根 据 另 一 根 , 然 在 区 间 ( n 内 , 而 可 以 求 出 参 数 的 值 。如 方 程 m, ) 从 ( +2 + m ) 2=0在 区 间 ( , ) 有 一 根 , 为 13上 因
l
^
t o
f。 , o 一 甜 ‘ 砷 ‘ 0 ’
I p0 ; ・∞0 ,《 t, -
=
} 。当 m=一l , 时 根 =一2 一3 0 , m= 一 ∈( ,) 即
{ f ’0 l t , ; - ,
( 2
1 满足题意; 当 = 时, :3 ( 30 , m 号 根 一 ,)故
j叶
。
l }・ f・ ,0 一0 L " £ 圭 ’ 一 , . ( ” ’ l 1^ ’ 、 ’ ’ \ f f /I j 厂
-
兰 f 。 厂
日 『 。 \ / 。
△ =0即 1m2 ( m +6 =0得 出 m = 一1或 m = 6 —42 )
P \
一
f/ \
l 一 ,) f ,‘ s 如‘ , C , c 似 ( - )0 ( , ,, , c 0 o 如 0 旧 - ) > ‘ o
lf\ l、 / ^ 厂
・
『 ’
_ f. /、 \ .、 厂' ”‘ }
to f , 。 0
一
名 _孵 “_ 叫 ~l ^_ 啊 融聱 f 睢 -^ —t . 蛊 _・ “^ 雌^ ) 一
5.1一元二次方程实根的分布

实系数一元二次方程实根分布1:当m 为何值时,方程03524222=--++m m mx x的两根异号?答案:(321<<-m )2:已知方程02322=-+-k kx x 的两个根都大于1,求k 的取值范围。
答案:(2≥k )3:已知集合A ={045|2≤+-x x x },B ={022|2≤++-a ax x x },且B ⊆A ,求实数a 的取值范围。
答案:(7181≤<-a )4、关于x 的方程0122=++x ax 至少有一个负的实根,则a_____________ (1≤a )5、01032=+-k x x 有两个同号且不相等的实根,则k__________- (3250<<k )6、要使关于x 的方程0322=+-kx x 的两个实根一个小于1,另一个大于1,则实数k 的取值范围是__( 5>k )7、已知抛物线m x m x y +-+=)3(2与x 轴的正半轴交于两点,则实数m 的取值范围是____。
(10<<m )8、设A ={01|2=-x x },B ={012|22=-+-a ax x x },若A ∩B =B ,则a 等于___。
(0=a )9、已知A ={01)2(|2=+++x p x x ,R x ∈},若A ∩R +=φ,则p 的范围是_____。
(4->p )10、已知方程0222=++-a ax x 的两根都在区间(1,4)内, 求a 的取值范围。
(7182<≤a )11、若关于x 的方程0532=+-a x x 的一个根在(-2,0)内,另一个根在(1,3)内,求a 的取值范围。
12、已知方程01222=+-+m mx x 的两个实根都大于2,求实数m 的取值范围。
(4316-≤<-m )13已知A ={023|2≤+-x x x },B ={02|2≤+-a ax x x ,R a ∈},且A ∩B =B ,求a 的取值范围。
一元二次方程根的分布

一元二次方程的形式为ax^2+bx+c=0,其中a、b、c为常数。
一元二次方程根的分布取决于方程的解的个数,有如下三种情况:1 两个不相等的实根:如果一元二次方程有两个不相等的实根,那么方程的解为x1=r1、x2=r2,其中r1和r2是方程的两个实根。
2 两个相等的实根:如果一元二次方程有两个相等的实根,那么方程的解为x1=x2=r,其中r是方程的两个相等的实根。
3 两个复数根:如果一元二次方程有两个复数根,那么方程的解为x1=r1+r2i、x2=r1-r2i,其中r1和r2是方程的两个复数根的实部和虚部。
一元二次方程的根分布可以通过求解方程的判别式来确定。
判别式为b^2-4ac,如果判别式>0,则方程有两个不相等的实根;如果判别式=0,则方程有两个相等的实根;如果判别式<0,则方程有两个复数根。
在数学中,一元二次方程是由一个二次项和一个一次项组成的方程。
它的形式为ax^2+bx+c=0,其中a、b、c为常数。
解决一元二次方程的方法有多种,常见的方法有求解公式法、因式分解法、二分法、牛顿迭代法等。
求解公式法是最常见的求解一元二次方程的方法,它的公式为:x1= (-b+sqrt(b^2-4ac))/(2a)x2= (-b-sqrt(b^2-4ac))/(2a)其中sqrt(b^2-4ac)表示根号内的值。
因式分解法是将一元二次方程写成两个一次方程的形式,然后分别求解两个一次方程的解。
二分法是一种数值解法,通过取方程的两个端点的中点来逐步缩小解的范围,最终得到方程的解。
牛顿迭代法是一种逐步迭代的方法,通过不断迭代来逼近方程的解,最终得到方程的解。
在解决一元二次方程时,应根据具体情况选择合适的方法。
一元二次方程实根的分布问题

专题二、一元二次方程的实根分布问题
问题: 已知方程0)3(2=+-+m x m x ,求实数m 的取值范围。
条件1:若方程有两个正根。
条件2:若方程的两个根均小于1。
条件3:若方程的一个根大于1,一个根小于1。
条件4:若方程的两个根均在( 0,2)内。
条件5:若方程的两个根有且仅有一个在( 0,2)内。
条件6:若方程的一个根在(–2 ,0),另一个根在(0 ,4)。
条件7:若方程的一个根小于2,另一个根大于4。
条件8:若方程有一个正根,一个负根且正根的绝对值较大。
1.若方程02)13(22=--++-m m x m x 在区间(0,1)、(1,2)上各有一个实根,求实数m 的取值范围。
2.若方程02)2(22=----m m x m x 的两根在区间[0,1]之外两旁,求实数m 的取值范围。
3.关于x 的方程023222=---k x kx 的二根,一个小于1,另一个大于1,则
求实数k 的取值范围。
4.若方程0122=-+-m mx x 在区间(–2,4)上有两根,求实数m 的取值范围。
高中数学 一元二次方程的根的分布问题教案 苏教版必修1

一元二次方程的根的分布问题 一、定理: 设:f (x )=ax 2+bx +c (a >0),△=b 2-4ac定理1 方程f (x )=0的两实根都大于(或小于)给定的实数m 的充要条件是 定理2 方程f (x)=0的两实根在区间(m ,n )的充要条件是 定理3 方程f (x)=0的两实根分别在区间(p ,q )与(q ,r )内的充要条件是⎪⎩⎪⎨⎧><>0)(0)(0)(r f q f p f定理4 方程f (x)=0的两实根分别在区间(p ,q )与(r ,s )(r ≥q )的充要条件是⎪⎪⎩⎪⎪⎨⎧><<>0)(0)(0)(0)(s f r f q f p f 定理5 方程f (x)=0的两实根中一根小于m ,另一根大于n (m <n )的充要条件是 定理6 方程f (x)=0的两实根x 1、x 2满足x 1<m <x 2的充要条件是x y o m -a b 2 -a b2 x y o mxyo -a b 2 m n p q rp q r s xy o m n m x 1 x 2小结:⑴若两实根分布在同一开区间...(m ,n ),则必须考虑三点:①判别式△≥0;②对称轴在所给区间内,即m <a b2 <n ;③在区间端点处函数值的符号,即f (m)>0且f (n)>0.⑵若两实根分布在两个不同的开区间...内,则只要考虑在区间端点处函数值的符号.二、例题:例1、若方程(k 2+1)x 2-2(k+1)x+1=0的两根在区间(0,1)内,求k 的取值范围.例2、求实数m ,使方程7x 2-(m+13)x+m 2-m -2=0有两实根,且它们分别在区间(0,1)与(1,2)中.例3、方程x 2+(a 2-1)x+a -2=0有一根大于1,另一根小于-1,求a 的取值范围.例4、若方程x 2-11x+m=0的两根都大于5,求m 的取值范围.例5、若方程x 2 l ga -2x+1=0的一根大于1,另一根小于1,求实数a 的取值范围.例6、若a >b >0,证明方程0112=+-+-b x a x ,有两相异实根,且一根在(b ,a )之间,另一根比b 小.练习题1、 已知方程x 2-2x+ l g (2a 2-a )=0有一正根和一负根,求实数a 的取值范围.2、求使方程x 2-2mx+m+1=0有两实根,且一根大于5,一根小于5的实数m 的取值范围.3、方程x 2+2(k+3)x+2k+4=0有两个相异实根, ⑴若一根大于3,另一根小于1,求k 的取值范围; ⑵若两根都在区间(-2,2)内,求k 的取值范围; ⑶若方程有且只有一个实根在(1,2)内,另一根不在其内,求k 的取值范围.4、设a 是任意实数,二次方程3x 2-1=a (2x -1)有两个不等的实根,证明两根中至少有一个在区间(0,1)之间.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.一元二次方程ax2+bx+c=0一根为正,另一根为负
y y
x1
o
x2
x
x1 o
x2
x
a>0 a< 0 或 x1<0<x2 f(0)>0 f(0)< 0
注:只要满足上述两个条件,就能判断函 数在指定区间内存在零点。
二、引入
问题:讨论方程ax2+bx+c=0 (a0) 的根的情况, (1)根的个数:a、b、c满足什么条件时,方程 有两个不等的实根?相等实根?无根实根? (2)根的大小:a、b、c满足什么条件时,方程 有两个正根?两个负根?两根异号?一根为零? (3)根的范围:a、b、c满足什么条件时,方程 两根都大于1?都小于1?一根大于1,一根小 于1?
4.一元二次方程ax2+bx+c=0两根都在区间(k1,k2)内
y 若方程 x2+ ( k+2 ) x-k=0 的两实根均在 区间(-1,1),求m的取值范围。 x2 k2 x
a 0 0 f(k1) k1 x1 x2 k2 f(k 2) 0 0 若是a<0,请同学们画出 b 图形,写出它的等价式 k1 k2 2a
①f ( ) f ( ) 0; ②f ( ) 0; (要验证) ③f ( ) 0 (要验证)
x
练一练
1.已知方程x +(m-2)x+2m-1=0 有且仅有一实根 在(0,1),求m的取值范围。 2.已知方程x +(m-2)x+2m-1=0 较大根在(0,1), 求m的取值范围。 3.已知方程x +(m-2)x+2m-1=0 较小根在(0,1), 求m的取值范围 变3.已知方程x +(m-2)x+2m-1=0 有根在(0,1), 求m的取值范围
x1 o
k1
三、巩固提高
已知A x x 2ax 1 0
2
B x x 2x 3 0
2
(1)若B A, 则a的范围? (2)若A B, 则a的范围?
作业
1、方程 5x2-ax-1=0(a∈R)的一个根在区间( -1, 0) 上,另一个在区间(1,2)上 ,求a的取值范围。 2、已知函数f(x)=mx2+(m-3)x+1的图象的零点至少 有一个在原点的右侧,求实数m的取值范围。
a>0
y
k x1 x2
b 2 4ac 0 ( f k) 0 b k 2a
o
k x1
x2 x
若a<0呢?
b2 4ac 0 af(k) 0 b k 2a
k x1 x2
(a≠0)
三、例题
一、知识铺垫
函数零点的定义: 对于函数y=f(x),我们把使f(x)=0的实数x叫做函数 y=f(x)的零点。
等价关系 方程f(x)=0有实数根 函数y=f(x)的图象与x轴有交点 函数y=f(x)有零点
零点存在判定法则
如果函数y=f(x)在区间[a,b]上的图象是连续
不断的一条曲线,并且有f(a)· f(b)<0,那么,函 数y=f(x)在区间(a,b) 内有零点,即存在c∈(a,b), 使得f(c)=0,这个c也就是方程f(x)=0的根。
三、例题
1.当m为何值时,方程 2 x 4 mx 3m 1 0
2
(1)有两个正根; 且负根的绝对值小于正根 (2)有两个负根; (3)有两个大于1的根;
0 注( 3) : x1 x2 2 是错的 x x 1 1 2
如:x 5 x 4 0
2 2 2 2
3.一元二次方程ax2+bx+c=0两根分别在区间(k1,k2) 以及(p1,p2)之间 y
k1
k2 p1 o x1
x2
p2
x
k1 x1 k2 p1 x2 p2
a 0 f( k ) 0 1 f( k 2 ) 0 f( p ) 1 0 0 f(P2)
af(0)< 0
推广:一元二次方程ax2+bx+c=0一根大于k,另一根小于k
y y
k
x1
o
x2
x
x1 o
k x2
a>0 a< 0 或 x1<k<x2 f(k)> 0 f(k)< 0
af(k)< 0
练一练 1.kx2+3kx+k-3=0的两根均为负,求k的取值范围。
2
两根为1、 4
四、归纳
1.一元二次方程ax2+bx+c=0(a>0)两根均为正根 y
b 2 4ac 0 f 0) c 0 ( b 0 2a
x1>0,x2 >0
o x1
x2
x
类比:一元二次方程ax2+bx+c=0(a>0)两根均为负根呢?
推广:一元二次方程ax2+bx+c=0(a>0)两根均为大于K
3.已知集合A={x|x2-7x+10≤0}, B={x|x2-(2-m)x+5-m≤0}, 且B A,求实数m的取值范围.
2.如果二次方程mx2-(m+1)x+3=0的两根均大于-1, 求m 的取值范围。 3.如果f(x)=x2+2(m-1)x+2m+6的一个零点大于2, 另一个零点小于2,求m 的取值范围。
例2. 求实数m的取值范围,使关于 x 的方程 x 2( m 1) x 2m 6 0,
2
(1)有两个根一个比 1大,另一个比 2小; (2)两个根均在区间( 2, 1)内; (3)有两个实根、 满足0 1 2; (4)只有一个根在区间( 2, 1)内; (5)只有一个根在区间[ 2, 1]内.
y f ( ) 0 f ( ) 0 (3)若两根在(, )之间, 则有 b 2a 0
x
f ( ) 0 则有 (4) 若一根小于,另一根大于 , f ( ) 0
y
(5) 若两根中只有一根在(, )之间,则有
