西安交大概率论上机实验报告材料
西安交大概率论上机实验报告

概率论上机实验报告班级:姓名:学号:一、实验目的1)熟悉Matlab中概率统计部分的常见命令与应用。
2)掌握运用Matlab解决概率问题的方法。
二、实验内容和步骤1.常见分布的概率密度及分布函数1)二项分布源码为:1.x=0:1:100;2.y1=binopdf(x,100,1/2); %求概率密度3.y2=binocdf(x,100,1/2); %求分布函数4.subplot(1,2,1)5.plot(x,y1)6.title('二项分布概率密度')7.subplot(1,2,2)8.plot(x,y2)9.title('二项分布分布函数')所得图形为:2)几何分布源码为:1.x=0:1:100;2.y1=geopdf(x,; %求概率密度3.y2=geocdf(x,; %求分布函数4.subplot(1,2,1)5.plot(x,y1)6.title('几何分布概率密度')7.subplot(1,2,2)8.plot(x,y2)9.title('几何分布分布函数')所得图形为:3)泊松分布源码为:1.x=0:1:100;2.y1=poisspdf(x,10); %求概率密度3.y2=poisscdf(x,10); %求分布函数4.subplot(1,2,1)5.plot(x,y1)6.title('泊松分布概率密度')7.subplot(1,2,2)8.plot(x,y2)9.title('泊松分布分布函数')所得图形为:4)均匀分布源码为:1.x=0:1:100;2.y1=unifpdf(x,0,100) %求概率密度3.y2=unifcdf(x,0,100); %求分布函数4.subplot(1,2,1)5.plot(x,y1)6.title('均匀分布概率密度')7.subplot(1,2,2)8.plot(x,y2)9.title('均匀分布分布函数')所得图形为:5)指数分布源码为:1.x=0:1:100;2.y1=exppdf(x,10); %求概率密度3.y2=expcdf(x,10); %求分布函数4.subplot(1,2,1)5.plot(y1)6.title('指数分布概率密度')7.subplot(1,2,2)8.plot(y2)9.title('指数分布分布函数')所得图形为:6)正态分布源码为:1.x=-10::10;2.y1=normpdf(x,0,1); %求概率密度3.y2=normcdf(x,0,1); %求分布函数4.subplot(1,2,1)5.plot(y1)6.title('正态分布分布概率密度')7.subplot(1,2,2)8.plot(y2)9.title('正态分布分布函数')所得图形为:7)卡方分布源码为:1.x=0::100;2.y1=chi2pdf(x,10); %求概率密度3.y2=chi2cdf(x,10); %求分布函数4.subplot(1,2,1)5.plot(y1)6.title('卡方分布分布概率密度')7.subplot(1,2,2)8.plot(y2)9.title('卡方分布分布函数')所得图形为:8)对数正态分布源码为:1.x=0::100;2.y1=lognpdf(x,2,1); %求概率密度3.y2=logncdf(x,2,1); %求分布函数4.subplot(1,2,1)5.plot(y1)6.title('对数正态分布分布概率密度')7.subplot(1,2,2)8.plot(y2)9.title('对数正态分布分布函数')所得图形为:9)F分布源码为:1.x=0::10;2.y1=fpdf(x,10,10); %求概率密度3.y2=fcdf(x,10,10); %求分布函数4.subplot(1,2,1)5.plot(y1)6.title('F分布分布概率密度')7.subplot(1,2,2)8.plot(y2)9.title('F分布分布函数')所得图形为:10)t分布源码为:1.x=-10::10;2.y1=tpdf(x,10); %求概率密度3.y2=tcdf(x,10); %求分布函数4.subplot(1,2,1)5.plot(y1)6.title('T分布分布概率密度')7.subplot(1,2,2)8.plot(y2)9.title('T分布分布函数')所得图形为:2.掷均匀硬币n次,检验正面出现的频率逼近1/21)思路:编写一个程序,验证随着n的增大,正面出现的频率越来越接近1/2。
西安交大概率论上机实验报告-西安交通大学概率论实验报告

概率论与数理统计上机实验报告一、实验内容使用MATLAB 软件进行验证性实验,掌握用MATLAB 实现概率统计中的常见计算。
本次实验包括了对二维随机变量,各种分布函数及其图像以及频率直方图的考察。
1、列出常见分布的概率密度及分布函数的命令,并操作。
2、掷硬币150次,其中正面出现的概率为0.5,这150次中正面出现的次数记为X ,(1) 试计算45=X 的概率和45≤X 的概率;(2) 绘制分布函数图形和概率分布律图形。
3、用Matlab 软件生成服从二项分布的随机数,并验证泊松定理。
4、设22221),(y x e y x f +-=π是一个二维随机变量的联合概率密度函数,画出这一函数的联合概率密度图像。
5、来自某个总体的样本观察值如下,计算样本的样本均值、样本方差、画出频率直方图。
A=[16 25 19 20 25 33 24 23 20 24 25 17 15 21 22 26 15 23 2220 14 16 11 14 28 18 13 27 31 25 24 16 19 23 26 17 14 30 21 18 16 18 19 20 22 19 22 18 26 26 13 21 13 11 19 23 18 24 28 13 11 25 15 17 18 22 16 13 12 13 11 09 15 18 21 15 12 17 13 14 12 16 10 08 23 18 11 16 28 13 21 22 12 08 15 21 18 16 16 19 28 19 12 14 19 28 28 28 13 21 28 19 11 15 18 24 18 16 28 19 15 13 22 14 16 24 20 28 18 18 28 14 13 28 29 24 28 14 18 18 18 08 21 16 24 32 16 28 19 15 18 18 10 12 16 26 18 19 33 08 11 18 27 23 11 22 22 13 28 14 22 18 26 18 16 32 27 25 24 17 17 28 33 16 20 28 32 19 23 18 28 15 24 28 29 16 17 19 18] 6. 利用Matlab 软件模拟高尔顿板钉试验。
西安交大数学建模实验报告

数学建模实验报告姓名:xxx 学号:xxxx 班级:xx 学院:xxxx1, 存货问题(一)问题描述每次订货费为500元,每月每吨保管费为50元,每月每吨货物缺货费为1500元,每吨材料的购价为1000元。
该企业欲采用周期性盘点的(s,S)策略来控制库存量,求最佳的S, S值。
(注:(s,S)策略指的是若发现存货量少于S时立即订货,将存货补充到S,使得经济效益最佳。
)(二)问题分析随机产生每个月需求量的概率,取遍每一个S和s的值,将每种S, s的组合对应的每月平均花费保存在数组money里,筛选数组,选出其中费用最小值,并求出对应的S和s。
模拟400个月的生产情况。
(三)程序代码clear;clc;need=0;remain=0;cost=0;mincostavg=inf;forsl=30:10:70forsh=80:10:140fornum=1:100000m=rand;if m<=0.1 need=50; elseif m<=0.3 need=60;elseif m<=0.45 need=70;elseif m<=0.7 need=80;elseif m<=0.75 need=90;elseif m<=0.85 need=100;elseif m<=0.95need=110;elseneed=120;endif remain<slcost=cost+(sh-remain)*1000+500;ifsh<needcost=cost+(need-sh)*1500;elsecost=cost+(sh-need)*50;remain=sh-need;endelseif remain<needcost=cost+(need-remain)*1500;remain=0;elsecost=cost+(remain-need)*50;remain=remain-need;endendendcostavg=cost/100000;ifcostavg<mincostavgmincostavg=costavg;propersl=sl;propersh=sh;endfprintf('s=%d, S=%d\nMonthly average cost=%.1f\n',sl,sh,costavg);cost=0;endendfprintf('\nWhen s=%d, S=%d\nThe least monthly averagecost=%.1f\n',propersl,propersh,mincostavg);(四)运行结果s=30, S=80Monthly average cost=85466.9s=30, S=90Monthly average cost=87007.6s=30, S=100Monthly average cost=87114.2 s=30, S=110Monthly average cost=87951.0s=30, S=120Monthly average cost=86778.9s=30, S=130Monthly average cost=86411.8 s=30, S=140Monthly average cost=86374.8 s=40, S=80Monthly average cost=83707.2s=40, S=90Monthly average cost=84026.6 s=40, S=100Monthly average cost=85089.1Monthly average cost=85386.0s=40, S=120Monthly average cost=86294.0 s=40, S=130 Monthly average cost=85148.0s=40, S=140Monthly average cost=84992.9s=50, S=80Monthly average cost=83693.0s=50, S=90Monthly average cost=82548.0 s=50, S=100 Monthly average cost=82730.9s=50, S=110Monthly average cost=83873.1 s=50, S=120 Monthly average cost=84029.5s=50, S=130Monthly average cost=84908.4s=50, S=140Monthly average cost=84134.1s=60, S=80Monthly average cost=83615.9s=60, S=90Monthly average cost=82503.9 s=60, S=100 Monthly average cost=81677.0s=60, S=110Monthly average cost=81905.5s=60, S=120Monthly average cost=82946.0s=60, S=130Monthly average cost=83449.2s=60, S=140Monthly average cost=83871.3s=70, S=80Monthly average cost=83522.6s=70, S=90Monthly average cost=82525.8s=70, S=100Monthly average cost=81627.9s=70, S=110Monthly average cost=81323.3s=70, S=120Monthly average cost=82005.5s=70, S=130Monthly average cost=82601.6s=70, S=140Monthly average cost=82858.3When s=70, S=110The least monthly average cost=81323.3(五)结果分析用计算机模拟的结果和用数学分析的结果有一定的差异,由于计算机模拟时一般情况都是要简化模型的,所以在一定程度上会有所差异,我们可以考虑能不能通过改进算法来消除该差异,但对于一般的生产要求亦可以满足。
西安交通大学概率论上机实验

西安交通⼤学概率论上机实验[公司名称]Matlab 上机实验尾号为7(题号5、8、9、12、16)第五题题⽬通过⾎检对某地区的N 个⼈进⾏某种疾病普查。
有两套⽅案:⽅案⼀是逐⼀检查;⽅案⼆是分组检查。
那么哪⼀种⽅案好?若这种疾病在该地区的发病率为0.1;0.05;0.01,试分析评价结果。
分析⽅案⼀需要检验N 次。
⽅案⼆:假设检验结果阴性为“正常”、阳性为“患者”,把受检者分为k 个⼈⼀组,把这k 个⼈的⾎混合在⼀起进⾏检验,如果检验结果为阴性,这说明k 个⼈的⾎液全为阴性,因⽽这k 个⼈总共只要检验⼀次就够了;如果结果为阳性,要确定k 个⼈的⾎液哪些是阳性就需要逐⼀再检查,因⽽这k 个⼈总共需要检查k+1次。
因此⽅案⼆在实施时有两种可能性,要和⽅案⼀⽐较,就要求出它的平均值(即平均检验次数)。
假设这⼀地区患病率(即检查结果为阳性的概率)为p ,那么检验结果为阴性的概率为,这时k 个⼈⼀组的混合⾎液是阴性的概率为,是阳性的概率为,则每⼀组所需的检验次数是⼀个服从⼆点分布的⼀个随机变量,下⾯的问题是,怎样确定k 的值使得次数最少?由以上计算结果可以得出:当,即时,⽅案⼆就⽐⽅案⼀好,总得检验次数为Y=。
当p=0.1时,⽤matlab 画出上述函数的图像: for i=1:1:101q p =-k q 1k q -ξ()1(1)11k k kE q k q k kq ξ=?++?-=+-1kk kq k +-p 11,k k kq q k f f()1k Nk kq k +-?k(i)=i;y(i)=(1+k(i)-k(i)*0.9^k(i))/k(i); end plot(k,y)可以看出,当k=4的时候最⼩,故此时每组⼈数应该取为4。
y=(1+k-k*0.9^k)/k*10000得到平均为5939次;P=0.05,k=5时,平均为4262次; P=0.01,k=32时,平均为3063次。
综上,采⽤合适的分组数时分组可以显著减少检验次数。
西安交通大学概率论实验报告-蒙特卡洛法

西安交通大学实验报告课程:概率论与数理统计实验日期:2013/12/22报告日期:2013/12/24专业班级:姓名:学号:实验内容:用蒙特卡洛方法估计积分值要求:(1)针对要估计的积分选择适当的概率分布设计蒙特卡洛方法;(2)利用计算机产生所选分布的随机数以估计积分值;(3)进行重复试验,通过计算样本均值以评价估计的无偏性;通过计算均方误差(针对第1类题)或样本方差(针对第2类题)以评价估计结果的精度。
目的:(1)能通过 MATLAB 或其他数学软件了解随机变量的概率密度、分布函数及其期望、方差、协方差等;(2)熟练使用 MATLAB 对样本进行基本统计,从而获取数据的基本信息;(3)能用 MATLAB 熟练进行样本的一元回归分析。
1用蒙特卡洛方法估计积分2sinx xdxπ⎰,2xe dx+∞⎰和22221x yx ye dxdy++≤⎰⎰的值,并将估计值与真值进行比较。
1)2sinx xdxπ⎰用区间为0-π/2的均匀分布产生;代码如下N=10000;x=unifrnd(0,pi/2,N,1); mean(x.*sin(x)*pi/2)计算出10次的数值计算出精确值:syms x ;int(x.*sin(x),0,pi/2)精确值为1;计算出均值:1.00158计算出均方误差:0.0000637580结论:这是一个计算积分的很好的近似,误差很小。
接下来考虑计算第二个积分:2)考虑2xe dx +∞⎰由对称性可以考虑正态分布N(0,1),代码如下:N=10000;x=normrnd(0,1,N,1)0.5*mean((sqrt(2.*pi)).*exp(-x.^2./2))求出均值为0.88598取0.8860计算出均方误差为:0.000018204说明误差允许范围内,可以用其作为积分的近似。
若考虑用参数为1的指数分布E(1)代码为:N=10000;x=exprnd(1,N,1)mean(exp(-x.^2./2+x))精确值为:0.8862计算出平均值为:1.25164计算出均方误差为:0.13356381和正态分布比相去甚远,效果不如正态分布3)22221x yx ye dxdy++≤⎰⎰利用代码计算出积分:N=10000;x=unifrnd(0,1,N,1) //已经转换为极坐标,r在[0,1]取值,取[0,1]均匀分布2*pi*mean(x.*exp(-x.^2))计算出十个值为:计算出平均值为:1.98397计算出均方误差为:0.000059其值与精确值非常接近,可以作为一个很好的近似第二类题:4) dx e x ⎰102用如下代码计算:N=10000;x=unifrnd(0,1,N,1) //[0,1]上的均匀分布mean(exp(x.^2))计算出平均值为:1.4619计算出标准偏差为:0.003304 ,说明波动性较小计算出均方误差为:0.000010其值与精确值非常接近,可以作为一个很好的近似5)22x y x d y +≤⎰⎰ 用如下代码计算:N=10000; x=unifrnd(0,2,N,1) //转换为极坐标后取[0,2]的均匀分布4*pi*mean(x./sqrt(1+x.^2)) 计算出平均值为:7.76363计算出标准偏差为:0.015241,说明波动性较小计算出均方误差为:0.000217其值与精确值非常接近,可以作为一个很好的近似。
概率论与数理统计上机实验报告

概率论与数理统计上机实验报告实验一【实验目的】熟练掌握 MATLAB 软件的关于概率分布作图的基本操作会进行常用的概率密度函数和分布函数的作图绘画出分布律图形【实验要求】掌握 MATLAB 的画图命令 plot掌握常见分布的概率密度图像和分布函数图像的画法【实验容】2 、设X : U (−1,1)(1 )求概率密度在 0 ,0.2 ,0.4 ,0.6 ,0.8,1 ,1.2 的函数值;(2 )产生 18 个随机数(3 行 6 列)(3 )又已知分布函数F ( x) = 0.45 ,求x(4 )画出X 的分布密度和分布函数图形。
【实验方案】熟练运用基本的MATLAB指令【设计程序和结果】1.计算函数值Fx=unifcdf(0, -1,1)Fx=unifcdf(0.2, -1,1)Fx=unifcdf(0.4, -1,1)Fx=unifcdf(0.6, -1,1)Fx=unifcdf(0.8, -1,1)Fx=unifcdf(1.0, -1,1)Fx=unifcdf(1.2, -1,1)结果Fx =0.5000Fx =0.6000Fx =0.7000Fx =0.8000Fx =0.9000Fx =1Fx =12.产生随机数程序:X=unifrnd(-1,1,3,6)结果:X =0.6294 0.8268 -0.4430 0.9298 0.9143 -0.7162 0.8116 0.2647 0.0938 -0.6848 -0.0292 -0.1565 -0.7460 -0.8049 0.9150 0.9412 0.6006 0.83153.求x程序:x=unifinv(0.45, -1,1)结果:x =-0.10004.画图程序:x=-1:0.1:1;px=unifpdf(x, -1,1);fx=unifcdf(x, -1,1);plot(x,px,'+b');hold on;plot(x,fx,'*r');legend('均匀分布函数','均匀分布密度');结果:【小结】运用基本的MATLAB指令可以方便的解决概率论中的相关问题,使数学问题得到简化。
西安交通大学汇编第二次上机实验报告范文

西安交通大学汇编第二次上机实验报告范文提交上机结果的模板文件第2次线上上机班级学号姓名1、循环程序设计-1(1)汇编、连接后的截图TODO:你的截图(必选)TODO:你的文字解释说明(可选)说明:mam某un得到某un.obj,某un.crf,某un.lt文件,通过link 某un得到某un.map文件,显示编译成功。
(2).lt文件的截图,TODO:你的截图(必选)TODO:你的文字解释说明(可选)说明:通过mam对程序进行编译时生成.lt文件,通过notepad++打开.lt文件,并进行截图(3)反汇编的截图TODO:你的截图(必选)TODO:你的文字解释说明(可选)说明:在debug环境下执行u指令,显示出反汇编代码。
(4)在完成DS赋值后,立即显示各个寄存器的值TODO:你的截图(必选)TODO:你的文字解释说明(可选)说明:按单步t之后,下方出现MOVDS,A某,即下一条即将执行的指令为MOVDS,A某,再按一次t,此时DS被赋值,此时执行的r指令显示的就是DS赋值后各个寄存器的值。
(5)在进行计算前,显示数组M开始的n+2个字的内存值的截图(只能显示这n+2个字的内存值,多显示、少显示均扣分)TODO:你的截图(必选)TODO:你的文字解释说明(可选)说明:在debug环境下,执行d指令显示内存,由于不能显示其他字的内存值,所以只能一行一行截图,可以看到,此时内存值与程序初始定义值相同。
(6)执行完计算后,立即显示各个寄存器的值TODO:你的截图(必选)TODO:你的文字解释说明(可选)说明:先执行g指令到执行回到do系统指令,此时显然已经执行完运算,此时执行r指令就获得执行完运算后各个寄存器的值。
(7)执行完计算后,显示数组M开始的n+2个字的内存值的截图(只能显示这n+2个字的内存值,多显示、少显示均扣分)TODO:你的截图(必选)TODO:你的文字解释说明(可选)说明:执行d指令显示出内存值,由于要求是不能显示其他字的值,所以只能一行一行截图,可以看到此时内存值与期望结果相同。
西安交通大学数学建模上机实验报告
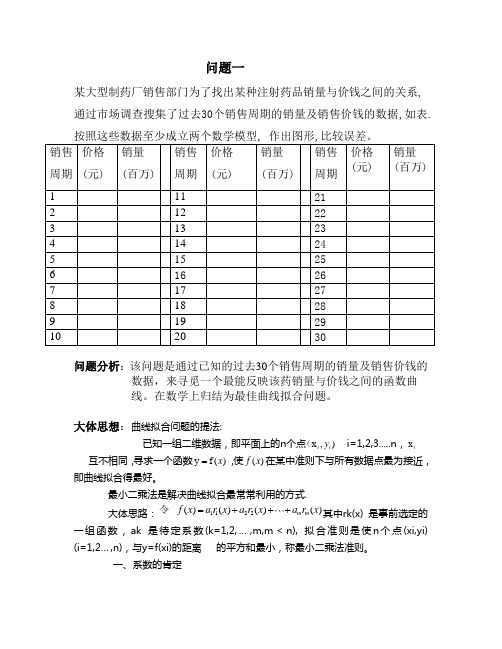
问题一某大型制药厂销售部门为了找出某种注射药品销量与价钱之间的关系,通过市场调查搜集了过去30个销售周期的销量及销售价钱的数据,如表.按照这些数据至少成立两个数学模型, 作出图形,比较误差。
问题分析:该问题是通过已知的过去30个销售周期的销量及销售价钱的 数据,来寻觅一个最能反映该药销量与价钱之间的函数曲 线。
在数学上归结为最佳曲线拟合问题。
大体思想:曲线拟合问题的提法:已知一组二维数据,即平面上的n 个点),x i i y ( i=1,2,3.....n ,i x 互不相同,寻求一个函数)(f y x =,使)(x f 在某中准则下与所有数据点最为接近,即曲线拟合得最好。
最小二乘法是解决曲线拟合最常常利用的方式.大体思路:1122 ()()()()m m f x a r x a r x a r x =+++令其中rk(x) 是事前选定的一组函数,ak 是待定系数(k=1,2,…,m,m <n), 拟合准则是使n 个点(xi,yi) (i=1,2…,n),与y=f(xi)的距离 的平方和最小,称最小二乘法准则。
一、系数的肯定22111 (,,)[()]n nm ii i i i J a a f x y δ====-∑∑记求m a a ,,1 使得使J 达到最小.0 (1,,)kJ k m a ∂==∂ 取得关于 m a a ,,1 的线性方程组:11111()[()]0 ()[()]0nmi k k i i i k n mm i k k i i i k r x a r x y r x a r x y ====⎧-=⎪⎪⎪⎨⎪⎪-=⎪⎩∑∑∑∑ 1 ,,().m a a f x 解出,即得散点图: 程序: x=[,,,,,,,,,,,,,,,,,,,,,,,,,,,,,]; y=[,,,,,,,,,,,,,,,,,,,,,,,,,,,,,]; plot(x,y,'r.')通过观察,结合实际情形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
概率论上机实验报告实验目的1. 学习使用MATLAB 中常见分布相关的命令;2. 学习绘制概率分布律与分布函数图形;3. 利用随机数对随机事件进行模拟;4. 体会随机事件发生频率与概率的关系,加深对概率论的理解。
实验内容1. 列出常见分布的概率密度及分布函数的命令,并操作。
2. 掷硬币150次,其中正面出现的概率为0.5,这150次中正面出现的次数记为X ,(1) 试计算45=X 的概率和45≤X 的概率;(2)绘制分布函数图形和概率分布律图形。
3. 用Matlab 软件生成服从二项分布的随机数,并验证泊松定理。
4. 设22221),(y x e y x f +-=π是一个二维随机变量的联合概率密度函数,画出这一函数的联合概率密度图像。
5. 来自某个总体的样本观察值如下,计算样本的样本均值、样本方差、画出频率直方图。
A=[16 25 19 20 25 33 24 23 20 24 25 17 15 21 22 26 15 23 22 20 14 16 11 14 28 18 13 27 31 25 24 16 19 23 26 17 14 30 21 18 16 18 19 20 22 19 22 18 26 26 13 21 13 11 19 23 18 24 28 13 11 25 15 17 18 22 16 13 12 13 11 09 15 18 21 15 12 17 1314 12 16 10 08 23 18 11 16 28 13 21 22 12 08 15 21 18 16 16 19 28 19 12 14 19 28 28 28 13 21 28 19 11 15 18 24 18 16 2819 15 13 22 14 16 24 20 28 18 18 28 14 13 28 29 24 28 14 18 18 18 08 21 16 24 32 16 28 19 15 18 18 10 12 16 26 18 19 3308 11 18 27 23 11 22 22 13 28 14 22 18 26 18 16 32 27 25 2417 17 28 33 16 20 28 32 19 23 18 28 15 24 28 29 16 17 19 18]6.利用Matlab软件模拟高尔顿板钉试验。
7.自己选择一个与以上问题不同类型的概率有关的建模题目,并解决. 实验任务及结果任务一、掌握常见分布的概率密度及分布函数的命令任务二、利用二项分布命令计算抛硬币实验题目分析:掷硬币是一种简单的随机试验,服从二项分布b(n,0.5),利用MATLAB中的概率密度命令与分布函数命令,取参数n为实验次数150,参数x为计算数值45,可以直接得到结果。
程序代码:p1=binopdf(45,150,0.5)p2=binocdf(45,150,0.5)x=0:1:150;y1=binopdf(x,150,0.5);y2=binocdf(x,150,0.5);figure(1)plot(x,y1);title('概率分布律');xlabel('x');ylabel('P(X=x)');figure(2)plot(x,y2);title('分布函数');xlabel('x');ylabel('P(X<=x)');运行结果与分析:(1)概率计算结果可知:45=X 的概率为 ;45≤X 的概率为 ;(2)概率分布律图形(3)分布函数图形任务三、使用随机数命令产生服从二项分布的随机数并验证泊松定理题目分析:1、利用binornd(n,p,m,s)可以直接产生m行s列服从b(n,p)的随机数。
2、泊松定理的内容是:在n重贝努力试验中,事件A在每次试验中发生的概率为p,出现A的总次数K服从二项分布b(n,p),当n很大p很小,λ=np大小适中时,二项分布可用参数为λ=np的泊松分布来近似。
为了验证泊松定理,可以设置参数n、p,通过二项分布命令binopdf与泊松分布命令poisspdf分别计算出分布律,并作图对比。
程序代码:%使用binornd命令产生服从二项分布b(n,p)的随机数n=10000;p=0.01;binornd(n,p,1,10) %产生服从b(n,p)的随机数x=50:150;y1=binopdf(x,n,p); %利用二项分布计算分布律,用空心圈绘出y2=poisspdf(x,n*p); %利用泊松分布计算分布律,用星号绘出plot(x,y1,'o',x,y2,'*');xlabel('x');ylabel('P(X=x)');运行结果与分析:(1)服从二项分布的随机数程序使用n=10000,p=0.01的二项分布,产生10个随机数结果如图,可以看出产生的10个随机数都在np=100附近。
(2)泊松定理的验证图中空心圈为利用二项分布计算分布律结果,星号为利用泊松分布计算分布律结果,从图可以看到,两种分布计算结果几乎完全重合,即在这种条件下二项分布完全可以用泊松分布逼近,验证了泊松定理。
任务四、画出二维随机变量的概率密度函数图像题目分析:利用MATLAB命令ezsurf可以非常简单地画出二维函数图像。
程序代码:ezsurf('1/(2*pi)*exp(-(x^2+y^2)/2)')运行结果与分析:任务五、调用MATLAB函数计算一组数据的均值、方差并绘直方图题目分析:MATLAB自带的mean命令可以直接计算一个向量内部数据的均值,var命令可以直接计算方差,hist命令可以直接绘出频数直方图,稍作调整就可以绘出频率直方图。
程序代码:A=[16 25 19 20 25 33 24 23 20 24 25 17 15 21 22 26 15 23 22 ...20 14 16 11 14 28 18 13 27 31 25 24 16 19 23 26 17 14 30 21 ...18 16 18 19 20 22 19 22 18 26 26 13 21 13 11 19 23 18 24 28 ...13 11 25 15 17 18 22 16 13 12 13 11 09 15 18 21 15 12 17 13 ...14 12 16 10 08 23 18 11 16 28 13 21 22 12 08 15 21 18 16 16 ...19 28 19 12 14 19 28 28 28 13 21 28 19 11 15 18 24 18 16 28 ...19 15 13 22 14 16 24 20 28 18 18 28 14 13 28 29 24 28 14 18 ...18 18 08 21 16 24 32 16 28 19 15 18 18 10 12 16 26 18 19 33 ...08 11 18 27 23 11 22 22 13 28 14 22 18 26 18 16 32 27 25 24 ...17 17 28 33 16 20 28 32 19 23 18 28 15 24 28 29 16 17 19 18];E=mean(A) %计算数据A的样本均值D=var(A) %计算数据A的样本方差[a,b]=hist(A);bar(b,a/sum(a));%将区间分为10个小区间绘制频率直方图xlabel('样本数据');ylabel('频率');title('频率直方图');运行结果与分析:(1)均值与方差计算结果:计算得这组数据均值为19.5176,方差为34.4025。
(2)频率分布直方图任务六、利用MATLAB模拟高尔顿板钉实验题目分析:高尔顿钉板实验如图,每一黑点表示钉在板上的一颗钉子,它们彼此的距离均相等,上一层的每一颗的水平位置恰好位于下一层的两颗正中间。
从入口处放进一个直径略小于两颗钉子之间的距离的小圆玻璃球,当小圆球向下降落过程中,碰到钉子后皆以1/2的概率向左或向右滚下,于是又碰到下一层钉子。
如此继续下去,直到滚到底板的一个格子内为止。
把许许多多同样大小的小球不断从入口处放下,只要球的数目相当大,它们在底板将堆成近似于正态的密度函数图形。
为了模拟高尔顿钉板实验,可以通过一个向量对钉子进行模拟,数值即为钉子的横坐标,每落下一次即根据随机数判断一次运动方向,如此便可以模拟任意球个数、任意钉板层数的高尔顿钉板实验。
程序代码:num=100000;ball=zeros(1,num); %产生num个球,横坐标为0floor=21; %floor层钉板for i=1:floorrd=binornd(1,0.5,1,num);%产生随机数向量%利用随机数向量对小球运动方向判断%随机数为0,小球向左运动;随机数为1,小球向右运动for j=1:numif rd(j)==0ball(j)=ball(j)-0.5;elseball(j)=ball(j)+0.5;endendendhist(ball,50)运行结果与分析:图为100000个小球经过21层钉板后的分布图,可以很明显的看出小球分布近似于正态分布的密度函数。
任务七、利用大量随机数实验模拟会面问题两人相约中午12时到13时在某地会面,双方约定,先到者必须等候对方15分钟,过了15分钟如果对方仍未到达则离去。
试模拟两人会面的概率问题分析:两人到达的时间可以认为是服从区间[0,60]上均匀分布的两个随机变量,两人会面的条件是两人到达时间之差的绝对值在15分钟以内,可以产生大量实验,在随机数的模拟值之差在一个范围内时,认为两人会面成功,计算两人会面的次数,与总实验次数之比即为两人会面概率的模拟值。
程序代码:n=1000000;k=0;x=rand(1,n);y=rand(1,n);for i=1:nif abs(x(i)-y(i))<1/4k=k+1;endendp=k/n运行结果与分析:两人会面的概率模拟值为0.4375,与理论计算值非常接近。
心得体会每次做完一个需要使用MATLAB的软件,我都会更加觉得MATLAB是一个强大的软件,竟然将这些常见的分布都做成了简单方便的命令可以直接调用,因为之前在计算均值、方差时,都是自己写程序来计算,这样似乎浪费了不少时间,达到的效果还不一定好。
因此,学无止境,要想用好MATLAB,还是要多加练习。
