二维插值
二维插值 原理

二维插值原理
二维插值是一种基于已知数据点的二维曲线或曲面估计方法。
它广泛应用于图像处理、地理信息系统、物理模拟等领域。
在二维插值中,我们假设已知的数据点位于一个二维平面上,每个数据点都有一个对应的数值。
我们的目标是通过这些已知数据点,来推断出未知位置上的数值。
常见的二维插值方法包括线性插值、拉格朗日插值和样条插值等。
线性插值是最简单的二维插值方法之一。
它假设在两个相邻数据点之间,数值的变化是线性的。
我们可以通过这两个相邻数据点之间的线段来估计未知位置上的数值。
拉格朗日插值则使用一个多项式来拟合已知数据点。
该多项式会经过所有已知数据点,并通过它们来估计未知位置上的数值。
它的优点是能够完全通过已知数据点来插值,但在高维情况下容易产生过拟合问题。
样条插值是一种基于局部插值的方法。
它通过在每个局部区域上拟合一个低阶多项式来实现插值。
这些局部多项式在相邻区域处满足平滑和连续性条件,从而得到整体平滑的插值结果。
除了上述方法外,还有其他一些二维插值方法,如反距离加权插值和克里金插值等。
总的来说,二维插值通过已知数据点之间的关系来估计未知位置上的数值。
不同的插值方法在计算复杂度、精度和平滑性等方面存在差异,根据具体应用场景的需求,选择合适的插值方法是非常重要的。
matlab interp2 用法

matlab interp2 用法关于MATLAB 中interp2 函数的用法在MATLAB中,interp2函数是一个用于二维插值的函数。
它可用于在给定的离散数据点之间进行插值,从而可以得到平滑的曲线或表面。
interp2函数的基本语法为:Vq = interp2(X,Y,V,Xq,Yq,method)其中,X和Y表示原始数据点的网格,V是在这些数据点上的测量值。
Xq和Yq是待插值点的坐标,Vq表示插值点所对应的值,method是用于插值的方法。
首先,让我们来看看如何准备要用于interp2函数的数据。
1. 创建原始数据点的网格首先,我们需要创建表示原始数据点的网格。
这可以通过使用meshgrid 函数来实现。
我们可以选择在一维数组上定义网格,然后使用meshgrid 函数来生成对应的二维网格。
例如,如果我们想要在x轴和y轴上分别有10个数据点,我们可以使用以下代码来创建网格:x = linspace(0,10,10);y = linspace(0,5,10);[X,Y] = meshgrid(x,y);这将创建一个10x10的网格,X和Y分别代表x和y坐标。
2. 创建原始数据点的测量值接下来,我们需要为每个数据点生成对应的测量值。
这些测量值可以是任意的,例如温度、压力、海拔等。
让我们用一个简单的函数来生成测量值,例如:V = sin(X).*cos(Y);这将为每个数据点生成一个sin(x)和cos(y)的乘积。
3. 进行插值接下来,我们可以使用interp2函数进行插值。
我们需要提供原始数据点的网格X和Y,以及每个数据点的测量值V。
我们还需要指定待插值点的坐标Xq和Yq,以及插值方法。
让我们使用与原始数据点相同的网格进行插值,并使用线性插值方法。
我们可以使用以下代码来实现:[Xq,Yq] = meshgrid(x,y);Vq = interp2(X,Y,V,Xq,Yq,'linear');注意,在这个例子中,我们使用的待插值点的坐标与原始数据点的网格相同。
二维插值算法原理

二维插值算法原理二维插值算法是一种在二维空间中根据已知的数据点来估计未知位置上的数值的算法。
它广泛应用于图像处理、地理信息系统和数值模拟等领域。
其原理是基于数学上的连续性和局部平滑性假设,通过利用已知数据点的信息,对未知位置上的数值进行估计。
二维插值算法的基本思想是根据已知的数据点的数值和位置,构建出一个合适的数学模型。
对于每一个未知位置,通过模型可以预测其数值。
这个模型常常是一个多项式函数或者其它形式的连续函数,以便于能够在整个二维空间中插值。
其中最常见的二维插值算法是双线性插值。
双线性插值法假设每个未知位置上的数值都是由其相邻四个已知点的数值线性插值得到的。
具体而言,假设已知的四个点为A、B、C、D,它们的数值分别为f(A)、f(B)、f(C)、f(D)。
对于未知位置P,可以通过以下公式计算得到其数值f(P):f(P) = (1 - u)(1 - v) f(A) + u(1 - v) f(B) + (1 - u)v f(C) + uv f(D)其中,u和v是分别表示未知位置在水平和垂直方向上的相对位置的权重。
这种方法实现简单,计算效率高,可以较为准确地插值出未知位置上的数值。
除了双线性插值之外,还有其它一些更复杂的二维插值算法,如三次样条插值、Kriging插值等。
这些算法在不同的应用场景下具有不同的优势。
例如,三次样条插值在处理光滑函数时效果较好,而Kriging插值则适用于处理具有空间相关性的数据。
选择适合的插值算法可以提高插值结果的质量。
在实际应用中,二维插值算法在处理图像、地理数据和模拟结果等方面具有重要意义。
通过插值算法,可以将有限的离散数据转换为连续的函数,从而对未知位置上的数值进行预测和分析。
同时,它也为数据的可视化提供了基础,使得我们能够更直观地理解数据的分布和变化规律。
总之,二维插值算法是一种有指导意义的数学工具,它通过在二维空间中根据有限的已知数据点估计未知位置上的数值。
matlab中二维插值函数用法

matlab中二维插值函数用法Matlab是一种强大的数学软件,可以对数据进行各种操作和分析。
在Matlab 中,二维插值函数是一种非常常用的工具,它可以帮助我们在已知数据点的基础上,估计其它位置的数值。
在本文中,我们将一步一步介绍二维插值函数的用法,希望对你有所帮助。
首先,我们需要明确一点,二维插值是用于处理二维平面上的数据,即x和y坐标都是变化的。
插值的目的是在这样的二维数据上,估计其它位置的数值,使得整个平面上的数值分布更加密集。
在Matlab中,二维插值函数主要是interp2函数。
该函数的基本语法如下:Vq = interp2(X, Y, V, Xq, Yq, method)其中,X和Y是已知数据点的x和y坐标,V是对应的数值;Xq和Yq是我们要估计数值的位置,Vq是估计得到的数值;method是插值方法,可以是‘linear’、‘nearest’、‘spline’等。
接下来,我们来演示一个具体的例子,以说明interp2函数的用法。
假设我们有一组二维数据如下:X = [1, 2, 3; 1, 2, 3; 1, 2, 3]Y = [1, 1, 1; 2, 2, 2; 3, 3, 3]V = [0, 1, 0; 1, 4, 1; 0, 1, 0]这里,X和Y分别是数据点的x和y坐标,V是对应的数值。
现在我们想要在位置(1.5, 1.5)处进行插值,估计其数值。
我们可以使用interp2函数来完成这个任务:Vq = interp2(X, Y, V, 1.5, 1.5, 'linear')这里,我们使用了‘linear’插值方法,得到的估计值Vq为2。
这就是在位置(1.5, 1.5)处的估计数值。
除了‘linear’插值方法,我们还可以尝试其它方法,比如‘nearest’和‘spline’。
这些方法在实际应用中有着不同的特点,需要根据具体情况选择合适的方法。
例如,‘nearest’方法会选择最近的数据点的数值作为估计值,‘spline’方法则会使用样条插值进行估计。
深入理解插值与卷积,1维插值,2维插值
a = 0.25 (a~c)
a = 1 (d~f)
a = 1.75 (g~i)
a = 0.5(j~l)
不同的a取值对于三次插值的效果。
•16.3.3 二维插值 •基本思想:先在某一维上进行一维插值,然后对这个中间结果的另外 一维进行一维插值。 •二维最近邻插值 •通过对x和y坐标分别取整,可以得到举例给定的连续点(x0,y0)最近的像 •素。
•16.3.2 以卷积方式描述插值 •对连续信号的重建可以描述为线性卷积运算。一般地,可以将插值表达 为给定离散函数g(u)和一连续插值内核w(x)的线性卷积。
• 可以理解为对离散函数的线性求和。 • 一维最近邻内插的插值内核为:
Байду номын сангаас
•线性插值的插值内核为:
最近邻插值(a-c)
线性插值(d-f)
•立方插值的插值内核为:
16.3 插值
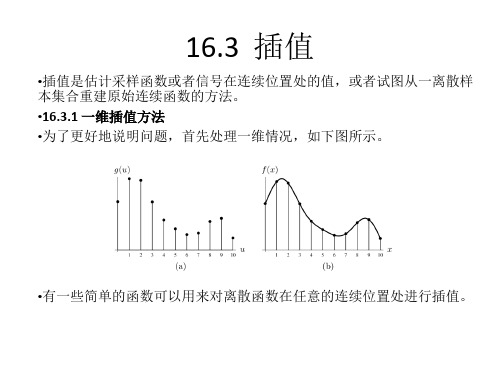
•插值是估计采样函数或者信号在连续位置处的值,或者试图从一离散样 本集合重建原始连续函数的方法。 •16.3.1 一维插值方法 •为了更好地说明问题,首先处理一维情况,如下图所示。
•有一些简单的函数可以用来对离散函数在任意的连续位置处进行插值。
•最近邻插值 •将连续坐标x近似为最近的整数值u0,并且用样本值g(u0)作为估计的函 数值。下图(a)为其示例。
•线性插值 •连续坐标x的估计值为最近两个样本g(u0)和g(u0+1)的加权求和的形式。 •下图(b)是其示例。
•数值计算中的三次Hermite插值 •给定离散点处的导数值和离散点处的函数值,可以在该离散点之间进行 插值,从而得到一个分段插值函数。该函数满足c1连续。这种插值方式 称为Hermite插值。以多项式构造插值函数则该多项式最多为3次。 •将该多项式写为 • f(x) =ax3 +bx2 + cx + d •例:求离散点0和离散点1之间的插值函数值: •1:约束条件 • f(0)= d; f(1)= a + b + c + d; • f’(0)=c; f’(1)=3a + 2b + c •2:求解上述四个方程,可以得到a,b,c,d的值从而求得插值函数 •三次插值(立方插值) •三次插值(立方插值)与Hermite插值之间的差别在于离散点处的导数 •值并不是事先已知的,而是通过相邻离散点之间的差分得到,如下式所 示 •f‘(0) = α[f(1)-f(-1)],f'(1) = α[f(2)-f(0)] •在上式中α是参数, α控制边缘处的锐化程度。当α =0.5时该插值又称为 •Catmull-Rom插值。
matlab中二维插值函数

matlab中二维插值函数Matlab中的二维插值函数是一种用于在给定有限数据点的情况下估算未知数据点的方法。
它可以用于图像处理、数据分析、数值计算等多个领域。
本文将介绍Matlab中常用的二维插值函数及其应用。
Matlab中的二维插值函数包括interp2、griddata和scatteredInterpolant等。
这些函数可以根据给定的数据点和相应的值,生成一个二维插值函数对象。
通过该对象,可以对未知数据点进行插值计算。
其中,interp2函数是最常用的二维插值函数之一。
它可以根据给定的数据点和相应的值,通过线性插值、样条插值或三次样条插值等方法,计算未知数据点的值。
interp2函数的使用方法如下:```Vq = interp2(X,Y,V,Xq,Yq)```其中,X和Y是二维网格的坐标,V是对应网格点的值,Xq和Yq 是待插值的点的坐标,Vq是插值得到的值。
通过interp2函数,可以将离散的数据点插值为连续的曲面,实现对未知数据点的估算。
除了interp2函数,griddata函数也是常用的二维插值函数之一。
它可以根据给定的散点数据和相应的值,生成一个二维插值函数对象。
griddata函数的使用方法如下:```F = griddata(x,y,v,xq,yq)```其中,x和y是散点数据的坐标,v是对应散点数据的值,xq和yq 是待插值的点的坐标,F是插值得到的函数对象。
通过griddata函数,可以实现对离散数据点的插值计算。
scatteredInterpolant函数也是常用的二维插值函数之一。
它可以根据给定的散点数据和相应的值,生成一个二维插值函数对象。
scatteredInterpolant函数的使用方法如下:```F = scatteredInterpolant(x,y,v)```其中,x和y是散点数据的坐标,v是对应散点数据的值,F是插值得到的函数对象。
通过scatteredInterpolant函数,可以实现对散点数据的插值计算。
griddata二维插值

griddata⼆维插值 对某些设备或测量仪器来说,采集的数据点的位置不是规则排列的⽹格结构(可参考),对于这种数据⽤散点图(每个采样点具有不同的值或权重)不能很好的展⽰其内部结构,因此需要对其进⾏插值,⽣成⼀个规则的栅格图像。
可采⽤griddata函数对已知的数据点进⾏插值,数据点(X, Y)不要求规则排列。
下图分别使⽤Nearest、Linear、Cubic三种插值⽅法对数据点进⾏插值。
插值算法都要⾸先⾯对⼀个共同的问题—— 邻近点的选择(利⽤靠近插值点附近的多个邻近点,构造插值函数计算插值点的函数值)。
应尽可能使所选择的邻近点均匀地分布在待估点周围。
因为使⽤适量的已知点对于插值的精度很重要,当已知点过多时,会使插值准确率下降,因为过多的信息量会掩盖有⽤的信息;被选择的邻近点构成的点分布不均匀,若某个⽅位上的数据点过多,或点集的某些数据点位置较集中,或者数据点过远,都会带来较⼤的插值误差。
griddata函数内部会先对已知的数据点进⾏Delaunay三⾓剖分,当完成三⾓剖分完成后,根据每个三⾓⽚顶点的数值,就可以对三⾓形区域内任意点进⾏线性插值(参考LinearNDInterpolator函数)。
对三⾓⽚内的插值点可采⽤质⼼插值,即是对插值点只考虑与该点最邻近周围点的影响,确定出插值点与最邻近的周围点之相互位置关系,求出与周围点的影响权重因⼦,以此建⽴线性插值公式(参考)。
"""Simple N-D interpolation.. versionadded:: 0.9"""## Copyright (C) Pauli Virtanen, 2010.## Distributed under the same BSD license as Scipy.### Note: this file should be run through the Mako template engine before# feeding it to Cython.## Run ``generate_qhull.py`` to regenerate the ``qhull.c`` file#cimport cythonfrom libc.float cimport DBL_EPSILONfrom libc.math cimport fabs, sqrtimport numpy as npimport scipy.spatial.qhull as qhullcimport scipy.spatial.qhull as qhullimport warnings#------------------------------------------------------------------------------# Numpy etc.#------------------------------------------------------------------------------cdef extern from"numpy/ndarrayobject.h":cdef enum:NPY_MAXDIMSctypedef fused double_or_complex:doubledouble complex#------------------------------------------------------------------------------# Interpolator base class#------------------------------------------------------------------------------class NDInterpolatorBase(object):"""Common routines for interpolators... versionadded:: 0.9"""def__init__(self, points, values, fill_value=np.nan, ndim=None,rescale=False, need_contiguous=True, need_values=True):"""Check shape of points and values arrays, and reshape values to(npoints, nvalues). Ensure the `points` and values arrays areC-contiguous, and of correct type."""if isinstance(points, qhull.Delaunay):# Precomputed triangulation was passed inif rescale:raise ValueError("Rescaling is not supported when passing ""a Delaunay triangulation as ``points``.")self.tri = pointspoints = points.pointselse:self.tri = Nonepoints = _ndim_coords_from_arrays(points)values = np.asarray(values)_check_init_shape(points, values, ndim=ndim)if need_contiguous:points = np.ascontiguousarray(points, dtype=np.double)if need_values:self.values_shape = values.shape[1:]if values.ndim == 1:self.values = values[:,None]elif values.ndim == 2:self.values = valueselse:self.values = values.reshape(values.shape[0],np.prod(values.shape[1:]))# Complex or real?self.is_complex = np.issubdtype(self.values.dtype, plexfloating) if self.is_complex:if need_contiguous:self.values = np.ascontiguousarray(self.values,dtype=plex128)self.fill_value = complex(fill_value)else:if need_contiguous:self.values = np.ascontiguousarray(self.values, dtype=np.double) self.fill_value = float(fill_value)if not rescale:self.scale = Noneself.points = pointselse:# scale to unit cube centered at 0self.offset = np.mean(points, axis=0)self.points = points - self.offsetself.scale = self.points.ptp(axis=0)self.scale[~(self.scale > 0)] = 1.0 # avoid division by 0self.points /= self.scaledef _check_call_shape(self, xi):xi = np.asanyarray(xi)if xi.shape[-1] != self.points.shape[1]:raise ValueError("number of dimensions in xi does not match x")return xidef _scale_x(self, xi):if self.scale is None:return xielse:return (xi - self.offset) / self.scaledef__call__(self, *args):"""interpolator(xi)Evaluate interpolator at given points.Parameters----------x1, x2, ... xn: array-like of floatPoints where to interpolate data at.x1, x2, ... xn can be array-like of float with broadcastable shape.or x1 can be array-like of float with shape ``(..., ndim)``"""xi = _ndim_coords_from_arrays(args, ndim=self.points.shape[1])xi = self._check_call_shape(xi)shape = xi.shapexi = xi.reshape(-1, shape[-1])xi = np.ascontiguousarray(xi, dtype=np.double)xi = self._scale_x(xi)if self.is_complex:r = self._evaluate_complex(xi)else:r = self._evaluate_double(xi)return np.asarray(r).reshape(shape[:-1] + self.values_shape)cpdef _ndim_coords_from_arrays(points, ndim=None):"""Convert a tuple of coordinate arrays to a (..., ndim)-shaped array."""cdef ssize_t j, nif isinstance(points, tuple) and len(points) == 1:# handle argument tuplepoints = points[0]if isinstance(points, tuple):p = np.broadcast_arrays(*points)n = len(p)for j in range(1, n):if p[j].shape != p[0].shape:raise ValueError("coordinate arrays do not have the same shape") points = np.empty(p[0].shape + (len(points),), dtype=float) for j, item in enumerate(p):points[...,j] = itemelse:points = np.asanyarray(points)if points.ndim == 1:if ndim is None:points = points.reshape(-1, 1)else:points = points.reshape(-1, ndim)return pointscdef _check_init_shape(points, values, ndim=None):"""Check shape of points and values arrays"""if values.shape[0] != points.shape[0]:raise ValueError("different number of values and points")if points.ndim != 2:raise ValueError("invalid shape for input data points")if points.shape[1] < 2:raise ValueError("input data must be at least 2-D")if ndim is not None and points.shape[1] != ndim:raise ValueError("this mode of interpolation available only for ""%d-D data" % ndim)#------------------------------------------------------------------------------# Linear interpolation in N-D#------------------------------------------------------------------------------class LinearNDInterpolator(NDInterpolatorBase):"""LinearNDInterpolator(points, values, fill_value=np.nan, rescale=False)Piecewise linear interpolant in N dimensions... versionadded:: 0.9Methods-------__call__Parameters----------points : ndarray of floats, shape (npoints, ndims); or DelaunayData point coordinates, or a precomputed Delaunay triangulation.values : ndarray of float or complex, shape (npoints, ...)Data values.fill_value : float, optionalValue used to fill in for requested points outside of theconvex hull of the input points. If not provided, thenthe default is ``nan``.rescale : bool, optionalRescale points to unit cube before performing interpolation.This is useful if some of the input dimensions haveincommensurable units and differ by many orders of magnitude.Notes-----The interpolant is constructed by triangulating the input datawith Qhull [1]_, and on each triangle performing linearbarycentric interpolation.Examples--------We can interpolate values on a 2D plane:>>> from scipy.interpolate import LinearNDInterpolator>>> import matplotlib.pyplot as plt>>> np.random.seed(0)>>> x = np.random.random(10) - 0.5>>> y = np.random.random(10) - 0.5>>> z = np.hypot(x, y)>>> X = np.linspace(min(x), max(x))>>> Y = np.linspace(min(y), max(y))>>> X, Y = np.meshgrid(X, Y) # 2D grid for interpolation>>> interp = LinearNDInterpolator(list(zip(x, y)), z)>>> Z = interp(X, Y)>>> plt.pcolormesh(X, Y, Z, shading='auto')>>> plt.plot(x, y, "ok", label="input point")>>> plt.legend()>>> plt.colorbar()>>> plt.axis("equal")>>> plt.show()See also--------griddata :Interpolate unstructured D-D data.NearestNDInterpolator :Nearest-neighbor interpolation in N dimensions.CloughTocher2DInterpolator :Piecewise cubic, C1 smooth, curvature-minimizing interpolant in 2D. References----------.. [1] /"""def__init__(self, points, values, fill_value=np.nan, rescale=False):NDInterpolatorBase.__init__(self, points, values, fill_value=fill_value, rescale=rescale)if self.tri is None:self.tri = qhull.Delaunay(self.points)def _evaluate_double(self, xi):return self._do_evaluate(xi, 1.0)def _evaluate_complex(self, xi):return self._do_evaluate(xi, 1.0j)@cython.boundscheck(False)@cython.wraparound(False)def _do_evaluate(self, const double[:,::1] xi, double_or_complex dummy): cdef const double_or_complex[:,::1] values = self.valuescdef double_or_complex[:,::1] outcdef const double[:,::1] points = self.pointscdef const int[:,::1] simplices = self.tri.simplicescdef double c[NPY_MAXDIMS]cdef double_or_complex fill_valuecdef int i, j, k, m, ndim, isimplex, inside, start, nvaluescdef qhull.DelaunayInfo_t infocdef double eps, eps_broadndim = xi.shape[1]start = 0fill_value = self.fill_valueqhull._get_delaunay_info(&info, self.tri, 1, 0, 0)out = np.empty((xi.shape[0], self.values.shape[1]),dtype=self.values.dtype)nvalues = out.shape[1]eps = 100 * DBL_EPSILONeps_broad = sqrt(DBL_EPSILON)with nogil:for i in range(xi.shape[0]):# 1) Find the simplexisimplex = qhull._find_simplex(&info, c,&xi[0,0] + i*ndim,&start, eps, eps_broad)# 2) Linear barycentric interpolationif isimplex == -1:# don't extrapolatefor k in range(nvalues):out[i,k] = fill_valuecontinuefor k in range(nvalues):out[i,k] = 0for j in range(ndim+1):for k in range(nvalues):m = simplices[isimplex,j]out[i,k] = out[i,k] + c[j] * values[m,k]return out#------------------------------------------------------------------------------# Gradient estimation in 2D#------------------------------------------------------------------------------class GradientEstimationWarning(Warning):pass@cython.cdivision(True)cdef int _estimate_gradients_2d_global(qhull.DelaunayInfo_t *d, double *data, int maxiter, double tol,double *y) nogil:"""Estimate gradients of a function at the vertices of a 2d triangulation.Parameters----------info : inputTriangulation in 2Ddata : inputFunction values at the verticesmaxiter : inputMaximum number of Gauss-Seidel iterationstol : inputAbsolute / relative stop tolerancey : output, shape (npoints, 2)Derivatives [F_x, F_y] at the verticesReturns-------num_iterationsNumber of iterations if converged, 0 if maxiter reachedwithout convergenceNotes-----This routine uses a re-implementation of the global approximatecurvature minimization algorithm described in [Nielson83] and [Renka84]. References----------.. [Nielson83] G. Nielson,''A method for interpolating scattered data based upon a minimum norm network''.Math. Comp., 40, 253 (1983)... [Renka84] R. J. Renka and A. K. Cline.''A Triangle-based C1 interpolation method.'',Rocky Mountain J. Math., 14, 223 (1984)."""cdef double Q[2*2]cdef double s[2]cdef double r[2]cdef int ipoint, iiter, k, ipoint2, jpoint2cdef double f1, f2, df2, ex, ey, L, L3, det, err, change# initializefor ipoint in range(2*d.npoints):y[ipoint] = 0## Main point:## Z = sum_T sum_{E in T} int_E |W''|^2 = min!## where W'' is the second derivative of the Clough-Tocher# interpolant to the direction of the edge E in triangle T.## The minimization is done iteratively: for each vertex V,# the sum## Z_V = sum_{E connected to V} int_E |W''|^2## is minimized separately, using existing values at other V.## Since the interpolant can be written as## W(x) = f(x) + w(x)^T y## where y = [ F_x(V); F_y(V) ], it is clear that the solution to# the local problem is is given as a solution of the 2x2 matrix# equation.## Here, we use the Clough-Tocher interpolant, which restricted to# a single edge is## w(x) = (1 - x)**3 * f1# + x*(1 - x)**2 * (df1 + 3*f1)# + x**2*(1 - x) * (df2 + 3*f2)# + x**3 * f2## where f1, f2 are values at the vertices, and df1 and df2 are# derivatives along the edge (away from the vertices).## As a consequence, one finds## L^3 int_{E} |W''|^2 = y^T A y + 2 B y + C## with## A = [4, -2; -2, 4]# B = [6*(f1 - f2), 6*(f2 - f1)]# y = [df1, df2]# L = length of edge E## and C is not needed for minimization. Since df1 = dF1.E, df2 = -dF2.E, # with dF1 = [F_x(V_1), F_y(V_1)], and the edge vector E = V2 - V1,# we have## Z_V = dF1^T Q dF1 + 2 s.dF1 + const.## which is minimized by## dF1 = -Q^{-1} s## where## Q = sum_E [A_11 E E^T]/L_E^3 = 4 sum_E [E E^T]/L_E^3# s = sum_E [ B_1 + A_21 df2] E /L_E^3# = sum_E [ 6*(f1 - f2) + 2*(E.dF2)] E / L_E^3## Gauss-Seidelfor iiter in range(maxiter):err = 0for ipoint in range(d.npoints):for k in range(2*2):Q[k] = 0for k in range(2):s[k] = 0# walk over neighbours of given pointfor jpoint2 in range(d.vertex_neighbors_indptr[ipoint],d.vertex_neighbors_indptr[ipoint+1]):ipoint2 = d.vertex_neighbors_indices[jpoint2]# edgeex = d.points[2*ipoint2 + 0] - d.points[2*ipoint + 0]ey = d.points[2*ipoint2 + 1] - d.points[2*ipoint + 1]L = sqrt(ex**2 + ey**2)L3 = L*L*L# data at verticesf1 = data[ipoint]f2 = data[ipoint2]# scaled gradient projections on the edgedf2 = -ex*y[2*ipoint2 + 0] - ey*y[2*ipoint2 + 1]# edge sumQ[0] += 4*ex*ex / L3Q[1] += 4*ex*ey / L3Q[3] += 4*ey*ey / L3s[0] += (6*(f1 - f2) - 2*df2) * ex / L3s[1] += (6*(f1 - f2) - 2*df2) * ey / L3Q[2] = Q[1]# solvedet = Q[0]*Q[3] - Q[1]*Q[2]r[0] = ( Q[3]*s[0] - Q[1]*s[1])/detr[1] = (-Q[2]*s[0] + Q[0]*s[1])/detchange = max(fabs(y[2*ipoint + 0] + r[0]),fabs(y[2*ipoint + 1] + r[1]))y[2*ipoint + 0] = -r[0]y[2*ipoint + 1] = -r[1]# relative/absolute errorchange /= max(1.0, max(fabs(r[0]), fabs(r[1])))err = max(err, change)if err < tol:return iiter + 1# Didn't converge before maxiterreturn 0@cython.boundscheck(False)@cython.wraparound(False)cpdef estimate_gradients_2d_global(tri, y, int maxiter=400, double tol=1e-6): cdef const double[:,::1] datacdef double[:,:,::1] gradcdef qhull.DelaunayInfo_t infocdef int k, ret, nvaluesy = np.asanyarray(y)if y.shape[0] != tri.npoints:raise ValueError("'y' has a wrong number of items")if np.issubdtype(y.dtype, plexfloating):rg = estimate_gradients_2d_global(tri, y.real, maxiter=maxiter, tol=tol) ig = estimate_gradients_2d_global(tri, y.imag, maxiter=maxiter, tol=tol) r = np.zeros(rg.shape, dtype=complex)r.real = rgr.imag = igreturn ry_shape = y.shapeif y.ndim == 1:y = y[:,None]y = y.reshape(tri.npoints, -1).Ty = np.ascontiguousarray(y, dtype=np.double)yi = np.empty((y.shape[0], y.shape[1], 2))data = ygrad = yiqhull._get_delaunay_info(&info, tri, 0, 0, 1)nvalues = data.shape[0]for k in range(nvalues):with nogil:ret = _estimate_gradients_2d_global(&info,&data[k,0],maxiter,tol,&grad[k,0,0])if ret == 0:warnings.warn("Gradient estimation did not converge, ""the results may be inaccurate",GradientEstimationWarning)return yi.transpose(1, 0, 2).reshape(y_shape + (2,))#------------------------------------------------------------------------------# Cubic interpolation in 2D#------------------------------------------------------------------------------@cython.cdivision(True)cdef double_or_complex _clough_tocher_2d_single(qhull.DelaunayInfo_t *d, int isimplex,double *b,double_or_complex *f,double_or_complex *df) nogil:"""Evaluate Clough-Tocher interpolant on a 2D triangle.Parameters----------d :Delaunay infoisimplex : intTriangle to evaluate onb : shape (3,)Barycentric coordinates of the point on the trianglef : shape (3,)Function values at verticesdf : shape (3, 2)Gradient values at verticesReturns-------w :Value of the interpolant at the given pointReferences----------.. [CT] See, for example,P. Alfeld,''A trivariate Clough-Tocher scheme for tetrahedral data''.Computer Aided Geometric Design, 1, 169 (1984);G. Farin,''Triangular Bernstein-Bezier patches''.Computer Aided Geometric Design, 3, 83 (1986)."""cdef double_or_complex \c3000, c0300, c0030, c0003, \c2100, c2010, c2001, c0210, c0201, c0021, \c1200, c1020, c1002, c0120, c0102, c0012, \c1101, c1011, c0111cdef double_or_complex \f1, f2, f3, df12, df13, df21, df23, df31, df32cdef double g[3]cdef double \e12x, e12y, e23x, e23y, e31x, e31y, \e14x, e14y, e24x, e24y, e34x, e34ycdef double_or_complex wcdef double minvalcdef double b1, b2, b3, b4cdef int k, itricdef double c[3]cdef double y[2]# XXX: optimize + refactor this!e12x = (+ d.points[0 + 2*d.simplices[3*isimplex + 1]]- d.points[0 + 2*d.simplices[3*isimplex + 0]])e12y = (+ d.points[1 + 2*d.simplices[3*isimplex + 1]]- d.points[1 + 2*d.simplices[3*isimplex + 0]])e23x = (+ d.points[0 + 2*d.simplices[3*isimplex + 2]]- d.points[0 + 2*d.simplices[3*isimplex + 1]])e23y = (+ d.points[1 + 2*d.simplices[3*isimplex + 2]]- d.points[1 + 2*d.simplices[3*isimplex + 1]])e31x = (+ d.points[0 + 2*d.simplices[3*isimplex + 0]]- d.points[0 + 2*d.simplices[3*isimplex + 2]])e31y = (+ d.points[1 + 2*d.simplices[3*isimplex + 0]]- d.points[1 + 2*d.simplices[3*isimplex + 2]])e14x = (e12x - e31x)/3e14y = (e12y - e31y)/3e24x = (-e12x + e23x)/3e24y = (-e12y + e23y)/3e34x = (e31x - e23x)/3e34y = (e31y - e23y)/3f1 = f[0]f2 = f[1]f3 = f[2]df12 = +(df[2*0+0]*e12x + df[2*0+1]*e12y)df21 = -(df[2*1+0]*e12x + df[2*1+1]*e12y)df23 = +(df[2*1+0]*e23x + df[2*1+1]*e23y)df32 = -(df[2*2+0]*e23x + df[2*2+1]*e23y)df31 = +(df[2*2+0]*e31x + df[2*2+1]*e31y)df13 = -(df[2*0+0]*e31x + df[2*0+1]*e31y)c3000 = f1c2100 = (df12 + 3*c3000)/3c2010 = (df13 + 3*c3000)/3c0300 = f2c1200 = (df21 + 3*c0300)/3c0210 = (df23 + 3*c0300)/3c0030 = f3c1020 = (df31 + 3*c0030)/3c0120 = (df32 + 3*c0030)/3c2001 = (c2100 + c2010 + c3000)/3c0201 = (c1200 + c0300 + c0210)/3c0021 = (c1020 + c0120 + c0030)/3## Now, we need to impose the condition that the gradient of the spline # to some direction `w` is a linear function along the edge.## As long as two neighbouring triangles agree on the choice of the# direction `w`, this ensures global C1 differentiability.# Otherwise, the choice of the direction is arbitrary (except that# it should not point along the edge, of course).## In [CT]_, it is suggested to pick `w` as the normal of the edge.# This choice is given by the formulas## w_12 = E_24 + g[0] * E_23# w_23 = E_34 + g[1] * E_31# w_31 = E_14 + g[2] * E_12## g[0] = -(e24x*e23x + e24y*e23y) / (e23x**2 + e23y**2)# g[1] = -(e34x*e31x + e34y*e31y) / (e31x**2 + e31y**2)# g[2] = -(e14x*e12x + e14y*e12y) / (e12x**2 + e12y**2)## However, this choice gives an interpolant that is *not*# invariant under affine transforms. This has some bad# consequences: for a very narrow triangle, the spline can# develops huge oscillations. For instance, with the input data## [(0, 0), (0, 1), (eps, eps)], eps = 0.01# F = [0, 0, 1]# dF = [(0,0), (0,0), (0,0)]## one observes that as eps -> 0, the absolute maximum value of the # interpolant approaches infinity.## So below, we aim to pick affine invariant `g[k]`.# We choose## w = V_4' - V_4## where V_4 is the centroid of the current triangle, and V_4' the# centroid of the neighbour. Since this quantity transforms similarly # as the gradient under affine transforms, the resulting interpolant# is affine-invariant. Moreover, two neighbouring triangles clearly# always agree on the choice of `w` (sign is unimportant), and so# this choice also makes the interpolant C1.## The drawback here is a performance penalty, since we need to# peek into neighbouring triangles.#for k in range(3):itri = d.neighbors[3*isimplex + k]if itri == -1:# No neighbour.# Compute derivative to the centroid direction (e_12 + e_13)/2. g[k] = -1./2continue# Centroid of the neighbour, in our local barycentric coordinates y[0] = (+ d.points[0 + 2*d.simplices[3*itri + 0]]+ d.points[0 + 2*d.simplices[3*itri + 1]]+ d.points[0 + 2*d.simplices[3*itri + 2]]) / 3y[1] = (+ d.points[1 + 2*d.simplices[3*itri + 0]]+ d.points[1 + 2*d.simplices[3*itri + 1]]+ d.points[1 + 2*d.simplices[3*itri + 2]]) / 3qhull._barycentric_coordinates(2, d.transform + isimplex*2*3, y, c) # Rewrite V_4'-V_4 = const*[(V_4-V_2) + g_i*(V_3 - V_2)]# Now, observe that the results can be written *in terms of# barycentric coordinates*. Barycentric coordinates stay# invariant under affine transformations, so we can directly# conclude that the choice below is affine-invariant.if k == 0:g[k] = (2*c[2] + c[1] - 1) / (2 - 3*c[2] - 3*c[1])elif k == 1:g[k] = (2*c[0] + c[2] - 1) / (2 - 3*c[0] - 3*c[2])elif k == 2:g[k] = (2*c[1] + c[0] - 1) / (2 - 3*c[1] - 3*c[0])c0111 = (g[0]*(-c0300 + 3*c0210 - 3*c0120 + c0030)+ (-c0300 + 2*c0210 - c0120 + c0021 + c0201))/2c1011 = (g[1]*(-c0030 + 3*c1020 - 3*c2010 + c3000)+ (-c0030 + 2*c1020 - c2010 + c2001 + c0021))/2c1101 = (g[2]*(-c3000 + 3*c2100 - 3*c1200 + c0300)+ (-c3000 + 2*c2100 - c1200 + c2001 + c0201))/2c1002 = (c1101 + c1011 + c2001)/3c0102 = (c1101 + c0111 + c0201)/3c0012 = (c1011 + c0111 + c0021)/3c0003 = (c1002 + c0102 + c0012)/3# extended barycentric coordinatesminval = b[0]for k in range(3):if b[k] < minval:minval = b[k]b1 = b[0] - minvalb2 = b[1] - minvalb3 = b[2] - minvalb4 = 3*minval# evaluate the polynomial -- the stupid and ugly way to do it,# one of the 4 coordinates is in fact zerow = (b1**3*c3000 + 3*b1**2*b2*c2100 + 3*b1**2*b3*c2010 +3*b1**2*b4*c2001 + 3*b1*b2**2*c1200 +6*b1*b2*b4*c1101 + 3*b1*b3**2*c1020 + 6*b1*b3*b4*c1011 +3*b1*b4**2*c1002 + b2**3*c0300 + 3*b2**2*b3*c0210 +3*b2**2*b4*c0201 + 3*b2*b3**2*c0120 + 6*b2*b3*b4*c0111 +3*b2*b4**2*c0102 + b3**3*c0030 + 3*b3**2*b4*c0021 +3*b3*b4**2*c0012 + b4**3*c0003)return wclass CloughTocher2DInterpolator(NDInterpolatorBase):"""CloughTocher2DInterpolator(points, values, tol=1e-6)Piecewise cubic, C1 smooth, curvature-minimizing interpolant in 2D. .. versionadded:: 0.9Methods-------__call__Parameters----------points : ndarray of floats, shape (npoints, ndims); or DelaunayData point coordinates, or a precomputed Delaunay triangulation. values : ndarray of float or complex, shape (npoints, ...)Data values.fill_value : float, optionalValue used to fill in for requested points outside of theconvex hull of the input points. If not provided, thenthe default is ``nan``.tol : float, optionalAbsolute/relative tolerance for gradient estimation.maxiter : int, optionalMaximum number of iterations in gradient estimation.rescale : bool, optionalRescale points to unit cube before performing interpolation.This is useful if some of the input dimensions haveincommensurable units and differ by many orders of magnitude.Notes-----The interpolant is constructed by triangulating the input datawith Qhull [1]_, and constructing a piecewise cubicinterpolating Bezier polynomial on each triangle, using aClough-Tocher scheme [CT]_. The interpolant is guaranteed to becontinuously differentiable.The gradients of the interpolant are chosen so that the curvatureof the interpolating surface is approximatively minimized. Thegradients necessary for this are estimated using the globalalgorithm described in [Nielson83]_ and [Renka84]_.Examples--------We can interpolate values on a 2D plane:>>> from scipy.interpolate import CloughTocher2DInterpolator>>> import matplotlib.pyplot as plt>>> np.random.seed(0)>>> x = np.random.random(10) - 0.5>>> y = np.random.random(10) - 0.5>>> z = np.hypot(x, y)>>> X = np.linspace(min(x), max(x))>>> Y = np.linspace(min(y), max(y))>>> X, Y = np.meshgrid(X, Y) # 2D grid for interpolation>>> interp = CloughTocher2DInterpolator(list(zip(x, y)), z)>>> Z = interp(X, Y)>>> plt.pcolormesh(X, Y, Z, shading='auto')>>> plt.plot(x, y, "ok", label="input point")>>> plt.legend()>>> plt.colorbar()>>> plt.axis("equal")>>> plt.show()See also--------griddata :Interpolate unstructured D-D data.LinearNDInterpolator :Piecewise linear interpolant in N dimensions.NearestNDInterpolator :Nearest-neighbor interpolation in N dimensions.References----------.. [1] /.. [CT] See, for example,P. Alfeld,''A trivariate Clough-Tocher scheme for tetrahedral data''.Computer Aided Geometric Design, 1, 169 (1984);G. Farin,''Triangular Bernstein-Bezier patches''.Computer Aided Geometric Design, 3, 83 (1986)... [Nielson83] G. Nielson,''A method for interpolating scattered data based upon a minimum norm network''.Math. Comp., 40, 253 (1983)... [Renka84] R. J. Renka and A. K. Cline.''A Triangle-based C1 interpolation method.'',Rocky Mountain J. Math., 14, 223 (1984)."""def__init__(self, points, values, fill_value=np.nan,tol=1e-6, maxiter=400, rescale=False):NDInterpolatorBase.__init__(self, points, values, ndim=2,fill_value=fill_value, rescale=rescale)if self.tri is None:self.tri = qhull.Delaunay(self.points)self.grad = estimate_gradients_2d_global(self.tri, self.values,tol=tol, maxiter=maxiter)def _evaluate_double(self, xi):return self._do_evaluate(xi, 1.0)def _evaluate_complex(self, xi):return self._do_evaluate(xi, 1.0j)@cython.boundscheck(False)@cython.wraparound(False)def _do_evaluate(self, const double[:,::1] xi, double_or_complex dummy):cdef const double_or_complex[:,::1] values = self.valuescdef const double_or_complex[:,:,:] grad = self.gradcdef double_or_complex[:,::1] outcdef const double[:,::1] points = self.pointscdef const int[:,::1] simplices = self.tri.simplicescdef double c[NPY_MAXDIMS]cdef double_or_complex f[NPY_MAXDIMS+1]cdef double_or_complex df[2*NPY_MAXDIMS+2]cdef double_or_complex wcdef double_or_complex fill_valuecdef int i, j, k, m, ndim, isimplex, inside, start, nvaluescdef qhull.DelaunayInfo_t infocdef double eps, eps_broadndim = xi.shape[1]start = 0fill_value = self.fill_valueqhull._get_delaunay_info(&info, self.tri, 1, 1, 0)out = np.zeros((xi.shape[0], self.values.shape[1]),dtype=self.values.dtype)nvalues = out.shape[1]eps = 100 * DBL_EPSILONeps_broad = sqrt(eps)with nogil:for i in range(xi.shape[0]):# 1) Find the simplexisimplex = qhull._find_simplex(&info, c,&xi[i,0],&start, eps, eps_broad)# 2) Clough-Tocher interpolationif isimplex == -1:# outside triangulationfor k in range(nvalues):out[i,k] = fill_valuecontinuefor k in range(nvalues):for j in range(ndim+1):f[j] = values[simplices[isimplex,j],k]df[2*j] = grad[simplices[isimplex,j],k,0]df[2*j+1] = grad[simplices[isimplex,j],k,1]w = _clough_tocher_2d_single(&info, isimplex, c, f, df)out[i,k] = wreturn outView Code 下图中红⾊的是已知采样点,蓝⾊是待插值的栅格点,三⾓形内部栅格点的数值可通过线性插值或其它插值⽅法计算出,三⾓形外部的点可在函数中指定⼀个数值(默认为NaN)。
二维插值算法原理

二维插值算法是一种用于在二维空间中估计未知数据点的方法。
它基于已知数据点的值和位置来推断未知数据点的值。
以下是常见的二维插值算法原理之一:双线性插值。
双线性插值是一种基于四个最近邻数据点进行估计的方法。
假设我们有一个二维网格,已知在四个顶点上的数据点的值和位置。
要估计某个位置处的未知数据点的值,双线性插值算法按照以下步骤进行:
1.找到目标位置的最近的四个已知数据点,通常称为左上、右上、左下和右下。
2.计算目标位置相对于这四个已知数据点的相对位置权重。
这可以通过计算目标位置到每个已知数据点的水平和垂直距离,然后根据距离来计算相对权重。
3.根据权重对四个已知数据点的值进行加权平均。
这里的加权平均可以使用线性插值进行计算。
4.得到目标位置的估计值作为插值结果。
双线性插值算法基于以下两个假设:
-在目标位置的附近,插值曲面在水平和垂直方向上是一致的,即呈现线性关系。
-已知数据点之间的变化不会很剧烈,即目标位置与附近已知数据点的值之间存在一定的连续性。
双线性插值算法是一种简单而有效的二维插值方法,适用于平滑、连续变化的数据。
但对于非线性、不规则的数据分布,或者存在边界情况的情况下,可能需要使用其他更复杂的插值算法来获得更准确的估计结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
返回
用MATLAB作散点数据的插值计算
z=griddata(x0,y0,z0,x,y,’method’)
被插值点 的函数值
插值节点 被插值点
注意:x0,y0,z0均为向量,长度相等。 Method可取 ‘nearest’,’linear’,’cubic’,’v4’; ‘linear’是缺省值。
上一页 下一页 主 页
1500
上一页 下一页 主 页
2000 X
2500
上一页 下一页 主 页
返回
上一页 下一页 主 页
范例2:船在该海域会搁浅吗?
在某海域测得一些点(x,y)处的水深z由下表给出, 船的吃水深度为5英尺,在矩形区域(75,200)* (-50,150)里的哪些地方船要避免进入。
x 129 140 103.5 88 185.5 195 105
上一页 下一页 主 页
引例1:如何绘制山区地貌图
上一页 下一页 主 页
Z
2000
1500
1000
500
0 0
1000 2000 3000 4000 5000 6000 0 X
上一页 下一页 主 页
5000 4000 3000 2000 1000 Y
引例1:如何绘制山区地貌图
y
•
•
•
•
•
••
•
••
假设:海底平滑 1.作出测量点的分布图; 2.求出矩形区域(75,200)*(-50,150)的 细分网格节点之横、纵坐标向量; 3.利用MATLAB中的散点插值函数求网格节点 的水深; 4.作出海底曲面图形和等高线图; 5.作出水深小于5的海域范围。
上一页 下一页 主 页
1.作出测量点的分布图
clear; x=[129 140 103.5 88 185.5 195 105.5 157.5 107.5 77 81 162 162 117.5]; y=[7.5 141.5 23 147 22.5 137.5 85.5…
再用
计算插值,即
上一页 下一页 主 页
返回
二维插值方法
网格节点插值法:
最邻近插值;
分片线性插值;
双线性插值;
双三次插值。
散点数据插值法:
修正Shephard法
返回
上一页 下一页 主 页
1.最邻近插值
y•
(x1•, y2) (x2,•y2)
•
•
•
•
•
••
(x1, y1) (x2, y1)
•
•
•实验目的
[1] 了解二维插值的基本原理,了解三 种网格节点数据的插值方法的基本思想; [2] 掌握用MATLAB计算二维插值的方法, 并对结果作初步分析; [3] 通过实例学习如何用插值方法解决 实际问题。
上一页 下一页 主 页
二维插值主要内容
引例1,引例2
二维插值的基本原理
上一页 下一页 主 页
返回
3.双线性插值
y
•
(x1•, y2)
•
(x2, y2)
•
•
• (x1•, y1) (x2•, y1) •
•
•
•
•
••
x
双线性插值是一片一片的空间二次曲面构成。 插值函数的形式如下:
f (x, y) (ax b)(cy d)
上一页 下一页 主 页
返回
用MATLAB作插值计算
z4
8
686
8
8
x 157.5 107.5 77 81 162 162 117.5
y -6.5 -81 3 56.5 -66.5 84 -33.5
z9
9
88
94
9
上一页 下一页 主 页
引例2:船在该海域会搁浅吗?
y
•
••
•
•
•
•
•
•
•
•
•
•
•
•
上一页 下一页 主 页
x
返回
插值的基本原理
二
第一种(网格节点)
上一页 下一页 主 页
用MATLAB作二维插值小结
2. 散点数据二维插值: 已有程序griddata ,e01sef 和e01sff
维 已知 mn个节点
插 (xi, xj, zij) ( i=1, 2, …,m; j=1, 2, …, n )
值 的
其中xi, yj互不相同,不妨设
提 a=x1<x2<…<xm=b
法 c=y1<y2<…<yn=d
求任一插值点(x*, y*) ( ≠(xi, yj) )处的插值Z*
上一页 下一页 主 页
end figure(5) meshc(px,py,pf),rotate3d
图2到4: 利用网格 节点的x,y坐标向量 px,py及其对应的z 坐标矩阵pf,作出网 格线图和填充曲面图, 水深5英尺处海底曲 面的等高线
上一页 下一页 主 页
150
100
50
0
-50 80
100
120
140
160
180
范例1:绘制山区地貌图
要在某山区方圆大约27平方公里范围内 修建一条公路,从山脚出发经过一个居民区, 再到达一个矿区。横向纵向分别每隔400米测 量一次,得到一些地点的高程:(平面区域 0<=x<=5600,0<=y<=4800),首先需作出该山 区的地貌图和等高线图。
上一页 下一页 主 页
范例1:绘制山区地貌图
500 0 0
2000
4000
4500 4000 3500 3000 2500 2000 1500 1000
500 0 0
2000
4000
上一页 下一页 主 页
Y Y
4200 4000 3800 3600 3400 3200 3000 2800 2600
1500
2000 X
2500
4200 4000 3800 3600 3400 3200 3000 2800 2600
x
注意:最邻近插值一般不连续。具有连续性的最简 单的插值是分片线性插值。
上一页 下一页 主 页
返回
2.分片线性插值
y
(xi, yj+1) (xi+1, yj+1)
•
•
•
••
•
(xi,•yj) (xi+1•, yj)
•
•
•
•
•
••
x
上一页 下一页 主 页
2.分片线性插值
四个插值点(矩形的四个顶点)处的函
-6.5 -81 3 56.5 -66.5 84 -33.5]; z=[-4 -8 -6 -8 -6 -8 -8 -9 -9 -8 -8 …
-9 -4 -9]; plot(x,y,'+'); pause
上一页 下一页 主 页
150
100
50
0
-50
-100 60
80
100
120
140
160
180
200
网格节点的插值计算; 散点数据的插值计算; 用MATLAB作插值计算小结
上一页 下一页 主 页
返回
网格节点数据的插值
例:测得平板表面3*5网格点处的温度
分别为:
x
82 81 80 82 84 • • • • •
79 63 61 65 81 • • • • •
84 84 82 85 86 • • • • •
di=1:.1:3;di=di'; wi=1:.1:5;
加密数据点
zlin=interp2(width,depth,temps,…
wi,di,'linear');
figure(2);
mesh(wi,di,zlin);
xlabel('Width of Plate'), ylabel('Depth of Plate') zlabel('Degrees Celsius'), axis('ij'),grid, pause; zlin=interp2(width,depth,temps,wi,di,…
注意:x0,y0为向量,但z0是矩阵,其 列数等于x0的长度,行数等于y0的长度。
上一页 下一页 主 页
width=1:5; depth=1:3;
M文件 wenduqm.m
temps=[82 81 80 82 84;79 63 61…
65 81;84 84 82 85 86];
mesh(width,depth,temps);pause
•
•
•
••
x
上一页 下一页 主 页
引例2:船在该海域会搁浅吗?
在某海域测得一些点(x,y)处的水深z由下表给 出,船的吃水深度为5英尺,在矩形区域(75,200) *(-50,150)里的哪些地方船要避免进入。
x 129 140 103.5 88 185.5 195 105
y 7.5 141.5 23 147 22.5 137.5 85.5
分别用最近邻点插值、线性插 值和三次插值加密数据点,并分别 作出这三组数据点的网格图。
注意观察双线性插值方法和双三 次插值方法的插值效果的差异。
上一页 下一页 主 页
上一页 下一页 主 页
上一页 下一页 主 页
上一页 下一页 主 页
4500 4000 3500 3000 2500 2000 1500 1000
'cubic'); figure(3); mesh(wi,di,zlin) xlabel('Width of Plate'), ylabel('Depth of Plate') zlabel('Degrees Celsius'), axis('ij'),grid
