圆周角与圆心角的关系练习题
鲁教版2020九年级数学圆周角与圆心角课后作业题3(附答案)

鲁教版2020九年级数学圆周角与圆心角课后作业题3(附答案)一.选择题(共10小题)1.如图,在半圆⊙O中,直径AB=4,点C、D是半圆上两点,且∠BOC=84°,∠BOD =36°,P为直径上一点,则PC+PD的最小值为()A.4B.2C.2D.22.如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,恰好经过点O,则与的关系是()A.=B.=C.=D.不能确定3.如图所示,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时处于弧AB上,则α取值范围是()A.36°≤α≤45°B.45°≤α≤54°C.54°≤α≤72°D.72°≤α≤90°4.如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为()A.4cm B.3cm C.5cm D.4cm5.如图,A、B、C在⊙O上,∠A=50°,则∠OBC的度数是()A.50°B.40°C.100°D.80°6.如图,AB是⊙O的直径,弦CD⊥AB于点E,连接OC、BD,若∠AOC=110°,则∠ABD的度数是()A.35°B.46°C.55°D.70°7.如图,在⊙O中,点C在优弧上,将弧沿BC折叠后刚好经过AB的中点D,连接AC,CD.则下列结论中错误的是()A.AC=CD B.+=C.OD⊥AB D.CD平分∠ACB 8.如图,四边形ABCD是⊙O内接四边形,若∠BAC=30°,∠CBD=80°,则∠BCD的度数为()A.50°B.60°C.70°D.80°9.如图,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是()A.120°B.80°C.100°D.60°10.如图,点A,B,C,D,E都是⊙O上的点,=,∠B=122°,则∠D=()A.58°B.116°C.122°D.128°二.填空题(共10小题)11.如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是.12.如图,已知点C,D是半圆上的三等分点,连接AC,BC,CD,OD,BC和OD相交于点E.则下列结论:①∠CBA=30°,②OD⊥BC,③OE=AC,④四边形AODC是菱形.正确的个数是.13.如图是两个半圆,点O为大半圆的圆心,AB平行于半圆的直径且是大半圆的弦且与小半圆相切,且AB=24,则图中阴影部分的面积是.14.已知⊙O的弦AB把圆分成两部分的比为1:5,若AB=3cm,则⊙O的半径等于cm.15.如图,五边形ABCDE内接于⊙O,BC=CD=DE,若∠B=98°,∠E=116°,则∠A =°.16.如图,AB为⊙O的直径,C为⊙O上一点,∠BOC=50°,AD∥OC,AD交⊙O于点D,连接AC,CD,那么∠ACD=.17.如图,四边形ABCD内接于⊙O,∠BOD=120°,则∠DCE=.18.如图,在圆内接四边形ABCD中,∠B=100°,则∠D的度数为.19.如图,四边形ABCD内接于⊙O,BC是⊙O的直径,AD∥BC,AC与BD相交于点P,若∠APB=50°,则∠PBC=.20.如图,点A,B,C,D都在⊙O上,C是的中点,AB=CD.若∠ODC=50°,则∠ABC的度数为°.三.解答题(共8小题)21.如图,弦AB和弦CD相交于⊙O内一点E,AD=CB,求证:AB=CD.22.如图,在⊙O中,=,∠A=40°,求∠D的度数.23.如图,在⊙O中,=(1)若∠C=75°,求∠A的度数;(2)若AB=13,BC=10,求⊙O的半径.24.如图,⊙O的弦AB、CD的延长线相交于点P,且AB=CD.求证:P A=PC.25.如图1,AB、EF是⊙O的直径,点C、F在AB上,且F是的中点,弦BC与FE交于点D,连接AC、BC、FC、FB、AE.(1)求证:AC∥EF;(2)如图2,过点C作FB的平行线,交EF于点N,M为线段CF的中点,连接MD并延长MD交AB于点H,连接FH.若EN=2,AB=6,求FH的长.26.如图,AB为圆O的直径,CD⊥AB于点E,交圆O于点D,OF⊥AC于点F (1)请写出三条与BC有关的正确结论;(2)当∠D=30°,CD=2时,求圆中阴影部分的周长.27.已知:四边形ABCD是⊙O的内接四边形.求证:∠ABC+∠ADC=180°.(用两种方法)28.如图,A、P、B、C是⊙O上四点,∠APC=∠CPB=60°.(1)求证:△ABC是等边三角形;(2)连接OA,OB,当点P位于什么位置时,四边形PBOA是菱形?并说明理由;(3)已知P A=a,PB=b,求PC的长(用含a和b的式子表示).参考答案与试题解析一.选择题(共10小题)1.如图,在半圆⊙O中,直径AB=4,点C、D是半圆上两点,且∠BOC=84°,∠BOD =36°,P为直径上一点,则PC+PD的最小值为()A.4B.2C.2D.2【解答】解:作点D关于AB的对称点DE,连接CE,交AB于点P,过点O作OF⊥CE,垂足为F,∵∠BOC=84°,∠BOD=36°,∴∠BOE=36°,∠COE=120°,∴∠C=30°,∵AB=4,∴OC=2,∴OF=1,CF=,∴CE=2,∴PC+PD的最小值为2,故选:B.2.如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,恰好经过点O,则与的关系是()A.=B.=C.=D.不能确定【解答】解:连接OC,BC,过O作OE⊥AC于D交圆O于E,∵把半圆沿弦AC折叠,恰好经过点O,∴OD=OE,∵AB是半圆O的直径,∴∠ACB=90°,∴OD∥BC,∵OA=OB,∴OD=BC,∴BC=OE=OB=OC,∴∠COB=60°,∴∠AOC=120°,∴=,故选:A.3.如图所示,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时处于弧AB上,则α取值范围是()A.36°≤α≤45°B.45°≤α≤54°C.54°≤α≤72°D.72°≤α≤90°【解答】解:∵在△AOB中,OA=OB,∠OAB=α∴∠OBA=α,∠AOB=180°﹣2α∴当α=36°时,∠AOB=180°﹣2×36°=108°108×5=540°∵转360°恰好位于点A,540°﹣360°=180°>108°∴此时不位于弧AB上,A错误;当α=60°时,∠AOB=60°,60×5=300°∴此时小华还没到达点A,故C错误;当α=60°时,∠AOB=60°,60×5=300°当α=90°时,点B在圆外,不符合题意,故D错误;故选:B.4.如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为()A.4cm B.3cm C.5cm D.4cm【解答】解:连接OD,OC,作DE⊥AB于E,OF⊥AC于F,∵∠CAD=∠BAD,∴=,∴∠DOB=∠OAC=2∠BAD,在△AOF和△ODE中,,∴△AOF≌△ODE,∴OE=AF=AC=3,在Rt△DOE中,DE==4,在Rt△ADE中,AD==4,故选:A.5.如图,A、B、C在⊙O上,∠A=50°,则∠OBC的度数是()A.50°B.40°C.100°D.80°【解答】解:∵∠BAC=50°,∴∠BOC=100°,∵BO=CO,∴∠OBC=(180°﹣100°)÷2=40°,故选:B.6.如图,AB是⊙O的直径,弦CD⊥AB于点E,连接OC、BD,若∠AOC=110°,则∠ABD的度数是()A.35°B.46°C.55°D.70°【解答】解:连接BC,∵∠AOC=110°,∴∠ABC=∠AOC═55°,∵CD⊥AB,∴=,∴∠ABD=∠ABC=55°,故选:C.7.如图,在⊙O中,点C在优弧上,将弧沿BC折叠后刚好经过AB的中点D,连接AC,CD.则下列结论中错误的是()A.AC=CD B.+=C.OD⊥AB D.CD平分∠ACB 【解答】解:A、过D作DD'⊥BC,交⊙O于D',连接CD'、BD',由折叠得:CD=CD',∠ABC=∠CBD',∴AC=CD'=CD,故①正确;B、∵AC=CD',∴,由折叠得:,∴=,故②正确;C、∵D为AB的中点,∴OD⊥AB,故③正确;D、延长OD交⊙O于E,连接CE,∵OD⊥AB,∴∠ACE=∠BCE,∴CD不平分∠ACB,故④错误;故选:D.8.如图,四边形ABCD是⊙O内接四边形,若∠BAC=30°,∠CBD=80°,则∠BCD的度数为()A.50°B.60°C.70°D.80°【解答】解:由圆周角定理得,∠CAD=∠CBD=80°,∴∠BAD=80°+30°=110°,∵四边形ABCD是⊙O内接四边形,∴∠BCD=180°﹣∠BAD=70°,故选:C.9.如图,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是()A.120°B.80°C.100°D.60°【解答】解:∵四边形ABCD为⊙O的内接四边形,∴∠A=180°﹣∠BCD=60°,由圆周角定理得,∠BOD=2∠A=120°,故选:A.10.如图,点A,B,C,D,E都是⊙O上的点,=,∠B=122°,则∠D=()A.58°B.116°C.122°D.128°【解答】解:连接AC、CE,∵点A、B、C、E都是⊙O上的点,∴∠AEC=180°﹣∠B=58°,∵=,∴∠ACE=∠AEC=58°,∴∠CAE=180°﹣58°﹣58°=64°,∵点A、C、D、E都是⊙O上的点,∴∠D=180°﹣64°=116°,故选:B.二.填空题(共10小题)11.如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是51°.【解答】解:如图,∵==,∠COD=34°,∴∠BOC=∠EOD=∠COD=34°,∴∠AOE=180°﹣∠EOD﹣∠COD﹣∠BOC=78°.又∵OA=OE,∴∠AEO=∠OAE,∴∠AEO=×(180°﹣78°)=51°.故答案为:51°.12.如图,已知点C,D是半圆上的三等分点,连接AC,BC,CD,OD,BC和OD相交于点E.则下列结论:①∠CBA=30°,②OD⊥BC,③OE=AC,④四边形AODC是菱形.正确的个数是①②③④.【解答】:如图,连接CD、AD、CO,,∵点C,D是半圆上的三等分点,∴∠AOC=∠COD=∠BOD=180°÷3=60°,∴∠CBA=∠AOC÷2=60°÷2=30°,即①正确;∵∠BEO=180°﹣∠BOD﹣∠CBA=180°﹣60°﹣30°=90°∴OD⊥BC,即②正确.∵OB=OC,OD⊥BC,∴E是BC的中点,又∵O是AB的中点,∴OE是△ABC的中位线,∴OE=AC,即③正确.∵AC⊥BC,OD⊥BC,∴AC∥OD,∵∠DCB=∠BOD÷2=60°÷2=30°,∠CBA=30°∴∠DCB=∠CBA,∴CD∥AB,∴四边形AODC是平行四边形,∵∠AOC=60°,OA=OC,∴△AOC是等边三角形,∴AO=AC,又∵四边形AODC是平行四边形,∴AO=OD=DC=CA,∴四边形AODC是菱形,即④正确.综上,可得正确的结论有:①②③④.故答案为①②③④.13.如图是两个半圆,点O为大半圆的圆心,AB平行于半圆的直径且是大半圆的弦且与小半圆相切,且AB=24,则图中阴影部分的面积是72π.【解答】解:将小圆向右平移,使两圆变成同心圆,如图,连OB,过O作OC⊥AB于C点,则AC=BC=12,∵AB是大半圆的弦且与小半圆相切,∴OC为小圆的半径,∴S阴影部分=S大半圆﹣S小半圆=π•OB2﹣π•OC2=π(OB2﹣OC2)=πBC2=72π.故答案为72π.14.已知⊙O的弦AB把圆分成两部分的比为1:5,若AB=3cm,则⊙O的半径等于3cm.【解答】解:∵弦AB将圆分成的两段弧所对的圆心角度数之比为1:5,∴∠AOB=×360°=60°,∵OA=OB,∴△AOB为等边三角形,∵⊙O的半径为3cm,∴AB=3cm.故答案为:3.15.如图,五边形ABCDE内接于⊙O,BC=CD=DE,若∠B=98°,∠E=116°,则∠A =102°.【解答】解:连接AC,AD,∵BC=CD=DE,∴==,∴设∠BAC=∠CAD=∠DAE=α,∵∠B=98°,∠E=116°,∴∠B+∠E﹣α=98°+116°﹣α=180°,∴α=34°,∴∠BAE=3α=102°,故答案为:102°.16.如图,AB为⊙O的直径,C为⊙O上一点,∠BOC=50°,AD∥OC,AD交⊙O于点D,连接AC,CD,那么∠ACD=40°.【解答】解:连接OD,∵AD∥OC,∴∠DAB=∠BOC=50°,∵OA=OD∴∠AOD=180°﹣2∠DAB=80°,∴∠ACD=∠AOD=40°故答案为40°17.如图,四边形ABCD内接于⊙O,∠BOD=120°,则∠DCE=120°.【解答】解:∵∠BOD=120°,∴∠BCD==60°.∴∠DCE=180°﹣60°=120°.故答案为:120°.18.如图,在圆内接四边形ABCD中,∠B=100°,则∠D的度数为80°.【解答】解:∵四边形ABCD是圆内接四边形,∴∠B+∠D=180°,∵∠B=100°,∴∠D=80°,故答案为80°.19.如图,四边形ABCD内接于⊙O,BC是⊙O的直径,AD∥BC,AC与BD相交于点P,若∠APB=50°,则∠PBC=25°.【解答】解:∵AD∥BC,∴=,∴∠PBC=∠PCB,∵∠APB=50°,∴∠PBC=25°,故答案为:25°.20.如图,点A,B,C,D都在⊙O上,C是的中点,AB=CD.若∠ODC=50°,则∠ABC的度数为100°.【解答】解:∵C是的中点,AB=CD.∴==,∵∠ODC=50°,∴∠A=∠ACB=∠COD=×(180°﹣2∠ODC)=×(180°﹣50°×2)=40°,∴∠ABC=180°﹣∠A﹣∠ACB=180°﹣40°×2=100°.故答案为:100.三.解答题(共8小题)21.如图,弦AB和弦CD相交于⊙O内一点E,AD=CB,求证:AB=CD.【解答】证明:∵AD=BC,∴=,∴=,∴CD=AB.22.如图,在⊙O中,=,∠A=40°,求∠D的度数.【解答】解:∵∠A=40°,∴劣弧BC的度数为80°,则优弧BC的度数为:360°﹣80°=280°,∴∠D=140°.23.如图,在⊙O中,=(1)若∠C=75°,求∠A的度数;(2)若AB=13,BC=10,求⊙O的半径.【解答】解:(1)∵在⊙O中,=,∴AB=AC.∴∠B=∠C=75°.∴∠A=180°﹣2×75°=30°;(2)如图,延长AO交BC于D,则AD⊥BC,BD=CD=BC=5,∴在直角△ABD中,由勾股定理,得AD===12.在直角△OBD中,由勾股定理,得OB2=(12﹣OB)2+52,解得OB=,即⊙O的半径是.24.如图,⊙O的弦AB、CD的延长线相交于点P,且AB=CD.求证:P A=PC.【解答】证明:连接AC,∵AB=CD,∴=,∴+=+,即=,∴∠C=∠A,∴P A=PC.25.如图1,AB、EF是⊙O的直径,点C、F在AB上,且F是的中点,弦BC与FE交于点D,连接AC、BC、FC、FB、AE.(1)求证:AC∥EF;(2)如图2,过点C作FB的平行线,交EF于点N,M为线段CF的中点,连接MD并延长MD交AB于点H,连接FH.若EN=2,AB=6,求FH的长.【解答】(1)证明:∵点F是的中点,∴∠BAC=∠BOC=∠BOF,∴AC∥EF;(2)解:如图2,∵CN∥FB,OA=OE=OB=OF,∴∠CNF=∠OFB=∠OBF=∠E,∴AE∥FB,∴CN∥AE,∵AC∥EF,∴四边形AENC是▱AENC,∴AC=EN=2,∵OC=OB,∠COF=∠BOF,∴DC=DB,OD⊥BC于点D,∵OD是△ABC的中位线,∴OD=AC=1,∵OB=3,∴BD=2,又∵MD是△BCE的中位线,∴MH∥FB,∴∠ODH=∠OFB=∠OBF=∠DHO,∴OD=OH,又∠DOH为公共角,∴△FOH≌△BOD,∴FH=BD=2.26.如图,AB为圆O的直径,CD⊥AB于点E,交圆O于点D,OF⊥AC于点F (1)请写出三条与BC有关的正确结论;(2)当∠D=30°,CD=2时,求圆中阴影部分的周长.【解答】解:(1)答案不唯一,只要合理均可.例如:①BC=BD;②OF∥BC;③∠BCD=∠A;④△BCE∽△OAF;⑤BC2=BE•AB;⑥BC2=CE2+BE2;⑦△ABC是直角三角形;⑧△BCD是等腰三角形.(2)∵CD=2,∴CE=,∵∠D=∠A=30°,∴AC=2,AB=4,∴==π,∴周长为:+227.已知:四边形ABCD是⊙O的内接四边形.求证:∠ABC+∠ADC=180°.(用两种方法)【解答】证法1:连接OA,OC,∵∠B=∠1,∠D=∠2,∴∠B+∠D=(∠1+∠2)=×360°=180°;证法2:如图2,连接CA,BD,∵∠1=∠2,∠3=∠4,∴∠ADC=∠1+∠3=∠2+∠4,∴∠ADC+∠ABC=∠2+∠4+∠ABC=180°.28.如图,A、P、B、C是⊙O上四点,∠APC=∠CPB=60°.(1)求证:△ABC是等边三角形;(2)连接OA,OB,当点P位于什么位置时,四边形PBOA是菱形?并说明理由;(3)已知P A=a,PB=b,求PC的长(用含a和b的式子表示).【解答】(1)证明:∵∠BAC=∠CPB=60°,∴∠ABC=∠APC=60°,∴∠ABC=∠BAC=∠ACB=60°,∴△ABC为等边三角形;(2)解:当点P位于的中点时,四边形PBOA是菱形.理由如下:连接OP,如图1,∵∠AOB=2∠ACB=120°,而P是的中点,∴∠AOP=∠BOP=60°,又∵OA=OP=OB,∴△OAP和△OBP都为等边三角形,∴OA=AP=OB=PB,∴四边形PBOA是菱形;(3)解:如图2,在PC上截取PD=P A,又∵∠APC=60°,∴△APD是等边三角形,∴P A=DA,∠DAP=60°,∵∠P AB+∠BAD=∠BAD+∠DAC,∴∠P AB=∠DAC,在△APB和△ADC中,∴△APB≌△ADC(ASA),∴PB=DC,又∵P A=PD,∴PC=PD+DC=P A+PB=a+b.。
中考数学复习指导:巧妙运用圆周角和圆心角的关系

巧妙运用圆周角和圆心角的关系圆周角和圆心角是圆中两类极其重要的角,它们之间有下列关系:一条弧所对的圆周角等于它所对的圆心角的一半.巧妙运用上述关系,可以解决与圆中的角有关的许多问题.一、由圆心角求圆周角例1 如图1,量角器外缘边上有A,P,Q 三点,它们所表示的读数分别是 180, 70,30,则∠PAQ 的大小为( )A.10°B.20°C.30°D.40° 解析:量角器上的读数就是相应圆心角的度数.为此设量角器的中心(即半圆的圆心)为O,连接OP,OQ,则圆心角∠POQ= 70- 30= 40.∴∠PAQ =21∠POQ= 20.故选B.. 温馨提示:本题求得圆心角的度数后,直接运用圆周角和圆心角的关系定理即可求解.二、由圆周角求圆心角例 2 如图2,⊙O 中OA BC ⊥,25CDA ∠=,则AOB ∠的度数为 . 解析:连接OC.∵OA BC ⊥,∴C A B A =,∴AOB ∠=∠AOC.∵25CDA ∠= ,∴∠AOC=2∠CDA=50°.∴ AOB ∠=50°.故填50°. 温馨提示:本题运用了圆周角和圆心角关系的另一种表述方式: 一条弧所对的圆心角等于它所对的圆周角的2倍.三、由圆周角求圆周角例3 如图3,AB 是⊙O 的直径,CD 是⊙O 的弦,连接AC AD ,,若35CAB ∠= ,则ADC ∠的度数为 .解析:连接BC.∵AB 是⊙O 的直径,∴∠ACB=90°,∴∠ABC= 90°-∠CAB=90°-35°=55°.因为ADC ∠和∠ABC 是C A所对的两个圆图2D 图3周角.∴ADC =∠ABC =55°. 故填55°.温馨提示:本题运用了圆周角和圆心角关系定理的推论:同弧所对的圆周角相等.当然,本题也可连接OC ,运用圆周角和圆心角关系定理求解,请同学们自己试一试.四、 解决实际问题例4 如图4,有一圆形展厅,在其圆形边缘上的点A 处安装了一台监视器,它的监控角度是65 .为了监控整个展厅,最少需在圆形边缘上共安装...这样的监视器 台. 解析:监控整个展厅,就是要监控的范围能覆盖整个圆,而360°的圆心角恰好能覆盖整个圆.∵∠A=65°,∴与∠A 所对同一条弧的圆心角度数为65°×2=130°.而130°×2<360°, 130°×3>360°,∴最少需要安装3台监控器才能监控整个展厅. 温馨提示:本题运用圆周角和圆心角的关系巧妙转化,让看似困难的问题简洁求解.图4。
初中数学 圆周角和圆心角的关系同步练习及答案

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分(每空xx 分,共xx分)试题1:在同圆中,同弦所对的圆周角 ( )A.相等 B.互补 C.相等或互补 D.互余试题2:如图3-63所示,A,B,C,D在同一个圆上,四边形ABCD的两条对角线把四个内角分成的8个角中,相等的角共有 ( )A.2对 B.3对 C.4对D.5对试题3:如图3-64所示,⊙O的半径为5,弦AB=,C是圆上一点,则∠ACB的度数是.试题4:如图,四边形 ABCD内接于⊙O,若∠BOD=100°,则∠DAB的度数为()A.50° B.80° C.100° D.130°试题5:如图是中国共产主义青年团团旗上的图案,点A、B、C、D、E五等分圆,则∠A+∠B+∠C+∠D+∠E的度数是() A.180° B.15 0° C.135° D.120°试题6:下列命题中,正确的命题个数是()①顶点在圆周上的角是圆周角;②圆周角度数等于圆心角度数的一半;③900的圆周角所对的弦是直径;④圆周角相等,则它们所对的弧也相等。
A、1个B、2个C、3个D、4个试题7:如图3-65所示,在⊙O中,∠AOB=100°,C为优弧ACB的中点,则∠CAB=.试题8:如图3-66所示,AB为⊙O的直径,AB=6,∠CAD=30°,则弦DC=.试题9:如图3-67所示,AB是⊙O的直径,∠BOC=120°,CD⊥AB,求∠ABD的度数.试题10:如图,已知AB是⊙O的直径,AD ∥ OC弧AD的度数为80°,则∠BOC=_________ 试题11:如图,⊙O内接四边形ABCD中,AB=CD则图中和∠1相等的角有______。
圆周角和圆心角的关系
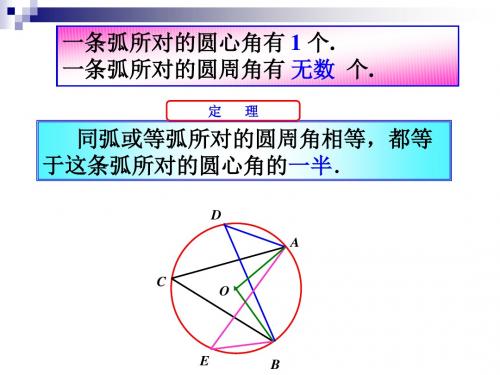
定 理
同弧或等弧所对的圆周角相等,都等 于这条弧所对的圆心角的一半.
D A C
O
·
B
E
1、说出图中相等的圆周角。
2、如图,已知△ABC内接⊙O,∠A=30°, BC=2.8cm,求⊙O直径长。
3、如图,AB为⊙O直径,∠ACB为多少度?
D A C O
·
B
E
【1】如图:求∠A +∠ B+∠ C+∠D+ ∠E=
.
【2】如图,P是△ABC的外接圆上的一点 ∠APC=∠CPB=60°。 求证:△ABC是等边三角形
【3】如图,∠A是⊙O的圆周角。 若∠B=250,∠C=200,求∠BOC的度数。
A O
B
C
定理
推 论
半圆(或直径)所对的圆周角是直角; 90°的圆周角所对的弦是直径.
C2 C1 C3
A
·
O
B
【4】如图,OA是⊙O的半径,以OA为直径的⊙C
与⊙O 的弦AB 相交于点D.
求证:D 是AB的中点.
【5】如图,AD是△ABC 的高,AE 是△ABC 的外接圆直径,求证:∠BAE=∠DAC.
定理
推 论
直径所对的圆周角是直角; 90°的圆周角所对的弦是直径.
C2 C1 C3
A
·
O
B
【例1】如图,AB为⊙O直径,BD是⊙O的弦, 延长BD到C,使AC=AB。BD与CD的大小有什么 关系?为什么?
4、如图,∠ BCD=100°,则∠BOD=___, ∠BAD=___,
四边形ABCD叫圆内接四边形。
BC AB AC 10 6 8
圆周角和圆心角的关系中考题目完整版

圆周角和圆心角的关系中考题目Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】圆周角和圆心角的关系-----中考链接能力提升题一.选择题(共12小题)1.(2013?自贡)如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、C两点,已知B(8,0),C(0,6),则⊙A的半径为()A. 3 B.4 C.5 D.82.(2013珠海)如图,ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为()A.36°B.46°C.27°D.63°3.(2013?湛江)如图,AB是⊙O的直径,∠AOC=110°,则∠D=()A.25°B.35°C.55°D.70°4.(2013?宜昌)如图,DC 是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是()A.B.AF=BF C.OF=CF D.∠DBC=90°5.(2013?绥化)如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,则AE的长为()A. 4 B.5 C.6 D.76.(2013?苏州)如图,AB是半圆的直径,点D是的中点,∠ABC=50°,则∠DAB等于()A.55°B.60°C.65°D.70°7.(2013?日照)如图,在△ABC中,以BC为直径的圆分别交边AC、AB于D、E两点,连接BD、DE.若BD平分∠ABC,则下列结论不一定成立的是()A.BD⊥AC B.AC2=2AB?AEC.△ADE是等腰三角形D.BC=2AD8.(2013?南宁)如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=∠BOD,则⊙O的半径为()A. 4B.5 C.4 D.39.(2013?济南)如图,AB是⊙O的直径,C是⊙O上一点,AB=10,AC=6,OD⊥BC,垂足是D,则BD的长为()A. 2 B.3 C.4 D.610.(2013?临沂)如图,在⊙O中,∠CBO=45°,∠CAO=15°,则∠AOB的度数是()A.75°B.60°C.45°D.30°11.(2013?红河州)如图,AB是⊙O的直径,点C在⊙O上,弦BD平分∠ABC,则下列结论错误的是()A. AD=DC B.C.∠ADB=∠ACB D.∠DAB=∠CBA12.(2013?黑龙江)如图,△ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O的直径,AD=6,那么AB的值为()A. 3 B.2C.3D.2二.填空题(共6小题)13.(2013?淄博)如图,AB是⊙O的直径,,AB=5,BD=4,则sin∠ECB=_________ .14.(2013?黔西南州)如图所示⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为_________ .15.(2013?盘锦)如图,⊙O直径AB=8,∠CBD=30°,则CD= _________ .16.(2013?常州)如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC= _________ .17.(2012?徐州)如图,已知AB是⊙O的直径,CD是弦,且CD⊥AB,AC=8,BC=6.则sin∠ABD=_________ .18.(2012?泰安)如图,在半径为5的⊙O中,弦AB=6,点C是优弧上一点(不与A,B重合),则cosC的值为_________ .三.解答题(共4小题)19.(2013?武汉)如图,已知△ABC是⊙O的内接三角形,AB=AC,点P是的中点,连接PA,PB,PC.(1)如图①,若∠BPC=60°.求证:AC=AP;(2)如图②,若sin∠BPC=,求tan∠PAB的值.20.(2013?温州)如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.(1)求证:∠B=∠D;(2)若AB=4,BC﹣AC=2,求CE的长.21.(2013?哈尔滨)如图,在△ABC中,以BC为直径作半圆O,交AB于点D,交AC于点E,AD=AE.(1)求证:AB=AC(2)若BD=4,BO=2,求AD的长.22.(2012?大庆)如图△ABC中,BC=3,以BC为直径的⊙O交AC于点D,若D是AC中点,∠ABC=120°.(1)求∠ACB的大小;(2)求点A到直线BC的距离.参考答案一.选择题(共12小题)1. C2. A.3. B.4. C.5. B.6. C.7. D.8. B.9. C.10. B.11. D.12. A.二.填空题(共6小题)13..14.50°.15. 4.16. 2.17..18..三.解答题(共4小题)19.解:(1)∵∠BPC=60°,∴∠BAC=60°,∵AB=AC,∴△ABC为等边三角形,∴∠ACB=∠ABC=60°,∴∠APC=∠ABC=60°,而点P是的中点,∴∠ACP=∠ACB=30°,∴∠PAC=90°,∴tan∠PCA==tan30°=,∴AC=PA;(2)过A点作AD⊥BC交BC于D,连结OP交AB于E,如图,∵AB=AC,∴AD平分BC,∴点O在AD上,连结OB,则∠BOD=∠BAC,∵∠BPC=∠BAC,∴sin∠BOD=sin∠BPC==,设OB=25x,则BD=24x,∴OD==7x,在Rt△ABD中,AD=25x+7x=32x,BD=24x,∴AB==40x,∵点P是的中点,∴OP 垂直平分AB,∴AE=AB=20x,∠AEP=∠AEO=90°,在Rt△AEO中,OE==15x,∴PE=OP﹣OE=25x﹣15x=10x,在Rt△APE中,tan∠PAE===,即tan∠PAB的值为.20.(1)证明:∵AB为⊙O的直径,∴∠ACB=90°,∴AC⊥BC,又∵DC=CB,∴AD=AB,∴∠B=∠D;(2)解:设BC=x,则AC=x﹣2,在Rt△ABC中,AC2+BC2=AB2,∴(x﹣2)2+x2=42,解得:x1=1+,x2=1﹣(舍去),∵∠B=∠E,∠B=∠D,∴∠D=∠E,∴CD=CE,∵CD=CB,∴CE=CB=1+.21.解:(1)连接BE,CD,∵BC是半圆O的直径,∴∠BDC=∠BEC=90°,∴∠ADC=∠AEB=90°,在Rt△ABE和Rt△ACD中,∵,∴△ABE≌△ACD,∴AB=AC.(2)∵BO=2,∴BC=4,在Rt△BDC中,CD==8,设AD=x,则AC=AB=x+4,在Rt△ADC中,82+x2=(x+4)2,解得:x=6.即AD=6.22.解:(1)连接BD,∵以BC为直径的⊙O交AC于点D,∴∠BDC=90°,∵D是AC中点,∴BD是AC的垂直平分线,∴AB=BC,∴∠A=∠C,∵∠ABC=120°,∴∠A=∠C=30°,即∠ACB=30°;(2)过点A作AE⊥BC于点E,∵BC=3,∠ACB=30°,∠BDC=90°,∴cos30°==,∴CD=,∵AD=CD,∴AC=3,∵在Rt△AEC中,∠ACE=30°,∴AE=×3=.。
圆周角和圆心角的关系(中考题目)

圆周角和圆心角的关系之青柳念文创作-----中考链接才能提升题一.选择题(共12小题)1.(2013•自贡)如图,在平面直角坐标系中,⊙A颠末原点O,而且分别与x轴、y轴交于B、C两点,已知B(8,0),C(0,6),则⊙A的半径为()A. 3 B. 4 C.5 D.82.(2013•珠海)如图,▱ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,毗连AE,则∠AEB 的度数为()A.36°B.46°C.27°D.63°3.(2013•湛江)如图,AB是⊙O的直径,∠AOC=110°,则∠D=()A.25°B.35°C.55°D.70°4.(2013•宜昌)如图,DC 是⊙O直径,弦AB⊥CD于F,毗连BC,DB,则下列结论错误的是()A.B.AF=BF C.O F=CF D.∠DBC=90°5.(2013•绥化)如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,则AE的长为()A. 4 B. 5 C.6 D.76.(2013•苏州)如图,AB是半圆的直径,点D是的中点,∠ABC=50°,则∠DAB等于()A.55°B.60°C.65°D.70°7.(2013•日照)如图,在△ABC中,以BC为直径的圆分别交边AC、AB于D、E两点,毗连BD、DE.若BD平分∠ABC,则下列结论纷歧定成立的是()A.BD⊥AC B. AC2=2AB•AEC.△ADE是等腰三角形D. BC=2AD 8.(2013•南宁)如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=∠BOD,则⊙O的半径为()A. 4B. 5 C.4 D.39.(2013•济南)如图,AB是⊙O的直径,C是⊙O上一点,AB=10,AC=6,OD⊥BC,垂足是D,则BD的长为()A. 2 B. 3 C.4 D.610.(2013•临沂)如图,在⊙O中,∠CBO=45°,∠CAO=15°,则∠AOB的度数是()A.75°B.60°C.45°D.30°11.(2013•红河州)如图,AB是⊙O的直径,点C在⊙O上,弦BD平分∠ABC,则下列结论错误的是()A. AD=DC B.C.∠ADB=∠ACB D.∠DAB=∠CBA 12.(2013•黑龙江)如图,△ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O的直径,AD=6,那末AB的值为()A. 3 B.2C.3D.2二.填空题(共6小题)13.(2013•淄博)如图,AB是⊙O的直径,,AB=5,BD=4,则sin∠ECB=_________ .14.(2013•黔西南州)如图所示⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为_________ .15.(2013•盘锦)如图,⊙O直径AB=8,∠CBD=30°,则CD= _________ .16.(2013•常州)如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC= _________ .17.(2012•徐州)如图,已知AB是⊙O的直径,CD是弦,且CD⊥AB,AC=8,BC=6.则sin∠ABD=_________ .18.(2012•泰安)如图,在半径为5的⊙O中,弦AB=6,点C是优弧上一点(不与A,B重合),则cosC的值为_________ .三.解答题(共4小题)19.(2013•武汉)如图,已知△ABC是⊙O的内接三角形,AB=AC,点P是的中点,毗连PA,PB,PC.(1)如图①,若∠BPC=60°.求证:AC=AP;(2)如图②,若sin∠BPC=,求tan∠PAB的值.20.(2013•温州)如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另外一个交点为E,毗连AC,CE.(1)求证:∠B=∠D;(2)若AB=4,BC﹣AC=2,求CE的长.21.(2013•哈尔滨)如图,在△ABC中,以BC为直径作半圆O,交AB于点D,交AC于点E,AD=AE.(1)求证:AB=AC(2)若BD=4,BO=2,求AD的长.22.(2012•大庆)如图△ABC中,BC=3,以BC为直径的⊙O 交AC于点D,若D是AC中点,∠ABC=120°.(1)求∠ACB的大小;(2)求点A到直线BC的间隔.参考答案一.选择题(共12小题)1. C2. A.3. B.4. C.5. B.6. C.7. D.8.B.9. C.10. B.11. D.12. A.二.填空题(共6小题)13..14.50°.15. 4.16. 2.17..18..三.解答题(共4小题)19.解:(1)∵∠BPC=60°,∴∠BAC=60°,∵AB=AC,∴△ABC为等边三角形,∴∠ACB=∠ABC=60°,∴∠APC=∠ABC=60°,而点P是的中点,∴∠ACP=∠ACB=30°,∴∠PAC=90°,∴tan∠PCA==tan30°=,∴AC=PA;(2)过A点作AD⊥BC交BC于D,保持OP交AB于E,如图,∵AB=AC,∴AD平分BC,∴点O在AD上,保持OB,则∠BOD=∠BAC,∵∠BPC=∠BAC,∴sin∠BOD=sin∠BPC==,设OB=25x,则BD=24x,∴OD==7x,在Rt△ABD中,AD=25x+7x=32x,BD=24x,∴AB==40x,∵点P是的中点,∴OP垂直平分AB,∴AE=AB=20x,∠AEP=∠AEO=90°,在Rt△AEO中,OE==15x,∴PE=OP﹣OE=25x﹣15x=10x,在Rt△APE中,tan∠PAE===,即tan∠PAB 的值为.20.(1)证明:∵AB为⊙O的直径,∴∠ACB=90°,∴AC⊥BC,又∵DC=CB,∴AD=AB,∴∠B=∠D;(2)解:设BC=x,则AC=x﹣2,在Rt△ABC中,AC2+BC2=AB2,∴(x﹣2)2+x2=42,解得:x1=1+,x2=1﹣(舍去),∵∠B=∠E,∠B=∠D,∴∠D=∠E,∴CD=CE,∵CD=CB,∴CE=CB=1+.21.解:(1)毗连BE,CD,∵BC是半圆O的直径,∴∠BDC=∠BEC=90°,∴∠ADC=∠AEB=90°,在Rt△ABE和Rt△ACD中,∵,∴△ABE≌△ACD,∴AB=AC.(2)∵BO=2,∴BC=4,在Rt△BDC中,CD==8,设AD=x,则AC=AB=x+4,在Rt△ADC中,82+x2=(x+4)2,解得:x=6.即AD=6.22.解:(1)毗连BD,∵以BC为直径的⊙O交AC于点D,∴∠BDC=90°,∵D是AC中点,∴BD是AC的垂直平分线,∴AB=BC,∴∠A=∠C,∵∠ABC=120°,∴∠A=∠C=30°,即∠ACB=30°;(2)过点A作AE⊥BC于点E,∵BC=3,∠ACB=30°,∠BDC=90°,∴cos30°==,∴CD=,∵AD=CD,∴AC=3,∵在Rt△AEC中,∠ACE=30°,∴AE=×3=.。
3.3 圆周角和圆心角的关系(2)圆周角定理

图1
图2
图3
自学与思考
1、圆周角定理的推论1、2、3的内容分别是什么? 你是怎样理解这些推论的? 2、从课本例2的学习中你认为证明等积式的一般思 路是怎样的? 3、例2是否还有其它证明方法?
例题精解
例:如图,AD是△ABC的高,AE是△ABC的外接圆直 径。求证:AB · = AE · AC AD A 分析:要证AB · = AE · AC AD
AC AD AE AB
△ADC∽ △ABE
或△ACE∽ △ADB
O B E D C
题后思:1、证明题的思路寻找方法;
2、等积式的证明方法;
小结与作业
1、本节课我们学习了哪些知识? 2、圆周角定理及其推论的用途你都知道了吗? 3、证明题思路的寻找方法如何? 4、证明等积式的一般思路你掌握了吗?
问题解答
1、圆周角定理的推论1: 同弧或等弧所对的圆周角相等;
用于找相 等的弧
同圆或等圆中,相等的圆周角所对的弧也相等。
2、圆周角定理的推论2: 半圆(或直径)所对的圆周角是直角; 用于找相等的 90°的圆周角所对的弦是直径。 角 3、圆周角定理的推论3: 如果三角形一边上的中线等于这边的一半,那么这 用于判断某 用于判断某个 条线是否过 圆周角是否是 个三角形是直角三角形。 圆心 直角 它的逆命题 也成立
九年级数学(下)第三章 圆
3. 圆周角和圆心角的关系 (2)圆周角定理
课前测验
11、一条弧所对的圆心角等于_______,所对的圆周角等于
100º _______。2、一弦分圆成两部分,其中一部分是另一部分的4
圆周角准则练习题A

圆周角准则练习题A
题目1:
已知:圆弧AB的弦长为12厘米,弦CD的弦长为8厘米,直径AC测得为10厘米。
问题:求圆心角AOB和圆心角COD的大小。
解答:
由圆周角准则可知,圆周角等于所对的圆弧所对应的弦长的一半除以半径的比值。
即:
圆周角 = (弦长 / 半径) × 180度/π
对于圆心角AOB,已知弦长为12厘米,直径为10厘米,可以求得半径为5厘米,所以:
圆心角AOB = (12 / 5) × 180度/π ≈ 138.08度
对于圆心角COD,已知弦长为8厘米,直径为10厘米,可以求得半径为5厘米,所以:
圆心角COD = (8 / 5) × 180度/π ≈ 92.05度
因此,圆心角AOB的大小约为138.08度,圆心角COD的大小约为92.05度。
题目2:
已知:圆的半径为6厘米,圆心角为60度。
问题:求对应的圆弧长度和弦长。
解答:
对于圆弧长度,根据圆周角准则,有:
圆弧长度 = 圆周角 ×半径× π / 180度
已知圆周角为60度,半径为6厘米,可以求得圆弧长度为:圆弧长度 = 60 × 6 ×π / 180度≈ 12.57厘米
对于弦长,根据圆周角准则,有:
弦长 = 2 ×半径 × sin(圆周角 / 2)
已知圆周角为60度,半径为6厘米,可以求得弦长为:
弦长= 2 × 6 × sin(60 / 2) ≈ 10.39厘米
因此,对应的圆弧长度约为12.57厘米,弦长约为10.39厘米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
随堂练习1.如图,在⊙O 中,∠BOC =50°,求∠BAC 的大小 解:在⊙O 中,∠BOC =50°
2.如图,哪个角与∠BAC 相等,你还能找到那些相等的角? 解:∠BAC =∠BDC ∠ADB =∠ACB ∠CAD =∠CBD ∠ABD =∠ACD 习题
1.如图,OA 、OB 、OC 都是⊙O 的直径,∠AOB =2 ∠BOC ,∠ACB 与∠BAC 的大小有什么关系,为什么? 解:∠BAC = 2 ∠ACB ,理由:
又∵∠AOB =2 ∠BOC
即∠BAC= 2∠ACB
2.如图,A 、B 、C 、D 是⊙O 上的四点,且∠BCD =100°,求∠BOD 与∠BAD 的大小
解:∵∠BCD =100°
∴优弧所对的圆心角∠BOD =2∠BCD =200° ∴劣弧所对的圆心角∠BOD =36O °-200°=160°
3.为什么电影院的作为排列呈弧形,说一说这设计的合理性.
答:有些电影院的坐位排列呈圆弧形,这样设计的理由是尽量保证同排的观众视
00
11502522
BAC BOC ∴∠=∠=⨯=
A
B
D
O
A
B
C 1
2
1
12AOB
∠=∠Q 1
22
BOC
∠=∠11
122222
AOB BOC BOC ∴∠=∠=⨯∠=∠=∠o
1
802BAD BOD ∴∠=∠=
角相等.
如图,A、B表示灯塔,暗礁分布在经过A、B两点的一个圆形
区域内,优弧AB上任一点C都是有触礁危险的临界点,
∠ACB就是“危险角”,当船位于安全区域时,∠α与“危险角”
有怎样的大小关系?
解:当船位于安全区域时,即船位于暗礁区域外(即⊙O外),与两个灯塔的
夹角∠α小于“危险角” .。
