串并联电路分析方法
串并联电路的电流和电压计算

串并联电路的电流和电压计算电路是电能传输和控制的基本载体,串并联电路是电路中常见的两种电路连接方式。
在实际应用中,我们需要根据电路中元件的连接方式计算电流和电压,以确保电路正常工作。
本文将介绍串并联电路的电流和电压计算方法。
一、串联电路串联电路是将多个电阻、电容或电感器按照一定顺序连接起来,电流依次流过每个元件。
在串联电路中,总电流贯穿整个电路,而电压在不同元件之间分配。
1. 电流计算在串联电路中,各元件的电流相等,即总电流等于各元件电流之和。
如果串联电路中有n个电阻,总电流I总可以通过以下公式计算:I总= I1 = I2 = …… = In其中,I1、I2、……、In分别为每个电阻的电流。
2. 电压计算在串联电路中,各元件的电压之和等于电源电压。
如果串联电路中有n个电阻,总电压U总可以通过以下公式计算:U总= U1 + U2 + …… + Un其中,U1、U2、……、Un分别为每个电阻的电压。
二、并联电路并联电路是将多个电阻、电容或电感器的一端连接起来,另一端连接在一起。
在并联电路中,各元件之间的电压相等,而电流在不同元件之间分配。
1. 电流计算在并联电路中,各元件电流之和等于总电流。
如果并联电路中有n个电阻,总电流I总可以通过以下公式计算:I总= I1 + I2 + …… + In其中,I1、I2、……、In分别为每个电阻的电流。
2. 电压计算在并联电路中,各元件之间的电压相等,即总电压等于各元件的电压。
如果并联电路中有n个电阻,总电压U总可以通过以下公式计算:U总= U1 = U2 = …… = Un其中,U1、U2、……、Un分别为每个电阻的电压。
三、综合计算在实际应用中,电路往往是由串联电路和并联电路组合而成。
此时,可以先计算每个串联电路的总电流和总电压,再计算整个并联电路的总电流和总电压。
四、总结串并联电路是电路中常见的两种连接方式,在实际应用中需要根据电路连接方式计算电流和电压。
通过本文的介绍,我们了解到串联电路中电流相等,电压分配;并联电路中电压相等,电流分配。
串并联电路的规律总结

串并联电路的规律总结导言:电路是电流和电压传输的路径,是电子设备中不可或缺的部分。
在电路中,串联和并联是两种常见的连接方式。
串联电路中,电流只有一条路径可走,而并联电路中,电流有多条路径可选择。
本文将总结串并联电路的规律,探讨其特点、计算方法和应用。
一、串联电路的规律1. 电流规律:串联电路中,电流在各元件之间保持不变。
这是因为串联电路中电流只有一条路径可走,电流通过每个元件时都会经过相同的电流大小。
2. 电压规律:串联电路中,总电压等于各个元件电压之和。
这是因为串联电路中电压在各个元件之间分配,总电压必须等于各个元件电压之和。
3. 电阻规律:串联电路中,总电阻等于各个元件电阻之和。
这是因为串联电路中电阻依次排列,电流通过每个元件时都要经过其电阻。
二、并联电路的规律1. 电流规律:并联电路中,总电流等于各个元件电流之和。
这是因为并联电路中电流有多条路径可选择,总电流等于各个路径的电流之和。
2. 电压规律:并联电路中,各个元件的电压相等。
这是因为并联电路中各个元件之间具有相同的电压,电压在各个元件之间保持不变。
3. 电阻规律:并联电路中,总电阻的倒数等于各个元件电阻倒数之和的倒数。
这是因为并联电路中电阻可以分为多个路径,电流在不同路径中分流,总电阻等于各个路径电阻倒数之和的倒数。
三、串并联电路的计算方法1. 串联电路计算方法:串联电路中,可以使用欧姆定律来计算电流和电压。
根据欧姆定律,电流等于电压除以电阻。
因此,在串联电路中,可以通过计算各个元件的电阻和总电压来求解电流。
2. 并联电路计算方法:并联电路中,可以使用欧姆定律和电流规律来计算电流和电压。
根据欧姆定律,电流等于电压除以电阻。
因此,在并联电路中,可以通过计算各个元件的电流和总电阻来求解电压。
四、串并联电路的应用串并联电路在电子设备和电路中广泛应用。
以下是几个常见的应用场景:1. 串联电路应用:串联电路常用于电压分压、信号传输和电阻匹配等场景。
如何进行电路的串并联计算

如何进行电路的串并联计算电路的串并联计算是电路分析中的基本内容之一,它可以帮助我们了解电路中元件的电流、电压以及功率等参数的分布情况。
在电子技术和电路设计领域中,电路的串并联计算是非常重要的一项技能。
本文将介绍电路的串并联计算的基本概念、计算方法和实际应用。
一、电路的串联计算在电路中,当多个电阻、电容、电感等元件按照一定的顺序依次相连时,我们称这些元件为串联连接,整个电路也称为串联电路。
在串联电路中,电流会依次通过每个元件,因此电流大小相同,而电压按照元件的大小依次分布。
1.电阻的串联计算在电路中,电阻的串联计算可以使用如下公式来求解:总电阻 = 电阻1 + 电阻2 + 电阻3 + ... + 电阻n例如,如果电路中有三个串联连接的电阻,其电阻分别为R1、R2和R3,则总电阻为:总电阻 = R1 + R2 + R32.电容的串联计算对于串联连接的电容元件,其总电容可以使用以下公式计算:总电容 = 1 / (1/电容1 + 1/电容2 + 1/电容3 + ... + 1/电容n)例如,如果电路中有三个串联连接的电容,其电容分别为C1、C2和C3,则总电容为:总电容 = 1 / (1/C1 + 1/C2 + 1/C3)3.电感的串联计算对于串联连接的电感元件,其总电感可以使用以下公式计算:总电感 = 电感1 + 电感2 + 电感3 + ... + 电感n例如,如果电路中有三个串联连接的电感,其电感分别为L1、L2和L3,则总电感为:总电感 = L1 + L2 + L3二、电路的并联计算在电路中,当多个电阻、电容、电感等元件同时相连在一个节点上时,我们称这些元件为并联连接,整个电路也称为并联电路。
在并联电路中,电压大小相同,而电流按照元件的大小依次分布。
1.电阻的并联计算在电路中,电阻的并联计算可以使用如下公式来求解:总电阻 = 1 / (1/电阻1 + 1/电阻2 + 1/电阻3 + ... + 1/电阻n)例如,如果电路中有三个并联连接的电阻,其电阻分别为R1、R2和R3,则总电阻为:总电阻 = 1 / (1/R1 + 1/R2 + 1/R3)2.电容的并联计算对于并联连接的电容元件,其总电容可以使用以下公式计算:总电容 = 电容1 + 电容2 + 电容3 + ... + 电容n例如,如果电路中有三个并联连接的电容,其电容分别为C1、C2和C3,则总电容为:总电容 = C1 + C2 + C33.电感的并联计算对于并联连接的电感元件,其总电感可以使用以下公式计算:总电感 = 1 / (1/电感1 + 1/电感2 + 1/电感3 + ... + 1/电感n)例如,如果电路中有三个并联连接的电感,其电感分别为L1、L2和L3,则总电感为:总电感 = 1 / (1/L1 + 1/L2 + 1/L3)三、电路串并联计算的实际应用电路的串并联计算在实际应用中非常重要,在电子电路设计、电力系统分析等领域都有广泛的应用。
初中物理电路故障分析常见情况(串并联)

一、短路、断路和开路1、短路:(1)电源短路:指导线不经过用电器而直接接到了电源的两极上。
会导致电路中电流过大而烧坏电源。
(2)用电器短路:指串联的多个用电器中的一个或多个(当然不是全部)在电路中不起作用,这种情况是由于接线的原因或者电路发生故障引起的。
(一般不会造成较大的破坏。
)2、断路:从电源的正极到负极,有且只有一条通路,若在某出断开,整个电路就成为断路。
可能是由于接触问题或者电流过大把用电器烧毁引起的。
3、开路:一般情况下等同于断路。
就是负载断开或者电路断开出现一个端口,一般是电路的干路没有连接电源正负极,也有可能是导线断了,或者是干路串联了电压表等特大电阻的元件。
二、电路故障分析(一)针对串联电路中的断路故障方法1:将完好的用电器与被测电路并联。
若用电器正常工作,说明被测电路上发生断路;若用电器不能工作,说明未测的电路上发生断路。
方法2:用导线与被测电路并联。
若未测电路正常工作,说明被测电路上发生断路;若未测电路不能工作,说明未测电路上发生断路。
(二)利用电流表的示数变化判断电路故障1.对于电路中原有电流表的示数变化情况分析。
(1)示数增大,说明电路(或支路)中部分用电器被短路(若所有用电器都被短路,则电流表烧毁)。
(2)示数减小,说明电路(或支路)中发生断路。
2.(针对串联电路)将电流表与被测电路并联分析。
(1)有示数,说明被测电路上发生断路。
(2)无示数,说明:未测电路上发生断路。
(三)利用电压表的示数变化判断电路故障1.对于电路中原有电压表的示数变化情况分析。
(1)示数增大,说明未与电压表并联的用电器被短路。
(2)示数减小,说明:与电压表并联的被测电路上发生短路或电压表与电源正负极间发生断路。
2.将电压表与被测电路并联分析。
(1)有示数,说明:电压表与电源正负极间是通路的。
(2)无示数,说明:与电压表并联的被测电路上发生短路或电压表与电源正负极间发生断路。
(四)串联电路的断路或局部短路故障现象如下表: 内容 断路 局部短路 实质某电阻(或导线)变为阻值无穷大。
初中物理电路分析方法(短路、串并联分析、滑动变阻器)

初中物理电教概括问题易面突破之阳早格格创做电教概括题历去是初中物理的易面,正在近几年的中考题中常常出现,由于试题概括性强,树坐障碍多,如果教死的教习前提不敷扎真,往往会感触很易.正在本量教教中,许多西席采与的是“题海战略”,无形加沉了教死教习的课业包袱.探索战矫正电教概括问题教教,是一项很有价格的处事.正在少久的初中教教试验中,自己逐步探索了一套电教概括问题教教规划,对付于教死突破电教概括问题中的障碍有一定效验.一、理浑“短路”观念.正在课本中,只给出了“完齐短路”的观念,“导线不通过用电器曲交跟电源二极连交的电路,喊短路.”而正在电教概括题中时常会出现局部短路的问题,如果导线不通过其余用电器而将某个用电器(或者某部分电路)尾尾贯串便产死局部短路.局部短路仅制成用电器不处事,本去不益坏用电器,果此是允许的.果它富于变更成为电教问题中的一个易面.局部短路观念抽象,教死易以明白.可用真验帮闲教死突破此易面.真验本理如图1,当启关S关合前,二灯均明(较暗);关合后,L1不明,而L2仍收光(较明).为了帮闲初中死明白,可将L1比做是电流需通过的“一座下山”而启关S的短路通讲则比做是“山里的一条隧洞”.有了“隧洞”,电流只会“走隧洞”而不会去“爬山”.二、辨别串并联电路电路图是电教的要害真量.许多电教题一启头便有一句“如图所示的电路中”如果把电路图辨别错了,电路中的电流强度、电压、电阻等物理量的估计也随之而错,制成“旗开得胜”的局里,所以分解电路是解题的前提.初中电教普遍只央供串联、并联二种基础的连交,不央供混联电路.区别串、并联电路是解电教概括题的又一个需要突破的易面.辨别串、并联有三种要领,⑴、电流法;⑵、等效电路法;⑶、去表法.⑴、电流法:即从电源正极出收,逆着电流的流背瞅电流的路径是可有分收,如果有,则所分的几个分收之间为并联,(分收前后有二个节面)如果电流的路径惟有一条(无分收面),则各元件之间为串联.此要领教死简单交受.⑵、等效电路法:此要领真量上使用了“电位”的观念,正在初中物理中,电压的观念,是通过“火位好”的类比中引进的.那么,可借帮于“下度好”举止类比,修坐“一般下的电位”观念.不妨通过类比脚法,比圆:如果某书院三层楼上有初三⑴、初三⑵、初三⑶三个班级,二层楼上有初二⑴、初二⑵、初二⑶三个班级,那么初三年级与初二年级任性二个班级之间的“下度好”是一般的,皆出进“一层楼”.果为初三年级各班处于“一般下”的三层楼上,而初二年级各班级处于“一般下”的二层楼上.正在电路中,也有“一般下电位”的观念.正在电路中,无论导线有多少,只消其间不用电器皆不妨瞅成是共一个面,即电位“一般下”.果此,咱们不妨找出各元件二端的大众面绘出简化的等效电路.图2、图3是对付各电阻的连交情况分解.图2图3如上图2白线上各个面皆与电源正极“电位一般下”,蓝线部分与电源背极“电位一般下”,不妨简化为图3.正在图3中,R1、R2、R3的并联关系也便隐而易睹了.⑶、去表法:由于电压表的内阻很大,并联正在电路中时,通过它的电流很小,可忽略不计.故正在电路中去掉电压表,不会做用电路结构,电压表地圆之处可视为启路.而电流表的内阻很小,串联正在电路中险些不做用电路的电流强度,果而,正在电路分解中,可视其为一根导线,去掉后改成一根导线即可.三、“表格分解法” 整治解题思路很多初中死反映,电教习题波及观念、公式多,解题头绪多,简单堕落.要突破那个易面,关键正在于整治出浑晰的解题思路.四、有关“电路变更”分解很多共教反映“变更的电路易,不知从何下脚”.那是果为分解变更的电路波及的真量广,思量的问题深.对付电阻、电流强度、电压及电功率相互关系的分解,稍有得慎便会制成连错反应,得堕落误的论断.那是电教概括问题的又一个易面.变更电路主假如通过启关或者滑动变阻器的改变去富于电路变更的.电路中有多个启关,通过启关关合战断启的状态变更,往往会使各用电器的连交关系爆收变更,而滑动变阻器则通过滑片去改变其连进电路的灵验电阻,进而使电路中的电压、电流、电功率等数值爆收变更(也有改变电路结构的).有关变更电路,应正在教会辨别“部分电路短交”战教会辨别串并联电路的前提上,掌握分解变更电路的基础思路.1、启关的通、断制成电路的变更当启关处正在分歧状态时,由于断路战短路,交进电路中的用电器,及其用电器之间的连交办法普遍要爆收变更,果此最先要正在本电路的前提上绘出百般情况下的本量电路.改绘时要根据电流的本量情况,使用“裁撤法”.裁撤法央供:⑴、去掉被断路的元件;⑵、去掉已被短路的元件;⑶、用“去表法”去表,其准则是“电压表处是断路,电流曲过电流表”.正在去掉电压表时,要分解电压表读出去的是哪部分电路二端的电压,可用等效电路法举止分解.例题:如图5所示电路中,电源电压脆持4伏,L1的电阻为4欧,L2、L3的电阻均为16欧供:⑴、S1、S2皆断启时,电流表战电压表的示数.⑵、S1、S2皆交通时,所有电路消耗的电功率.例题分解:正在题中的当启关处于关合或者断启的二种情况下电路结构爆收了变更,可举止电路的改绘,睹图6.注:图中真线部分是要去掉的部分.正在用“去表法”去掉电流表电压表后,要分解它们分别丈量哪一个用电器的哪一个物理量.电压表可借帮于“等电位”举止分解.正在图7中,白线、蓝线、乌线分别是三个“共电位面”,由图7中可睹,L1与电压表V均加正在蓝线与乌线之间,所以电压表是L二端的电压.解:当S1、S2皆断启时,L1、L3串联.电流表读数电压表读数当S1、S2皆交通时,L2、L3并联.总电阻总功率2.滑动变阻器变更问题滑动变阻器连进电路中的灵验电阻爆收变更了,或者是引起电路结构的变更,或者是引起电路中电压、电流、电功率的变更.典型例题:如图8所示电路中,电源电压稳定,当滑动变阻器的滑片背左滑动时,电流表战电压表的示数变更情况是[]A 、电流表战电压表的示数变大;B、电流表战电压表的示数变小;C、电流表示数变小,电压表示数变大;D、电流表示数变大,电压表示数变小.有关滑动变阻器的此典型问题,解题关键是:⑴、弄浑滑动变阻器本理,滑片滑动时电阻是变大仍旧变小?⑵、弄浑物理量是可变更,普遍去道,电源的电压,定值电阻的阻值是稳定,其余的物理量皆是变更的;⑶、弄浑电压表读数读出的是哪一个电器二端的电压;⑷、利用表格整治分解问题的思路.上例题表格分解如下:有关R1 有关R2 总电路关系电流I1 I2 I ?串联电流相等电压U1 ?U总稳定U总=U1+U2电阻R1 稳定R2 ↑R总R总=R1+R2由电阻横背关系可知,果R1稳定,R2变大,故R总将变大;再由总电路纵背关系可知,R总变大,U总稳定,故I将变小(电流表读数);果串联电路电流相等I1=I;再由有关R1纵背关系可知,I1变小,R1稳定,故U 1将变小(电压表读数变小).。
初中物理10种复杂电路分析方法
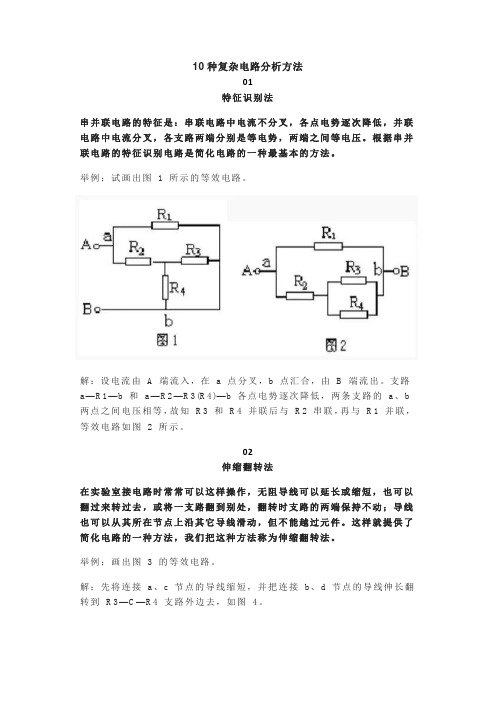
10种复杂电路分析方法01特征识别法串并联电路的特征是:串联电路中电流不分叉,各点电势逐次降低,并联电路中电流分叉,各支路两端分别是等电势,两端之间等电压。
根据串并联电路的特征识别电路是简化电路的一种最基本的方法。
举例:试画出图 1 所示的等效电路。
解:设电流由 A 端流入,在 a 点分叉,b 点汇合,由 B 端流出。
支路a—R1—b 和a—R2—R3(R4)—b 各点电势逐次降低,两条支路的a、b 两点之间电压相等,故知R3 和R4 并联后与R2 串联,再与R1 并联,等效电路如图 2 所示。
02伸缩翻转法在实验室接电路时常常可以这样操作,无阻导线可以延长或缩短,也可以翻过来转过去,或将一支路翻到别处,翻转时支路的两端保持不动;导线也可以从其所在节点上沿其它导线滑动,但不能越过元件。
这样就提供了简化电路的一种方法,我们把这种方法称为伸缩翻转法。
举例:画出图 3 的等效电路。
解:先将连接a、c 节点的导线缩短,并把连接b、d 节点的导线伸长翻转到R3—C—R4 支路外边去,如图4。
再把连接a、c节点的导线缩成一点,把连接b、d 节点的导线也缩成一点,并把R5 连到节点 d 的导线伸长线上(图5)。
由此可看出R2、R3 与R4 并联,再与R1 和R5 串联,接到电源上。
03电流走向法电流是分析电路的核心。
从电源正极出发(无源电路可假设电流由一端流入另一端流出)顺着电流的走向,经各电阻绕外电路巡行一周至电源的负极,凡是电流无分叉地依次流过的电阻均为串联,凡是电流有分叉地分别流过的电阻均为并联。
举例:试画出图 6 所示的等效电路。
解:电流从电源正极流出过 A 点分为三路(AB 导线可缩为一点),经外电路巡行一周,由 D 点流入电源负极。
第一路经R1 直达 D 点,第二路经R2 到达 C 点,第三路经R3 也到达 C 点,显然R2 和R3 接联在AC 两点之间为并联。
二、三路电流同汇于 c 点经R4 到达 D 点,可知R2、R3 并联后与R4 串联,再与R1 并联,如图7 所示。
初二物理串联、并联分析及电路图练习分析

L1 B
L2 A K
L2
K2
C
L3
B
V1 L1
D
V2
G
A
E
A
K1
F
K1、K2断开 L2 K2
C
L3
B
V1 L1
D
V2
G
A
E
A
K1
F
L3
V1
V1 2
L1
A
A
K1断开、K2闭合 L2
C
L3
B
V1 L1
D
V2
G
A
E
A
K1
F
L2 L3 L1
V1
V2
A
K1闭合、K2断开 L2 K2
C
L3
B
V1 L1
串联电路
1、定义
2、连实物图,画电路图 3 、观察实验现象,得出特点 4、串联电路知识结构方框图
串联电路的定义
实验演示: 如左图,把 两只小灯泡,顺 次连接在电路里, 一只灯泡亮时另 一只灯泡也亮。 像这样把元件逐
个顺次连接起来
-----称串联电路。
串联电路图
实物图:
电路图:
连接要点:在串联电路中,电流从
并联电路知识结构方框图
连接特点 各用电器(包括跟用电 器相连的开关)各自接 在电路两点之间。 某一条支路断开时,其 他支路上的用电器照常 工作。 干路上的开关可以控制 所有用电器,而支路上 的开关只能控所在支路 上的用电器。
A
B
D
C
电源被短路
六、用”正负号”法判断两种”短路”现象. 方法:
电源正负极分别标“+” “-”号。可 以从正极开始标符号“+”,根据 相同的点标相同符号的原则,直 至遇到电压表或用电器停止(电 路表相当于导线);再从负极开 始根据相同的原则标上符号“-” , 直至将点电路图中所有相交而连 结的点标上符号。这时观察若从 正极(或负极)开始用相同的符 号一直标到负极(正极),这就 是一条短路;若某个用电器或电 压表(电流表相当于导线)两端 的符号相同了,这个用电器就被 “短路”,可以去掉。
物理判断串并联电路的方法
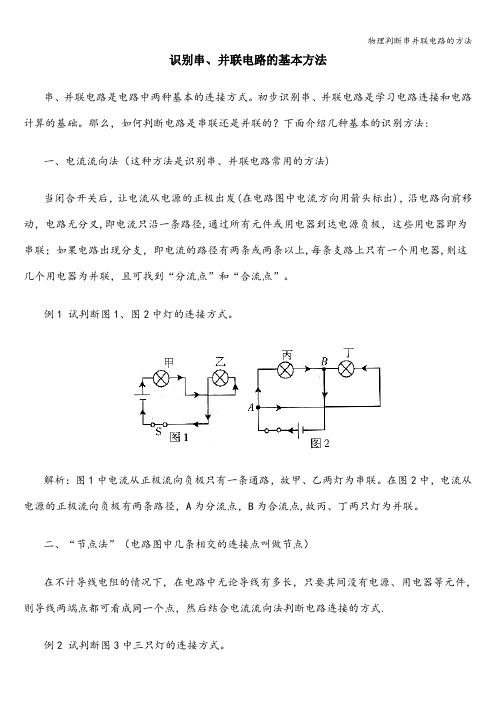
识别串、并联电路的基本方法串、并联电路是电路中两种基本的连接方式。
初步识别串、并联电路是学习电路连接和电路计算的基础。
那么,如何判断电路是串联还是并联的?下面介绍几种基本的识别方法:一、电流流向法(这种方法是识别串、并联电路常用的方法)当闭合开关后,让电流从电源的正极出发(在电路图中电流方向用箭头标出),沿电路向前移动,电路无分叉,即电流只沿一条路径,通过所有元件或用电器到达电源负极,这些用电器即为串联;如果电路出现分支,即电流的路径有两条或两条以上,每条支路上只有一个用电器,则这几个用电器为并联,且可找到“分流点”和“合流点”。
例1 试判断图1、图2中灯的连接方式。
解析:图1中电流从正极流向负极只有一条通路,故甲、乙两灯为串联。
在图2中,电流从电源的正极流向负极有两条路径,A为分流点,B为合流点,故丙、丁两只灯为并联。
二、“节点法”(电路图中几条相交的连接点叫做节点)在不计导线电阻的情况下,在电路中无论导线有多长,只要其间没有电源、用电器等元件,则导线两端点都可看成同一个点,然后结合电流流向法判断电路连接的方式.例2 试判断图3中三只灯的连接方式。
解析:在图3所示的电路中先定节点。
把共线(线中没有用电器)的点用同一符号A、B表示,如图4所示。
从电源正极流向负极的电流在节点A分流到三个灯泡,在节点B汇合后,回到电源负极,画出等效电路图,显然灯是并联在A、B两点之间。
如图5所示,故三只灯的连接方式为并联。
三、断路观法(这种方法是识别较难电路常用的方法)在多个用电器组成的电路中,把其中一个用电器断路(如去掉该用电器),如果其他用电器不能工作了(如电灯不发光了)则这个电路是串联的.如果其他用电器仍能工作,则这个电路是并联的。
该方法的依据是串联电路各元件间相互影响,相互干扰。
并联电路各元件相互独立,互不影响。
例3 试判断图6中三只灯的连接方式。
解析:如图6所示电路,用“断路观察法”来判断,可以发现具有“断二通一”或“断一通二"的特点,即在中任意断开两个(或一个),其他一个(或两个)能构成通路,如图7所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
串并联电路分析方法
串并联电路是电路中常见的两种基本连接方式。
在实际的电路分析
计算中,正确应用串并联电路的分析方法对于求解电压、电流以及电
阻等参数具有重要意义。
本文将介绍串并联电路的基本概念和分析方法。
1. 串联电路的分析方法
串联电路是将电路中的元件依次连接,形成一个电流沿着一条路径
流动的电路。
串联电路的分析方法可以分为以下几个步骤:(1)计算总电阻:串联电路中的元件电阻依次相加,得到总电阻。
(2)计算总电流:根据欧姆定律,总电流等于电压除以总电阻。
(3)计算各元件电压:根据欧姆定律,各元件的电压等于电流乘
以电阻。
(4)计算功率和能量:根据功率和能量公式,可以计算各元件的
功率和能量。
2. 并联电路的分析方法
并联电路是将电路中的元件分成多个支路,每个支路的两端连接在
一起,形成一个电压相同的电路。
并联电路的分析方法可以分为以下
几个步骤:
(1)计算总电导:并联电路中的元件电导依次相加,得到总电导。
(2)计算总电流:根据欧姆定律,电流等于电压乘以总电导。
(3)计算各元件电流:根据欧姆定律,各元件的电流等于总电流
乘以各元件的电导。
(4)计算功率和能量:根据功率和能量公式,可以计算各元件的
功率和能量。
3. 串并联电路的分析方法
串并联电路是包含了串联和并联连接的电路。
在分析串并联电路时,可以将电路分割成多个包含串联或并联连接的小部分,然后利用串联
和并联电路的分析方法求解。
(1)划分电路:将串并联电路中的元件根据串联和并联的关系划
分成多个小部分。
(2)使用串联电路和并联电路的分析方法求解每个小部分的电压、电流以及电阻等参数。
(3)根据串联和并联的关系,将各小部分的电压、电流以及电阻
合并得到最终的结果。
总结:
串并联电路的分析方法是电路分析的基础,正确应用这些方法可以
帮助我们求解电路中的各种参数。
在实际应用中,可以根据具体情况
选择串联或并联电路的分析方法,也可以结合串并联对电路进行综合
分析。
掌握串并联电路的分析方法,可以为我们理解和设计电路提供有效的工具和方法。
