八年级数学几何培优资料经典题型,图形面积例题加解析
专题在平面直角坐标系中求图形的面积(四大题型)(原卷版)
1.上面题主要考查坐标与图形性质,解题的关键是明确题意,画出相应的图形,利用数形结合的思想解答.
2.由于点的位置不明确,因此在解题时要注意分情况讨论.
【变式41】已知点A(1,0),B(0,2),点P在x轴的负半轴上,且△PAB的面积为5,则点P的坐标为( )
A.(0,﹣4)B.(0,﹣8)C.(﹣4,0)D.(6,0)
(2)直接写出A1,B1,C1三点的坐标;
(3)求△ABC的面积.
【例题3】(2022春•长安区校级月考)如图所示,在平面直角坐标系中,点A(4,0),B(3,4),C(0,2),则四边形ABCO的面积为( )
A.9B.10C.11D.12
解题技巧提炼
1、当四边形的其中有一边在坐标轴上(或与坐标轴平行)时,可以用分割法;
【变式45】(2022秋•渭滨区期末)如图所示,在平面直角坐标系中,已知A(0,1)、B(2,0)、C(4,3).
(1)在平面直角坐标系中画出△ABC,则△ABC的面积是;
(2)若点D与点C关于y轴对称,则点D的坐标为;
(3)已知P为x轴上一点,若△ABP的面积为1,求点P的坐标.
【变式46】(2022•天津模拟)如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b﹣3)2=0.
【变式24】(2022春•雷州市期末)如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标;
(2)求出S△ABC.
【变式25】在如图所示的正方形网格中,每个小正方形的边长均为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(﹣4,5)、(﹣1,3).
(1)请在如图所示的网格平面内画出平面直角坐标系;
初中数学培优专题学习专题25 图形面积的计算
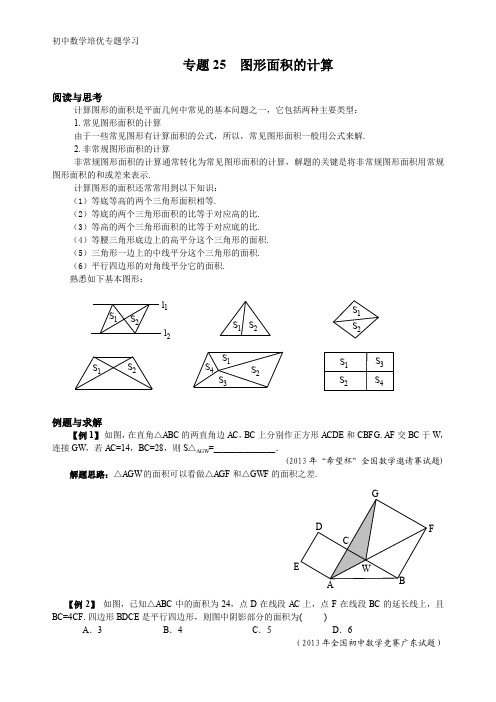
专题25 图形面积的计算阅读与思考计算图形的面积是平面几何中常见的基本问题之一,它包括两种主要类型: 1.常见图形面积的计算由于一些常见图形有计算面积的公式,所以,常见图形面积一般用公式来解. 2.非常规图形面积的计算非常规图形面积的计算通常转化为常见图形面积的计算,解题的关键是将非常规图形面积用常规图形面积的和或差来表示.计算图形的面积还常常用到以下知识:(1)等底等高的两个三角形面积相等.(2)等底的两个三角形面积的比等于对应高的比. (3)等高的两个三角形面积的比等于对应底的比. (4)等腰三角形底边上的高平分这个三角形的面积. (5)三角形一边上的中线平分这个三角形的面积. (6)平行四边形的对角线平分它的面积. 熟悉如下基本图形:S 3S 4S 3S 4S 1S 2S 1S 2S 1S 2S 1S 2S 1S 2S 2S 1l 2l 1例题与求解【例1】 如图,在直角△ABC 的两直角边AC ,BC 上分别作正方形ACDE 和CBFG .AF 交BC 于W ,连接GW ,若AC =14,BC =28,则S △AGW =______________.(2013年“希望杯”全国数学邀请赛试题)解题思路:△AGW 的面积可以看做△AGF 和△GWF 的面积之差.WFGEDCBA【例2】 如图,已知△ABC 中的面积为24,点D 在线段AC 上,点F 在线段BC 的延长线上,且BC =4CF .四边形BDCE 是平行四边形,则图中阴影部分的面积为( )A .3B .4C .5D .6(2013年全国初中数学竞赛广东试题)解题思路:设△ABC 底边BC 上的高为h .本例关键是通过适当变形找出h 和DE 之间的关系.FC BDEA【例3】 如图,平行四边形ABCD 的面积为30cm 2,E 为AD 边延长线上的一点,EB 与DC 交于F 点,已知三角形FBC 的面积比三角形DEF 的面积大9cm 2,AD =5cm ,求DE 长.(北京市“迎春杯”竞赛试题)解题思路:由面积求相关线段,是一个逆向思维的过程,解题的关键是把条件中图形面积用DE 及其它线段表示.BACFDE【例4】 如图,四边形ABCD 被AC 与DB 分成甲、乙、丙、丁4个三角形,已知BE =80 cm ,CE =60 cm ,DE =40 cm ,AE =30 cm ,问:丙、丁两个三角形面积之和是甲、乙两个三角形面积之和的多少倍?(“华罗庚杯”竞赛决赛试题)解题思路:甲、乙、丙、丁四个三角形面积可通过线段的比而建立联系,找出这种联系是解本例的突破口.丁乙丙甲E BCDA【例5】 如图,△ABC 的面积为1,D ,E 为BC 的三等分点,F ,G 为CA 的三等分点,求四边形PECF 的面积.解题思路:连CP ,设S △PFC =x ,S △PEC =y ,建立x ,y 的二元一次方程组.QP F GEDCBA【例6】如图,E ,F 分别是四边形ABCD 的边AB ,BC 的中点, DE 与AF 交于点P ,点Q 在线段DE 上,且AQ ∥PC .求梯形APCQ 的面积与平行四边形ABCD 的面积的比值.(2013年”希望杯“数学邀请赛试题)解题思路:连接EF ,DF ,AC ,PB ,设S □ABCD =a ,求得△APQ 和△CPQ 的面积.FEPQDCBA能力训练A 级1.如图,边长为1的正方形ABCD 的对角线相交于点O .过点O 的直线分别交AD ,BC 于E ,F ,则阴影部分面积是______.FOEDCB A(海南省竞赛试题)2.如图,在长方形ABCD 中,E 是AD 的中点,F 是CE 的中点,若△BDF 的面积为6平方厘米,则长方形ABCD 的面积是_____________平方厘米.EFDCBA(“希望杯”邀请赛试题)3.如图,ABCD 是边长为a 的正方形,以AB ,BC ,CD ,DA 分别为直径画半圆,则这四个半圆弧所围成的阴影部分的面积是____________.DCBA(安徽省中考试题)4.如图,已知AB ,CD 分别为梯形ABCD 的上底、下底,阴影部分总面积为5平方厘米,△AOB 的面积是0.625平方厘米,则梯形ABCD 的面积是_________平方厘米.DOCBA(“祖冲之杯”邀请赛试题)5.如图,长方形ABCD 中,E 是AB 的中点,F 是BC 上的一点,且CF =BC 31,则长方形ABCD的面积是阴影部分面积的( )倍.A .2B . 3C . 4D .5DF CBEA6.如图,是一个长为a ,宽为b 的长方形,两个阴影图形都是一对长为c 的底边在长方形对边上的平行四边形,则长方形中未涂阴影部分的面积为( ).A .c b a ab )(+-B . c b a ab )(--C .))((c b c a --D .))((c b c a +-cccc7.如图,线段AB =CD =10cm ,BC 和DA 是弧长与半径都相等的圆弧,曲边三角形BCD 的面积是以D 为圆心、DC 为半径的圆面积的41,则阴影部分的面积是( ). A .25π B . 100 C .50π D .200CBD A(“五羊杯”竞赛试题)8.如图,一个大长方形被两条线段AB 、CD 中分成四个小长方形,如果其中图形Ⅰ,Ⅱ,Ⅲ的面积分别为8,6,5,那么阴影部分的面积为( ). A .29 B .27 C .310 D .815 ⅢⅡⅠCBDA9.如图,长方形ABCD 中,E ,F 分别为AD ,BC 边上的任一点,△ABG ,△DCH 的面积分别为15和20,求阴影部分的面积.HGEDCF B A(五城市联赛试题)10.如图,正方形ABCD ,正方形BEFG 和正方形RKPF 的位置如图所示,点G 在线段DK 上,已知正方形BEFG 的边长为4,求△DEK 的面积.RKP GF EC B AD(广西壮族自治区省南宁市中考试题)B 级1.如果图中4个圆的半径都为a ,那么阴影部分的面积为_____________.(江苏省竞赛试题)2.如图,在长方形ABCD 中,E 是BC 上的一点,F 是CD 上的一点,若三角形ABE 的面积是长方形ABCD 面积的31,三角形ADF 的面积是长方形ABCD 面积的52,三角形CEF 的面积为4cm 2,那么长方形ABCD 的面积是_________cm 2.DCFE BA(北京市“迎春杯”邀请赛试题)3.如图,边长为3厘米与5厘米的两个正方形并排放在一起,在大正方形中画一段以它的一个顶点为圆心,边长为半径的圆弧,则阴影部分的面积为___________________.(“希望杯”邀请赛试题)4.如图,若正方形APHM ,BNHP ,CQHN 的面积分别为7,4,6,则阴影部分的面积是_____.CMNDQPB A(“五羊杯”竞赛试题)5.如图,把等边三角形每边三等分,使其向外长出一个边长为原来的31的小等边三角形,称为一次“生长”,在得到的多边上类似“生长”,一共“生长”三次后,得到的多边形的边数=________,面积是原三角形面积的______倍.第2次生长第1次生长原图(“五羊杯”竞赛试题)6.如图,在长方形ABCD 中,AE =BG =BF =21AD =31AB =2,E ,H ,G 在同一条直线上,则阴影部分的面积等于( ).A .8B .12C .16D .20F BGCHDE A7.如图,边长分别为8cm 和6cm 的两个正方形,ABCD 与BEFG 并排放在一起,连接EG 并延长交AC 于K ,则△AKE 的面积是( ).A .48cm 2B .49cm 2C .50cm 2D .51cm 2KGFEC B A D(2013年“希望杯”邀请赛试题)8.在一个由8×8个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆经过的所有小方格的圆内部分的面积之和记为S 1,把圆周经过的所有小方格的圆外部分的面积之和记为S 2,则21S S 的整数部分是( ).A .0B .1C .2D .3(全国初中数学联赛试题)9.如图,△ABC 中,点D ,E ,F 分别在三边上,E 是AC 的中点,AD ,BE ,CF 交于一点G ,BD =2DC ,S △GEC =3,S △GDC =4,则△ABC 的面积是( ).A .25B .30C .35D .40GFE CBDA10.已知O (0,0),A (2,2),B (1,a ),求a 为何值时,S △ABO =5?11.如图,已知正方形ABCD 的面积为1,M 为AB 的中点,求图中阴影部分的面积.GCBMAD(湖北省武汉市竞赛试题)12.如图,△ABC 中,21===FA FB EC EA DB DC .求的面积△的面积△ABC GHI 的值. G IHEDCBFA(“华罗庚金杯”邀请赛试题)。
(完整版)八年级数学几何经典题【含答案】
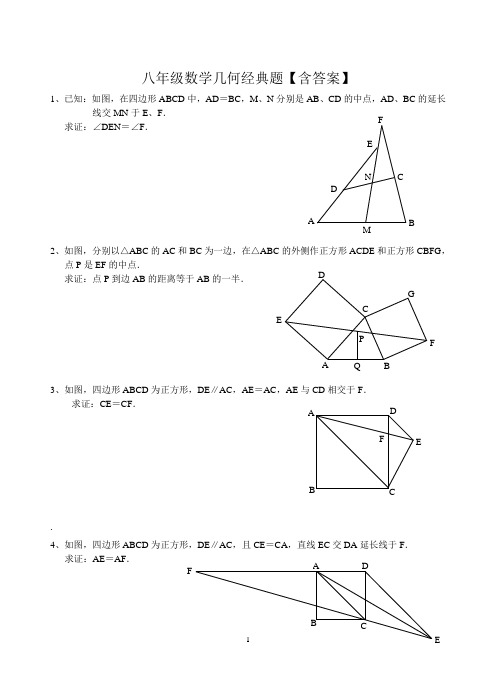
F八年级数学几何经典题【含答案】1、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .2、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.3、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF ..4、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .B5、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .6、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .7如图,△ABC 中,∠C 为直角,∠A=30°,分别以AB 、AC 为边在△ABC 的外侧作正△ABE 与正△ACD ,DE 与AB 交于F 。
求证:EF=FD 。
8如图,正方形ABCD 中,E 、F 分别为AB 、BC 的中点,EC 和DF 相交于G ,连接AG ,求证:AG=AD 。
9、已知在三角形ABC 中,AD 是BC 边上的中线,E 是AD 上的一点,且BE=AC,延长BE 交AC 与F,求证AF=EFD FEP CB AFPDE CBA,九年级数学【答案】1.如下图连接AC 并取其中点Q ,连接QN 和QM ,所以可得∠QMF=∠F ,∠QNM=∠DEN 和∠QMN=∠QNM ,从而得出∠DEN =∠F 。
2.过E,C,F 点分别作AB 所在直线的高EG ,CI ,FH 。
可得PQ=2EGFH。
由△EGA ≌△AIC ,可得EG=AI ,由△BFH ≌△CBI ,可得FH=BI 。
中考培优竞赛专题经典讲义 第12讲 四边形与面积
256
D.
9
【巩固练习】
1、如图,在一个平行四边形中,两对平行于边的直线将这个平行四边形分为九个小平行四边形,
如果原来这个平行四边形的面积为 100cm2,而中间那个小平行四边形(阴影部分)的面积为
20 平方厘米,则四边形 ABDC 的面积是(
)
A.40 cm2 B.60 cm2 C.70 cm2 D.80 cm2
个正方形的对称中心,则阴影部分的面积为
.
5、如图,在矩形 ABCD 中,AD=6,AB=4,点 E、G、H、F 分别在 AB、BC、CD、AD 上,且
AF=CG=2,BE=DH=1,点 P 是直线 EF、GH 之间任意一点,连结 PE、PF、PG、PH,则△PEF
和△PGH 的面积和等于
.
1
6、如图,矩形 ABCD 长为 a,宽为 b,若 S1=S₂= (S3+S4),则 S4=
【解析】
1
1
可知 S△BEC=S△DFC= S 平行四边形 ABCD∴S△AFD+S△BFC= S 平行四边形=S△EBC∴S3+S4+①+S1+②=①+S2+②
2
2
∴S4=S2-S1-S3=12-2-3=7 故选 D
【巩固练习】
1、已知△ABC,面积为 12,点 D 在边 BC 上,满足 CD:BD=1:2,点 E 为 AC 的中点,连接
积等于
.
2、以□ABCD 的四条边为边,在其形外分别作正方形,如图②,连结 EF、GH、IJ、KL.若□ABCD
的面积为 5,则图中阴影部分四个三角形的面积和为
.
例题 5、如图,四边形的两条对角线 AC、BD 所成的锐角为 45°,当 AC+BD=18 时,四边形 ABCD
人教版八年级数学培优题精选18例(含答案)

A、1.5B、2C、2.25D、2.5爬到点 B ,如果它运动的路径是最短,则 AC 的长度是多少?少?车是否超速?例题6、对实数 a , b ,定义新运算☆如下: a ☆ b =八年级数学培优题精选18例(含答案)例题7、计算八年级数学培优题精选18例(含答案)例题9、点 A(3x + 2y , -2)关于 y 轴的对称点为 B(-1 ,2x + 4y), 则点 M (x , y)关于 x 轴的对称点的坐标为多少?答案:(1,1)。
例题10、如图所示,在平面直角坐标系中有 A , B 两点:八年级数学培优题精选18例(含答案)(1)写出 A , B 两点的坐标;(2)若线段 AB 各顶点的横坐标不变,纵坐标都乘以 -1 ,请你在同一坐标系中描出对应的点 A1 ,B1 ,并连接 A1B1 ,所得的线段 A1B1 与线段 AB 有怎样的位置关系?(3)在(2)的基础上,纵坐标不变,横坐标都乘以 -1 ,请你在同一坐标系中描出对应的点 A2,B2 ,并连接这两个点,所得的线段 A2B2 与线段 AB 有怎样的位置关系?解:(1)点 A 的坐标为(1,2),点 B 的坐标为(3,1);(2)如图所示,线段 A1B1 与线段 AB 关于 x 轴对称;(3)如图所示,线段 A2B2 与线段 AB 关于原点对称。
例题11、甲乙两人赛跑,所跑路程与时间的关系如图所示。
根据图像得到如下四个信息,其中错误的是(C )八年级数学培优题精选18例(含答案)A、这是一次 1500 m 赛跑B、甲、乙两人中先到达终点的是乙C、甲、乙同时起跑D、甲在这次赛跑中的速度为 5 m/s例题12、如图,BE 是∠ABD 的角平分线,CF 是∠ACD 的角平分线,BE 与CF 交于点 G ,∠BDC = 140°,∠BGC = 110°,则∠A 的度数为(C)八年级数学培优题精选18例(含答案)A、70°B、75°C、80°D、85°例题13、如图所示,已知 AB∥DE ,一个弯形管道 ABCDE 的拐角∠EDC = 140°,∠CBA = 150°,则∠C = ?八年级数学培优题精选18例(含答案)答案:∠C = 70°。
初二数学 勾股定理、面积精典例题含参考答案

直角三角形、勾股定理、面积精典例题+跟踪训练+参考答案知识考点:了解直角三角形的判定与性质,理解直角三角形的边角关系,掌握用勾股定理解某些简单的实际问题。
它的有关性质广泛应用于线段计算、证明线段倍分关系、证明线段平方关系及与面积有关的问题等方面。
精典例题:【例1】如图,在四边形ABCD 中,∠A =600,∠B =∠D =900,BC =2,CD =3,则AB =? 分析:通过作辅助线,将四边形问题转化为三角形问题来解决,其关键是对内分割还是向外补形。
答案:833 ABCD E23图1例AB CP Q图2例【例2】如图,P 为△ABC 边BC 上一点,PC =2PB ,已知∠ABC =450,∠APC =600,求∠A CB 的度数。
分析:本题不能简单地由角的关系推出∠ACB 的度数,而应综合运用条件PC =2PB 及∠APC =600来构造出含300角的直角三角形。
这是解本题的关键。
答案:∠ACB =750(提示:过C 作CQ ⊥AP 于Q ,连结BQ ,则AQ =BQ =CQ ) 探索与创新:【问题一】如图,公路MN 和公路PQ 在点P 处交汇,且∠QPN =300,点A 处有一所中学,AP =160米,假设汽车行驶时,周围100米以内会受到噪声的影响,那么汽车在公路MN 上沿PN 方向行驶时,学校是否会受到噪声的影响?如果受影响,已知汽车的速度为18千米/小时,那么学校受影响的时间为多少秒?分析:从学校(A 点)距离公路(MN )的最近距离(AD =80米)入手,在距A 点方圆100米的范围内,利用图形,根据勾股定理和垂径定理解决它。
略解:作AD ⊥MN 于D ,在Rt △ADP 中,易知AD =80。
所以这所学校会受到噪声的影响。
以A 为圆心,100米为半径作圆交MN 于E 、F ,连结AE 、AF ,则AE =AF =100,根据勾股定理和垂径定理知:ED =FD =60,EF =120,从而学校受噪声影响的时间为:t ==120180001150(小时)=24(秒)评注:本题是一道存在性探索题,通过给定的条件,判断所研究的对象是否存在。
【八年级数学培优竞赛-素养提升】专题06 四边形的面积问题
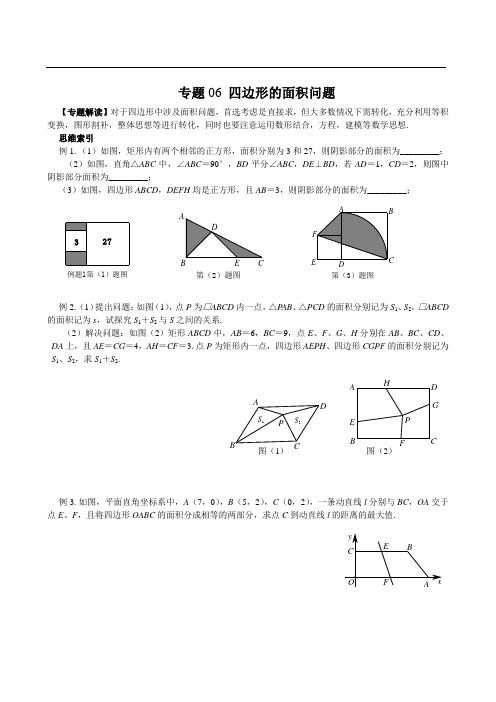
专题06 四边形的面积问题【专题解读】对于四边形中涉及面积问题,首选考虑是直接求,但大多数情况下需转化,充分利用等积变换,图形割补,整体思想等进行转化,同时也要注意运用数形结合,方程,建模等数学思想. 思维索引例1.(1)如图,矩形内有两个相邻的正方形,面积分别为3和27,则阴影部分的面积为_________; (2)如图,直角△ABC 中,∠ABC =90°,BD 平分∠ABC ,DE ⊥BD ,若AD =1,CD =2,则图中阴影部分面积为_________;(3)如图,四边形ABCD ,DEFH 均是正方形,且AB =3,则阴影部分的面积为_________;例题1第(1)题图第(2)题图第(3)题图例2.(1)提出问题:如图(1),点P 为□ABCD 内一点,△P AB 、△PCD 的面积分别记为S 1、S 2,□ABCD 的面积记为s ,试探究S 1+S 2与S 之间的关系.(2)解决问题:如图(2)矩形ABCD 中,AB =6,BC =9,点E 、F 、G 、H 分别在AB 、BC 、CD 、DA 上,且AE =CG =4,AH =CF =3.点P 为矩形内一点,四边形AEPH 、四边形CGPF 的面积分别记为S 1、S 2,求S 1+S 2.图(1)ADCBPS 2S 1图(2)AD CBE F GHP例3.如图,平面直角坐标系中,A (7,0),B (5,2),C (0,2),一条动直线l 分别与BC ,OA 交于点E 、F ,且将四边形OABC 的面积分成相等的两部分,求点C 到动直线l 的距离的最大值.素养提升1.已知正方形ABCD 的边长为10,AE 长为8,CG 长为2.则图中阴影部分面积为 ( )A .16B .20C .25D .36第1题图A E BGF第2题图第3题图CDEA2.如图,ABCD 与BEFG 是并列放在一起的两个正方形.O 是BF 与EG 的交点.如果正方形ABCD 的面积是9,CG =2,则△DEO 的面积为( ) A .1B .94C .4D .2543.如图,已知△ABC 的面积为12,点D 在线段AC 上,点F 在线段BC 的延长线上,且BC =4CF ,四边形DCFE 是平行四边形,则图中S △ADE +S △BDE 的值为( )A .2B .3C .4D . 64.如图,四边形AOEF 是平行四边形,点B 为OE 的中点,延长FO 至点C ,使FO =3OC ,连接AB 、AC 、BC ,则S △ABO :S △AOC :S △BOC 的值为( )A .6:2:1B .3:2:1C .6:3:2D .4:3:2第4题图BCAEFOM第5题图第6题图AEDCB5.已知图中三十六个小等边三角形的面积都等于1,则三角形ABC 的面积为 ( ) A .21 B .22 C .23 D .246.已知如图,AB =3,AC =1,以AC ,BC 为边分别向上作等边△ACD 和等边△BCE ,则S △BDE =________.7.如图所示,在△ABC 中,∠ACB =90°,AC =8,BC =6.分别以AC 、BC 为边作正方形AEDC 、BCFG ,则△BEF 的面积为________.第7题图BCDEF GBCD E F GH A MNPQ m 4m 3m 2m1l 1l 2l 3l 4第8题图第9题图B8.如图,已知直线l 1、l 2、l 3、l 4及m 1、m 2、m 3、m 4分别互相平行,且S 四边形ABCD =100,S 四边形EFGH =60.则S 四边形PQMN = ________.9.如图,四边形ABCD 中,AD 平行BC ,E 为CD 中点,EF ⊥AB ,若AB =6,EF =4,则四边形ABCD 的面积是________. 10.四边形ABCD 的四边长为ABBCCDDA,一条对角线BD,其中m ,n 为常数,且0<m <7,0<n <5,那么四边形ABCD 的面积为________.11.如图,在四边形ABCD 中,设∠BAD +∠ADC =270°,且E 、F 分别为AD 、BC 的中点,EF =4,以AB 、CD 为直径作半圆,求这两个半圆面积的和.BDEFA12.△ABC 中,AB =14,AC =15,BC =13,分别以AB ,AC ,BC 为边向外作正方形ABFG ,正方形ACDE ,正方形BCMN ,连接DE ,NF ,GE ,求六边形DEGFNM 的面积.N M B CD EFGA13.如图,在矩形ABCD 中,AD =6,CD =8,菱形EFGH 的三个顶点E 、G 、H 分别在矩形ABCD 的边AB 、CD 、DA 上,AH =2,连接CF .(1)当DG =2时,求证:四边形EFGH 是正方形; (2)当△FCG 的面积为2时,求DG 的值.BCDEFGH A14.如图1,A 、D 分别在x 轴和y 轴上,CD ∥x 轴,BC ∥y 轴.点P 从D 点出发,以1cm /s 的速度,沿五边形OABCD 的边匀速运动一周.记顺次连接P 、O 、D 三点所围成图形的面积为Scm 2,点P 运动的时间为t s ,S 与t 之间的函数关系如图2中折线段OEFGHI 所示. (1)求A 、B 两点的坐标;(2)若直线PD 将五边形OABCD 分成面积相等的两部分,确定此时点P 的位置。
八年级数学几何经典题【含答案】.docx

八年级数学几何经典题【含答案】1、已知:如图,在四边形ABCD中, AD= BC, M、 N 分别是 AB、 CD的中点, AD、 BC的延长线交MN于 E、 F.F 求证:∠ DEN=∠ F.EN CDA BM2、如图,分别以△ABC的 AC 和 BC 为一边,在△ABC的外侧作正方形ACDE和正方形 CBFG,点P是 EF 的中点.D求证:点 P 到边 AB的距离等于 AB的一半.GECPFA QB3、如图,四边形ABCD为正方形, DE∥ AC, AE= AC, AE与 CD相交于 F.求证: CE=CF.ADF EB C.4、如图,四边形ABCD为正方形, DE∥ AC,且 CE= CA,直线 EC交 DA延长线于F.求证: AE=AF.A DFB CE5、设 P 是正方形ABCD一边 BC上的任一点,PF⊥ AP, CF平分∠ DCE.A求证: PA=PF.D FBP C E 6、平行四边形ABCD中,设 E、F 分别是 BC、 AB 上的一点, AE 与 CF 相交于 P,且AE= CF.求证:∠ DPA=∠ DPC.A DFPB E C7 如图,△ ABC中,∠ C为直角,∠ A=30°,分别以AB、AC为边在△ ABC的外侧作正△ ABE与正△ACD, DE与 AB交于 F。
求证: EF=FD。
8 如图,正方形 ABCD中,E、F 分别为 AB、BC的中点, EC和 DF 相交于 G,连接 AG,求证: AG=AD。
9、已知在三角形ABC中 ,AD 是 BC边上的中线 ,E 是 AD上的一点 , 且 BE=AC,延长 BE交 AC与 F, 求证AF=EF,九年级数学【答案】1. 如下图连接 AC并取其中点 Q,连接 QN和 QM,所以可得∠QMF=∠F,∠QNM=∠DEN和∠QMN=∠ QNM,从而得出∠DEN=∠ F。
2. 过 E,C,F 点分别作 AB 所在直线的高 EG ,CI ,FH 。
