NOIP2010模拟试题
冲刺NOIP2010模拟试题六

冲刺NOIP2010模拟试题六(提高组复赛)试题:1.油滴扩展【问题描述】在一个长方形框子里,最多有N(0≤N≤6)个相异的点。
在其中任何一个点上给一个很小的油滴,那么这个油滴会一直扩展,直到接触到其他油滴或者框子的边界。
必须等一个油滴扩展完毕才能放置下一个油滴。
那么应该按照怎样的顺序在这N个点上放置油滴,才能使放置完毕后所有油滴占据的总体积最大呢?(不同的油滴不会相互融合)注:圆的面积公式V=pi*r*r,其中r为圆的半径。
【输入】第一行一个整数N。
第二行为长方形边框一个顶点及其对角顶点的坐标,x,y,x’,y’。
接下去N行,每行两个整数xi,yi,表示盒子内N个顶点的坐标。
以上所有的整数都在[-1000,1000]内。
【输出】一行,一个整数,长方形盒子剩余的最小空间(结果四舍五入输出)。
【输入样例】,20 0 10 103 37 7【输出样例】502.数列(sequence)【问题描述】虽然msh长大了,但她还是很喜欢找点游戏自娱自乐。
有一天,她在纸上写了一串数字:1,1,2,5,4。
接着他擦掉了一个1,结果发现剩下1,2,4都在自己所在的位置上,即1在第1为,2在第2为,4在第4位。
她希望擦掉某些数后,剩下的数列中在自己的位置上的数尽量多。
她发现这个游戏很好玩,于是开始乐此不彼地玩起来…不过她不能确定最多能有多少个数在自己的位置上,所以找到你,请你帮忙计算一下!【输入】第一行为一个数n,表示数列的长度。
接下来一行为n个用空格隔开的正整数,第i行表示数Ai。
【输出】一行一个整数,表示擦掉某些数后,最后剩下的数列中最多能有多少个数在自己的位置上,即Ai=i最多能有多少。
【样例】sequence.in51 12 5 4sequence.out3数据规模对于20%的数据,n≤20对于60%的数据,n≤100对于100%的数据,n≤10003.SOFTW ARE一个软件开发公司同时要开发两个软件,并且要同时交付给用户,现在公司为了尽快完成这一任务,将每个软件划分成m个模块,由公司里的技术人员分工完成,每个技术人员完成同一软件的不同模块的多用的天数是相同的,并且是已知的,但完成不同软件的一个模块的时间是不同的,每个技术人员在同一时刻只能做一个模块,一个模块只能有一个人独立完成而不能由多个人协同完成。
NOIP2010模拟试题

NOIP2010 模拟试题故事背景:话说小FF在经历了上次“寻找古代王族遗产”的探险后,成为了世界上最伟大的探险家并拥有了一大笔财富。
当然他不能坐吃山空,必须创造财富!!于是他买下了传说中的Greed Island并优先发展那里的采矿业……他还将其称为Greed Island的“NewBe_One”计划。
试题一:新的开始【题目描述】发展采矿业当然首先得有矿井,小FF花了上次探险获得的千分之一的财富请人在岛上挖了n口矿井,但他似乎忘记考虑的矿井供电问题……为了保证电力的供应,小FF想到了两种办法:1、在这一口矿井上建立一个发电站,费用为v(发电站的输出功率可以供给任意多个矿井)。
2、将这口矿井与另外的已经有电力供应的矿井之间建立电网,费用为p。
小FF希望身为”NewBe_One" 计划首席工程师的你帮他想出一个保证所有矿井电力供应的最小花费。
【输入格式】第一行一个整数n,表示矿井总数。
第2~n+1行,每行一个整数,第i个数v[i]表示在第i口矿井上建立发电站的费用。
接下来为一个n*n的矩阵P,其中p[ i , j ]表示在第i口矿井和第j口矿井之间建立电网的费用(数据保证有p[ i, j ] = p[ j, i ], 且p[ i, i ]=0)。
【输出格式】仅一个整数,表示让所有矿井获得充足电能的最小花费。
【输入样例】454430 2 2 22 03 32 3 0 42 3 4 0【输出样例】9输出样例说明:小FF可以选择在4号矿井建立发电站然后把所有矿井都与其建立电网,总花费是3+2+2+2 = 9。
【数据范围】对于30%的数据:1<=n<=50;对于100%的数据:1<=n<=300; 0<=v[i], p[i,j] <=10^5.试题二工业时代【试题描述】小FF的第一片矿区已经开始运作了,他着手开展第二片矿区……小FF的第二片矿区,也是”NewBe_One“计划的核心部分,因为在这片矿区里面有全宇宙最稀有的两种矿物,科学家称其为NEW矿和BE矿。
Noip2010模拟题由朱全民老师提供1

Noip2010模拟题由朱全民老师提供PROBLEM 1. SHLQSH数问题描述:我们把t1 , t2 (包括t1 , t2 (1<=t1<t2<=10000000))之间的所有数的约数个数和n 称为t1 , t2的shlqsh数;问题是给出数据t1 , t2后,求t1 , t2的shlqsh数;输入输入文件 shlqsh.in 仅包含一行,共有两个整数,表示t1 t2 (用空格分开)输出输出文件shlqsh.out 仅有一个整数,表示t1 , t2之间的shlqsh数。
输入样例:2 6输出样例:13样例说明:(说明部分不必输出)2的约数有1,2 (2个);3的约数有1,3 (2个);4的约数有1,2,4 (3个);5的约数有1,5 (2个);6的约数有1,2,3,6 (4个)。
所以2 6 的shlqsh数为13【数据规模】对于50 %的数据,保证有t1,t2<=5000000对于全部的数据,保证有t1,t2<=10000000PROBLEM 2.石材切割问题描述:某人得到一块N*M个小格的矩形石材(可能是玉石),经专家分析,把这个矩形石材的每个小格都有一个价值(使用一个绝对值不大于10的整数来描述),现在将这块石材切割成两块矩形石材,注意,切割只能与该矩形边平行,也就是说不能把矩形的小格切碎,假设每块矩形石材的价值为该矩形中所有小格子价值之和。
问怎样切割,才能使得这两个矩形的价值乘积最大。
如下图是一种比较好的切割方式。
输入格式:输入文件BRICK.IN的第一行为2个正整数N和M,表示石材被划分为N*M个格子。
接下来N行,每行有M个整数,代表这个格子的价值。
输出格式:输出文件BRICK.OUT只有一行,包含一个整数,为两个矩形的价值的最大乘积。
数据范围对于30%的数据,满足N,M≤5。
对于100%的数据,满足N,M≤100。
每个小格的伤害值的绝对值不超过10。
一切数据及中间变量不超过longint范围。
NOIP10(pty)
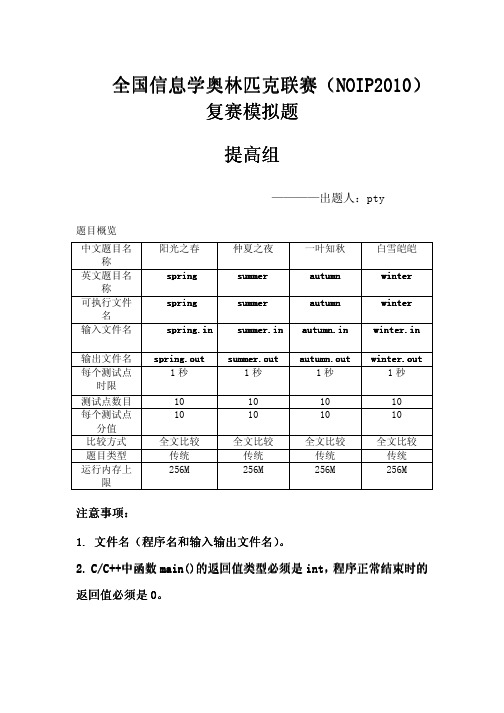
全国信息学奥林匹克联赛全国信息学奥林匹克联赛((NOIP2010NOIP2010))复赛模拟题复赛模拟题提高组提高组————出题人:pty题目概览 中文题目名称 阳光之春 仲夏之夜 一叶知秋 白雪皑皑 英文题目名称 spring spring summer summer autumn autumn winter winter 可执行文件名 spring spring summer summer autumn autumn winter winter 输入文件名 spring spring..in in s ummer ummer.in .in .in autumn autumn.in .in .in w inter inter.in .in .in 输出文件名 spring spring.out .out .out s ummer ummer.out .out .outa utumn utumn.out .out .out winter winter.out .out .out 每个测试点时限 1秒1秒1秒1秒测试点数目 10 10 10 10 每个测试点分值 10 10 10 10 比较方式 全文比较 全文比较 全文比较 全文比较 题目类型 传统 传统 传统 传统 运行内存上限256M256M256M256M注意事项注意事项::1. 1. 文件名文件名文件名((程序名和输入输出文件名程序名和输入输出文件名)。
)。
C/C++2. C/C++中函数中函数main()main()的返回值类型必须是的返回值类型必须是int int,,程序正常结束时的返回值必须是0。
1、阳光之春阳光之春spring.pas/c/cpp).pas/c/cpp)(spring.pas/c/cpp)【问题描述】春天静悄悄地来了。
HJ站在窗前,欣赏着这和谐的万物。
他背着手,慢步踱行,吟诵道:“春色满园关不住,一枝红杏出墙来”,好诗啊!(HJ不愧是有知识的人)。
金华一中信息学奥林匹克联赛(NOIP2010)复赛模拟试题(十八)

金华一中信息学奥林匹克联赛(NOIP2010)复赛模拟试题(十八)一、题目概览二、运行内存限制1.买鱼方案(fish.pas)【问题描述】对于每种鱼,每个人最多每一条,并且有些鱼不能一起买,因为他们之间会互相争斗吞食。
现在资金有限,希望买最多的鱼,如果有多个方案都能买最多的鱼,输出花费资金最多的方案。
【输入格式】第一行两个正整数M(M<=1000)和N(N<=30),分别表示资金和鱼的种类数。
一下N行,每行两个正整数,S(1<=S<=N)和T(T<=1000),分别表示某种鱼的编号和价格。
接下来每行有两个整数数P和Q。
当P,Q均大于0时,表示P,Q不能共处,当P,Q均等于0时,表示输入文件的结束。
【输出格式】第一行两个正整数X,Y,分别表示所买鱼的条数和总花费。
接下来X行,每行一个正整数,表示所买鱼的编号,编号按升序排列输出。
若存在多解,只需要输出其中的一种。
【输入样例】170 71 702 503 304 405 406 307 201 41 73 43 55 76 70 0【输出样例】4 16024562. 公路建设(road.pas)【问题描述】A国有N个城市,按1,2,3…,N编号。
政府想大搞公路建设,提供了优惠政策:对于每一个投资方案的预计总费用,政府负担50%,并允许投资的公司对过往的汽车收取连续5年的养路费。
世界各地的大公司纷纷投资,并提出了自己的建设方案,方案内容包括:公路连接的两座城市的编号,预计的总费用(假设他们的预计总是准确的)。
作为A国公路规划局的总工程师,有权利决定每一个方案是否接受,但是政府的要求是:(1)要保证各个城市之间都有公路直接或者间接相连(2)政府负担最少的费用(3)因为大公司并不是同时提出方案,政府希望每接到一个方案,就可以知道当前需要负担的最小费用和接受的投资方案,以便随时开工。
关于你给投资公司的回复可以等到开工以后再给。
A国一开始是没有公路的。
2010 NOIP初赛模拟试题2——prn

二.问题求解(共2题,每题5分,共计10分)21. 自然数按右图所示的方法排列。问:射线b上第1995个数是 22. 2999最后两位数是
四、阅读程序(共4题,每题8分,共计32分)
23. #include "stdio.h" #define N 7 int fun1(char s[],char a,int n) {int j; j=n; while(a<s[j] && j>0) j--; return j; } int fun2(char s[],char a,int n) {int j=1; while(a>s[j] && j<=n) j++; 程 序: return j; } int main() {char s[N+1];
五、完善程序(前5空,每空2分,后6空,每空3 分,共28分)
1、假设一个剧场有N*N个座位,顾客买票时可以提出任意有效的座号请
求。下面用二维数组a[N] [N],模拟剧场中的座位,a[i] [j]等于0表示 第i排第j列(0≤I,j≤N-1)的票尚未售出。 函数 int Find(int a [][N],int R,int*row,int *col)的功能 是:在部分票已售出的情况下,找出剧场中的R*R个空座位,要求这些 座位的排列形成一个正方形。若找到满足要求的一个座位排列,则函数 返回1,并算出该正方左上角的行、列号;若未找到,返回0。 例如,一个7×7个座位的剧场如下图(a)所示,已售出部分座位 的剧场如下图(b)所示,图中阴影部分表示已售出的座位,从图(b) 中找出的3×3正方形空座位如图(c)中斜线区所示。
NOIP初赛模拟试题 (C语言)
一、单项选择题(共20题,每题1.5分,共计30分。每题有 且仅有一个正确答案。)
NOIP2010信息学奥赛初赛普及组模拟试题(二)

NOIP2010初赛模拟试题(六)(普及 Pascal语言二小时完成)●●全部试题答案均要求写在答卷纸上,写在试卷纸上一律无效●●一.单项选择题(共20题,每题1.5分,共计30分。
每题有且仅有一个正确答案。
)1、.在所有由两个1和六个0组成的8位二进制整数(补码)中,最小的数是:()A.-127B.-64 C.-128 D.-652、.在一棵二叉树结点的先根序列、中根序列和后根序列中,所有叶子结点的先后顺序()A.都不相同B.完全相同C.先序和中序相同,而与后序不同D.中序和后序相同,而与先序不同3、下面有效的IP地址是:()A.202.280.130.45 B.130.192.33.45C.192.256.130.45 D.280.192.33.4564、一台具有1024*768分辨率、可显示65 536种颜色的显示器,其显示适配器(显示卡)上显示存储器容量的配置为:()A.512K B.1MB C.大于1.6MB,小于2MB D.2MB5、进行二分法查找,则线性表()A.必须顺序方式存储B.必须以链接方式存储,且数据元素已按值排好序C.必须以链接方式存储D.必须以顺序方式存储,且数据元素已按值排好序6、机器语言是用()编写的。
A.二进制码B.ASCII码C.十六进制码D.国标码7、一棵含有101个结点的完全二叉树存储在数组A[1..101]中,对1≤k≤101,若 A[k]是叶子结点,则k的最小值是:()A.51 B.50 C.49 D.488、不同的计算机,其指令系统也不相同,这主要取决于()A. 所用的操作系统B. 系统的总体结构C. 所用的CPUD. 所用的程序设计语言9、计算机主机是由CPU 与()构成的。
A.控制器B。
输入、输出设备C.运算器D.内存储器10、计算机系统总线上传送的信号有()。
A.地址信号与控制信号B.数据信号、控制信号与地址信号C.控制信号与数据信号D.数据信号与地址信号11、计算机的运算速度取决于给定的时间内,它的处理器所能处理的数据量。
冲刺Noip2010模拟试题七

冲刺Noip2010模拟试题七1、数列(Sequence.pas/c/cpp)问题描述一个数列定义如下:f(1) = 1,f(2) = 1,f(n) = (A * f(n - 1) + B * f(n - 2)) mod 7。
给定A,B和n的值,要求计算f(n)的值。
输入格式输入文件(sequence.in)仅一行包含3个整数A,B和n,其中(1≤ A, B ≤1000, 1 ≤n≤100,000,000)。
输出格式输出文件(sequence.out)仅一行,一个整数,即f(n)的值。
输入样列1 1 3输出样列2说明:若输入样例为1 2 10,则输出为5。
数据规模20%的数据,n≤1,00040%的数据,n≤100,000100%的数据,n≤100,000,0002、最长路(path.pas/c/cpp)问题描述设G为有n个顶点的有向无环图,G中各顶点的编号为1到n,且当<i,j>为G中的一条边时有i < j。
设w(i,j)为边<i,j>的长度,请设计算法,计算图G中<1,n>间的最长路径。
输入格式输入文件path.in的第一行有两个整数n和m,表示有n个顶点和m条边,其中(2≤n≤1500,m≤50000),接下来m行中每行输入3个整数a ,b,v表示从a点到b点有条边,边的长度为v。
输出格式输出文件path.out,一个整数,即1到n之间的最长路径.如果1到n之间没连通,输出-1。
输入样例2 11 2 1输出样例1说明:若输入样例为2 0,则输出为-1。
数据规模20%的数据,n≤100,m≤100040%的数据,n≤1,000,m≤10000100%的数据,n≤1,500,m≤500003、木棍(wooden.cpp/pas/c)问题描述有n根木棍,每根的长度l和重量w已知。
这些木棍将被一台机器一根一根的加工。
机器需要一些启动时间来做准备工作,启动时间与木棍被加工的具体情况有关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
NOIP2010 模拟试题
故事背景:
话说小FF在经历了上次“寻找古代王族遗产”的探险后,成为了世界上最伟大的探险家并拥有了一大笔财富。
当然他不能坐吃山空,必须创造财富!!于是他买下了传说中的Greed Island并优先发展那里的采矿业……他还将其称为Greed Island的“NewBe_One”计划。
试题一:
新的开始
【题目描述】
发展采矿业当然首先得有矿井,小FF花了上次探险获得的千分之一的财富请人在岛上挖了n口矿井,但他似乎忘记考虑的矿井供电问题……
为了保证电力的供应,小FF想到了两种办法:
1、在这一口矿井上建立一个发电站,费用为v(发电站的输出功率可以供给任意多个矿井)。
2、将这口矿井与另外的已经有电力供应的矿井之间建立电网,费用为p。
小FF希望身为”NewBe_One" 计划首席工程师的你帮他想出一个保证所有矿井电力供应的最小花费。
【输入格式】
第一行一个整数n,表示矿井总数。
第2~n+1行,每行一个整数,第i个数v[i]表示在第i口矿井上建立发电站的费用。
接下来为一个n*n的矩阵P,其中p[ i , j ]表示在第i口矿井和第j口矿井之间建立电网的费用(数据保证有p[ i, j ] = p[ j, i ], 且p[ i, i ]=0)。
【输出格式】
仅一个整数,表示让所有矿井获得充足电能的最小花费。
【输入样例】
4
5
4
4
3
0 2 2 2
2 0
3 3
2 3 0 4
2 3 4 0
【输出样例】
9
输出样例说明:
小FF可以选择在4号矿井建立发电站然后把所有矿井都与其建立电网,总花费是3+2+2+2 = 9。
【数据范围】
对于30%的数据:1<=n<=50;
对于100%的数据:1<=n<=300; 0<=v[i], p[i,j] <=10^5.
试题二
工业时代
【试题描述】
小FF的第一片矿区已经开始运作了,他着手开展第二片矿区……
小FF的第二片矿区,也是”NewBe_One“计划的核心部分,因为在这片矿区里面有全宇宙最稀有的两种矿物,科学家称其为NEW矿和BE矿。
矿区是被划分成一个n*m的矩形区域。
小FF探明了每一小块区域里的NEW矿和BE矿的蕴藏量,并且小FF还在矿区的北边和西边分别设置了NEW矿和BE矿的收集站。
你的任务是设计一个管道运输系统,使得运送的NEW矿和BE矿的总量最多。
管道的型号有两种,一种是东西向,一种是南北向。
在一个格子内你能建造一种管道,但不能两种都建。
如果两个同类型管道首位相接,它们就可以被连接起来。
另外这些矿物都十分不稳定,因此它们在运送过程中都不能拐弯。
这就意味着如果某个格子上建有南北向管道,但是它北边的格子建有东西向管道,那么这根南北向管道内运送的任何东西都将丢失。
进一步地,运到NEW矿收集站的BE矿也会丢失,运到BE矿收集站的NEW 矿也会丢失。
【输入格式】
第一行包含两个整数n和m,表示矿区大小。
以下n行,每行m个整数,其中第i行第j个整数G[ i , j ] 描述各个格子上的BE矿数量。
接下来以类似的矩阵表示各个格子上的NEW矿数量。
【输出格式】
仅一个整数,表示最多可以采集到的NEW矿和BE矿的总量。
【输入样例】
4 4
0 0 10 9
1 3 10 0
4 2 1 3
1 1 20 0
10 0 0 0
1 1 1 30
0 0 5 5
5 10 10 10
【输出样例】
98
【数据范围】
对于30%的数据:0<= n,m <=100;
对于100%的数据:0<= n, m <=1000;
0<= G[ i, j ] <=1000.
试题三:
杀蚂蚁
【题目描述】
说“善有善报,恶有恶报,不是不报……”。
小FF一心只顾自己企业的壮大而没顾及自己的采矿业对Greed Island上生态环境的破坏,Greed Island的环境日益恶劣。
终于,岛上的蚂蚁们变异了,它们决定对小FF的矿区进行攻击,欲将岛上的人类驱逐出去……面对蚂蚁
们的进攻,人类节节败退。
无奈之下,小FF请来了全宇宙最强的防御系统制造商派来的工程机器人——SCV,希望能够阻挡蚂蚁的攻势。
经过小FF的研究,他发现蚂蚁们每次都走同一条长度为n个单位的路线进攻,且蚂蚁们的经过一个单位长度所需的时间为T秒。
也就是说,只要小FF在条路线上布防且给蚂蚁造成沉痛伤害就能阻止蚂蚁的进军。
SCV擅长制造的防御塔有三种,分别是激光塔,放射塔和干扰塔,他们可以在一个单位长度内修建一座防御塔。
三种防御塔的作用如下:
激光塔:使用高能激光,当蚂蚁从塔前经过时每秒对蚂蚁造成r点伤害。
放射塔:释放放射性元素,当蚂蚁经过这座塔后,每一秒受到g点伤害。
干扰塔:干扰塔负责干扰蚂蚁们的信息素,使得蚂蚁在经过这座塔后,经过之后每一个单位长度的时间变成T+b。
当然,放射塔和干扰塔的效果是可以叠加的,也就是说如果敌人经过x座放射塔,那么敌人每秒钟会受到x*g点伤害;同理,如果敌人经过y座干扰塔,那么敌人经过一个单位长度的时间将变为T+y*b。
现在距离蚂蚁的下一轮进攻还有足够长的时间,你这个“NewBe_One”计划的首席工程师现在被任命为战略总参谋长,因此你必须设计一个给蚂蚁们造成最大伤害的布塔方案。
【输入格式】
输入数据仅一行,5个整数n, r, g, b, T中间用一个空格隔开。
它们分别表示你可以布防的总长度,激光塔的效果、放射塔的效果和干扰塔的效果。
【输出格式】
输出仅一个整数,代表你的方案给敌人带来的最大伤害值。
【输入样例】
5 4 3 2 1
【输出样例】
82
输出样例解释:
第1号位置为放射塔,第2,3号位置建造干扰塔,第4,5号位置建造激光塔。
【数据范围】
对于30%的数据:1<=n<=20;
对于60%的数据:1<=n<=1024;
0<=r, g, b<=65536;
0<=T<=3;
对于另外40%的数据:
1<=n<=400;
0<=r, g, b<=2^31-1;
0<=t<=1000.
试题四
贪婪大陆
【题目描述】
面对蚂蚁们的疯狂进攻,小FF的Tower defence宣告失败……人类被蚂蚁们逼到了Greed Island上的一个海湾。
现在,小FF的后方是一望无际的大海,前方是变异了的超级蚂蚁。
小FF还有大好前程,他可不想命丧于此,于是他派遣手下最后一批改造SCV布置地雷以阻挡蚂蚁们的进攻。
小FF最后一道防线是一条长度为N的战壕,小FF拥有无数多种地雷,而SCV每次可以在[ L , R ]区间埋放同一种不同于之前已经埋放的地雷。
由于情况已经十万火急,小FF在某些时候可能会询问你在[ L' , R'] 区间内有多少种不同的地雷,他希望你能尽快的给予答复。
【输入格式】
第一行为两个整数n和m;n表示防线长度,m表示SCV布雷次数及小FF询问的次数总和。
接下来有m行,每行三个整数Q,L , R;若Q=1 则表示SCV在[ L , R ]这段区间布上一种地雷,若Q=2则表示小FF询问当前[ L , R ]区间总共有多少种地雷。
【输出格式】
对于小FF的每次询问,输出一个答案(单独一行),表示当前区间地雷总数。
【输入样例】
5 4
1 1 3
2 2 5
1 2 4
2 3 5
【输出样例】
1
2
【数据范围】
对于30%的数据:0<=n, m<=1000;
对于100%的数据:0<=n, m<=10^5.。
