作业答案水利学与泵第2章静力学PPT
流体力学第2章水静力学--用.ppt

说明:(1)在连通的同种的静止液体中,水平面必定是
等压面。 (2)静止液体的自由液面是一个水平面。 (3)两种液体的分界面是水平面。 成立条件:静止、连通及均质液体
在等压面上有:
等压面有以下性质:
dp dW 0
1、等压面必为等势面。 由前述可知,若dp=0 ,必有dW=0 , 即 W= 常数,可见,等压面就是等势面。 2、在静止流体中质量力与等压面相垂直(正交)。 Xdx Ydy Zdz 0 从(2-2)可得等压面方程为:
1 1 1 dy dz px dy dz pn dx dy dz X 0 2 2 6
证明步骤如下:
1 1 1 dy dz px dy dz pn dx dy dz X 0 2 2 6 1 p p dx X 0 化简得: x n 3
1 )以应力单位表示 : 压强用单位面积上受力的大小, 2 即应力单位表示,为:N / m 2或Pa,kPa,可记为 kN / m 2)以大气压表示:工程中:1工程大气压=98kPa 3)水柱高表示:由于水的容重为常量,水柱高h p 的数值反映了压强的大小。
(h
)
三者关系: 1 P工程=1.0Kgf/cm2=10mH2O=98KPa 1 P标准 = 101.3KPa =760mmHg=10.336mH2O
2. 大小特性:证明 选择微小四面体进行分析,见右 图,四面体的受力合为零。
命题:当四面体OABC无限地缩小到O
点时,平均压强 px=py=pz=pn?
第2章 水静力学
证明步骤如下:
1) 设四面体的质点为M(x,y,z); 2) 分析作用于四面体的表面力—压力:
1 Px dy dz px 2
习题 水静力学PPT课件

解:当下游无水时: 水平分力
Px rhC1 Ax1 9.813 261 3312.4KN (水平向右) 垂直分力 Pz rV1 9.8 梯形abcd1 9.8 0.5 (2618) 41 862.4KN (竖直向下)
第28页/共54页
当下游有水时 水平分力 Px rhC1 Ax1 rhc2 Ax2 3312.4 9.8 3 6 1 3316KN (水平向右z \ z) 垂直分离 Pz rV1 rV2 862.4 9.8 三角形efg 1 862.4 9.8 0.5 3 6 1 950.6KN (竖直向下)
1 ctg 60 1.73 2
1.73 P(sin 60
e)
第34页/共54页
拉T力 9.8 1 (2 0.845) .662 131.56KN 2
(h2)3当 h2 1.73m 时, AB闸门上的压强分布如AacB,
P1
9.8 1
1.73 sin 60
58.8KN
对A点取矩
T • ctg60 1.73 9.8 1 ctg 60 1.73
• 1. A、B两点之压差为多 少?
• 2. A、B两点中有无真空
第5页/共54页
• 1-2解:
• (1) 由图知道A点喝B点得压差是由h1高度得
两种密度不同PB 引 P起A 的(,0 即密A )度gh1差引起的
• 所以
0.52kPa
• (2)存在真空PA Ags m gh
• 由A点在的等压面 知5.89KN / m2 PAK 5.89KN / m2
第33页/共54页
解:
(h1)3当 0
AB 闸门上的压强分布图如AabB,
9.8
1.73
第二章水静力学

第二章 水静力学
四面体的体积D V为
Z D Pn Px A Py
D
V=
1
6
Dx
Dy
Dz
C
O B Pz X
Y
总质量力在三个坐标方向的投影为
Fx
=1 6
Dx Dy
Dz X
Fy
=
1 6
Dx Dy Dz Y
Fz
=1 6
Dx Dy
Dz
Z
第二章 水静力学
按照平衡条件,所有作用于微 小四面体上 的外力在各坐标轴 上投影的代数和应分别为零
第二章 水静力学
Pa
四、测压管高度,测压 管水头及真空度
一个密闭容器,P0>Pa
则:在水力学中,hA高度
P0
hA
即为测压管高度。
这种测量压强的管子叫测压管。
h
在容器内有 pA = p0 h
A
在右管中有 pA = pa hA
ZA
因此 p0 h = pa hA
hA
=
pA
pa
可写成: p = p0 z
第二章 水静力学
对于液体中各点来说,一般用各点在液面以下的深
度 h 代替 z , 因此将 h = z 代入上式得:
p = p0 h 静水全压强
上式即为水静力学基本方程式的另一种形式 它说明:
1、在静止的液体中,压强随深度线性规律变化
p 2、静止液体中任一点的压强 等于表面压强 p0
x
y
z
由此得: X = U ,Y = U , Z = U
x
y
z
《水力学》第二章答案

第二章:水静力学 一:思考题2-1.静水压强有两种表示方法,即:相对压强和绝对压强2-2.特性(1)静水压强的方向与受压面垂直并指向手压面;(2)任意点的静水压强的大小和受压面的方位无关,或者说作用于同一点上各方向的静水压强都相等. 规律:由单位质量力所决定,作为连续介质的平衡液体内,任意点的静水压强仅是空间坐标的连续函数,而与受压面的方向无关,所以p=(x,y,z)2-3答:水头是压强的几何意义表示方法,它表示h 高的水头具有大小为ρgh 的压强。
绝对压强预想的压强是按不同的起点计算的压强,绝对压强是以0为起点,而相对压强是以当地大气压为基准测定的,所以两者相差当地大气压Pa.绝对压强小于当地大气压时就有负压,即真空。
某点负压大小等于该点的相对压强。
Pv=p'-pa2-4.在静水压强的基本方程式中C g p z =+ρ中,z 表示某点在基准面以上的高度,称为位置水头,g p ρ表示在该点接一根测压管,液体沿测压管上升的高度,称为测压管高度或压强水头,g p z ρ+称为测压管水头,即为某点的压强水头高出基准面的高度。
关系是:(测压管水头)=(位置水头)+(压强水头)。
2-5.等压面是压强相等的点连成的面。
等压面是水平面的充要条件是液体处于惯性坐标系,即相对静止或匀速直线运动的状态。
2-6。
图中A-A 是等压面,C-C,B-B 都不是等压面,因为虽然位置高都相同,但是液体密度不同,所以压强水头就不相等,则压强不相等。
2-7.两容器内各点压强增值相等,因为水有传递压强的作用,不会因位置的不同压强的传递有所改变。
当施加外力时,液面压强增大了Ap∆,水面以下同一高度的各点压强都增加Ap∆。
2-8.(1)各测压管中水面高度都相等。
(2)标注如下,位置水头z,压强水头h,测压管水头p.图2-82-9.选择A2-10.(1)图a 和图b 静水压力不相等。
因为水作用面的面积不相等,而且作用面的形心点压强大小不同。
作业答案_水利学与泵_第2章_静力学
Δh2
h3
h2
h1
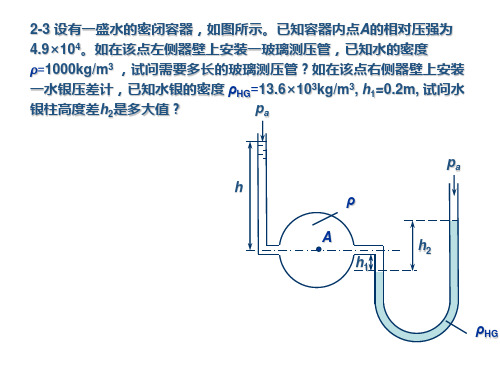
2-10 设有一盛有油和水的圆柱形澄清桶,如图所示。油和水之间的分 界面借玻璃管A来确定,油的上表面借玻璃管B来确定。若已知圆桶直 径D=0.4m, h1=0.5m, h2=1.6m, 油的密度ρ0=840kg/m3,水的密度 ρ=1000kg/m3。试求桶内的水和油体积各为多少? 若已知h1=0.2m ,h2=1.2m ,h3=1.4m ,试求油的密度ρ0。 (1)根据题意 pa
p2
p1
4
D (2 h)
2
4
d2 h
Δh ρ0
Δh
h 200 h
A点压强 pA p1 Oil ( H h)
B点压强 pB p2 Oil ( H h h) Water h B
H h A
ρ
p A pB
p1 Oil ( H h) p2 Oil ( H h h) Water h p1 p2 Oil (2h h) Water h Water 0.01
pa
h
ρ A h2
h1
ρHG
pa h p A h
p A pa
4.9 104 1000 9.807
pa Hg h2 p A h1 h2 p A pa h1
Hg
4.9 104 1000 9.807 0.2 13.6 103 9.807
Байду номын сангаасVOil
4
D 2 ( h3 h1 )
VWater
4
D h1
水力学第二章(3)

主要内容: §2-6 作用在曲面上的静水总压力
§2-7 浮体的平衡与稳定 §2-8 在重力与惯性力同时作用下 液体的相对平衡
2.6
作用在曲面上的静水总压力
在水利工程上常遇到受压面为曲面的情况,如拱坝坝面、
弧形闸墩、弧形闸门等。
A′ B′
作用在曲面上静水总 压力分解为水平分力
θ
和铅直分力分别计算,
δ
T
2 T Px p 2 r
p T r
图 2.6.4
5 3
A
r
1 . 5 10 4 10 5 10
2
1 . 2 10 ( kN/m
4
2
)
2.7
浮体的平衡与稳定
2.7.1 浮力及物体的沉浮
y
z
浸没于液体中的物体受到的x轴方向静水总压力应 为零
Px 左 = Px 右
(a)
(b)
(c)
图 2.7.2
不稳定平衡:重心C在浮心D之上,重力与浮力组 成使物体继续倾斜的力矩,这种状态下的平衡为 不稳定平衡。
随遇平衡:当重心C与浮心D重合时,潜体在液体 中的方位是任意的,称为随遇平衡。
(a)
(b)
(c)
注意:要使潜体处于稳定平衡状态,必须使其重 心位于浮心之下。
图 2.7.2
Z
图 2.6.1
静水总压力的铅直分力
作用在曲面AB上的静水总压力的铅直分力Pz
Pz
dP sin
A
hdA sin
AZ
h ( dA ) Z
A′ B′
h(dA)z是微小曲面和它在自
由水面延长面上的投影之间
水力学-第二章水静力学

13
水力学 液体平衡的全微分方程 2.
Xdx Ydy Zdz
第 二 章 水 静 力 学
3、等压面
1
dp
Xdx Ydy Zdz 0
W X x W Y y W Z z
力势函数
W W W dx dy dz dp x y z
p g (
2r 2
2g
z) c
由边界条件:x = y = z = 0,p = p0 则得
C=p0
p p 0 g (
则
r
2 2
2g
z)
47
水力学
静水总压力Static Surface Forces
第 二 章 水 静 力 学
平面压力Forces on plane areas
水力学
相对压强
第 二 章 水 静 力 学
pr pabs pa
真空压强
pv pa pabs
A
A点相 对压强 大气压强 pa A点绝 对压强
压强
相对压强基准
B
B点真空压强
B点绝对压强 绝对压强基准
O
O
水力学
p 3、 z C 的物理意义和几何意义 g
第 二 章 水 静 力 学
p dxdydz Xdxdydz 0 x
10
水力学
以ρdxdydz 除以上式各项,并化简,
第 二 章 水 静 力 学
得x方向的液体平衡微分方程。同 理可得出其他两个方向的液体平衡微分 方程
(Differential equation of liquid equilibrium)。
11
作用 点…… 记住了 吗? ?
第二章水静力学水力学PPT课件

第二章
1
《水力学》精品课程多媒体课件
§2-1 静水压强及特性
一、静水压强定义
lim
A0
P A
N/m2 (Pa) KN/m2 (KPa)
二、特性
1、垂直指向作用面
Ⅰ
N
N
Ⅱ
Ⅱ
2、任意点上各方向p相等
用牛顿第二定律证明
F=0
① 说明该性质的含义(结合图形)
2
《水力学》精品课程多媒体课件
则该点存在真空,又称“负
压”真空度:pv pa p'
理论上:pv pa 实际中达不到。
真空高度:h v
pv
16
《水力学》精品课程多媒体课件
理论上:hv=10m;实际上:hv=7~8m 举例:
讨论分布规律:
p 2r2
(2-13)式变形为
z (2-14)
r 2g
等压面方程: 2r 2 z c
2g
可见等压面为旋转抛物面,自由面亦为等压
面,其上p=0。自由液面方程:
12
2r2
z
(2-15)
2g
《水力学》精品课程多媒体课件
由(2-15)式可知: 2 r 2
2g
表示A点处自由面高出x0y平面的
dpd(g)
积分得:
pzc(2-10)
d(z p) 0
积分得 :zp c
说明:在重力作用下,均质不可压缩液体中,各点的
(z p ) 值相等。
在自由面上:
zz0;pp0;cz0p0 9
pp0(z0 z)
pp0 h(2-11)
二、几种质量力同时作用
取坐标研究,液体相对于坐标及 处于平衡状态。属相对静止。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
pa ρ
3 1
4
2
ρHG
p2 p1 Hg (1 2 ) pa Hg (1 2 )
p3 p2 (3 2 ) pa Hg (1 2 ) (3 2 )
p4 p3 Hg ( 3 4 ) pa ( 3 2 ) Hg (1 2 3 4 )
Oil (2h h) Water h 0.01 Water
h 200 h
h 0.11m
2-9 设有一容器盛有三种各不相同的密度且各不相混的液体,如图所示。 已知ρ1=700kg/m3, ρ2=1000kg/m3, ρ3=1200kg/m3,试求三根测压 管内的液面到容器底的高度h1、 h2和 h3、 解:根据题意
如图建立坐标
根据题意,容器内任意一点(x, z)的 流体质点所受到的质量力为: az a
h3 2 2.83 4.83 m
Δh2
h3
h2
h1
2-10 设有一盛有油和水的圆柱形澄清桶,如图所示。油和水之间的分 界面借玻璃管A来确定,油的上表面借玻璃管B来确定。若已知圆桶直 径D=0.4m, h1=0.5m, h2=1.6m, 油的密度ρ0=840kg/m3,水的密度 ρ=1000kg/m3。试求桶内的水和油体积各为多少? 若已知h1=0.2m ,h2=1.2m ,h3=1.4m ,试求油的密度ρ0。 (1)根据题意 pa
VOil
4
D 2 ( h3 h1 )
VWater
4
D h1
2
ρ0
B
A
ρ h1
h3
h2
D
pA Water (h2 h1 ) Oil (h3 h1 )
Water 1000 h3 (h2 h1 ) h1 (1.6 0.5) 0.5 1.309 Oil 840
pa
2 1
pab 101325 9807 0.3 9.83810 Pa
4
相对压强
p 水h1 2942 Pa
h2
水 0.3 h2 h1 =0.0221m pa Hg 13.6
h1 ρHg 水
ρ
2-6 设有两盛水的密闭容器,其间连以空气压差计,如图a所示。已知点 A、点B位于同一水平面,压差计左右两肢水面铅垂高差为h,空气重量 可略去不计,试以式表示点A、点B两点的压强差值。 若为了提高精度,将上述压差计倾斜放置某一角度θ=30°,如图b所示。 试以式表示压差计左右两肢水面距离l。 ρa
h1 6
m
1 1.4 m 2
2m 2m 2m
h1 2 2 1 h1 2
pa ρ1 ρ2 ρ3
h2 4 h1 5.4 m
h2 3 2 1 2 2
Δh1
2 h2 2 1 2.83 m 3
pa h p A h
p A pa
4.9 104 1000 9.807
pa Hg h2 p A h1 h2 p A pa h1
Hg
4.9 104 1000 9.807 0.2 13.6 103 9.807
2-4 设有一盛水的密闭容器,连接一复式水银测压计,如图所示。已知 各液面的高程分别为,▽1=2.3m, ▽2=1.2m, ▽3=2.5m, ▽4=1.4m, ▽5=3.0m, 水的密度 ρ=1000kg/m3, ρHG=13.6×103kg/m3 , 试求密闭容器内水面上 压强p0的相对压强值。 p0
(2)根据试求油的密度ρ0
pa B
Oil
(h2 h1 ) Water (h3 h1 )
ρ0
1.2 0.2 1000 833.3 1.4 0.2
A
ρ h1
h3
h2
D
2-16 设有一敞口容器(如图所示)以3.0m/s2的等加速度沿α=30°的 倾斜轨道向上运动,试求容器内自由表面方程及其与水平面所成的角 度θ
p pA pB h1
h1 ρ A B A
l
l
)
h1 sin
B
2-8 杯式微压计,上部盛油,下部盛水, 圆杯直径D=40 mm, 圆管直径 d=4mm, 初始平衡位置读数h=0。当p1-p2=10mmH2O时, 在圆管中读得 的h(如图所示)为 多大?油的密度 ρ=918 kg/m3,水的密度 ρ=1000 kg/m3 。 根据题意,显然
p5 p0 p4 ( 5 4 ) pa ( 3 2 5 4 ) Hg (1 2 3 4 ) 13.6 103 9.807 (2.3 1.2 2.5 1.4) 1.0 103 9.807 (2.5 3.0 1.2 1.4) 2.650103
2-5 设有一盛空气的密闭容器,在其两侧各接一测压装置,如图所示。 已知h1=0.3m。试求容器内空气的绝对压强值和相对压强值,以及水银 真空计左右两肢水银液面的高差h2。(空气重度略去不计)。 解:容器内的绝对压强
pab p1 p2 pa 水h1 pa Hg h2
p2
p1
4
D (2 h)
2
4
d2 h
Δh ρ0
Δh
h 200 h
A点压强 pA p1 Oil ( H h)
B点压强 pB p2 Oil ( H h h) Water h B
H Oil ( H h) p2 Oil ( H h h) Water h p1 p2 Oil (2h h) Water h Water 0.01
