2010年数学建模C、D题解析
2010高教社杯全国大学生数学建模竞赛C题

同上的解法求得方案一最佳。
问题一的解答:
2、当共用管线和非共用管线费用不相同时要考
虑方案二中的各部分管线的总费用并与方案一
中的费用对比,得出最优方案。经过查阅资料
得知某非共用管道5万元/千米;共用管道8万 元/千米;方案一的费用为
C1 5 l 2 (a b 方案二的费用为:) 2
;
2010高教社杯全国大学生数学建模 竞赛 C题 输油管线设计的数学模型
阐述的主要问题
某油田计划在铁路线一侧建造两家炼油厂,同 时在铁路线上增建一个车站,用来运送成品油。 由于这种模式具有一定的普遍性,油田设计院 希望建立管线建设费用最省的模型。
针对这个问题,通过三个小问题 进行解答:
1.针对两炼油厂到铁路线距离和两炼油厂间距离的各种不同情形, 提出设计方案。若有共用管线,考虑其共用管线费用与非共用管 线费用相同或不同的情形。 B 2. 两炼油厂的具体位置其中A厂位于郊区(Ⅰ), 厂位于城区 Ⅱ (Ⅱ),两个区域有明显的分界线。若所有管线的铺设费用均相 同, 铺设在城区的管线还需增加拆迁和工程补偿等附加费用, 根据三家工程咨询公司对此项附加费用的估计,为设计院给出管 线布置方案及相应的费用。 3. 为进一步节省费用,炼油厂根据生产能力,选用相适应的油管。 这时的管线铺设费用就各不相同,拆迁等附加费用同上。给出管 线最佳布置方案及相应的费用。
,
2 3 l ,解得 C1 C2 3
问题一的解答:
2)同理:当 a b
当 a b 时,解得C1 C 2。当 a
3 10 3 3a 3b l 时, 2 C l 3 3 3
3l
8
b时,解得
C1 C 2。即方案一最佳。
问题二的解答:
2010年数学建模集训小题目解答

试分别按以下两种形式建立 y 对 x 的回归方程,画出散点图和回归曲线,并根据适当 的指标判断哪一种好。 (1)
1 b =a+ ; y x
j = 1,2,3 )表示生产第 i 种糖用的第 j 种原料的量, ai 表示第 i 种糖果的需求量, b j 表示第 j 种原料的可供量。
总利润为销售总收入与原料总成本之差,总利润
z = 24( x11 + x12 + x13 ) + 15( x21 + x22 + x23 ) − 20( x11 + x21 ) − 12( x12 + x22 ) − 8( x13 + x23 ) = 4 x11 + 12 x12 + 16 x13 − 5 x21 + 3 x22 + 7 x23
原料 A B C 可供量(公斤) 500 750 625 成本(员/公斤) 20 12 8
订单至少需要生产 600 公斤高级奶糖,800 公斤水果糖,为求最大利润,试建立线性规 划模型并求解。 用 j = 1,2,3 分别表示原料 A, B, C。 设 xij ( i = 1,2 , 解: 用 i = 1,2 分别表示高级奶糖和水果糖,
解:Matlab 程序如下。 clc, clear a=[1 0.4 53 158 64 10 12.6 58 112 2 0.4 23 163 60 11 10.9 37 111 3 3.1 19 37 71 12 23.1 46 114 4 0.6 34 157 61 13 23.1 50 134 5 4.7 24 59 54 14 21.6 44 73 6 1.7 65 123 77 15 23.1 56 168 7 9.4 44 46 81 16 1.9 36 143 8 10.1 31 117 93 17 26.8 58 202 9 11.6 29 173 93 18 29.9 51 124 x=a(:,[2:4,7:9]); x=[x(:,1:3);x(:,4:6)]; y=[a(:,5);a(:,10)]; xx=[ones(18,1),x]; %注意数据的格式 [s1,s2,s3,s4,s5]=regress(y,xx)
2010高教社杯全国大学生数学建模竞赛官方题目(含ABCD)
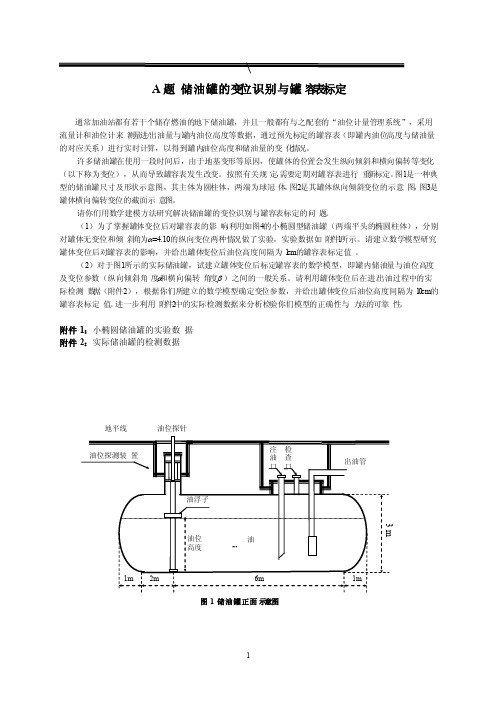
\A 题 储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm 的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β )之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm 的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
附件1:小椭圆储油罐的实验数据 附件2:实际储油罐的检测数据油油浮子出油管油位探测装置注油口 检查口地平线 2m6m1m1m3 m油位高度图1 储油罐正面示意图油位探针油位探针α地平线 图2 储油罐纵向倾斜变位后示意图油油浮子出油管油位探测装置注油口 检查口水平线(b) 小椭圆油罐截面示意图α油油浮子出油管油位探针注油口水平线2.05mcm 0.4m1.2m1.2m1.78m(a) 小椭圆油罐正面示意图图4 小椭圆型油罐形状及尺寸示意图图3 储油罐截面示意图(b )横向偏转倾斜后正截面图地平线β地平线垂直线油位探针(a )无偏转倾斜的正截面图油位探针油位探测装置地平线油3m油B题2010年上海世博会影响力的定量评估2010年上海世博会是首次在中国举办的世界博览会。
数学与统计学学院2010年数学建模竞赛试题

数学与统计学学院2010年数学建模竞赛试题(请先仔细阅读竞赛要求)A题、武汉房地产价格问题房地产价格是一个备受关注的问题。
现在请你就以下几个方面的问题进行讨论1.给出你的房地产价格指标的定义(考虑房子所处的位置(交通,学校,医院,商场…),房子的户型,房子的楼层,房子的朝向,小区的内环境(绿化,容积率…等等),房子的开发商,物业,房子的质量,小区的大小,噪音大小,空气等等…);2.请搜集武汉近两年来的房子日销售情况表(至少搜集10天的武汉的房子日销售情况表);对你的上述房地产价格指标的定义做简化,给出一个简化的武汉的房地产价格指标的定义;并且假设:以你搜集到的10天的武汉的房子日销售情况表中时间最早的那一天武汉的房地产价格指标为100,利用你的简化的武汉的房地产价格指标的定义,计算其他天的武汉的房地产价格指标;3.请搜集相应10天的武汉(或者全国)的物价指标,请你建立武汉的房地产价格指标与武汉(或者全国)的物价指标的关系模型,并假设有一天武汉(或者全国)的物价指标,是你搜集到的10天的武汉的房子日销售情况表中时间最早的那一天的武汉(或者全国)的物价指标的100倍,请你预测那一天的武汉的房地产价格指标;4.如果某人准备在武汉买房,请你给他买房的时机的建议。
中南民族大学数学与统计学学院2010年首届数学建模竞赛要求1、参赛者为中南民族大学任意在校本科生, 以队为单位参赛。
学生自愿组队,每队有且仅有三人,鼓励学生跨院系组队。
比赛开始后不允许更换队员。
2、竞赛时间为:2010年4月9日16时至4月14日16时。
3、竞赛按照甲、乙组分别命题,甲组(参加对象为2007,2008级学生)分为A,B两题,乙组(2009级学生)分为C,D两题,每个参赛队可任选一题,4月9日16时起可在院网页上下载试题。
4、竞赛采取开放的竞赛方式,竞赛期间参赛队员可以使用各种图书资料、计算机和软件,在国际互联网上浏览,但不得与队外任何人(包括在网上)讨论。
2010研究生C题

2010年全国研究生数学建模竞赛C题神经元的形态分类和识别大脑是生物体内结构和功能最复杂的组织,其中包含上千亿个神经细胞(神经元)。
人类脑计划(Human Brain Project, HBP)的目的是要对全世界的神经信息学数据库建立共同的标准,多学科整合分析大量数据,加速人类对脑的认识。
作为大脑构造的基本单位,神经元的结构和功能包含很多因素,其中神经元的几何形态特征和电学物理特性是两个重要方面。
其中电学特性包含神经元不同的电位发放模式;几何形态特征主要包括神经元的空间构象,具体包含接受信息的树突,处理信息的胞体和传出信息的轴突三部分结构。
由于树突,轴突的的生长变化,神经元的几何形态千变万化。
电学特性和空间形态等多个因素一起,综合表达神经元的信息传递功能。
(1a) (1b) (1c)图1,(1a) 鼠中海马的CA1锥体神经元.(1b) 关键位置: D, 树突; S, 胞体; AH, 轴突的开始阶段轴丘; A,轴突; T,轴突末端. 树突的类型: e, 单个树突的等价圆柱体; a, 树突顶端; b, 树突基端; o, 树突倾斜. 树突的水平: (p)最近端, (m) 中间端, 和 (d) 最远端-相对细胞胞体.(1c)神经元局部形态的简单几何特征:D树干直径,T顶端直径,L树干长度,△A树干锥度,R分支比例(前后分支的长度关系),ν分支幂律(前后分支的直径关系),α分支角度.对神经元特性的认识,最基本问题是神经元的分类。
目前,关于神经元的简单分类法主要有:(1)根据突起的多少可将神经元分为多极神经元;双极神经元和单极神经元。
(2)根据神经元的功能又可分为主神经元,感觉神经元,运动神经元和中间神经元等。
主神经元的主要功能是输出神经回路的信息。
例如大脑皮层的锥体神经元,小脑皮层中的普肯野神经元等。
感觉神经元,它们接受刺激并将之转变为神经冲动。
中间神经元,是介于感觉神经元与运动神经元之间起联络作用的。
运动神经元,它们将中枢发出的冲动传导到肌肉等活动器官。
全国大学生数学建模竞赛D题解析

汇报人:
CONTENTS
PRT ONE
PRT TWO
竞赛名称:全国大学生数学建模竞 赛
竞赛目的:培养大学生数学建模能 力提高解决实际问题的能力
添加标题
添加标题
竞赛级别:国家级
添加标题
添加标题
竞赛影响:促进大学生数学建模技 术的发展选拔优秀人才
竞赛起始于XXXX年 每年举办一次 参赛对象为全国大学生 竞赛目的是提高大学生数学建模能力和科技创新能力
组建合适的团队分工明确
制定详细的计划合理安排时间
充分准备所需的知识和技能
准备阶段:研究 题目收集资料建 立模型
实施阶段:编程 实现模拟实验优 化模型
总结阶段:撰写 论文整理思路提 炼经验
反思阶段:总结 得失分析原因改 进策略
赛题分析:对竞赛题目进行深入剖析明确解题思路和要点 经验教训:总结竞赛过程中遇到的问题和不足提出改进措施 团队协作:评估团队成员在竞赛中的表现和贡献提出优化建议 未来规划:根据竞赛经验和教训制定个人和团队未来的学习和发展计划
模型验证:通过对比实际数据和模型预测结果对模型的准确性和可靠性进行评估和改进
数据清洗:去除异常值、缺失值和重复值 数据筛选:根据需求筛选有效数据 数据转换:对数据进行必要的转换以适应分析需求 数据可视化:通过图表、图像等形式直观展示数据
确定问题类型和目 标函数
确定算法的输入和 输出
设计算法的流程图 和伪代码
培养团队协作精神 提升大学生数学应用能力
促进学科交叉融合
为国家和社会培养创新型人 才
PRT THREE
题目背景:全国大学生数学建模竞赛D题 题目要求:分析D题所涉及的数学建模方法和技巧 题目内容:对D题进行解析包括问题分析、模型建立、求解过程等 题目难度:对D题的难度进行评估并给出解题建议
2010数学建模竞赛C题解答
2010高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)C题输油管的优化布置某油田计划在铁路线一侧建造两家炼油厂,同时在铁路线上增建一个车站,用来运送成品油。
由于这种模式具有一定的普遍性,油田设计院希望建立管线建设费用最省的一般数学模型与方法。
1. 针对两炼油厂到铁路线距离和两炼油厂间距离的各种不同情形,提出你的设计方案。
在方案设计时,若有共用管线,应考虑共用管线费用与非共用管线费用相同或不同的情形。
2. 设计院目前需对一更为复杂的情形进行具体的设计。
两炼油厂的具体位置由图1所示,其中A厂位于郊区(图中的Ⅰ区域),B厂位于城区(图中的Ⅱ区域),两个区域的分界线用图中的虚线表示。
图中各字母表示的距离(单位:千米)分别为a = 5,b = 8,c = 15,l = 20。
图1 两炼油厂的具体位置图若所有管线的铺设费用均为每千米7.2万元。
铺设在城区的管线还需增加拆迁和工程补偿等附加费用,为对此项附加费用进行估计,聘请三家工程咨询公司(其中公司一具有甲级资质,公司二和公司三具有乙级资质)进行了估算。
估算结果如下表所示:请为设计院给出管线布置方案及相应的费用。
3. 在该实际问题中,为进一步节省费用,可以根据炼油厂的生产能力,选用相适应的油管。
这时的管线铺设费用将分别降为输送A厂成品油的每千米5.6万元,输送B厂成品油的每千米6.0万元,共用管线费用为每千米7.2万元,拆迁等附加费用同上。
请给出管线最佳布置方案及相应的费用。
2010高教社杯全国大学生数学建模竞赛C题解答问题1:如图1,设P的坐标为(x, y),(x≥ 0,y≥ 0),共用管道的费用为非共用管道的k倍,模型可归结为2222)()()(),(min ybxlyaxkyyxf-+-+-++=只需考虑21<≤k的情形(不妨假设ba≤)。
对上述二元费用函数求偏导,令()()()()()()()()⎪⎪⎩⎪⎪⎨⎧=-+----+--==-+----+=,,22222222ybxlybyaxyakyxfybxlxlyaxxyxfyx(*)结合图1,将(*)式改写为⎩⎨⎧=+=-kβαβαsinsincoscos,易知:24coscos,2sinsin2kk-====βαβα所以24tantankk-==βα,故经过AP和BP的直线方程分别为:xkkay24--=-①()lxkkby--=-24②联立①、②解方程组得交点()()⎥⎦⎤⎢⎣⎡--+=⎥⎥⎦⎤⎢⎢⎣⎡---=22421,421kklbayabkklx因为x≥ 0,y≥ 0,所以l应满足:()a b k k l --≥24 且()a b kk l +-≤24 (a )当 )(42a b kk l --≤时,此时交点在y 轴上,将0=x 代入①式,可得),0(a P =,即交点P 与A 点重合(如图2)。
2010年数学建模试题(全部)
2010高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)A 题 储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm 的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β )之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学的罐地平线 图1 储油罐正面示意图 油位探针2010高教社杯全国大学生数学建模竞赛题目 (请先阅读“全国大学生数学建模竞赛论文格式规范”)B 题 2010年上海世博会影响力的定量评估 20101851年伦互联网数据,定量评估2010年上海世博会的影响力。
2010高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)C 题 输油管的布置某油田计划在铁路线一侧建造两家炼油厂,同时在铁路线上增建一个车站,用来运送成品油。
2010年数学建模C、D题解析
4 − k2 l a+b k 1 P =( (b − a) + , − l ) ,此时 f min = [k (a + b) + l 4 − k 2 ] ; 2k 2 2 2 2 4 − k2
*
ab 4 − k2 (3)当 l ≥ (b + a ) 时, P* = ( , 0) ,此时 f min = (a + b) 2 + l 2 . a+b k 对共用管道与非共用管道相同的情况,只需令 k = 1 即可. 此问的优化模型实际上有两个约束条件 x ≥ 0, y ≥ 0 . 上面得到(1)(2)(3) 、 、 ,
关于学生论文中的几种情形
1.讨论不全面,很多队没有给出什么条件下不用公 用管道;有些虽有讨论,但不清晰,一定要用已知参数的 关系来讨论. 2.有些同学用镜面反射,Ferma定理,这些只适用于 各种管道费用相同的情形,即只适用第1问中的特殊情形 ,后面仍然要建立优化模型,对整个论文并没有增添什么 色彩. 之所以采用这两种方法,主要是参考了《两城镇取 水管线的最短铺设》和《泵站选址与水管铺设》两篇论文 . 不少学生根本就没有弄清Ferma定理,叙述Ferma定理就 不正确. 另外,用了文章就应引用为参考文献. 3.不少论文叙述混乱,符号混淆,图形不合理.
2012-4-28 费浦生 feipusheng@
关于C题《输油管的布置》的第3问
3.设输送 A 厂的管线为 k1 = 5.6 万元/km,输送 B 厂的管线为 k2 = 6.0 万 元/km,共用管线费用为 k3 = 7.2 万元/km,拆迁等附加费用同上. 请给出管 线最佳布置方案及相关费用. 总费用表达式为
2010数学建模C题论文
C题输油管的布置某油田计划在铁路线一侧建造两家炼油厂,同时在铁路线上增建一个车站,用来运送成品油。
由于这种模式具有一定的普遍性,油田设计院希望建立管线建设费用最省的一般数学模型与方法。
1. 针对两炼油厂到铁路线距离和两炼油厂间距离的各种不同情形,提出你的设计方案。
在方案设计时,若有共用管线,应考虑共用管线费用与非共用管线费用相同或不同的情形。
2. 设计院目前需对一更为复杂的情形进行具体的设计。
两炼油厂的具体位置由附图所示,其中A厂位于郊区(图中的I区域),B厂位于城区(图中的II 区域),两个区域的分界线用图中的虚线表示。
图中各字母表示的距离(单位:千米)分别为a = 5,b = 8,c = 15,l = 20。
若所有管线的铺设费用均为每千米7.2万元。
铺设在城区的管线还需增加拆迁和工程补偿等附加费用,为对此项附加费用进行估计,聘请三家工程咨询公司(其中公司一具有甲级资质,公司二和公司三具有乙级资质)进行了估算。
估算结果如下表所示:请为设计院给出管线布置方案及相应的费用。
3. 在该实际问题中,为进一步节省费用,可以根据炼油厂的生产能力,选用相适应的油管。
这时的管线铺设费用将分别降为输送A厂成品油的每千米5.6万元,输送B厂成品油的每千米6.0万元,共用管线费用为每千米7.2万元,拆迁等附加费用同上。
请给出管线最佳布置方案及相应的费用。
输油管的布置摘要:本文主要讨论了在建设费用最省的前提下输油管线的布置问题。
问题一分别讨论了有无共用管线及费用不同的情况下输油管线的铺设问题,以铺设费用最省为目标,建立了非线性优化模型,分别给出了铺设方案。
问题二在问题一的基础上讨论了有附加费的情况,利用改进层次分析法确定三家咨询公司的权重,进而确定附加费用为21.424万元/千米,最终得出铺设方案及最省费用为282.3134万元。
问题三在问题二的基础上进一步讨论了输油管线价格不同时输油管线的布置问题,给出了具体的铺设方案和对应的最省费用为251.5841万元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A b a C l
2011-8-3 费浦生 feipusheng@
D
此问中,未给出具体数据,设计方案中必须以 a , b , l 的解析表达式表 示.有无公共管线,必须根据这些参数来加以讨论.费用可以按公用或非公 用分别用常数表示. 实际上,设计费用只与两种费用之比有关,可以将共 用管道与非公用管道费用之比设为 k. 如图,设 P ( x , y ) ( x ≥ 0, y ≥ 0) , A (0, a ) , B (l , b ) ,则模型优化为 求函数 f ( x , y ) = ky + y B
2011-8-3 费浦生 feipusheng@
评阅时着重考虑
模型的正确性、结果推导的合理性 和完整性,以及数值结果的正确性, 对后两问有解析表达式比仅有数值结 果好.
2011-8-3
费浦生 feipusheng@
关于2010年数学建模竞赛D题 《对学生宿舍设计方案的评价》
4 − k2 4 − k2 (2)当 (b − a ) < l < (b + a ) 时, k k
4 − k2 l a+b k 1 P =( (b − a) + , − l ) ,此时 f min = [k (a + b) + l 4 − k 2 ] ; 2k 2 2 2 2 4 − k2
*
ab 4 − k2 (3)当 l ≥ (b + a ) 时, P* = ( , 0) ,此时 f min = (a + b) 2 + l 2 . a+b k 对共用管道与非共用管道相同的情况,只需令 k = 1 即可. 此问的优化模型实际上有两个约束条件 x ≥ 0, y ≥ 0 . 上面得到(1)(2)(3) 、 、 ,
2011-8-3 费浦生 feipusheng@
关于C题《输油管的布置》的第3问
3.设输送 A 厂的管线为 k1 = 5.6 万元/km,输送 B 厂的管线为 k2 = 6.0 万 元/km,共用管线费用为 k3 = 7.2 万元/km,拆迁等附加费用同上. 请给出管 线最佳布置方案及相关费用. 总费用表达式为
2011-8-3
费浦生 feipusheng@
学生宿舍的设计必须考虑经济性、舒适性和安全 性等问题. 经济性:建设成本、运行成本、和收费标准等; 舒适性:人均面积、使用方便、互不干扰、采光 和通风等; 安全性:人员疏散和防盗等. 附件是四件比较典型的学生宿舍的设计方案. 请用 数学建模的方法就它们的经济性、舒适性和安全性作 出综合量化评价和比较.
关于学生论文中的几种情形
1.讨论不全面,很多队没有给出什么条件下不用公 用管道;有些虽有讨论,但不清晰,一定要用已知参数的 关系来讨论. 2.有些同学用镜面反射,Ferma定理,这些只适用于 各种管道费用相同的情形,即只适用第1问中的特殊情形 ,后面仍然要建立优化模型,对整个论文并没有增添什么 色彩. 之所以采用这两种方法,主要是参考了《两城镇取 水管线的最短铺设》和《泵站选址与水管铺设》两篇论文 . 不少学生根本就没有弄清Ferma定理,叙述Ferma定理就 不正确. 另外,用了文章就应引用为参考文献. 3.不少论文叙述混乱,符号混淆,图形不合理.
2011-8-3 费浦生 feipusheng@
1.题目的要求中,重要的是“用数学建模的方法”和“ 量化评价和比较”. 2.题目要求综合评价,综合评价下面有三个子目标—— 经济性、舒适性和安全性,每个子目标下面题目又给了几个 子目标. 讨论时这些子目标中还可再分,例如运行成本又可认 为由几个方面构成,使用方便又由几个因素决定等等. 论文必须清楚表述所建立的综合评价模型及其求解过程, 说明模型和解法是合理的. . 3.题目简短,附录只是平面图,对有关问题作出合理假 设是必要的,但假设不能违背现实生活. 4.题目未给出任何数据,要求对各个因素实行量化. 例 如,安全性包含人员疏散和防盗,如何从设计图定出这两个 指标的量化计算. 有些因素如建设成本、运行成本和收费标准 的量化则需要采集数据,甚至还要进行分解,并结合有关假 设来决定. 5.根据模型计算的结果给出综合评价结论.
关于2010年数学建模竞赛
C、D题情况说明
2011-8-3 费浦生 feipusheng@
关于2010年数学建模竞赛C题 《输油管的布置》的说明
2011-8-3
费浦生 feipusheng@
关于C题《输油管的布置》的第1问
1.针对两炼油厂到铁路线距离和两炼油厂间距离的各种不 同情形提出你的设计方案.若有共有管线,应考虑共有管线费用 与非共有管线费用相同或不同的情形. B
2011-8-3 费浦生 feipusheng@
C
H c
D x
公司一 21
公司二 24
公司三 20
首先要确定附加费用,可用加权平均办法: p = 21k1 + 24k2 + 20k3 . 根据题意应有 k1 ≥ k2 = k3 ≥ 0 , k1 + k2 + k3 = 1 . 设管线布置在城乡结合处的点为 Q (c, z ) ,链接炼油厂 A 和点 Q 到铁路线输油 管最优布置可采用第 1 问中的结果,一般情况下可取 1(2)的结果,总费用最省 的模型为 1 p 求函数 g ( z ) = (a + z + 3c) + t (b − z ) 2 + (l − c) 2 的最小值,其中 t = . 2 7.2 l−c 1 当 z* = b − 时, g ( z ) 取最小值 g ( z * ) = [(a + b + 3c) + (l − c) 4t 2 − 1]. 2 4t 2 − 1 (1)模型可不用第 1 问的结果,而可以把第 1 问的目标函数嵌入进来,得到 三个变量的优化模型: 求函数 f ( x, y, z ) = y + x 2 + (a − y )2 + (c − x)2 + ( z − y )2 + t (b − z )2 + (l − c)2 的最小值,其中 x ≥ 0, y ≥ 0, z ≥ 0. 在解析求解过程中,需要讨论.
实际上是结合了求偏导求极值,而当极值点不满足 x ≥ 0 时,令 x = 0 ,得情形(1) , 不满足 y ≥ 0 时,令 y = 0 ,得情形(3).
2011-8-3 费浦生 feipusheng@
关于C题《输油管的布置》的第2问
2.A 厂位于郊区(图中区域Ⅰ) 厂位于 ,B 城区(图中区域Ⅱ) a = 5, b = 8, c = 15, l = 20. , 若所有管线铺设费用均为 7.2 万元/km,铺 设在城区的管线还需增加拆迁和工程补偿等附 加费用. 聘请三家工程咨询公司(其中公司一具有 甲级资质,公司二和公司三具有乙级资质)进 行了估算,估算结果如下表: y Ⅰ Ⅱ B Q A P E l 工程咨询公司 附加费用(万元/km) 请给出管线布置方案及相应费用.
2011-8-3 费浦生 feipusheng@
(2)这一问给出了具体数据,可以不求解的解析形式,而 直接用软件求数值. 两种极端情况下的数值结果如下: (ⅰ) k1 = 1, k2 = k3 = 0 , P (5.4593, 1.8481), Q (15, 7.564) , 最小费用 280.1771 万元; (ⅱ) k1 = k2 = k3 , P (5.4462, 1.8556), Q (15, 7.3715) ,最小 费用 283.5373 万元. (3)此问模型为简化的原因,采用了 1(2)的结果,恰好 此题数据满足 1(2)的条件(事后检验) 3( z − a) ≤ c 3( z + a). : 如果不满足此条件,这就有问题了. 而将问题 1 的目标函数嵌入 问题 2 中,就包含了各种情形. ( 4) 决定权数时, 不能将公司估计的附加费用作为因素(不 . 适合用层次分析)
x 2 + (a − y )2 + (l − x ) 2 + (b − y ) 2 的最小值
P H D x
C
2011-8-3
费浦生 feipusheng@
只需考虑 1 ≤ k < 2 的情形(只有两个炼油厂的油经此管道) ,不妨设 a ≤ b.
4 − k2 (1)当 l ≤ (b − a) 时, P* = (0, a) ,此时 f min = ka + (b − a )2 + l 2 ; k
F ( x, y, z) = k1 x2 + (a − y)2 + k2 (c − x)2 + ( z − y)2 + k4 (b − z)2 + (l − c)2 ,
其中 k4 = k2 + p , x ≥ 0, y ≥ 0, z ≥ 0. 可写出解析表达式再代入数据计算,也可以直接用软件求解.
2011-8-3 费浦生 feipusheng@
让我们一起思考,共同 研究,为我省数学建模竞赛 谱写新的篇章! +
谢谢大家! 谢谢大家!
2011-8-3 费浦生 feipusheng@
