河北省邯郸市育华 人教版九年级二次函数题库分类题型(无答案)
【初三数学】邯郸市九年级数学上(人教版)第22章二次函数检测试卷(解析版)

人教版九年级上册第二十二章二次函数单元检测(含答案)(5)一.选择题(30分)1.已知二次函数2y x bx c =++的图象上有38-(,)和58--(,)两点,则此抛物线的对称轴是( )A .直线4x =B .直线3x =C .1x =-D .x =-2.已知二次函数2y ax bx c =++的图象如图所示,则abc ,24b ac -, 2a b +,a b c ++这四个式子中,值为正数的有(A .4个B .3个C .2个D .1个3.以知二次函数()20y ax c a =+≠,当x 取1212x x x x ≠,()时,函数值相等,则当x 取12x x +时,函数值为( )A .a c +B .a c -C .c -D .c 4.函数2y ax bx c =-+,的图象经过10-(,)则a b cb c c a a b+++++ 的值是( ) A .3- B .3 C .12 D .12- 5.把二次函数253212++=x x y 的图象向右平移2个单位后,再向上平移3个单位,所得的函数图象顶点是( ) A .(-5,1) B .(1,-5) C .(-1,1) D .(-1,3) 6.若点(2,5),(4,5)在抛物线y =ax 2+bx +c 上,则它的对称轴是直线( )A .ab x -= B .x =1 C .x =2 D .x =37.已知函数4212--=x x y ,当函数值y 随x 的增大而减小时,x 的取值范围是( ) A .x <1 B .x >1 C .x >-2 D .-2<x <48.二次函数y =a(x +k)2+k ,当k 取不同的实数值时,图象顶点所在的直线是( )A .y =xB .x 轴C .y =-xD .y 轴9.已知二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,有下列结论:①abc >0;②a +b +c =2;21>a ③;④b <1.其中正确的结论是( )A .①②B .②③C .②④D .③④ 10.下列命题中,正确的是( ) ①若a +b +c =0,则b 2-4ac <0;②若b =2a +3c ,则一元二次方程ax 2+bx +c =0有两个不相等的实数根; ③若b 2-4ac >0,则二次函数y =ax 2+bx +c 的图象与坐标轴的公 共点的个数是2或3;④若b >a +c ,则一元二次方程ax 2+bx +c =0有两个不相等的实数根.A .②④B .①③C .②③D .③④二.填空题11.抛物线y =-x 2+15有最______点,其坐标是______.12.若抛物线y =x 2-2x -2的顶点为A ,与y 轴的交点为B ,则过A ,B 两点的直线的解析式为____________.13.若抛物线y =ax 2+bx +c(a≠0)的图象与抛物线y =x 2-4x +3的图象关于y 轴对称,则函数y =ax 2+bx +c 的解析式为______.14.若抛物线y =x 2+bx +c 与y 轴交于点A ,与x 轴正半轴交于B ,C 两点,且BC =2,S △ABC=3,则b =______.15.二次函数y =x 2-6x +c 的图象的顶点与原点的距离为5,则c =______. 16.二次函数22212--=x x y 的图象在坐标平面内绕顶点旋转180°,再向左平移3个单位,向上平移5个单位后图象对应的二次函数解析式为___________. 17.抛物线22y x x m =--+,若其顶点在x 轴上,则m=___________.18.顶点为25-(-,)且过点114(,-)的抛物线的解析式为 ___________. 三.解答题 19.把二次函数43212+-=x x y 配方成y =a(x+m)2+k 的形式,并求出它的图象的顶点坐标.对称轴方程,y <0时x 的取值范围,并画出图象.20.已知二次函数y =ax 2+bx +c(a≠0)的图象经过一次函数323+-=x y 的图象与x 轴.y 轴的交点,并也经过(1,1)点.求这个二次函数解析式,并求x 为何值时,有最大(最小)值,这个值是什么?21.已知二次函数223y ax ax =-+的图象与x 轴交于点A ,点B ,与y 轴交于点C ,其顶点为D ,直线DC 的函数关系式为3y kx =+,又45CBO ∠=︒(1)求二次函数的解析式和直线DC 的函数关系式 (2)求的面积22.已知抛物线y =-x 2+bx +c 与x 轴的两个交点分别为A (m ,0),B (n ,0),且4=+n m ,⋅=31n m 人教新版九年级上学期第22章《二次函数》单元测试卷(含答案)(1)一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列函数中,是反比例函数的是( )A .y =3x -1B .y =0.1xC .y =-13 D.yx =22.反比例函数y =22x的图像在( ) A .第一、二象限 B .第一、三象限 C .第二、三象限 D .第二、四象限 3.若点A(a ,b)在反比例函数y =2x 的图像上,则代数式ab -4的值为( )A .-2B .0C .2D .-6 4.下列函数中,y 随x 的增大而减小的函数是( )A .y =-1xB .y =1xC .y =-1x (x >0)D .y =1x(x <0)5.某学校要种植一块面积为100 m 2的长方形草坪,要求两边长均不小于5 m ,则草坪的一边长y(单位:m)随另一边长x(单位:m)的变化而变化的图像可能是( )6.如图,在平面直角坐标系中,点A 是双曲线y =1x (x >0)上的一个动点,过点A 作x 轴的垂线,交x 轴于点B ,点A 运动过程中△AOB 的面积将会( )A B C△A .保持不变B .逐渐变小C .逐渐增大D .先增大后减小7.对于反比例函数y =k 2+1x,下列说法正确的是( )A .y 随x 的增大而减小B .图像是中心对称图形C .图像位于第二、四象限D .当x <0时,y 随x 的增大而增大 8.已知反比例函数y =-9x,当1<x <3时,y 的最大整数值是( )A .-6B .-3C .-4D .-19.一次函数y =ax -a 与反比例函数y =ax (a ≠0)在同一平面直角坐标系中的图像可能是( )10.已知A(-1,y 1),B(2,y 2)两点在双曲线y =3+2mx上,且y 1>y 2,则m 的取值范围是( )A .m >0B .m <0C .m >-32D .m <-3211.一次函数y 1=ax +b 与反比例函数y 2=kx 的图像如图所示,当y 1<y 2时,x 的取值范围是( )A .x <2B .x >5C .2<x <5D .0<x <2或x >512.在平面直角坐标系中,直线y =x +b 与双曲线y =-1x 只有一个公共点,则b 的值是( )A .1B .±1C .±2D .213.如图,已知双曲线y =kx (x >0)经过矩形OABC 的边AB ,BC 的中点F ,E ,且四边形OEBF的面积为2,则k 的值为( )A .2B .4C .3D .114.反比例函数y =mx的图像如图所示,以下结论:①常数m <-1;②在每个象限内,y 随x 的增大而增大;③若点A(-1,h),B(2,k)在图像上,则h <k ;④若点P(x ,y)在图像上,则点P ′(-x ,-y)也在图像上.其中正确结论的个数是( ) A .1 B .2 C .3 D .415.如图,在平面直角坐标系xOy 中,菱形AOBC 的一个顶点O 在坐标原点,一边OB 在x 轴的正半轴上,sin ∠AOB =45,反比例函数y =48x 在第一象限内的图像经过点A ,与BC 交于点F ,则△AOF 的面积等于( )A .30B .40C .60D .8016.定义新运算:a ⊕b =⎩⎪⎨⎪⎧a b (b >0),-ab (b <0).例如:4⊕5=45,4⊕(-5)=45,则函数y =2⊕x(x≠0)的图像大致是( )A B C D二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有2个空,每空3分.把答案写在题中横线上)17.如图,矩形ABCD 在第一象限,AB 在x 轴的正半轴上,AB =3,BC =1,直线y =12x -1经过点C 交x 轴于点E ,双曲线y =kx经过点D ,则k 的值为 .18.如图,过点C(2,1)作AC ∥x 轴,BC ∥y 轴,点A ,B 都在直线y =-x +6上.若双曲线y =kx(x >0)与△ABC 总有公共点,则k 的取值范围是 .19.如图,在函数y =8x (x >0)的图像上有点P 1,P 2,P 3,…,P n ,P n +1,点P 1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P 1,P 2,P 3,…,P n ,P n +1分别作x 轴、y 轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分的面积从左至右依次记为S 1,S 2,S 3,…,S n ,则S 1= ,S n = (用含n 的代数式表示).三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤) 20.(本小题满分8分)已知反比例函数的图像过点A(-2,2).(1)求函数的表达式;(2)y 随x 的增大而如何变化?(3)点B(-4,2),点C(3,-43)和点D(22,-2)哪些点在图像上?21.(本小题满分9分)已知反比例函数y =k -1x的图像的两个分支分别位于第一、三象限. (1)求k 的取值范围;(2)若一次函数y =2x +k 的图像与该反比例函数的图像有一个交点的纵坐标是4,试确定一次函数与反比例函数的表达式,并求当x =-6时,反比例函数y 的值.22.(本小题满分9分)如图,一次函数y =kx +b 的图像与坐标轴分别交于A ,B 两点,与反比例函数y =nx 的图像在第一象限的交点为C ,CD ⊥x 轴,垂足为D.若OB =3,OD =6,△AOB的面积为3.(1)求一次函数与反比例函数的表达式;(2)直接写出当x >0时,kx +b -nx<0的解集.解:23.(本小题满分9分)一般情况下,中学生完成数学家庭作业时,注意力指数随时间x(分钟)的变化规律如图所示(其中AB ,BC 为线段,CD 为曲线的一部分).(1)分别求出线段AB 和曲线CD 的函数表达式;(2)若学生的注意力指数不低于40为高效时间,根据图中信息,求出一般情况下,完成一份数学家庭作业的高效时间是多少分钟?解:24.(本小题满分10分)如图,四边形ABCD 是平行四边形,点A(1,0),B(3,1),C(3,3).反比例函数y =mx (x >0)的图像经过点D ,点P 是一次函数y =kx +3-3k(k ≠0)的图像与该反比例函数图像的一个公共点.(1)直接写出D 点的坐标,并求反比例函数的表达式;(2)连接人教版九年级上册第二十二章二次函数单元检测(含答案)(6)一、选择题:1、下列对二次函数y=x 2﹣x 的图象的描述,正确的是( ) A .开口向下 B .对称轴是y 轴C .经过原点D .在对称轴右侧部分是下降的2、已知二次函数y =x 2﹣4x +2,关于该函数在﹣1≤x ≤3的取值范围内,下列说法正确的是( ) A .有最大值﹣1,有最小值﹣2 B .有最大值0,有最小值﹣1C .有最大值7,有最小值﹣1D .有最大值7,有最小值﹣2 3、二次函数y =(x ﹣1)2+3图象的顶点坐标是( )A .(1,3)B .(1,﹣3)C .(﹣1,3)D .(﹣1,﹣3)4、在平面直角坐标系中,已知a ≠b ,设函数y=(x+a )(x+b )的图象与x 轴有M 个交点, 函数y=(ax+1)(bx+1)的图象与x 轴有N 个交点,则( ) A .M=N-1或M=N+1B .M=N-1或M=N+2C .M=N 或M=N+1D .M=N 或M=N-15、(2019济宁)将抛物线265y x x =-+向上平移两个单位长度,再向右平移一个单位长度后,得到的抛物线解析式是( ) A .2(4)6y x =-- B .2(1)3y x =-- C .2(2)2y x =--D .2(4)2y x =--6、已知二次函数y=ax 2+2ax +3a 2+3(其中x 是自变量),当x ≥2时,y 随x 的增大而增大,且﹣2≤x ≤1时,y 的最大值为9,则a 的值为( ) A .1或﹣2 B .或C .D .17、已知a ,b 是非零实数,|a |>|b |,在同一平面直角坐标系中,二次函数y 1=ax 2+bx 与一次函数y 2=ax +b 的大致图象不可能是( )A .B .C .D .8、对于题目“一段抛物线L :y=﹣x (x ﹣3)+c (0≤x ≤3)与直线l :y=x +2有唯一公共点,若c 为整数,确定所有c 的值,”甲的结果是c=1,乙的结果是c=3或4,则( ) A .甲的结果正确 B .乙的结果正确C .甲、乙的结果合在一起才正确D .甲、乙的结果合在一起也不正确9、在平面直角坐标系中,抛物线(5)(3)y x x =+-经过变换后得到抛物线(3)(5)y x x =+-,则这个变换可以是( ) A .向左平移2个单位 B .向右平移2个单位 C .向左平移8个单位D .向右平移8个单位10、如图是二次函数y=ax 2+bx +c 图象的一部分,且过点A (3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )A .b 2<4acB .ac >0C .2a ﹣b=0D .a ﹣b +c=011、如图,抛物线2y ax c =+与直线y mx n =+交于A (-1,P ),B (3,q )两点,则不等式2ax mx c n ++>的解集是( ).A. 1<x<3B.-3<x<1C.x<-3或x>1D.x>3或x<-112、如图,若二次函数y=ax 2+bx +c (a ≠0)图象的对称轴为x=1,与y 轴交于点C ,与x 轴交于点A 、点B (﹣1,0),则 ①二次函数的最大值为a +b +c ; ②a ﹣b +c <0;③b 2﹣4ac <0;④当y >0时,﹣1<x <3,其中正确的个数是( )A .1B .2C .3D .4二、填空题:13、已知抛物线y =-x 2+bx +4经过(-2,n )和(4,n )两点,则n 的值为 .14、已知坐标平面上有一直线L ,其方程式为y +2=0,且L 与二次函数y=3x 2+a 的图形相交于A ,B 两点:与二次函数y=﹣2x 2+b 的图形相交于C ,D 两点,其中a 、b 为整数.若AB=2,CD=4.则a +b= .15、将抛物线y=x 2﹣6x +21向左平移2个单位后,得到新抛物线的解析式为 . 16、在平面直角坐标系中,垂直于x 轴的直线l 分别与函数y =x -a +1和y =x 2-2ax 的图象相交于P ,Q 两点.若平移直线l ,可以使P ,Q 都在x 轴的下方,则实数a 的取值范围是__________. 17、在平面直角坐标系xOy 中,已知点M ,N 的坐标分别为(﹣1,2),(2,1),若抛物线y=ax2﹣x+2(a≠0)与线段MN有两个不同的交点,则a的取值范围是.18、已知二次函数y=﹣(x﹣h)2(h为常数),当自变量x的值满足2≤x≤5时,与其对应的函数值y的最大值为﹣1,则h的值为.19、若对于任意非零实数a,抛物线y=ax2+ax﹣2a总不经过点P(x0﹣3,x02﹣16),则符合条件的点P .20、当a≤x≤a+1时,函数y=x2﹣2x+1的最小值为1,则a的值为.21、如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n)与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②﹣1≤a≤﹣;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为个.22、如图,在足够大的空地上有一段长为20米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD面积为450平方米,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.其中所利用旧墙AD的长为米.三、解答题:23、已知函数y=x2+bx+c(b,c为常数)的图象经过点(–2,4).(1)求b,c满足的关系式;(2)设该函数图象的顶点坐标是(m,n),当b的值变化时,求n关于m的函数解析式;24、某景区商店销售一种纪念品,每件的进货价为40元.经市场调研,当该纪念品每件的销售价为50元时,每天可销售200件;当每件的销售价每增加1元,每天的销售数量将减少10件.(1)当每件的销售价为52元时,该纪念品每天的销售数量为 件;(2)当每件的销售价x 为多少时,销售该纪念品每天获得的利润y 最大?并求出最大利润.25、已知直线l :y=kx +1与抛物线y=x 2﹣4x .(1)求证:直线l 与该抛物线总有两个交点;(2)设直线l 与该抛物线两交点为A ,B ,O 为原点,当k=﹣2时,求△OAB 的面积.26、已知抛物线G :y =mx 2-2mx -3有最低点.(1)求二次函数y =mx 2-2mx -3的最小值(用含m 的式子表示);(2)将抛物线G 向右平移m 个单位得到抛物线G 1.经过探究发现,随着m 的变化,抛物线G 1顶点的纵坐标y 与横坐标x 之间存在一个函数关系,求这个函数关系式,并写出自变量x 的取值范围;(3)记(2)所求的函数为H ,抛物线G 与函数H 的图象交于点P ,结合图象,求点P 的纵坐标的取值范围.27、(2019镇江)如图,二次函数245y x x =-++图象的顶点为D ,对称轴是直线1,一次函数215y x =+的图象与x 轴交于点A ,且与直线DA 关于l 的对称直线交于点B . (1)点D 的坐标是 ;(2)直线l 与直线AB 交于点C ,N 是线段DC 上一点(不与点D 、C 重合),点N 的纵坐标为n .过点N 作直线与线段DA 、DB 分别交于点P 、Q ,使得DPQ ∆与DAB ∆相似. ①当275n =时,求DP 的长; ②若对于每一个确定的n 的值,有且只有一个DPQ ∆与DAB ∆相似,请直接写出n 的取值范围.参考答案:一、选择题:1、C2、D3、A4、C5、D6、D7、D8、A9、B10、D11、C12、B二、填空题:13、-414、115、y=(x﹣4)2+3.16、a>1或a<-117、a ≤﹣1或≤a <18、1或619、有且只有2个20、﹣1或221、422、10三、解答题: 23、(1)将点(–2,4)代入y =x 2+bx +c ,得–2b +c =0,∴c =2b ;(2)m 2b =-,n244c b -= 人教版九年级上册第二十二章二次函数单元检测(含答案)(6)一、选择题:1、下列对二次函数y=x 2﹣x 的图象的描述,正确的是( )A .开口向下B .对称轴是y 轴C .经过原点D .在对称轴右侧部分是下降的2、已知二次函数y =x 2﹣4x +2,关于该函数在﹣1≤x ≤3的取值范围内,下列说法正确的是( )A .有最大值﹣1,有最小值﹣2B .有最大值0,有最小值﹣1C .有最大值7,有最小值﹣1D .有最大值7,有最小值﹣23、二次函数y =(x ﹣1)2+3图象的顶点坐标是( ) A .(1,3) B .(1,﹣3) C .(﹣1,3) D .(﹣1,﹣3)4、在平面直角坐标系中,已知a ≠b ,设函数y=(x+a )(x+b )的图象与x 轴有M 个交点, 函数y=(ax+1)(bx+1)的图象与x 轴有N 个交点,则( )A .M=N-1或M=N+1B .M=N-1或M=N+2C .M=N 或M=N+1D .M=N 或M=N-15、(2019济宁)将抛物线265y x x =-+向上平移两个单位长度,再向右平移一个单位长度后,得到的抛物线解析式是( )A .2(4)6y x =--B .2(1)3y x =--C .2(2)2y x =--D .2(4)2y x =--6、已知二次函数y=ax 2+2ax +3a 2+3(其中x 是自变量),当x ≥2时,y 随x 的增大而增大,且﹣2≤x ≤1时,y 的最大值为9,则a 的值为( )A .1或﹣2B .或C .D .17、已知a ,b 是非零实数,|a |>|b |,在同一平面直角坐标系中,二次函数y 1=ax 2+bx 与一次函数y 2=ax +b 的大致图象不可能是( )A .B .C .D . 8、对于题目“一段抛物线L :y=﹣x (x ﹣3)+c (0≤x ≤3)与直线l :y=x +2有唯一公共点,若c 为整数,确定所有c 的值,”甲的结果是c=1,乙的结果是c=3或4,则( ) A .甲的结果正确B .乙的结果正确C .甲、乙的结果合在一起才正确D .甲、乙的结果合在一起也不正确9、在平面直角坐标系中,抛物线(5)(3)y x x =+-经过变换后得到抛物线(3)(5)y x x =+-,则这个变换可以是( )A .向左平移2个单位B .向右平移2个单位C .向左平移8个单位D .向右平移8个单位10、如图是二次函数y=ax 2+bx +c 图象的一部分,且过点A (3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )A .b 2<4acB .ac >0C .2a ﹣b=0D .a ﹣b +c=011、如图,抛物线2y ax c =+与直线y mx n =+交于A (-1,P ),B (3,q )两点,则不等式2ax mx c n ++>的解集是( ).B. 1<x<3 B.-3<x<1C.x<-3或x>1D.x>3或x<-112、如图,若二次函数y=ax 2+bx +c (a ≠0)图象的对称轴为x=1,与y 轴交于点C ,与x 轴交于点A 、点B (﹣1,0),则①二次函数的最大值为a +b +c ;②a ﹣b +c <0;③b 2﹣4ac <0;④当y >0时,﹣1<x <3,其中正确的个数是( )A .1B .2C .3D .4二、填空题:13、已知抛物线y =-x 2+bx +4经过(-2,n )和(4,n )两点,则n 的值为 .14、已知坐标平面上有一直线L ,其方程式为y +2=0,且L 与二次函数y=3x 2+a 的图形相交于A ,B 两点:与二次函数y=﹣2x 2+b 的图形相交于C ,D 两点,其中a 、b 为整数.若AB=2,CD=4.则a +b= .15、将抛物线y=x 2﹣6x +21向左平移2个单位后,得到新抛物线的解析式为 .16、在平面直角坐标系中,垂直于x 轴的直线l 分别与函数y =x -a +1和y =x 2-2ax 的图象相交于P ,Q 两点.若平移直线l ,可以使P ,Q 都在x 轴的下方,则实数a 的取值范围是__________.17、在平面直角坐标系xOy 中,已知点M ,N 的坐标分别为(﹣1,2),(2,1),若抛物线y=ax 2﹣x +2(a ≠0)与线段MN 有两个不同的交点,则a 的取值范围是 .18、已知二次函数y=﹣(x ﹣h )2(h 为常数),当自变量x 的值满足2≤x ≤5时,与其对应的函数值y的最大值为﹣1,则h的值为.19、若对于任意非零实数a,抛物线y=ax2+ax﹣2a总不经过点P(x0﹣3,x02﹣16),则符合条件的点P .20、当a≤x≤a+1时,函数y=x2﹣2x+1的最小值为1,则a的值为.21、如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n)与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②﹣1≤a≤﹣;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为个.22、如图,在足够大的空地上有一段长为20米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD面积为450平方米,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.其中所利用旧墙AD的长为米.三、解答题:23、已知函数y=x2+bx+c(b,c为常数)的图象经过点(–2,4).(1)求b,c满足的关系式;(2)设该函数图象的顶点坐标是(m,n),当b的值变化时,求n关于m的函数解析式;24、某景区商店销售一种纪念品,每件的进货价为40元.经市场调研,当该纪念品每件的销售价为50元时,每天可销售200件;当每件的销售价每增加1元,每天的销售数量将减少10件.(1)当每件的销售价为52元时,该纪念品每天的销售数量为 件;(2)当每件的销售价x 为多少时,销售该纪念品每天获得的利润y 最大?并求出最大利润.25、已知直线l :y=kx +1与抛物线y=x 2﹣4x .(1)求证:直线l 与该抛物线总有两个交点;(2)设直线l 与该抛物线两交点为A ,B ,O 为原点,当k=﹣2时,求△OAB 的面积.26、已知抛物线G :y =mx 2-2mx -3有最低点.(1)求二次函数y =mx 2-2mx -3的最小值(用含m 的式子表示);(2)将抛物线G 向右平移m 个单位得到抛物线G 1.经过探究发现,随着m 的变化,抛物线G 1顶点的纵坐标y 与横坐标x 之间存在一个函数关系,求这个函数关系式,并写出自变量x 的取值范围;(3)记(2)所求的函数为H ,抛物线G 与函数H 的图象交于点P ,结合图象,求点P 的纵坐标的取值范围.27、(2019镇江)如图,二次函数245y x x =-++图象的顶点为D ,对称轴是直线1,一次函数215y x =+的图象与x 轴交于点A ,且与直线DA 关于l 的对称直线交于点B . (1)点D 的坐标是 ;(2)直线l 与直线AB 交于点C ,N 是线段DC 上一点(不与点D 、C 重合),点N 的纵坐标为n .过点N 作直线与线段DA 、DB 分别交于点P 、Q ,使得DPQ ∆与DAB ∆相似. ①当275n =时,求DP 的长; ②若对于每一个确定的n 的值,有且只有一个DPQ ∆与DAB ∆相似,请直接写出n 的取值范围 .参考答案:一、选择题:1、C2、D3、A4、C5、D6、D7、D8、A9、B10、D11、C12、B二、填空题:13、-414、115、y=(x﹣4)2+3.16、a>1或a<-117、a ≤﹣1或≤a <18、1或619、有且只有2个20、﹣1或221、422、10三、解答题: 23、(1)将点(–2,4)代入y =x 2+bx +c ,得–2b +c =0,∴c =2b ;(2)m 2b =-,n244c b -= 人教版九年级上册单元检测:第二十二章二次函数(含答案)(1)一.选择题1.下列函数表达式中,一定是二次函数的是( )A .y =3x ﹣1B .y =ax 2+bx +cC .y =3x 2﹣2x +1D .y =x 2+2.抛物线y =﹣x 2+2x +6的对称轴是( )A .直线x =1B .直线x =﹣1C .直线x =﹣2D .直线x =23.在平面直角坐标系中,对于二次函数y =(x ﹣2)2+1,下列说法中错误的是( )A .y 的最小值为1B .图象顶点坐标为(2,1),对称轴为直线x =2C .当x <2时,y 的值随x 值的增大而增大,当x ≥2时,y 的值随x 值的增大而减小D .它的图象可以由y =x 2的图象向右平移2个单位长度,再向上平移1个单位长度得到4.二次函数y =﹣x 2+mx ,对称轴为直线x =3,若关于x 的一元二次方程﹣x 2+mx ﹣t =0(t 为实数)在2<x <7的范围内有解,则t 的取值范围是( )A .t >﹣7B .﹣7<t <8C .8<t ≤9D .﹣7<t ≤95.若正比例函数y =mx (m ≠0),y 随x 的增大而减小,则它和二次函数y =mx 2+m 的图象大致是( )A .B .C.D.6.把抛物线y=﹣2x2向上平移1个单位,再向右平移1个单位,得到的抛物线是()A.y=﹣2(x+1)2+1 B.y=﹣2(x﹣1)2+1C.y=﹣2(x﹣1)2﹣1 D.y=﹣2(x+1)2﹣17.如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是()A.球不会过网B.球会过球网但不会出界C.球会过球网并会出界D.无法确定8.若函数y=(a﹣2)x2﹣2ax+a﹣与x轴有交点,且关于x的不等式组无解,则符合条件的整数a的值有()个A.3 B.4 C.5 D.69.在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给以下结论:①abc<0;②c+2a<0;③9a﹣3b+c=0;④a﹣b≥m(am+b)(m为实数);⑤4ac﹣b2<0.其中错误结论的个数有()A.1个B.2个C.3个D.4个10.如图,抛物线y=a(x+1)(x﹣3)的图象与x轴交于A,B两点(点A在点B的左边),与y轴正半轴交于点C,点D为抛物线的顶点.点P为线段BC上的动点,以AC,AP为邻边构造▱APEC,连结BE.若△ACP的面积与△BEP的面积之比为1:2时,ED⊥BD,则a 的值为()A.﹣1 B.﹣C.﹣D.﹣2二.填空题11.已知一个二次函数的图象开口向上,顶点坐标为(2,3),那么这个二次函数的解析式可以是.12.某斜拉索大桥主索塔呈抛物线,主索塔底部在水面部分的宽度AB=50米,主索塔的最高点E距水面的垂直距离为100米,桥面CD距水面的咨度为36米,桥的宽度CD米.13.某二次函数的图象过点(﹣3,m)和(7,m),则此二次函数的图象的对称轴为.14.抛物线y=﹣x2+bx+c的部分图象如图所示,已知关于x的一元二次方程﹣x2+bx+c=0的一个解为x1=1,则该方程的另一个解为x2=.15.抛物线y=3x2﹣6x+a与坐标轴只有一个公共点,则a取值范围为.16.已知二次函数y=x2+4x+3的顶点为A,与y轴交于点B,作它关于以P(1,0)为中心的中心对称的图象顶点为C,交y轴于点D,则四边形ABCD面积为.三.解答题17.如图,已知抛物线y=x2+bx+c与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.(1)求抛物线的函数表达式;(2)设D为抛物线的顶点,连接DA、DB,试判断△ABD的形状,并说明理由;(3)设P为对称轴上一动点,要使PC﹣PB的值最大,求出P点的坐标.18.如图,已知抛物线y=﹣x2+bx+c的顶点C的坐标为(﹣3,2),此抛物线交x轴于点A,B两点,交y轴于点D,点P为直线AD上方抛物线上一点,过点P作PE⊥x轴垂足为E,交直线AD于点N,连接AP,PD.(1)求抛物线和直线AD的解析式;(2)求线段PN的最大值;(3)当△APD的面积是△ABC的面积的时,求点P的坐标.19.已知抛物线y=ax2+bx+c(a、b、c是常数,a≠0)的对称轴为直线x=﹣1.(1)b=;(用含a的代数式表示)(2)当a=﹣1时,若关于x的方程ax2+bx+c=0在﹣4<x<1的范围内有解,求c的取值范围;(3)若抛物线过点(﹣1,﹣1),当0≤x≤1时,抛物线上的点到x轴距离的最大值为4,求a的值.20.如图,一隧道的横截面是由一段抛物线及矩形的三边围成的,隧道宽BC=10米,矩形部分高AB=3米,抛物线型的最高点E离地面OE=6米,按如图建立一个以BC为x轴,OE为y轴的直角坐标系.(1)求抛物线的解析式;(2)如果该隧道内设有双车道,现有一辆货运卡车高4.5米,宽3米,这辆货运卡车能顺利通过隧道吗?21.某服装超市购进单价为30元的童装若干件,物价部门规定其销售单价不低于每件30元,不高于每件60元.销售一段时间后发现:当销售单价为60元时,平均每月销售量为80件,而当销售单价每降低10元时,平均每月能多售出20件.同时,在销售过程中,每月还要支付其他费用450元.设销售单价为x元,平均月销售量为y件.(1)求出y与x的函数关系式,并写出自变量x的取值范围.(2)当销售单价为多少元时,销售这种童装每月可获利1800元?(3)当销售单价为多少元时,销售这种童装每月获得利润最大?最大利润是多少?22.如图,抛物线y=﹣x2﹣x+c与x轴交于A,B两点,且点B的坐标为(3,0),与y 轴交于点C,连接AC,BC,点P是抛物线上在第二象限内的一个动点,点P的横坐标为a,过点P作x轴的垂线,交AC于点Q.(1)求A,C两点的坐标.(2)请用含a的代数式表示线段PQ的长,并求出a为何值时PQ取得最大值.(3)试探究在点P运动的过程中,是否存在这样的点Q,使得以B,C,Q为顶点的三角形是等腰三角形?若存在,请写出此时点Q的坐标;若不存在,请说明理由.23.在平面直角坐标系中,如果某点的横坐标与纵坐标的和为10,则称此点为“合适点”例如,点(1,9),(﹣2019,2029)…都是“合适点”.(1)求函数y=2x+1的图象上的“合适点”的坐标;(2)求二次函数y=x2﹣5x﹣2的图象上的两个“合适点”A,B之间线段的长;(3)若二次函数y=ax2+4x+c的图象上有且只有一个合适点”,其坐标为(4,6),求二次函数y=ax2+4x+c的表达式;(4)我们将抛物线y=2(x﹣n)2﹣3在x轴下方的图象记为G1,在x轴及x轴上方图象记为G2,现将G1沿x轴向上翻折得到G3,图象G2和图象G3两部分组成的记为G,当图象G上恰有两个“合适点”时,直接写出n的取值范围.参考答案一.选择题1.解:A、是一次函数,故此选项错误;B、当a=0时,y=ax2+bx+c不是二次函数,故此选项错误;C、是二次函数,故此选项正确;D、含有分式,不是二次函数,故此选项错误;故选:C.2.解:∵抛物线y=﹣x2+2x+6=﹣(x﹣1)2+7,∴该抛物线的对称轴是直线x=1,故选:A.3.解:二次函数y=(x﹣2)2+1,a=1>0,∴该函数的图象开口向上,对称轴为直线x=2,顶点为(2,1),当x=2时,y有最小值1,当x>2时,y的值随x值的增大而增大,当x<2时,y的值随x值的增大而减小;故选项A、B的说法正确,C的说法错误;根据平移的规律,y=x2的图象向右平移2个单位长度得到y=(x﹣2)2,再向上平移1个单位长度得到y=(x﹣2)2+1;故选项D的说法正确,故选:C.4.解:∵抛物线y=﹣x2+mx的对称轴为直线x=3,∴﹣=3,解得m=6,∴抛物线解析式为y=﹣x2+6x=﹣(x﹣3)2+9,抛物线的顶点坐标为(3,9),当x=2时,y=﹣x2+6x=8;当x=7时,y=﹣x2+6x=﹣7,∵关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在2<x<7的范围内有解,∴抛物线y=﹣x2+6x与直线y=t在2<x<7的范围内有公共点,∴﹣7<t<8.故选:B.5.解:∵y=mx(m≠0),y随x的增大而减小,∴m<0,∴二次函数y=mx2+m的图象的开口向下,与y则交于负半轴上,故选:A.6.解:∵函数y=﹣2x2的顶点为(0,0),∴向上平移1个单位,再向右平移1个单位的顶点为(1,1),∴将函数y=﹣2x2的图象向上平移1个单位,再向右平移1个单位,得到抛物线的解析式为y=﹣2(x﹣1)2+1,故选:B.7.解:∵球与O点的水平距离为6m时,达到最高2.6m,∴抛物线为y=a(x﹣6)2+2.6过点,∵抛物线y=a(x﹣6)2+2.6过点(0,2),∴2=a(0﹣6)2+2.6,解得:a=﹣,故y与x的关系式为:y=﹣(x﹣6)2+2.6,当x=9时,y=﹣(x﹣6)2+2.6=2.45>2.43,所以球能过球网;当y=0时,﹣(x﹣6)2+2.6=0,解得:x1=6+2>18,x2=6﹣2(舍去)故会出界.故选:C.8.解:,解不等式①得:x≤a,解不等式②得:x>5,∵关于x的不等式组无解,∴a≤5.①当二次函数y=(a﹣2)x2﹣2ax+a﹣与x轴有交点时,方程(a﹣2)x2﹣2ax+a﹣=0的△=(﹣2a)2﹣4(a﹣2)(a﹣)≥0,解得:a≥,∴≤a≤5.又∵a≠2,整数有1,3,4,5,共4个.②当函数y=(a﹣2)x2﹣2ax+a﹣是一次函数时,a﹣2=0,此时a=2.综上所述,整数有1,2,3,4,5,共5个.故选:C.9.解:①由抛物线可知:a>0,c<0,对称轴x=﹣<0,∴b>0,∴abc<0,故①正确;②由对称轴可知:﹣=﹣1,∴b=2a,∵x=1时,y=a+b+c=0,∴c+3a=0,∴c+2a=﹣3a+2a=﹣a<0,故②正确;③(1,0)关于x=﹣1的对称点为(﹣3,0),∴x=﹣3时,y=9a﹣3b+c=0,故③正确;④当x=﹣1时,y的最小值为a﹣b+c,∴x=m时,y=am2+bm+c,∴am2+bm+c≥a﹣b+c,即a﹣b≤m(am+b),故④错误;⑤抛物线与x轴有两个交点,∴△>0,。
初三__二次函数基础分类练习题(含答案)(2)(K12教育文档)

初三__二次函数基础分类练习题(含答案)(2)(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(初三__二次函数基础分类练习题(含答案)(2)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为初三__二次函数基础分类练习题(含答案)(2)(word版可编辑修改)的全部内容。
12二次函数练习题练习一 二次函数1、 一个小球由静止开始在一个斜坡上向下滚动,通过仪器观察得到小球滚动的距离s(米)与时间t (秒)的数据如下表:时间t(秒) 1 2 3 4 …距离s(米)2 8 18 32 …写出用t 表示s 的函数关系式:2、 下列函数:① 23yx ;② 21y x x x ;③ 224y x x x ;④ 21yx x ;⑤ 1y x x ,其中是二次函数的是 ,其中a,b ,c3、当m 时,函数2235y mx x(m 为常数)是关于x 的二次函数二次函数 4、当____m 时,函数2221mm ym m x 是关于x 的5、当____m时,函数2564mm ymx +3x 是关于x的二次函数 6、若点 A ( 2, m ) 在函数 12-=x y 的图像上,则 A 点的坐标是____.7、在圆的面积公式 S =πr 2中,s 与 r 的关系是( )A 、一次函数关系B 、正比例函数关系C 、反比例函数关系D 、二次函数关系 8、正方形铁片边长为15cm,在四个角上各剪去一个边长为x(cm)的小正方形,用余下的部分做成一个无盖的盒子.(1)求盒子的表面积S(cm 2)与小正方形边长x (cm )之间的函数关系式; (2)当小正方形边长为3cm 时,求盒子的表面积. 9、如图,矩形的长是 4cm,宽是 3cm ,如果将长和宽都增加 x cm , 那么面积增加 ycm 2, ① 求 y 与 x 之间的函数关系式.3② 求当边长增加多少时,面积增加 8cm 2。
人教版九年级上二次函数练习试卷7

人教版九年级上二次函数练习试卷7一、选择题(共10小题;共50分)1. 把二次函数配方成顶点式为A. B.C. D.2. 若二次函数配方后为,则值为A. B. C.3. 已知和是二次函数图象上的两点,若,下列不等式一定成立的是A. B. C. D.4. 下列函数是二次函数的是A. B.C. D.5. 如图,四边形的两条对角线互相垂直,,则四边形的面积最大值是A. B. C. D.6. 已知实数,满足,则以,的值为两边长的等腰三角形的周长是A. 或B.C. D. 以上答案均不对7. 关于二次函数,下列说法中正确的是A. 图象的开口向上B. 当时,随的增大而增大C. 图象的顶点坐标是D. 当时,有最小值是8. 如图,已知二次函数在坐标平面上的图象经过,两点.若,,则的值可能为A. B. C. D.9. 已知函数的图象与轴有交点,则得取值范围是A. B. C. D.10. 已知二次函数的图象如图,它与轴的两个交点分别为,.对于下列命题:①;②;③;④.其中正确的有A. 个B. 个C. 个D. 个二、填空题(共6小题;共30分)11. 若可取任意有理数,则的最小值是.12. 抛物线的顶点坐标是,对称轴是.13. 二次函数化成的形式是.14. 已知,那么.15. 把抛物线绕着顶点逆时针旋转,所得新图形与轴交于点,,则.16. 关于的方程,当满足时,一个根小于,另一个根大于.三、解答题(共8小题;共104分)17. 在同一直角坐标系内画出函数和的图象,并说明抛物线是由抛物线怎样移动得到的.18. 求抛物线的顶点坐标..顶点坐标为.19. 图中有条抛物线,其中顶点为坐标原点的抛物线为,请写出其他几条抛物线的表达式.20. 利用图象判断方程是否有解,若有解,请写出它的解(结果精确到).21. 在同一坐标系中画出下列函数的图象:(1);(2);(3).22. 如图,若二次函数的图象与轴交于,两点(点在点的左侧),与轴交于点.(1)求,两点的坐标;(2)若为二次函数图象上一点,求的值.23. 已知二次函数,该函数与自变量的部分对应值如下表:(1)求该二次函数的表达式.(2)不等式的解集为;不等式的解集为.24. 抛物线的顶点坐标为,点也在图象上,求出它的函数解析式.答案第一部分1. B2. D 【解析】,又,.故选D.3. A 【解析】函数的对称轴为,而,所以.4. D 【解析】A、,是一次函数,故此选项错误;B、,不是整式方程,故此选项错误;C、,是一次函数,故此选项错误;D、,是二次函数,故此选项正确.故选:D.5. B【解析】设,则,,,,当时,有最大值为.6. B7. B8. D9. C 【解析】由题意,若即时,,为一次函数,与轴有交点,符合,若,则,所以,所以且,所以综上,.10. B【解析】根据图象可得,,对称轴为,①因为它与轴的两个交点分别为,,所以对称轴是,所以,所以,所以①错误;②因为,所以,因为,所以,所以②错误;③因为,所以,所以,又由①得,所以,所以③正确;④根据图象知,当时,,所以,由①知,,所以,所以④正确,所以正确的有③④.第二部分11.12. ,直线13.14.15.【解析】抛物线,抛物线开口向上,顶点为:,旋转前的对应点,的纵坐标为,把代入得:,解得:,,,.故答案为:.16.【解析】提示:由题意可得,当与时,.第三部分17. 图略,抛物线是由抛物线向右平移个单位,再向下平移个单位得到的.18. ;;19. ;①;②;③;④;⑤;⑥;20. 有解.,.21.22. (1)当时,,解得,,所以,.(2)把代入得,解得,,所以的值为或.23. (1)设该二次函数的关系式为,顶点坐标为,,该二次函数过点,,解得,即.(2)或;【解析】当时,或,抛物线开口向上,不等式的解集为或;当时,或,抛物线开口向上,不等式的解集为.24. 设抛物线的解析式为,因为点在抛物线上,所以,则,所以解析式为.。
人教版九年级上二次函数练习试卷10

人教版九年级上二次函数练习试卷10一、选择题(共10小题;共50分)1. 已知抛物线的顶点坐标是,则和的值分别是A. , C.2. 抛物线的对称轴是A. 直线B. 直线C. 直线D. 直线3. 已知点,在函数的图象上,则,,的大小关系是A. B. C. D.4. 圆的面积公式中,与之间的关系是A. 是的正比例函数B. 是的一次函数C. 是的二次函数D. 以上答案都不对5. 某幢建筑物,从高的窗口处用水管向外喷水,喷出的水成抛物线形状(抛物线所在平面与地面垂直),如果抛物线的最高点离墙(如图),则水流落地点离墙的距离是6. 已知实数,满足,则以,的值为两边长的等腰三角形的周长是A. 或B.C. D. 以上答案均不对7. 如图,二次函数的图象经过点,,下列说法正确的是A. B.C. D. 图象的对称轴是直线8. 抛物线的顶点坐标是A. B.9. 若、是方程的两个根,则实数,,,的大小关系为A. B. C. D.10. 已知抛物线与轴最多有一个交点,现有以下结论:①;②该抛物线的对称轴在轴左侧;③关于的方程有实数根;④对于自变量的任意一个取值,都有,其中正确的为A. ①②B. ①②④C. ①②③D. ①②③④二、填空题(共6小题;共30分)11. 用一个的值说明”是错误的,这个值可以是.12. 把二次函数化成的形式是.13. 抛物线的顶点坐标是.14. 已知抛物线经过点,它的对称轴是,则它的函数表达式是15. 如果抛物线与轴的两个交点分别为和,则当时,的值为.16. 若,是关于的方程的两根,且,则,,,的大小关系用“”连接的结果是.三、解答题(共8小题;共104分)17. 能否通过左右平移函数的图象,使得到的新的图象过点?如果能,说出平移的方向和距离;如果不能,说明理由.18. 在平面直角坐标系中,抛物线与轴的交点为,.(1)求抛物线的顶点坐标.(2)横、纵坐标都是整数的点叫做整点.①当时,求线段上整点的个数.②若抛物线在点,之间的部分与线段所围成的区域内(包括边界)恰有个整点,结合函数的图象,求的取值范围.19. 填表:20. 利用图象判断方程是否有解,若有解,请写出它的解(结果精确到).21. 不画出图象,你能说明抛物线与抛物线之间的关系吗?22. 将抛物线向右平移个单位所得抛物线的顶点为,向左平移个单位所得抛物线的顶点为,两条抛物线的交点为,求的面积.23. 已知二次函数,该函数与自变量的部分对应值如下表:(1)求该二次函数的表达式.(2)不等式的解集为.(3)不等式的解集为.24. 已知二次函数的图象过三个点,,,求这个二次函数的解析式.答案第一部分1. B2. C3. B4. C 【解析】圆的面积公式中,和之间的关系是二次函数关系.5. B6. B7. D 【解析】由图象可知图象与轴交点位于轴正半轴,故,A选项错误;函数图象与轴有两个交点,所以,B选项错误;观察图象可知时,所以,C选项错误;根据图象与轴交点可知,对称轴是,两点的中垂线,,即为函数对称轴,D选项正确.8. D 【解析】抛物线的顶点坐标为.9. C 【解析】由,,所以,同正,,同负,又,,所以.10. B第二部分(任意负数都可以)【解析】用一个的值说明”是错误的,这个值可以是(任意负数都可以).12.【解析】.13.14.15.16.第三部分17. 能,向右平移个单位长度.18. (1)解法一:对称轴,当时,,抛物线的顶点坐标为.【解析】解法二:,抛物线的顶点坐标为.(2)①当时,,令,得到,;则线段上的整数点有,,,共个.②顶点为,所以整点只能落在顶点和轴上.有个整数点,所以轴上应该有个.根据对称性知,当二次函数经过点和之间(包括)时,符合题意.将代入二次函数,得;将代入,得;的取值范围为.19. 第一列:向上、轴、;第二列:向上、轴、;第三列:向上、轴、;第四列:向上、轴、.20. 有解.,.21. 抛物线的顶点坐标为;抛物线的顶点坐标为.抛物线与抛物线形状相同,开口方向都向下,对称轴分别是轴和直线.抛物线是由抛物线向左平移个单位长度而得到的.22. 抛物线向右平移个单位所得抛物线为:顶点,向左平移个单位所得抛物线顶点,,联立解得,,点的坐标是,即的高,的面积是.23. (1)将点,,代入原函数可得,,,二次函数为.(2)或【解析】函数过点,,开口向上,解集为或.(3)【解析】,,,开口向上,的解集为.24. 设这个二次函数的解析式为,将,,三点坐标代入得解得这个二次函数的解析式为.。
新人教版九年级上册数学:《二次函数》基础练习及答案(5套)
基础知识反应卡·时间:10 分钟满分: 25 分一、选择题(每题3 分,共6 分 )21.若 y = mx + nx - p(此中 m , n , p 是常数 )为二次函数,则 ( )C .m ≠0D .m ≠0,或 p ≠02.当 ab>0 时, y = ax 2 与 y = ax + b 的图象大概是 ()二、填空题 (每题 4 分,共 8 分 )3.若 y = x m -1+ 2x 是二次函数,则 m = ________.4.二次函数 y = (k + 1)x 2 的图象如图 J22-1-1,则 k 的取值范围为 ________.图 J22-1-1三、解答题 (共 11 分 )5.在如图 J22-1-2 所示网格内成立适合直角坐标系后,画出函数2和 y =-1 2 的 y = 2x x(设小方格的边长为 1) :2图象,并依据图象回答以下问题图 J22-1-2(1)说出这两个函数图象的张口方向,对称轴和极点坐标;(2)抛物线 y = 2x 2 ,当 x______时,抛物线上的点都在 x 轴的上方,它的极点是图象的最______点;1 2,关于全部 x 的值,总有函数 y______0;当 x______时, y 有最 ______(3)函数 y =- x 2值是 ______.基础知识反应卡 ·时间: 10 分钟满分: 25 分一、选择题 (每题 3 分,共 6 分 )1.以下抛物线的极点坐标为 (0,1)的是 ( )A . y = x 2+ 1B . y = x 2- 1C .y = (x + 1)22D .y = (x - 1)2.二次函数 y =- x 2 +2x 的图象可能是 ()二、填空题 (每题 4 分,共 8 分 ) 3.抛物线 y = x 2+1的张口向 ________,对称轴是 ________.44.将二次函数 y = 2x 2+ 6x + 3 化为 y = a(x - h)2+ k 的形式是 ________. 三、解答题 (共 11 分 ) 5.已知二次函数 y =- 1x 2+ x + 4.2(1)确立抛物线的张口方向、极点坐标和对称轴; (2)当 x 取何值时, y 随 x 的增大而增大?当x 取何值时, y 随 x 的增大而减小?*基础知识反应卡·时间:10 分钟满分:25 分一、选择题 (每题 3 分,共 6 分 )1.已知二次函数的图象过(1,0), (2,0)和 (0,2) 三点,则该函数的分析式是()A . y= 2x2+ x+ 2B . y= x2+ 3x+ 2C.y= x2- 2x+ 3 D . y= x2- 3x+ 22.若二次函数的图象的极点坐标为(2,- 1),且抛物线过(0,3),则二次函数的分析式是()A . y=- (x- 2)2- 1B. y=-1(x- 2)2-1 2C.y= (x- 2)2- 1 D. y=1(x- 2)2- 1 2二、填空题 (每题 4分,共8 分 )3.如图 J22-1-3,函数 y=- (x- h)2+ k 的图象,则其分析式为____________.图 J22-1-34.已知抛物线y= x2+(m- 1)x-14的极点的横坐标是2,则m 的值是________.三、解答题(共 11 分)5.已知当x= 1 时,二次函数有最大值5,且图象过点(0,- 3),求此函数关系式.基础知识反应卡 ·22.2时间: 10 分钟 满分: 25 分一、选择题 (每题 3 分,共6 分 )1.下表是二次函数 y = ax 2+ bx +c 的自变量 x 的值与函数 y 的对应值,判断方程 ax 2+bx + c = 0(a ≠ 0, a , b , c 为常数 )的一个解的范围是 ( )x 6.17 6.18 6.19 6.20 y = ax 2+ bx + c- 0.03- 0.010.020.04A.6< x<6.17 B . 6.17<x<6.18C .6.18< x<6.19D . 6.19< x<6.202.二次函数 y =2x2+3x - 9 的图象与 x 轴交点的横坐标是 ()33 A. 2和 3 B.2和- 3 C .-3和 2 D .-3和- 22 2二、填空题 (每题 4 分,共 8 分 )3.已知抛物线y =x 2- x -1 与 x 轴的交点为 (m,0),则代数式m 2-m + 2 011 的值为__________.4.如图 J22-2-1 是抛物线 y = ax 2+bx + c 的图象,则由图象可知,不等式ax 2 +bx + c<0的解集是 ________.图 J22-2-1三、解答题 (共 11 分 )5.如图 J22-2-2,直线 y = x + m 和抛物线 y = x 2+ bx + c 都经过点 A(1,0), B(3,2). (1)求 m 的值和抛物线的关系式;(2)求不等式 x 2+bx + c>x + m 的解集 (直接写出答案 ).图 J22-2-2基础知识反应卡·22.3时间: 10 分钟满分: 25 分一、选择题 (每题 3分,共 6分 )2,1.在半径为 4 cm 的圆中,挖去一个半径为x cm 的圆,剩下一个圆环的面积为y cm 则 y 与 x 的函数关系为 ()22A . y=πx - 4 B. y=π(2-x)C.y=- (x2+ 4) D. y=-πx2+ 16πt(s)的关系式是 h=-52.已知某种礼炮的升空高度h(m)与飞翔时间t2+ 20t+ 1.若此礼2炮在升空到最高处时引爆,则引爆需要的时间为()A . 3 s B. 4 s C. 5 s D. 6 s二、填空题 (每题 4分,共 8分 )3.销售某种手工艺品,若每个赢利x 元,一天可售出 (8 - x) 个,则当 x= ________元,一天销售该种手工艺品的总收益y 最大.4.如图 J22-3-1,某省大学的校门是一抛物线形水泥建筑物,大门的地面宽度为8 m,双侧距地面 4 m 的高处各有一个挂校名横匾用的铁环,两铁环的水平距离为 6 m,则校门的高度为 (精准到 0.1 m,水泥建筑物厚度忽视不计)________ .图 J22-3-1三、解答题 (共 11 分 )5.杂技团进行杂技表演,演员从跷跷板右端 A 处弹跳到人梯顶端椅子 B 处,其身体(看成一个点)的路线是抛物线y=- 3x2+ 3x+ 1 的一部分,如图5J22-3-2.(1)求演员弹跳离地面的最大高度;(2)已知人梯高BC= 3.4 米,在一次表演中,人梯到起跳点 A 的水平距离是 4 米,问这次表演能否成功?说明原因.图 J22-3-2基础知识反应卡 ·1. C 2.D 3.3 4.k>- 1 5. 解: 图略.(1)函数 y = 2x 2 的图象张口向上,对称轴为 y 轴,极点坐标为 (0,0). 函数 y =- 1x 2 的图象张口向下,对称轴为y 轴,极点坐标为 (0,0).2(2)≠ 0 低 (3)≤ = 0 大 0 基础知识反应卡 ·1. A 2.Bx + 3 2- 33.上 y 轴 4.y = 22 21 21 2 9 5. 解: (1) 将二次函数 y =- x+ x + 4 配方,得 y =- (x - 1)+ .2 229因此抛物线的张口向下,极点坐标为1, 2 ,对称轴为 x = 1.(2)当 x>1 时, y 随 x 的增大而减小;当x<1 时, y 随 x 的增大而增大.*基础知识反应卡 ·1.D2.C3.y =- (x + 1)2+ 54.- 35.解: 由题意可设函数关系式为 y = a(x - 1)2+ 5,∵图象过点 (0,- 3),∴ a(0- 1)2+ 5=- 3,解得 a =- 8.∴ y =- 8(x - 1)2+ 5,即 y =- 8x 2+ 16x - 3.基础知识反应卡 ·22.21. C 2.B 3.2 012 4.- 2<x<3 5. 解: (1) ∵直线 y = x +m 经过点 A(1,0) ,∴ 0= 1+m.∴m =- 1. 即 m 的值为- 1. ∵抛物线 y = x 2+ bx + c 经过点 A(1,0), B(3,2),0= 1+ b + c ,b =- 3,∴解得2= 9+ 3b +c , c = 2.∴二次函数的关系式为 y =x 2- 3x + 2.(2){ x|x<1 或 x>3} . 基础知识反应卡 ·22.31. D2.B3.44.9.1 m3 25. 解: (1)y =- x + 3x + 15=- 35 2 19 5 x - 2 + 4 .故函数的最大值是 19,419米.∴演员弹跳离地面的最大高度是(2)当 x = 4 时, y =- 3×424+3× 4+ 1= 3.4= BC.5∴此次表演成功.基础知识反应卡 ·23.11. D 2.A3.∠ D ∠E DE DC 4. C 顺时针 905. 解: (1) 旋转中心是点 B. (2)旋转了 90 度.(3)AC 与 EF 垂直且相等.。
人教版九年级数学下册二次函数测试习题及答案【推荐下载】

B . y3> y1= y2
C. y1> y2> y3
D .y1= y2>y3
6.(毕节中考 ) 一次函数 y= ax+ b(a≠ 0)与二次函数 y= ax2+ bx+ c(a≠0) 在同一平面直角坐标系
中的图象可能是 ( )
7. (兰州中考 )二次函数 y=ax2+bx+ c 的图象如图所示,对称轴是直线 x=- 1,有以下结论: ① abc>0;② 4ac<b2;③ 2a+ b= 0;④ a- b+ c> 2.其中正确的结论的个数是 ( )
0
解析:根据已知条件,画出函数图象,如图所示.由已知得
a< 0,
-1
解
- ≤- 1,
2a
得- 12≤ a< 0.
14. (1+ 2, 2)或 (1- 2, 2) 解析:∵△ PCD 是以 CD 为底的等腰三角形,∴点 P 在线段 CD 的垂直平分线上.过 P 作 PE⊥ y 轴于点 E,则 E 为线段 CD 的中点.∵抛物线 y=- x2+ 2x+3 与 y 轴交于点 C,∴ C 点坐标为 (0, 3).又∵ D 点坐标为 (0, 1),∴ E 点坐标为 (0 ,2) ,∴ P 点纵坐
第 11 题图
第 14 条图
12. (台州中考 )竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔
1 秒依次竖直向
上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后
1.1 秒时到达相同的最大离地
高度,第一个小球抛出后 t 秒时在空中与第二个小球的离地高度相同,则
t= ________.
时, y 随 x 的增大而减小;当 x> 2 时, y 随 x 的增大而增大;
(2)解方程 x2- 4x+ 3= 0 得 x1= 3,x2= 1,即 A 点的坐标是 (1,0) ,B 点的坐标是 (3, 0).如图,
(word完整版)人教版九年级二次函数练习题(含答案),推荐文档
本大题共 4 小题,每小yo xyo x人教版九年级数学二次函数单元试卷时间 90 分钟满分:100 分一、选择题(本大题共 10 小题,每小题3分,共 30 分)1.下列函数不属于二次函数的是()A.y=(x-1)(x+2)1B.y= (x+1)22C. y=1-3 x2D. y=2(x+3)2-2x22.函数 y=-x2-4x+3 图象顶点坐标是()A.(2,-1)B.(-2,1)C.(-2,-1)D.(2, 1)3.抛物线y =1 (x + 2)2 + 1 的顶点坐标是()2A.(2,1)B.(-2,1)C.(2,-1)D.(-2,-1)4. y=(x-1)2+2 的对称轴是直线()A.x=-1 B.x=1 C.y=-1 D.y=1)5.已知二次函数y =mx 2 +x +m(m - 2) 的图象经过原点,则m 的值为(A.0 或2 2B. 0 C. 2 D.无法确定6.二次函数y=x 的图象向右平移3 个单位,得到新的图象的函数表达式是()A. y=x2+3B. y=x2-3C. y=(x+3)2D. y=(x-3)27.函数y=2x2-3x+4 经过的象限是()A.一、二、三象限B.一、二象限C.三、四象限D.一、二、四象限8.下列说法错误的是()A.二次函数 y=3x2中,当x>0 时,y 随x 的增大而增大B.二次函数 y=-6x2中,当x=0 时,y 有最大值 0C.a 越大图象开口越小,a 越小图象开口越大D.不论 a 是正数还是负数,抛物线 y=ax2(a≠0)的顶点一定是坐标原点19.如图,小芳在某次投篮中,球的运动路线是抛物线y=-5x2+3.5 的一部分,若命中篮圈中心,则他与篮底的距离l 是()A.3.5m B.4m C.4.5m D.4.6m10.二次函数y=ax2+bx+c 的图象如图所示,下列结论错误的是()A.a>0.B.b>0.C.c<0.D.abc>0.y(第 9 题) 3.05mx(第 10 题)二、填空题( 2.5 Ol 题3分,共 12 分)11.一个正方形的面积为 16cm2,当把边长增加 x cm 时,正方形面积为 y cm2,则 y 关于x的函数为 。
人教版九年级数学上册 第二十二章 二次函数 求二次函数的解析式 专题练习题.docx
初中数学试卷桑水出品人教版九年级数学上册第二十二章二次函数求二次函数的解析式专题练习题1.如图,在平面直角坐标系xOy中,正方形OABC的边长为2,点A,C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A,B和D(4,-23),求抛物线的解析式.2.如图,二次函数y=ax2+bx+c的图象与x轴交于A,B两点,其中点A(-1,0),点C(0,5),D(1,8)都在抛物线上,M为抛物线的顶点.(1)求抛物线的函数解析式;(2)求直线CM的解析式;(3)求△MCB的面积.3.已知一个二次函数,当x=1时,y有最大值8,其图象的形状、开口方向与抛物线y=-2x2相同,则这个二次函数的解析式是( )A.y=-2x2-x+3 B.y=-2x2+4C.y=-2x2+4x+8 D.y=-2x2+4x+64.已知某二次函数的最大值为2,图象的顶点在直线y=x+1上,并且图象经过点(2,1),求二次函数的解析式.2(2)画出此函数图象;(3)结合函数图象,当-4<x≤1时,写出y的取值范围.6.已知一个二次函数的图象经过点A(-1,0),B(3,0)和C(0,-3)三点;(1)求此二次函数的解析式;(2)对于实数m,点M(m,-5)是否在这个二次函数的图象上?说明理由.7.已知抛物线在x轴上截得的线段长是4,对称轴是x=-1,且过点(-2,-6),求该抛物线的解析式.8.已知y=x2+bx+c的图象向右平移2个单位长度,再向下平移3个单位长度,得到的图象对应的函数解析式为y=x2-2x-3.(1)b=____,c=____;(2)求原函数图象的顶点坐标;(3)求两个图象顶点之间的距离.9.如图,已知抛物线y=-x2+bx+c的对称轴为直线x=1,且与x轴的一个交点为(3,0),那么它对应的函数解析式是.10.如图,抛物线与x轴交于A,B两点,与y轴交于C点,点A的坐标为(2,0),点C的坐标为(0,3),它的对称轴是直线x=-1 2 .(1)求抛物线的解析式;(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标.答案:1. 解:y=16x2-13x-22. 解:(1)y=-x2+4x+5(2)y=-x2+4x+5=-(x-2)2+9,则M点坐标为(2,9),可求直线MC的解析式为y=2x+5(3)把y=0代入y=2x+5得2x+5=0,解得x=-52,则E点坐标为(-52,0),把y=0代入y=-x2+4x+5得-x2+4x+5=0,解得x1=-1,x2=5,则B点坐标为(5,0),所以S△MCB =S△MBE-S△CBE=12×152×9-12×152×5=153. D4. 解:∵函数的最大值是2,则此函数顶点的纵坐标是2,又顶点在y=x+1上,那么顶点的横坐标是1,设此函数的解析式是y=a(x-1)2+2,再把(2,1)代入函数中可得a(2-1)2+2=1,解得a=-1,故函数解析式是y=-(x-1)2+2,即y=-x2+2x+15. 解:(1)由表知,抛物线的顶点坐标为(-1,4),设y=a(x+1)2+4,把(0,3)代入得a(0+1)2+4=3,解得a=-1,∴抛物线的解析式为y=-(x+1)2+4,即y=-x2-2x+3(2)图象略(3)-5<y≤46. 解:(1)设二次函数的解析式为y=a(x+1)(x-3),由于抛物线的图象经过C(0,-3),则有-3=a(0+1)(0-3),解得a=1,∴二次函数的解析式为y=(x+1)(x-3),即y=x2-2x-3 (2)由(1)可知y=x2-2x-3=(x-1)2-4,则y的最小值为-4>-5,因此无论m取何值,点M都不在这个二次函数的图象上7. 解:∵抛物线的对称轴为x=-1,在x轴上截得的线段长为4,∴抛物线与x轴的交点坐标为(-3,0),(1,0),设抛物线解析式为y=a(x+3)(x-1),把(-2,-6)代入得a·(-2+3)·(-2-1)=-6,解得a=2,所以抛物线解析式为y=2(x+3)(x-1),即y=2x2+4x-6 8. (1) 2 0(2)(-1,-1)(3)由平移知两个图象顶点之间的距离=22+32=139. y=-x2+2x+310. 解:(1)y=-12x2-12x+3(2)由y=0得-12(x+12)2+258=0,解得x1=2,x2=-3,∴B(-3,0).①当CM=BM时,∵BO=CO=3,即△BOC是等腰直角三角形,∴当M点在原点O时,△MBC是等腰三角形,∴M点坐标为(0,0);②当BC=BM时,在Rt△BOC中,BO =CO=3,由勾股定理得BC=OC2+OB2=32,∴BM=32,∴M点坐标(32-3,0).综上所述,M点坐标为(32-3,0)或(0,0)。
九年级二次函数基础分类练习题.doc
二次函数基础分类练习题(练习一)1、下列函数:① y =』3x2;® y = x2 -x(14-x);③ y = x2(x2 +x)-4 ;④y=」+x;⑤j = x(l-x),其屮是二次函数的是 _________________ ,其屮,b = _______ ,c = _________2、当加 ____ 时,函数y =伽一2)++3兀一5 (m为常数)是关于x的二次函数3、当加二 ____ 时,函数),=(/沪+加卜八2恥|是关于%的二次函数4、当加二 ____ 时,函数y = (m-4)x,,,2-5w,+6+3x是关于x的二次函数5、若点A(2, m )在函数y = F 一】的图像上,则A点的坐标是 ______________ -6、在圆的面积公式S=7ir2屮,s与r的关系是( )A、一次函数关系B、正比例函数关系C、反比例函数关系D、二次函数关系7、如图,矩形的长是4cm,宽是3cm,如果将长和宽都增加xcm,那么面积增加ycm2, ①求y与x Z间的函数关系式•②求当边长增加多少时,面积增加8cm2.8、已知二次函数y = ax2-kc(a^O),当x=l时,y=-l;当x=2时,y=2,求该函数解析式.9、富根老伯想利用一边长为a米的II」墙及可以围成24米长的111木料,建造猪舍三间,如图, 它们的平血图是一排大小相等的长方形.(1)如果设猪舍的宽AB为x米,则猪舍的总面积S与x有怎样的函数关系?(2)请你帮富根老伯计算一下,如果猪舍的总面积为32米2,应该如何安排猪舍的长BC和宽AB的长度?III墙的长度是否会对猪舍的长度有影响?怎样影响?B C二次函数基础分类练习题(练习二)函数y = ax 2的图象与性质 1 r1、填空:(I )抛物线y = -x 2的对称轴是 ______ (或 _________ ),顶点坐标是 _______ ,当X ______ 时,y 随X 的增大而增大,当X ___ 时,y 随X 的增大而减小,当x= ______ 时, 该函数有最 值是 ____________ ;1 9(2)抛物线y = 的对称轴是 _______ (或 ________ ),顶点坐标是 _______ ,当x 时,y 随x 的增大而增大,当x _______ 时,y 随x 的增大而减小,当⑴ ________ 时,该函 数有最 ____ 值是 ________ :2、对于函数y = 2x 2下列说法:①当x 取任何实数时,y 的值总是正的;②x 的值增大,y 的值也增大;③y 随x 的增大而减小;④图象关于y 轴对称.其屮正确的是 _________3、抛物线y=—X?不具有的性质是( )A 、开口向下B 、对称轴是y 轴C 、与y 轴不相交D 、最高点是原点 4、苹果熟了,从树上落下所经过的路程s 与下落时间t 满足S=ygt 2 (g=9.8),则s 与7、二次函数y = 在其图彖对称轴的左侧,y 随x 的增大而增大,求m 的值.求加的值.8、二次函数『=一2/,当xi>x2>OH'i,求yi与y2的大小关系.9、己知函数),=(加+ 2)*宀心是关于x的二次函数,求:(1)满足条件的m的值;(2)m为何值时,抛物线有最低点?求出这个哉低点,这时x为何值时,y随x的增大而增大;(3)m为何值时,抛物线有最大值?最大值是多少?当x为何值时,y随x的增大而减小?10、如果抛物线y = 与直线y = x_{交于点@,2),求这条抛物线所对应的二次函数的关系式.二次函数基础分类练习题(练习三)函数y = ax2 + c的图象与性质1、抛物线y = -lx2-3的开口__________ ,对称轴是______ ,顶点坐标是_______ ,当x时,y随x的增大而增大,当x ______ 时,y随x的增大而减小.1 02、______________________________________________________________ 将抛物线y二-F向下平移2个单位得到的抛物线的解析式为__________________________ ,再向上平移3个单位得到的抛物线的解析式为_________________ ,并分别写出这两个函数的顶点坐标_______ 、_________ .3、任给一些不同的实数k,得到不同的抛物线y 当k取o, ±1时,关于这些抛物线有以下判断:①开口方向都相同;②对称轴都相同;③形状相同;④都有最底点.其屮判断正确的是________ .4、____________________________________________________________ 将抛物线y = 2.? -1向上平移4个单位后,所得的抛物线是____________________________ ,当x= _____ 时, 该抛物线有最—(填大或小)值,是_________ .5、已知函数y = mx2 + (in2 - m)x + 2的图象关于y轴对称,则m= ______6、二次函数),=0?+。
河北省邯郸市育华中学九年级2019-2020学年第一学期开学收心考试数学试卷(含答案)
育华中学九年级2019-2020学年第一学期数学开学收心考试测试范围:二次函数(主)、数据分析、勾股定理、平行四边形一、选择题(本题共16个小题,1-10题每题3分,11-16题每题2分,共42分)1. 下列y关于x的函数中,属于二次函数的是( )A. y=x−1B. y=C. y=(x−1)2−x2D. y=−2x2+12.下列能够成直角三角形的是()A. 1,2,3B. 3,4,5C. 5,6,7D.12,13,183.二次函数 y =- 2 ( x + 3 ) 2 - 1 的顶点坐标是()A.( 3 , 1 ) B.( 3 ,- 1 )C.(- 3 , 1 )D.(- 3 ,- 1 )4.二次函数y=(x−1)2−4的图象先向左平移2个单位,再向上平移3个单位,所得函数解析式为( )A. y=(x−1)2+1B. y=(x−3)2−1C. y=(x+1)2−1D. y=(x+2)2+15.二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如下:x …−3 −2 −1 0 1 …y …−3 −2 −3 −6 −11 …则该函数图象的对称轴是( )A. 直线x=−3B. 直线x=−2C. 直线x=−1D. 直线x=06.一条开口向上的抛物线的顶点坐标是(−1,2),则它有( )A. 最大值1B. 最大值−1C. 最小值2D. 最小值−27. 如图,以Rt△ABC的三边为直角边分别向外作等腰直角三角形.若AB=5,则图中阴影部分的面积为()A. 6B. 25/2C. 25/4D. 258. 如图,在平行四边形ABCD中,CE⊥AB,E为垂足.如果∠A=119°,则∠BCE=()A、61°B、29°C、39°D、51°9.为了解某社区居民的用电情况,随机对该社区10户居民进行了调查,下表是这10户居民2014年4月份用电量的调查结果: 居民(户) 1 3 2 4 月用电量(度/户) 40 50 55 60那么关于这10户居民月用电量(单位:度),下列说法错误的是( )A. 中位数是55B. 众数是60C. 方差是29D. 平均数是5410.对于抛物线y=−31(x+4)2+2,下列结论:①抛物线的开口向下;②对称轴为直线x=4;③顶点坐标为(−4,2);④x>4时,y 随x 的增大而减小,其中正确结论的个数为( )A. 1个B. 2个C. 3个D. 4个11. 某种植基地2016年蔬菜产量为80吨,预计2018年蔬菜产量达到300吨,求蔬菜产量的年平均增长率,设蔬菜产量的年平均增长率为x,则可列方程为( )A. 80(1+x)2=300 B. 80 (1+3x)=300C. 80+80(1+x) +80(1+x)2=300D. 80(1+x)3 =30012. 当ab>0时,y=ax2与y=ax+b 的图象大致是( ) A. B. C. D.13. 为增强身体素质,小明每天早上坚持沿着小区附近的矩形公园ABCD 练习跑步,爸爸站在的某一个固定点处负责进行计时指导。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
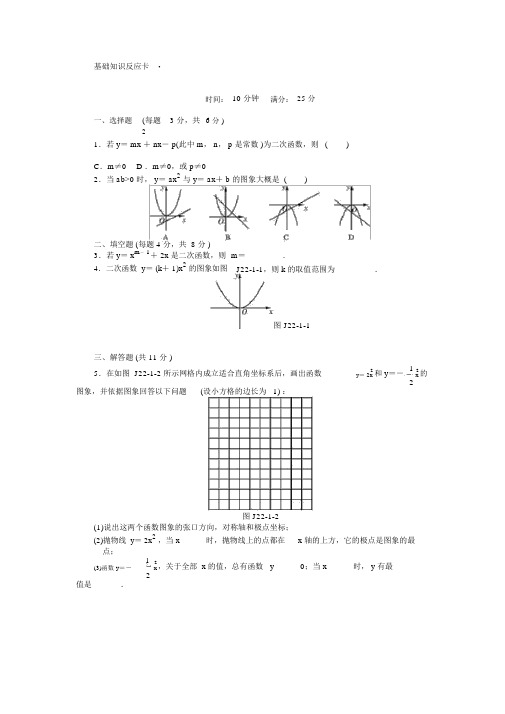
一、二次函数定义、解析式 (1)二、二次函数对称轴、顶点 (2)三、二次函数图像分析 (3)四、二次函数判别式△ (4)五、二次函数与一元二次方程关系 (4)六、二次函数函数值大小比较 (5)七、二次函数平移 (6)八、二次函数自变量范围求解 (8)九、二次函数与X轴交点问题 (8)十、二次函数动点问题 (9)十一、二次函数与三角形、平行四边形结合 (13)十二、二次函数与实际问题结合 (17)二次函数分类汇编 二次函数定义、解析式1. (2016~2017·育华·单元测试)下列关系式中,属于二次函数的是(x 为自变量)( )A. 218y x =B. 21y x =-C.21y x= D. 22y a x =2.(2016~2017·育华·单元测试)抛物线c bx x y ++=2经过A (-1,0),B (3,0)两点,则这条抛物线的解析式为_______________。
3.(2016~2017·育华·单元测试)(本题10分)若二次函数的图象的对称轴方程是32x =,并且图象过A (0,-4),和B (4,0)(1) 直接写出此二次函数的图象上点A 关于对称轴32x =对称的点A '的坐标。
(2) 求此二次函数的解析式。
4. (2017~2018·育华·第1次月考)(8分)如图,已知抛物线的顶点为A (1,4)、抛物线与y 轴交于点B (0,3),与x 轴交于点C 、D 两点。
点P 是x 轴上的一个动点。
(1) 求此抛物线的解析式。
(2) 求C 、D 两点坐标。
二次函数对称轴、顶点5. (2016~2017·育华·单元测试)函数223y x x =-+的图象的顶点坐标是( )A.(1,-4 )B.(-1,2)C.(1,2)D. (0,3)6. (2016~2017·育华·单元测试)抛物线4412-+-=x x y 的对称轴是( )A. 2-=xB. 2=xC. 4-=xD. 4=x7. (2016~2017·育华·单元测试)抛物线c x x y +-=82的顶点在x 轴上,则c 等于( )A. -16B. -4C. 8D. 168. (2016~2017·育华·第1次月考)对于抛物线3)5(312+--=x y ,下列说法正确的是( )A .开口向下,顶点坐标(5,3)B. 开口向上,顶点坐标(5,3)C. 开口向下,顶点坐标(-5,3)D. 开口向上,顶点坐标(-5,3)9. (2016~2017·育华·第2次月考)对于二次函数2)1(2+-=x y 的图象,下列说法正确的是( )A .开口向下B. 对称轴是1-=xC. 顶点坐标是(1,2)D. 与x 轴有两个交点10. (2016~2017·育华·第3次月考)抛物线3)2(2+--=x y 的顶点坐标是( )A . (-2,3) B.(2,3) C.(2,-3) D. (-2,-3)11. (2016~2017·育华·第4次月考)二次函数的解析式为1)2(2+-=x y ,则它的图象的顶点坐标是( )A. (-2,1)B. (2,-1)C. (2,1)D. (1,2)12. (2016~2017·育华·开学考试)对于二次函数2)1(2+-=x y 的图象,下列说法正确的是( )A .开口向下B .对称轴是x =-1C .顶点坐标是(1,2)D .与x 轴有两个交点13. (2017~2018·育华·第1次月考)函数223y x x =-+的图象的顶点坐标是( )A. (1,4)-B. (1,2)-C. (1,2)D. (0,3)14. (2017~2018·育华·第1次月考)对于抛物线3)5(312+--=x y ,下列说法正确的是( )A .开口向下,顶点坐标(5,3)B. 开口向上,顶点坐标(5,3)C. 开口向下,顶点坐标(-5,3)D. 开口向上,顶点坐标(-5,3)15. (2016~2017·育华·第2次月考)已知抛物线222++-=x x y ,则该抛物线的顶点坐标是________。
16. (2016~2017·育华·单元测试)若将二次函数322+-=x x y 配方为k h x y +-=2)(的形式,则k =___________。
17. (2016~2017·育华·单元测试)公路上行驶的汽车急刹车的刹车距离S (m )与时间t (s )的函数关系为2520S t t -=,当遇到紧急情况时,司机急刹车,但由于惯性,汽车要滑行_______米才能停下来。
18. (2016~2017·育华·第1次月考)二次函数32+=x y 的最小值是________。
19. (2016~2017·育华·第1次月考)已知,二次函数的表达式为x x y 842+=。
写出这个函数图象的对称轴和顶点坐标,并求图象与x 轴的交点坐标。
二次函数图像分析20. (2016~2017·育华·单元测试)二次函数2y ax bx c =++的图象如图所示,则点(b,ac )在第( )象限 A.一 B. 二 C. 三 D. 四21. (2016~2017·育华·单元测试)若一次函数b ax y +=的图象经过第二、三、四象限,则二次函数bx ax y +=2的图象只可能是( )22. (2016~2017·育华·第1次月考)在同一坐标系内,一次函数b ax y +=与二次函数b x ax y ++=82的图象可能是( )A B C D23. (2016~2017·育华·第4次月考)如图为二次函数c bx ax y ++=2的图象,则一次函数a bx y +=的图象不经过( ) A.第一象限B. 第二象限C. 第三象限D. 第四象限24. (2016~2017·育华·第2次模拟)二次函数()20y ax bx c a =++≠的大致图象如图4所示,关于该二次函数,下列说法错误的是A .函数有最小值B .对称轴是直线x =21C .当x <21时,y 随x 的增大而减小D .当 -1 < x < 2时,y >025. (2017~2018·育华·第1次月考)已知二次函数2y ax bx c =++的图象如图所示,则下列结论正确的是( ) A. ab >0, c >0 B. ab >0,c <0 C. ab <0, c >0D. ab <0,c <0O-1 xy2图426. (2016~2017·育华·第5次模拟)平面直角坐标系中,有线段MN ,M (1,1),N (2,2),若抛物线2axy =与线段MN 没有公共点,则a 的取值范围是( ) A. 0<aB. 2101<<>a a 或C. 21010<<><a a a 或或 D.121<<a 二次函数判别式△27. (2016~2017·育华·单元测试)抛物线)1(3)2(2-++-=m x m x y 与x 轴( )A. 一定有两个交点B. 只有一个交点C .有两个或一个交点 D. 没有交点28. (2016~2017·育华·第1次月考)在平面直角坐标系中,抛物线12-=x y 与x 轴的交点个数是( )A. 3B. 2C. 1D. 029. (2016~2017·育华·第1次月考)若函数362+-=x kx y 的图象与x 轴有交点,则k 的取值范围是( )A. 3<kB. 03≠<k k 且C. 3≤kD. 03≠≤k k 且二次函数与一元二次方程关系30. (2016~2017·育华·单元测试)抛物线c bx ax y ++=2如图,考察下述结论:①0<b ;②0>+-c b a ; ③ac b 42>; ④02<+b a .正确的有() A. ①②B. ①②③C. ②③④D. ①②③④31. (2016~2017·育华·第1次月考)已知二次函数)0(2≠++=a c bx ax y 的图象如图所示,下列结论:①0<b ;②024<++c b a ;③0>+-c b a ;④22)(b c a <+。
其中正确的结论是( )A. ①②B. ①③C. ①③④D. ①②③④32. (2016~2017·育华·第2次月考)已知二次函数)0(2≠++=a c bx ax y 的图象如下图所示,且关于x 的用一元二次方程02=-++m c bx ax 没有实数根,有下列结论:①042>-ac b ;②0<abc ;③2>m 。
其中,正确结论的个数是( ) A. 0B. 1C. 2D. 333. (2016~2017·育华·第3次月考)已知二次函数)0(2≠++=a c bx ax y 的图象如图所示,则下列结论:①ac >0;②方程02=++c bx ax 的两根之和大于0;③y 随x 的增大而增大;④a -b +c <0,其中正确的有( )A. 4个B.3个C.2个D. 1个34. (2016~2017·育华·第3次模拟)抛物线c bx ax y ++=2如图,考察下述结论:①0<b ; ②0>+-c b a ; ③ac b 42>; ④02<+b a .正确的有() A. ①② B. ①②③ C. ②③④ D. ①②③④ 35. (2016~2017·育华·第4次模拟)已知二次函数)0(2≠++=a c bx ax y 的图象如图所示,有下列结论:①0>+-c b a ;②0>abc ;③024>+-c b a ;④042>-ac b ;⑤03>+c a ;⑥0>-c a .其中正确结论的个数是( ) A. 2 B. 3 C. 4 D. 536. (2016~2017·育华·第5次月考)已知二次函数)0(2≠++=a c bx ax y 的图象如图所示,且关于x 的一元二次方程92=-++m c bx ax 没有实数根,有下列结论:①042>-ac b ;②abc <0;③7->m ,其中,正确结论的个数是() A. 0B. 1C. 2D. 3二次函数函数值大小比较37. (2016~2017·育华·单元测试)已知抛物线和直线l 在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线1-=x ,P 1(x 1,y 1),P 2(x 2,y 2)是抛物线上的点,P 3(x 3,y 3)是直线l 上的点,且-1<x 1<x 2,x 3<-1,则y 1,y 2,y 3的大小关系是( ) A .y 1<y 2<y 3 B .y 2<y 3<y 1 C .y 3<y 1<y 2 D . y 2<y 1<y 338. (2016~2017·育华·第2次月考)二次函数c bx ax y ++=2的图象,如图所示,其对称轴为直线1=x ,若点A (-1,y 1),B (2,y 2)是它图象上的两点,则y 1与y 2的大小关系是( )A. 21y y <B. 21y y =C. 21y y >D. 不能确定39. (2017~2018·育华·第1次月考)二次函数2(1)2y x =-+图像上三点A (-2,a ),B (-1,b ),C (2,c ),比较a , b , c 大小( )A. a >b >cB. b >a >cC. c >a >bD. a >c >b二次函数平移40. (2016~2017·育华·单元测试)把抛物线1422++-=x x y 的图象向左平移2个单位,再向上平移3个单位,所得的抛物线的函数关系式是( ) A .6)1(22+--=x yB. 6)1(22---=x yC .6)1(22++-=x yD. 6)1(22-+-=x y41. (2016~2017·育华·第1次月考)将抛物线3)1(2+-=x y 向左平移1个单位,再向下平移3个单位后所得抛物线的解析式为( ) A. 2)2(-=x yB. 6)2(2+-=x yC. 62+=x yD. 2x y =42. (2016~2017·育华·第2次月考)在平面直角坐标系中,将二次函数22x y =的图象向上平移2个单位,所得图象的解析式为( ) A. 222-=x yB. 222+=x yC. 2)2(2-=x yD. 2)2(2+=x y43. (2016~2017·育华·第3次月考)把抛物线2x y =向上平移1个单位,向左平移2个单位,得到的解析式为( ) A. 1)2(2+-=x yB. 1)2(2--=x yC. 1)2(2++=x yD. 1)2(2-+=x y44. (2016~2017·育华·第5次模拟)抛物线x x y --=2的图象向右平移一个单位并沿x 轴做翻折称为第一次操作,再向右平移一个单位并沿x 轴翻折称为第二次操作……那么第2015次操作得到的抛物线解析式为__________________。
