自动调节器典型调节规律及调节过程分析(1)
2 调节器和调节系统的调节过程

图1-13 积分控制规律
比例控制规律使控 制器反应迅速,积分 控制规律能消除系统 静态偏差。在制冷空 调系统中,较少采用 纯积分控制器;在控 制质量要求较高的场 合,选用比例控制器 或比例积分控制器。
图1-14 比例积分控制规律
控制规律
微分控制
若流入量和流出量存在着不平衡,等到在被控参 数的偏差量上充分反映出来时,实际上已落后了一 段时间。当被调对象中一旦出现流入量与流出量不 平衡时,立即就有一个与此不平衡流量成正比的被 调量偏差的变化速度出现。由于控制对象总有一定 的容量,所以此时偏差变化量尚未形成(或十分小), 因此,被调量偏差的变化速度信号在时间上快于偏 差变化信号。如果利用被控参数的变化速度(即被控 参数对时间的导数)作为控制器的输入信号,就可克 服偏差控制作用不及时的现象。这就引入了微分控 制器。理想微分控制器的输出信号与输入信号变化 速度成正比。即
(2)电动比例调节器
电动比例积分两通调节阀
优点:
①电源问题容易解决; ②作用距离长,一般情况下不受限制; ③调节精度高的电动调节器一般容易做到; ④可实现微机化。
缺点:
①电气装置、继电器和电子元件在动作频繁的工作条 件下,只能使用一定的期限; ②电动调节器的使用和调整比较复杂,对维护技术要 求亦高; ③电器接点有火花产生,电器元件带电,不利于防火 防爆。
Байду номын сангаас
3、调节器元件
调节器可分为直接作用式和间接作用式。 间接作用式调节器的优点是:调节器灵敏 度高,作用距离长,输出功率大,便于集中控 制及采用计算机控制等。其缺点是:常需要辅 助能源,结构较复杂,价格较贵等。 直接作用式调节器的优点是:结构简单、 紧凑、价格便宜,密封性好,因此被广泛用于 制冷、空调系统的一般控制中。但它灵敏度及 精度差,因此在调节质量要求高的场合不能适 用。
第二章 调节器的特性及调节过程(2006.9)

⑷、比例系数和比例带的概念及物理意义
①、在比例控制中,输出信号的变化量与输入信号的 u t 变化量之比,称为比例系数,即:
Kp
e t
②、通常用比例系数的倒数来表示调节器的输入与
输出之间的比例关系,即:
u t
1
e t
1 100% Kp
δ称为比例调节器的比例带(比例度);
Δ Qf
θ + e -θz
g
1 2
ε
ε
1 2
P
θc
K4
电加热器
+
K1
τ 1 T1
θa
恒温室
对象
双位调节器
T2
敏感元件(传感器)
2.3、比例调节器特性及调节过程分析
⑴、比例调节器的定义: 能使输出变量与输入变量按比例关系调节的调节器称为比 例调节器(也称P调节器); ⑵、调节器的输出信号u与偏差信号e有如下关系:
h H hman hmin
hman-液位标尺的最高刻度(mm) hmin-液位标尺的最低刻度(mm)
由于比例调节器的输入信号和输出信号成比例,即:L∝H
H h / hman hmin h lman lmin L l / lman lmin l hman hmin
H h / hman hmin h lman lmin 100% 100% L l / lman lmin l hman hmin
h lman lmin 250 300 10 0 100% 100% 50% l hman hmin 5.0 2.5 400 0
1 3
调节器及调节作用规律

K p测
K F测 l2 F反 l3
F为波纹管的截面积,两者一般相等
l为力臂,一般固定不变
K为负数—负作用(作用方式)
§1-3-2 比例作用规律
DLMU
K F测 l2 F反 l3
如何调整比例带(比例系数)?
改变反馈力臂的长度,来调整比例系数(K比例带PB), 实物上通过比例带旋钮可以左右移动反馈波纹管的位置来实 现。
微分阀Rd开度越大,微分消失得越快,即微分时间Td 越 短,微分作用越弱;反之亦然。
当微分消失后,调节器的输出大小与偏差成比例,比例 作用的强弱由负反馈波纹管的位置进行调整。
§1-3-3 比例微分作用规律
DLMU
小结
1、微分作用具有超前调节的功能,输出减小的过程即为微分 消失过程;
2、微分作用不能单独用作调节器,一般与比例或者比例积分 一起构成PD或者PID调节器;
Company name
调节器及调节作用规律
轮机自动化教研室
DLMU
引言
r(t)
+-
e(t) 调节器
p(t)
b(t)
执行 q(t) 机构
测量 单元
f(t)
控制 y(t) 对象
DLMU
引言
– 系统为偏差驱动 – 调节器的输入是被控量的偏差值 – 调节器的输出是控制量 – 可看作一个对象或环节 – 调节器的作用规律:
§1-3-2 比例作用规律
DLMU
2、比例带δ(或 PB):是指调节器的相对输入量与相对输出 量之比的百分数.
PB( ) e / X imax 100% X Omax e 100 R 100%
p / X O max
第一章 调节系统的基本原理与调节

2.自动调节系统的 任务:以预定的精 度,确保被控量等 于给定值,或与给 定值保持确定的函 数关系。
3.自动调节系统的组成
自动调节系统由调节对象、发信器、调节 器和执行器组成的闭环系统。 发信器、调节器和执行器的总和又可以称 为自动调节设备。 自动调节系统是由调节对象和自动调节设 备组成。
定义:调节系统在阶跃干扰作用下,系统的平 衡状态遭到破坏,从一个稳态过渡到另一个稳 态的过程,也就是被调参数随时间而变化的过 程,称为过渡过程。
静态(稳态)——动平衡。对于定值调节系统, 当对象的流入量与流出量相等时被调参数处于 相对平衡状态,此时被调参数不随时间而变化。
流入 调节对象
流出
例:冷藏箱——调节对象,被调参数——箱内 的温度,给定值θ 0 。当干扰加入后,箱内温度 会偏离θ 0 ,原来的平衡被破坏。由于调节作用, 克服了干扰的影响,是被调参数逐渐趋近于给定 值。这一过程,被调参数是随时间t变化的。
+-
自动调节系统是个闭合回路,故为闭环系统。 另外,系统的输出是被调参数,但它经过发信器 后又返回到调节器的输入端。这种把系统的输出 信号又引到系统输入端的作法叫做反馈。
如果反馈信号使被调参数的变化减小,称为负 反馈,反之,称为正反馈。 负反馈信号(即被调参数的测量值z)进入比较元 件时取负值,而给定值r取正值,所以比较元件输 出的偏差信号为 e=r-z。 在自动调节系统中一般都采用负反馈。它是按 偏差进行控制的,所以,产生偏差是自动调节的 必要条件。
空调系统中采用的开环控制系统方框图如下
按干扰补偿的控制系统方框图
这种控制方式的原理是需要控制受控对象 (调节对象),而测量的是破坏系统正常工作 的干扰。利用干扰信号产生控制作用,以补偿 干扰对被调参数的影响,所以称干扰补偿。 信号源干扰经测量、计算、执行诸元件至 对象的被控量,是单向传递的,所以是开式控 制。 由于测量的是干扰,所以只能对可测干扰 进行补偿。不可测干扰以及对象各功能部件参 数变化给被控量造成的影响,系统自身无法控 制。因此,控制精度受到原理上的限制。
调节器及其调节规律

• 三、比例微分调节规律PD: • 1、概念: • 理想的比例微分调节规律,其表达式为:
P
Kp(e
Td
de dt
)
• 式中:Kp—比例系数;Td—微分时间;
•
de/dt—偏差的变化速度;
• 比例微分调节器的输出等于比例作用的输出和 微分作用的输出之和。比例度和微分时间是比例 微分调节器的两个重要特性参数。其大小反映了 比例作用和微分作用的强弱。
•
dP dt
= KIe
• 可见,只要偏差存在,调节器的输出就会变
化,只有e=0,输出信号才不再继续变化,执
行器才停止动作,系统才能稳定不来。
2、实例分析:
• 3、特点:
• a)积分调节完毕,能消除被控参数的静差。 • b)积分调节作用比较缓慢。 • c)积分作用的引入,会降低系统的稳定 • 性,最大动态偏差较大,调节时间增加。 • d)积分调节规律,容易使调节器输出产 • 生饱和状态。 • 总之,积分调节规律动态性能差,在实际
• 当t=T,PD= A( Kd-1)e-T/T=0.368 A( Kd-1)
• 可见:微分作用的输出下降了63.2%所需的时间
•
为时间常数T。
•
∴微分时间Td=Kd×T
• 3、不同时间常数下的阶跃响应曲线:
T1>T2>T3
• 微分时间Td表征微分作用的强弱,当T大,Td长, 微分作用强;反之Td短,微分作用弱。
• d)只适用于惯性较大的系统。
• 二、微分器:
• 1、何为微分器:
•
即比例微分调节,比例带PB=100%。对
阶
跃输入,输出瞬时增大到某数值,然后慢慢降
到和阶跃输入相等的值。
第四节 调节器的基本调节规律

2.比例积分调节规律及积分时间
比例调节规律是输出信号与输人偏差成 比例,因此作用快,但有余差;积分调节规 律能消除余差,但作用慢;比例积分调节规 律具有以上两种调节规律的优点,是生产 上常用的一种调节规律(常用PI表示)。比例 积分调节规律可用下式表示:
由于比例积分调节器具有比例和积分
两种调节器的优点,同时比例度、积分时 间两个参数均可以调整,因此适用面比较 广,多数系统都可采用。只有在对象纯滞 后时间特别大时,调节时间较长,最大偏 差较大;在负荷变化特别强烈时,由于积分 作用迟缓,调节作用不能及时,这时可增 加微分作用。
双位调节是位式调节的最简单形式。 双位调节的动作规律是,测量值大于给定 值时,调节器的输出为最小;测量值小于给 定值时,调节器的输出为最大(也可以是相 反的情况)。因此,双位调节只有两个输出 值,相应的调节机构也只有两个极限位置, 即不是最大就是最小。没有中间位置。而 且从一个位置变到另一个位置是很快的、 如图7-14所示。
第四节 调节器的基本调节规律
调节器接受偏差信号后,其输出随输人 变化的规律,即是调节器的基本调节规律。 在工业自动调节系统中最基本的调节规律 有:位式调节、比例调节、积分调节和微分 调节四种。
各种调节规律是为了适应不同的生产要 求设计的。因此,必须根据生产的要求来 选用适当的调节规律。
一、双位调节
2.ห้องสมุดไป่ตู้例积分微分调节规律
比例微分调节的结果是存在余差的。为
了消除余差,生产上常将比例、积分、微 分三种调节规律结合起来,称例积分微分 调节,习惯上用PID表示。
PID调节器综合了各类调节器的优点, 因此具有较好的调节性能。但这并不意味 着在任何条件下采用这种调节器都是最好 的,要从生产实际和经济价值等方面来选 用调节器。
调节器调节规律
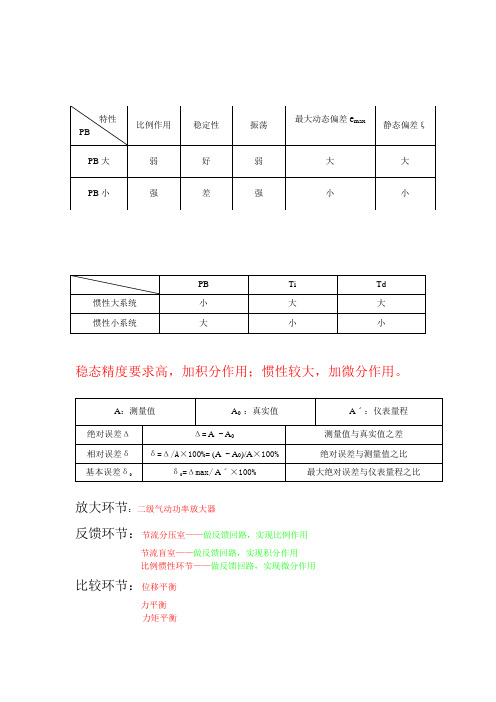
稳态精度要求高,加积分作用;惯性较大,加微分作用。
放大环节:二级气动功率放大器反馈环节:节流分压室——做反馈回路,实现比例作用节流盲室——做反馈回路,实现积分作用比例惯性环节——做反馈回路,实现微分作用比较环节:位移平衡力平衡力矩平衡所有气动仪表的构成原理如图3-1-7所示,都是由三个基本环节(放大、反馈、比较)构成。
其中,放大环节起信号放大作用,要求它具有较高的灵敏性和足够大的功率输出;反馈环节起信号的运算作用,通常是把仪表的输出信号P 出通过反馈回路,送回到仪表的输入端与输入信号进行综合,如果放大环节放大倍数足够大,仪表的信号传递关系只决定于反馈回路的信号传递关系。
这样,可消除放大环节各种非线性因素的影响,提高仪表的精度。
同时,在调节器中,采用不同的反馈回路,可实现不同的调节作用规律;比较环节起信号比较作用,使输入信号与反馈信号在此比较,其输出信号等于各信号的代数和。
总之,只要我们掌握了放大、反馈和比较等三个基本环节,就能比较容易地分析一台仪表的工作原理及功能。
图3-1-7 气动仪表的组成原理1.气动仪表的放大环节前面介绍过,几乎所有气动仪表,在喷嘴挡板机构的输出端,都要串联一个气动功率放大器。
在结构上两者往往组成一体,称为二级气动功率放大器。
其中喷嘴挡板机构为一级放大。
图3-1-8是耗气型二级气动放大器的原理图。
这种类型的二级气动功率放大器的输入与输出之间的传递关系为:h K P B ∆⋅=∆式中,K =K 1·K 2是二级气动放大器的放大倍数;K 1是喷嘴挡板机构的放大倍数;K 2是耗气型气动放大器的放大倍数。
图3-1-8 耗气型二级气动放大器原理图2.气动仪表的反馈环节 基于反馈控制原理,如果仪表放大环节的放大倍数足够大,则仪表的信号传递关系只决定于反馈回路的信号传递关系。
因此,在气动仪表中,总是把输出端的输出信号引回到输入端,构成负反馈气路,但除1∶1的负反馈外,在调节器中引用不同的反馈气路,就可以实现比例、积分和微分的作用规律。
自动调节器典型调节规律及调节过程分析

第八章 调节器调节规律及其对过程影响第一节 自动调节器典型调节规律及调节过程分析调节器的基本调节规律是模拟运行人员的基本操作,是运行人员调节动作精华的总结。
选择合适的调节器动作规律是热工自动人员的职责范畴,但运行人员如果能理解各种动作的调节过程,就能够使用好相应的自动调节系统。
自动调节的目的是要及时准确地进行调节,前面我们已经讲到基本环节由比例、积分、惯性、微分、迟延组成。
因为惯性、迟延环节不符合及时准确的要求,所以我们可考虑的就只有比例、积分、微分这三种特性了(积分、微分调节规律一般不能单独使用)。
自动调节器的典型动作规律按照环节特性可分为比例(P )、比例积分(PI )、比例微分(PD )、比例积分微分(PID )。
一、典型调节规律1. 比例(P )调节规律比例调节作用简称为P 作用,是所有调节器必不可少的一种典型调节作用。
P 作用实质上就是典型环节中的比例作用。
不过这个环节一般用电子元件构成的电路来实现,其输入输出都是电信号。
比例环节的传递函数P K W =,P K 称为比例环节的比例放大系数;而在比例(P )调节作用中,传递函数习惯上表示成δ1=P W , (8-1) 式中 PK 1=δ——调节器的比例带(比例度),δ越大,比例作用越弱。
下面以如图8-1所示的采用浮子式比例调节器的水位调节系统为例,说明比例调节器的调节规律。
该系统的被调对象是有自平衡能力的单容水箱;浮子起到检测器的作用,用于感受水位的变化;比例调节器就是杠杆本身,杠杆以O 点为支点可以顺时针或逆时针转动。
给定值的大小与给定值连杆的长短有关;选择流入侧阀门作为调节阀,由调节器来控制它的开度变化。
当某种扰动使水位升高时(说明此时流入量1q >流出量2q ),浮子随之升高,通过杠杆作用使阀门芯下移,关小调节阀,流入量1q 减小直至等于流出量2q 。
反之,当某种扰动使水位降低时(说明此时流入量1q <流出量2q ,浮子随之降低,通过杠杆作用使阀门芯上移,开大调节阀,流入量1q 加大直至等于流出量2q 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八章 调节器调节规律及其对过程影响第一节 自动调节器典型调节规律及调节过程分析调节器的基本调节规律是模拟运行人员的基本操作,是运行人员调节动作精华的总结。
选择合适的调节器动作规律是热工自动人员的职责范畴,但运行人员如果能理解各种动作的调节过程,就能够使用好相应的自动调节系统。
自动调节的目的是要及时准确地进行调节,前面我们已经讲到基本环节由比例、积分、惯性、微分、迟延组成。
因为惯性、迟延环节不符合及时准确的要求,所以我们可考虑的就只有比例、积分、微分这三种特性了(积分、微分调节规律一般不能单独使用)。
自动调节器的典型动作规律按照环节特性可分为比例(P )、比例积分(PI )、比例微分(PD )、比例积分微分(PID )。
一、典型调节规律 1. 比例(P )调节规律比例调节作用简称为P 作用,是所有调节器必不可少的一种典型调节作用。
P 作用实质上就是典型环节中的比例作用。
不过这个环节一般用电子元件构成的电路来实现,其输入输出都是电信号。
比例环节的传递函数P K W =,P K 称为比例环节的比例放大系数;而在比例(P )调节作用中,传递函数习惯上表示成δ1=P W , (8-1)式中 PK 1=δ——调节器的比例带(比例度),δ越大,比例作用越弱。
下面以如图8-1所示的采用浮子式比例调节器的水位调节系统为例,说明比例调节器的调节规律。
该系统的被调对象是有自平衡能力的单容水箱;浮子起到检测器的作用,用于感受水位的变化;比例调节器就是杠杆本身,杠杆以O 点为支点可以顺时针或逆时针转动。
给定值的大小与给定值连杆的长短有关;选择流入侧阀门作为调节阀,由调节器来控制它的开度变化。
当某种扰动使水位升高时(说明此时流入量1q >流出量2q ),浮子随之升高,通过杠杆作用使阀门芯下移,关小调节阀,流入量1q 减小直至等于流出量2q 。
反之,当某种扰动使水位降低时(说明此时流入量1q <流出量2q ,浮子随之降低,通过杠杆作用使阀门芯上移,开大调节阀,流入量1q 加大直至等于流出量2q 。
这样,就可以自动地把水位H 维持在某个高度附近,完成水位的自动调节。
↓↑⇒μh ,↑↓⇒μh ,动作方向始终正确,朝着减小被调量波动的方向努力。
比例调节器的动画演示见光盘第八章目录下”比例调节器流出侧扰动(阶跃减少)”和“比例调节图示中连杆长度为L ,水位如图8-1所示。
假设在目前调节阀门开度μ下流入流出正好平衡,水位稳定不变。
此时,将给定值连杆变短后重新装入,由于连杆变短,水位还是原数值没有变化,所以调节器杠杆右侧下降左端升高,调节阀门开度阶跃开大,使流入量1q 阶跃增加,21q q >,进而引起水位H 上升,水位上升的同时,调节杠杆右侧又不断回升,杠杆左端下移,调节阀开度不断关小,使1q 减小,当21q q =时,水位处于新的平衡状态。
这个新的水位高于原来的水位,所以给定值连杆长度变短相当于给定值的增加,给定值连杆的长度就代表给定数值的大小。
自动调节系统主体是由被调对象(单容水箱)、调节机构(流入侧阀门)、检测器(浮子)、调节器(杠杆)、执行器(阀门杆)组成,方框图如图8-2所示。
图8-2 比例调节系统方框图图中mK代表检测器(浮子)传递函数,此系统mK=1;(为了分析方便,对调节系统进行简化,假设检测器和执行器的传递函数都等于1(实际系统虽然不等于1但等于常数),故图8-2上省略执行器);1μK反映流入侧阀门开度和流量之间的关系;δ1为调节器传函,此系统ba=δ1;As1反映水箱这一环节净流量与水位的关系;2R代表水箱流出侧阀门阻力;λ代表流出侧阀门开度扰动;2μK反映流出侧阀门开度与流量之间的关系。
选择给定值G为输入,水位H为输出,传递函数可化简为1)1(1)1(212212121221221221+++=++=+++=sRKARRKRKRKsARRKsARRKsARRKWμμμμμμμδδδδδδδ(8-2)是一个一阶惯性环节,稳态放大系数2121RKRKKμμδ+=(8-3)当给定值扰动为幅值为x的阶跃扰动时,输出水位的稳态值为2121)(xRKRKhμμδ+=∞(8-4)δδδδμμμμ2121212111)()()(RKxRKxxRKRKxhGe+=+=+-=∞-=∞(8-5)可以看出,静态偏差与δ成正比。
如图8-2所示系统,给定值单位阶跃扰动仿真曲线如图8-3所示,从图中可知,随着δ↑,静态偏差)(∞e也相应↑,但响应曲线始终体现为一阶惯性环节特性,为非周期响应,系统始终很稳定。
Matlab文件见光盘第八章目录下“BiLiXT01.mdl”。
10;1,121===ARKμ图8-3 给定值单位阶跃响应给定值G不变,流出侧阶跃扰动时,H的仿真曲线如图8-4所示,从曲线上可以看出,流出侧阀门开大时(λ↑),水位H↓,且随着δ↑,静差e(∞)↑,响应曲线为非周期响应。
Matlab文件见光盘第八章目录下“BiLiXT02.mdl”。
8-5所示,测量变送器q1+-G+执行器We调节器WcE调节机构μWμy干扰通道q2+调节通道W oμW m调节量W oλλ++e mμ调节器采用比例(P)调节器,δ1=cW;(8-7)被调对象为有自平衡多容对象,调节通道等效传函表示为1)1(nooo sTKW+=μμμ(8-8)干扰通道等效传函表示为2)1(nooo sTKW+=λλλ(8-9)给定值G加入单位阶跃扰动的双容对象调节系统仿真曲线如图8-6所示,从图上可以看出,随着比例带δ的增大,响应曲线振荡程度逐渐减小,系统稳定性提高,但静态偏差也逐渐加大。
动画演示见光盘第八章目录下“比例调节器配双容水箱”。
Matlab文件见光盘第八章目录下“BiLiXT03.mdl”。
2)120(1+=s W o μ 图8-6给定值单位阶跃扰动响应(比例调节器配接双容对象)对方框图8-5进行等效变换,化简出给定值作为输入时的系统等效传函为:2222222121121)1(111)1(11T s T s T Ts s T Ts Ts W δδδδδδδδ+++=+++=+•++•= (8-10) 可看出该系统属于振荡环节,与振荡环节标准传函2222nn ns s K W ωζωω++=比较 可得出⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+=+=+=δωδζδ11111111T K n 同时↓↑⇒<<n K ωδζ11 (8-11)随着↑δ,↓K ,静态偏差↑∞)(e ,静态准确性指标变坏;↑ζ,系统稳定程度提高,对提高系统稳定性有利;↓n ω,振荡频率↓f ,响应曲线振荡周期加大(调节时间加长)。
通过上面分析,可以得出比例调节作用的优点:动作方向始终正确,且加大比例带δ对提高系统的稳定性有利(多容对象);缺点:存在静态偏差,且静差与比例带成正比。
因为现场对象多数是多容对象,所以,当调节比例带时,其对系统稳定性和准确性的影响正好相反。
2. 积分(I )调节规律比例调节的最大缺点是存在静态偏差,要想静差为0,比例带就要选择的非常小,而这会使系统的稳定性大大降低,这是我们不希望的。
积分调节器就是前面研究过的积分环节,输入信号是误差e ,输出信号是阀门开度μ。
表达式如下⎰=edt T i1μ,此式表明调节阀的开度变化与误差对时间的积分成正比。
只有当误差为0时,调节阀开度才能保持不变。
传递函数为sT W i I 1=(8-12) i T ——积分时间常数,i T 越小输出的变化就越快,称为积分作用越强。
所以,采用积分调节器可以消除被调量的静态偏差,这是积分调节规律的主要特点,也是它的优点。
对于如图8-5所示的单回路调节系统,调节器采用积分调节器,传函为sTWic1=,对象采用有自平衡单容对象,调节通道传函表示为1+=sTKWoooμμμ;选择给定值G作为输入,被调量y作为输出,构成的负反馈回路如图8-7所示,系统传递函数为图8-7 积分调节系统方框图(配接有自平衡单容对象)μμμμμμμμμμμμoioooiooioioooiooiTTKsTsTTKKsTsTTKsTKsTsTKsTW++=++=+⋅++⋅=11111122(8-13)与二阶系统的标准传函222nnssKWωζω++=比较,列出联立方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧===μμμμμζωωωonoionoionTTTKTTKK1222(8-14)解之得⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧===μμμμζωooioionTKTTTKK2112(8-15)由上式可知,1=K与其它变量无关,对于给定值为幅值为x的阶跃扰动,)(xKxy==∞,静态偏差0)()(=-=∞-=∞xxyGe。
分析得出积分作用的优点:可以消除静态偏差。
比例作用配接有自平衡的单容对象构成的系统总是稳定的,而采用积分作用当121<=μμζooiTKT时,系统响应则为衰减振荡,说明引入积分作用降低了系统的稳定性,造成振荡。
ζ的大小与积分时间i T成正比,即iT减小,ζ减小,系统稳定性下降,振荡加剧。
积分调节器配接单容水箱的演示文件见光盘第八章目录下“积分调节器”(使用时先选择“水位升高”或“水位降低”按钮后再选择绿色的“播放”按钮。
对于积分作用来说,只要存在误差,积分环节的输出就会一直朝某方向变化,这种变化作用在对象的输入端(调节作用),目的是消除误差。
例如单容水箱当Gh>时,偏差0)(<-hGe,数值为负,所以积分调节器输出减小,进而关小调节阀门减小流入量。
Gh<水位偏低会加大流入量。
但这种调节只以水位是否等于给定值作为调节目标,而不是以流入流出量平衡作为调节目标。
假设给定值G 不变,对象受到流出侧扰动,水位响应曲线如图8-11所示,在20t t →时刻,G h >,0<e ,积分输出持续减小,会关小流入侧阀门;在42t t →时刻,G h <,0>e ,积分输出持续增大,会开大流入侧阀门。
而水位的变化是反映流入与流出是否平衡的标志,10t t →、43t t →阶段水位上升说明流入大于流出,正确调节应关小流入侧阀门;31t t →水位下降说明流入小于流出,应开大流入侧阀门。
采用积分作用,在10t t →阶段,应该关小且实际调节也关小,方向正确;在21t t →阶段,应该开大而实际调节关小,方向错误;在32t t →阶段,应该开大且实际调节也开大,方向正确;在43t t →阶段,应该关小而实际调节开大,方向错误。
一个周期内有一半的时间调节方向是错误的,这种错误调节会引起过调现象的产生,过调是引起系统输出振荡的原因。
通过分析可以得出积分作用的缺点:过程中容易产生过调,引起被调量反复振荡,系统稳定性下降。
积分时间越小其积分作用越强,输出的变化越快,过调就越严重,系统的振荡就越剧烈。
