风筝模型和梯形蝴蝶定理
2018四年级奥数.几何.风筝模型和梯形蝴蝶定理(B级).学生版

MSDC 模块化分级讲义体系
四年级奥数.几何.风筝模型和梯形蝴蝶定理(B).学生版
Page 2 of 9
【巩固】在△ABC 中 BD =2:1, AE =1:3,求 OB =?
DC
EC
OE
【例 3】 如图,平行四边形 ABCD 的对角线交于 O 点,△CEF 、△OEF 、 △ODF 、△BOE 的面积依次 是 2、4、4 和 6.求:⑴求 △OCF 的面积;⑵求 △GCE 的面积.
【巩固】如右上图,已知 BO=2DO,CO=5AO,阴影部分的面积和是 11 平方厘米,求四边形 ABCD 的面积。
【例 4】 如图,边长为 1 的正方形 ABCD 中, BE 2EC , CF FD ,求三角形 AEG 的面积.
A
D
G F
B
EC
MSDC 模块化分级讲义体系
四年级奥数.几何.风筝模型和梯形蝴蝶定理(B).学生版
方厘米,则四边形 PMON 的面积是
平方厘米。
MSDC 模块化分级讲义体系
四年级奥数.几何.风筝模型和梯形蝴蝶定理(B).学生版
Page 6 of 9
课堂检测
【随练 1】 如图, S2 2 , S3 4 ,求梯形的面积.
【随练 2】 如左下图,E 是长方形 ABCD 边 AB 的中点,已知三角形 EBF 的面积是 1 平方厘米,求长方形 ABCD 的面积。
A
D
O
B
C
MSDC 模块化分级讲义体系
四年级奥数.几何.风筝模型和梯形蝴蝶定理(B).学生版
Page 4 of 9
【巩固】在梯形 ABCD 中,上底长 5 厘米,下底长 10 厘米, S BOC 20 平方厘米,则梯形 ABCD 的面积是 平方厘米。
四年级下册数学扩展专题练习:几何.风筝模型和梯形蝴蝶定理(B级)全国通用

风筝模型:
板块一风筝模型:(又叫任意四边形模型)
S 4
S 3S 2S 1O
D
C B
A
①1243::S S S S 或者1324S S S S ②1243
::AO OC S S S S 风筝模型为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.板块二梯形模型的应用
梯形中比例关系(“梯形蝴蝶定理”
):A
B C D
O
b
a S 3S 2S 1S 4①2213
::S S a b ②22
1324
::::::S S S S a b ab ab ;③S 的对应份数为2a b .梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.
(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明) 知识框架
风筝模型和梯形蝴蝶定理。
多边形的面积几何模型篇风筝模型和蝴蝶模型【五大考点】-2024-2025学年五年级数学上册(解析版)

篇首寄语我们每位老师都希望把最好的教学资料留给学生使用,所以在平时教学时,能够快速找到高质量、高效率、高标准的资料显得十分重要。
编者以前常常游走于各大学习网站寻找自己所需的资料,可却总在花费大量时间与精力后才能找到自己心仪的那份,这样费时费力不讨好,实在有些苦恼。
正因如此,每次在寻找资料时,编者就会想,如果是自己来创作一份资料那又该如何呢?那么这份资料应该首先满足自身教学需要,并达到我的高标准要求,然后才能为他人提供参考。
于是,本着这样的想法,在结合自身教学需求和学生实际情况后,最终酝酿出了一个既适宜课堂教学,又适应课后作业,还适合阶段复习的大综合系列。
《2024-2025学年五年级数学上册典型例题系列》,它基于教材知识和常年真题进行总结与编辑,该系列主要分为典型例题篇、专项练习篇、单元复习篇、思维素养篇、分层试卷篇等五个部分。
1.典型例题篇,按照单元顺序进行编辑,主要分为计算和应用两大部分,其优点在于考题典型,考点丰富,变式多样。
2.专项练习篇,从高频考题和期末真题中选取专项练习,其优点在于选题经典,题型多样,题量适中。
3.单元复习篇,汇集系列精华,高效助力单元复习,其优点在于综合全面,精练高效,实用性强。
4.思维素养篇,新的学年,新的篇章,从课本到奥数,从方法到思维,从基础技能到核心素养,其优点在于由浅入深,思维核心,方法易懂。
5.分层试卷篇,根据试题难度和水平,主要分为A卷·基础巩固卷、B卷·素养提高卷、C卷·思维拓展卷,其优点在于考点广泛,分层明显,适应性广。
时光荏苒,转眼之间,《典型例题系列》已经历三个学年三个版本,在过去,它扬长补短,去粗取精,日臻完善;在未来,它承前启后,不断发展,未有竟时。
黄金无足色,白璧有微瑕,如果您在使用资料的过程中有任何宝贵意见,请留言于我,欢迎您的使用,感谢您的支持!101数学创作社2024年9月16日第二单元多边形的面积·几何模型篇·风筝模型和蝴蝶模型【五大考点】【考点一】风筝模型(任意四边形模型)问题一:基础应用 (3)【考点二】风筝模型(任意四边形模型)问题二:进阶应用 (4)【考点三】风筝模型(任意四边形模型)问题三:拓展应用 (7)【考点四】蝴蝶模型(梯形蝶形定理)问题一:基本应用 (8)【考点五】蝴蝶模型(梯形蝶形定理)问题二:添加辅助线构建蝴蝶模型 (11)【第三篇】典型例题篇【考点一】风筝模型(任意四边形模型)问题一:基础应用。
奥数专题:蝴蝶定理和风筝定理
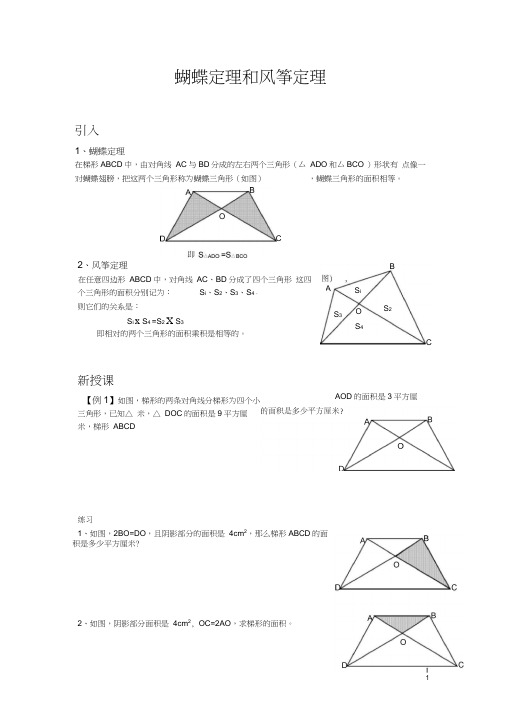
蝴蝶定理和风筝定理引入1、蝴蝶定理在梯形ABCD 中,由对角线 AC 与BD 分成的左右两个三角形(厶 ADO 和厶BCO )形状有 点像一对蝴蝶翅膀,把这两个三角形称为蝴蝶三角形(如图),蝴蝶三角形的面积相等。
2、风筝定理在任意四边形 ABCD 中,对角线 AC 、BD 分成了四个三角形 这四个三角形的面积分别记为: S i 、S 2、S 3、S 4。
则它们的关系是:S i x S 4 =S 2 X S 3即相对的两个三角形的面积乘积是相等的。
新授课【例1】如图,梯形的两条对角线分梯形为四个小三角形,已知△ 米,△ DOC 的面积是9平方厘米,梯形 ABCD练习1、如图,2BO=DO ,且阴影部分的面积是 4cm 2,那么梯形ABCD 的面积是多少平方厘米?2、如图,阴影部分面积是 4cm 2, OC=2AO ,求梯形的面积。
CBAS i S 2O S 3S 4CAOD 的面积是3平方厘【例2】如图,BD , CF 将长方形ABCD 分成四块,红色三角形的面积是4平方厘米,黄色三角形的面积是 8平方厘米,那么绿色四边形的面积是多少平方厘米?练习1如图,BD ,CF 将长方形ABCD 分成4块,红色三角形面积是 面积是6平方厘米,则绿色四边形的面积是多少平方厘米?2、如图,平行四边形 ABCD 的面积是36平方厘米,对角线 AC 、BD 交于0点,E 为CD 上一点,已知四边形 EFOG 的面积是3平方厘米,则阴影部分的面积为多少平方厘米?【例3】如图,四边形ABCD 是边长为18厘米的正方形,已知CE 的长是ED 的2倍。
求:(1)三角形CEF 的面积,(2)DF 的长度练习 正方形ABCD 的边长是12厘米,已知DE 是EC 长度的2倍。
三角形DEF 的面积是多少平 方厘米? CF 长多少厘米?4平方厘米,黄色三角形DDFC【例4】正方形ABCD 和正方形CEFG ,且正方形 ABCD 边长为10厘米,则图中三角形BDF 面积为多少平方厘米?2、三个正方形 ABCD 、BEFG 、FHKP 如图排列,正方形 BEFG 的边长是3厘米,求三角形 DEK 的面积。
风筝模型和梯形蝴蝶定理

风筝模型和梯形蝴蝶定理知识框架板块一风筝模型:(又叫任意四边形模型)① S! :S2 S4:S3 或者S I S3 S2 S4② AO :OC Si S2: S4 S3风筝模型为我们提供了解决不规则四边形的面积问题的一个途径•通过构造模型,一方面可以使不规则四边形的面积矢系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例矢系•板块二梯形模型的应用梯形中比例矢系(“梯形蝴蝶定理”):① S1 :S3 a2:b222②Si:S3:S2: S4 a2:b2:ab:ab ;③S的对应份数为a b 2•梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间矢系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果・(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)例题精讲【例1】图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷・那么最大的一个三角形的面积是多少公顷?C巩固】如图,某公园的外轮廓是四边形ABCD,被对角线AC、BD分成四个部分,△ AOB面积为1平方千米,△ BOC面积为2平方千米,△ COD的面积为3平方千米,公园由陆地面积是6・92平方千米和人工湖组成,求人工湖的面积是多少平方千米?例2】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC的面积;⑵ AG:GC ?BD 巩固】在△ ABC 中=2:1,AEEC求0BOE 例3】如图相邻两个格点间的距离是1,则图中阴影三角形的面积为A巩固】如图,每个小方格的边长都是1 '求三角形ABC 的面积・例4】如图,平行四边形ABCD的对角线交于O点,ACEF、AOEF、AODF、ABOE的面积依次是2、4、4和6 •求:⑴求△ OCF的面积;(2)求△ GCE的面积•巩固】如右上图,已知BO=2DO,CO=5AO,阴影部分的面积和是11平方厘米,求四边形ABCD的面积。
2018四年级奥数.几何.风筝模型和梯形蝴蝶定理(A级).学生版

知识框架板块一风筝模型:(又叫任意四边形模型)S 4S 3S 2S 1O DCBA ①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++风筝模型为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.板块二梯形模型的应用梯形中比例关系(“梯形蝴蝶定理”):A BCDO ba S 3S 2S 1S 4①2213::S S a b =②221324::::::S S S S a b ab ab =;③S 的对应份数为()2a b +.梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)风筝模型和梯形蝴蝶定理例题精讲【例1】图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷.那么最大的一个三角形的面积是多少公顷?【巩固】如图,某公园的外轮廓是四边形ABCD,被对角线AC、BD分成四个部分,△AOB面积为1平方千米,△BOC面积为2平方千米,△COD的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?【例2】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC AG GC ?的面积;⑵:欢迎关注:奥数轻松学余老师薇芯:69039270【巩固】在△ABC 中DC BD =2:1,EC AE =1:3,求OEOB=?【例3】如图相邻两个格点间的距离是1,则图中阴影三角形的面积为.【巩固】如图,每个小方格的边长都是1,求三角形ABC 的面积.【例4】如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.【巩固】如右上图,已知BO=2DO,CO=5AO,阴影部分的面积和是11平方厘米,求四边形ABCD 的面积。
四年级奥数风筝模型和梯形蝴蝶定理(A级)

板块一 风筝模型:(又叫任意四边形模型)① 1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++风筝模型为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.板块二 梯形模型的应用梯形中比例关系(“梯形蝴蝶定理”):①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)S 4S 3S 2S 1O DCBA A BCDO baS 3S 2S 1S 4知识框架风筝模型和梯形蝴蝶定理【例 1】 图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷.那么最大的一个三角形的面积是多少公顷?【巩固】 如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?【例 2】 如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC 的面积;⑵:AG GC ?76EDCBA76OCDBA321GDCBA 例题精讲【巩固】 在△ABC 中DC BD =2:1, EC AE =1:3,求OEOB=?【例 3】 如图相邻两个格点间的距离是1,则图中阴影三角形的面积为 .【巩固】 如图,每个小方格的边长都是1,求三角形ABC 的面积.【例 4】 如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.DCBAOGF EDC BA【巩固】 如右上图,已知BO=2DO ,CO=5AO ,阴影部分的面积和是11平方厘米,求四边形ABCD 的面积。
四年级奥数.几何.风筝模型和梯形蝴蝶定理

板块一 风筝模型:(又叫任意四边形模型)S 4S 3S 2S 1O DC BA①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++风筝模型为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.板块二 梯形模型的应用梯形中比例关系(“梯形蝴蝶定理”):A BCDO baS 3S 2S 1S 4①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)知识框架风筝模型和梯形蝴蝶定理【例 1】 图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷.那么最大的一个三角形的面积是多少公顷?76EDCBA76【巩固】 如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?OCDBA【例 2】 如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC的面积;⑵:AG GC ?321GDCBA【巩固】 在△ABC 中DC BD =2:1, EC AE =1:3,求OEOB=? 例题精讲【例 3】 如图相邻两个格点间的距离是1,则图中阴影三角形的面积为 .BA【巩固】 如图,每个小方格的边长都是1,求三角形ABC 的面积.A B【例 4】 如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.OGF EDC BA【巩固】 如右上图,已知BO=2DO ,CO=5AO ,阴影部分的面积和是11平方厘米,求四边形ABCD 的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
风筝模型和梯形蝴蝶定理
知识框架
板块一 风筝模型:(又叫任意四边形模型)
S 4
S 3
S 2
S 1O D
C B
A
①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++
风筝模型为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.
板块二 梯形模型的应用
梯形中比例关系(“梯形蝴蝶定理”):
A B
C
D
O b
a
S 3
S 2
S 1S 4
①2213::S S a b =
②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2
a b +.
梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)
例题精讲
【例 1】 图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角
形的面积分别是6公顷和7公顷.那么最大的一个三角形的面积是多少公顷?
7
6
E
D
C B
A
7
6
【巩固】 如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千
米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?
O
C
D
B
A
【例 2】 如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC
的面积;⑵:AG GC ?
C
B
【巩固】 在△ABC 中
DC BD =2:1, EC AE =1:3,求OE
OB
=?
【例 3】 如图相邻两个格点间的距离是1,则图中阴影三角形的面积为 .
B
A
【巩固】 如图,每个小方格的边长都是1,求三角形ABC 的面积.
A B
【例 4】 如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依次
是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.
O
G
F E
D
C B
A
【巩固】 如右上图,已知BO=2DO ,CO=5AO ,阴影部分的面积和是11平方厘米,求四边形ABCD 的面积。
【例 5】 如图,22S =,34S =,求梯形的面积.
S 4
S 3
S 2
S 1
【巩固】 如下图,梯形ABCD 的AB 平行于CD ,对角线AC ,BD 交于O ,已知AOB △与BOC △的面积
分别为25 平方厘米与35平方厘米,那么梯形ABCD 的面积是________平方厘米.
3525O
A
B
C
D
【例 6】 梯形ABCD 的对角线AC 与BD 交于点O ,已知梯形上底为2,且三角形ABO 的面积等于三角形
BOC 面积的
2
3
,求三角形AOD 与三角形BOC 的面积之比.
O
A B C
D
【巩固】 如下图,四边形ABCD 中,对角线AC 和BD 交于O 点,已知1AO =,并且
3
5
ABD CBD =三角形的面积三角形的面积,
那么OC 的长是多少?
A
B
C
D
O
【例 7】 梯形的下底是上底的1.5倍,三角形OBC 的面积是29cm ,问三角形AOD 的面积是多少?
A
B
C
D
O
【巩固】 如图,梯形ABCD 中,AOB ∆、COD ∆的面积分别为1.2和2.7,求梯形ABCD 的面积.
O
D
C
B
A
【例 8】 如下图,一个长方形被一些直线分成了若干个小块,已知三角形ADG 的面积是11,三角形BCH
的面积是23,求四边形EGFH 的面积.
H
G F
E
D
C
B A
【巩固】 如图,长方形中,若三角形1的面积与三角形3的面积比为4比5,四边形2的面积为36,则三
角形1的面积为________.
3
21
【例 9】 如图,正方形ABCD 面积为3平方厘米,M 是AD 边上的中点.求图中阴影部分的面积.
【巩固】 在下图的正方形ABCD 中,E 是BC 边的中点,AE 与BD 相交于F 点,三角形BEF 的面积为1
平方厘米,那么正方形ABCD 面积是 平方厘米.
A
B
C
D
E
F
【例 10】 如图所示,BD 、CF 将长方形ABCD 分成4块,DEF ∆的面积是5平方厘米,CED ∆的面积是
10平方厘米.问:四边形ABEF 的面积是多少平方厘米?
F
A
B
C
D
E
10
5
【巩固】 如图所示,BD 、CF 将长方形ABCD 分成4块,DEF ∆的面积是4平方厘米,CED ∆的面积是6
平方厘米.问:四边形ABEF 的面积是多少平方厘米?
6
4A
B
C
D
E
F
【例 11】 如图,正六边形面积为6,那么阴影部分面积为多少?
【巩固】 如图,在一个边长为6的正方形中,放入一个边长为2的正方形,保持与原正方形的边平行,现
在分别连接大正方形的一个顶点与小正方形的两个顶点,形成了图中的阴影图形,那么阴影部分的面积为 .
课堂检测
【随练1】 如图,每个小方格的边长都是1,求三角形ABD 的面积.
【随练2】 如图所示,在梯形ABCD 中,AB ∥CD ,对角线AC ,BD 相交于点O 。
已知AB=5,CD=3,且梯形ABCD
的面积为4,求三角形OAB 的面积。
A B
C
D
O
【随练3】 如左下图,E 是长方形ABCD 边AB 的中点,已知三角形EBF 的面积是1平方厘米,求长方形ABCD
的面积。
课后作业
【作业1】如图,四边形ABCD中,AC和BD相交于O点,三角形ADO的面积=5,三角形DOC的面积=4,三角形AOB的面积=15,求三角形BOC的面积是多少?
【作业2】(2003北京市第十九届小学生“迎春杯”数学竞赛)
四边形ABCD的对角线AC与BD交于点O(如图)所示。
如果三角形ABD的面积等于三
角形BCD的面积的1
3
,且2
AO=,3
DO=,那么CO的长度是DO的长度的_________
倍。
D
A
O
C
B
【作业3】正方形ABCD的边长为6,E是BC的中点(如图)。
四边形OECD的面积为。
O E D C
B
A
【作业4】如图面积为12平方厘米的正方形ABCD中,,E F是DC边上的三等分点,求阴影部分的面积.
O
F
E D
C
B
A
【作业5】 如图,长方形ABCD 被CE 、DF 分成四块,已知其中3块的面积分别为2、5、8平方厘米,那
么余下的四边形OFBC 的面积为___________平方厘米.
8
5
2O A B
C
D
E
F
【作业6】 在梯形ABCD 中,上底长5厘米,下底长10厘米,20=∆BOC S 平方厘米,则梯形ABCD 的面积是
( )平方厘米。
