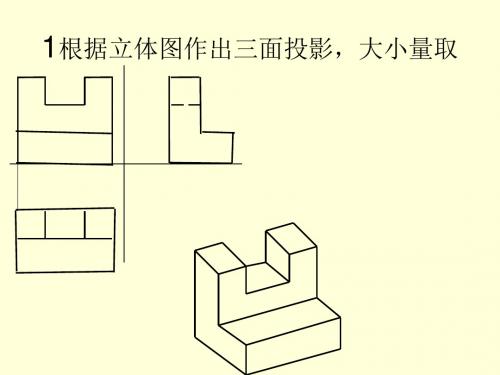
教材例题画法几何
合集下载
画法几何1习题答案PPT课件
b'
(c') a' c b
(a)
b"
c" a"
9-4画出圆柱的W面投影及其表面上各线的另两面投影。
a'
a"
b'
b"
d'
(c')
c"
d"
c
d ab
33
9-5 已知圆柱表面各转向线EE1、FF1、GG1、MM1投影， 求作其表面曲线ABC的另两面投影。
e'
b'
a'
e1'
b"
a"
d' (c')
d" c"
917完成切口三棱锥的水平投影和侧面投影919完成切口三棱锥的水平投影和侧面投影
9-1 画出正五棱柱表面上各点及线的另二面投影。
9-2 画出正六棱柱的W面投影及其表面上各线的另两面投影。
b' ca'
c' d'
b" a"
c" d"
c
b
d
a
b'
c' d' a'
d c
b a
b"
d"
c"
a"
32
9-3 画出圆柱表面上各点的另二面投影。
54
12-9 补画正立面图
12-10 补画正立面图
55
12-11 补画正立面图。
12-12 补画平面图。
56
12-13 补全投影图中所缺漏的图线。
12-14 补全投影图中的漏线。
画法几何全主编习题集答案
db cab ’ a ’c’ d ’ Xb 1'd 1'c 1'a 1'c 1d 1m 1n 1'b 1（a 1）m 1'm’n ’nmX1X2n 12-4 直线与平面、平面与平面的相对位置1.求直线AB与平面的交点，并判别直线的可见性。
4.求两平面的交线。
6.作一直线使与两交叉直线AB,CD相交，同时平行于直线KL。
作直线AE平行于直线KL；求CD与平面（AE和AB确定）的交点M；作MN平行于KL。
7.过点C作CD平行于AB，且点D于A,B等距。
距离说明：为使图形清晰，将AB 的正面投影改变了一些方向。
过AB 的中点E 作AB 的中垂面；求CD 与中垂面的交点D 。
其中MN 为PH 中垂面的交线。
8.求点K 到直线AB 的距离。
距离9.求点A 到三角形BCD 的距离。
说明：为使图形清晰，将A 点的水平投影 往上移动了一些。
11.已知线段AB,CD正交，作线段AB的正面投影。
13.过点K作直线与交叉两直线AB和CD相交。
交叉二直线DE,FG相交，并垂直于三角形ABC。
作直线BC垂直于平面；求三角形ABC的实形（略);90°减角ABC即为所求（略)。
15.求直线与平面之间的夹角。
作直线EM垂直于三角形ABC;求FG与平面（DE和EM确定）的交点K；过K作EM的平行线KN。
16.已知菱形ABCD的一边AD在直线AE上，另一边AB平行于三角形LMN，点B在直线FG上，求作菱形的两面投影。
Y坐标差16.过点A作平行于三角形LMN的平面；求FG与平面的交点B;求AB的实长，AE的实长，在AE上截取AD=AB,得D;再作AB,AD的平行线即可。
2-5 投影变换1.用换面法求直线AB的实长及其与H面的倾角α。
2.已知AB垂直于BC，补全BC的水平投影。
4.已知点A与三角形DEF的距离为10，求A的正面投影。
7.已知两平行直线AB及CD相距15mm,求CD的水平投影。
《画法几何》习题集及题解完整版
b′ d′ a′ c′ X d a c b
AB
∥
CD
3-13 判别下列AB与CD两直线的相对位置。（2）
a′
c′ b′ d′
X c a b d
AB 相交于
CD
3-13 判别下列AB与CD两直线的相对位置。（3）
a′
1 4(3)
d′
c′
X c
2
b′
3
1(2) 4
b
ห้องสมุดไป่ตู้
a
d
AB 相叉于
CD
3-13 判别下列AB与CD两直线的相对位置。（4）
d
8页
2005习题集第8页—点
2-6 已知Ａ点的两面投影,求点Ｂ、C 、D的三面投影,使 B点在A点的正下方10,C点在A点的正前方10,D 点在A点 的正左方15,并判断可见性。(单位mm)
d′
15
(a′ ) c′
10
Z
( a〞 〞c〞 )d
b′ X (b) a d
10
b〞
O
YW
c
YH
8页
2005习题集第9页—直线1
a
L
b a (b) d
c
L
c b
(a)
(b)
(c)
11页
2005习题集第11页—直线3 3–12 下列各图中,表示两交叉直线的图是( c ) 。
a′ b′ d′ a′ d′ d a b c a
(a)
c′ b′ a′
c′
b′
c′
d′ d
a c(d) b c b
(b)
(c)
11页
3-13 判别下列AB与CD两直线的相对位置。（1）
a′ d′ 1(2) 3 c′ d b′ b″ d″ a″
AB
∥
CD
3-13 判别下列AB与CD两直线的相对位置。（2）
a′
c′ b′ d′
X c a b d
AB 相交于
CD
3-13 判别下列AB与CD两直线的相对位置。（3）
a′
1 4(3)
d′
c′
X c
2
b′
3
1(2) 4
b
ห้องสมุดไป่ตู้
a
d
AB 相叉于
CD
3-13 判别下列AB与CD两直线的相对位置。（4）
d
8页
2005习题集第8页—点
2-6 已知Ａ点的两面投影,求点Ｂ、C 、D的三面投影,使 B点在A点的正下方10,C点在A点的正前方10,D 点在A点 的正左方15,并判断可见性。(单位mm)
d′
15
(a′ ) c′
10
Z
( a〞 〞c〞 )d
b′ X (b) a d
10
b〞
O
YW
c
YH
8页
2005习题集第9页—直线1
a
L
b a (b) d
c
L
c b
(a)
(b)
(c)
11页
2005习题集第11页—直线3 3–12 下列各图中,表示两交叉直线的图是( c ) 。
a′ b′ d′ a′ d′ d a b c a
(a)
c′ b′ a′
c′
b′
c′
d′ d
a c(d) b c b
(b)
(c)
11页
3-13 判别下列AB与CD两直线的相对位置。（1）
a′ d′ 1(2) 3 c′ d b′ b″ d″ a″
画法几何习题集答案
a’
bc于m,作
m’
m’m ∥oz,交
n’
b’c’于m’,连接
b’
a’m’,作c’n’
⊥am交于n’,
b
作nn’ ⊥am交
a
于n,利用直角
mn
三角形求出
倾角β
c
31 判别直线AB是否平行于平面CDEF
• 作法：
c’
b’
f’ • 作e’f’ ∥a’b’,
a’
交c’d’于m’,
e’
m’
作mm’ ∥oz,
33 过A点作平面平行∆ DEF
a’
d’ a
d
e’
n’ • 作法：
• 作a’m’
f’ ∥e’f’,作am
m’
∥ef, mm
∥oz.
e
• 作a’n’
∥d’f’,作an
n
∥df, nn’
∥oz.
f m
34 过直线AB作平面平行于直线CD
b’
m’ a’
c’
b
a
c
m
• 作法：
• 作am ∥cd,
d’
作a’m’
d’
• 做法：
c’
k’
b’ • 过k 点作kk’
a’
∥oz交a’b’于
e’ k’.b’k’为实线，
a
中段为虚线，
k
d
e 下段为实线。
c
b
37 作出直线AB与∆ CDE的交点并判别可见性
d’
a’ m’
k’
c’
n’
b’
e’
• 做法：连接 mm’,nn’ ∥oz, 连接mn交ab于 k,作kk’
∥oz,a’k’,bk为
画法几何习题集答案
a’
bc于m,作
m’
m’m ∥oz,交
n’
b’c’于m’,连接
b’
a’m’,作c’n’
⊥am交于n’,
b
作nn’ ⊥am交
a
于n,利用直角
mn
三角形求出
倾角β
c
31 判别直线AB是否平行于平面CDEF
• 作法：
c’
b’
f’ • 作e’f’ ∥a’b’,
a’
交c’d’于m’,
e’
m’
作mm’ ∥oz,
b’ p’ o’ n1’’
a’
c’
4’
m’
a c
po
4 m
n1 b
• 做法：
2’ • 延长 ac .34交
于m,求出 m’,
延长2‘1’交点
3’ 为o’,p,’ 在ab
求出p,bc利用
3 定比性求出o, 连接po交21
于n,求出n’,连
2
接mn,m’n’.
42 已知直线AB平行于平面CDE求直线的正面投影
33 过A点作平面平行∆ DEF
a’
d’ a
d
e’
n’ • 作法：
• 作a’m’
f’ ∥e’f’,作am
m’
∥ef, mm
∥oz.
e
• 作a’n’
∥d’f’,作an
n
∥df, nn’
∥oz.
f m
34 过直线AB作平面平行于直线CD
b’
m’ a’
c’
b
a
c
m
• 作法：
• 作am ∥cd,
d’
作a’m’
20mm b1 X2
67用换面法确定两交错直线间的距离返回做出投影
画法几何习题集及题解
14页
2005习题集第15页—平面2 4-4 下列各图中，表示点K属于△ABC的是图 (b) 。
k′ b′b′ a′ k′
a′ X
xk a
k
b
a (a)
k′ b′
k′
a′
c′
a′
OX
cc′
ox
a
c
k
b
a (b) .
b′
b′
b
a′ k′
c′
c′
OX
a′ O
k
c c′
c
aox
ck
b
a
(c)
48 k
15页
b′
a′
a′
＝30°
X
b
a
有2 解
X
b
a 有2 解
.
18
10页
3–5 已知C点属于线段AB, 且AC︰CB＝3 ︰1, 求作C点 的V、H投影。
(1)
a′
X a
c′ b′
c b
(2)
a′
c′ X b′
b c
a
.
19
10页
3–6 已知线段AB的投影,试取属于AB的一点K,使 AK＝25,求
作K点的投影k、k′,并求出直线的迹点。
30°
e′ b′
c′
f′
d′
X
e b 30° d c
a
f
.
41
13页
2005习题集第14页—平面1
4-1 已知相交二直线决定的平面P的投影,试求其迹线。
n2′
n1′ b′ PV
a′
c′
a
b
m1′ PH
.
c
2005习题集第15页—平面2 4-4 下列各图中，表示点K属于△ABC的是图 (b) 。
k′ b′b′ a′ k′
a′ X
xk a
k
b
a (a)
k′ b′
k′
a′
c′
a′
OX
cc′
ox
a
c
k
b
a (b) .
b′
b′
b
a′ k′
c′
c′
OX
a′ O
k
c c′
c
aox
ck
b
a
(c)
48 k
15页
b′
a′
a′
＝30°
X
b
a
有2 解
X
b
a 有2 解
.
18
10页
3–5 已知C点属于线段AB, 且AC︰CB＝3 ︰1, 求作C点 的V、H投影。
(1)
a′
X a
c′ b′
c b
(2)
a′
c′ X b′
b c
a
.
19
10页
3–6 已知线段AB的投影,试取属于AB的一点K,使 AK＝25,求
作K点的投影k、k′,并求出直线的迹点。
30°
e′ b′
c′
f′
d′
X
e b 30° d c
a
f
.
41
13页
2005习题集第14页—平面1
4-1 已知相交二直线决定的平面P的投影,试求其迹线。
n2′
n1′ b′ PV
a′
c′
a
b
m1′ PH
.
c
画法几何试题
5-15 补全三棱锥截切后的水平投影和侧面投影。
5-16 补全三棱锥穿孔后的水平投影和侧面投影。
36
5-17 求作直线AB与三棱柱的贯穿点，并求其侧面投影。
5-18 求作直线AB与三棱锥的贯穿点，并求其侧面投影。
5-19 求作直线AB、CD与三棱柱的表面交点。
5-20 求直线AB与该平面体的表面交点，并求其侧面投影。
34
5-9 补全四棱柱截切后的水平投影和正面投影。
5-10 补全四棱柱经两次截切后的水平投影和正面投影。
5-11 补全四棱台切口后的水平投影和侧面投影。
5-12 补全四棱台切口后的水平投影和侧面投影。
35
5-13 补全四棱锥截切后的水平投影和侧面投影。
5-14 补全四棱锥截切后的正面投影和侧面投影。
班级
姓名
学号
2-5 根据点的两面投影，求第三投影，并判定其相对位置。 (1)
(1) D(30、20、25），E（30、10、25），F（20、15、10），G（10、0、20） (2)
__ 在 __ 之左 __ 在 __ 之后 __ 在 __ 之上
__ 在 __ 之右 __ 在 __ 之前 __ 在 __ 之下
3
已知点B在点A的正上方10，点C在点B的正左方10， 求A、B、C的三面投影，并标明其可见性。
已知两直线AB和CD的端点坐标分别为A（30、5、20），B（5、20、 10），C（40、10、0），D（10、30、0）。做出两直线的投影图。
根据点的坐标值，判定投影的可见性（可见的画√， 不可见的画×）。
二、点、直线和平面
2-1 根据点的空间位置，画出点的投影图。
班级
姓名
学号
u 1
画法几何及土木工程制图试题
画法几何及土木工程制图试题（高教朱育万）一、填空题（每空2分，共40分）1．由空间的三维形体转变为平面上的二维图形是通过__________ 实现的。
2．工程上常哀告的图示法有_________、__________ 、______ 和_______ 。
3．空间平面相对于投影面有三种类型_________、__________ 、____________ 。
4．如果平面包含一条垂直于另一平面的直线，由该两平面_______。
5．棱锥被平行于其底面的平面截割，截面与底面间的部分为________ 。
6．直线与多面体表面相交，产生交点，称为___________ 。
7．距离画面不同远近的同样高度的直线，其透视高度不同，距离画面愈远，其透视愈_________ ，相反就愈_________ 。
8．当圆锥正放（锥顶朝上）时，等高线的高程值愈_____，则圆的直径愈__ 。
当圆锥倒放时，等高线的高程值愈______ ，则圆的直径也愈_____。
9．尺寸起止符号一般用________ 线画，其倾斜方向应与尺寸界线成顺时针____角，长度宜为____________ 。
二、名词解释（每题4分，共12分）1．斜投影法：2．正等轴测投影：3．量点法：三、简答题（每题5分，共30分）1．土木工程制图的任务是什么？2．在作辅助投影时，设置新投影面必须遵循的原则是什么？3．直角投影法则是什么？4．简述曲线的投影性质？5．运用辅助球面法必须具务哪些条件？6．工程图上对标注尺寸有哪些要求？四、绘图题（每题9分，共18分）1．如图所示，己知点K属于△ABC平面，试作出点K的V面投影K。
2．己知地形面与一斜坡平面相交，如图所示，试作地面与斜坡平面的交线的标高投影。
画法几何及土木工程制图试题（高教朱育万）答案一、填空题（每空2分，共40分）1．投影法。
2。
多面正投影法、轴测投影法、透视投影法、标高投影法。
3。
投影面平行面、投影面垂直面、一般位置平面。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
例2-15：判定点K是否在两平行直线AB和CD所决定的平面内 （图2－49（a））。 分析：如果点K在给定的平面内，它必在该平面内的一条直 线上。因此，只要通过点K的某一投影在（或k‘），在给定的 平面内作一条直线的投影，看点K的另一投影k’（或k）是否在 该直线的同面投影上，即可判定点K是否在所给定的平面内。
例3-10：判定图3-14（a）所示的直线AB与平面P是否垂直。 分析：如果AB⊥P，则AB的水平投影ab，必垂直于平面P内 水平线的水平投影；同时AB的正面投影a’b’，必垂直于平面 P内正平线的正面投影。
例 3-11：判定图 3-15所示的直线 AB与铅垂面P是否垂直。 分析判定：因为铅垂面P内水平线的水平投影，与它的水平 投影p重合；铅垂面内平行于V面的直线，又只能是铅垂线；所 以与铅垂面P垂直的直线，一定是水平线，而且其水平投影与 平面的水平投影（有积聚性）垂直。从图中可以看出，虽然 ab⊥P，但a’b’不平行于OX轴，故直线 AB与铅垂面P不垂直。 同理，与正垂面垂直的直线，一定是正平线，而且其正面投 影与正垂面的正面投影垂直，由此可判定，直线与正垂面是否 垂直。
例2—16：已知平面四边形ABCD的水平投影abcd和正面投 影a’b’d’，完成该四边形的正面投影见图2—50（a）。 分析：因为ABCD为一平面四边形，所以点C必在ABD所决 定的平面内，因此点C的正面投影C’可运用在平面内取点的 方法求得。
例2—17：在两平行直线AB、CD所决定的平面内，作一距 H 面为15的水平线，如图(2-52(a)) 分析：水平线的正面投影平行于OX轴，它到OX轴的距离， 反映水平线到H面的距离，虽然平面内所有的水平线，其正 面投影都平行于OX轴，但距OX轴为15的只有一条，故应先作 其正面投影，再求其水平投影。
例2—19：求ΔABC（alc，a’b’c’）与 H 面的倾角，见图 2 一55（a）。 分析：ΔAB C与H 面的倾角，就是该平面的最大坡度线 与H 面的倾角。因此，只要求出该平面的最大坡度线的两个 投影，然后利用直角三角形法，即可求得最大坡度线与H 面 的倾角α。
例2－20 包含点A（a，a‘）作一用迹线表示的铅垂面P， 且与V面的倾角为300［图2-56（a）］。 分析：因为铅垂面的水平迹线有积聚性，所以PH必通过点 A的水平投影a；又因水平迹线与OX轴的夹角，反映该平面与 V面的倾角，故PH的方向可定。
例3-12：过点 A作一平面，与两条平行线DE和FG所决定的平 面平行，如图 3-17。 分析：由两平面互相平行的几何条件可知，只要过点A作两 条相交直线，与已知平面内的两条相交直线对应平行（其同 面投影都对应平行），则过点A的这两条相交直线所决定的平 面，必与已知平面平行。
例3-13：判定图 3-18（a）所示的ΔABC与ΔDEF是否平行。 分析：如果ΔABC∥ΔDEF，则在ΔDEF内必能作出两相交 直线，与ΔABC的两边对应平行（其同面投影都对应平行）， 否则ΔABC不平行于ΔDEF。
例3－3：判定直线AB与正垂面P是否平行（图3-4） 分析判定：正垂面P内的所有直线（包括水平投影与ab平 行的直线）的正面投影，都积聚在Pv上。因为题中给出 a’b’∥Pv，故可以判定直线AB与正垂面互相平行。
例3－4:求直线AB与铅垂面P的交点K，并判定投影的可见性 (3－6（a）)。 分析：因为交点K是直线AB与铅垂面P的公有点，铅垂面P的 水平投p有积聚性，所以直线AB的水平投影ab与p的交点k，即 为AB与平面P交点K的水平投影。
例2-2： 已知点B的正面投影b‘和侧面投影b”，求其水平投影 b，如图2—10（a）所示。
例2－3：已知点A的坐标为（20、10 、15），求作点A的三面 投影a、a’和a”。 分析：从点 A的三个坐标值可知，点 A 到 W 面的距离为 20，到 V 面的距离为 10倒 H 面的距离为15。根据点的投影 规律和点的三面投影与其3个坐标的关系，即可求得点A的3个 投影。
例3－7：求图 3-10（a）所示的直线 AB与ΔCDE的交点， 并判定投影的可见性。
பைடு நூலகம்
例3-8：过点M作直线MN垂直于ΔABC，并求其垂足，如图312（a）所示。
例3-9：过点A作平面与直线MN垂直（图3-13（a））。 分析：由直线与平面垂直的几何条件可知，只要过点A作两条 相交直线均与MN垂直，则这两条相交直线所决定的平面，既包 含点A，又与MN垂直。
例2-1：已知点A的水平投影a和正面投影a’，求其侧面投影a”， 如图2－9(a)所示。 分析：由点的投影规律得知，点的正面投影与侧面投影的 连线垂直于OZ轴，故a”必在过a’所作的OZ轴的垂线（OX轴的平 行线）上。又知点的侧面投影到OZ轴的距离等于水平投影到OX 轴的距离，即a”az=aax。因此，只要在过a’对OZ轴所作的垂线上 截取aza”＝aax，即可得a”。
例2-7 :已知直线AB的水平投影ab和点A的正面投影a’，并 知AB对H 面倾角为300，求: AB的正面投影a’b’。 分析：由于点A的正面投影a’（即其z坐标）已知，所以 只要求出A、B两点的z坐标差，即可确定点B的正面投影b’。 由上述直角三角形法的原理可知，以ab为一直角边，作一锐 角为300的直角兰角形，则300角所对的直角边，即为A、B两 点的Z坐标差。
例2-6：已知直线AB的正面投影 a’b’和点 A的水平投影 a，并 知AB=25，求AB的水平投影ab及AB对V面的倾角β，如图2-23(a) 所示。 分析：由点的投影规律可知，b应在过b’所作的OX轴的垂线 上，因此只要求出AB两点的y坐标差，即可确定b。根据直角三 角形法的原理，以a’b’为一直角边。以25为斜边作一直角三角形， 它的另一直角边即为AB两点的y坐标差，y坐标差所对的角即为 AB对V面的倾角β。本题有两个解。
例2－21：包含水平线AB作一与H 面倾角为300的平面，见图 2—57（a）。 分析：平面对H 面的倾角α，就是该平面最大坡度线与H 面的倾角；最大坡度线又与平面内的水平线垂直；因此只要作 一条与AB相交垂直、且与H 面成300角的直线（即为所求平面 的最大坡度线），该直线与AB所决定的平面，即为所求的平面。
例2-10：已知：直线AB和CD相交于点K，并知AK：KB=1：2，根 据图给的投影，求AB的正面投影a’b’和CD的水平投影cd 分析：由直线上的点分线段为定比的性质可知，若AK：KB=1： 2，则ak：bk 也必等于1：2，由此可求得交点K的水平投影。 又因交点K是两直线AB和CD的公有点，故k’必在c’d’上。点C的水 平投影和点B的正面投影分别位于dk和a’k’的延长线上。
例3-1：过点 A作一水平线 AB，与ΔCDE平行，见图3-2（a）。 分析：ΔCDE（Δcde，c’d’e’）的空间位置一经给定，该平 面水平线的方向也就随之而定。虽然过点A可作无数条水平线， 而与ΔCDE平行的直线只有一条，它必与ΔCDE内的水平线平行。
例3-2: 判定直线AB与ΔCDE是否平行（图3-3（a））。 分析：由直线与平面平行的几何条件可知，如果AB∥ΔCDE， 则在西CDE内必能作出与AB平行的直线，否则AB不平行于ΔCDE。
例3－21：判定图 3-31（a）所示的平面 P与ΔABC是否 垂直。 分析：由两平面垂直的几何条件可知，如果P⊥ΔABC， 则在ΔABC内必包含平面P的垂线。因此，欲判定P与ΔABC 是否垂直，可过ΔABC内的任一点作平面P的垂线，然后根 据直线在平面内的几何条件，判定该垂线是否在ΔABC内。
例3-22：判定图3-32（a）所示的ΔABC与铅垂面P是否垂直。 分析：由于与铅垂面垂直的直线只能是水平线，所以欲判定 ΔABC与铅垂面P是否垂直，只要看ΔABC内的水平线的水平投 影，与铅垂面的水平投影p是否垂直即可。
例2-18:过ΔABC的顶点B，作该平面内的正平线见图2-53 （a）。 分析：由直线在平面内的几何条件可知，过顶点 B作直线 L，平行于西ABC的一条直线，则直线L必在该平面内。如果所 作的直线L，平行于ΔABC的一条正平线，则直线L即为该平面 内过顶点B的正平线。因此，欲过顶点B作该平面内的正平线， 须在ΔABC内先任作一条正平线。
例2-8：根据图2－26（a）所示，在直线AB上找一点K，使 AK：KB=3：2 分析：由上述投影特性可知，AK：KB=3：2，则其投影 ak： kb=a’k’：k’b’＝3：2。因此，只要用平面几何作图的方法， 把ab或a’b’为3：2，即可求得点K的投影。
例2－9：判定点K是否在侧平线AB上（图2－27a〕。 分析：由直线上点的投影特性可知，如果点K在直线AB上， ak：kb=a’k’：k’b’，因此，可用这一等比关系来判定K是否在 直线AB上。另外，如果点K在直线AB上，则k”应在a”b”上。所 以，也可作出它们的侧面投影来判定。
例3-14：求图 3－21 (a) 所示的铅垂面 P与ΔABC的交线， 并判定其投影的可见性。
例3-15：求图3－22 (a)所示的正平面ΔABC与铅垂面P的 交线，并判定其投影的可见性。
例3-16：求图3—23（a）所示的ΔABC与水平面P的交 线，并判定其投影的可见性。
例3-17：求图3－25（a）所示的ΔABC与ΔDEF的交线， 并判定其投影的可见性。 分析：为了作图简便起见，求交点时所选的直线， 最好与相交平面的各投影都有重影部分（因为只有这样 的直线与平面的交点，才有可能在平面图形的范围之 内），如DE、DF与ΔABC的两投影，以及 AC与ΔDEF的 两投影都有重影部分，所以宜在 DE、DF和AC中任选两 条，求与另一平面的交点。
例3-18：求图3－26（a）所示的ΔABC与ΔDEF的交线， 并判定其投影的可见性
例3-19：求图3-28（a）所示的ΔABC与ΔDEF的交线。
例3-20：包含直线MN作一平面，与ΔABC垂直，如图3-30（a） 所示。 分析：由两平面垂直的几何条件可知，只要过直线MN上的 任一点，作一条直线与ΔABC垂直，则这两条相交直线所决定 的平面必与ΔABC垂直。