材料力学习题课
材料力学课后习题答案详细

变形厚的壁厚:
(R r) | (R r) | 30 0.009 29.991(mm)
[习题 2-11] 受轴向拉力 F 作用的箱形薄壁杆如图所示。已知该材料的弹性
常数为 E, ,试求 C 与 D 两点间的距离改
22
N 22 A
10 103 N 400mm 2
25MPa
33
N 33 A
10 103 N 400mm 2
25MPa
[习题 2-3] 试求图示阶梯状直杆横截面 1-1、2-2 和平 3-3 上的轴力,并作
轴力图。若横截面面积 A1 200mm2 , A2 300mm2 , A3 400mm2 ,并求各横截 面上的应力。
A1 11.503cm2 1150.3mm2
AE
N EA A
366.86 103 N 2 1150.3mm2
159.5MPa
EG
N EG A
357.62 103 N 2 1150.3mm2
155.5MPa
[习题 2-5] 石砌桥墩的墩身高 l 10m ,其横截面面尺寸如图所示。荷载
22
N 22 A2
10 103 N 300mm 2
33.3MPa
3
33
N 33 A
10 103 N 400mm 2
25MPa
[习题 2-4] 图示一混合屋架结构的计算简图。屋架的上弦用钢筋混凝土制
成。下面的拉杆和中间竖向撑杆用角钢构成,其截面均
为两个 75mm 8mm 的等边角钢。已知屋面承受集度为
《习题课材料力学》PPT课件

(4)物理关系
由此得:
p.12
例题
例题
解:(1)以整体为研究对象,易见A处的水平约束反力为零
即
XA=0
(2) 以AB为研究对象
(3)以杆BD为研究对象
(4)杆的应力为
p.13
例题
例题
8. 某拉伸试验机的示意图如图所示。设试验机的CD杆与试样AB同 为低碳钢制成,p=200MPa,s=240MPa,b=400MPa。试验机的 最大拉力为100kN。 (1)用这试验机作拉断试验时试样最大直径可达多少? (2)设计时若取安全系数n=2,则CD杆的截面面积为多少? (3)若试样的直径d=10mm,今欲测弹性模量E则所加拉力最大不 应超过多少?
p.3
例题
例题
AB杆发生弯曲变形。 (3)求n-n截面内力:取杆BC为研究对象,截开n-n截面
BC杆发生拉伸变形
2.拉伸试件A、B两点的距离l称为标距,在拉力作用 下,用引伸仪量出两点距离的增量为Δl=5×10-2mm若 l的原长为l=10cm,试求A、B两点间的平均应变。
p.4
例题
例题
解:平均应变为
3.图示三角形薄板因受外力而变形。角点B 垂 直 向 上 的 位 移 为 0.03mm,但AB和BC仍保持为直线。试求沿OB的平均应变,并求 AB、BC两边在B点夹角的变化。
解:(1) OB方向的平均线应变
(2)AB与BC两边的角应变
p.5
例题
1
例题
5
第二章2Leabharlann 拉压、剪切与挤压4
3
p.6
例题
例题
4.试求图示各杆1-1、2-2、3-3截面的轴力,并作轴力图。
(2)由平衡方程得
习题课材料力学资料

解:(1)横截面上剪应力分布为:
(2)将四分之一截面上的力系向O点简化
p.48
例题
例题
(3) Ro与x轴之间的夹角
(4)将Ro和Mo进一步简化为一合力R,即将Ro平移
31.钻头简化成直径为20mm的圆截面杆,在头部受均布阻抗扭矩m 的作用,许用剪应力为[τ]=70MPa。(1).求许可的Me;(2).若 G=80GPa,求上、下两端的相对扭转角。
截面2-2 (2)画扭矩图
(c) (1)用截面法求内力
p.38
例题
例题
截面1-1
截面2-2 截面3-3 截面4-4 (2)画扭矩图
p.39
例题
例题
25.发电量为1500kW的水轮机主轴如图示。D=550mm,d=300mm ,正常转速n=250r/min。材料的许用剪应力[τ]=500MPa。试校核水 轮机主轴的强度。
21.图示螺钉受拉力P作用,已知材料的剪切 许用应力[]与拉伸许用应力[]的关系为[]= 0.6[],试求螺钉直径d与钉头高度h的合理 比值。
p.30
例题
例题
解:(1) 螺钉的剪切面面积
(2)剪切强度条件
(3)拉伸强度条件
(4)由已知条件 故
p.31
例题
例题
22.木榫接头如图所示。a=b=120mm,h=350mm,c=45mm, P=40kN。试求接头的剪切和挤压应力。
解:(1) 外力扭矩
(2)内力扭矩
p.46
例题
例题
(3)计算AB段的直径d1和BC段的直径d2
强度条件
刚度条件
故取
p.47
例题
例题
(4)若AB和BC两段选用同一直径,则取d1=d2=84.6mm
(完整版)材料力学课后习题答案
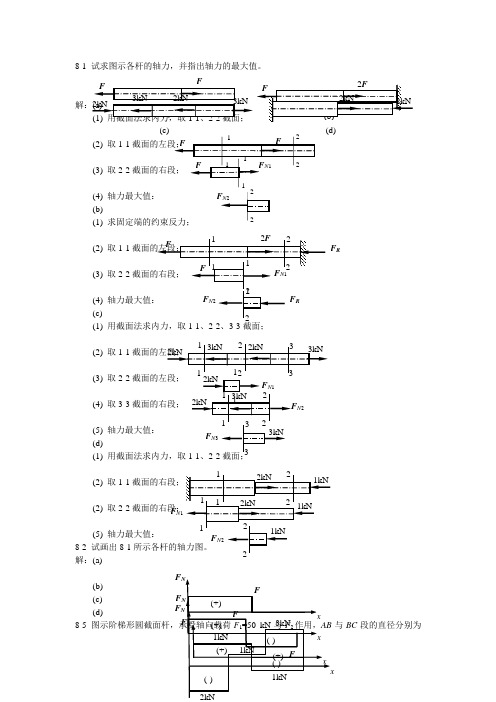
8-1 试求图示各杆的轴力,并指出轴力的最大值。
(2) 取1-1(3) 取2-2(4) 轴力最大值: (b)(1) 求固定端的约束反力; (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力,取1-1、2-2、3-3截面;(2) 取1-1(3) 取2-2 (4) 取3-3截面的右段;(5) 轴力最大值: (d)(1) 用截面法求内力,取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值: 8-2 试画出8-1解:(a) (b) (c) (d) 8-5与BC 段的直径分别为(c) (d)F RN 2F N 3 F N 1F F Fd 1=20 mm 和d 2=30 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求载荷F 2之值。
解:(1) 用截面法求出(2) 求1-1、2-28-6 题8-5段的直径d 1=40 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求BC 段的直径。
解:(1)用截面法求出1-1、2-2截面的轴力;(2) 求1-1、2-2截面的正应力,利用正应力相同;8-7 图示木杆,承受轴向载荷F =10 kN 作用,杆的横截面面积A =1000 mm 2,粘接面的方位角θ= 450,试计算该截面上的正应力与切应力,并画出应力的方向。
解:(1) (2) 8-14 2=20 mm ,两杆F =80 kN 作用,试校核桁架的强度。
解:(1) 对节点A(2) 列平衡方程 解得: (2) 8-15 图示桁架,杆1A 处承受铅直方向的载荷F 作用,F =50 kN ,钢的许用应力[σS ] =160 MPa ,木的许用应力[σW ] =10 MPa 。
解:(1) 对节点A (2) 84 mm 。
8-16 题8-14解:(1) 由8-14得到的关系;(2) 取[F ]=97.1 kN 。
8-18 图示阶梯形杆A 2=100 mm 2,E =200GPa ,试计算杆AC 的轴向变形 解:(1) (2) AC 8-22 图示桁架,杆1与杆2的横截面面积与材料均相同,在节点A 处承受载荷F 作用。
《材料力学练习》word版

第1章1-1 什么是构件的强度、刚度和稳定性?1-2 材料力学对变形固体有哪些假设?第2章2-1 试作图示各杆的轴力图,并确定最大轴力| FN |max 。
2-2 试求图示桁架各指定杆件的轴力。
2-3 试作图示各杆的扭矩图,并确定最大扭矩| T|max 。
2-4 图示一传动轴,转速n=200 r/min ,轮C为主动轮,输入功率P=60 kW ,轮A、B、D均为从动轮,输出功率为20 kW,15 kW,25 kW。
(1)试绘该轴的扭矩图。
(2)若将轮C与轮D对调,试分析对轴的受力是否有利。
2-5 试列出图示各梁的剪力方程和弯矩方程。
作剪力图和弯矩图,并确定| Fs |max及|M |max值。
2-6 试用简易法作图示各梁的剪力图和弯矩图,并确定| F s |max及| M|max值,并用微分关系对图形进行校核。
2-7 图示起重机横梁AB承受的最大吊重F P=12kN,试绘出横梁A B的内力图。
2-8 图示处于水平位置的操纵手柄,在自由端C处受到一铅垂向下的集中力F p作用。
试画出AB段的内力图。
第3章3-1图示圆截面阶梯杆,承受轴向荷载F1=50kN与F2的作用,AB与BC段的直径分别为d1=20mm与d2=30mm,如欲使AB与BC段横截面上的正应力相同,试求荷载F2之值。
3-2变截面直杆如图所示。
已知A1=8cm2,A2=4cm2,E=200GPa 。
求杆的总伸长量。
3-3 在图示结构中,AB为刚性杆,CD为钢斜拉杆。
已知F P1=5kN ,F P2=10kN ,l=1m ,杆CD的截面积A=100mm2 ,钢的弹性模量E=200GPa 。
试求杆CD的轴向变形和刚性杆AB在端点B的铅垂位移。
3-4 一木柱受力如图所示。
柱的横截面为边长200mm的正方形,材料可认为符合胡克定律,其弹性模量E=10GPa。
如不计柱的自重,试求:(1)作轴力图;(2)各段柱横截面上的应力;(3)各段柱的纵向线应变;(4)柱的总变形。
材力习题集.
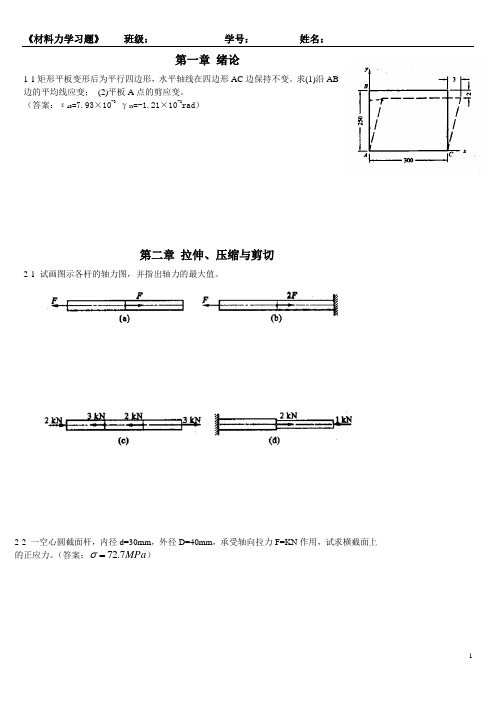
第一章 绪论1-1矩形平板变形后为平行四边形,水平轴线在四边形AC 边保持不变。
求(1)沿AB边的平均线应变; (2)平板A 点的剪应变。
(答案:εAB =7.93×10-3 γXY =-1.21×10-2rad )第二章 拉伸、压缩与剪切2-1 试画图示各杆的轴力图,并指出轴力的最大值。
2-2 一空心圆截面杆,内径d=30mm ,外径D=40mm ,承受轴向拉力F=KN 作用,试求横截面上的正应力。
(答案:MPa 7.72=σ)2-3 题2-1 c 所示杆,若该杆的横截面面积A=502m m ,试计算杆内的最大拉应力与最大压应力(答案:MPa t 60max ,=σ MPa c 40max ,=σ)2.4图示轴向受拉等截面杆,横截面面积A=5002m m ,载荷F=50KN 。
试求图示截面m-m 上的正应力与切应力,以及杆内的最大正应力与最大切应力。
(答案:MPa MPa MPa MPa 50 ; 100 ; 24.49 ; 32.41max max ==-==τστσαα)2.5如图所示,杆件受轴向载荷F 作用。
该杆由两根木杆粘接而成,若欲使粘接面上的正应力为其切应力的二倍,则粘接面的方位角θ应为何值(答案: 6.26=θ)2.6 等直杆受力如图所示,试求各杆段中截面上的轴力,并绘出轴力图。
2.7某材料的应力-应变曲线如图所示,图中还同时画出了低应变去区的详图,试确定材料的弹性模量E 、屈服极限s σ、强度极限b σ、与伸长率δ,并判断该材料属于何种类型(塑性或脆性材料)。
2.8某材料的应力-应变曲线如图所示,试根据该曲线确定: (1)材料的弹性模量E 、比例极限P σ与屈服极限2.0σ; (2)当应力增加到MPa 350=σ时,材料的正应变ε, 以及相应的弹性应变e ε与塑性应变p ε2.9图示桁架,杆1与杆2的横截面均为圆形,直径分别为d1=30mm 与d2=20mm ,两杆材料相同,许用应力[]σ=160MPa ,该桁架在节点A 处承受铅垂方向的载荷F=80KN 作用。
材料力学全部习题解答

弹性模量
b
E 2 2 0 M P a 2 2 0 1 0 9P a 2 2 0 G P a 0 .1 0 0 0
s
屈服极限 s 240MPa
强度极限 b 445MPa
伸长率 ll010000m ax2800
由于 280;故0该50 材0料属于塑性材料;
13
解:1由图得
弹性模量 E0 3.550110063700GPa
A x l10.938m m
节点A铅直位移
A ytan 4 l150co sl4 2503.589m m
23
解:1 建立平衡方程 由平衡方程
MB 0 FN1aFN22aF2a
FN 2 FN1
得: FN12F1N22F
l1
l2
2.建立补充方程
3 强度计算 联立方程1和方
程(2);得
从变形图中可以看出;变形几何关
l
l0
断面收缩率
AAA110000d22d22d2121000065.1900
由于 2故.4 属6 % 于 塑5 性% 材料;
15
解:杆件上的正应力为
F A
4F D2 -d2
材料的许用应力为
要求
s
ns
由此得
D 4Fns d2 19.87mm
s
取杆的外径为
D19.87m m
16
FN1 FN 2
Iz= I( za) I( zR ) =1 a2 4
2R4 a4 R 4 =
64 12 4
27
Z
解 a沿截面顶端建立坐标轴z;,y轴不变; 图示截面对z,轴的形心及惯性矩为
0 .1
0 .5
y d A 0 .3 5 y d y2 0 .0 5 y d y
材料力学习题及答案

材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆,两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量,并确定其大小。
解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其大小等于M。
1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力σ与切应力τ。
解:应力p与斜截面m-m的法线的夹角α=10°,故σ=p cosα=120×cos10°=118.2MPaτ=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为σmax=100 MPa,底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量,并确定其大小。
图中之C点为截面形心。
解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解:第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最大值。
解:(a) F N AB=F, F N BC=0, F N,max=F(b) F N AB=F, F N BC=-F, F N,max=F(c) F N AB=-2 kN, F N2BC=1 kN, F N CD=3 kN, F N,max=3 kN(d) F N AB=1 kN, F N BC=-1 kN, F N,max=1 kN2-2 图示阶梯形截面杆AC,承受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
80.8 MPa
满足强度要求
例8-2 已知[]=120MPa 试设计轴径d
z d 4kN x y A
解:1。外力分析
FC FD 14 kN M C M D (10 4) 10 3 250 10 3 1.5 kN m
3 3 3 Pl 9 Pl 10 Pl ' '' st f D fD EI EI EI
2h 2hEI Kd 1 1 1 1 st 5Pl 3
最大动挠度发生在D点,有
f D d
2hEI 10 Pl 3 K d st 1 1 3 5Pl EI
危险点位置 危险点应 力公式 强度条件
抵抗变形刚度
主要考虑 : 危险截面距中性 轴最远点 危险截面周边各点 其次考虑 : 危险截面中性轴上
max
FNmax A
bs
Fbs Abs
max
M x max WP
max
max
EA
max bs bs
d Kd st
强度条件
d m a x [ ]
1、自由落体冲击
2h Kd 1 1 st
2、水平冲击
Kd
2
g st
例8-1
已知: FQ、 h、d、E 、a
求:
Kd
FQ h a
2h Kd 1 1 st
st
Mc
EI
M xc
GIp
a
2 1 2 aFQ a a 1 FQ a 3 GI P EI 2 3
实验:
1.低碳钢拉伸分几个阶段,画出其应力应变图, 在图中标出相应阶段的力学指标。
2.材料的强度指标、塑性指标是什么?写出其表 达式。 3.画出低碳钢、铸铁拉伸、扭转、压缩的断口形 状,试用应力状态解释其破坏的原因 。
例4-1、列图示内力(FQ, M) 方程,作FQ` M 图
qa2 q
解:1.求支反力
11 X1 1F 0
D C X1 A X1 F B
X1 4. 计算各系数.求解
M c F N c 1 1 2 1 aa a l 1 1 11 EI 2 3 EA EI EA
a3 l 3EI EA
FN
1
1 F
1
M c 1 1
1F
外力 基本变形
轴向拉伸 F 轴力 FN
F
剪 切
F F Me
圆轴扭转 Me 扭矩 Mx Mx Mx
平面弯曲 剪力 FQ FQ 弯矩 M M
横 截 面 的 内 力 横 截 面 的 应 力
强 度 计 算
内力种类 符号规定 危险截面 计算公式 应力分布
剪力 FQ
等直杆F图 Fmax 变截面杆 分段 Fmax
最大动挠度发生在D点,有
f D d
2hEI 10 Pl 3 K d st 1 1 3 5Pl EI
第十一章 静不定结构
• 解题步骤 (1)判断静不定次数,选取适当静定基; (2)建立相应的变形协调方程或力法正则方 程; (3)求变形或力法正则方程系数; (4)解静不定问题。
3 5 Fa 5 2 a Fa 6 EI EI EI 3 2
FQ
F/2
x
Fa
例 4-5 试画出图示梁的剪力图和弯矩图
例 4-6 试画出图示梁的剪力图和弯矩图
例 4-7 试画出图示梁的剪力图和弯矩图(作内力图)
4-8、作图示梁的内力图。
第八章 组合变形
1.两个平面弯曲的组合(斜弯曲)
2.拉伸(压缩)与弯曲的组合
偏心拉伸或压缩 3.弯曲和扭转拉伸(压缩)和扭转
拉伸(压缩),弯曲和扭转
组合变形
• 1、斜弯曲:
max
M y max Wy M z max Wz
同一点
max
2 2 My max M z max
W
圆轴
2、拉弯组合:
max
M max FN W A 1 2 M 2 Mx W
FQ 1
M
FQ a
Mx
M
FQ a a
a
Mx
FQ a
a
st
FQ h
Mc
EI
M xc
GIp
2 1 2 aFQ a a 1 FQ a 3 GI P EI 2 3
a
a
2 FQ a 3
3EI GIP 32FQ a 3 4 1 4 d 3E G
FQ a 3
剪切面 挤压面
F N A
均布 危险截面任意点
实用计算 Fbs F Q bs Abs A
等直轴 Mx图Mxmax 等直梁 M图 塑性 Mmax 阶梯轴 分段 Mmax 脆性 +Mmax Mmax
M x IP
Mx
假设均布
危险截面任意点
max
FQ A
FQ S 矩形 My I Z b 截面 IZ max M max
3。强度计算---设计d
d 3 1 2 M max M x2max 32
32 2 d M max M x max 2
3
y
A
C 4kN 10kN
B
D
400
1.5kNm
400
300
Mx
3.5kNm 4.2kNm
3
32 120 10 6
4200 2 1500 2
当结构有弹簧、制造误差、温度变化时,用变 形比较法物理意义更直观
例11-1 已知 AB梁EI , CD杆EA, F 求: CD杆内力
D F C a D X1 A X1 a B A l
方法1 解: 1.一次静不定.
2.将AB,CD在C处拆开 加一 对相对力X1。 3. C处的相对位移为0,即
C
F B
3。强度计算---设计d
1 2 r3 M max M x2 max W 1 2 W M max M x max 2 d 3 1 2 M max M x2max 32
2.1kNm
4.2kNm 4.2kNm
3.5kNm
M
z d
4kN x 10kN
2hd 4 Kd 1 1 1 3 4 32FQa 3E G
例8-2、重量为P的质量块由高度h下落到D点,设梁ABD 抗弯刚度EI为常数,杆BC抗拉刚度为EA,且EI=4EAl2, 不考虑杆BC失稳问题,求跳板中最大动挠度;如果杆 BC为刚体,定性说明冲击时梁ABD中的最大动应力是增 大还是减少?(15分)
3、拉、弯、扭组合:
r 3 1 3 2 4 2
r4
1 2 2 2 1 2 2 3 3 1 2 1 2 2 2 3 M 2 0.75M x W
例8-1 矩形截面的铝合金杆承受偏心压力如图。a=20mm, b=120mm, h=180mm, 若杆侧面 A点处的纵向应变 =500×106,E=70GPa, [] =100MPa,试求载荷F,并校核强度。 解:
由第三强度理论,有
1 2 2 r3 M Mx W 1 2 2 M Mx 3 d / 32
73.5MPa
结构安全
第十二章 动载荷
动静法 动 能量法 静
Fd d d 动荷系数 K d F st st
Fd K d F
d Kd st
M
7 2 .3 1 0 3 m
取d
=74mm
例8-3、水平放置钢制圆截面直角曲拐,直径d=100mm ,l=2m,q=1kN/m,Fy=2kN,[σ]=160MPa, 试校核该杆 的强度。
解:危险截面为固定端A,有
M x Fl 4kN m 1 2 M Fl ql 6 kN m 2
x3
D
A
qa/2
x1
a
C x2
a
B
3qa/2
2.列FQ,M 方程
AC段 FQ1=qa/ 2 M1=qax1/ 2 CB段
qa FQ2 q ( x2 a ) 2
a
qa
FQ
qa/2
M
qa2/2
qa/2
qa q ( x2 a ) 2 2 M2 x2 qa 2 2 FQ3 qx3
例 4-2 试画出图示梁的剪力图和弯矩图(作内力图)
q 2qa2 a
FQ qa 3qa M
2qa 2a qa 5qa
2qa
a
2qa2
2qa2
例 4-3 试画出图示梁的剪力图和弯矩图
例4-4 试画出图示梁的剪力图和弯矩图(作内力图)
F 2a F/2 F/2 F/2 F/2 F/2 M Fa/2 x a F a
F 46 139 108 201F =E
Eε 70 109 500 106 F 174.5kN 201 201
4. 强度计算
F My F Mz z y 20 A 180
F My Mz A A Wy Wz
1 6 6 102 12 9 102 120180106 1202 180106 1201802 106
BD段
qa2/2
3qa2/8
qa2/2
2 qx3 M3 2
绘制FQ、M 图的简便方法
一. 正确求出支反力。 二. 有集中力F 作用处, FQ 图有突变, 方向与F一致(左),突变值 =F ,M 图有折线
