定积分分部积分法
定积分的分部积分法经典例题
定积分的分部积分法经典例题
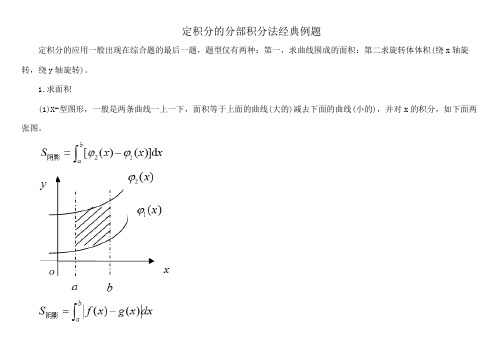
定积分的应用一般出现在综合题的最后一题，题型仅有两种：第一，求曲线围成的面积；第二求旋转体体积(绕x轴旋转，绕y轴旋转)。
1.求面积
(1)X-型图形，一般是两条曲线一上一下，面积等于上面的曲线(大的)减去下面的曲线(小的)，并对x的积分，如下面两张图。
求面积首要问题是画出草图，图形的上下位置(或者左右位置)，交点一定要做得准确。
通常曲线，例直线、抛物线、双曲线、指数、对数、三角函数的图像要画得熟练、准确。
求出结果后要检验，这样的题型是一个实际问题，所得结果要合乎逻辑。
(2)Y-型，一般是两条曲线一左一右，面积等于右边的曲线(大的)减去左边的曲线(小的)，并对y的积分，如下图
2.旋转体体积
求旋转体体积时要充分发挥几何空间想象能力，要想象出旋转出的体积大概是什么形状的。
(1)X-型图形
绕x轴旋转所得图形的体积
绕y轴旋转所得图形的体积
(2)Y-型图形
绕x轴旋转所得图形的体积
绕y轴旋转所得图形的体积
常考题型如下：。
定积分的分部积分法广义积分
b
(5.3.3)
分部积分法
例(补充)
计算
0
4
0
xdx . 1 cos 2 x
2
解 1 cos2x 2cos x,
4
0
xdx 1 cos 2x
4
4
xdx 2 cos x
2
0
4
4
0
x d tan x 2
1 1 x tan x 0 2 2 1 4
dx
1
dx x
lim
1
b 1
b
dx x
令 x t，则x t 2，dx 2tdt 且x 1 t 1 ，x b t b
b 2tdt lim 2dt lim 2t b 1 b t
lim
b 1
b
b 1
lim 2( b 1)
1 x
dx
b 0
lim (arctan x)
a
a
lim (arctan x)
b
b
(0 lim arctan a) ( lim arctan b 0)
2
注意 有限区间上 定积分的计 算和对积分 结果求极限 的运算的正 确性.
2
广义积分
b
b
1 1
所以，广义积分
-x
e dx 收敛 .
0
广义积分
例3 求广义积分
解
0
定积分的分部积分法
§6.5 定积分的分部积分法因为vdu udv uv d +=)(，两边从a 到b 取定积分有：⎰⎰⎰+==b abab ab avdu udv uv uv d ][)(，所以 ⎰⎰-=bab a ba vdu uv udv ][ 例1⎰⎰⎰-=-=5151515151]ln [ln ])[(ln ln dx xx x x x xd x x xdx 45ln 5][05ln 551-=--x例2 11|][1110110=+-=-=-==⎰⎰⎰xx xxx x x e e e e dxe xe xde dx xe例3211|c o s 0s i n|s i n s i n c o s 0000-=--=+=-==⎰⎰⎰πππππx dx x x x x xd xdx x例4⎰⎰⎰-==ee e e xd x x x x xd xdx x 1121221ln 21]ln [21)2(ln ln=414|212122122122122+=⋅-=-⎰e x e dx x x e e e例5⎰⎰=2ln 0222ln 032221dx e x dx e x x x 令2x t =，则原式=⎰⎰⎰-==2ln 02ln 02ln 02ln 021][212121dt e te tde dt te tt t t =212ln 212212ln |212)2(ln 212ln 0-=+⋅-=-⋅t e 例6 求⎰⎰=2020c o s c o s ππx xx d e xd xe =dx x e x d e e x x xx⎰⎰+-=-⋅202020sin 1cos |cos πππ=⎰⎰-⋅+-=+-202020sin ])[(sin 1sin 1πππx d e e x xde x xx=xdx e e x cos 1202⎰-+-ππ∴ 1cos 2220-=⎰ππe xdx e x∴ ⎰-=202)1(21cos ππe x e x例7⎰342s i n ππdx xx=⎰⎰+-=-343434cot ]cot [cot ππππππxdx x x x xd=++-=⎰dx x x 34sin cos 493ππππ⎰++-=34sin sin 493ππππx xd 34]sin [ln 493ππππx ++-=23ln 21493++-ππ 利用定积分还可以求某些和的近似值。
(完整版)定积分的分部积分法
n 102 sin n2xdx n 102 sin n xdx
n 1In2 n 1In
In
n
n
1
I
n2
,
积分递推公式.
预科部：melinda
In2
n n
3 2
In4
,
,
直到
In
的下标 n 递减
到0或1为止.于是
I2m
2m 1 2m
2m 2m
3 2
2m 2m
5 4
...5 6
3 4
1 2
I0
I 2 m1
2m 2m
1
2m 2 2m 1
2m 2m
4 3
... 6 7
4 5
2 3
I1
m 1,2,3,...
预科部：melinda
I0
2
0
sin
0
xdx
2
, I1
2
0
sin
xdx
1
In
2
0
sin
n
xdx
n
n
1 n 1
n n n
3 2 3
... ...
3 4 4
1 2 2
，n为正偶数，
定积分的分部积分法
一、分部积分法 二、例题
预科部：melinda
一、分部积分法
1.分部积分公式 设函数 u ux,v vx
在a,b 上具有连续导数 u,v, 则
b
a
uvdx
uv
b a
b
a
uvdx；
或
b
a
udv
uv
b a
b
a
vdu
2.说明
6.5.1定积分分部积分法
△ 冗1
冗In 2
——llnsec x 10 =-82 0 8 4
经济数学--微积分
o
定积分分部积分法
三、举例-幕函数乘对数函数
经济数学
例5 计算 J： (In x)3 dx
：一 解原式=x (In x )3
J 3(ln x)2 dx
】 =e _ 3 x(In x)2
-1J2 In xdx
J =e - 3(e - 2 In xdx)
) =1 [[xf '(2 x )]1 -1 (2 x dx
1
1
=2 f'(2) - 4 [f (2 x )]0
=2 - 4 [f (2) - f (0)] = 2.
经济数学
fx2 sin t i
“ ——d t, 求[xf (x )dx.
*
解因为沖没有初等形式的原函数， t
无法直接求出f (x),所以釆用分部积分法
f兀
2
2x
Jo o
si1n 2 ■xdxd
cos2x
x sin 2 xdx = 2 Jo
=1
JO
x cos
2
x
兀1
2
1,
cos 2 xdx
2 Jo o
= ——sin2 x71
n
24
02
3
勿 2 1 + cos 2x ,
例3计算f x dx.
00 2
解原式万 d ( x + § sin 2 x)
经济数学--微积分
—厂 f X x)=
-2 x = ,
xx
1
1
.・J0 xf(x)dx = 2 f⑴ _ -J： x2f，(x)dx
定积分的分部积分法
(3) 4 3 xdx; 1
(4) (sin x cos x)dx; 0
(7)
2
sin 2
x
dx;
0
2
1
(8) (
x 1 3x )dx.
0
第三节 定积分的换元法
例1 求 4 dx .
0 1 x
解法1
dx 1
x
令
x
t
2tdt 1 t
2
(1
1
1
1．计算
(1) d x ln(1 t2 )dt ; dx 1
2．计算下列各定积分
x
tan tdt
(2) lim x0
0
x3
.
（1）2|1 x | dx;
2
(2) | sin x | dx;
0
0
(5)
0 1
3x4 3x2 1 x2
1dx;
(6) 4 tan2 xdx; 0
4 dx
1 x x
2 2tdt 1 t2 t
2 2dt 2 d (t 1) 2
1 t 1 1 t 1
2
ln(t
1)
|12
2(ln
3
ln
2)
2
ln
3 2
.
例4 求 2 3cos2 xsin xdx. 0
解 设u cos x，则du sin xdx，当x 0时，u 1；当x 时，u 0.于是 2
与下方部分面积的代数和，如图6－2所示，有
b
a f (x)dx A1 A2 A3
定积分的分部积分法
b
(1 b ) ln(1 b ) (1 a ) ln(1 a ) ( x
2 2 2 2
2 b a
)
2
(1 b ) ln(1 b ) (1 a ) ln(1 a ) (b a )
2 2 2 2 2
例3 计算 解 设
x
2
4 0
特别： sin x dx
2 0 2
2 0
1 2 dx 2 0 4
sin x dx
4
1 cos x dx I 2 I 0 2
2
2 0
2 0
3 3 1 cos x dx I 4 I 2 I 0 4 4 2
4
3 3 dx 8 16
ln( 2 1) 2 1
例5：计算定积分 ln( 1 x 2 )dx
0
1
解：原式 ( x) ln( 1 x )dx
2 0
1
x ln( 1 x ) x[ln( 1 x )]dx
2 1 0 2 0
1
2x (1 x ) 1 ln 2 dx ln 2 2 dx 2 2 0 1 x 0 1 x
“反” “对”
反三角函数. 对数函数.
“幂” “指”
“三”
幂函数. 指数函数.
三角函数.
基本类型及分部方式:
(1) Pn ( x)e
a b ax b
dx
b
a
1 ax b Pn ( x)[ e ]dx a
b a
(2) Pn ( x) cos( ax b)dx
定积分的分部积分法
例4 证明定积分公式
I n 02 sin n xdx 02 cos n xdx
n 1 n 3 ... 3 1 ，n为正偶数， n n2 4 2 2 n 1 n 3 ... 4 2 ,n为大于1的正奇数. n n2 5 3
预科部：melinda
二、例题
例1 计算
解
1
0 xe dx .
x x 1
1
x xe dx x de 0 0
xe
x 1 0
e dx
1 x 0
e e
x 1 0
1
预科部：melinda
例2 计算 4 sin xdx .
0
2
解
0
2
4
sin xdx
t x , dx 2tdt x 0, t 0; x
b b a b
预科部：melinda
(1)应用分部积分公式不需要变换积分限，对 于不含积分号的 uv 项需将积分上下限代入求 差，另一项
a vdu 仍按定积分继续计算.
b
(2)应用分部积分公式时,被积函数 u 和 v 的选
取与不定积分的方法一样，需注意的是由于求 定积分，应观察积分区间是否关于原点对称， 被积函数是否是奇函数或偶函数，以利用特殊 定积分公式简化定积分的运算.
到0或1为止.于是
I 2m
2m 2m 2 2m 4 6 4 2 I 2 m1 ... I1 2m 1 2m 1 2m 3 7 5 3
m 1,2,3,...
预科部：melinda
I 0 sin xdx , I1 02 sin xdx 1 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
In
n1 n In2
积分I n关于下标的递推公式
I n2
n n
3 2
In4
, 直到下标减到0或1为止
I2m
2m 1 2m
2m 2m
3 2
5 6
3 4
1 2
I0,
(m 1,2, )
2m 2m 2 6 4 2
I2m1
2m
1
2m
1
7
5
3 I1,
I0
2
dx
,
0
2
I1
2 sin xdx 1,
已积出的部分 要求值
解 原式
2 xdex
1
xex 12
2 exdx
1
2e2 e ex 12
2e2 e e2 e e2
定积分的分部积分法
已积出的部分要求值
2 4 x tan2 xdx 0
解
原式
4 0
x
x sec2
tan x 4
x 1
4
dx tan
4 xd 0
1
例2 计算 2 arcsin xdx. 0
解 令 u arcsin x, dv dx,
则 du dx , v x, 1 x2
1
2 arcsin xdx
0
x
arcsin
1
x2 0
1 2
0
1
1
1 2
2 6 20
1 d(1 x2 ) 1 x2
xdx 1 x2
12
1
1 x2
x
2dx 2
1 2
cos x2
1 0
1 (cos1 1). 2
例6 证明定积分公式
In
2 sinn xdx
0
2 cosn xdx
0
n
n
n
1 1
n n n
3 2 3
3 4 4
1 2 2,
2
,
n为正偶数 n为大于1的正奇数
n n2 5 3
证 设 u sinn1 x, dv sin xdx,
abuvdx
例(5)2 计算 01e xdx
解解解解 010101eee xxxddxx令令令 xxttt22 010101eeetttttdtddttt222010101t01tddtedeetett t
22[t[etet]t1]010220101eettddtt22ee22[[eett]]1010 22
xdx
tan
2
x
x2 2
4 0
0
0
32
2
4
ln
cos x
4 0
32
ln 2 2
4 2 32
3 2 e2x sin 2xdx 0
解 原式 1
2 e2xd cos 2x
20
1 2
e2
x
cos
2
x
2 0
1 2
2 cos 2x e2x (2)dx
0
1 1 e
1
一、分部积分公式
设函数u( x)、v( x) 在区间a,b上具有连续
导数，则有abudv
uv b a
b
a vdu
.
定积分的分部积分公式
推导
uv uv uv,
b
a (uv
)dx
b
uv a
,
uv
b a
b
a
uvdx
b
a
uvdx,
b
udv
b
uv
b
vdu.
a
aa
◆定积分的分部积分法
例1 1 2 xexdx 1
2 e2xd sin 2x
2
20
1 1 e 2
1 2
e2 x
sin
2
x
2 0
1 2
2 sin 2xde2x
0
1 1 e
2 e2x sin 2xd x
2
0
所以
2
e 2 x
sin 2xdx
1
1 e
0
4
分部积分过程：
abuvdxabudv[uv]ba abvdu[uv]ba abuvdx
0
于是
I2m
2m 1 2m
2m 3 2m 2
531 642
, 2
I2m1
2m 2m
1
2m 2 2m 1
6 7
4 5
2. 3
二、小结
定积分的分部积分公式
b udv
b
uv
b
vdu.
a
aa
（注意与不定积分分部积分法的区别）
思考题
设 f ( x) 在 0,1 上 连 续 ， 且 f (0) 1 ，
2
0
3 1.
12 2
例3 计算 4
xdx .
0 1 cos 2x
解 1 cos 2x 2cos2 x,
4
xdx
0 1 cos 2x
4
xdx
0 2cos2 x
4
0
xdtan x
2
1 2
x
tan
x
4
0
1 2
4
0
tan xdx
8
1 2
ln
sec
x
4 0
ln 2 . 84
x)10
5 ln 2 3
ln
3.
例5
设 f (x)
x2 sin t
1
dt, 求 xf ( x)dx.
1t
0
解 因为sin t 没有初等形式的原函数，
t
无法直接求出 f ( x)，所以采用分部积分法
1
0 xf ( x)dx
11
2 0
f ( x)d( x2 )
1 2
x2
f
(
x)
1 0
1 2
1
0
x
2df
(
x
)
1 2
f
(1)
11
2 0
x2
f
( x)dx
x2 sin t
f ( x) 1
dt , t
f
(1)
1 sin
1 t
t
dt
0,
f
( x)
sin x2 x2
2x
2sin x
x2
,
1
0
xf
( x)dx
1 2
f
(1)
11
2 0
x2
f
( x)dx
1 2
1
0
2
x
sin
x 2dx
1 2
1
0
sin
例(41)
1
计算 02 arcsinxdx
1
11
解
02 arcsinxdx
[x arcsin x]2 0
02 xd
arcsin x
1 2
6
1
02
x 1 x2
dx
12
1 2
1
02
1 d(1 x2) 1 x2
[
1
x2
1
]2
3 1
12
0 12 2
分部积分过程：
abuvdx
b
audv
[uv]ba
abvdu[uv]ba
du (n 1)sinn2 x cos xdx, v cos x,
In
sinn1 x cos x
2
0
(n
1)
2 sinn2 x cos2 xdx
0
0
1 sin2 x
In
(n
1) 2 0
sin n 2
xdx
(n
1) 2 0
sin n
xdx
(n 1)In2 (n 1)In
f
(2)
3，
f
(2)
5
，求 1 0
xf
(2
ቤተ መጻሕፍቲ ባይዱ
x )dx
.
思考题解答
1
0
xf
(2 x )dx
1 2
1
0
xdf
(2
x)
1 2
xf
(2 x)10
1 2
1
f (2x)dx
0
1 2
f
(2)
1
4
f
(2 x )10
5 1 f (2) f (0) 2.
24
练习题
一、填空题：
1、设 n 为正奇数，则 2 sinn xdx ___________； 0
1 ln(1 x)
例4 计算 0 (2 x)2 dx.
解
1
0
ln(1 (2
x
x) )2
dx
1 0
ln(1
x)d
2
1
x
ln(1 x 2 x
)1 0
1
0
2
1
x
d
ln(1
x)
ln 2 1 1 1 dx
3 0 2 x 1 x
11 1 x 2 x
ln 2 3
ln(1
x)
ln(2