材料动态特性实验报告,SHPB实验报告
高性能混凝土的SHPB测试技术
高性能混凝土的SHPB测试技术摘要高性能混凝土是一种特殊的混凝土，由于其具有高强度、高耐久性、高耐久性和较低的渗透性等特点，广泛应用于建筑结构、道路、桥梁等领域。
为了更好地了解高性能混凝土的力学性能，研究人员常使用SHPB测试技术进行测试。
本文将介绍高性能混凝土的SHPB测试技术，包括其原理、测试步骤和应用。
1. 引言高性能混凝土是一种以高强度和高性能为目标的特殊混凝土。
它具有一系列优异的力学性质，如高强度、高耐久性、较低的渗透性和较小的收缩。
在建筑结构、道路和桥梁等领域应用广泛。
为了更好地了解高性能混凝土的力学性能，研究人员常使用Split Hopkinson Pressure Bar（SHPB）技术进行测试。
SHPB是一种高速压力杆技术，可用于测量材料的高应变率动态力学特性。
2. 原理SHPB技术是一种在很短时间内施加高压脉冲到试样上的方法，主要用于测量在单向动态拉伸或压缩载荷下材料的动态力学性能。
技术的核心部分是两个导杆通过脉冲形成器与被测试材料相连。
当形成器发出一个很短的脉冲压缩后导杆相互碰撞，导致两个导杆的快速运动。
因此，SHPB测试的载荷速率比传统试验方法的载荷速率高得多。
试验与试样的动应变和动应力可通过记录两个导杆的速度波形来计算测量。
结果可用于绘制应变-应力曲线，通过不同载荷下的测试来计算材料性能。
3. 测试步骤3.1 试样准备试样应按照标准要求进行制备和切割。
在测试之前，试样的尺寸和形状应量取并与标准匹配。
试样应保持在一定的温度和湿度环境中，以避免影响测试结果。
3.2 实验条件设置SHPB测试中, 时间、应变速率和温度是需要优先设置的实验条件。
应定期检测系统参数以保证测试结果的准确性。
实验室环境的温度和湿度也应被监测，以保证测试的可靠性。
试验时，应在适当的电子显微镜下观察试样的损伤，为后续的研究提供支持。
3.3 数据采集和处理在测试中，应负责记录数据。
应根据实验标准对数据进行统计和分析，以根据结果计算出高性能混凝土的动态力学性质，同时另一方面需要根据数据进行可靠性分析。
材料动态特性实验报告,SHPB实验报告
机械工程学院研究生研究型课程考试答卷课程名称：材料动态特性实验（SHPB实验）考试形式：□专题研究报告□论文√大作业□综合考试评阅人：时间：年月日材料动态特性实验实验目的：1、了解霍普金森杆的实验原理和实验步骤；2、会用霍普金森杆测试材料动态力学性能。
1.SHPB 组成：Kolsky 在Hopkinson 压杆技术的基础上提出采用分离式 Hop-kinson 压杆 SHPB )技术来测定材料在一定应变率范围的动态应力 ── 应变行为 ,该实验的理论基础是一维应力波理论, 它通过测定压杆上的应变来推导试样材料的应力 ── 应变关系, 是研究材料动态力学性能最基本的实验方法之一。
为了测出A3钢（又称Q235钢）的屈服极限、弹性模量以及其他性能参数。
用SHPB 实验就行数据测量。
SHPB 的实现装置如下图：分离式Hopkinson 压杆装置示意图它由压缩气枪、撞击杆、测时仪、输入杆（入射杆）、超动态应变仪、试件、透射杆、吸收杆、阻尼器和数据处理系统组成。
2.实验原理：SHPB 技术建立在两个基本假定的前提上：（1）杆中应力波是一维波；（2）试件应力/应变沿其长度均匀分布。
根据垂直入射应力波在界面出的反射、透射原理和上述假定由：应力相等：)()()(t t t T R I σσσ=+ (1)应变相等：)()()(t t t T R I εεε=+ (2)式中()I t σ和()R t σ分别为入射杆的入射应力和反射应力，()T t σ为透射杆的透射应力，()I t ε和()R t ε为入射杆的入射应变和反射应变，()Tt ε为透射杆的透射应变。
图1 输入杆-试件-输出杆相对位置如图2所示，在满足一维应力波假定的条件下，一旦测得试件与输入杆的界面X 1处的应力，可理论推导得： []112()(,)(,)(,)2S I R T SA t X t X t X t A σσσσ=++ （3） SR I T S S L t X v t X v t X v L t X v t X v t ),(),(),(),(),()(11212--=-=ε （4） []⎰⎰--==t R I T S t S S dt t X v t X v t X v L dt t 01120),(),(),(1)(εε （5）式中：A 为压杆的横截面积，s A 为试件的横截面积，S L 为试件的长度。
高应变率下混凝土动态力学性能SHPB实验
２ Ｅｎｇｉｅｅ ｉ ｇ Ｉ ｔｔ ｔ ． ｎ ｒｎ ｎｓ ｉｕ ｅ，Ａ ｉ ｒ Ｆｏｒ ｅ Ｅｎｇ ｎｅ ｉ ｇ Ｕ ｎ ｖ ｓｔ ｃ ｉ ｅｒｎ ｉ ｅｒ ｉｙ，Ｘ ｉ ｎ ７１ ０３ ａ ０ ８，Ｃｈ ｎ ｉ ａ；
证 了实验 结果 的有 效性 、 一致性 和 试样 中的应 力均 匀性 问题 ， 到 了混 凝土 材料 在较 高应 变率 范 围内的动 态 得 应力一 应 变关 系。 究表 明 ， 凝 土材料 的 动 态应力一 应 变呈 非线性 关 系； 研 混 混凝 土材料 为应 变率敏 感性 材料 ，
在 较 高应 变率 范 围 内混凝 土材 料 的动 态应 力一 应 变 关 系是 与 应 变率相 关的 ； 混凝 土材 料 的破 坏 应 力和破 坏
Ａ ｓ ｒ ｃ ：Ｔｈ ｐ ｉ Ｈｏ ｋ ｎ ｏ ｒ ｓ ｕ ｅ Ｂａ （ Ｈ Ｐ ｂ ｔａ ｔ ｅ Ｓ ｌ ｐ ｉ ｓ ｎ Ｐ ｅ ｓ ｒ ｒ Ｓ ｔ Ｂ）ｏ ｆ
１ ０ ｍ ｍ ｓ ｕ ｅ ｏ ｉ ｖ ｓ ｉ ａ ｅ ｔ ｅ ｄ ｎ ｍｉ ０ ｗａ ｓ ｄ ｔ ｎ ｅ ｔｇ ｔ ｈ ｙ ａ ｃ
（． 安 交 通 大 学 土 木 工 程 系 ， 西 西 安 ７０ ４ ；２ 空 军 工 程 大 学 工 程 学 院 ， １西 陕 １０９ ． 陕西 西 安 ７ ０ ３ ； １ ０ ８ ３ 空 军 后 勤 部 机 场 营房 部 ， 京 １ ０ ２ ） ． 北 ０ ７０
摘
要 ： 用ｊ ｌ Ｏｍｍ 霍普金 森 压 杆试 验设 备 ， 究 了混凝 土材 料在 冲击荷 栽 下 的动 态压 缩性 能 ， 析验 利 ２ Ｏ 『 研 分
素混凝土材料的SHPB实验及其参数敏感性与不确定性分析
素混凝土材料的SHPB实验及其参数敏感性与不确定性分析混凝土材料是最重要的工程结构建筑材料之一。
由于混凝土结构在使用过程中经常承受动态冲击荷载,混凝土材料的动态力学性能一直是工程结构研究关注的重要课题。
SHPB实验设备是被广泛用于测试各种材料动态力学性能的实验设备。
然而,在混凝土材料的SHPB实验中,许多参数存在着不确定性,这些不确定性会对实验结果造成重要影响。
本文首先开展了素混凝土材料的SHPB实验,通过对实验数据的分析验证了实验的有效性;其次,建立了数值模型并把数值模拟的结果与实验结果进行对比,验证了数值模型的有效性;然后,基于数值模型对素混凝土材料SHPB实验中的端面摩擦效应参数进行了敏感性与不确定性分析;最后,基于数值模型对素混凝土材料SHPB实验中的整体参数进行了敏感性与不确定性分析。
本文的主要研究工作如下:(1)完成了两种强度的素混凝土材料在3种应变率下的SHPB实验,并通过实验数据分析对实验的有效性进行了验证。
首先,介绍了SHPB实验装置的主要组成部分、基本原理;其次,描述了两种强度的素混凝土材料的制备过程;然后,完成了两类素混凝土材料在3个应变率下的SHPB实验,通过对实验记录的波形进行三波分析验证了实验的有效性,得到了6种工况下素混凝土材料的应力-应变曲线和对应的应变率;最后,分析了材料强度和应变率对动态力学性能的影响,包括动态抗压强度、动态吸能特性、破坏模式和高速摄像下的裂纹扩展。
(2)建立了素混凝土材料SHPB实验的数值模型,并通过与实验对比验证了模型的有效性。
首先,建立了与本文实验尺寸相同的SHPB实验的数值模型;其次,介绍了用于模拟素混凝土材料的Drucker-Prager材料模型参数的意义及其取值;最后,对数值模型进行求解和分析,分析了压杆中应力波的传播过程,验证了应力波传播的一维性,对比了数值模拟和实验得到的三个波形,验证了加载过程的一致性,对比了6种工况下数值模拟和实验得到的应力-应变曲线,验证了数值模型的有效性。
霍普金森压杆实验报告
(Байду номын сангаас)
νⅠ = ν2 = ν i +ν r = −c(ε i − ε r )
′ = ν t = −cε t νⅡ = ν 2
(t= ε )
νⅡ −νⅠ
l0 c l0
=
t
c (ε i − ε r − ε t ) l0 − ε r − ε t )dt
ε= (t )
∫ (ε
0
i
(2)
由 (1) 、 (2) 式进而可得试件材料的应力应变关系。根据均匀假定，可得
1. 霍普金森压杆(SHPB)实验装置、基本原理及用途
1.1 实验装置及用途
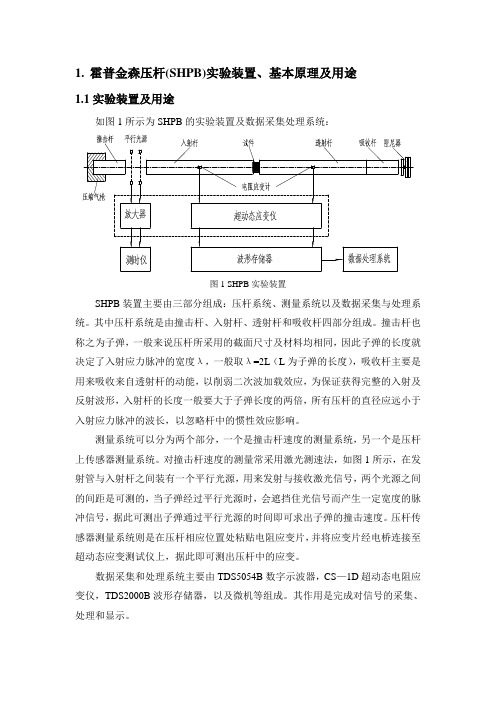
如图 1 所示为 SHPB 的实验装置及数据采集处理系统：
图 1 SHPB 实验装置
SHPB 装置主要由三部分组成：压杆系统、测量系统以及数据采集与处理系 统。其中压杆系统是由撞击杆、入射杆、透射杆和吸收杆四部分组成。撞击杆也 称之为子弹， 一般来说压杆所采用的截面尺寸及材料均相同，因此子弹的长度就 决定了入射应力脉冲的宽度λ，一般取λ=2L（L 为子弹的长度） ，吸收杆主要是 用来吸收来自透射杆的动能， 以削弱二次波加载效应，为保证获得完整的入射及 反射波形， 入射杆的长度一般要大于子弹长度的两倍，所有压杆的直径应远小于 入射应力脉冲的波长，以忽略杆中的惯性效应影响。 测量系统可以分为两个部分，一个是撞击杆速度的测量系统，另一个是压杆 上传感器测量系统。对撞击杆速度的测量常采用激光测速法，如图 1 所示，在发 射管与入射杆之间装有一个平行光源，用来发射与接收激光信号，两个光源之间 的间距是可测的， 当子弹经过平行光源时，会遮挡住光信号而产生一定宽度的脉 冲信号， 据此可测出子弹通过平行光源的时间即可求出子弹的撞击速度。压杆传 感器测量系统则是在压杆相应位置处粘贴电阻应变片， 并将应变片经电桥连接至 超动态应变测试仪上，据此即可测出压杆中的应变。 数据采集和处理系统主要由 TDS5054B 数字示波器，CS—1D 超动态电阻应 变仪，TDS2000B 波形存储器，以及微机等组成。其作用是完成对信号的采集、 处理和显示。
霍普金森压杆实验报告
1.1 实验装置及用途
如图 1 所示为 SHPB 的实验装置及数据采集处理系统：
图 1 SHPB 实验装置
SHPB 装置主要由三部分组成：压杆系统、测量系统以及数据采集与处理系 统。其中压杆系统是由撞击杆、入射杆、透射杆和吸收杆四部分组成。撞击杆也 称之为子弹， 一般来说压杆所采用的截面尺寸及材料均相同，因此子弹的长度就 决定了入射应力脉冲的宽度λ，一般取λ=2L（L 为子弹的长度） ，吸收杆主要是 用来吸收来自透射杆的动能， 以削弱二次波加载效应，为保证获得完整的入射及 反射波形， 入射杆的长度一般要大于子弹长度的两倍，所有压杆的直径应远小于 入射应力脉冲的波长，以忽略杆中的惯性效应影响。 测量系统可以分为两个部分，一个是撞击杆速度的测量系统，另一个是压杆 上传感器测量系统。对撞击杆速度的测量常采用激光测速法，如图 1 所示，在发 射管与入射杆之间装有一个平行光源，用来发射与接收激光信号，两个光源之间 的间距是可测的， 当子弹经过平行光源时，会遮挡住光信号而产生一定宽度的脉 冲信号， 据此可测出子弹通过平行光源的时间即可求出子弹的撞击速度。压杆传 感器测量系统则是在压杆相应位置处粘贴电阻应变片， 并将应变片经电桥连接至 超动态应变测试仪上，据此即可测出压杆中的应变。 数据采集和处理系统主要由 TDS5054B 数字示波器，CS—1D 超动态电阻应 变仪，TDS2000B 波形存储器，以及微机等组成。其作用是完成对信号的采集、 处理和显示。
图 6 透射波波形
万试屋 – 材料测试仪器方法资源小站/test_house
2.5 试件应力-应变曲线
工程应力曲线：
图 7 试样的工程应力曲线
工程应变曲线：
图 8 试样的工程应变曲线
混凝土动态性能实验报告(3篇)
第1篇一、实验目的本实验旨在研究混凝土在不同动态载荷作用下的力学性能，包括抗压强度、抗拉强度、抗剪强度等，以期为混凝土结构设计提供理论依据。
二、实验原理混凝土动态性能实验主要基于霍普金森压杆（SHPB）试验方法。
SHPB试验方法是一种非破坏性试验方法，通过高速加载使试件在极短时间内承受高应变率下的动态载荷，从而研究混凝土在不同动态载荷作用下的力学性能。
三、实验材料1. 混凝土试件：采用C30级混凝土，试件尺寸为100mm×100mm×100mm，分别进行抗压、抗拉、抗剪试验。
2. 加载设备：霍普金森压杆试验机，加载速度范围为10～100m/s。
3. 测量设备：高速数据采集系统、应变片、力传感器等。
四、实验步骤1. 准备试件：将混凝土试件切割成100mm×100mm×100mm的立方体，试件表面磨光，确保试件尺寸和形状符合要求。
2. 安装试件：将试件放置于试验机的加载平台上，确保试件中心与加载平台中心对齐。
3. 连接传感器：将应变片和力传感器安装在试件上，确保传感器与试件连接牢固。
4. 设置试验参数：根据试验要求设置加载速度、应变率等参数。
5. 进行试验：启动试验机，使试件在高速加载下承受动态载荷，记录试验数据。
6. 数据处理与分析：对试验数据进行处理和分析，得出混凝土在不同动态载荷作用下的力学性能。
五、实验结果与分析1. 抗压强度实验结果表明，C30级混凝土在不同动态载荷作用下的抗压强度随应变率的增加而降低。
在应变率为10m/s时，抗压强度为50.2MPa；在应变率为100m/s时，抗压强度为45.6MPa。
这说明混凝土在高速加载下抗压强度有所降低，且应变率对其抗压强度有显著影响。
2. 抗拉强度实验结果表明，C30级混凝土在不同动态载荷作用下的抗拉强度随应变率的增加而降低。
在应变率为10m/s时，抗拉强度为2.8MPa；在应变率为100m/s时，抗拉强度为2.5MPa。
材料动态特性实验(南京理工大学)
的弥散可以忽略不计。 第二个办法是数据处理时尽量选用透射波以及在打击端附 上一层柔性介质。 经过试件的透射波形及经柔性介质过滤的入射波形的高频振荡 均已大大减弱。 (2)惯性效应 SHPB 试验是在冲击载荷作下进行的,试件的变形速率很高,因此,作用在试件 上的外力做功,除转化为试件的应变能以外,尚有部分转化为试件的横向动能和 纵向动能。这就是试件质点的运动所引起的惯性效应。 (3)摩擦效应 在应力脉冲作用下,界面处压杆和试件的横向运动不同,由此产生的摩擦力 破坏了试件的一维应力状态,影响了径向应力应变分布的均匀性,使测得的应力 应变曲线高出真正的曲线。此即所谓界面的摩擦效应。 (4)波动效应 在 SHPB 试验中,波在试样内只需经过两、三个来回,即可使试样的状态均匀, 又由于脉冲的宽度远大于试件的厚度,因此在应力脉冲作用的大部分时间内,试 件处于均匀状态。 然而,在应力脉冲作用的最初阶段,试件内部的状态是不均匀的,
处理带来不便,因此在数据处理时不考虑摩擦效应。 这就要求在试验时,尽量减少 摩擦,使误差降到最低程度。SHPB 系统已在测试材料动态力学性能中得到了广泛 的应用,但是该系统测试的精度受到一些不利因素的干扰,影响测试结果的可信 度。影响 SHPB 试验精度的主要因素如下: (1)弥散效应 在 SHPB 试验技术中,一切分析都是以一维假定作为基础的。根据一维假定,任意 一个应力脉冲都是以 C。(仅与材料性质有关的常数)的速度在压杆中传播。然而 这一假定忽略了杆中质点的横向惯性运动,即忽略了杆的横向收缩或膨胀对动能 的贡献,因此是一个近似假定。 用电阻应变片测得的应变波形中,波峰上叠加的高 频振荡就是波形弥散的结果。 由此而求得的应力应变曲线中的上下震荡常常掩盖 了材料本身的特性,造成了数据处理上的困难,有时还容易将曲线中的第一个振 荡误认为是材料的上、下屈服点。为了尽量减少弥散效应对试验的影响,通常由 两个办法:第一个办法是减小压杆的半径,要求半径 r 与应力脉冲宽度 的比值
压实粘性土动态力学性能的SHPB试验
压实粘性土动态力学性能的SHPB试验刘俊新;陈忠富;徐伟芳;何鹏【摘要】Because of soils' low wave velocity and impedance and large deformation, it is unable to obtain their reliable and accurate dynamic stress-strain curves with a conventional SHPB(split Hopkinson pressure bar) experimental device. To investigate the compressive mechanic properties of compacted clays under strain rates varying from 600 to 2 500 s-1, compacted clay specimens were subjected to axial impact with different projectile speeds by using the improved SHPB with a diameter of 25 mm made of polycarbonate and a small pellet of vacuum seal cement as pulse shaper, and the validity of the experiment was discussed by considering the stress equilibrium and constant strain rate. The results show that the polycarbonate SHPB device can be used to the dynamic experiment of compacted clays, the dynamic stress and strain of a compacted clay are sensitive to strain rate, and the relationship between dynamic stress and strain rate may be expressed by an exponential function.%为解决因土体波阻抗及波速较低且变形较大,采用传统的分离式Hopkinson压杆(SHPB)实验装置不能准确获得土体的动态应力-应变曲线的问题,采用直径25 mm的聚碳酸脂SHPB 实验装置和真空封泥小球丸作为波形整形器,以不同的轴向速度撞击试件,测试试件在应变率600 ～2 500 s-1之间的动态力学性能,并通过应力平衡和常应变率分析对试验结果的有效性进行了讨论.结果表明:用聚碳酸脂SHPB装置对压实粘性土进行动态试验是可行的；土体的动态应力与应变具有显著的应变率效应,动态应力与应变率成指数关系.【期刊名称】《西南交通大学学报》【年(卷),期】2011(046)006【总页数】6页(P960-965)【关键词】聚碳酸脂;压实粘性土;波形整形技术;高应变率;动态力学性能【作者】刘俊新;陈忠富;徐伟芳;何鹏【作者单位】中国工程物理研究院总体工程研究所,四川绵阳621900;西南科技大学土木工程与建筑学院,四川绵阳621010;中国工程物理研究院总体工程研究所,四川绵阳621900;中国工程物理研究院总体工程研究所,四川绵阳621900;中国工程物理研究院总体工程研究所,四川绵阳621900【正文语种】中文【中图分类】TU411.8钻地武器，是指携带钻地弹头(侵彻战斗部)能够钻入地下目标深层后再引爆的精确制导武器.由于钻地武器钻入地下目标过程中或钻入目标内部后延时爆炸，都涉及到对目标组成部分在冲击荷载作用下的动力响应问题.这些目标主要由岩土介质和混凝土组成，包括压实粘土.因此，压实粘土在冲击荷载作用下的动力响应是防护工程和武器设计中一个相对热门的课题.目前，材料动载特性研究的理想设备主要是分离式Hopkinson压杆(SHPB).与硬质材料不同，对于软质材料，如土和塑料泡沫等，由于其波阻抗和波速较低，且变形较大，采用传统的SHPB实验装置已不能准确地获得可靠的动态应力-应变曲线.为确保这类材料SHPB实验结果的有效性和精度，从而得出正确的结论，必须对现有的SHPB实验装置进行改进.根据SHPB实验装置的原理以及应力波理论，解决这个问题通常有2种方法:一种是减小透射杆的横截面积或弹性模量，或者两者同时减小.例如胡时胜等利用铝杆，并采用灵敏度系数较高的半导体应变片代替电阻应变片测试泡沫铝的动态力学性能[1］;又如W.Chen等利用空心铝质透射杆测量低阻抗材料的应力-应变曲线[2］.另一种是直接选用与试件波阻抗相近的非金属材料(如尼龙、有机玻璃、聚碳酸酯(简称PC)等聚合物材料)作为透射杆[3］，以有效地增大透射波信号.如谢若泽等用PC 杆对泡沫铝合金的动态力学性能进行研究[4］.目前对于土体动态力学性能的研究主要集中在较低的应变率范围[5-9］，而较高应变率下土体动态力学性能的研究只有零星的报导.如Screwvala通过弹道摆法试验，发现土对加载应变率的依赖性，其应变率介于 15 ～ 23 s－1之间[10］;Young 和Japp通过双端口高速液压测试仪研究了应变率在1～20 s－1之间时土的应力-应变关系，结果显示动态强度与应变率的常用对数成线性关系[11］.我国学者皮爱如、李小雷等利用SHPB装置研究了土体的动态力学性能，结果表明土体具有明显的应变率效应[12-13］.本文中试验土样为西南红层泥岩粉碎土，采用特制钢质模具压制而成，用PC杆SHPB装置对压实粘性土(干密度 2.02 g/cm3，含水量 12.54%，压实度100%)进行了单轴压缩动态试验，并对试验结果的有效性进行了讨论，在此基础上对压实粘性土的动态压缩力学性能进行了研究，其成果对研究武器触地侵彻过程中弹头强度和刚度、炸药的安定性等问题以及战斗部入地后的爆炸破坏效应具有重要意义.1 SHPB实验装置1.1 实验系统及原理动态试验采用直径为φ25的聚碳酸脂SHPB装置，波导杆的弹性模量为2.379 GPa，密度为1.18 t/m3，弹性波波速为 1 420 m/s，弹性极限为50 MPa.子弹长0.3 m，波导杆杆长为 1.0 m.应变片贴于距离试件0.5 m处，每处对称贴2个应变片，桥路为1/4桥，取2个应变片的平均值作为计算值.除波导杆外，系统还包括空气炮发射机构、激光片光源测速系统和软回收装置等.采用一维应力假定和均匀性假定，利用测试得到的反射脉冲εr和透射脉冲εt，采用两波法(试件两端处于应力平衡状态)，由式(1)～(3)得到试件的应变率˙εs，应变εs和应力σs与时间的关系，进而得到材料在各应变率下的应力-应变关系:式中:c为压杆的弹性波速，m/s;ls为试件的初始长度，m;E为压杆的弹性模量，Pa;A为压杆的横截面积，m2;As为试件的横截面积，m2.1.2 波形整形由于压实粘性土的波速低且具有较大的变形能力，因此，为保证试件恒应变率变形、应力均匀以及增加脉冲宽度的需要，采用了脉冲整形技术.采用的整形方法与文献[4］相同，即用手戳成的真空封泥小球丸作为整形器，其大小为不影响入射波和反射波的分离，直径一般为2～3 mm.1.3 实验装置有效性的验证为保证SHPB实验装置的有效性，必须满足试件两端应力平衡和常应变率加载.同时考虑到PC杆为粘弹性杆，按文献[14］的方法对波形进行了修正，对修正后的典型试验曲线进行了应力平衡和常应变率分析(图1).从图1可见:修正后的试验曲线基本满足应力平衡和常应变率加载条件;透射波电压信号达到最大值后，随入射波和反射波的减小同步减小，而反射波电压信号并没有反向.根据SHPB实验装置的原理可知，反射波代表应变率的变化，透射波代表作用在试件两端应力的变化，说明在应变增大的同时，由于应变率减小，导致应力减小. 图1 试件典型曲线的应力平衡和常应变率分析(撞击速度15.1 m/s)Fig.1 Typical curves of stress equilibrium and constant rate analyses at a projectile velocity of 15.1 m/s2 试验结果及分析考虑到PC杆为粘弹性杆，按文献[14］的方法对透射波进行修正，图2为修正后的应力-应变曲线.图2 压实粘性土的动态应力-应变曲线Fig.2 Dynamic stress-strain curves of compacted clay under different strain rates从图2可知，压实粘性土的应力-应变曲线表现出明显的“四阶段”特征，即弹性段、屈服平台段、致密段以及由于应变率降低引起的卸载段.应力-应变曲线从弹性段到屈服平台段时，出现峰值跳跃现象，这是由于土体颗粒从静止状态转变为运动状态，颗粒之间的摩擦由静摩擦变为动摩擦(动摩擦因子小于静摩擦因子)，同时也需要克服颗粒之间的粘聚力.从图2还可以看到，随着应变率增大，压实粘性土的动态应力和可压缩变形均大大提高，说明随应变率的增大，应力强化效应不断增强.根据文献[15］，主要原因有:(1)在冲击荷载作用下，由于材料的惯性作用，限制了试件侧向应变的发展，并且限制作用随应变率的提高而增强.这种紧箍作用使试件近似处于被动围压状态，从而使其动态应力随应变率增大而增大.(2)土体由大量颗粒组成，颗粒之间的接触面为潜在破坏面，与准静态试验不同，在SHPB试验中，滑动面没有足够的时间沿与试件最大主应力作用面成45°+φ/2的弱面扩展.试件中产生运动、破坏的颗粒数目随应变率增大而增加，相应地能量需求也随之增大.由于冲击荷载作用的时间往往极短，试件没有足够的时间用于能量分配和耗散，根据冲量定理，试件只有通过提高应力的办法来平衡外部的冲量，因而动态应力将随应变率的增大而增大.(3)由于试件本身的压密作用，导致其摩擦角和粘聚力提高.(4)由于试件的动态强度随应变率的增大而增大，因此试件抵抗变形的能力也增强.此外，试件破坏需要一定的时间积累，而应变率越高，撞击速度越大，这也是导致动态变形能力随应变率增大的原因.为研究土体的应变率效应，对屈服应力、应变为10%，20%的应力和卸载前的峰值应力随应变率的变化进行了分析，结果见图3～5和表1.动态应力与应变率的关系用式 (4)拟合，可见，拟合参数随应变率的增大呈显出减小的趋势.图3 屈服应力随应变率的变化Fig.3 The yield stress of compacted clayvs.strain rate图4 应力与应变率关系的拟合曲线Fig.4 The fitting curves of stress and strain rate图5 卸载前峰值应力随应变率的变化Fig.5 The peak stress of compacted clay vs.strain rate before unloading图6 比能量吸收随应变率的变化Fig.6 Specific energy absorption of compacted clay vs.strain rate式中:σd为动态应力，MPa;为应变率，1/s;A为拟合参数，MPa;B为拟合参数，1/s.同时，采用比能量吸收(eea)来表征试件的变形性[16］.其物理意义是单位体积试件吸收的应力波能量的大小，可表示为:式中:eea为比能量吸收，J/cm3;t0和εi(t)分别为卸载前时刻和入射脉冲应变.从图6可知，能量吸收能力具有显著的应变率相关性——随应变率的提高，比能量吸收呈指数关系增大，拟合公式见式(6)，拟合参数见表1.式中:C为拟合参数，J/cm3;D为拟合参数，1/s.表1 拟合参数Tab.1 Fitting parameters in equations(4)and(6)3 结论利用改进的聚碳酸脂SHPB装置对压实粘性土的动态力学性能进行了试验研究，结果表明:(1)用聚碳酸脂SHPB装置对压实粘性土进行动态试验是可行的.(2)压实粘性土的动态应力-应变曲线从弹性段到屈服平台段时，出现峰值跳跃现象，这是由于土体的颗粒从静止状态转为运动状态，颗粒之间的摩擦由静摩擦变为动摩擦(动摩擦因子小于静摩擦因子)，同时也需要克服颗粒之间的粘聚力.(3)压实粘性土的动态应力与应变均表现出显著的应变率效应，动态应力随应变率增大呈指数关系增大，拟合参数随应变率增大呈现出减小的趋势.(4)压实粘性土的能量吸收能力具有显著的应变率相关性，随应变率增大而呈指数关系增大.传统的理论分析认为应力减小主要是由于:(1)应变减小导致卸载;(2)应变持续增大，使应力超过材料的强度，从而导致材料发生软化.而对应变率减小(并没有反向，意味着应变是持续增大的)而导致的应力卸载却未见相关报导，因此，与此相关的理论有待进一步完善.参考文献:【相关文献】[1]胡时胜，王悟，潘艺，等.泡沫材料的应变率效应[J］.爆炸与冲击，2003，23(1):13-18.HU Shisheng，WANG Wu，PAN Yi，et al.Strain rate effect on the properties of foam materials[J］.Explosion and Shock Waves，2003，23(1):13-18.[2]CHEN W， ZHANG B， FORRESTALMJ. Split Hopkinson bar techniques for low impedance materials[J］.Experimental Mechanics，1999，39(1):81-85.[3]ZHAO H，GRAY G，KLEPACZKO J R.On the use of a visco-elastic splitHopkinson pressure bar[J］.International JournalofImpactEngineering，1997，19(4):319-330. [4]谢若泽，卢子兴，陈成军，等.聚碳酸脂SHPB系统测量泡沫铝合金动态压缩性能力[J］.航空学报，2009，30(8):1435-1439.XIE Ruoze， LU Zixing， CHEN Chengjun， etal.Measurementofdynamic compressive behaviorof aluminum-alloy foams by polycarbonate SHPB system[J］.Acta Aeronautica et Astronautica Sinica，2009，30(8):1435-1439.[5]OLSON R E，KANE H.Dynamic Shearing properties of compacted clay at high pressure[C］∥ Proceedings of the Sixth International Conference on Soi l Mechanics and Foundation Engineering.Montreal:University of Toronto Press，1965:328-332.[6]OLSON R E， PAROLA JF. Dynamicshearing properties of compacted clay[C］∥Proceedings of the InternationalSymposium on WavePropagation and Dynamic Properties of Earth Minerals.Albuquerque，NM:University of New Mexico Press，1967:173-182.[7]KOVACS W D，SEED H B，CHAN C K.Dynamic moduli and damping ratios for a soft clay[J］.Journal of the Soil Mechanics and Foundations Division，1971，97(1):59-75. [8]RICHARDSON A M，WHITMAN R V.Effect of a strain rate upon undrained shearresistance ofa saturated remolded fat clay[J］.Geotechnique，1963，13:310-324.[9]KONDNER R L.KRIZEK R J.Dynamic response of cohesive soils for earthquake considerations[C］∥Proceedings of the Third World Conference on Earthquake Engineering.New Zealand: National Committee on Earthquake Engineering Press，1965:96-104.[10]SCREWVALA F N，KHERA R P.Ballistic pendulums and dynamic testing of clays[J］.Journal of the Geotechnical Engineering Division，1979，105(8):927-938.[11]YOUNG R N，JAPP R D.A flow law for clays in dynamic compression[C］∥Proceedings of the International Symposium on Wave Propagation and Dynamic Properties of Earth Materials. Albuquerque， NM:University of New Mexico Press，1967:183-188.[12]皮爱如，沈兆武，王肖钧.土壤冲击特性的实验研究[J］.振动与冲击，2003，22(3):28-31.PI Airu，SHEN Zhaowu，WANG Xiaojun.Experimental study of impact characteristic ofsoil[J］.Journal of Vibration and Shock，2003，22(3):28-31.[13]李小雷，张振宇，卢芳云.土的动态性能实验研究[J］.实验技术与实验机，2006(2):22-25.LI Xiaolei，ZHANG Zhenyu，LU Fangyun.Study on the dynamic characteristic of asoil[J］.Test Technology and Machine，2006(2):22-25.[14]刘孝敏，胡时胜，陈智.粘弹性Hopkisnon压杆中波的衰减和弥散[J］.固体力学学报，2002，23(1):81-86.LIU Xiaomin，HU Shisheng，CHEN Zhi.The wave propagation attenuation and dispersion in a viscoelastic Hopkinson pressure bar[J］.Acta Mechanic Solida Sinica，2002，23(1):81-86.[15]刘军忠，许金余，吕晓聪，等.冲击压缩荷载下角闪岩的动态力学性能实验研究[J］.岩石力学与工程学报，2009，28(10):2113-2120.LIU Junzhong， XU Jinyu， LU Xiaocong， etal.Experimental study on dynamic mechanical properties of amphibolites under impact compressive loading[J］.Chinese Journal of Rock Mechanics and Engineering，2009，28(10):2113-2120.[16]余同希，卢国兴.材料与结构的能量吸收:耐撞性、包装、安全防护[M］.北京:化学工业出版社，2006:209-212.。
SHPB实验及其在钛合金材料中的研究
SHPB实验及其在钛合金材料中的研究摘要:钛合金材料在航空航天等工程领域中得到了广泛应用，对其动态冲击力学性能的研究需借助分离式霍普金森压杆(SHPB) 实验完成。
研究了影响SHPB 实验结果的因素。
通过对钛合金材料冲击动态力学性能进行研究发现:钛合金材料的流动应力和屈服强度往往会随着应变率的升高而升高，随温度的升高而降低。
关键词: 钛合金；SHPB；动态力学性能0 引言分离式霍普金森压杆(SHPB)装置是研究金属材料在102～104s-1应变率范围内动态力学特性的主要实验手段。
通过测试两个杆中的应力脉冲信号，可以得到杆件与试件端面的应力、位移和时间关系，进而求解试样的应力－应变关系。
利用长弹性杆中应力波的传播来测量动态过程的压力脉冲，研究了应力波在长杆中的传播特征。
钛合金材料因密度低、强度高和抗腐蚀性等优点，在航空航天、船舶及化学工业中被广泛应用。
钛合金可用于制造飞机的任何部分：机身、引擎机舱、飞机起落架、机翼和尾翼等，它已成为现代飞机不可缺少的结构材料。
众所周知，安全性能一直是航空飞行器的首要任务。
大鸟撞击导致飞机损坏严重威胁着航空安全，据民航局数据统计，全世界每年大约发生1万次鸟撞飞机事件，而在撞机过程中，钛合金作为结构材料经常会承受高速冲击载荷：这就对钛的强度、使用寿命和可靠性提出了更高的要求，需要其在规定的冲击载荷下保证结构的完整性和连续性，具有良好的动态承载能力。
由于实际工作环境的复杂性，钛合金必然会承受动态冲击载荷，动态冲击载荷所引起的高应变率和高温等因素使得材料的力学性能较静态载荷时有显著的不同，因此对钛合金材料的动态力学性能的研究受到越来越多的关注。
本文通过对 SHPB 实验装置及其原理的研究，分析影响SHPB实验结果的因素，并在该实验系统上对钛合金材料动态力学性能研究中的应用进行研究，以便为进一步提升SHPB实验装置的测试精度和工程应用提供重要参考。
1.SHPB实验装置组成及其影响实验结果因素分析1.1 SHPB 实验装置组成及原理SHPB实验装置是基于一维假定和应力均匀假定基本假设而成立的:（1）在导杆的横向尺寸与应力波的波长相比很小时，应力波在细长杆中传播，弹性杆的每个截面始终保持为平面状态，任意一个应力波在杆中的传播速度为定值，仅与材料有关; （2）应力波在试件中反复2～3个来回，试件中的应力处处相等。
脆性材料shpb实验技术的研究
脆性材料shpb实验技术的研究
脆性材料SHPB实验技术的研究
脆性材料是指在一定载荷范围内，物理性能变化较大的材料，是衡量材料力学特性的重要参数。
SHPB实验技术是一种新型实验技术，用于研究脆性材料的力学特性，它可以模拟脆性材料在短时间内的变形和断裂行为。
SHPB实验技术的原理是将材料的内部应力分布在一定的载荷范围内，以衡量材料在一定载荷下的弹性和破坏性能。
在实验中，材料被放置在一个均匀的横截面板上，然后将这个材料放在一个专用的高速冲击装置中，前后运动使材料受到一个时间和位移梯度的脉冲载荷。
SHPB实验技术的研究可以帮助我们更好的了解脆性材料的力学特性，从而有助于精确的设计和消能材料的应用。
它有助于我们了解材料在拉伸、压缩、翻转和切削等强度条件下的行为特性，从而使我们更好地利用这些材料。
此外，SHPB实验技术还可以用于研究脆性材料中复杂破坏过程中的拉伸、压缩、断裂和持久化等行为，从而更好地利用脆性材料在不同场合中的应用，比如汽车制造业，航空航天等。
总之，SHPB实验技术是一种新型实验技术，可以有效模拟脆性材料力学性能，为我们设计和应用脆性材料提供有价值的理论参考。
霍普金森杆试验报告
霍普金森压杆(SHPB)试验报告一、SHPB试验目的及用途1、了解霍普金森压杆(SHPB)测试的试验原理，掌握试验的基本操作步骤；2、霍普金森压杆(SHPB)测试技术主要用来测试材料在高应变率下的力学性能。
此试验主要通过霍普金森压杆(SHPB)测试技术，来测试泡沫铝(37mm×21mm)的力学性能，获取应力-应变曲线。
二、SHPB试验装置及其示意图1—发射气枪2—撞击杆3—激光发射器4—激光接收器5—电阻应变片6—入射杆7—试件8—透射杆9—吸收杆10—缓冲装置11—超动态应变仪12—波形存贮器13—数据处理系统三、试验原理1、三种波形的获取过程通过发射气枪作用，赋予撞击杆一定的初速度，此初速度可以由激光发射器和接收器测出间隔时间，然后计算得出。
撞击杆以此速度撞击入射杆，输入入射波脉冲，随着入射波的传播，在试件表面产生反射和穿透。
入射、反射、透射脉冲均可以通过电阻应变片测出，进而通过超动态应变仪传递到波形存贮器进行保存三种波形，从而利用入射、反射和透射脉冲来推导出试件中的应力、应变和应变率。
2、应力应变曲线获取的原理利用这些脉冲信号来获得材料在高应变率下的应力-应变曲线原理如下：图SHPB系统加载示意图上图是SHPB系统加载过程的示意图，Iε、Rε、Tε分别表示的是应变片测量到的入射、反射和透射信号。
1、2分别是试件的两个端面，S A是试件的横截面积，L是试件的长度，A和E分别是压杆的横截面积和弹性模量。
根据一维应力波理论，试件的两个端面的位移1u和2u可分别表示为1010t u C dt ε=⎰ (1) 2020tu C dt ε=⎰ (2)式中，1ε、2ε分别是试件两个端面的应变，0C 是压杆的弹性波速。
由于入射波到达杆与试样接触端是立刻会有反射波产生，因此入射杆与试件接触面上的应变1ε既包括了向右传播的应变脉冲I ε，又包括向左传播的反射应变脉冲R ε，即：1I R εεε=+ (3)因此界面1上的位移1u 就可以表示为：100()t I R u C dt εε=-⎰ (4)而界面2处的位移2u 只与透射脉冲T ε有关，故有：200t T u C dt ε=⎰ （5）这里的应变均是压应变。
钙质砂的SHPB实验技术及其动态力学性能
钙质砂的SHPB实验技术及其动态力学性能吕亚茹;王明洋;魏久淇;廖斌【摘要】开展了11组南海钙质砂和福建石英砂的分离式霍普金森压杆(SHPB)实验,试样相对密实度为90％,厚度分别为10、30和50 mm,得到了冲击荷载下钙质砂和石英砂的应变率时程曲线、应变时程曲线和应力应变关系.实验结果表明:通过严格装样技术可以减小实验设备产生的误差,改变试样厚度、子弹长度、整形器等是实现钙质砂应力平衡和恒应变率的主要手段.在相同的密实度和加载条件下,钙质砂的体积模量和剪切模量约为石英砂的10％,压缩强度和抗剪强度约为石英砂的30％.冲击荷载作用下钙质砂的动态力学性能与石英砂存在较大的差异,因此不能将已有石英砂的研究结果直接用于钙质砂.【期刊名称】《爆炸与冲击》【年(卷),期】2018(038)006【总页数】9页(P1262-1270)【关键词】钙质砂;霍普金森压杆;冲击特性;应力应变曲线【作者】吕亚茹;王明洋;魏久淇;廖斌【作者单位】河海大学力学与材料学院,江苏南京210098;香港科技大学土木与环境学系,香港999077;陆军工程大学爆炸冲击防灾减灾国家重点实验室,江苏南京210007;陆军工程大学爆炸冲击防灾减灾国家重点实验室,江苏南京210007;陆军工程大学爆炸冲击防灾减灾国家重点实验室,江苏南京210007;陆军工程大学爆炸冲击防灾减灾国家重点实验室,江苏南京210007【正文语种】中文【中图分类】O347.4霍普金森压杆(split Hopkinson pressure bar, SHPB)实验是研究中高应变率下材料力学性能最主要、可靠的实验方法之一，是冲击动力学实验技术的重要组成部分，利用霍普金森杆不仅可以实现高应变率(102～104 s-1)单轴压缩、剪切加载，还可实现动态压-剪复合加载，主、被动围压复杂加载，以及100～101 s-1中应变率加载[1]。
早在1967年，E.Fletcher等[2]首次通过SHPB研究了土的动态特性，由于土体为散体材料，实验时需要通过套筒和垫块将土样固定，土样夹在垫块之间如同“三明治”，通过粘贴在入射杆和透射杆上的高灵敏度应变片采集试样的应力、应变时程曲线[3]。
材料动态冲击实验技术(09-11-10)
撞击杆的长度可变，并且可以将撞击杆设计成不同的规格形状，如：
柱形、台锥形和台阶形等，以实现不同的加载应力波形。 输入杆与撞击杆相同材料，相同直径，以使得撞击应力波无反射地传
入输入杆。同时，由于撞击杆自由面的反射，输入杆中应力波的持续长
度是撞击杆长度的两倍。
3．测试分析仪表
1) 速度测量 SPHB技术要求准确测定撞击杆撞击输入杆时的末速度。当 撞击杆撞击输入杆时，将会依次遮挡第一、第二激光束，通 过光电放大转换电路可以得到撞击杆通过两激光束的时间差， 由于两激光束的距离L已知，因而即可求得撞击杆的末速度
实验技术
实验技术
1)试验分类
蠕变试验：应变率范围 10 ~ 10 / s ； 5 1 准静态试验：应变率范围 10 ~ 10 / s ；
8 5
试验装置-----材料试验机
Instron拉压试验机、Instron液压伺服材料试验机； MTS伺服式疲劳试验机、MTS电液伺服试验系统； 附加刚性框架辅助吸能装置
实验结果
100
A 100
应力 (MPa)
B
80
80
60
60
40
O
20
40
20
应变
0 0.000 0.005 0.010 0.015 0.020 0.025 0.030
0 0.000
0.002
0.004
0.006
0.008
0.010
0.012
混凝土和加筋混凝土实验测量应力应变曲线
材料动态冲击实验技术--SHPB
V
2) 应变测量 应变测量由粘贴在输入、输出杆上的应变片、超动态应变仪 和信号记录、存储、显示仪器组成的系统完成，可采用所示 的瞬态应变测试系统。 对应变片，要求应变片的基长应满足
SHPB与混凝土材料动态力学性能研究
181
第三届全国爆炸力学实验技术学术会议论文集
应力—应变曲线 。 H.Zhao 在同一篇文章中还提出了利用反向计算（inverse calculation）的方法进行数据处 理，即利用实测到的一部分波形（入射波）加上假设的试件材料虚拟的本构关系，通过二维 数值模拟求得另一部分波形（透射波和反射波） ，并和实测到的这些波形比较，根据两者的 差异修正假设的本构关系，再重复上述过程，直至模拟结果与实测的一致，而最终假设的本 构关系则为我们所需的试件材料的本构关系。 然而， 这种反向计算方法不仅迭代过程十分繁 杂，而且对实验操作技能要求高，很难推行。 1.4.4 直锥变截面式φ74 SHPB 装置
1.2 多孔介质
泡沫塑料（橡胶） 、泡沫金属等多孔介质大多具有很好的吸能特性，因此可广泛应用于 缓冲、 减振以及防爆震等方面， 而所有这些应用都需要通过 SHPB 实验来研究这些多孔介质 的动态力学性能，了解应变率、密度（孔隙率）等对其应力—应变关系的影响。然而在利用 SHPB 装置测定这些多孔介质的应力—应变关系时会遇到一些具体问题。第一，多孔介质的 泡孔尺寸， 尤其是一些低密度 （高孔隙率） 的材料， 其泡孔尺寸相对于 SHPB 装置的杆径 （通 常较细）已是一个不可忽略的量。为了确保实验数据的可靠性，要求所使用的 SHPB 装置的 杆径要大一些，应比泡孔尺寸大一个量级以上。第二，多孔介质中的弹性波速很低，比压杆 中的弹性波速小一、二个量级，例如泡沫硅橡胶的弹性波波速只有几十米/秒，波在这些试 件内来回一次的时间较长，于是试件内部的应力不均匀性变得十分突出，需要认真考虑。周
180
第三届全国爆炸力学实验技术学术会议论文集
撞击杆 v
输入杆
输入杆应变计 试件应变计
输出杆应变计 输出杆
材料动态力学冲击实验技术-shpb。高温下SHPB相关实验技术。
二、基本理论
霍普金森压杆(SHPB)测试中两种数据处理方法。
6
三、高温实验方法及应该注意到的问题
高温SHPB研究的发展
7
三、高温实验方法及应该注意到的问题
利用SHB测量材料高温下的动态力学性能主要面临两方面的问题：
实验装置设计上的困难 实验数据处理上也有一定的难度
消除温度影响的方法主要分为两类：
利用特殊设计的实验装置，降低进而忽略温度梯度的影响 处理实验数据时设法消除温度梯度场的影响
8
三、高温实验方法及应该注意到的问题
目前高温SHPB装置的实验方案之一：局部导杆和试件共同加热
9
三、高温实验方法及应该注意到的问题
目前高温SHPB装置的实验方案之二：高温动态实验技术则通过单独 对试件加热，待试件加热完成后，再利用机械装置将导杆与试件快 速组装
实现的实验的两种做法
10
三、高温实验方法及应该注意到的问题
目前高温SHPB装置的实验方案之三：采用温度不敏感材料来避开温 度梯度影响的实验方法。
例如：在压杆和试件之间添加耐高温、高强度的铝陶瓷短杆，实验时将其和试样 同时加热，既可保证试件温度场恒定，同时又可避开压杆温度场对应力波传播的 影响。
11
材料与结构的冲击行为
高温下SHPB相关实验技术
材料动态力学冲击实验技术 -shpb
我是个魔鬼 2019年11月26日
目录 一、背景与任务 二、基本理论 三、冲击加载条件下动态力学行为的研究是许多涉及冲 击加载问题的工程设计的基础
3
二、基本理论
三、高温实验方法及应该注意到的问题
目前高温SHPB装置的实验方案之三：采用温度不敏感材料来避开温 度梯度影响的实验方法。
混凝土材料的SHPB实验技术研究
混凝土材料的SHPB实验技术研究张柱;晋艳娟【摘要】In order to improve the precision and comparability of SHPB testing results of concrete materials,some studies on the SHPB technique for concrete are carried out by combining with the experimental process of concrete in this paper,which include the dispersion effect of waveguide bars,the analysis of stress and strain uniformities in specimen and the radial inertial effect of specimen.The results show that experiments meet the requirements of one-dimensional stress wave assumption andstress/strain uniformity assumption.Whether there is enough time to achieve stress and strain uniformities or not depends on the maximum strain and strain rate of concrete specimen.Pulse shaping technique and constant strain rate test technique are used in the experiments,and the experiment data is processed by using the formula of three waves,which can increase the effective loading time of concrete and reduce the inertia effect of specimen on experiment results.When the strain rate is close to or more than 104,it is necessary to consider the radial inertia effect of specimen.%为提高混凝土材料的SHPB实验结果的精度和可比性,结合混凝土的实验过程,对波导杆的弥散效应、试件内应力应变均匀性和试件的径向惯性效应进行了研究。
SHPB
在0～30s-1之间，在第一个极值出现之前，随着冲击
速度或者应变率的增加，由动态应力—应变曲线可以 看出，曲线越接近直线，但是，曲线之间的偏离比较 明显，重叠性不好，从曲线中也看不出完全意义上的 直线，表现出其具有明显的应变率效应，若用割线法
计算弹性模量，可以看出，随着应变率的不断增加，
弹性模量会有显著的增加。阶段是明显的不同的。
各领域的重视，研究这类材料在各种冲击载荷下的力 学行为已经成为有关设计部门日益关注的问题。 武器工程设计与分析中，大量涉及材料的动态力 学性能方面的研究课题，如武器服役的安全性及抗事
故能力、爆炸驱动下材料的高速变形与破坏等等。
Company Logo
二、霍普金森压杆实验技术
分离式霍普金森压杆（简称SHPB）实验技术发 明至今已有60多年的历史，已成为测量材料动态力学 性能的主要手段之一。 国内有关科研单位为了不同的研究目的，相继建 立起尺寸不同的SHPB装置，我校土木建筑学院冲击 动力学研究室的SHPB装置于2009年开始工作。
SHPB实验技术及其工程应用
力学系 刘文震
LOGO
一、前言
我国的煤炭资源是相当丰富的，储量和产量都位 于世界的前列。
煤炭资源是我国的主要能源，预计即使到 2050 年，煤炭在能源构成中所占比重仍为50%以上。
受诸多因素影响，长期以来，块煤率较低、煤尘 较高的现状改变缓慢。
提高块煤率、通过试验确定相关参数，这些都具 有重要的理论和科研意义。
Company Logo
二波法公式：
Company Logo
三、煤的动态冲击试验
我们选用直径为50mm的锥形变截面钢杆进行 煤的动态力学性能试验。
1、试件加工制作
在试件尺寸的设计方面，为了消除横向惯性运动
煤矿砂岩SHPB动态压缩力学性能试验与分析
安徽 理工 大学 学报 （ 自然 科学 版 ）
Ｊ ｏ ｕ ｒ ｎ ａ ｌ ｏ ｆ Ａ ｎ ｈ ｕ ｉ Ｕ ｎ ｉ ｖ ｅ ｒ ｓ ｉ ｔ ｙ ｏ ｆ Ｓ ｃ ｉ ｅ ｎ ｃ ｅ ａ ｎ ｄ Ｔ ｅ ｃ ｈ ｎ ｏ ｌ ｏ ｇ ｙ （ Ｎ ａ ｔ ｕ ｒ ａ ｌ Ｓ ｃ ｉ ｅ ｎ ｃ ｅ ）
ｉ ｎ ａ ｎ Ａｎ ｈ ｕ ｉ ２ ３ ２ ０ ０１，Ｃ ｈ ｉ ｎ ａ ；２ ．Ｔ ｈ ｅ Ｋｅ ｙ Ｌａ ｂ ｏ ｒ ａ ｔ ｏ ｒ ｙ ｏ ｆ Ｃ ｏ ｌ ａ Ｍｉ ｎ ｅ Ｓ ａ ｆ ｅ ｔ ｙ ａ ｎ ｄ Ｅ ｆ ｉ ｆ ｃ ｉ ｅ ｎ ｔ Ｅ ｘ ｐ ｌ ｏ ｉ ｔ ａ ｔ ｉ ｏ ｎ ｏ ｆ Ｍｉ ｎ ｉ ｓ ｔ ｒ ｙ ｏ ｆ Ｅｄ ｕ ｃ ａ ｔ ｉ ｏ ｎ；Ａｎ ｈ ｕ ｉ
淮南
２ ３ ２ ０ ０ １ ； ２ ． 安徽 理工大学 煤矿安全 高效开 采省部共 建
摘
要： 为研 究煤矿砂 岩 冲 击载荷 作 用下的 动 态力 学特性 ， 利 用分 离式 Ｈ ｏ ｐ ｋ ｉ ｎ ｓ ｏ ｎ压杆 对 皖 北
矿 区祁 东煤矿 的砂 岩试 件进行 冲击压 缩试验 ， 得 到 了试 件 应 变率 变化 时程 曲 线和 动 态应 力 一
Ｑ ｉ ｄ ｏ ｎ ｇ ｍｉ ｎ ｅ ｉ ｎ Ｗａ ｎ ｂ ｅ ｉ Ｍｉ ｎ ｉ ｎ ｇ Ａ ｒ ｅ ａ ．Ｓ ｔ ｒ ａ ｉ ｎ ｒ ａ ｔ ｅ ｈ ｉ ｓ ｔ ｏ ｒ ｙ ｃ ｕ ｒ ｖ ｅ ａ ｎ ｄ ｄ ｙ ｎ ａ ｍｉ ｃ ｓ ｔ ｒ ｅ ｓ ｓ —ｓ ｔ ｒ ａ ｉ ｎ ｃ ｕ ｒ ｖ ｅ ａ ｒ ｅ ｏ ｂ ｔ ａ ｉ ｎ ｅ ｄ ．
Ｖｏ １ ． ３ ３ Ｎｏ ． ４
软材料动态拉伸试验
软材料动态拉伸试验摘要：因为实验困难，测定软材料动态力学响应一直是项挑战。
分体式霍普金森拉杆（shtb ）是一种常用的表征高强度工程材料的设备。
不过，当这个标本是软的，设计必要的夹头来保证测量微弱信号传输和标本达到动态平衡是具有挑战性的。
在这项工作中，我们修改了shtb 的加载脉冲、力平衡检测系统和试样几何形状。
使用这个修改后的设备所取得的成果描述一个软橡胶表明，试样动态应力平衡条件下的变形近恒应变速率。
软的动态特性材料的轴向和径向惯性效应经常会面临降到最低。
关键词：分离式霍普金森拉杆 冲击试验 动态平衡 惯性的影响 软质材料介绍非生物、机械阻抗低的软质材料已被广泛用作冲击吸收部件，其机械性能，特别是冲击载荷条件下的机械性能，在有效地利用这些之前需要了解材料在汽车、航空航天、交通运输和便携式电子产品中应用。
此外，生物组织被列为一类软质材料，因为其具有机械阻抗低的优点。
软材料的机械性能，如橡胶和生物组织材料应变率通常是非常敏感的[1，2]。
动态响应和高速率下加载材料的破坏行为，如发生碰撞和碰撞射入，跟静态载荷下不同。
因此，有必要确定动态等效软质材料，在高速率响应下的行为，优化发展可靠率相关材料模型设计工程元件或人类对高速率的负荷保护系统。
软质材料的动态压缩性能得到了广泛的调查与最近开发可靠的技术实验[1-3]。
高速率拉伸行为是这些软质材料的动态响应另一个方面的重要认识。
然而，准确地确定所需的动态拉伸实验的挑战进展有限。
霍普金森压杆（SHPB 实验），最初由Kolsky 开发[4]，已被广泛用于研究率依赖压缩流动行为韧性的金属，通常的应变率范围210到4101-S [4]。
这种方法一直延伸到用于各个版本的霍普金森拉杆（SHTB ）动态拉伸特性[5-7]。
SHTB 技术常见的工程材料开发，如金属[8，9]、聚合物[10，11]、和复合材料[12，13]中。
在一个理想的分离式霍普金森杆实验中，一个几乎恒定的应变率下的试样变形动态平衡单轴应力状态[14]。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
机械工程学院研究生研究型课程考试答卷课程名称：材料动态特性实验（SHPB实验）考试形式：□专题研究报告□论文√大作业□综合考试评阅人：时间：年月日材料动态特性实验实验目的：1、了解霍普金森杆的实验原理和实验步骤；2、会用霍普金森杆测试材料动态力学性能。
1.SHPB 组成：Kolsky 在Hopkinson 压杆技术的基础上提出采用分离式 Hop-kinson 压杆 SHPB )技术来测定材料在一定应变率范围的动态应力 ── 应变行为 ,该实验的理论基础是一维应力波理论, 它通过测定压杆上的应变来推导试样材料的应力 ── 应变关系, 是研究材料动态力学性能最基本的实验方法之一。
为了测出A3钢（又称Q235钢）的屈服极限、弹性模量以及其他性能参数。
用SHPB 实验就行数据测量。
SHPB 的实现装置如下图：分离式Hopkinson 压杆装置示意图它由压缩气枪、撞击杆、测时仪、输入杆（入射杆）、超动态应变仪、试件、透射杆、吸收杆、阻尼器和数据处理系统组成。
2.实验原理：SHPB 技术建立在两个基本假定的前提上：（1）杆中应力波是一维波；（2）试件应力/应变沿其长度均匀分布。
根据垂直入射应力波在界面出的反射、透射原理和上述假定由：应力相等：)()()(t t t T R I σσσ=+ (1)应变相等：)()()(t t t T R I εεε=+ (2)式中()I t σ和()R t σ分别为入射杆的入射应力和反射应力，()T t σ为透射杆的透射应力，()I t ε和()R t ε为入射杆的入射应变和反射应变，()Tt ε为透射杆的透射应变。
图1 输入杆-试件-输出杆相对位置如图2所示，在满足一维应力波假定的条件下，一旦测得试件与输入杆的界面X 1处的应力，可理论推导得： []112()(,)(,)(,)2S I R T SA t X t X t X t A σσσσ=++ （3） SR I T S S L t X v t X v t X v L t X v t X v t ),(),(),(),(),()(11212--=-=ε （4） []⎰⎰--==t R I T S t S S dt t X v t X v t X v L dt t 01120),(),(),(1)(εε （5）式中：A 为压杆的横截面积，s A 为试件的横截面积，S L 为试件的长度。
()S t σ、()S t ε和()S t ε为试件的平均应力、应变和应变率，1(,)I v X t 、1(,)R v X t 分别为入射应力波在界面X 1处的入射质点速度和反射质点速度，2(,)T v X t 为透射应力波在2X 处的透射质点速度。
在弹性压杆的情况下，由一维应力波分析可知，应变与应力和质点速度之间存在如下线性关系：()()()[]()()()()()[]()()⎪⎪⎩⎪⎪⎨⎧===-=+=====+=+==),(,,),(),(,,,),(,,),(),(,,,2022211011112222111111t X C t X v t X v v t X t X C t X v t X v t X v v t X E t X t X t X t X E t X t X t X T T R I R I T T R I R I εεεεσσσεεσσσσ （6） 可见，上述问题就转化为如何测界面X 1处的入射应变波),(1t X I ε和反射应变波),(1t X R ε，以及界面2X 处的透射应力波),(2t X T ε。
因为，只要压杆保持弹性状态，不同位置上的波形均相同。
这样，最后由应变片1G 和2G 所测信号就可以确定材料的动态应力()S t σ和动态应变()S t ε。
[]),(),(),()(211t X A EA t X t X A EA t G T SG R G I S S εεεσ=+= （7） []⎰⎰-=-=t G T G I S t G R S S dt t X t X L C dt t X L C t 0210010),(),(2),(2)(εεεε （8）于是，在入射应变波),(1t X G I ε、反射应变波),(1t X G R ε和透射应变波),(2t X G T ε中，实际上测量两个就足以测量材料的动态应力()S t σ和动态应变()S t ε。
在消去时间参量t 后，就可以获得材料的动态应力-应变曲线。
（8）式对时间求导可以求出应变率：),(2)(10t X L C t G R SS εε-= （9） 故可以由（7）（8）（9）三式可以得到试件的应力-应变，应变率-时间的曲线图，由图中得到试件的屈服极限以及弹性模量等其他参数。
3.实验步骤：（1）搭建该实验装置，检查压气舱的气压是否达到实验要求，0.2个大气压左右。
调试动态应变仪，波形存储器是否处于良好的工作状态。
电压调到5V 。
记录压杆（入射杆和透射杆）的材料、直径和杆件长度（要求两杆件的参数相同）。
（2）对试件A3钢进行清洁，测量尺寸(直径、厚度)并记录。
试验前对试件应变片进行静标。
试件左右端面涂抹凡士林(应检查试件的表面粗糙情况)，与输入、输出杆(万向头)端面磨合，并夹紧对直。
用布条缠绕包好以减小外部干扰；（2）打开气压阀，按照选定的气体压力进行发射子弹（或撞击杆）；（3）利用平行光源进行测速，并记录下显示屏上的时间，以便计算发射子弹的速度。
（4）当撞击杆撞击到入射杆，输入应力波，可以通过贴在上面的应变片测量入射应立波，同时应力波传播到试件上面进行反射和透射，在透射杆上测量透射应力，在入射杆上的应变片测反射应力，应变片的数据通过超动态应变仪进入到波形存储，最后进入到数据处理系统，进过转换得到最终测量的材料动态本构方程。
（5）检查试件破损情况并记录撞击后A3钢试件的直径和厚度。
收拾实验装置，将相关部件归位。
4.数据处理：(1)数据前期处理：打开波形记录仪记录的入射波和透射波的相关数据，将excel内的ch1和ch3通道的数据粘贴复制到Origin8的表格中，然后分别对两列数据取反：即右击鼠标，在下拉菜单中选择set column value，弹出对话框，在空白处输入-col（a）点击ok键后将其取反.如图二所示：图2然后点击File，在下拉菜单中选择export，将数据输出保存，以同样的方式将Ch3通道的数据也取反，并输出保存。
之后以记事本的格式将两组数据打开复制到excel将数据与起初的时间相对应，然后全部复制，保存在记事本中，形成一个三列的矩阵。
如图3;图3（2）数据处理：编写MATLAB程序，将此矩阵a数据复制到程序中，如下图4所示：图4需要指出的是矩阵a数据没有全部采用,只是采用了中间数据段的1470行，这是因为前期的2019行的数据是还没有计时时采集的数据，亦即外界的杂波由记录仪形成的数据，需要剔除，之后的数据是波在A3钢内形成的弹塑性波进过反射和透射后两个应变片记录的数据，而在后期结果并非是单纯试件在弹塑性阶段形成的波，而是进过多次的反射和折射后叠加而形成的波形数据，故也要剔除。
然后运行图标后出现三个图如下：图5该图中包含两个图，上图是数据记录仪中未经过处理的入射和透射波随时间变化的波形，下图为经过滤波后的入射和透射波随时间变化的波形，从图中可以入射波和透射波波形是对称的，这表明没有反射波的出现。
图六该图是应力-应变曲线图，从图形可以看出，该曲线图比较符合实际A3钢的应力应变曲线图。
只是在强化结果出现的较为大幅度的波动，这可能是有一定的干扰存在。
另外可以看出在应变为40（这里的横轴不是真正的应变，而是经过放大后的应变）时为屈服极限（这里取下屈服极限为屈服极限）。
具体的数据可由MATLAB中workspace内进行查找。
图7该图是应变率波形图，该图和应力应变图很相似。
（3）相关参数的求解：屈服极限：在应力应变曲线图六中，屈服极限应是应力上升在下降后的最低点，在workspace中双击trueos《1477*1double》查找符合该特性的数据如图8图8可以看出最低点为4.2125e+04单位为MPA，这里的应力是经过放大200倍后的值，所以用该值除以200，最终得到屈服强度：210.626mpa。
弹性模量：按照弹性模量的定义：σ=Eε。
这里只限制在弹性阶段阶段，所以弹性模量也为图六比例阶段的斜率，为了求解出这个斜率，可以截取比例阶段部分的应力应变值进行一次线性拟合。
如图9：图:9画出来的线性曲线图：图10图形只能大致符合线性规律得到的斜率k=0.8513*e4,但是这里的应变是放大了200倍后取得是千分单位，故真正的弹性模量为E=k*200*1000,最终弹性模量的值为163.06Gpa屈服应变:屈服应变应是在外界力卸载后应力恢复为零时试件的应变值。
在卸载过程中，应力和应变是按照直线规律变化的。
这里相当于将比例极限段的往右平移且过屈服极限点，直线交横轴的左边就是塑性应变，可以直接进行数值求解过屈服极限点的直线，斜率k=0.8513*e4,过点（40，4.2125e04），得到直线方程为：y-4.2125*e04=0.8513*e4(x-40)整理后为：y=0.8513x*e4-2.984e5令y=0得到x=35.05,从而得到塑性应变值为3.505%。
5.实验总结：在该实验中充分应用了弹塑性波的原理，通过分析数据求出了A3钢的相关参数，通过网上查阅资料可知A3钢（也称Q235）的屈服极限为235Mpa,处理的结果为210.626mpa，误差为（235-210.626）/235=10.37%,误差较小，弹性模量值在2.058*e11,实验测得的数据为1.63*e11,误差率为（2.05-1.63）/2.05=20.49%误差率较大，存在这样的原因主要有：①数组a数据的取舍过于粗糙，没有进一步的论证，只是确定在适当的范围后进行粗糙的估计，这方面可以进一步改进。
②波形图的数据本身在记录是就有外界干扰波的存在，这是难以避免的。
③在拟合线性方程时，为了图方便只是截取了非常少量的应力应变数据来求解弹性模量，这与严谨的数据求解拟合的方式是相悖的。
存在较大的误差也是必然的（从图10）能够明显的看出来。
这里可以进一步分析后较为精确的取值来缩小误差。