附表4 F值表
食品试验设计与统计分析常用公式及步骤

17
教材P120 例5-2 处理内重复数相等的单向分组资料的方差分析 (K个处理n个等观察值)
变异来源
处理间 误差
SS t
SS
DF
C
S2
F
F0.05
2
F0.01
Tt 2
n
DFt k 1 S t2
2 Se
SSe SST SSt DFe k (n 1)
▲方法步骤: 教材P77例4-2例4-3
(1)提出假设: H o: o
H A: o
(2)确定显著水平,查附表3 得:当 n 1 时,t 0.05 和 t 0.01值 (3)测验计算:
x x n
s
2 ( x ) x2 n n 1
sx
s n
x t sx
x1 x 2 x3 x n 平均数 x n
x
n
平方和SS
( x
x)
2
方差S 2
( x x)2 n 1
Hale Waihona Puke x2 (n 1
x) 2 n
标准差S
S2
几何平均数G n x1 x2 x3 xn
变异系数CV s 100% x
●单个平均数U测验:
(2)确定显著水平,查附u表,得u临界值
x1 ˆ1 p (3)测验计算: n1
S pˆ pˆ
1
2
(4)推断:
u u0.05 u u0.05 u u o . o1
x1 x2 p n1 n2 ˆ1 p ˆ2 p 1 1 p(1 p)( ) u Sp n1 n2 ˆ p ˆ
概率论-分布及其分位数

U—分布 正态总体样本均值的分布
设总体 X ~ N , 2 , X1, X2,..., Xn 是 X 的一
个样本, 则样本均值服从正态分布X1 nFra bibliotekn i 1
Xi
~
N
,
2
n
U
X
1 n
n i1
Xi
~
N 0,1
n n
概率分布的分位数(分位点)
定义 对总体X和给定的 (0<<1),若存在x,
f(y)
上分位数或上侧临界值,
其几何意义见图5-5所示.
其中f(y)是 2-分布的概率密度. O
图5-5 2(n) x
显然,在自由度n取定以后,2(n)的值只与有关.
例如,当n=21,=0.05时,由附表3(P254)可查得,
02.05(21) 32.67 即 P 2(21) 32.67 0.05.
即 t(n)≈u , n>45.
一般的t分布临界值表中,详列至n=30,当 n>30就用标准正态分布N(0, 1)来近似.
四、F分布
定义5.5 设随机变量X~ 2(n1)、Y~ 2(n2),且
与相互独立,则称随机变量
F
X Y
n1 n2
服从第一自由度为n1,第二自由度为n2的F分布,
记作 F~F(n1,n2).
02.1(9)≈查 14.684.
故
表
≈
14.684x
16 9
≈26.105
n2) F 2
图6-4
(n1,
n2)
x
例 设总体X~N( , 42), X1,X2,…,X10是n=10简
单随机样本, S2为样本方差,已知P{S2>}=0.1,求
第8章思考与练习0801217
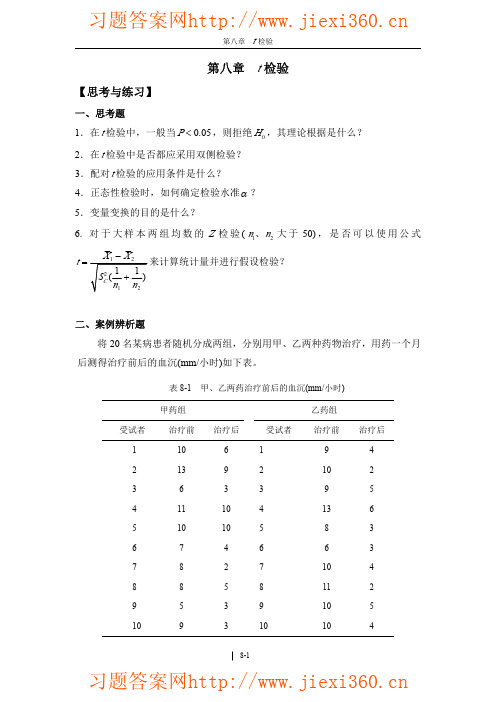
Z KURT = 0.360 1.334 < 1.96 Z KURT = 0.232 1.334 < 1.96
故,甲药,、乙药两组资料的差值 d1、d 2 均服从正态分布。 (2) 方差齐性检验 1) 建立检验假设,确定检验水准
2 ,两差值总体方差相等 H 0 :σ 12 = σ 2
2 ,两差值总体方差不等 H1:σ 12 ≠ σ 2
g d Valid N (listwise) d Valid N (listwise)
Group Statist ic s Std. Error Std. Deviation Mean 1.93218 .61101 1.81353 .57349
g d
N 10 10
Mean 3.2000 5.8000
8-3
习题答案网
习题答案网
第八章
t 检验
7. 为研究两种方法的检测效果,将 24 名患者配成 12 对,采用配对 t 检验进行统 计分析,则其自由度为: A. 24 B. 12 C. 11 D. 23 E. 2 四、综合分析题 1. 大量研究表明健康成年男子脉搏的均数为 72 次/min。某医生在某山区随机调 查了 16 名健康成年男子,测得其脉搏(次/min)资料如下: 69 72 74 68 73 74 80 73 75 74 73 75 74 79 72 74
Z KURT = 1.403 1.334 < 1.96 Z KURT = 0.751 1.334 < 1.96
Z SKEW = 0.088 0.687 < 1.96
故,甲、乙两组资料均服从正态分布。 (2) 假设检验
2 2 由甲、乙两组数据得: X甲 = 5.5, X 乙 = 3.8, S甲 = 3.12 , S乙 = 1.32
医学统计学 方差分析

100.66
110.31
4
367.60
5
80.57
97.90
115.76
103.56
4
397.79
6
102.77
81.20
90.30
138.54
4
412.81
ni
6
6
6
6
24( n )
Xi
550.01
537.30
618.19
726.28
2431.78( X )
Xi
91.67
89.55
103.03
2 =32 得: F0.05(2,32) 3.30, F0.01(2,32) 5.34 ,P<0.01。按 =0.05 水准,拒绝 H0 ,
差别有统计学意义,可以认为喂养三种不同饲料的大鼠红细胞数的总体均数不 全相同。
随机区组设计的两因素方差分析
例9.2 利用随机区组设计研究不同温
度对家兔血糖浓度的影响,某研究者进行 了如下实验:将 24只家兔按窝别配成6个 区组, 每组 4 只, 分别随机分配到温度 15℃、 20℃、 25℃、 30℃的4个处理组 中,测量家兔的血糖浓度值(mmol/L),结 果如下表9.4所示,分析4种温度下测量家 兔的血糖浓度值是否不同?
23
3742.5521
3
1247.5174 8.2717
1491.2744
5
298.2549 1.9776
2262.2511
15
150.8167
P
<0.01 >0.05
3. 确定 P 值,作出统计推断
根据处理组 F 值的分子的自由度处理 ,分母的自由度 误差 ;区组 F 值的分子的 自由度区组 ,分母的自由度 误差 查 F 界值表(附表 4),得到处理组和区组的 P 值。 根据表 9.6,按 =0.05 水准,对于不同区组间,不拒绝 H0 ,尚不能认为不同窝 别家兔血糖浓度值不同;对于不同处理组间,拒绝 H0 ,接受 H1 ,差异具有统 计学意义,可以认为 4 种温度下家兔血糖浓度值不全相同,即处理组 4 个总体 均数中至少有 2 个不同。
统计临界值表格

目录附表一:随机数表 _________________________________________________________________________ 2附表二:标准正态分布表 ___________________________________________________________________ 3附表三:t分布临界值表____________________________________________________________________ 4附表四:2分布临界值表__________________________________________________________________ 5附表五:F分布临界值表(α=0.05)________________________________________________________ 7附表六:单样本K-S检验统计量表___________________________________________________________ 9附表七:符号检验界域表 __________________________________________________________________ 10附表八:游程检验临界值表 _________________________________________________________________ 11附表九:相关系数临界值表 ________________________________________________________________ 12附表十:Spearman等级相关系数临界值表 ___________________________________________________ 13附表十一:Kendall等级相关系数临界值表 ___________________________________________________ 14附表十二:控制图系数表 __________________________________________________________________ 15附表一:随机数表(查表时注意:v是指自由度,并分单侧和双侧两种类型)(左侧的示意图是单侧检验的情形)附表四:2分布临界值表附表五:F分布临界值表(α=0.05)F分布临界值表(α=0.01)附表六:单样本K-S 检验统计量表[])(1)()(sup 0d D P x F x F D n n x n ≤-=-=α附表七:符号检验界域表附表十二:控制图系数表。
统计学t检验简介(二)

n1 n2
12 12
2019/7/5
15
(3)确定P值 作出推断结论 ν =12+12-2=22,查t界值 表,得t0.005/2,22=3.119, t0.001/2,22=3.505,现t0.005/2,22<t< t0.002/2,22, 故 0.005>P>0.002。按α水准,拒绝H0,接受H1,差异有统计学 意义。可以认为银屑病患者与正常人的血清IL-6平均水平不同, 银屑病患者血清IL-6平均水平较高。
2019/7/5
20
第四节 正态性检验和两总体方差的齐性检验
一、正态性检验
正态性检验只介绍以下基本概念。定量资料的假设检验方 法,如t 检验、F检验等大都要求资料服从于正态分布,通过 频数分布表可近似的看出资料的分布形态,但要确定资料是否 为正态分布要通过假设检验的方法。
(一)图示法:常用的图示法包括P-P图法和Q-Q图法。图 中数据呈直线关系可认为呈正态分布,不呈直线关系可认为呈 偏态分布。主要通过SAS或SPSS统计软件实现的。
2019/7/5
26
偏度系数g1和峰度系数g2的计算和假设检验主要通过SAS或 SPSS统计软件完成,两种检验方法都是P>0.05时,不拒绝H0; P≤0.05时,拒绝H0。一般认为两种检验方法均为P>0.05时,才 能认为总体分布为正态分布。
2019/7/5
27
二、两样本方差的齐性检验
两样本均数比较的t检验,要求相应的两总体方差相等,即
2019/7/5
5
如果在总体标准差σ0已知的情况下,样本均数与总体均数 比较可用z检验,因为z值符合标准正态分布,其计算公式为:
z X 0 0 / n
第14章思考与练习
第十四章 直线回归分析【思考与习题】一、思考题1.试述建立直线回归方程的步骤以及散点图的作用。
2.如何将方差分析运用于回归系数的假设检验简述其思想。
3.简述直线相关和直线回归的区别与联系。
4.对回归系数进行假设检验可以采用哪些方法二、案例辨析题某研究采用火箭电泳法对已知浓度的标准血清进行测量,其免疫球蛋白IgA 浓度(μg/ml)和火箭电泳高度(mm)如表14-1所示。
研究者据此数据建立直线回归方程,用于测定未知样品血清中的IgA 浓度,以上分析正确吗~表14-1 标准品的IgA 浓度(μg/ml)和火箭电泳高度(mm)】采用最小二乘法建立直线回归方程,得到ˆ 5.335 1.599yx =+,经假设检验得001.0<P ,故此回归方程可用于测定未知样品血清中的IgA 含量。
标准品的IgA 浓度 x火箭电泳高度 y…。
三、最佳选择题 |1. 对于一组服从双变量正态分布的资料,经直线相关分析得相关系数0r >,若对该资料拟合回归直线,其回归系数 A .0b > B .0b < C .0b = D .11b -<< E .1>b2. 一组服从双变量正态分布的资料,经直线相关分析得相关系数1r =-,则有 A .SS =残总SS B .SS SS =残回 C .SS SS =总回 【D .回残MS MS =E .回总MS MS =3.直线回归中x 与y 的标准差相等时,则有 A .b a = B .b r =C .1b =D .1r =E .1a =4.若直线回归系数0b =,则一定有 A .截距等于0 @B .截距等于yC .SS 残等于0D .SS 总等于0E .SS 残等于SS 回5.两组服从双变量正态分布的资料,若两样本12b b =,12n n >,则有A .12r r >B .12b b t t =C .12r r >D .11b r t t =E .12r r t t =]6.最小二乘法的原理是各观测点A .距回归直线的纵向距离相等B .距回归直线的纵向距离平方和最小C .距回归直线的垂直距离相等D .距回归直线的垂直距离平方和最小E .距回归直线的纵向距离最小7.直线回归分析中,按直线方程ˆ0.0040.0588yx =+,代入两点绘制回归直线,以下选项中正确的是A .所有实测点都应在回归直线上B .所绘回归直线必过点(,)x yC .回归直线必过原点-D .x 的取值范围为[1,1]-E .实测值与估计值之差的平方和必小于零8.同一资料进行直线回归与直线相关分析时,下列说法正确的是 A .0ρ=时,则0r = B .||0r >时,则0b >C .0r <时,则0b >D .0r <时,则0b <E .||1b ≤四、综合分析题 ~1. 为了研究女大学生胸围(cm)与肺活量(L)的关系,随机抽取某高校一年级女生15名,测量其胸围与肺活量数据如表14-2所示。
GSM-R手持机使用说明书
GSM-R手持机使用说明(本说明适用于GPH610和OPH810型号)GSM-R手持机是指专门为铁路通信设计的综合专用数字移动通信系统手机,简称为吉时玛手机。
GSM-R配的SIM卡称为MSISDN号,如。
吉时玛手机的功能菜单有“呼叫记录”“薄”“工具”“短消息”“GSM-R”等功能菜单,其中“GSM-R”为铁路吉时玛手机专用菜单,配合专用SIM使用的。
其它菜单同普通手机一样。
“GSM-R”菜单功能又受到所配SIM卡的权限限制。
如工区所配SIM卡不能注册司机车次功能号,不能发起210组呼等限制。
吉时玛手机使用说明如下:1. GSM-R手持台用户类别调度通信用户:司机、助理值班员(车务应急值守人员)、随车机械师;其它用户:通信、信号、工务、供电维护人员,列车长,公安人员,有关管理人员。
2. GSM-R手持台呼叫方式2.1 常规功能的使用(1)GSM-R手机只能实现手机与铁路的互打,不支持与移动、联通、电信的互打。
(2)GSM-R手机拨打GSM-R手机,直接拨打对方(如,手机上会显示来电和来电)。
(3)使用GSM-R手机拨打铁路:901—0441—铁路5位(其中0441为铁路长途区号)。
(4)铁路拨打GSM-R手机:018—0—手机。
(其中018为铁路区号,3字头的铁路暂时不能拨打GSM-R手机)。
2.2 功能号呼叫方式该拨叫方式适合调度通信用户,列车长。
使用功能号呼叫前提是被叫用户必须进行功能号网络注册(注册方式见下文“3. ”)。
用户直接拨打功能号即可发起呼叫。
例1:通过车次功能号呼叫D333次动车司机,可以直接拨打2006833381(“2”表示使用车次功能号呼叫,“0068”表示“D”,“333”表示1-5位可变长度的车次号数字位,“81”表示本务司机手持台);如果呼叫D333次列车长,可以拨打2006833310(最后2位“10”表示列车长)。
车次功能号呼叫,除直接按齐拔打外,也可通过菜单:“GSM-R”—“铁路通讯拨号”—“车次功能号”—【输入车次号】栏输入D333,—【输入功能码】栏输入81或按“选择”键选择“本务司机手持台”项后拔打,通过本菜单可减少手工换算功能码的程序。
混凝土强度标准值
附表22注:1.计算现浇钢筋混凝土轴心受压及偏心受压构件时,如截面的长边或直径小于 300mm ,则表中混凝土 的强度设计值应乘以系数 0.8;当构件质量(如混凝土成型、截面和轴线尺寸等)确定保证时,可不受此限制;2.离心混凝土的强度设计值应按有关专门标准取用。
2) E 2.20 2.55 2.80 3.00 3.15 3.25 3.35 3.45 3.55 3.60 3.65 3.70 3.75 3.80c γ ρ γ ρ0.740.800.860.931.0注:如采用蒸汽养护时,养护温度不宜超过 600C ,如超过时,应按计算需要的混凝土强度设计值提高 20%。
2)E c f1.1 1.2 1.3 1.4 1.5 1.55 1.6 1.65 1.7 1.75 1.8 1.851.92)2)注:1.钢绞线直径 d系指钢绞线外接圆直径,即钢绞线标准 GB/T5224中的公称直径 Dg;2.各种直径钢绞线、钢丝、钢筋的公称截面面积如附录 B所示。
3.消除应力光面钢丝直径 d为 4~9mm,消除应力螺旋肋钢丝直径 d为 4~8mm。
2)注:1.在钢筋混凝土结构中,轴心受拉和小偏心受拉的钢筋抗拉强度设计值大于300N/mm2时,仍应按300N/mm2取用;2.构件中配有不同种类的钢筋时,每种钢筋应采用各自的强度设计值。
2)注:当预应力钢绞线、钢丝的强度标准值不符合表 4.2.2—2的规定时,其强度设计值应进行换算。
2)钢绞线10注:必要时钢绞线可采用实测的弹性模量。
2)注:1.当纵向受拉钢筋采用闪光接触对焊接头时,其接头处钢筋疲劳应力幅限值应按表中数值乘以系数0.8;2.RRB400级钢筋须经试验严正吼,方可用于需做疲劳验算的构件。
注:当f 2)ρ p 不小于 0.9 时,不必作钢筋疲劳验算。
附表 13混凝土构件中纵向受力钢筋的最小配筋百分率 min (%)注:1.轴心受压构件、偏心受压构件全部纵向钢筋的配筋率以及各类构件一侧受压钢筋的配筋率应按构件的全截面面积计算;轴心受拉构件及小偏心受拉构件一侧受拉钢筋的配筋率应按构件的全截面面积计算;受弯梁类构件、大偏心受拉构件一侧受拉钢筋的配筋率应按全截面面积扣除受压边缘面积//( b f − b) h f 后的截面面积计算。
方差齐性检验
但是,方差齐性检验也可以在 F 检验结果为多个样本所属总体平均数差异显著的情况下进行,因为 F 检验之后,如果多个样本所属总体平均数差异不显著,就不必再进行方差齐性检验。
Levene 方差齐性检验也称为Levene 检验(Levene's Test). 由H.Levene 在1960 年提出[1] .M.B.Brown 和A.B.Forsythe 在1974年对Levene 检验进行了扩展[2], 使对原始数据的数据转换不但可以使用数据与算术平均数的绝对差, 也可以使用数据与中位数和调整均数(trimmed mean) 的绝对差. 这就使得Levene 检验的用途更加广泛.Levene 检验主要用于检验两个或两个以上样本间的方差是否齐性. 要求样本为随机样本且相互独立. 国内常见的Bartlett 多样本方差齐性检验主要用于正态分布的资料,对于非正态分布的数据, 检验效果不理想.Levene 检验既可以用于正态分布的资料, 也可以用于非正态分布的资料或分布不明的资料, 其检验效果比较理想.方差分析的条件之一为方差齐,即各总体方差相等。
因此在方差分析之前,应首先检验各样本的方差是否具有齐性。
常用方差齐性检验( test for homogeneity of variance )推断各总体方差是否相等。
本节将介绍多个样本的方差齐性检验,本法由Bartlett 于1937 年提出,称Bartlett 法。
该检验方法所计算的统计量服从分布。
用自由度查界值表,若值大于等于界值,则P值小于等于相应的概率,反之,P值大于相应的概率。
如果未经校正的值小于界值,则校正后的值更小,可不必再计算校正值。
J J例5.7对照组、A降脂药组、B降脂药组和C降脂药组家兔的血清胆固醇含量 (mmol/L)的均数分别为5.845 、2.853 、2.972 和1.768 ,方差分别为5.941、2.370 、0.517 和0.581 ,样本含量分别为6、6、 6 和7,问四样本的方差是否齐同?J J本例自由度为,查界值表,得0.025>P>0.01 ,按=0.05水准拒绝H0,接受H1,可以认为四总体方差不同或不全相同。
