西安交通大学苏州附属中学
关于西交大苏州附中

关于西交大苏州附中,很多家长会拿它与苏大附中、甚至其他学校作对比,不妨先来搞清楚西交大苏州附中的相关信息:西安交通大学苏州附属中学,也就是原先苏州家长比较熟知的“园三”演变而来,是苏州工业园区管理委员会直属公办四星级全日制中学,2004年建校,2011年晋升为江苏省四星级高中。
师资力量:目前全校共有专任教师138人,100%本科及以上学历,中、高级职称者达81.4%,特级教师3名,大市级学科带头人8 名,硕士研究生33名,在读14名,学校师资队伍先后被评为苏州市“优秀教师群体”、苏州市“先进青蓝文明岗”、苏州市“教育系统工人先锋号”。
学校数学教研组和英语教研组被评为江苏省教改实验先进单位。
升学成绩:2010年本一达线率53.4%,本二以上达线率87.64%;2011年本一达线率46.8%,本二以上达线率 85.34%;2012年文科本一上线率50.5%、文科本二上线率83.2%、理科本一上线率53.4%、理科本二上线率80.3%、艺体本二上线率 100%、总计本二以上上线率83.51%(不含出国学生)、囊括园区文理科状元、各项指标值均稳居园区第一、本二以上总计上线率市区第二的优异成绩,这一成绩延续了2010、2011年的高位发展水平并取得新的突破。
2012年高考质量更是获得园区教育局、管委会肯定,苏州市区排名第二,获得2012年度园区科学发展奖。
一大批学生被复旦大学、南京大学、浙江大学、上海交通大学、西安交通大学、同济大学、中国美术学院等985知名高校录取,多次受到苏州市教育局和园区教育局的表彰,被媒体称为“苏州最年轻的名校”。
中考录取分数线:2009年2010年2011年2012年2013年统招分数线637 639 639 647 650择校分数线617 635 629 643 646单从录取分数线来说,相信家长也可以看得出,“园三”一直是在走上坡的路线,分数线逐年走高。
关于签约:2013年西安交大苏州附中签约信息招生情况和班级设置:学校的招生说明会一般会在初三一模考试之后。
江苏省苏州市工业园区西安交通大学苏州附属初级中学2022-2023学年九年级上学期数学第十三周周测卷

2022-2023学年第一学期西附初中初三数学第十三周周测卷一.选择题(共8小题,满分24分,每小题3分)1.⊙O的半径为2,线段OP=4,则点P与⊙O的位置关系是()A.点P在圆内B.点P在圆上C.点P在圆外D.无法确定2.下列命题中,正确的是()A.平面上三个点确定一个圆B.等弧所对的圆周角相等C.弦是直径D.同圆或等圆中,相等的弦所对的圆周角相等3.已知点A(3,y1),B(4,y2),C(5,y3)均在抛物线y=2x2﹣4x+m上,下列说法中正确的是()A.y3<y2<y1B.y2<y1<y3C.y3<y1<y2D.y1<y2<y34.若抛物线y=x2﹣bx+8的顶点在x轴的负半轴上,则b的值为()A.±4B.﹣4C.﹣2D.±25.如图,∠DCE是⊙O内接四边形ABCD的一个外角,若∠DCE=82°,那么∠BOD的度数为()A.160°B.162°C.164°D.170°6.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为()A.15°B.28°C.29°D.34°7.如图,BC是半圆O的直径,D,E是上两点,连接BD,CE并延长交于点A,连接OD,OE.如果∠A=70°,那么∠DOE的度数为()A.35°B.38°C.40°D.42°8.如图,⊙O中,BC为直径,A为BC弧的中点,点D在AC弧上,BD与AC相交于M,若CD=1,BC =,则DM的长是()A.B.C.D.(第5题)(第6题)(第7题)(第8题)二、填空题(共8小题,满分24分,每小题3分)9.如图,AB是⊙O的直径,点C、D在⊙O上,若∠ADC=58°,则∠BAC=°.10.如图,△ABC中,∠C=90°,tan B=3,MN垂直平分AB,AN=10,则BC=.11.如图,由边长为1的小正方形组成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C和点D,则tan∠ADC=.12.如图,弦CD垂直于⊙O的直径AB,垂足为H,CD=6,BD=,则OH的长为.(第9题)(第10题)(第11题)(第12题)13.如图,△ABC、△FED区域为驾驶员的盲区,驾驶员视线PB与地面BE的夹角∠PBE=43°,视线PE 与地面BE的夹角∠PEB=20°,点A,F为视线与车窗底端的交点,AF∥BE,AC⊥BE,FD⊥BE.若A 点到B点的距离AB=1.6m,则盲区中DE的长度是.(参考数据:sin43°≈0.7,tan43°≈0.9,sin20°≈0.3,tan20°≈0.4)(第13题)(第14题)14.如图,在平面直角坐标系中,⊙M经过原点,且与x轴交于点A(﹣4,0),与y轴交于点B(0,2),点C在第二象限⊙M上,且∠AOC=60°,则OC=.15.如图,某同学用圆规BOA画一个半径为4cm的圆,测得此时∠O=90°,为了画一个半径更大的同心圆,固定A端不动,将B端向左移至B′处,此时测得∠O′=120°,则BB′的长为.(第15题)(第16题)16.如图,在四边形ACBD中,AB=BD=BC,AD∥BC,若CD=4,AC=2,则AB的长为.三、解答题(共8小题,满分82分)17.(本题满分8分)计算:(1)2tan45°•sin30°+cos30°•tan60°;(2)cos60°﹣cos45°+3tan230°.18.(本题满分8分)解方程:(1)x2﹣2x﹣3=0.(2)3x2+6x﹣4=0.19.(本题满分6分)如图,在平面直角坐标系中,点A的坐标为(0,7),点B的坐标为(0,3),点C 的坐标为(3,0).(1)若△ABC的外接圆的圆心为M,则圆心M的坐标为;(2)△ABC的外接圆与x轴的另一个交点坐标是.20.(本题满分12分)如图,在平面直角坐标系中,二次函数y=ax2+bx+3(a≠0)的图象经过点A(﹣1,0),点B(3,0),与y轴交于点C.(1)求a,b的值;(2)若点P为直线BC上一点,点P到A,B两点的距离相等,将该抛物线向左(或向右)平移,得到一条新抛物线,并且新抛物线经过点P,求新抛物线的顶点坐标.21.(本题满分12分)如图,AB是⊙O的直径,点D,E在⊙O上,连接AE,ED,DA,连接BD并延长至点C,使得∠DAC=∠AED.(1)求证:AC是⊙O的切线;(2)若点E是的中点,AE与BC交于点F;①求证:CA=CF;②当BD=5,CD=4时,请直接写出BF的长为.22.(本题满分12分)如图,某无人机爱好者在一小区外放飞无人机,当无人机飞行到一定高度D点处时,无人机测得操控者A的俯角为75°,测得小区楼房BC顶端点C处的俯角为45°.已知操控者A和小区楼房BC之间的距离为45米,小区楼房BC的高度为15米.(1)求此时无人机的高度;(2)在(1)条件下,若无人机保持现有高度沿平行于AB的方向,并以5米/秒的速度继续向前匀速飞行.问:经过多少秒时,无人机刚好离开了操控者的视线?(假定点A,B,C,D都在同一平面内.参考数据:tan75°=2+,tan15°=2﹣.计算结果保留根号)23.(本题满分12分)已知:抛物线y=﹣x2+2x+m﹣2交y轴于点A(0,2m﹣7).与直线y=2x交于点B、C(B在右、C在左).(1)求抛物线的解析式;(2)在线段AB的下方是否存在点G,使得∠GBA = 45°且AG = AB,存在的话,请求出点G的坐标;(3)设抛物线的顶点为E,在抛物线的对称轴上是否存在一点F,使得∠BFE=∠CFE?若存在,求出点F 的坐标;若不存在,说明理由.24.(本题满分12分)已知⊙O为△ABC的外接圆,AC=BC,点D是劣弧上一点(不与点A,B重合),连接DA,DB,DC.(1)如图1,若AB是直径,将△ADC绕点C逆时针旋转得到△BCE.若CD=4,求四边形ADBC的面积;(2)如图2,若AB=AC,半径为2,设线段DC的长为x,四边形ADBC的面积为S.①用含有x的代数式表示S;②若点M,N分别在线段CA,CB上运动(不含端点),经过探究发现,点D运动到每一个确定的位置.△DMN的周长有最小值t,随着点D的运动,t的值会发生变化.则所有t值中的最大值是,此时四边形ADBC的面积S为.。
江苏省苏州市西安交通大学苏州附属初级中学2024~2025学年上学期八年级数学试卷(无答案)
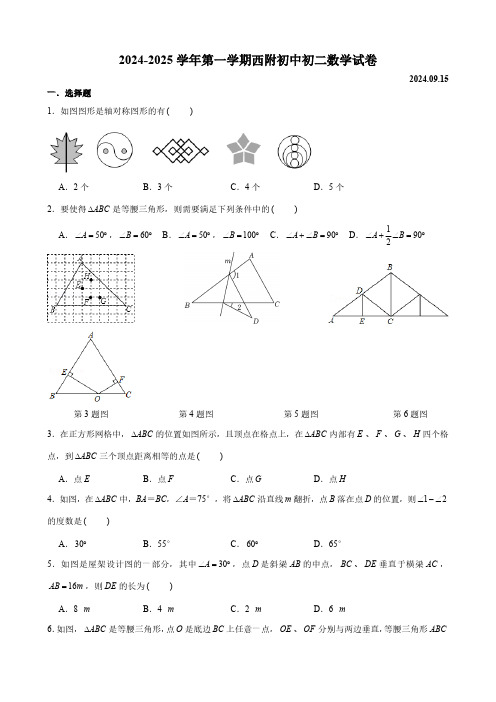
2024-2025学年第一学期西附初中初二数学试卷2024.09.15一.选择题1.如图图形是轴对称图形的有 A .2个B .3个C .4个D .5个2.要使得是等腰三角形,则需要满足下列条件中的 A ., B ., C . D .第3题图 第4题图 第5题图 第6题图3.在正方形网格中,的位置如图所示,且顶点在格点上,在内部有、、、四个格点,到三个顶点距离相等的点是 A .点B .点C .点D .点4.如图,在中,BA =BC ,∠A =75°,将沿直线翻折,点落在点的位置,则的度数是 A .B .55°C .D .65°5.如图是屋架设计图的一部分,其中,点是斜梁的中点,、垂直于横梁,,则的长为 A .8 B .4 C .2 D .6 6.如图,是等腰三角形,点是底边上任意一点,、分别与两边垂直,等腰三角形()ABC ∆()50A ∠=︒60B ∠=︒50A ∠=︒100B ∠=︒90A B ∠+∠=︒1902A B ∠+∠=︒ABC ∆ABC ∆E F G H ABC ∆()E F G HABC ∆ABC ∆m B D 12∠-∠()30︒60︒30A ∠=︒D AB BC DE AC 16AB m =DE ()m m m mABC ∆O BC OE OF ABC的腰长为5,面积为12,则的值为 A .4B .C .15D .87.如图“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪“能三等分任一角.这个三等分角仪由两根有槽的棒,组成,两根棒在点相连并可绕转动,点固定,,点、可在槽中滑动,若,则的度数是 A .B.C .D .第7题图 第9题图 第10题图8.已知,,是的三边长,且,则的形状为 A .钝角三角形 B .等边三角形 C .直角三角形 D .等腰直角三角形9.如图,点是内任意一点,,点和点分别是射线和射线上的动点,周长的最小值是,则的度数是 A .B .C .D .10.如图,在中,,,点从点出发以每秒的速度向点运动,点从点同时出发以每秒的速度向点运动,其中一个动点到达端点时,另一个动点也随之停止运动,当是以为底的等腰三角形时,运动的时间是 A .2.5秒B .3秒C .3.5秒D .4秒二、填空题11.一个汽车牌照号码在水中的倒影为,则该车牌照号码为 .12.如图所示是的方格纸,请在其中选取一个白色的方格并涂黑,使图中阴影部分是一个轴对称图形,这样的涂法有 种.13.已知等腰三角形的两边长分别为4和8,则它的周长是 .14.如果等腰三角形的两个角的比是,那么底角的度数为 .15.等腰三角形腰长为,腰上的高为.那么这个三角形的顶角是 度.OE OF +()245OA OB O O C OC CD DE ==D E 75BDE ∠=︒CDE ∠()70︒75︒80︒85︒a b c ABC ∆222a b c ab ac bc ++=++ABC ∆()P AOB ∠5OP cm =M N OA OB PMN ∆5cm AOB ∠()25︒30︒35︒40︒ABC ∆20AB cm =12AC cm =P B 3cm A Q A 2cm C APQ ∆PQ ()45⨯2:56cm 3cm第12题图 第16题图 第17题图 第18题图16.如图,在中,,,是上一点,将沿折叠,使点落在边上的处,则等于 .17.已知,是的平分线,点为上一点,过作直线,垂足为点,且直线交于点,如图所示.若,则 .18.如图所示,是一钢架,且,为了使钢架更加坚固,需在其内部添加一些钢管,,,添加的钢管长度都与相等,则最多能添加这样的钢管 根.三、作图题19.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点和(格点为网格线的交点),以及过格点的直线.(1)画出关于直线对称的△;(2)将向右平移1个单位长度,再向下平移3个单位长度,画出平移后的△;(3)填空: .20.如图:(1)在AB 公路一侧有C 、D 两村庄,想在公路上找一点P ,使C 、D 、P 三点组成的三角形的周长最短。
西安交通大学苏州附属中学
35
教授级特级教师
苏州市名教师
发展研究中心专家
数学
通技
周书琴
女
27
本科
硕士
数学
蒋亚军
男
25
本科
本科
中学
二级
4
市青年教师基本功大赛一等奖省教学竞赛二等奖
英语
周 兵
男
44
专科
硕士
中学
高级
23
园区学科带头人
教研组长
高三英语
备课组长
英语
陈瑞娟
女
30
本科
本科
中学
一级
8
市高中班主任比赛三等奖
苏州市教师教育技术能力竞赛暨十佳网络教学团队一等奖
中学
二级
7
区青年教师基本功竞赛二等奖
物理
徐卫兵
男
44
本科
本科
中学
高级
26
江苏省特级教师
大市学科带头人
发展研究中心主任
物理
通技
宋海荣
男
36
大专
本科
中学
一级
14
市级教学能手
市教育系统新长征突击手
化学
王小阳
女
52
本科
本科
中学
高级
外借科教
创新区
化学
王晓珍
女
29
本科
本科
中学
一级
7
区化学教学设计比赛一等奖
高二化学
备课组长
化学
成素萍
女
39
本科
本科
中学
高级
17
园区学科带头人
区学科能力把握竞赛三等奖
江苏省苏州市西安交通大学苏州附属中学2023-2024学年七年级下学期5月月考数学试题

江苏省苏州市西安交通大学苏州附属中学2023-2024学年七年级下学期5月月考数学试题一、单选题1.下列计算正确的是( )A .33634a a a +=B .23a a a ⋅=C .623a a a ÷=D .()235a a = 2.一个不等式组的解在数轴上表示如图,则这个不等式组的解是( )A .13x -<<B .13x -≤<C .13x -<≤D .13x -≤≤ 3.如图,下列条件中,可以判定DE AB ∥的是( )A .E DCA ∠=∠B .DCE E ∠=∠C .180E BCD ∠+∠=︒ D .180ACE E ∠+∠=︒4.若m n >,则下列不等式中不成立...的是( ) A .22m n +>+ B .22m n ->- C .2>2m n -- D .22m n > 5.如图,已知ABC DEF ≌△△,且7040A B ∠=︒∠=︒,,则F ∠的度数是( )A .40°B .50°C .60°D .70° 6.若多项式2429a ka -+可以写成一个整式的平方,则常数k 的值为( ) A .12 B .12± C .6 D .6±7.从A 地到B 地需要经过一段上坡路和一段平路,小明上坡速度为4km /h ,平路速度为5km /h ,下坡速度为6km /h .已知他从A 地到B 地需用35min ,从B 地返回A 地需用24min .问从A 地到B 地全程是多少千米?我们可将这个实际问题转化为二元一次方程组问题,如果设未知数x 、y ,且列出一个方程为354560x y +=,则另一个方程是( ) A .244560x y += B .244660x y += C .245660x y += D .246560x y += 8.如图,ABC V 中,3∠=∠ABC C ,E 分别在边BC ,AC 上,24EDC ︒∠=,3ADE AED ∠=∠,ABC ∠的平分线与ADE ∠的平分线交于点F ,则F ∠的度数是( )A .54°B .60°C .66°D .72°二、填空题9.“沉睡数千年,一醒惊天下”,三星堆遗址在5号坑提取的牙雕制品,最细微处仅为0.00005米,该数据用科学记数法表示为.10.若52m n a a ==,,则m n a -的值为 .11.命题“如果a b =,那么a b =”,则它的逆命题是命题(填“真”或“假”). 12.一个三角形的两边长为5和7,则第三边a 的取值范围是.13.若()()232x a x x x b +-=+-,则a b -=.14.若关于x ,y 的方程组3632x y k x y +=-⎧⎨+=⎩的解满足1x y +=,则k 的值为. 15.若不等式组2111x x m -<⎧⎨+>⎩恰有四个整数解,则m 的取值范围是. 16.将一副三角板按如图放置,则下列结论:①如果∠2=30°.则AC ∥DE ;②∠2+∠CAD =180°;③如果BC ∥AD ,则有∠2=60°;④如果∠CAD =150°,必有∠4=∠C ;其中正确的结论有.17.如图,C 是AB 上一点,分别以AC 、BC 为边画正方形ACDE 与正方形BCFG ,连接CG 、DG .已知 92AB =,CDG V 的面积为74,则正方形ACDE 与正方形BCFG 的面积的和为.18.如图,将ABC V 纸片先沿DE 折叠,再沿FG 折叠,若12228∠+∠=︒,则34∠+∠=.三、解答题19.解方程组2128x y x y +=⎧⎨-=⎩20.因式分解:(1)39-t t ;(2)()()41y y y +--.21.求不等式组273102113x x x +≤+⎧⎪⎨-<-⎪⎩①②的整数解. 22.如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.仅用无刻度的直尺完成下列作图.(1)画出ABC V 向右平移4个单位后的图形111A B C △;(2)画出ABC V 的中线CD ;(3)在图中存在满足QBC △与ABC V 面积相等的格点Q (与点A 不重合)共有个. 23.如图,点A 、C 、D 在同一条直线上,BC AD ⊥,垂足为C ,BC CD =,点E 在BC 上,AC EC =,连接AB ,DE .(1)求证ABC EDC △≌△;(2)写出AB 与DE 的位置关系,并说明理由.24.某景区对基础设施提档升级,计划购置一批A 型和B 型器材.购买1套A 型器材比购买1套B 型器材多50元;购买2套A 型器材和3套B 型器材共需1350元.(1)购买1套A 型器材和1套B 型器材各需多少元?(2)根据景区的实际情况,需购买A 、B 型器材的总数为50套,购买A 、B 型器材的总费用不超过14500元.①请问A 型器材最多购买多少套?②从游客的实际需要出发,其中A 型器材购买的数量不少于B 型器材数量的3倍,该景区共有几种购买方案?试写出所有的购买方案.25.已知关于x 、y 的方程组325233x y a x y a -=-⎧⎨+=+⎩. (1)求方程组的解(用含a 的代数式表示);(2)若方程组的解满足条件0231x y ≤-≤,求a 的取值范围;(3)若x 、y 是等腰三角形的两条边,且等腰三角形的周长为9,求a 的值;(4)若无论a 取何值,等式222x by a b +=+-总成立,求b 的值.26.如图,直线PQ MN ∥,一副三角板(90ABC CDE ∠=∠=︒,30ACB ∠=︒,60BAC ∠=︒,45DCE DEC ∠=∠=︒)按如图①放置,其中点E 在直线PQ 上,点B ,C 均在直线MN 上,且CE 平分ACN ∠.(1)求DEQ ∠的度数;(2)如图②,若将ABC V 绕B 点以每秒5︒的速度按逆时针方向旋转(A ,C 的对应点分别为F ,G ).设旋转时间为t 秒()036t ≤≤;①在旋转过程中,若边BG CD ∥,求t 的值;②若在ABC V 绕B 点旋转的同时,CDE V 绕E 点以每秒4°的速度按顺时针方向旋转.请直接写出旋转过程中CDE V有一边与BG 平行时t 的值.。
西安交通大学苏州附属中学高三10月月考试题数学

西安交通大学苏州附属中学高三10月月考试题高三数学2014.10注意事项:1.本试卷共4页.满分160分,考试时间120分钟.2.请将填空题的答案和解答题的解题过程写在答题卡的规定区域,在本试卷上答题无效. 3.答题前,务必将自己的姓名、学校、考试号写在答题卡的指定位置.一、填空题:本大题共14小题,每小题5分,共计70分,请把答案直接填写在答题卡相应位置.......上. 1.已知集合{|},{|12},()R A x x a B x x AC B R =<=<<=且,则实数a 的取值范围是 ▲ .2.命题“若a 2+b 2=0,则a=0且b=0”的逆否命题是 ▲ . 3.已知函数3()2log cos x f x x x =++,则()=f x ' ▲ . 4的值域是[0,)+∞,则实数m 的取值范围是▲ .5.已知定义域为R 的函数)(x f为奇函数.且满足)()2(x f x f -=+,当[]1,0∈x 时,12)(-=x x f ,则6.若sinx 3)(+=x x f ,则满足不等式0)3()12(>-+-m f m f 的m 的取值范围为 ▲ .7.已知函数3()y f x x =+为偶函数,且(10)10,f =若函数()()4g x f x =+,则(10)g -= ▲ .89.已知函数f(x)=x 2-3x +m ,g(x)=2x 2-4x ,若f(x)≥g(x)恰在x ∈[-1,2]上成立,则实数m 的值为 ▲ . 10.一个人喝了少量酒后,血液中的酒精含量迅速上升到0.3mg/mL,在停止喝酒后,血液中的酒精含量以每小时25%的速度减少,为了保障交通安全,某地根据《道路交通安全法》规定:驾驶员血液中的酒精含量不得超过0.09 mg/mL,那么,一个喝了少量酒后的驾驶员,至少经过 ▲ 小时,才能开车(精确到1小时). 11.已知函数123()=+1234xx x x f xx x x x +++++++++,则5522f f ⎛⎛-+- ⎝⎝= ▲ . 12.()f x 的定义域为实数集R 对于任意的x R ∈都有(1)(1)f x f x +=-.若在区间[1,3]-上函数()()g x f x mx m =--恰有四个不同的零点,则实数m 的取值范围是 ▲ .13.设函数f(x)=ax 2+bx +c(a<0)的定义域为D ,若所有点(s ,f(t))(s 、t ∈D )构成一个正方形区域,则a 的值为▲ .14.定义在),0(+∞上的函数)(x f 满足:①当[)3,1∈x 时,;②)(3)3(x f x f =.设关于x 的函数a x f x F -=)()(的零点从小到大依次为*12,,,,()n x x x n N ∈.若(1,3)a ∈,则=++++-n n x x x x 21221 ▲ .(用n 表示)二、解答题:本大题共6小题,共计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题卡的指定区域内. 15.(本小题满分14分)设命题p :实数x 满足22430x ax a -+<,其中0a >,命题q :实数x 满足2260,280.x x x x ⎧--≤⎪⎨+->⎪⎩.(1)若1a =且p q ∧为真,求实数x 的取值范围;(2)若p ⌝是q ⌝的充分不必要条件,求实数a 的取值范围.16.(本小题满分14分)已知四边形ABCD 是矩形,AB =,BC =,将△ABC 沿着对角线AC 折起来得到1AB C ∆,且顶点B 1在平面AB=CD 上射影O 恰落在边AD 上,如图所示.(1)求证:AB 1⊥平面B 1CD ;(2)求三棱锥B 1﹣ABC 的体积1B -ABC V .17.(本小题满分14分)过去的2013年,我国多地区遭遇了雾霾天气,引起口罩热销.某品牌口罩原来每只成本为6元,售价为8元,月销售5万只.(1) 据市场调查,若售价每提高0.5元,月销售量将相应减少0.2万只,要使月总利润不低于原来的月总利润(月总利润=月销售总收入-月总成本),该口罩每只售价最多为多少元?(2) 为提高月总利润,厂家决定下月进行营销策略改革,计划每只售价x(x ≥9)元,并投入265(x -9)万元作为营销策略改革费用.据市场调查,每只售价每提高0.5元,月销售量将相应减少0.2(x -8)2万只.则当每只售价x为多少时,下月的月总利润最大?并求出下月最大总利润.18.(本小题满分16分)(1)若函数)(x f 在2=x 时取得极值,求实数a 的值;(2)若0)(≥x f 对任意),1[+∞∈x 恒成立,求实数a 的取值范围.19.(本小题满分16分)已知函数()()()2log 41,x f x kx k =++∈R 是偶函数. (1)求k 的值;(2)设函数()24log 23x g x a a ⎛⎫=⋅- ⎪⎝⎭,其中0.a >若函数()f x 与()g x 的图象有且只有一个交点,求a 的取值范围.20.(本小题满分16分)已知函数()ln f x ax x x =+的图象在点x e =(e 为自然对数的底数)处的切线的斜率为3. (1)求实数a 的值;(2)若2()f x kx ≤对任意0x >成立,求实数k 的取值范围; (3)当1n m >>*(,)m n N ∈时,证明:参考答案1.2≥a 【解析】通过数轴分析得:2≥a . 考点:集合的交并补 2.若0a ≠或0b ≠,则220a b +≠【解析】试题分析:原命题:若p 则q .逆否命题为:若q ⌝则p ⌝.注意“且”否之后变“或”. 考点:命题的逆否命题. 3. 4.[][)0,19,+∞【解析】试题分析:由题意得:函数1)3(2+-+=x m mx y 的值域包含[0,)+∞,当0=m 时,),,0[13+∞⊃∈+-=R x y 满足题意;当0≠m 时,要满足值域包含[0,)+∞,需使得.0,0≥∆>m 即9≥m 或10≤<m ,综合得:实数m 的取值范围是[][)0,19,+∞.考点:函数值域5【解析】解:因为定义域为R 的函数)(x f为奇函数.且满足)()2(x f x f -=+,周期为4,当[]1,0∈x 时,12)(-=x x f ,则6.m>-2 【解析】 试题分析:因为sinx3)(+=x x f 的定义域为R 关于原点对称切满足()()f x f x -=-,所以函数()f x 为奇函数,又因为'()3cosx>0f x =+,所以函数f(x)在R 上单调递增.则(21)(3)0(21)(3)f m f m f m f m -+->⇒->--(21)(3)213f m f m m m ⇒->-⇒->-⇒m>-2,故填m>-2.考点:奇偶性 单调性 不等式 7.2014 【解析】试题分析:由函数3()y f x x =+为偶函数,且(10)10,f =得2010)10(10)10()10()10(33=-⇒+=-+-f f f 从而2014420104)10()10(=+=+-=-f g ,故应填入2014.考点:函数的奇偶性. 8.3 【解析】考点:对数运算. 9.2【解析】由题意,x 2-3x +m ≥2x 2-4x ,即x 2-x -m ≤0的解集是[-1,2],所以m =2. 10.5【解析】设x 小时后,该驾驶员血液中的酒精含量不超过0.09mg/mL,则有0.3·()x≤0.09,即()x≤0.3,估算或取对数计算得至少5小时后,可以开车. 11.答案:8解析:因为f(x)=xx +1+x +1x +2+x +2x +3+x +3x +4=4-⎝⎛⎭⎫1x +1+1x +2+1x +3+1x +4.设g(x)=1x +1+1x +2+1x +3+1x +4, 则g(-5-x)=-⎝⎛⎭⎫1x +4+1x +3+1x +2+1x +1, 所以g(x)+g(-5-x)=0,从而f(x)+f(-5-x)=8, 故f ⎝⎛⎭⎫-52+2+f ⎝⎛⎭⎫-52-2=8.12【解析】试题分析:因为对任意的x R ∈都有(1)(1)f x f x +=-,所以函数()f x 的周期为 2. 由在区间[1,3]-上函数()()g x f x mx m=--恰有四个不同的零点,即函数()f x mx m=+在[1,3]-上有四个不同的零点.即函数()y f x =与函数()h x mx m =+在[1,3]-有四个不同的交点.所以0(3)1h <≤.解得考点:1.分段函数的性质.2.函数的周期性.3.函数的等价变换. 13.答案:-4 解析:|x 1-x 2|=f max (x),b 2-4aca 2=4ac -b 24a,|a|=2-a ,∴ a =-4. 14.6(31)n - 【解析】试题分析:由①当[)3,1∈x 时,()f x 在[)1,3上的图象,根据②)(3)3(x f x f =,只要将()f x 在[)1,3上的图象沿x 轴伸长到原来的3倍,再沿y 轴伸长到原来的3倍即可得到()f x 在[)3,9上的图象,以此类推,可得到在[)[)9,27,27,81上的图象,关于x 的函数a x f x F -=)()(的零点,可看成函数()y f x =与y a=图象交点的横坐标,由函数()y f x =图象的对称性可知:,如图,所以就有)()212126136636363313n n n x x ---+++=+⨯+⨯++⨯==-因此122126(31)n n nx x x x-++++=-考点:函数图象与性质及等比数列求和.15.解析:由22430x ax a -+<得(3)()0x a x a --<,又0a >,所以3a x a <<, 当1a =时,1<3x <,即p 为真时实数x 的取值范围是1<3x <.由2260280x x x x ⎧--≤⎪⎨+->⎪⎩,得23x <≤,即q 为真时实数x 的取值范围是23x <≤.若p q ∧为真,则p 真且q 真,所以实数x 的取值范围是23x <<.(Ⅱ)p ⌝是q ⌝的充分不必要条件,即p ⌝⇒q ⌝,且q ⌝⇒/p⌝,设A={|}x p ⌝,B={|}x q ⌝,则AB ,又A={|}x p ⌝={|3}x x a x a ≤≥或,B={|}x q ⌝={23x x ≤>或}, 则0<2a ≤,且33a >所以实数a 的取值范围是12a <≤. 16.解析:(1)1B O ⊥Q 平面ABCD ,CD ⊂平面ABCD ,∴1B O CD ⊥,又CD ⊥AD ,AD I 1B O =O∴CD ⊥平面1AB D ,又1AB ⊂平面1AB D∴1AB CD ⊥,又11AB B C ⊥,且1B C CD C =I1AB ∴⊥平面1B CD(2)由于1AB ⊥平面1B CD ,1B D ⊂平面ABCD ,所以11AB B D ⊥ 在1Rt AB D ∆中,17.解:(1) 设每只售价为x 元,则月销售量为⎝⎛⎭⎫5-x -80.5×0.2万只,由已知得⎝⎛⎭⎫5-x -80.5×0.2(x -6)≥(8-6)×5,(3分)∴ 25x 2-535x +2965≤0,即2x 2-53x +296≤0,(4分) 解得8≤x ≤372,(5分)即每只售价最多为18.5元.(6分)(2) 下月的月总利润y =⎣⎢⎡⎦⎥⎤5-x -80.5×0.2(x -8)2·(x -6)-265(x -9)(9分) =2.4-0.4x x -8-15x +234-1505=-0.4(x -8)-0.8x -8-15x +845 =-⎣⎢⎡⎦⎥⎤45(x -8)+x -85+745,(10分) ∵ x ≥9,∴45(x -8)+x -85≥2425=45,(12分) 当且仅当45(x -8)=x -85,即x =10,y min =14,(13分)答:当x =10时,下月的月总利润最大,且最大利润为14万元.(14分) 18.(1,依题意有:0)2('=f ,即此时:函数)(x f 在)2,1(上单调递减,在),2(+∞上单调递增,满足在2=x 时取得极值分 (2)依题意:)(≥x f 对任意),1[+∞∈x 恒成立等价转化为0)(min ≥x f 在),1[+∞∈x 恒成立 6分令0)('=x f 得:1,1221=-=x a x 8分当112≤-a 即1≤a 时,函数)('≥x f 在),1[+∞恒成立,则)(x f 在),1[+∞单调递增,于是022)1()(min ≥-==a f x f ,解得:1≤a ,此时:1≤a 10分②当112>-a 即1>a 时,函数)(x f 在]12,1[-a 单调递减,在),12[+∞-a 单调递增,于是022)1()12()(min <-=<-=a f a f x f ,不合题意,此时:Φ∈a综上所述:实数a 的取值范围是1≤a 12分. 说明:本题采用参数分离法或者先用必要条件0)1(≥f 缩小参数范围也可以.考点:1.函数的极值与导数;2.函数的最值与导数;3.分类讨论的思想. 19.解:(1)∵2()log (41)()x f x kx k =++∈R 是偶函数,∴2()log (41)()x f x kx f x --=+-=对任意x R ∈,恒成立 2分 即:22log (41)2log (41)x x x kx kx +--=++恒成立,∴1k =- 5分 (2)由于0a >,所以24()log (2)3x g x a a =⋅-定义域为24(log ,)3+∞, 也就是满足423x >7分 ∵函数()f x 与()g x 的图象有且只有一个交点, ∴方程224log (41)log (2)3x x x a a +-=⋅-在24(log ,)3+∞上只有一解 即:方程414223x xx a a +=⋅-在24(log ,)3+∞上只有一解 9分 令2,xt =则43t >,因而等价于关于的方程 24(1)103a t at ---=(*)在4(,)3+∞上只有一解 10分①当1a =时,解得34(,)43t =-∉+∞,不合题意; 11分 当01a <<时,记24()(1)13h t a t at =---,其图象的对称轴203(1)a t a =<- ∴函数24()(1)13h t a t at =---在(0,)+∞上递减,而(0)1h =- ∴方程(*)在4(,)3+∞无解 13分 ②当1a >时,记24()(1)13h t a t at =---,其图象的对称轴203(1)a t a =>- 所以,只需4()03h <,即1616(1)1099a a ---<,此恒成立 ∴此时a 的范围为1a > 15分 综上所述,所求a 的取值范围为1a > 16分19.20.解析:(1)∵()ln f x ax x x =+,∴'()ln 1f x a x =++, 1分 又∵()f x 的图象在点x e =处的切线的斜率为3,∴'()3f e =,即ln 13a e ++=,∴1a =; 2分 (2) 由(1)知,()ln f x x x x=+,∴2()f x kx ≤对任意0x >成立对任意0x >成立, 4分,则问题转化为求()g x 的最大值,,解得1x =, 5分 当01x <<时,'()0g x >,∴()g x 在(0,1)上是增函数;当1x >时,'()0g x <,∴()g x 在(1,)+∞上是减函数. 6分 故()g x 在1x =处取得最大值(1)1g =,∴1k≥即为所求; 8分(3分 由(2)知,1ln (0)x x x ≥+>,∴'()0h x ≥, 10分 ∴()h x 是(1,)+∞上的增函数,∵1n m >>,∴()()h n h m >,即分∴ln ln ln ln mn n n n mn m m m ->-, 12分 即ln ln ln ln mn n m m mn m n n +>+,ln ln ln ln mnm mn nnm m n +>+,ln()ln()n m m n mn nm >, 13分∴()()n mm nmn nm >,∴ 14分。
江苏省苏州市吴中区西安交通大学苏州附属中学2023-2024学年七年级上学期12月月考数学试题

江苏省苏州市吴中区西安交通大学苏州附属中学2023-2024学年七年级上学期12月月考数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题A .1个B .2个7.对有理数x ,y 定义运算:x y ax by =+※,其中那么a ,b 的取值范围是()A .1a <-,1b >B .1a >-,1b <三、计算题19.计算:四、作图题六、应用题24.王老师到商场购买了甲、乙两种笔记本,购买甲种笔记本15个,乙种笔记本20个,共花费250元,已知购买一个甲种笔记本比购买一个乙种笔记本多花费5元.(1)求购买一个甲种、一个乙种笔记本各需多少元?(2)某天王老师想再次购买两种笔记本共35个,正好赶上商场对商品价格进行调整,甲种笔记本售价比上一次购买时减价2元,乙种笔记本按上一次购买时售价的8折出售,如果王老师此次购买甲、乙两种笔记本的总费用不超过225元,求至多能购买多少个甲种笔记本?七、计算题25.定义:对于一个两位数x,如果x满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“相异数”,将一个“相异数”的个位数字与十位数字对调后得到一个八、问答题26.【阅读理解】我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,解决此类问题时一般要进行转化,其中“作差法”就是常用的方法之一.其依据是不等式(或等式)的性质:若0x y ->,则x y >;若0x y -=,则x y =;若0x y -<,则x y <.例:已知2M a ab =-,2N ab b =-,其中a b ¹,求证:M N >.证明:()222M N a ab ab b a b -=--+=-,因为a b ¹,所以()20a b ->,故M N >,【新知理解】(1)比较大小:3x -______2x +.(填“>”,“=”,“<”)【问题解决】(2)甲、乙两个平行四边形,其底和高如图所示(a 为正整数),其面积分别为1S ,2S .请比较1S ,2S 的大小关系.【拓展应用】(3)请用“作差法”解决下列问题:初中生小明暑假准备去游泳,已知游泳馆在暑假期间对学生优惠开放,游泳票为30元一张,有A ,B 两种方案可供选择,A 方案:每次按原价打9折收费;B 方案:前5次按照原价收费,从第6次起每次打8折.请问小明选择哪种方案更合算?27.如图,将等边ABC 放在数轴上,点B 与数轴上表示6-的点重合,点C 与数轴上(1)折叠后,点A与数轴上的数______(2)若点D为AC的中点,点E表示()=+,其中EC、CA代表线段长度.L EA EC CA向运动,动点Q从点E出发,沿时停止运动,已知动点P在DC上运动速度为秒;动点Q的速度为1单位/秒,设运动时间为①当t为何值时,动点P、Q表示同一个数;L PQ的表达式(用t表示)②求()③请直接写出:当t为多少秒时,。
西安交通大学苏州附属中学
校青年教师优秀课特等奖
区把握学科能力竞赛一等奖
语文
陈兴才
男
41
专科
本科
中学
高级
22
苏州市学科带头人
区指导学生自学先进教师
全国说课展示活动一等奖
教研组长
语文
周 静
女
34
本科
本科
中学
一级
12
区指导学生自学先进教师
语文
黄莉萍
女
28
本科
本科
中学
一级
7
校优秀工作者
校优秀助理班主任
语文
李倩
女
36
本科
本科
中学
一级
区解题基本功竞赛二等奖
高二英语
备课组长
英语
商三英
女
34
本科
硕士
中学
一级
12
区解题基本功竞赛二等奖
英语
金 萍
女
36
专科
本科
中学
高级
16
市解题基本功竞赛三等奖
高一英语
备课组长
英语
刘丹萍
女
35
本科
本科
中学
一级
12
区高中英语优质课评比一等奖
市高中英语教师评优课二等奖
英语
鲁华
女
33
本科
本科
中学
二级
9
苏州市高中英语优质课三等奖
数学
张祖银
男
40
专科
本科
中学
高级
19
园区教学能手
市网络教学团队一等奖
高一数学
备课组长
数学
黄红霞
女
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
备课组长
地理
张燕妮
女
29
本科
本科
中学
一级
7
市学科能力竞赛二等奖
学科优秀录像课评比二等奖
地理
王晨光
男
38
本科
本科
中学
一级
15
园区学科带头人
昆山市优秀班主任
高二地理
备课组长
体育
沈文玺
男
本科
本科
中学
二级
7
区体育教师基本功竞赛一等奖
体育
陆超武
男
39
本科
本科
中学
一级
16
县级市学科带头人
工会
负责人
体育
钱秀英
女
39
本科
本科
中学
高级
16
园区教学能手
政治
齐芹芹
女
30
硕士
硕士
1
校优秀助理班主任
历史
张连合
男
43
本科
本科
中学
高级
20
市青年优秀骨干教师
历史
李秦苏
女
28
本科
本科
中学
二级
6
园区教坛新秀
苏州海外联谊会周氏德育奖
校办副
主任
历史
殷莲子
女
27
本科
本科
中学
二级
5
园区教坛新秀
历史
钱珍
女
37
本科
本科
中学
高级
16
教研组长
生物
蒋玲玲
女
30
本科
本科
中学
二级
9
市区优质课评比一等奖
区把握学科能力竞赛一等奖
高二生物备课组长
生物
张桂花
女
37
专科
本科
中学
高级
15
区学科带头人
高三生物
备课组长
生物
陈蓉芳
女
27
本科
本科
中学
二级
3
市区高基本功竞赛三等奖
政治
朱桂友
男
46
本科
本科
中学
高级
23
园区学科带头人
校长助理
政治
李晓艳
女
36
本科
西安交通大学苏州附属中学
专任教师情况表
学科
姓名
性别
年龄
学历
专技
职称
任教
年限
荣誉称号
或获奖情况
备注
最初
最高
语文
许国庆
男
48
本科
本科
中学
高级
26
苏州市学科带头人
省优秀青少年科技教育校长
副校长
语文
卜延中
男
50
专科
本科
中学
高级
27
园区学科带头人
全国说课展示活动一等奖
教科室
主任
语文
周洁
女
31
本科
本科
中学
一级
8
男
40
专科
本科
中学
高级
19
园区教学能手
市网络教学团队一等奖
高一数学
备课组长
数学
黄红霞
女
31
本科
本科
中学
二级
8
市把握学科能力竞赛二等奖
数学
周苗
女
26
本科
本科
中学
二级
4
市教师基本功比赛三等奖
数学
孟广进
男
35
本科
本科
中学
一级
12
市数学竞赛一等奖
区把握学科能力竞赛一等奖
高三数学
备课组长
数学
秦卫东
男
41
专科
本科
中学
高级
20
区优秀教育工作者
区教学能手
数学
季红善
男
40
本科
本科
中学
高级
17
区把握学科能力竞赛一等奖
数学
姜竹岭
女
28
本科
本科
中学
二级
5
校优秀工作者
校优秀助理班主任
数学
施积林
男
45
本科
本科
中学
高级
25
苏州市学科带头人
市教师基本功评比二等奖
教研组长
数学
谈杰
男
31
本科
本科
中学
一级
8
园区教坛新秀
市教师教育技术竞赛二等奖
教研组长
美术
葛鑫
男
28
本科
本科
中学
二级
5
园区教师基本功竞赛二等奖
信息技术
郭松柏
男
33
中师
本科
中学
一级
14
校优秀工作者
教研组长
信息技术
潘婷
女
29
本科
本科
中学
二级
7
园区教师优秀课评比二等奖
信息技术
范子韬
男
26
本科
本科
中学
二级
3
校优秀助理班主任
园区教学能手
园区优秀教育工作者
教研组长
高一历史
备课组长
历史
周密
女
26
本科
本科
中学
二级
4
校优秀助理班主任
高三历史
备课组长
历史
夏勤
女
38
本科
硕士
中学高级
17
区把握学科能力竞赛一等奖
高二历史备课组长
高二年
级组长
历史
潘海燕
女
31
本科
硕士
中学
二级
9
校十佳班主任
历史
崔恒祥
男
32
本科
硕士
中学
一级
11
县优秀青年教师
英语
浦璇彦
女
26
本科
本科
中学
二级
4
区高中英语优质课评比二等奖
英语
诸葛
女
27
本科
本科
中学
二级
4
校优秀工作者
校优秀班主任
英语
王静静
女
29
本科
本科
中学
二级
7
市高中班主任比赛一等奖
英语
朱莹颖
女
26
本科
本科
中学
二级
3
区高中英语解题竞赛三等奖
英语
姚倩汝
女
25
本科
本科
中学
二级
2
校教学基本功竞赛二等奖
英语
刘献瑶
女
27
男
49
本科
本科
中学
高级
27
市区学科带头人
副校长
数学
杨原明
男
35
专科
本科
中学
一级
14
园区优秀教育工作者
园区教学能手
高三数学
备课组长
数学
王剑
男
36
本科
本科
中学
一级
15
江苏省优秀教育工作者
市数学教师评优课一等奖
教务处
主任
数学
张元建
男
42
本科
本科
中学
高级
18
市指导学生自学先进教师
区高考模拟卷命题二等奖
数学
张祖银
中学
二级
7
区青年教师基本功竞赛二等奖
物理
徐卫兵
男
44
本科
本科
中学
高级
26
江苏省特级教师
大市学科带头人
发展研究中心主任
物理
通技
宋海荣
男
36
大专
本科
中学
一级
14
市级教学能手
市教育系统新长征突击手
化学
王小阳
女
52
本科
本科
中学
高级
外借科教
创新区
化学
王晓珍
女
29
本科
本科
中学
一级
7
区化学教学设计比赛一等奖
高二化学
本科
中学
一级
13
园区教坛新秀
园区指导学生自学先进教师
高一政治
备课组长
政治
张斌
男
41
专科
本科
中学
高级
20
园区教学能手
园区优秀教育工作者
教研组长
高三政治
备课组长
政治
刘雁
女
35
专科
硕士
中学
高级
15
园区学科带头人
省高中评优课一等奖
高三年
级组长
政治
张建平
男
43
专科
本科
中学
高级
21
园区优秀党员
高二政治备课组长
政治
园区教坛新秀
全国说课展示活动二等奖
语文
宋亦琴
女
29
本科
本科
中学
二级
6
校优秀工作者
校优秀助理班主任
语文
张富玉
女
36
本科
本科
中学
一级
12
园区教科研学术带头人
园区优秀共产党员
高三语文
备课组长
语文
张兰芳
