多电子原子的结构
11 多电子原子系统及其壳层结构

多电子原子系统及其壳层结构
注意: 注意:常用支壳层电子组态表明原子结构 例碳原子:原子系数为6,核外有6个电子 例碳原子:原子系数为 ,核外有 个电子
各壳层最多可容纳的电子数: 各壳层最多可容纳的电子数: 壳层符号 K L M 1 3 主量子数 n 2
N 4 Nn 2 8 18 32 各支壳层最多可容纳的电子数: 各支壳层最多可容纳的电子数: (2l +1) 2 p d 支壳层符号 s f 3 1 2 角量子数 l 0 2 10 14 6 Nl
1s 2s 2 p
多电子原子系统及其壳层结构
例:钾原子核外有19个电子 钾原子核外有 个电子
各壳层最多可容纳的电子数: 各壳层最多可容纳的电子数: 壳层符号 K L M 1 3 主量子数 n 2
N 4 Nn 2 8 18 32 各支壳层最多可容纳的电子数: 各支壳层最多可容纳的电子数: (2l +1) 2 p d 支壳层符号 s f 3 1 2 角量子数 l 0 2 10 14 6 Nl
l
多电子原子系统及其壳层结构
两个原理: 二 两个原理: 1)泡利不相容原理(Pauli exclusion principle) )泡利不相容原理( ) 在原子系统内, 在原子系统内,不可能有两个或两个以上的 电子具有相同的状态, 电子具有相同的状态,亦不可能具有相同的四 个量子数。 个量子数。 因对应一个量子数为n的壳层 的壳层, 因对应一个量子数为 的壳层, 由此可知: 由此可知: 还有n个不同的角量子态 还有 个不同的角量子态 [l = 0.1.2L(n 1)] 对应每个角量子态还有 (2l +1)磁量子态 此外对应每个磁量子数还 [m = 0. ±1. ± 2L± l] 个自旋磁量子态。 有2个自旋磁量子态。 mS = ±1/ 2] 个自旋磁量子态 [
原子物理学5

同一电子组态在j-j耦合中和L-S耦合中形成的原子 态的数目相同,代表原子态的J值也是相同的。
例题:
若某原子的两个价电子处于2s2p组态,利用j-j耦合, 求可得到其原子态的个数。
同一电子组态在j-j耦合中和L-S耦合中形成的原 子态对应的能级间隔不同。
1P 1
( 1 3 , )1 2 2 1 3 , )2 2 2
1P 1 1S 0
三重态 2s3p 2s3s
3P 2 3P 1 3P 0 3S 1
2s2p 2s2s 1 2 3 4
1P 1 1S 0
2s2p 1 3
3P 2 3P 1 3P 0
2s2s在三层结构中没有对应的能级
例题2: 铍(Be)原子共有四个电子,已知其中三个始终处于 基态。 (1)写出铍原子的三个最低能量的电子组态; (2)用L-S耦合模型画出这三个最低能量电子组 态的全部能级; (3)画出上述能级间全部可能发生的跃迁。
1P , 3P 1 2,1,0
Pb:6p7s (j-j)
1 1 3 1 , , , 2 2 1 , 0 2 2 2 ,1
碳族元素在激发态ps的能级比较 C Si Ge Sn Pb
3 1 ( , )1 2 2 3 1 ( , )2 2 2
1P 3P
1 2
3P
3P
倒序排列:
3P > 3P > 3P 0 1 2
能级的形成:
基态:两个电子都处于最低的1s 态 激发态:所有能级都是由一个电子处于基态,另 一个电子被激发到较高能态形成的。 能级图上注明的数码就是第二个电子的主量子 数 试计算一下如果两个电子都处于激发态至少 需要多少能量?
单层结构 n
7.62eV
第八章 原子结构(2)
电负性( P)变化
主 族 元 素
元素的原子半径变化趋势
第四周期元素 r/pm 第五周期元素
Sc 161 Y
Ti 145 Zr
V 132 Nb
Cr 125 Mo
r/pm 第六周期元素 r/pm
181 Lu 173
160 Hf 159
143 Ta 143
146 W 137
镧系元素从左到右,原子半径减小幅 度更小,这是由于新增加的电子填入外数 第三层上,对外层电子的屏蔽效应更大, 外层电子所受到的 Z* 增加的影响更小。镧 系元素从镧到镱整个系列的原子半径减小 不明显的现象称为镧系收缩。
同一周期:
短周期:从左到右,Z*显著增加。 长周期:从左到右,前半部分有Z*增加 不多,后半部分显著增加。 同一族:从上到下,Z*增加,但不显著。
2. 原子半径
在同一周期中,从左到右减小 主 由于核电荷的增加,核外电子受核的引 族 力增大,原子半径减小。 元 素 在同一族中,从上到下增加 由于主量子数 n 的增加,原子半径一般增 加。 过渡元素:从左到右r 缓慢减小; 从上到下r略有增大。
Z=56,Ba: [Xe] 6s2 。
四个量子数小结:
原子中每个电子的运动状态可以用n,l,m, ms四个量子数来描述:主量子数n决定电子层 数和主要电子的能量;角量子数l决定原子轨道
的形状,同时也影响电子的能量;磁量子数m
决定原子轨道在空间的伸展方向;自旋量子数
ms决定电子自旋的方向。四个量子数确定后,
3. 电离能
第一电离能——处于基态的1mol气态原子失去 1mol电子成为气态一价正离子所需的能量,称 为该元素的第一电离能。 同一周期中 自左至右,第一电离能一般增加,但有一 些波动。当电子结构为全充满或半充满时, 其第一电离能相应较大。 同一族中 主族,自上而下第一电离能依次减小。
多电子原子的原子结构

第三节多电子原子的原子结构外层只有一个电子时,由于该电子仅受到核的吸引如氢原子或类氢原子,可以精确求解出波函数。
但多电子原子核外有2个以上的电子,电子除受核的作用外,还受到其他电子对它的排斥作用,情况要复杂得多,只能作近似处理。
但上述氢原子结构的某些结论还可用到多电子原子结构中:在多电子原子中,每个电子都各有其波函数ψi,其具体形式也取决一组量子数n、l、m。
多电子原子中的电子在各电子层中可能占据的轨道数,与氢原子中各电子层轨道数相等。
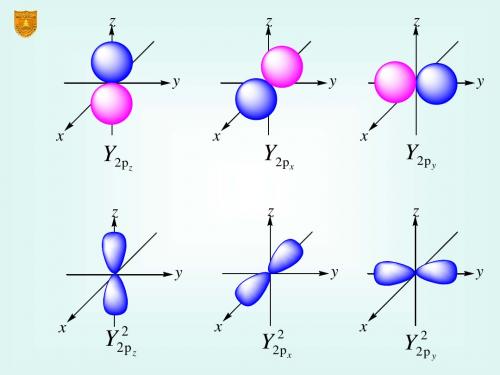
多电子原子中每个电子的波函数的角度部分Y(θ,φ)和氢原子Y(θ,φ)相似,所以多电子原子的各个原子轨道角度分布图与氢原子的各个原子轨道的角度分布图相似。
同理两者的Y 2图也相似。
处理多电子原子问题时,认为其他电子对某个电子i的排斥,相当于其他电子屏蔽住原子核,抵消了一部分核电荷对电子i的吸引力,称为其他电子对电子i的屏蔽作用(screening effect),引进屏蔽常数σ(screening constant)表示其他电子所抵消掉的核电荷。
这样多电子原子中电子i的能量公式可表示为式中(Z –σ)= Z′称为有效核电荷(effective nuclear charge)。
多电子原子电子的能量和Z、n、σ有关。
Z愈大,相同轨道的能量愈低,如基态氟原子1s电子的能量比基态氢原子1s电子的能量低;n愈大,能量愈高;起屏蔽作用的电子愈多,总的屏蔽作用愈强。
σ愈大,能量愈高。
影响σ有以下因素:1. 外层电子对内层电子的屏蔽作用可以不考虑,σ=0;2. 内层 (n-1层)电子对最外层(n层)电子的屏蔽作用较强,σ=,离核更近的内层(n-2层)电子对最外层电子的屏蔽作用更强,σ=;3. 同层电子之间也有屏蔽作用,但比内层电子的屏蔽作用弱,σ=,1s之间σ=。
n相同l不同时,l愈小的电子,它本身的钻穿能力愈强,离核愈近,它受到其他电子对它的屏蔽作用就愈弱,能量就愈低E n s <E n p <E n d <E n f。
多电子原子结构知识点

多电子原子结构知识点电子结构是物质性质的重要基础,而多电子原子结构的研究成为了化学和物理学领域必须面对的重要难题。
掌握多电子原子结构的知识对于理解元素周期表、化学键和化学反应等过程具有重要意义。
本文将介绍多电子原子结构的几个重要知识点,以帮助读者更好地理解和应用这一领域的知识。
1. 原子结构回顾在开始讨论多电子原子结构之前,我们首先回顾一下单电子原子结构的基本知识。
原子由原子核和绕核运动的电子组成。
电子可以分布在不同的能级和轨道上,能级越高,电子离原子核越远。
每个轨道可以容纳一定数量的电子,满足一定的填充顺序规则,如Aufbau原理和Hund规则等。
2. 多电子原子结构的挑战对于多电子原子结构的研究,面临了许多复杂的挑战。
首先是电子之间的相互作用问题。
由于电子带有负电荷,它们之间会发生斥力作用,使得电子在原子中的运动变得困难。
其次,由于电子的自旋和轨道运动,使得电子的能级分裂形成能级结构,增加了研究的复杂性。
3. 电子构型与元素周期表电子构型是描述原子中电子分布的方式。
通过填充顺序规则,我们可以确定每个元素的电子构型。
电子构型的特点与元素周期表的排布有密切关系。
元素周期表按照电子构型的特点将元素分类,帮助我们更好地理解元素的性质和规律。
4. 能级分裂与塞曼效应在外部磁场的作用下,电子能级会发生分裂,形成能级子。
这种现象被称为塞曼效应。
根据电子的自旋和轨道运动,能级子可以进一步分为塞曼项。
这个现象对于理解原子光谱以及应用与磁共振等领域具有重要意义。
5. 电子互斥原理和双电子积分电子互斥原理指出,由于两个电子都是费米子,它们不能同时处于同一个电子轨道中。
这一原理对于多电子体系的描述具有重要意义。
双电子积分则是用于计算多电子体系能量的基本方法,通过对电子波函数的积分,得到多电子体系的能量。
6. 配位化合物与电子排布配位化合物是指由一个中心金属离子和周围的配体离子或分子组成的化合物。
配位化合物中的电子排布对于其性质和反应有重要影响。
2014级大学化学 原子结构及元素性质的周期性(II)

氮原子中的各p电子,其量子数组合是
B. ⑴ ⑶ ⑸ 或⑵ ⑷ ⑹
D. ⑵ ⑷ ⑸
自测题:
原子序数为33的元素,其原子在 n=4,l=1,
m=0的轨道中的电子数为
A. 1 B. 2 D. 4 C. 3
自测题:
多电子原子中,各电子有以下量子数,其中能
量最高的是
A. 2, 1, 0, 1/2 C. 2, 1, 1, 1/2
B. 3, 2, 2, -1/2 D. 3, 1, -1, 1/2
特例:等价轨道处于全充满(p6、d10、f14)、半
充满(p3、d5、f7)或全空(p0、d0、f0)的状 态时,体系能量较低,状态较稳定。 例:
电子填入轨道的次序图
Filling the p Orbitals
Filling the d Orbitals
例:氦原子的1s 轨道中的两个电子
1 n 1, l 0, m 0, m s 2 1 n 1, l 0, m 0, m s 2
电子层中电子最大容量表
⑶ Hund 规则
电子分布到能量相同的等价轨道时, 总是尽先以自旋相同的方向,单独占据能 量相同的轨道,或者说成在等价轨道中自 旋相同的单电子越多,体系就越稳定。 等价轨道:n、l 相同的轨道,即同 一电子分层上的各个轨道。
4. 钻穿效应 主要是指 n 相同、l 不同的轨道,由于电子云径向 分布不同,电子穿过内层钻穿到核附近回避其它 电子屏蔽的能力不同,从而使其能量不同的现象。
用钻穿效应解释能级分裂现象:
如: E3s< E3p < E3d
电子钻得越深, 它受其它电子的 屏蔽作用就越小, 受核的吸引力越 强,因而能量也 越低。即钻穿作 用越大的电子的 能量越低。
第三章 多电子原子的结构

子半径逐渐收缩,这个现象称为镧系收缩。从 72 号 Hf 开始重新填充 5d 轨道,到 79 号 Au 5d 轨道填 满,形成第三过渡元素系。由于镧系收缩,第三过 渡系的元素与第二过渡系的元素中同族元素的原子 离子半径很相近,化学性质很相近。第七周期的 5f 轨道参与成键的程度比第六周期 4f 轨道要大(由于 5f 轨道有节面,4f 轨道没有节面,5f 轨道电子云分 布比 4f 更为弥散,离原子核更远)。从 Ac 到 Lr 的离子都具有 fx 的组态,化学性质很相似,称为锕 系元素。
§3 原子中电子的排布和元素周期表 3.1 原子中电子排布的原则
基态原子核外电子的分配遵从如下三条原则: (1)泡利原理:在同一原子中不能有两个或两个以 上的电子具有完全相同的四个量子数,即每一个原 子轨道最多只能填充两个自旋相反的电子。 (2)最低能量原理:在符合泡利原理的前提下,电 子填充后尽可能使体系的能量最低。 (3)洪特规则:在等价轨道(量子数 n、l 都相同) 上排布的电子尽可能分占不同的轨道,且自旋平行。
3. 第三周期填 3s 和 3p 轨道,可以填 8 个电子。3d 轨 道虽然可填 10 个电子,但由于优先填充 4s 比优先 填充 3d 的体系总能量更低,所以 3p 轨道填满后, 先填 4s 轨道,4s 填满后再填 3d,然后再填 4p,4d 和 5s 情况类似。这样就造成第三周期填充的轨道为 3s、3p,总数仍是 8 个电子。
上面四式中,η1 和 η2 是对称的,而 η3 和 η4 是 非对称的,但可将 η3 和 η4 线性组合成两个等价的自 旋波函数 (3-23) (3-24) 其中 η5 是对称的,η6 是反对称的。
包括空间坐标与自旋坐标的多电子体系的完全波 函数是否必须是对称或反对称的呢?并且是对称的还 是反对称的呢?泡利(Pauli)在总结大量实验结果的 基础上得出泡利原理。
第一章:原子结构

n 光谱符号
1 K
2 L
3 M
4 N
5 O
· · · · · ·
对氢原子来说,电子能量完全由n决定:
2.181018 Z 2 E J 2 n
四 个 量 子 数
B:角量子数:l 取值:0、1,2,3,. n-1
它表示原子轨道和电子云的形状 ,l与能级或称电子亚层对应。
(也是决定能量高低的因素)
自然界的物质种类繁多,性质各异,但它们都是由种类不同的原子组成,
原子以不同的种类.数目和方式结合,形成了无数的物种,因此,原子结构的
知识是了解物质结构和性质的基础。 化学变化包含着旧的化学键断裂和新的化学键的形成,化学变化一般 只涉及核外电子运动状态的变化,所以研究原子结构时,主要研究核外电子
的运动状态。
∴|ψ|2 ∝电子的几率密度
电子云角度分布图表示出电子在空间不同角度所出现的几率密度大小。
三、波函数的空间图象
B:电子云角度分布图 ︱Y(θ.φ) ︱2
z
+
→ θ.φ 作图,就得到电子云角度分布图
z y
+
z
+
x
-
x
+ -
x
pz z
x
s px z z x s px x x pz x py y
py
三、波函数的空间图象
E 光子 E E 2 E1 h 2.18 10
18
Z n 2n 2 2 1
2
1
←波长
青
氢原子光谱的一部分
课堂小结
玻尔理论最大贡献:建立微观粒子量子化特性,成功地解释了氢
原子光谱是线状光谱,为化学键理论奠定了基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E=E1+E2++En
i,Ei
实际上电子间的相互作用是不可忽略的!
1. 单电子近似法:
既不忽略电子间的相互作用,又用单电子波函 数描述多电子原子中单个电子的运动状态,而体系 的状态函数可以用单电子波函数的乘积来表示,为 此所作的近似称为单电子近似。
近似的物理基础:
每个电子都是在原子核和其它电子形成的有效 平均势场中“独立”地运动。
§2.4 多电子原子的结构
多电子原子由于电子间存在复杂的瞬时相互 作用,其势能函数比较复杂,精确求解比较困 难,一般采用近似解法。
§2.4.1 原子单位制
1. 国际单位制的基本单位:m, kg, s 2. cm, g, s 单位制
3. 原子单位制: 质量:me=9.110-31 kg 长度:a0=0.529 Å=0.529 10-10 m 时间:s
(2) 对所考虑的壳层,外层电子没有影响;
(3) 同一层每一个其它电子贡献0.35(1s层每一电子 0.30)
(4) 对s,p层,(n-1)层每个电子贡献0.85,更内层每 个电子为1.00;
(5) 对d层或f层,每一内层电子均为1.00。
Hˆ ii Eii
Hˆ i
1 2
i
2
Z ri
E4s
(Z
4s )2
2n 2
(19 16.8)2 2 42
0.134 Hartree
3.66eV
所以4s电子的电离能为3.66 eV
3. 自洽场方法(SCF: Self-consistent field)
(1,2,3…n)=1(1)2(2)3(3)···n(n)
Slater公式
与i对应的原子轨道能为:
Ei
(Z * )2 2n2
●原子中电子的第一电离能等于该电子所在原子 轨道 能的负值。
例:K原子(2881),求4s电子电离能?
(最外层电子受各层屏蔽作用常数为: 1.00,1.00,0.85)
解:4s=2×1.00+8×1.00+8×0.85=18.80
屏蔽模型-中心力场的半经验处理
物理基础:其它电子对电子i的排斥作用相当于
抵消了原子核中i个正电荷对该电子的吸引
屏蔽常数
U
i
(i)
i
ri
有效核电荷
Vi
Z ri
i
ri
Z i
ri
Z ri
Slater提出估算屏蔽常数的方法:
(1) 电子分层: 1s | 2s 2p | 3s 3p | 3d | 4s 4p | 4d | 4f | …… 每层具有不同的屏蔽常数;
j 2 d j ri j
电子j对电子i的排斥作用
其它n-1个电子对电子i的排斥作用:
n
Ui (i)
ji
j 2 d j
rij
电子i的单电子S方程:
2
(
1 2
i
2
Z ri
n ji
j d
rij
j
) i
Ei i
迭代法
2
Ei
Ti
Z ri
Vi (i)
Z ri
U i (i)
第i个电子所受的势能仅和其本身的坐标有关,
而与其它电子的位置无关
对于电子i:Hˆ i
1 2
i
2
Z ri
U i (i)
Hˆ ii Eii
i,Ei
(1,2,3…n)=1(1)2(2)3(3)···n(n) n(n):轨道-空间轨道
n ji
j d j
rij
Ei
n
Ti
i 1
n ( Z ) n
i1 ri
i 1
n ji
j 2 d j
rij
E
n i 1
(
1 2
i2 )
n i1
(
Z ri
)
n i 1
ji
1 rij
n
E Ei i 1
n
ri j
单电子原子的能级:En
Z2 n2
R
Z2 2n 2
§2.4.2 多电子原子体系的S方程
核固定近似下的哈密顿算符
1. He原子
Hˆ Tˆ Vˆ
1 2
12
1 2
22Fra bibliotek2 r1
2 r2
1 r12
2. Li原子
Hˆ Tˆ Vˆ
1 2
12
1 2
2
2
1 2
常用的单电子近似法有: (1)中心力场近似方法 (2)自洽场方法
2. 中心力场近似:
在多电子原子中,每个电子所受其它电子的排 斥作用近似为每个电子处于其它电子形成的具 有球对称的平均势场的作用
Ui(i)具有球对称性 吸引能项-Z/ri具有球对称性 整个势能函数具有球对称性
可以利用变量分离法求解 Hˆ ii Eii
引出单位: 电荷:e=1.6010-19 C 能量:Hartree=2R=27.2 eV 角动量: ħ
基本单位
3. 在原子单位制下的物理量对应的算符:
电子动能:Tˆ 2 2
2me
核对电子的吸引能: Ze 2
4 r
Tˆ 1 2 2
Z r
电子间的排斥能: e2
1
4ri j
Ei E 电子间的排斥能
i 1
库仑积分
电子i和电子j间的排斥能:
i
2 j 2 d i d j
rij
J ij
n
Ei E Jij
i 1
i j
32
3 r1
3 r2
3 r3
1 r12
1 r13
1 r23
3. 原子序数为Z的n电子体系
Hˆ Tˆ Vˆ
n i1
(
1 2
i
2
)
n ( Z ) i1 ri
n i1
ji
1 rij
其S方程为: Hˆ E
为n个电子坐标的函数: (x1,y1,z1; x2,y2,z2… xn,yn,zn)
写作:
(1,2…n)
§2.4.3 多电子原子S方程的求解
多电子原子S方程中包含许多rij项,无法分离
变量,不能精确求解,需设法求近似解。
一种很粗略的方法就是忽略电子间的相互作用, 即舍去第三项。
设(1,2,,n)=1(1)2(2)n(n), 则可分离变量成为n个方程:Ĥii(i)=Eii(i) ,
