关系代数表达式总结-数据库
关系代数等价变换规则

投影关于 笛 卡尔乘积 的 分配公式 : 设 E1 和 E2 是两个关 系代数表 达 式, A1,A2,…,An 是 E1 的属性变元,B1,B2,…,Bm 是 E2 的属性变元,则如下等价公 式成立: ∏A1,A2, ,An,B1,B2, ,Bm (E1 × E2) ≡ ∏ A1,A2, ,An (E1) × ∏ B1,B2, ,Bm (E2)
34
数据库理论及应用基础
3. 笛卡尔乘积与连接间的转换公式 设 E1 和 E2 是两个关系代数表达式, A1,A2,…,An 是 E1 的属性变元,B1,B2,…,Bm 是 E2 的属性变元,F 为形如 E1AiE2Bj 所组成的合取式,则如下等价公式成立: σ F (E1 × E2) ≡ E1 E2
σ F1∧ F2 (E)) ≡ σ F1 (σ F2 (E))
数据库理论及应用基础
33
(2) 投影运算串接公式 设 E 是一个关系代数表达式,B1,B2,…,Bm 是 E 中的某些属性名,而{A1,A2,…,An} 是{B1,B2,…,Bm}的子集,则以下等价公式成立: ∏A1,A2, An ( ∏ B1,B2, Bm (E)) ≡ ∏B1,B2 Bm (E)
F
例 4-2 我们可以将例 4-1 中表达式 Q1 转化成 Q2,同时也可以将 Q2 转化为 Q3。 用选择的串接等价公式将 Q1 转化为 Q*2: ∏ Sn (σ S.S#=SC.S# ∧SC.C# =C5(S × SC))= ∏Sn (σ SC.C#=C5 (σ S.S#=SC.S# (S × SC)) 用笛卡尔乘积与连接运算的转换公式将 Q*2 转换为 Q2: ∏ Sn (σ SC.C#=C5 (σ S.S#=SC.S# (S × SC)) ≡ ∏Sn (σ SC.C#=C5 (S SC)) 用选择运算与笛卡尔乘积交换公式,将 Q2 转化成 Q3: ∏ Sn (σ SC.C#=C5 (S SC) ≡ ∏Sn (S σ SC.C#=C5 (SC))
关系数据库关系代数运算

• 是一种抽象的查询语言
SQL
• 介于关系代数和关系演算之间 • 集DDL、DML和DCL一身的关系数据语言
2.2 关系数据结构的形式化定义
关系模型建立在集合代数基础上,从集合论角度讨论 关系的形式化定义
定义1:域(Domain)-形式化表示为D
• 一组具有相同数据类型的值的集合,如整数、实数等。定义
张三 女
802
李四 男
803
王五 男
804
赵六 女
805
钱七 男
01
19
01
20
01
20
02
20
02
19
专业号 01 02 03
专业名 信息 数学 计算机
关系间的引用
例2 学生、课程、学生与课程之间的多对多联系
学生(学号,姓名,性别,专业号,年龄) 课程(课程号,课程名,学分) 选修(学号,课程号,成绩)
外码说明
关系R和S不一定是不同的关系 目标关系S的主码Ks 和参照关系的外码F必
须定义在同一个(或一组)域上 关于取名
外码并不一定要与相应的主码同名 当外码与相应的主码属于不同关系时,往往取
相同的名字,以便于识别
参照完整性举例
例1:学生实体与专业实体间的关系: 外码 学生(学号,姓名,性别,专业号,年龄) 专业(专业号,专业名)
04
90
04
88
关系间的引用
例3 学生实体及其内部的领导联系(一对多)
学生(学号,姓名,性别,专业号,年龄,班长)
学号
801 802 803 804 805
姓名
张三 李四 王五 赵六 钱七
性别
女 男 男 女 男
《数据库原理及应用》-关系代数操作复习

关系代数操作复习实例:职工(职工编号,职工姓名,年龄,性别);E(ENO ,ENAME,AGE,SEX);社团(社团编号,社团名称);C(CNO ,CNAME);参加(职工编号,社团编号,参加时间);EC(ENO ,CNO,TIME);说明:(1)加粗的为主键;(2)参加表中的职工编号参照职工表中的职工编号,参加表中的社团编号参照社团表中的社团编号写出如下检索关系代数表达式:(1)检索年龄在30到50岁之间的职工编号和职工姓名AGE '30'AGE '50',((E))ENO ENAME σ>=∧<=∏(2)检索年龄在30到50岁之间的职工参加的社团名称AGE '30'AGE '50'((E C EC))CNAME σ>=∧<=∞∞∏(3)检索参加‘妇女之家’的职工编号''(())CNAME ENO C EC σ=∞∏妇女之家(4)检索参加‘书法社’或‘篮球队’的职工姓名''''AME ((E C EC))CNAME CNAME EN σσ=∨=∞∞∏书法社篮球队(5)检索既参加‘书法社’又参加‘篮球队’的职工姓名''''AME AME ((E C EC))((E C EC))CNAME CNAME EN EN σσ==∞∞∞∞∏∏ 书法社篮球队注意:不能将结果写成:''''AME ((E C EC))CNAME CNAME EN σσ=∧=∞∞∏书法社篮球队不能使指定的社团名称既是‘书法社’又是‘篮球队’。
假设社团表的信息如下:‘篮球队’,从表格中可以看出一个名称对应一个编号!(6)检索‘2014’年参加社团的职工信息'2014'NO,ENAME,AGE,SEX ((C EC))TIME E σ=∞∏(7)检索‘王小毛’参加的社团名称ENAME ''CNAME ((E C EC))σ=∞∞∏王小毛(8)检索没有参加任何社团的职工编号ENO ENO (E)-(EC)∏∏(9)检索没有参加‘篮球队’的职工姓名CNAME=''ENAME ENAME (E)-(E C EC )σ∞∞∏∏篮球队()。
数据库关系代数表达式学习

数据库关系代数表达式学习关系代数是关系数据库系统查询语言的理论基础一、关系代数的9种操作:关系代数中包括了:并、交、差、乘、选择、投影、联接、除、自然联接等操作。
五个基本操作:并(∪)、差(-)、笛卡尔积(×)、投影(σ)、选择(π)四个组合操作:交(∩)、联接(等值联接)、自然联接(R S)、除法(÷)注2:等值连接表示先做笛卡尔积(×)之后,对相应列进行选择或等值关联后的结果(仅筛选行、不筛选列) 注2:自然连接表示两个关系中若有相同名称的属性,则自动作为关联条件,且仅列出一列二、关系代数表达式:由关系代数运算经有限次复合而成的式子称为关系代数表达式。
这种表达式的运算结果仍然是一个关系。
可以用关系代数表达式表示对数据库的查询和更新操作。
三、举例说明:设教学数据库中有3个关系:学生关系S(SNO, SNAME,AGE,SEX)学习关系SC(SNO,CNO,GRADE)课程关系C(CNO,CNAME,TEACHER)(1) 检索学习课程号为C2的学生学号与成绩------------------------------------SELECT SNO,GRADEFROM SCWHERE CNO='C2'------------------------------------π SNO, GRADE (σ CNO='C2' (SC))************************************(2) 检索学习课程号为C2的学生学号与姓名------------------------------------SELECT SC.SNO,S.SNAMEFROM SC,SWHERE SC.SNO=S.SNOAND O='C2'------------------------------------π SNO,SNAME (σ CNO='C2' (S SC))此查询涉及S和SC,先进行自然连接,然后再执行选择投影操作。
关系运算----关系代数

R − S = {t | t ∈ R ∧ t ∉ S} 式中“-”为差运算符,t 为元组变量,结果 R-S 为一个新的与 R、S 同类的关系,该 关系是由属于 R 而且不属于 S 的元组构成的集合,即在 R 中减去与 S 中相同的那些元组。
c1
d1
a1
b1
c2
d2
a3
b3
c1
d1
a3
b3
c2
d2
图 2.12 关系 P1×R、P2×R 和 P3×R
3. 关系的联结——广义笛卡尔乘积运算
查询常常需要由多个关系生成一个新的关系。为了有效处理这种情况,引入广义笛卡尔 乘积运算。
设有关系 R、S,其中关系 R 有 r 个属性分量、m 个元组,关系 S 有 s 个属性分量、n 个元组,则二者的广义笛卡尔乘积(Cartesian Product)运算定义为:
2. 关系元组选定——选择运算
为了完成关系元组的选择,引入选择运算。 选择(Selection)也是一元关系运算,用于选取某个关系上我们感兴趣的某些行(满足一定 的条件的行),并且将它们组成一个新的关系。
Sn
Sa
刘刚
21
Class 2003A
王建
22
张华
21
李倩
20
2003A 2003A 2003A
A
B
C
a1
b1
c1
a1
b2
c2
a1
b2
c2
a2
b2
c1
a2
b2
c1
a2
b2
数据库期末复习资料-关系代数补充例题

2021/3/18
4
3. 关系代数表达式
关系代数表达式是由关系和关系运算符通过有限次 连接组成的表达式,用以表示对数据库数据的一组查询。
实例 对关系:s(sno,sname,sex)、c(cno,cname)、sc(sno,cno,score), 用关系代数表达式表示以下查询,并写出相应的T-SQL语句。
用这种方法解决选修所有课程的学生202131811相信梦想是价值的源泉相信眼光决定未来的一切相信成功的信念比成功本身更重要相信人生有挫折没有失败相信生命的质量来自决不妥协的信念
20XX年复习资料
大学复习资料
专 业: 班 级: 科目老师: 日 期:
例题
关系代数
2021/3/18
2
关系代数
关系代数是关系型数据库的重要理论基础。关系数据库系统 采用数学方法处理数据库中的数据,是建立在严密的数学理论基 础上的一种数据组织与存储方式。
单字段用not in 否则用not exists
或 SELECT sno FROM s WHERE NOT EXISTS
(SELECT * FROM sc WHERE sc.sno=s.sno AND cno='c001')
2021/3/18
7
实例3
查询选修“数据库应用”课程的学生的学号 关系代数表达式:
1001 c001 1001 c001
SELECT DISTINCT sc1.sno
1001 1001
c001 c001
1001 1003
c002 c001
√
FROM sc AS sc1,sc AS sc2 WHERE sc1.sno=sc2.sno AND o<>o
数据库关系代数
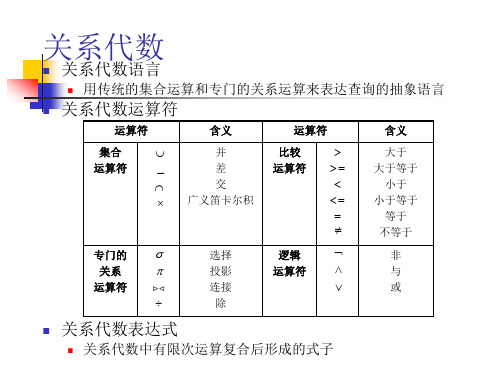
R S {trts | tr R ts S}
RS
AB
C
a1 b1 c1
a1 b2 c2
a2 b2 c1
a1 b3 c2
码.
( Sno
Cno = ‘1’
(SC))
2)在学以生上号S码-C.数据Sno库( 中C,no查= ‘询1’选v 修Cno了=‘13’号课程或3号课程的
(SC))
Sno( Cno = ‘1’ (SC)) U
( Sno
Cno = ‘1’
(SC))
关系代数:综合应用
2)查询选修了2号课程的学生的学号
19
IS
95004 张立 男
19
IS
Sno Sname Ssex Sage Sdept
95002 刘晨 女
19
IS
95003 王敏 女
18
MA
95004 张立 男
19
IS
关系代数:投影
定义:从关系R中选择出满足条件F的若 干属性列并组成新的关系,列选
F(R) {t[A] | t R}
A2,…,An中的一部分,则A称为属性列或域列 t[A]=(t[Ai1],t[Ai2],…,t[Aik])表示元组t在属性列A上
诸分量的集合
A 则表示{A1,A2,…,An}中去掉{Ai1,Ai2,…,Aik}
后剩余的属性组
传统的集合运算 若R和S是同类关系(即它们都具有n个属性且相应属性
第四步:判断包含关系
关系代数表达式的优化

1.2关系代数表达式的优化算法 1.优化算法
利用优化策略再结合等价变换规则我们 可以得到一个优化算法。 算法:关系代数表达式的优化。 输入:一个关系代数表达式的查询树。 输出:一个优化后的查询树。
2.优化步骤:
①利用规则(4),将查询树中的每个选择运算变成 选择串。
②利用规则(4)~(8)把查询树中的每一个选择 运算尽可能地移近树的叶节点。
③利用规则(3)、(5)、(9)、(10),把查询 树中的投影运算均尽可能地移近树的叶节点。若 某一投影是针对某一表达式中的全部属性,则可 消去这一投影运算。
④利用规则(3)~(5),把选择和投影运算合并 成单个选择、单个投影、选择后跟随投影等三种 情况。
⑤对经上述步骤后得到的查询树中的内部节点分组。 ⑥找出查询树中的公共子树Ti,并用该公共子树的
结果关系Ri代替查询树中的每一个公共子树Ti。 ⑦输出经优化后的查询树。
1.3关系代数表达式的优化策略 结合上面的变换规则和优化算法,下面给出三个简
实用的优化策略: 1)将选Байду номын сангаас尽可能转向叶结点。即尽可能先做选择运
算。在优化策略中这是最重要、最基本的一条。 2)合并可能的投影 3)将投影尽可能转向叶结点
数据库原理与应用
关系代数表达式的优化
1.1关系代数表达式的等价变换规则 (1)连接、笛卡儿积交换律 (2)连接、笛卡儿积的结合律 (3)投影的串接定律 (4)选择的串接定律 (5)选择与投影的交换律
(6)选择和笛卡儿积的交换律 (7)选择与并的交换 (8)选择与差的交换 (9)投影与笛卡儿积的交换 (10)投影与并的交换
数据库原理与应用
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关系代数表达式总结一、并例1 求选修了课程号为1或2的课程的学生学号。
分析:可以先求出选修了课程号为1的课程的学生学号,再求出选修了课程号为2的课程的学生学号,最后使用并运算的方法求出选修课程号为1或2的课程的学生学号。
本例也可以使用或条件来表示。
πSno(σCno=’1’(SC))∪πSno(σCno=’2’(SC)) 或πSno(σCno=’1’∨Cno=’2’(SC))二、交例2 检索至少选修课程号为2和3的课程的学生学号。
分析:方法一:只涉及到一个表,但不能直接用∧(为什么?)特别注意,本例不能写为:πSno(σCno=’2’∧Cno=’3’(SC))因为选择运算为行运算,在同一行中Cno不可能既为2,又为3。
第一步:转换(SC×SC)笛卡尔积将垂直的条件展开为水平的条件。
选修课程号为2和3的学生:σ1=4∧2=’2’∧5=’3’(SC×SC)最后取出学生的学号:π1(σ1=4∧2=’2’∧5=’3’(SC×SC))方法二:πSno(σCno=’2’(SC))∩πSno(σCno=’3’(SC))三、差例3 将学生信息(‘95001’,’李勇’,‘男’,20,‘CS’)从Student表删除。
分析:可以将这行数据看成由一个元组构成的表,将Student表与该表进行差运算。
因此,该删除操作可表示为:Student-{‘95001’,’李勇’,‘男’,20,‘CS’}注意:但是当查询涉及到否定或全部值时,上述形式就不能表达了,就要用到差操作或除操作。
例4 求没有选修课程号为2的课程的学生学号。
分析:可以认为是在全部学号中去掉选修课程号为2的课程的学生学号,就得出没有选修课程号为2的学生学号。
由于在并、交、差运算中,参加运算的关系要求是兼容的,故应当先投影,再进行差运算。
πSno(Student)- πSno(σCno=’2’(SC))特别注意,本题不能写为:πSno(σCno≠’2’(SC))。
因为,选择运算为行运算,并且SC 表中包含的只是选修了课程的学生学号,对那些没选任何课程的学生学号,在SC中找不到。
根据题意,要查询没有选修课程号为‘2’课程的学生学号,显然包括没选任何课程的学生学号。
当查询涉及到针对“否定”特征含义的查询要求,如“不”、“没有”等字眼,一般要用差运算表示。
四、自然连接例5 检索不学“2”号课程的学生姓名与年龄。
分析:首先考虑“差”的问题。
先求出全体学生的姓名和年龄,再求出学了”2”号课程的学生的姓名和年龄,最后执行两个集合的差操作。
πSname,Sage(Student)- πSname,Sage(σCno=’2’(Student SC))例6 查询至少选修了一门其直接先行课为“5”号课程的学生姓名。
分析:(1)根据题目确定要输出的列为:Sname,都在Student表中;(2)根据题意,先行课程名为“5”,则选择的条件为Cpno=’5’,因为Cpno在Course表中,所以也要用到Course表;(3)根据1,2两步确定用到的表名集为{Student,Course};(4)因为表名集中两个表,则要用自然连接将它们连接起来,但因为这个两表不存在共同的列,不能进行自然连接。
因此要加入中间表,中间表中应含有能与其它两个表进行自然连接的公共列,这个表就是SC。
将选择条件Cpno=‘5’作用于自然连接后产生的新表上,并用投影操作选取要输出的Sno,Cno。
综上,该查询的关系代数表达式为:πSname(σCpno=’5’(Course)SCπSno,Sname(Stuent))或πSname(πSno(σCpno=’5’(Course)SC)Stuent))五、除1.除法定义中的含义分析:(1)前提:两个关系R(X,Y)和S(Y,Z)应该有公共属性列。
(2)运算结果为P(X),元组来自于R关系,只包含X属性列(3)R关系中的哪些元组呢?对于T[X]的象集包含∏Y(S)2.除法运算的步骤(1)将被关系R的属性分成两个部分,即与除关系相同的属性部分Y,和与除关系不同的属性部分X。
(2)在除关系中,求Y的投影,得到目标数据集。
(3)将被除关系进行分组。
(分组原则是“值”一样的为一组)(4)考虑被除关系中已分好的每一元组,如果它的象集包含目标数据集(投影结果),则其值为商。
例如,R SR÷SAa1(c)分析:在关系R中,A可以取四个值{a1,a2,a3,a4}。
其中:a1的象集为{(b1,c2),(b2,c3),(b2,c1)}a2的象集为{(b3,c7),(b2,c3)}a3的象集为{(b4,c6)}a4的象集为{(b6,c6)}S在(B,C)上的投影为{(b1,c2),(b2,c1),(b2,c3)}显然只有a1的象集(B,C)a1包含了S在(B,C)属性组上的投影,所以R÷S={a1}。
例,R表示选修课程,S1、S2、S3表示课程情况3.除法的物理意义(1)除法的含义:R÷S1表示至少选修S1关系中列出课程的学生的学号和姓名;R÷S2表示至少选修S2关系中列出课程的学生的学号和姓名;(2)求选修所有课的同学姓名:(S、SC、C)说明:针对“全部”特征含义的查询要求,如“全部”、“至少”、“包含”等字眼,一般要用除法运算。
4.有时需要构造被除数与除数除操作是同时从行和列角度进行运算(S是R的子集),构造被除数与除数。
用除法的第一种情况例7 检索至少选修课程号为1和2的学生学号。
分析:(1)至少选修课程号为1和2的关系(表)。
(2)考虑用除法来做(3)构造一个临时表K=πCno(σCno=’1’∨Cno=’2’(Course))(4)构造被除数与除数πSno,Cno(SC)÷K用除法的第二种情况例8 查询选修了全部课程的学生的学号。
1) 确定目标属性:学号Sno;2) 确定目标条件:如果学号x被查询到,说明在临时关系πSno,Cno(SC)表中学号x的像集就是所有课程号Cno组成的集合;3) 确定目标关系:根据1)、2)的分析,可以确定该查询是在πsno,cno(SC)和Course两个关系上进行除法运算。
其中,关系SC提供选修信息,而Course提供全部的课程号信息。
4) 画查询树:图3 例题2 的查询树5) 写出关系代数表达式:πsno,cno(SC)÷πcno(Course)。
例9 查询选修全部课程的学生号码和姓名。
(结果需同时满足多个关系的时候用除法)。
πSno,Cno(SC)÷πCno(Course)πSno,Sname(Student)六、综合实例1、设有如下所示的关系:学生表S(S#,SNAME,AGE,SEX)、课程表C(C#,CNAME,TEACHER)和学生选课表SC(S#,C#,GRADE),其中:S#为学号,SNAME 为姓名,AGE为年龄,SEX为性别,C#为课程号,CNAME为课程名,GRADE为成绩, TEACHER为教师。
S#SNAME AGE SEX1李强23男2刘丽22女3张友22男C#CNAME TEACHERK1C语言王华K5数据库原理程军K8编译原理程军(1)检索“程军”老师所授课程的课程号(C#)和课程名(CNAME)。
(2)检索年龄大于21的男学生学号(S#)和姓名(SNAME)。
(3)检索至少选修“程军”老师所授全部课程的学生姓名(SNAME)。
(4)检索“李强”同学不学课程的课程号(C#)。
(5)检索至少选修两门课程的学生学号(S#)。
(6)检索全部学生都选修的课程的课程号(C#)和课程名(CNAME)。
(7)检索选修课程包含“程军”老师所授课程之一的学生学号(S#)。
(8)检索选修课程号为K1和K5的学生学号(S#)。
(9)检索选修全部课程的学生姓名(SNAME)。
(10)检索选修课程包含学号为2的学生所修课程的学生学号(S#)。
(11)检索选修课程名为“C语言”的学生学号(S#)和姓名(SNAME)。
解:本题各个查询语句对应的关系代数表达式表示如下:(1)πC#,CNAME(σTEACHER=‘程军’(C))(2)πS#,SNAME(σAGE>21∧SEX=‘男’(S))(3)πSNAME(Sw v(πS#,C#(SC)÷πC#(σTEACHER=‘程军’(C))))(4)πC#(C)-πC#(σSNAME=‘李强’(S) w v SC)(5)πS#(σ1=4∧2≠5(SC ×SC))(6)πC#,CNAME(Cw v(πS#,C#(SC)÷πS#(S)))(7)πS#(SCw vπC#(σTEACHER=‘程军’(C)))(8)πS#,C#(SC)÷πC#(σC#=’k1’∨C#=’k5’(C))(9)πSNAME(Sw v(πS#,C#(SC)÷πC#(C)))(10)πS#,C#(SC)÷πC#(σS#=’2’(SC))(11)πS#,SNAME(Sw v(πS#(SCw vσCNAME=‘C语言’(C))))2、设有如下所示的关系:学生表S(S#,SNAME,AGE,SEX)、课程表C(C#,CNAME,TEACHER)和学生选课表SC(S#,C#,GRADE),其中:S#为学号,SNAME 为姓名,AGE为年龄,SEX为性别,C#为课程号,CNAME为课程名,GRADE为成绩, TEACHER为教师。
(1)检索LIU老师所授课程的课程号和课程名;(2)检索年龄大于23岁的男学生的学号和姓名;(3)检索学号为S3学生所学课程的课程名与任课教师名;(4)检索至少选修LIU老师所授课程中一门课的女学生姓名;(5)检索WANG同学不学的课程的课程号;(6)检索既选修了LIU老师的课程、又选修了LI老师课程的学生学号;(7)全部学生都选修的课程的课程号与课程名;(8)检索选修课程包含LIU老师所授全部课程的学生学号。
解:本题各个查询语句对应的关系代数表达式表示如下:(1)πC#,CNAME(σTEACHER=‘LIU’(C))(2)πS#,SNAME(σAGE>23∧SEX=‘男’(S))(3)πCNAME,TEACHER(σS#=‘S3’(SCw v C))(4)πSNAME(σSEX=’女’∧TEACHER=‘LIU’(Sw v SCw v C))(5)πC#(C)-πC#(σSNAME=‘WANG’(Sw v SC))(6)π1(σ1=4∧2≠5(SC×SC))(7)πC#,CNAME(Cw v(πS#,C#(SC)÷πS#(S)))(8)πS#,C#(SC)÷πC#(σTEACHER=‘LIU’(C))。
