数据结构实验3二叉树
实验报告二叉树

递归遍历右子树输出根结点数data}void postOrder1 (struct btnode *bt){概念栈,结点参数p,prebt入栈While(栈或p是不是为空){提取栈顶元素值if判定p是不是为空或是pre的根结点输出根结点数data栈顶元素出栈栈顶元素p赋给pre记录else if右结点非空将右结点压栈if左结点将左结点压栈}}void main(){struct btnode *root=NULL;root=createbt(root);preOrder(root); midOrder(root); postOrder(root);preOrder1(root); midOrder1(root); postOrder1(root);
数据结构二叉树实验报告
一 、实验目的和要求(1)掌握树的相关概念,包括树、节点的度、树的度、分支节点、叶子节点、孩子节点、双亲节 点、树的深度、森林等定义。
(2)掌握树的表示,包括树形表示法、文氏图表示法、凹入表示法和括号表示法等。
(3)掌握二叉树的概念,包括二叉树、满二叉树和完全二叉树的定义。
(4)掌握二叉树的性质。
(5)重点掌握二叉树的存储结构,包括二叉树顺序存储结构和链式存储结构。
(6)重点掌握二叉树的基本运算和各种遍历算法的实现。
(7)掌握线索二叉树的概念和相关算法的实现。
(8)掌握哈夫曼树的定义、哈夫曼树的构造过程和哈夫曼编码的产生方法。
(9)掌握并查集的相关概念和算法。
(10)灵活运用二叉树这种数据结构解决一些综合应用问题。
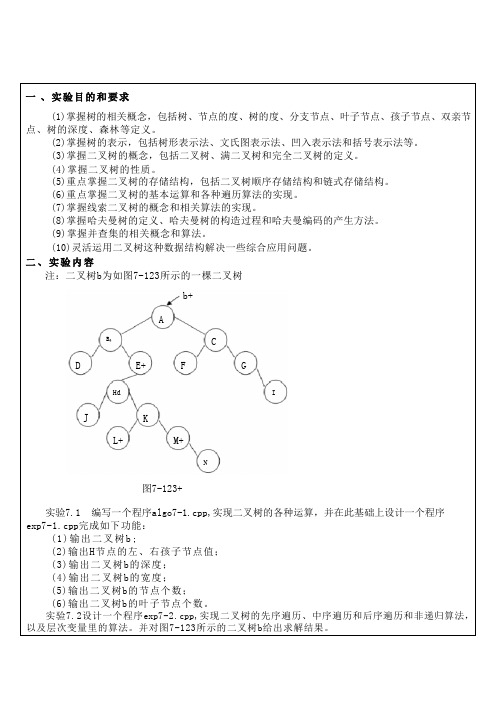
二、实验内容注:二叉树b 为如图7-123所示的一棵二叉树图7-123+实验7.1 编写一个程序algo7-1.cpp,实现二叉树的各种运算,并在此基础上设计一个程序exp7-1.cpp 完成如下功能:(1)输出二叉树b ;(2)输出H 节点的左、右孩子节点值; (3)输出二叉树b 的深度; (4)输出二叉树b 的宽度; (5)输出二叉树b 的节点个数;(6)输出二叉树b 的叶子节点个数。
实验7.2设计一个程序exp7-2.cpp,实现二叉树的先序遍历、中序遍历和后序遍历和非递归算法, 以及层次变量里的算法。
并对图7-123所示的二叉树b 给出求解结果。
b+ACF GIKL+NM+E+HdJD₄B臣1607-1.CPPif(b?-HULL)re3P4+;Qu[rear]-p-b;Qu[rear].1no=1;while(reart=front){Front++;b=Qu[front]-P;lnum-Qu[front].1no;if(b->Ichildt=NULL)rpar+t;Qu[rear]-p=b->1child;Qu[rear].Ino-lnun+1;if(D->rch11d?=NULL)1/根结点指针入队//根结点的层次编号为1 1/队列不为空1/队头出队1/左孩子入队1/右孩子入队redr+t;qu[rear]-p=b->rchild;Qu[rear].1no-lnun*1;}}nax-0;lnun-1;i-1;uhile(i<=rear){n=0;whdle(i<=rear ge Qu[1].1no==1num)n+t;it+;Inun-Qu[i].1n0;if(n>max)nax=n;}return max;田1607-1.CPPreturn max;}elsereturn o;口×int Modes(BTNode *D) //求二叉树D的结点个数int nun1,nun2;if(b==NULL)returng,else if(b->ichild==NULL&D->rchild==NULL)return 1;else{num1-Hodes(b->Ichild);num2=Nodes(b->rchild);return(num1+nun2+1);LeafNodes(BINode *D) //求二叉树p的叶子结点个数int num1,num2;1f(D==NULL)return 0;else if(b->1chi1d==NULLc& b->rch11d==NULL)return 1;else{num1-LeafModes(b->lchild);num2=LeafNodes(b->rchild);return(nun1+nun2);int程序执行结果如下:xCProrn FlslirosfViu l SudiollyPrjecslro7 LJebuglFoj7 ex<1)输出二叉树:A<B<D,E<H<J,K<L,M<,N>>>>),C<F,G<,I>>)<2)'H’结点:左孩子为J石孩子为K(3)二叉树b的深度:7<4)二叉树b的宽度:4(5)二叉树b的结点个数:14(6)二叉树b的叶子结点个数:6<?>释放二叉树bPress any key to continue实验7 . 2程序exp7-2.cpp设计如下:坠eTPT-2.EPP#include<stdio.h》winclude<malloc.h>deFn Masie 00typde chr ElemTyetypede sruct nde{ElemType data;stuc node *lclldstruct node rchild;》BTHode;extern vod reaeBNodeBTNode extrn void DispBTHode(BTNodeuoid ProrderBTNode *b)if(b?-NULL)- 回1 / 数据元素1 / 指向左孩子1 / 指向右孩子*eb car *str)xb1 / 先序遍历的递归算法1 / 访问根结点/ / 递归访问左子树1 7 递归访问右子树/ / 根结点入栈//栈不为空时循环/ / 退栈并访问该结点/ / 右孩子入栈{》v oidprintf(*c“,b->data); Preorder(b->lchild); Pre0rder(b->rchild);Preorder1(BTNode *b)BTNode xSt[Maxsize],*p;int top=-1;if(b!-HULL)top++;St[top]-b;uhle (op>-)p-St[top];top--;printf("%c“,p->data);if(p->rchild?-HULL)A约e程p7-2.CPPprintF(”后序逅历序列:\n");printf(" 递归算法=");Postorder(b);printf("\n");printf(“非递归算法:“);Postorder1(b);printf("\n");序执行结果如下:xCAPrograFleicsoftVisal SudlyrjecsProj 2Debuzlroj72ex"二叉树b:A(B(D,ECH<J,K(L,M<,N)>))),C(F,GC.I>))层次遍历序列:A B C D E F G H I J K L M N先序遍历序列:递归算法:A B D E H J K L M N C F G I非归算法:A B D E H J K L M N C F G I中序遍历序列:递归算法: D B J H L K M N E A F C G I非递归算法:D B J H L K M N E A F C G I后序遍历序列:递归算法: D J L N M K H E B F I G C A非递归算法:D J L N H K H E B F I G C APress any key to continue臼p7-3.CPP15Pp a t h[p a t h l e n]-b->d a t a;//将当前结点放入路径中p a t h l e n t+;/7路任长度培1Al1Path1(b->ichild,patn,pathlen);1/递归扫描左子树Al1Path1(b->rchild,path,pathlen); //递归扫描右子树pathlen-- ; //恢复环境uoid Longpath(BTNode *b,Elemtype path[1,int pathlen,Elemtype longpath[],int elongpatnien) int i;1f(b==NULL){if(pathlen>longpatnlen) //若当前路径更长,将路径保存在1ongpatn中for(i-pathlen-1;i>-8;i--)longpath[i]=path[1];longpathlen-pathlen;elsepath[pathlen]=b->data; pathlen4; //将当前结点放入路径中//路径长度增1iongPath(b->lchild,path₇pathlen,langpath,longpathien);//递归扫描左子树LongPath(b->rchiid,path,pathien,longpath,longpathien);//递归扫描石子树pathlen--; /7饮其环境oid DispLeaf(BTNode xb)- 口凶uoid DispLeaf(BTNode xb)iE(D!=NULL){ if(b->1child--HULL B& b->rchild--HULL)printf("3c“,b->data);elsepispLeaf(b->ichild);DispLeaf(b->rchild);oid nain()8TNodexb;ElenType patn[Maxsize],longpath[Maxsize];int i.longpathien-U;CreateBTNode(b,"A(B(D,E(H(J,K(L,H(,N))))),C(F,G(,I)))");printf("\n二灾树b:");DispBTNode(b);printf("\n\n*);printf(”b的叶子结点:");DispLeaf(b);printf("\n\n");printf("A11Path:");A11Path(b);printf("m");printf("AiiPath1:n");AliPath1(b.path.);printf("");LongPath(b,path,8,longpath,longpathlen);printf(”第一条量长路径长度=d\n”,longpathlen);printf(”"第一茶最长路径:");for(i=longpathlen;i>=0;i--)printf("c",longpatn[1]);printf("\n\n");。
数据结构实验报告 二叉树

数据结构实验报告二叉树数据结构实验报告:二叉树引言:数据结构是计算机科学中的重要基础,它为我们提供了存储和组织数据的方式。
二叉树作为一种常见的数据结构,广泛应用于各个领域。
本次实验旨在通过实践,深入理解二叉树的概念、性质和操作。
一、二叉树的定义与性质1.1 定义二叉树是一种特殊的树结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。
二叉树可以为空树,也可以是由根节点和左右子树组成的非空树。
1.2 基本性质(1)每个节点最多有两个子节点;(2)左子树和右子树是有顺序的,不能颠倒;(3)二叉树的子树仍然是二叉树。
二、二叉树的遍历2.1 前序遍历前序遍历是指首先访问根节点,然后按照先左后右的顺序遍历左右子树。
在实际应用中,前序遍历常用于复制一颗二叉树或创建二叉树的副本。
2.2 中序遍历中序遍历是指按照先左后根再右的顺序遍历二叉树。
中序遍历的结果是一个有序序列,因此在二叉搜索树中特别有用。
2.3 后序遍历后序遍历是指按照先左后右再根的顺序遍历二叉树。
后序遍历常用于计算二叉树的表达式或释放二叉树的内存。
三、二叉树的实现与应用3.1 二叉树的存储结构二叉树的存储可以使用链式存储或顺序存储。
链式存储使用节点指针连接各个节点,而顺序存储则使用数组来表示二叉树。
3.2 二叉树的应用(1)二叉搜索树:二叉搜索树是一种特殊的二叉树,它的左子树上的节点都小于根节点,右子树上的节点都大于根节点。
二叉搜索树常用于实现查找、插入和删除等操作。
(2)堆:堆是一种特殊的二叉树,它满足堆序性质。
堆常用于实现优先队列,如操作系统中的进程调度。
(3)哈夫曼树:哈夫曼树是一种带权路径最短的二叉树,常用于数据压缩和编码。
四、实验结果与总结通过本次实验,我成功实现了二叉树的基本操作,包括创建二叉树、遍历二叉树和查找节点等。
在实践中,我进一步理解了二叉树的定义、性质和应用。
二叉树作为一种重要的数据结构,在计算机科学中有着广泛的应用,对于提高算法效率和解决实际问题具有重要意义。
数据结构实验三实验报告

数据结构实验三实验报告数据结构实验三实验报告一、实验目的本次实验的目的是通过实践掌握树的基本操作和应用。
具体来说,我们需要实现一个树的数据结构,并对其进行插入、删除、查找等操作,同时还需要实现树的遍历算法,包括先序、中序和后序遍历。
二、实验原理树是一种非线性的数据结构,由结点和边组成。
树的每个结点都可以有多个子结点,但是每个结点只有一个父结点,除了根结点外。
树的基本操作包括插入、删除和查找。
在本次实验中,我们采用二叉树作为实现树的数据结构。
二叉树是一种特殊的树,每个结点最多只有两个子结点。
根据二叉树的特点,我们可以使用递归的方式实现树的插入、删除和查找操作。
三、实验过程1. 实现树的数据结构首先,我们需要定义树的结点类,包括结点值、左子结点和右子结点。
然后,我们可以定义树的类,包括根结点和相应的操作方法,如插入、删除和查找。
2. 实现插入操作插入操作是将一个新的结点添加到树中的过程。
我们可以通过递归的方式实现插入操作。
具体来说,如果要插入的值小于当前结点的值,则将其插入到左子树中;如果要插入的值大于当前结点的值,则将其插入到右子树中。
如果当前结点为空,则将新的结点作为当前结点。
3. 实现删除操作删除操作是将指定的结点从树中移除的过程。
我们同样可以通过递归的方式实现删除操作。
具体来说,如果要删除的值小于当前结点的值,则在左子树中继续查找;如果要删除的值大于当前结点的值,则在右子树中继续查找。
如果要删除的值等于当前结点的值,则有三种情况:- 当前结点没有子结点:直接将当前结点置为空。
- 当前结点只有一个子结点:将当前结点的子结点替代当前结点。
- 当前结点有两个子结点:找到当前结点右子树中的最小值,将其替代当前结点,并在右子树中删除该最小值。
4. 实现查找操作查找操作是在树中寻找指定值的过程。
同样可以通过递归的方式实现查找操作。
具体来说,如果要查找的值小于当前结点的值,则在左子树中继续查找;如果要查找的值大于当前结点的值,则在右子树中继续查找。
[精品]【数据结构】二叉树实验报告
![[精品]【数据结构】二叉树实验报告](https://img.taocdn.com/s3/m/5d561ae96e1aff00bed5b9f3f90f76c661374c27.png)
[精品]【数据结构】二叉树实验报告二叉树实验报告一、实验目的:1.掌握二叉树的基本操作;2.理解二叉树的性质;3.熟悉二叉树的广度优先遍历和深度优先遍历算法。
二、实验原理:1.二叉树是一种树形结构,由n(n>=0)个节点组成;2.每个节点最多有两个子节点,称为左子节点和右子节点;3.二叉树的遍历分为四种方式:前序遍历、中序遍历、后序遍历和层次遍历。
三、实验环境:1.编程语言:C++;2.编译器:Dev-C++。
四、实验内容:1.定义二叉树节点结构体:struct BinaryTreeNode{int data; // 节点数据BinaryTreeNode *leftChild; // 左子节点指针BinaryTreeNode *rightChild; // 右子节点指针};2.初始化二叉树:queue<BinaryTreeNode *> q; // 使用队列存储节点q.push(root);int i = 1; // 创建子节点while (!q.empty() && i < length){BinaryTreeNode *node = q.front();q.pop();if (data[i] != -1) // 创建左子节点 {BinaryTreeNode *leftChild = new BinaryTreeNode;leftChild->data = data[i];leftChild->leftChild = nullptr;leftChild->rightChild = nullptr;node->leftChild = leftChild;q.push(leftChild);}i++;if (data[i] != -1) // 创建右子节点 {BinaryTreeNode *rightChild = new BinaryTreeNode;rightChild->data = data[i];rightChild->leftChild = nullptr;rightChild->rightChild = nullptr;node->rightChild = rightChild;q.push(rightChild);}i++;}return root;}3.前序遍历二叉树:五、实验结果:输入:int data[] = {1, 2, 3, 4, -1, -1, 5, 6, -1, -1, 7, 8};输出:前序遍历结果:1 2 4 5 3 6 7 8中序遍历结果:4 2 5 1 6 3 7 8后序遍历结果:4 5 2 6 8 7 3 1层次遍历结果:1 2 3 4 5 6 7 8通过本次实验,我深入理解了二叉树的性质和遍历方式,并掌握了二叉树的基本操作。
数据结构二叉树的实验报告

数据结构二叉树的实验报告数据结构二叉树的实验报告一、引言数据结构是计算机科学中非常重要的一个领域,它研究如何组织和存储数据以便高效地访问和操作。
二叉树是数据结构中常见且重要的一种,它具有良好的灵活性和高效性,被广泛应用于各种领域。
本实验旨在通过实际操作和观察,深入了解二叉树的特性和应用。
二、实验目的1. 理解二叉树的基本概念和特性;2. 掌握二叉树的创建、遍历和查找等基本操作;3. 通过实验验证二叉树的性能和效果。
三、实验过程1. 二叉树的创建在实验中,我们首先需要创建一个二叉树。
通过输入一系列数据,我们可以按照特定的规则构建一棵二叉树。
例如,可以按照从小到大或从大到小的顺序将数据插入到二叉树中,以保证树的有序性。
2. 二叉树的遍历二叉树的遍历是指按照一定的次序访问二叉树中的所有节点。
常见的遍历方式有前序遍历、中序遍历和后序遍历。
前序遍历是先访问根节点,然后再依次遍历左子树和右子树;中序遍历是先遍历左子树,然后访问根节点,最后再遍历右子树;后序遍历是先遍历左子树,然后遍历右子树,最后访问根节点。
3. 二叉树的查找二叉树的查找是指在二叉树中寻找指定的节点。
常见的查找方式有深度优先搜索和广度优先搜索。
深度优先搜索是从根节点开始,沿着左子树一直向下搜索,直到找到目标节点或者到达叶子节点;广度优先搜索是从根节点开始,逐层遍历二叉树,直到找到目标节点或者遍历完所有节点。
四、实验结果通过实验,我们可以观察到二叉树的特性和性能。
在创建二叉树时,如果按照有序的方式插入数据,可以得到一棵平衡二叉树,其查找效率较高。
而如果按照无序的方式插入数据,可能得到一棵不平衡的二叉树,其查找效率较低。
在遍历二叉树时,不同的遍历方式会得到不同的结果。
前序遍历可以用于复制一棵二叉树,中序遍历可以用于对二叉树进行排序,后序遍历可以用于释放二叉树的内存。
在查找二叉树时,深度优先搜索和广度优先搜索各有优劣。
深度优先搜索在空间复杂度上较低,但可能会陷入死循环;广度优先搜索在时间复杂度上较低,但需要较大的空间开销。
数据结构 实验报告

数据结构实验报告一、实验目的数据结构是计算机科学中非常重要的一门课程,通过本次实验,旨在加深对常见数据结构(如链表、栈、队列、树、图等)的理解和应用,提高编程能力和解决实际问题的能力。
二、实验环境本次实验使用的编程语言为C++,开发工具为Visual Studio 2019。
操作系统为 Windows 10。
三、实验内容1、链表的实现与操作创建一个单向链表,并实现插入、删除和遍历节点的功能。
对链表进行排序,如冒泡排序或插入排序。
2、栈和队列的应用用栈实现表达式求值,能够处理加、减、乘、除和括号。
利用队列实现银行排队系统的模拟,包括顾客的到达、服务和离开。
3、二叉树的遍历与操作构建一棵二叉树,并实现前序、中序和后序遍历。
进行二叉树的插入、删除节点操作。
4、图的表示与遍历用邻接矩阵和邻接表两种方式表示图。
实现图的深度优先遍历和广度优先遍历。
四、实验步骤及结果1、链表的实现与操作首先,定义了链表节点的结构体:```cppstruct ListNode {int data;ListNode next;ListNode(int x) : data(x), next(NULL) {}};```插入节点的函数:```cppvoid insertNode(ListNode& head, int val) {ListNode newNode = new ListNode(val);head = newNode;} else {ListNode curr = head;while (curr>next!= NULL) {curr = curr>next;}curr>next = newNode;}}```删除节点的函数:```cppvoid deleteNode(ListNode& head, int val) {if (head == NULL) {return;}ListNode temp = head;head = head>next;delete temp;return;}ListNode curr = head;while (curr>next!= NULL && curr>next>data!= val) {curr = curr>next;}if (curr>next!= NULL) {ListNode temp = curr>next;curr>next = curr>next>next;delete temp;}}```遍历链表的函数:```cppvoid traverseList(ListNode head) {ListNode curr = head;while (curr!= NULL) {std::cout << curr>data <<"";curr = curr>next;}std::cout << std::endl;}```对链表进行冒泡排序的函数:```cppvoid bubbleSortList(ListNode& head) {if (head == NULL || head>next == NULL) {return;}bool swapped;ListNode ptr1;ListNode lptr = NULL;do {swapped = false;ptr1 = head;while (ptr1->next!= lptr) {if (ptr1->data > ptr1->next>data) {int temp = ptr1->data;ptr1->data = ptr1->next>data;ptr1->next>data = temp;swapped = true;}ptr1 = ptr1->next;}lptr = ptr1;} while (swapped);}```测试结果:创建了一个包含 5、3、8、1、4 的链表,经过排序后,输出为 1 3 4 5 8 。
数据结构实验报告—二叉树

数据结构实验报告—二叉树数据结构实验报告—二叉树引言二叉树是一种常用的数据结构,它由节点和边构成,每个节点最多有两个子节点。
在本次实验中,我们将对二叉树的基本结构和基本操作进行实现和测试,并深入了解它的特性和应用。
实验目的1. 掌握二叉树的基本概念和特性2. 熟练掌握二叉树的基本操作,包括创建、遍历和查找等3. 了解二叉树在实际应用中的使用场景实验内容1. 二叉树的定义和存储结构:我们将首先学习二叉树的定义,并实现二叉树的存储结构,包括节点的定义和节点指针的表示方法。
2. 二叉树的创建和初始化:我们将实现二叉树的创建和初始化操作,以便后续操作和测试使用。
3. 二叉树的遍历:我们将实现二叉树的前序、中序和后序遍历算法,并测试其正确性和效率。
4. 二叉树的查找:我们将实现二叉树的查找操作,包括查找节点和查找最大值、最小值等。
5. 二叉树的应用:我们将探讨二叉树在实际应用中的使用场景,如哈夫曼编码、二叉搜索树等。
二叉树的定义和存储结构二叉树是一种特殊的树形结构,它的每个节点最多有两个子节点。
节点被表示为一个由数据和指向其左右子节点的指针组成的结构。
二叉树可以分为三类:满二叉树、完全二叉树和非完全二叉树。
二叉树可以用链式存储结构或顺序存储结构表示。
- 链式存储结构:采用节点定义和指针表示法,通过将节点起来形成一个树状结构来表示二叉树。
- 顺序存储结构:采用数组存储节点信息,通过计算节点在数组中的位置来进行访问和操作。
二叉树的创建和初始化二叉树的创建和初始化是二叉树操作中的基础部分。
我们可以通过手动输入或读取外部文件中的数据来创建二叉树。
对于链式存储结构,我们需要自定义节点和指针,并通过节点的方式来构建二叉树。
对于顺序存储结构,我们需要定义数组和索引,通过索引计算来定位节点的位置。
一般来说,初始化一个二叉树可以使用以下步骤:1. 创建树根节点,并赋初值。
2. 创建子节点,并到父节点。
3. 重复步骤2,直到创建完整个二叉树。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
}
else
{
Q->front=(Q->front+1)%MAXSIZE;
*x=Q->data[Q->front];
return1;
}
}
voiddestory_seqqueue(Pseqqueue*Q)
{
if(*Q)
free(*Q);
*Q=NULL;
}
voidPreOrder(BTreet)
一、 实验目的
1. 进一步掌握指针变量的含义。
2. 掌握二叉树的结构特征,以及各种存储结构的特点及使用范围。
3. 掌握用指针类型描述、访问和处理二叉树的运算。
二、 实验要求
1. 认真阅读和掌握本实验的参考程序。
2. 按照对二叉树的操作需要,在创建好二叉树后再通过遍历算法验证创建结果。
3. 保存程序的运行结果,并结合程序进行分析。
}SeqStack,*PSeqStack;
PSeqStackInit(void)
{
PSeqStackS;
S=((PSeqStack)malloc(sizeof(SeqStack)));
if(S)
{
S->top=-1;
returnS;
}
}
intEmpty(PSeqStackS)
{
if(S->top==-1)
{
inth1,h2;
if(t==NULL) return 0;
else
{
h1=Height(t->lchild);
h2=Height(t->rchild);
if(h1>h2) return h1+1;
elsereturn h2+1;
}
}
intmain()
{
BTreeT;
inta=0;
intb=0;
T=create();
return;
}
intleaf(BTreeT)
{
if(T == NULL)
return0;
if(T->lchild== NULL && T->rchild== NULL)
return1;
returnleaf(T->lchild) + leaf(T->rchild);
}
intHeighபைடு நூலகம்(BTreet)
{
if(t)
{
printf("%c",t->data);
PreOrder(t->lchild);
PreOrder(t->rchild);
}
}
voidPostOrder2(BTreet)
{
PSeqStackS;
DataSq;
BTreep=t;
S=Init();
while(p||!Empty(S))
{
if(p)
{
Sq.flag=0;Sq.node=p;
Push(S,Sq);
p=p->lchild;
}
else
{
Pop(S,&Sq);
p=Sq.node;
if(Sq.flag==0)
{
Sq.flag=1;
Push(S,Sq);
p=p->rchild;
}
else
{
printf("%c",p->data);
p=NULL;
}
returnQ;
}
intempty_seqqueue(PseqqueueQ)
{
if(Q&&Q->rear==Q->front)
return1;
else
return0;
}
intin_seqqueue(PseqqueueQ,BTreex)
{
if((Q->rear+1)%MAXSIZE==Q->front)
{
printf("队满");
return-1;
}
else
{
Q->rear=(Q->rear+1)%MAXSIZE;
Q->data[Q->rear]=x;
return0;
}
}
intout_seqqueue(PseqqueueQ,BTree*x)
{
if(empty_seqqueue(Q))
{
printf("队空");
return0;
else
{
*x=S->Data[S->top];
S->top--;
return1;
}
}
Pseqqueueinit_seqqueue(void)
{
PseqqueueQ;
Q=(Pseqqueue)malloc(sizeof(seqqueue));
if(Q)
{
Q->front=0;
Q->rear=0;
while(!empty_seqqueue(q))
{
out_seqqueue(q,&p);
printf("%c",p->data);
if(p->lchild)in_seqqueue(q,p->lchild);
if(p->rchild)in_seqqueue(q,p->rchild);
}
destory_seqqueue(&q);
return1;
else
return0;
}
intPush(PSeqStackS,Datax)
{
if(S->top==MAXSIZE-1)
return0;
else
{
S->top++;
S->Data[S->top]=x;
return1;
}
}
intPop(PSeqStackS,Data*x)
{
if(Empty(S))
typedefstruct{
BTreedata[MAXSIZE];
intfront,rear;
}seqqueue,*Pseqqueue;
typedefstruct{
BNode*node;
intflag;
}Data;
typedefstructnode
{
DataData[MAXSIZE];
inttop;
PostOrder2(T);
printf("\n");
HBiTree(T);
printf("\n");
a=Height(T);
printf("深度为:%d\n",a);
b=leaf(T);
printf("叶子数:%d\n",b);
return0;
}
实验结果如下:
三、 实验内容
以下参考程序是按完全二叉树思想将输入的字符串生成二叉树,并通过遍历来验证二叉树创建正确与否,但不能创建非完全二叉树,请认真研究该程序,然后模仿教材例6.4初始化方式创建二叉树:所有的空指针均用#表示,如教材图6-13对应的二叉树,建立时的初始序列为:AB#D##CE##F##。然后通过遍历算法验证二叉树是否正确(先递归验证后非递归验证)。
}
returnT;
}
voidHBiTree(BTreet)
{
Pseqqueueq;
q=init_seqqueue();
if(t==NULL) return;
BTreep=t;
printf("%c",p->data);
if(p->lchild)in_seqqueue(q,p->lchild);
if(p->rchild)in_seqqueue(q,p->rchild);
参考程序略
程序代码如下:
#include "stdio.h"
#include "stdlib.h"
typedefcharDatatype;
#define MAXSIZE 100
typedefstructbnode
{
Datatypedata;
structbnode*lchild,*rchild;
}BNode,*BTree;
}
}
}
}
BTreecreate()
{
BTreeT;
charc;
scanf("%c",&c);
if('#' == c)
T=NULL;
else
{
T=(BTree)malloc(sizeof(BNode));
T->data = c;
T->lchild=create();
T->rchild=create();
