第04讲 基本不等式(达标检测)(原卷版)
第04讲 基本不等式及其应用(十八大题型)(课件)-高考数学一轮复习(新教材新高考)

【典例1-1】下列不等式证明过程正确的是( )
A.若, ∈ R,则 + ≥ 2
⋅ =2
C.若x<0,则 + 4 ≥ −2 ⋅ 4 = −4
B.若x>0,y>0,则lg + lg ≥ 2 lg ⋅ lg
D.若x<0,则2 + 2− > 2 2 ⋅ 2− = 2
解析二: − 2 − = 0 ⇒ − 1 − 2 = 2,
则 + 2 = − 1 + 2 − 4 + 5 ≥ 2 2 − 1 − 2 + 5 = 9,
=3
− 1 = 2 − 4
⇒
等号成立时
,所以 + 2的最小值是9.
+ 2 = 9
=3
故答案为:9.
,解方程得
或
2
=1
= 1
=2
【方法技巧】
1、通过添项、拆项、变系数等方法凑成和为定值或积为定值的形式.
2、注意验证取得条件.
题型突破·考法探究
题型三:常规凑配法求最值
【变式3-1】若 > −2,则 = +
1
的最小值为
+2
.
【答案】0
1
【解析】由 > −2,得 + 2 > 0, +2 > 0,
所以() = +
1
+2
当且仅当 + 2 =
故答案为:0
=+2
1
即
+2
1
+
+2
第04讲 利用导数研究不等式恒成立问题(含新定义解答题)(分层精练)(原卷)-25年高考数学一轮复习

两个实数
x 1
,x
2
,且
x1
x2 ,若不等式
f
x1 f x2
x1 x2
1恒成立,则实数 a 的取值范围为(
)
A.9,
B.7,
C.9,
D.7,
4.(22-23
高二下·广东揭阳·阶段练习)已知函数
f
(x)
ex
x2
2ax, x 1 (a 3) x
a
2,
x
,若关于 1
x
的不等式 f (x) 0恒成立,则实数 a 的取值范围为( )
A. 1 e
B.1
C. e
D. e 1
7.(23-24 高二下·重庆·阶段练习)已知函数 f (x) 2x ln x ( ln 2 1)x ,若对 x(0,) ,
都有 f x 0 ,则实数 的取值范围是( )
A.
(,
1 e
]
B.
[
e
1 ln
2
,
)
C.[1 , ) e
D.[ln 2, )
(北 京)股 份有限 公司
8.(2024·辽宁·一模)已知函数 f x e2x e2x ax ,若 x 0 时,恒有 f x 0 ,则 a 的取
值范围是( )
A. , 2
B. , 4
C.2,
D.4,
二、多选题
9.(2023·全国·模拟预测)设函数 f x x 1ln x 1(x 0) ,若 f x k 1 x 1恒成
11.(2024 高三·全国·专题练习)若不等式 xex-ex ln x>mx-ex 恒成立,则正整数 m 的最
大值为
.
12.(22-23 高二下·黑龙江齐齐哈尔·阶段练习)如果存在函数 g x ax b ( a,b 为常数),
2020高考数学《专题04 等式性质与不等式性质、基本不等式》(原卷版)

专题四 等式性质与不等式性质、基本不等式 核心素养练习一、核心素养聚焦考点一 逻辑推理-利用不等式的性质证明不等式例题9. 若a >b >0,c <d <0,e <0,求证:e (a -c )2>e (b -d )2.考点二 数学运算-利用基本不等式求条件最值例题10.已知x >0,y >0,且满足8x +1y=1.求x +2y 的最小值.考点三 数学建模素养-利用基本不等式解决实际问题例题11、如图,动物园要围成相同面积的长方形虎笼四间,一面可利用原有的墙,其他各面用钢筋网围成.现有36 m 长的钢筋网材料,每间虎笼的长、宽分别设计为多少时,可使每间虎笼面积最大?二、学业质量测评一、选择题1.(2019·全国高一课时练习)若0a b >>,则下列不等式成立的是 ( )A. 2a b a b +>>>B.2a b a b +>>>C. 2a b a b +>>>D. 2a b a b +>>> 2.(2019·全国高一课时练习)已知实数()()120,1,0,1a a ∈∈,记12121M a a N a a ==+-,,则( )A .M N <B .M N >C . M N =D .大小不确定3.(2019·全国高一课时练习)已知正数,a b 满足10ab =,则2+a b 的最小值是 ( )A. B. C. D. 4.(2019·全国高一课时练习)已知1x >,则41x x +-的最小值为 A .3 B .4 C .5D .6 5.(2019·全国高一课时练习)已知14a b ≤+≤,12a b -≤-≤,则42a b -的取值范围是( )A.[]4,10-B.[]3,6-C.[]2,14-D.[]2,10-6.(2019·全国高一课时练习)盐水溶液的浓度公式为()b p a b a =>盐的量克盐水的量克,向盐水中再加入m 克盐,那么盐水将变得更咸,下面哪一个式子可以说明这一事实( ) A. bb m a a m +<+ B. bb m a a m +>+ C. bb m a a +< D. bb m a a+>二、填空题7.(2019·全国高一课时练习)已知实数a 、b ,满足02a b <<<,则-a b 的取值范围是_____________.8.(2019·全国高一课时练习)设a =2b =+,a b 的大小关系为 . 9.(2019·全国高一课时练习)周长为12的矩形,其面积的最大值为____________;10.(2019·全国高一课时练习)已知0,0a b >>,122a b +=,则a b +的最小值为_______________; 三、解答题11.(2019·全国高一课时练习)已知0a >,0b >,试比较11a b M a b =+++与11b a N a b =+++的大小.12.(2019·全国高一课时练习)(1)已知0x >,求42y x x=--的最大值; (2)已知112x -<<,求()()112y x x =+-的最大值.13.(2018·全国高二课时练习)某住宅小区为了使居民有一个优雅、舒适的生活环境,计划建一个八边形的休闲小区,其主体造型的平面图是由两个相同的矩形ABCD 和矩形EFGH 构成的面积是200m 2的十字形区域,现计划在正方形MNPQ 上建一花坛,造价为4 200元/m 2,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元/m 2,再在四个空角上铺草坪,造价为80元/m 2.(1)设总造价为S 元,AD 的边长为x m ,试建立S 关于x 的函数解析式;(2)计划至少要投多少万元才能建造这个休闲小区?。
2024年高考数学 高三大一轮复习专题04 基本不等式

专题04 基本不等式【知识精讲】一、基本不等式12a b+≤(1)基本不等式成立的条件:0,0a b >>. (2)等号成立的条件,当且仅当a b =时取等号. 2.算术平均数与几何平均数设0,0a b >>,则a 、b 的算术平均数为2a b+,基本不等式可叙述为:两个正数的算术平均数不小于它们的几何平均数. 3.利用基本不等式求最值问题(1)如果积xy 是定值P ,那么当且仅当x y =时,x +y 有最小值是简记:积定和最小)(2)如果和x +y 是定值P ,那么当且仅当x y =时,xy 有最大值是24P .(简记:和定积最大) 4.常用结论(1)222(,)a b ab a b +≥∈R (2)2(,)b aa b a b+≥同号 (3)2()(,)2a b ab a b +≤∈R (4)222()(,)22a b a b a b ++≤∈R(5)2222()()(,)a b a b a b +≥+∈R(6)222()(,)24a b a b ab a b ++≥≥∈R(7)222(0,0)1122a b a b ab a b a b++≥≥≥>>+ 二、常见求最值模型 模型一:)0,0(2>>≥+n m mn x nmx ,当且仅当mn x =时等号成立; 模型二:)0,0(2)(>>+≥+−+−=−+n m ma mn ma ax na x m a x n mx ,当且仅当mna x =−时等号成立;模型三:)0,0(2112>>+≤++=++c a bac xc b ax c bx ax x ,当且仅当acx =时等号成立; 模型四:)0,0,0(4)21)()(22mnx n m m n mx n mx m m mx n mx mx n x <<>>=−+⋅≤−=−(,当且仅当mnx 2=时等号成立. 【题型精讲】题型一 利用基本不等式求最值【例1-1】对勾函数 求下列函数的最值(1)已知54x <,则函数1445y x x =+−的最大值为___________.【答案】3 【解析】 【分析】由于5,4504x x <−< ,需要构造函数,才能运用基本不等式.【详解】因为54x <,所以450x −<,540x −>,()1144554545y x x x x =+=−++−−()()11545254535454x x x x ⎡⎤=−−++≤−−⋅=⎢⎥−−⎣⎦当且仅当15454x x−=−,即1x =时,等号成立.故当1x =时,y 取最大值,即max 3y =.故答案为:3.(2)已知54x >,则函数1445y x x =+−的最小值为___________.【答案】3 【解析】 【分析】由于5,4504x x >−> ,需要构造函数,才能运用基本不等式.【详解】因为54x >,所以450x −>,()1144554545y x x x x =+=−++−−()14555745x x ⎡⎤=−++≥=⎢⎥−⎣⎦当且仅当14545x x −=−,即32x =时,等号成立.故当32x =时,y 取最小值,即min7y=.故答案为:3.(3)已知2x ≥,则函数1445y x x =+−的最小值为___________. 【答案】325 【例1-2】最值定理(1)已知01x <<,则(43)x x −取得最大值时x 的值为________.【答案】 23【解析】 【分析】(1)积的形式转化为和的形式,利用基本不等式求最值,并要检验等号成立的条件; 【详解】解:(1)2113(43)4(43)3(43)3323x x x x x x +−⎡⎤−=⨯−≤⨯=⎢⎥⎣⎦, 当且仅当343x x =−,即23x =时,取等号. 故答案为:23.(2)若x ,y 为实数,且26x y +=,则39x y +的最小值为( )A .18B .27C .54D .90【答案】C 【解析】 【分析】利用基本不等式可得答案. 【详解】由题意可得2393322754x y x y +=+≥=⨯=, 当且仅当233x y =时,即2x y =等号成立. 故选:C .【例1-3】“1”的妙用 (1)若正实数,a b 满足32a b +=,则11a b+的最小值为___________.【答案】22 【解析】 【分析】用“1”的代换凑配出定值后用基本不等式求得最小值. 【详解】1111113(3)2()22222b a a b a b a b a b ⎛⎫+=++=++≥+ ⎪⎝⎭,当且仅当3b a a b =时,即a b ==时,11a b +的最小值为2.故答案为:2.(2)已知0x >,0y >,且22x y +=,则433x y x y++的最小值为__________.【答案】3【解析】 【分析】将目标式中4代换成24x y +,展开由基本不等式可得. 【详解】 因为22x y +=所以432434333333x y x y x y y x x y x y x y ++++=+=++≥+= 当且仅当4322yx x y x y ⎧=⎪⎨⎪+=⎩,即3x y ==时,取等号,所以433x y x y ++的最小值为3故答案为:3【例1-4】分离常数法 当2x >−时,函数2462++=+x x y x 的最小值为___________.【答案】【解析】 【分析】将函数解析式变形为()222y x x =+++,利用基本不等式可求得结果. 【详解】因为2x >−,则20x +>,则()()22224622222x x x y x x x x ++++===+++++≥=当且仅当2x 时,等号成立,所以,当2x >−时,函数2462++=+x xy x 的最小值为故答案为:【例1-5】换元法 已知正数x ,y 满足21133x y x y+=++,则x y +的最小值( )AB .34+CD .38+ 【答案】A 【解析】 【分析】利用换元法和基本不等式即可求解. 【详解】令3x y m +=,3x y n +=,则211m n+=, 即()()()334m n x y x y x y +=+++=+,∴21121344424444m n m n m n x y m n n m +⎛⎫⎛⎫+==++=+++≥ ⎪⎪⎝⎭⎝⎭33244=+=,当且仅当244m n n m=,即2m =1n =时,等号成立, 故选:A.【例1-6】消元法 已知正实数a ,b 满足220ab a +−=,则4a b +的最小值是( )A.2 B .2 C .2 D .6【答案】B 【解析】 【分析】根据220ab a +−=变形得22a b =+,进而转化为a b b b +=++842, 用凑配方式得出()b b ++−+8222,再利用基本不等式即可求解. 【详解】由220ab a +−=,得22a b =+,所以()a b b b b b b +=+=++−⋅=+++888422222222,当且仅当,a b b b ==+++28222,即a b ==22取等号. 故选:B.【例1-7】一元二次不等式法 已知x ,y R ∈,2291x xy y −+=,则3x y +的最大值为________.【解析】 【分析】由229123x y xy x y +=+⋅⋅,可推出15xy ,而222(3)6917x y x xy y xy +=++=+,代入所得结论即可. 【详解】解:2291x xy y −+=,22916x y xy xy ∴+=+,即15xy ,当且仅当3x y =,即15x y ⎧=⎪⎪⎨⎪=⎪⎩或x y ⎧=⎪⎪⎨⎪=⎪⎩时,等号成立,222112(3)69171755x y x xy y xy ∴+=++=+≤+⨯=,∴3x y +≤3x y ∴+【例1-8】拆项法,,a b c 是不同时为0的实数,则2222ab bca b c +++的最大值为( )A .12 B .14CD【答案】A 【解析】 【分析】对原式变形,两次利用基本不等式,求解即可. 【详解】因为a ,b 均为正实数,则2222222ab bc a c a c a b c b b ++=≤++++12==≤=, 当且仅当222a c b b +=,且a c =取等,即a b c ==取等号,即则2222ab bc a b c +++的最大值为12,故选:A .【练习1-1】(1)已知1x >−,求函数27101x x y x ++=+的值域;(2)已知0x >,0y >,且280x y xy +−=,求:x y +的最小值. 【答案】(1)[)9,+∞;(2)18. 【解析】 【分析】(1)设1t x =+,得到0t >,且1x t =−,化简2710451x x y t x t ++==+++,结合基本不等式(对勾函数法),即可求解;(2)由280x y xy +−=,得到821x y +=,化简()822810x yx y x y x y y x ⎛⎫+=++=++ ⎪⎝⎭,结合基本不等式(“1”的妙用),即可求解. 【详解】(1)设1t x =+,因为1x >−,可得0t >,且1x t =−,故22710(1)7(1)10451x x t t y t x t t ++−+−+===+++,因为44t t+≥,可得459t t ++≥,当且仅当2t =时,即1x =时,等号成立.所以函数2710(1)1x x y x x ++=>−+的值域为[)9,+∞.(2)由280x y xy +−=,可得28x y xy +=,即821x y +=,则()82x y x y x y ⎛⎫+=++ ⎪⎝⎭281010218x y y x =++≥+=. 当且仅当28x y y x=,即12x =且6y =时,等号成立, 所以x y +的最小值为18.【练习1-2】已知正实数a ,b 满足26a b +=,则212a b ++的最小值为( )A .45B .43C .98D .94【答案】C 【解析】 【分析】利用乘1法即得. 【详解】 ∵26a b +=,∴()214114122222822a b a b a b a b ⎛⎫+=+=+++ ⎪+++⎝⎭()(42121941582288b a b a +⎡⎤=+++≥⨯+=⎢⎥+⎣⎦, 当且仅当()42222b ab a+=+,即23b =,83a =时,取等号. 故选:C.【练习1-3】已知对任意正实数x ,y ,恒有()2222x y a x xy y +−+≤,则实数a 的最小值是___________. 【答案】2 【解析】 【分析】证明220x xy y −+>,由()2222x y a x xy y +−+≤,即2222x y a x xy y +−+≤,22222211x y xy x xy y x y +=−+−+结合基本不等式求出2222max x y x xy y ⎛⎫+ ⎪−+⎝⎭,即可得出答案. 【详解】解:因为0,0x y >>,则()2220x xy y x y xy −+=−+>, 则()2222x y a x xy y +−+≤,即2222x y a x xy y +−+≤, 又22222211x y xy x xy y x y +=−+−+, 因为222x y xy +≥,所以22112xy x y −≥+,所以22121xy x y ≤−+, 即22222x y x xy y+≤−+,当且仅当x y =时,取等号, 所以2222max2x y x xy y ⎛⎫+= ⎪−+⎝⎭, 所以2a ≥,即实数a 的最小值是2.故答案为:2.【练习1-4】已知正数a ,b 满足426a b ab ++=,则4a b +的最小值为( )A .1BC .4D .5【答案】C 【解析】 【分析】由基本不等式得出关于4a b +的不等式,解之可得. 【详解】由已知2146(4)2()22a b a b ab +−+=≤⋅,当且仅当4a b =时等号成立, 所以2(4)8(4)480a b a b +++−≥,(44)(412)0a b a b +−++≥, 又0,0a b >>,所以44a b +≥,即4a b +的最小值是4,此时12,2a b ==. 故选:C .【练习1-5】设0a >,0b >,若221a b +=2ab −的最大值为( )A .3+B .C .1D .2+【答案】D 【解析】 【分析】法一:设c b =−,进而将问题转化为已知221a c +=,求ac 的最大值问题,再根据基本不等式求解即可;法二:由题知221()14a b +=进而根据三角换元得5cos ,(0)62sin a b πθθθθ⎧=⎪<<⎨=⎪⎩,再根据三角函数最值求解即可. 【详解】解:法一:(基本不等式)设c b =−2ab −=)a b ac −=,条件222211a b a c +=⇔+=,2212a c ac +=+≥,即2≤ac 故选:D.法二:(三角换元)由条件221()14a b +=,故可设cos sin 2a b θθ⎧=⎪⎪⎨⎪=⎪⎩,即cos ,2sin a b θθθ⎧=⎪⎨=⎪⎩, 由于0a >,0b >,故cos 02sin 0θθθ⎧>⎪⎨>⎪⎩,解得506πθ<<所以,5cos ,(0)62sin a b πθθθθ⎧=⎪<<⎨=⎪⎩,22sin 22ab θ−=≤当且仅当4πθ=时取等号.故选:D.题型二 求数、式的范围【例2-1】若正数a ,b 满足ab =a +b +3,则 (1)ab 的取值范围是__ ; (2)a +b 的取值范围是__ __. 【答案】(1)_[9,+∞) (2)[6,+∞) [解析] (1)∵ab =a +b +3≥2ab +3,令t =ab >0,∴t 2-2t -3≥0,∴(t -3)(t +1)≥0. ∴t ≥3即ab ≥3,∴ab ≥9,当且仅当a =b =3时取等号. (2)∵ab =a +b +3,∴a +b +3≤(a +b 2)2.今t =a +b >0,∴t 2-4t -12≥0,∴(t -6)(t +2)≥0. ∴t ≥6即a +b ≥6,当且仅当a =b =3时取等号. 【例2-2】已知0m >,0xy >,当2x y +=时,不等式24mx y+≥恒成立,则m 的取值范围是 。
基本不等式(精讲)(原卷版)
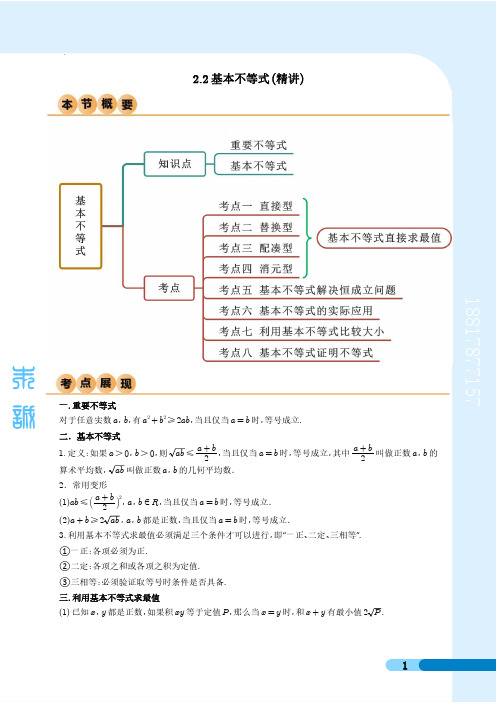
188****71572.2基本不等式(精讲)一.重要不等式对于任意实数a ,b ,有a 2+b 2≥2ab ,当且仅当a =b 时,等号成立.二.基本不等式1.定义:如果a >0,b >0,则ab ≤a +b 2,当且仅当a =b 时,等号成立,其中a +b 2叫做正数a ,b 的算术平均数,ab 叫做正数a ,b 的几何平均数.2.常用变形(1)ab ≤a +b 22,a ,b ∈R ,当且仅当a =b 时,等号成立.(2)a +b ≥2ab ,a ,b 都是正数,当且仅当a =b 时,等号成立.3.利用基本不等式求最值必须满足三个条件才可以进行,即“一正、二定、三相等”.①一正:各项必须为正.②二定:各项之和或各项之积为定值.③三相等:必须验证取等号时条件是否具备.三.利用基本不等式求最值(1)已知x ,y 都是正数,如果积xy 等于定值P ,那么当x =y 时,和x +y 有最小值2P .(2)已知x,y都是正数,如果和x+y等于定值S,那么当x=y时,积xy有最大值14S2.一.利用基本不等式求条件最值的常用方法1.配凑法求最值:主要是配凑成“和为常数”或“积为常数”的形式.2.常数代换法:主要解决形如“已知x+y=t(t为常数),求a x+b y的最值”的问题,先将a x+b y转化为ax+by·x+y t,再用基本不等式求最值.3.当所求最值的代数式中的变量比较多时,通常考虑利用已知条件消去部分变量后,凑出“和为常数”或“积为常数”的形式,最后利用基本不等式求最值.4.构建目标式的不等式求最值,在既含有和式又含有积式的等式中,对和式或积式利用基本不等式,构造目标式的不等式求解.二.利用基本不等式比较实数大小(1)利用基本不等式比较大小,常常要注意观察其形式(和与积).(2)利用基本不等式时,一定要注意条件是否满足a>0,b>0.三.利用基本不等式解决实际问题的步骤1.先理解题意,设变量.设变量时一般把要求最大值或最小值的变量定为函数.2.建立相应的函数关系式.把实际问题抽象为函数的最大值或最小值问题.3.在定义域内,求出函数的最大值或最小值.4.正确写出答案.四.利用基本不等式证明不等式1.无附加条件的不等式的证明,其解题思路是:观察要证不等式的结构特征,若不能直接使用基本不等式,则要结合左、右两边的结构特征,进行拆项、变形、配凑(加减项或乘除某个实系数)等,使之满足使用基本不等式的条件.2.有附加条件的不等式的证明,其解题思路是:观察已知条件与要证不等式之间的关系,条件的巧妙代换是一种较为重要的变形.另外,解题过程中要时刻注意等号能否取到. 考点一直接型1.【例1-1】(2023春·陕西榆林)已知a>0,b>0,a+4b=2,则ab的最大值为( )A.14B.12C.1D.22.【例1-2】(2023·陕西)已知0<x<1,则当x(5-5x)取最大值时,x的值为( )A.54B.12C.13D.34188****7157【一隅三反】1.(2023春·湖南邵阳)已知a >0,b >0,a +b =6,则ab 的最大值为( )A.6B.9C.12D.362.(2023·高一课时练习)已知x ,y ∈R +,x +y =2,c =xy ,那么c 的最大值为( )A.1B.12C.22D.143.(2023福建省)已知nm =2,则m 2+n 2的最小值为( )A.1B.2C.3D.44.(2023安徽)已知x <0,则x +1x的最大值为( )A.2 B.-12 C.-2 D.12考点二替换型3.【例2-1】(2023·江西景德镇)已知x ,y ∈R *,x +2y =1,则1x +2y的最小值( )A.8 B.9 C.10D.114.【例2-2】(2023春·浙江温州)已知正数a ,b 满足a +b =1,则a +6b +3ab最小值为( )A.25 B.19+26 C.26D.195.【例2-3】(2023·浙江)已知正实数x ,y 满足x +2y =1,则1x +1+2y +1的最小值为( )A.12+2 B.3+22 C. 94 D.34156.【例2-4】(2023春·河南周口·高一校联考期末)已知a >0,b >0,2a +1b=1,则a 2+4b 2的最小值为( )A.8B.16C.24D.32【一隅三反】1.(2023西藏)已知a>0,b>0,a+b=2,则y=1a+4b的最小值是( )A.72B.4C.92D.52.(2023春·福建福州)若正数x,y满足x+2y=2,则yx+1y的最小值为( )A.2+1B.22+1C.2D.523.(2023春·江苏南京)已知非负数x,y满足x+y=1,则1x+1+9y+2的最小值是___________.4.(2023·重庆)已知正数m、n,满足2m+3n-mn=0,则2m+3n的最小值为_________ _.考点三配凑型7.【例3-1】(2023·广西)函数f x =2x2+x+3x x<0的最大值为________.8.【例3-2】(2022·江苏·高一专题练习)当x>0时,函数y=3+x+x21+x的最小值为( )A.23B.23-1C.23+1D.4【一隅三反】1.(2023·全国·高一专题练习)函数y=x2+x+3x-2x>2的最小值为_________.2.(2023·福建)已知x>-1,则函数y=x2+x+4x+1的最小值是______.3.(2022秋·上海浦东新·高一校考期中)函数y=2xx2-x+4的值域是__________.考点四消元型188****71579.【例4】(2023·全国·高一专题练习)已知x >0,y >0,且xy +2x +y =6,则2x +y 的最小值为( ).A.4B.6C.8D.12【一隅三反】1.(2023·北京)设b >0,ab +b =1,则a 2b 的最小值为( )A.0B.1C.2D.42.(2023·重庆沙坪坝)已知x >0,y >0,xy +2x -y =10,则x +y 的最小值为( )A.22-1B.22C.42D.42-13.(2023·全国·高一专题练习)已知x >0,y >0,若x +3y +4xy =6,则x +3y 的最小值为______.考点五基本不等式解决恒成立问题10.【例5-1】(2023·江苏)若对x >0,y >0,有(x +2y )⋅2x +1y≥m 恒成立,则m 的取值范围是( )A.m ≤4 B.m >4 C.m <0D.m ≤811.【例5-2】(2023浙江)若两个正实数x ,y 满足1x +4y =1,且不等式x +y 4<m 2-3m 有解,则实数m 的取值范围是( )A.(-1,4)B.(-4,1)C.(-∞,-1)∪(4,+∞)D.(-∞,0)∪(3,+∞)【一隅三反】1.(2022秋·黑龙江哈尔滨)已知x >0,y >0,且2x +1y=1,若2x +y >m 恒成立,则实数m 的取值范围是( )A.-∞,9 B.7,+∞ C.9,+∞D.-∞,7 2.(2023·重庆沙坪坝)已知正实数x ,y 满足2x +3y -xy =0,若3x +2y ≥t 恒成立,则实数t 的取值范围是( )A.t≤25B.t<25C.t≤24D.t≥243.(2023·北京)已知x≥4,y≥4,且x+4y-xy=0,若不等式a≤x+y恒成立,则a的最大值为______.考点六基本不等式的实际应用12.【例6】(2023春·湖南)某社区计划在一块空地上种植花卉,已知这块空地是面积为1800平方米的矩形ABCD,为了方便居民观赏,在这块空地中间修了如图所示的三条宽度为2米的人行通道,则种植花卉区域的面积的最大值是( )A.1208平方米B.1448平方米C.1568平方米D.1698平方米【一隅三反】1.(2023·湖南)近日,随着新冠肺炎疫情在多地零星散发,为最大程度减少人员流动,减少疫情发生的可能性,高邮政府积极制定政策,决定政企联动,鼓励企业在国庆期间留住员工在本市过节并加班追产,为此,高邮政府决定为波司登制衣有限公司在国庆期间加班追产提供x x∈0,20(万元)的专项补贴.波司登制衣有限公司在收到高邮政府x(万元)补贴后,产量将增加到t=(x+3) (万件).同时波司登制衣有限公司生产t(万件)产品需要投入成本为7t+81t+3x(万元),并以每件8+42 t元的价格将其生产的产品全部售出.注:收益=销售金额+政府专项补贴-成本.(1)求波司登制衣有限公司国庆期间,加班追产所获收益y(万元)关于政府补贴x(万元)的表达式;(2)高邮政府的专项补贴为多少万元时,波司登制衣有限公司国庆期间加班追产所获收益y(万元)最大?2.2(2023春·广西南宁·高一校联考开学考试)某游泳馆拟建一座占地面积为200平方米的矩形188****7157泳池,其平面图形如图所示,池深1米,四周的池壁造价为400元/米,泳池中间设置一条隔离墙,其造价为100元/米,泳池底面造价为60元/平方米(池壁厚忽略不计),设泳池的长为x 米,写出泳池的总造价f x ,问泳池的长为多少米时,可使总造价f x 最低,并求出泳池的最低造价.考点七利用基本不等式比较大小13.【例7-1】(2023·甘肃)已知a 、b 为正实数,A =a +b 2,2H =1a +1b,G =ab ,则( )A.G ≤H ≤A B.H ≤G ≤A C.G ≤A ≤HD.H ≤A ≤G 14.【例7-2】(2022秋·湖南张家界·高一张家界市民族中学校考阶段练习)设0<a <b ,则下列不等式成立的是( )A.ab <a +b 2<a <b B.a <a +b 2<ab <b C.ab <a <a +b 2<b D.a <ab <a +b 2<b 【一隅三反】1.(2023·云南)若0<a <1,0<b <1,a ≠b ,则a +b ,2ab ,2ab ,a 2+b 2中最大的一个是______.2.(2023·河北邯郸·高一校考期末)(多选)若a >0,b >0,且a ≠b ,则( )A.a +b 2>a 2+b 22B.a +b 2<a 2+b 22C.ab ≤a +b 2 D.ab <a +b 23.(2023·河北唐山·)(多选)已知b <a <0,则下列不等式正确的是( )A.b 2>abB.a +1b <b +1aC.b a +a b >2D.a 2+1a <b 2+1b考点八基本不等式证明不等式15.【例8-1】(2023·河南郑州·高一校考阶段练习)若0<a <b ,则下列不等式成立的是( )A.ab <a <a +b 2<bB.ab ≤a +b 2<a <b C.a <ab <a +b 2<b D.a <a +b 2≤ab <b 16.【例8-2】(2023·江苏)已知a >0,b >0,c >0,且a +b +c =1.求证:a +1a+b +1b +c +1c ≥10.17.【例8-3】(2023·全国·高一假期作业)已知a >0,b >0,c >0,求证:bc a +ca b+ab c ≥a +b +c .【一隅三反】1.(2023·吉林长春)下列不等式恒成立的是( )A.a +b ≥-2ab ;B.a +b ≤2ab ;C.a 2+b 2≤2ab ;D.a 2+b 2≥-2ab .2.(2023·全国·高一假期作业)已知a >0,b >0,且a +b =1,求证:1+1a 1+1b≥9.3.(2023·贵州黔南)设a,b,c均为正数,且a+b+c=1,证明:(1)a2+b2+c2≥13;(2)a2b+b2c+c2a≥1.188****7157。
数学课时过关检测(四) 基本不等式

课时过关检测(四) 基本不等式A 级——基础达标1.“a >b >0”是“ab <a 2+b 22”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:选A 由a >b >0,可知a 2+b 2>2ab ,充分性成立,由ab <a 2+b 22,可知a ≠b ,a ,b ,∈R ,故必要性不成立.2.已知x >0,y >0,且x +2y =2,则xy ( ) A .有最大值为1 B .有最小值为1 C .有最大值为12D .有最小值为12解析:选C 因为x >0,y >0,x +2y =2,所以x +2y ≥2x ·2y ,即2≥22xy ,xy ≤12,当且仅当x =2y ,即x =1,y =12时,等号成立.所以xy 有最大值,且最大值为12.3.(2021·湖北八校第一次联考)已知x >0,y >0,且1x +9y =1,则x +y 的最小值为( )A .12B .16C .20D .24解析:选B 法一:由题意x +y =⎝⎛⎭⎫1x +9y (x +y )=1+y x +9x y +9≥1+2y x ×9xy +9=16,当且仅当⎩⎨⎧x >0,y >0,1x +9y =1,y x =9x y ,即{x =4,y =12时取等号,故选B.法二:由1x +9y =1得9x +y -xy =0,即(x -1)(y -9)=9,可知x >1,y >9,所以x +y =(x -1)+(y -9)+10≥2(x -1)(y -9)+10=16,当且仅当⎩⎪⎨⎪⎧x >1,y >9,1x +9y =1,x -1=y -9=3,即⎩⎪⎨⎪⎧x =4,y =12时取等号,故选B.4.已知f (x )=x 2+3x +6x +1(x >0),则f (x )的最小值是( )A .2B .3C .4D .5解析:选D f (x )=x 2+3x +6x +1=(x +1)2+x +1+4x +1=x +1+4x +1+1,因为x >0,所以x +1>0,则x +1+4x +1+1≥24+1=5⎝ ⎛⎭⎪⎫当且仅当x +1=4x +1,即x =1时取“=”,故f (x )的最小值是5.故选D. 5.(多选)(2021·泉州市高三模拟)若x ≥y ,则下列不等式中正确的是( ) A .2x ≥2y B.x +y2≥xyC .x 2≥y 2D .x 2+y 2≥2xy解析:选AD 由指数函数的单调性可知,当x ≥y 时,有2x ≥2y ,故A 正确; 当0>x ≥y 时,x +y2≥xy 不成立,故B 错误;当0≥x ≥y 时,x 2≥y 2不成立,故C 错误;x 2+y 2-2xy =(x -y )2≥0成立,即x 2+y 2≥2xy 成立,故D 正确. 6.(多选)若正实数a ,b 满足a +b =1,则下列选项中正确的是( ) A .ab 有最大值14B.a +b 有最小值 2C.1a +1b 有最小值4 D .a 2+b 2有最小值22解析:选ABC 因为a >0,b >0,且a +b =1,所以ab ≤⎝ ⎛⎭⎪⎫a +b 22,所以ab ≤14,当且仅当a =b =12时取等号, 所以ab 有最大值14,所以选项A 正确;a +b ≤ 2 a +b 2=2,当且仅当a =b =12取等号,所以a +b 的最小值是2,所以B 正确;因为1a +1b =a +b ab =1ab ≥4,当且仅当a =b =12时取等号,所以1a +1b 有最小值4,所以C正确;因为a 2+b 2≥(a +b )22=12,当且仅当a =b =12时取等号,所以a 2+b 2的最小值不是22,所以D 错误.故选A 、B 、C.7.若x >1,则x +4x -1的最小值为________. 解析:x +4x -1=x -1+4x -1+1≥4+1=5. 当且仅当x -1=4x -1,即x =3时等号成立. 答案:58.当3<x <12时,函数y =(x -3)(12-x )x的最大值为________.解析:y =(x -3)(12-x )x =-x 2+15x -36x=-⎝⎛⎭⎫x +36x +15≤-2 x ·36x+15=3, 当且仅当x =36x ,即x =6时取等号, 所以y max =3. 答案:39.某游泳馆拟建一座平面图形为矩形且面积为200平方米的泳池,池的深度为1米,池的四周墙壁建造单价为每米400元,中间一条隔壁建造单价为每米100元,池底建造单价每平方米60元(池壁厚忽略不计).则泳池的长设计为______米时,可使总造价最低.解析:设泳池的长为x 米,则宽为200x 米,总造价f (x )=400×⎝⎛⎭⎫2x +2×200x +100×200x +60×200=800×⎝⎛⎭⎫x +225x +12 000≥1 600x ·225x +12 000=36 000(元),当且仅当x =225x(x >0),即x =15时等号成立.即泳池的长设计为15米时,可使总造价最低.答案:1510.若a >0,b >0,且a +b =4,则下列不等式恒成立的是________(填序号).①1ab ≤14;②1a +1b≤1;③ab ≥2;④a 2+b 2≥8. 解析:4=a +b ≥2ab (当且仅当a =b 时,等号成立),即ab ≤2,ab ≤4,1ab ≥14,故①③不成立;1a +1b =a +b ab =4ab ≥1,故②不成立;a 2+b 2=(a +b )2-2ab =16-2ab ≥8,故④成立.答案:④11.(1)当x <32时,求函数y =x +82x -3的最大值;(2)设0<x <2,求函数y =x (4-2x )的最大值. 解:(1)y =12(2x -3)+82x -3+32=-⎝ ⎛⎭⎪⎫3-2x 2+83-2x +32.当x <32时,有3-2x >0,∴3-2x 2+83-2x≥23-2x 2·83-2x=4, 当且仅当3-2x 2=83-2x ,即x =-12时取等号.于是y ≤-4+32=-52,故函数的最大值为-52.(2)∵0<x <2,∴2-x >0, ∴y =x (4-2x )=2·x (2-x )≤ 2·x +2-x 2=2,当且仅当x =2-x ,即x =1时取等号, ∴当x =1时,函数y =x (4-2x )的最大值为 2.12.已知x >0,y >0,且2x +8y -xy =0,求: (1)xy 的最小值; (2)x +y 的最小值.解:(1)由2x +8y -xy =0,得8x +2y =1. 又x >0,y >0,则1=8x +2y ≥28x ·2y =8xy,得xy ≥64, 当且仅当8x =2y ,即x =16且y =4时,等号成立.所以xy 的最小值为64.(2)由2x +8y -xy =0,得8x +2y =1, 则x +y =⎝⎛⎭⎫8x +2y (x +y ) =10+2x y +8yx ≥10+22x y ·8y x =18.当且仅当2x y =8yx ,即x =12且y =6时等号成立,所以x +y 的最小值为18.B 级——综合应用13.《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F 在半圆O 上,点C 在直径AB 上,且OF ⊥AB ,设AC =a ,BC =b ,则该图形可以完成的无字证明为( )A.a +b2≥ab (a >0,b >0)B .a 2+b 2≥2ab (a >0,b >0) C.2ab a +b ≤ab (a >0,b >0) D.a +b 2≤a 2+b 22(a >0,b >0) 解析:选D 由AC =a ,BC =b ,可得圆O 的半径r =a +b2,又OC =OB -BC =a +b 2-b =a -b2,则FC 2=OC 2+OF 2=(a -b )24+(a +b )24=a 2+b 22, 再根据题图知FO ≤FC ,即a +b 2≤a 2+b 22,当且仅当a =b 时取等号. 故选D.14.已知a >b >0,则a 2+16b (a -b )的最小值为( )A .15B .16C .17D .26解析:选B 因为a >b >0,所以a -b >0.所以b (a -b )≤⎣⎢⎡⎦⎥⎤b +(a -b )22=a 24.所以a 2+16b (a -b )≥a 2+64a 2≥2a 2·64a2=16. 当a 2=64a 2且b =a -b ,即a =22,b =2时等号成立.所以a 2+16b (a -b )的最小值为16.故选B.15.某厂家拟定在2021年举行促销活动,经调查测算,该产品的年销量(即该厂的年产量)x 万件与年促销费用m (m ≥0)万元满足x =3-km +1(k 为常数).如果不搞促销活动,那么该产品的年销量只能是1万件.已知2021年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).(1)将2021年该产品的利润y 万元表示为年促销费用m 万元的函数; (2)该厂家2021年的促销费用投入多少万元时,厂家利润最大? 解:(1)由题意知,当m =0时,x =1(万件), 所以1=3-k ⇒k =2,所以x =3-2m +1(m ≥0),每件产品的销售价格为1.5×8+16xx(元), 所以2021年的利润y =1.5x ×8+16x x -8-16x -m =4+8x -m =4+8⎝ ⎛⎭⎪⎫3-2m +1-m =-⎣⎢⎡⎦⎥⎤16m +1+(m +1)+29(m ≥0).(2)因为m ≥0时,16m +1+(m +1)≥216=8,所以y ≤-8+29=21,当且仅当16m +1=m +1⇒m =3(万元)时,y max =21(万元).故该厂家2021年的促销费用投入3万元时,厂家的利润最大为21万元.C 级——迁移创新16.某单位拟建一个扇环形状的花坛(如图所示),该扇环是由以点O 为圆心的两个同心圆弧和延长后通过点O 的两条直线段围成.按设计要求,扇环的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x 米,圆心角为θ(弧度).已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比值为y ,求当y 最大时,x 的值.解:由题意得30=θ(10+x )+2(10-x ),所以θ=10+2x 10+x ,花坛的面积为12θ(102-x 2)=(5+x )(10-x )=-x 2+5x +50(0<x <10),装饰总费用为9θ(10+x )+8(10-x )=170+10x ,所以花坛的面积与装饰总费用的比值y =-x 2+5x +50170+10x =-x 2-5x -5010(17+x ).令t =17+x ,t ∈(17,27),则y =3910-110⎝⎛⎭⎫t +324t ≤310,当且仅当t =18时取等号,此时x =1,θ=1211.所以当x =1时,花坛的面积与装饰总费用的比值y 最大.。
第04讲 基本不等式高考数学大一轮复习核心题型讲与练+易错重难点专项突破(新高考版)

G ( x )万元,且 G ( x )=
2 + 120,0 < ≤ 50,
4 900
201+
− 2 100,50 < ≤ 100,
200万元,且全年内生产的该产品当年能全部销售完.
每台该产品的售价为
(1)写出年利润 W ( x )(单位:万元)关于年产量 x (单位:台)的函数解析式(利润=销售
2.几个重要的不等式
2ab
1a2+b2≥______a,b∈R;
b a
2
2a+b≥___a,b同号且不为零;
当且仅当a=b
2
a+b
3ab≤
时等号成立
a,b∈R;
2
2
2
2
a +b
a+b
4
a,b∈R.
≤
2
2
(2)[2024宁夏银川模拟]已知0< x <4,则 (4 − ) 的最大值为 2
[解析] 0< x <4,则0<4- x <4,由基本不等式可得 (4
.
+4−
− ) ≤
=2,
2
当且仅当 x =4- x ,即 x =2时,等号成立.故 (4 − ) 的最大值为2.
角度2 常数代换法
−4
8
−4
>0,因为 a >0,所以 a >4,所以8 a + b =8 a
+5]≥8×(2 4 +5)=72,当且仅当 a =6时取等号.故选C.
8
4
8
4
解法二 ∵8 a +4 b = ab , a >0, b >0,∴ + =1,∴8 a + b =(8 a + b )( + ) =
2024年高考语文一轮复习讲练测专题六 文言文阅读第04讲 文言文翻译(练习)(原卷版)

第04讲文言文翻译(基础题和拔高题)自古文体变易多矣。
梁简文帝及庾肩吾之属,始为轻浮绮靡之词,名曰宫体。
自后沿袭,务于妖艳,谓之摛锦布绣焉。
其有敦尚风格,颇存规正者,不复为当时所重。
讽谏比兴,由是废缺。
物极则变,理之常也。
圣唐受命,斫雕为朴,开元之际,王纲复举,浅薄之风兹焉渐革。
其时作者,凡十数辈颇能以雅参丽,以古杂今,彬彬然,灿灿然,近建安之遗范矣。
南阳岑公,声称尤著。
公讳参,代为本州冠族。
曾太公文本,大父长倩,伯父羲,皆以学术德望,官至台辅。
早岁孤贫,能自砥砺,遍览史籍,尤工缀文,属辞尚清,用意尚切,其有所得,多入佳境。
每一篇绝笔,则人人传写,虽闾里士庶,戎夷蛮貊,莫不讽诵吟习焉。
时议拟公于吴均、何逊,亦可谓精当矣。
天宝三载,进士高第,解褐右内率府兵曹参军,转右威卫录事参军。
入为右补阙,频上封章,指述权佞。
改太子中允兼殿中侍御史,充关西节度判官。
圣上潜龙藩邸总戎陕服参佐僚史皆一时之选由是委公以书奏之任出为嘉州刺史。
副元帅相国杜公鸿渐,表公职方郎中兼侍御史,列于幕府。
无几使罢,寓居于蜀。
时四川节度因乱(注)受职,本非朝旨,其部统之内,文武衣冠附会阿谀以求自结,皆曰:中原多故,剑外小康,可以庇躬,无暇向阙。
公乃著《招蜀客归》一篇,申明逆顺之理,折挫邪佞之计,有识者感叹,奸谋者惭沮,播德泽于梁益,畅皇风于邛僰。
旋轸有日,犯俟时,吉往凶归,呜呼不禄。
岁月逾迈,殆三十年。
嗣子佐公,复纂前绪,亦以文采,登名翰场,有公遗文,贮之筐箧。
确忝同声后辈,受命编次,因令缮录,区分类聚,勒成八卷。
倘后之词人有所观览,亦由聆广乐者识清商之韵,游名山者仰翠微之色,足以莹彻心府,发挥高致焉。
把文中画横线的句子翻译成现代汉语。
(1)其有敦尚风格,颇存规正者,不复为当时所重。
(2)中原多故,剑外小康,可以庇躬,无暇向阙。
阅读下面的文言文,完成各题。
为司徒公与宁南侯书侯方域顷待罪师中,每接音徽,嘉壮志,又未尝不叹以将军之材武,所向无前,而掎角无人,卒致一篑遗恨。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7.(2020春•顺庆区校级月考)在 中,点 为线段 上任一点(不含端点),若 ,则 的最小值为
A.1B.8C.2D.4
8.(2019秋•开封期末)已知 , , ,若不等式 对已知的 , 及任意实数 恒成立,则实数 的取值范围是
A. , B. , C. , D. ,
9.(2020•中卫二模)《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为 和 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄 和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形,该矩形长为 ,宽为内接正方形的边长 .由刘徽构造的图形可以得到许多重要的结论,如图3.设 为斜边 的中点,作直角三角形 的内接正方形对角线 ,过点 作 于点 ,则下列推理正确的是
[B组]—强基必备
1.(2019秋•南城县校级期末)已知正数 , 满足 ,且 ,则 的最大值为
A. B. C.2D.4
2.(2020春•武侯区校级期中)已知正数 , 满足 ,若 恒成立,则实数 的取值范围是.
《基本不等式》达标检测
[A组]—应知应会
1.(2020春•南关区校级期中)若 ,则 的最小值为
A. B. C.1D.
2.(2020•历下区校级模拟)已知 , ,且 ,则 的最小值为
A.100B.81C.36D.9
3.(2020•海南一模)如图,矩形花园 的边 靠在墙 上,另外三边是由篱笆围成的.若该矩形花园的面积为4平方米,墙 足够长,则围成该花园所需要篱笆的
19.(2020•全国Ⅰ卷模拟)若 , ,且 .
(1)求 的最小值;
(2)是否存在 、 ,使得 ?并说明理由.
20.已知 , 均为正实数,且 .
(Ⅰ)求 的最小值;
(Ⅱ)若 对任意的 , 恒成立,求实数 的取值范围.
21.(2020•赣州模拟)已知正实数 , 满足 .
(1)求 的最小值.
(2)证明: .
14.(2020•江苏模拟)已知正实数 , 满足 ,则 的最小值为.
15.2020•南开区二模)已知 ,则 的最小值为.
16.(2019秋•淄博期末)若两个正实数 , 满足 ,且不等式 恒成立,则实数 的取值范围是.
17.(2020春•克东县期中)已知 .
(1)求 的最大值;
(2)求 的最小值.
18.(2019秋•历城区校级期末)有一批材料,可以建成长为240米的围墙如图,如果用材料在一面靠墙的地方围成一块矩形的场地,中间用同样材料隔成三个相等面积的矩形,怎样围法才可取得最大的面积?并求此面积.
A.最大长度为8米B.最大长度为 米
C.最小长度为8米D.最小长度为 米
4.(2020春•诸暨市校级期中)坐标 满足 ,且 , ,则 的最小值为
A.9B.6C.8D.
5.(2020春•金华期中)已知实数 , 满足 ,且 ,则 的最小值为
A.21B.24C.25D.27
6.(2020•河东区一模)已知实数 、 , ,则 的最大值为
A. 的最小值为 B. 的最大值为
C. 的最小值为2D. 的最小值为2
12.(2020•昌平区二模)已知 ,则 的最小值为.
13.(2020•北京模拟)为净化水质,向一个游泳池加入某种化学药品,加药后池水中该药品的浓度 (单位: 随时间 (单位: 的变化关系为 ,则经过 后池水中药品的浓度达到最大.
①由图1和图2面积相等可得 ;②由 可得 ;
③由 可得 ;④由 可得 .
A.①②③④B.①②④C.②③④D.①③
10.(多选)(2020•德州二模)若正实数 , 满足 ,则下列说法正确的是
A. 有最大值 B. 有最大值
C. 有最小值2D. 有最大值
11.(多选)(2020春•锡山区校级期中)设正实数 、 满足 ,则下列说法正确的是
