夫妻过河问题
求解夫妻过河问题

曲靖师范学院本科生毕业论文论文题目: matlab求解夫妻过河问题作者、学号:郭彩虹2010111212学院、年级:数学与信息科学学院2010级学科、专业:数学数学与应用数学指导教师:郭昀完成日期:2013年12月27日曲靖师范学院教务处摘要渡河问题.[]1始于公元8 世纪,至今它仍是一个逻辑难题,许多数学建模教材上已经提到.这个问题指的是:有不同的对象或生物,他们其中一些相互不共存,逐步地让一小群体从河的一岸到另一岸,经过有限步后,该群体全部从一岸达到另一岸,并且要求没有任何损失.在渡河问题的夫妻过河问题中我们发现状态转移问题有时不一定有解,有时的解又不一定有规律,本文对于夫妻过河问题利用图解法和matlab编写程序求解5对、6对夫妻过河是否有解,并推广到n对夫妻与船的运载能力m对于能否安全渡河时它们之间的关系。
关键词:多步决策 matlab 数学模型渡河问题Problem of couples across the riverAbstract: the problem of crossing the river. In the 8th century, it still is a logical problem, many mathematical modeling teaching material has been mentioned. The question is: have different objects or creatures, they lack some mutual coexistence, gradually to a small group from one bank to another bank of the river, after finite steps, the group all from one side to the other shore, and requires no losses. In crossing the river problem of couples across the river, we found that state transition problem sometimes does not necessarily have a solution, sometimes the solution is not necessarily regular, in this paper, using the graphical method for the problem of couples across the river and the matlab program to solve the 5, 6 for couple across a river if there is a solution,And derived to n couple with the ability to run m to safe crossing the river when the relationship between them.Keywords: Multistep decision Matlab Mathematical model Problem of crossing the river目录1 引言 (1)2 文献综述 (1)2.1 国内外研究现状 (1)2.2 国内外研究现状评价 (2)2.3 问题提出 (2)3 模型假设 (2)4 符号说明 (2)5 重述3、4对夫妻过河问题的解 (3)5.1 3对夫妻过河的解 (3)5.2 4对夫妻过河的解 (3)6 五对夫妻过河模型 (4)6.1 模型构成 (4)6.2 模型建立 (4)6.3 模型求解 (4)6.31 Matlab编程求解 (4)6.32 图解法 (7)7 六对夫妻过河模型 (8)7.1 模型构成 (8)7.2 模型求解 (9)8 n对夫妻过河情况 (10)8.1 求解 (10)8.2 验证 (11)9 总结与展望 (12)9.1 总结 (12)9.2后续研究工作展望 (13)参考文献 (14)附录 (15)1 引言这是一个古老的阿拉伯数学问题。
求解夫妻过河问题

求解夫妻过河问题曲靖师范学院本科生毕业论文论文题目: matlab求解夫妻过河问题作者、学号:郭彩虹2010111212学院、年级:数学与信息科学学院2010级学科、专业:数学数学与应用数学指导教师:郭昀完成日期:2013年12月27日曲靖师范学院教务处摘要渡河问题.[]1始于公元8 世纪,至今它仍是一个逻辑难题,许多数学建模教材上已经提到.这个问题指的是:有不同的对象或生物,他们其中一些相互不共存,逐步地让一小群体从河的一岸到另一岸,经过有限步后,该群体全部从一岸达到另一岸,并且要求没有任何损失.在渡河问题的夫妻过河问题中我们发现状态转移问题有时不一定有解,有时的解又不一定有规律,本文对于夫妻过河问题利用图解法和matlab编写程序求解5对、6对夫妻过河是否有解,并推广到n对夫妻与船的运载能力m对于能否安全渡河时它们之间的关系。
关键词:多步决策 matlab 数学模型渡河问题Problem of couples across the riverAbstract: the problem of crossing the river. In the 8th century, it still is a logical problem, many mathematical modeling teaching material has been mentioned. The question is: have different objects or creatures, they lack some mutual coexistence, gradually to a small group from one bank to another bank of the river, after finite steps, the group all from one side to the other shore, and requires no losses. In crossing the river problem of couples across the river, we found that state transition problem sometimes does not necessarily have a solution, sometimes the solution is not necessarily regular, in this paper, using the graphical method for the problem of couples across the river and the matlab program to solve the 5, 6 for couple across a river if there is a solution,And derived to n couple with the ability to run m to safe crossing the river when the relationship between them.Keywords: Multistep decision Matlab Mathematical model Problem of crossing the river目录1 引言 (1)2 文献综述 (1)2.1 国内外研究现状 (1)2.2 国内外研究现状评价 (2)2.3 问题提出 (2)3 模型假设 (2)4 符号说明 (2)5 重述3、4对夫妻过河问题的解 (3)5.1 3对夫妻过河的解 (3)5.2 4对夫妻过河的解 (3)6 五对夫妻过河模型 (4)6.1 模型构成 (4)6.2 模型建立 (4)6.3 模型求解 (4)6.31 Matlab编程求解 (4)6.32 图解法 (7)7 六对夫妻过河模型 (8)7.1 模型构成 (8)7.2 模型求解 (9)8 n对夫妻过河情况 (10)8.1 求解 (10)8.2 验证 (11)9 总结与展望 (12)9.1 总结 (12)9.2后续研究工作展望 (13)参考文献 (14)附录 (15)1 引言这是一个古老的阿拉伯数学问题。
借船过河:一个据说能看穿你的人性和欲望的心理测试
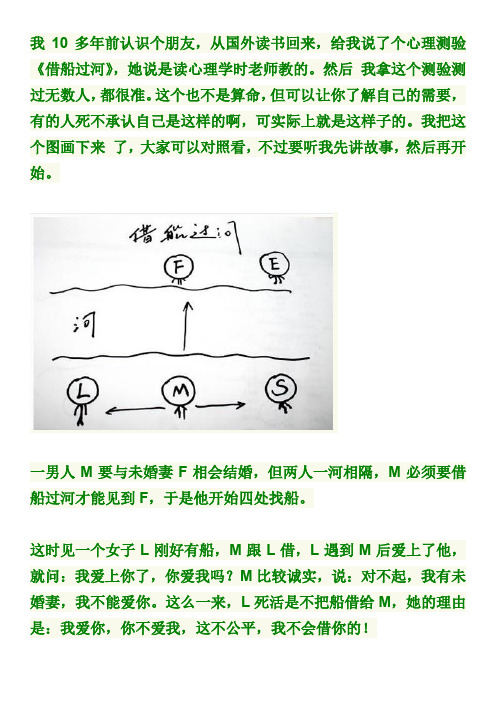
我10多年前认识个朋友,从国外读书回来,给我说了个心理测验《借船过河》,她说是读心理学时老师教的。
然后我拿这个测验测过无数人,都很准。
这个也不是算命,但可以让你了解自己的需要,有的人死不承认自己是这样的啊,可实际上就是这样子的。
我把这个图画下来了,大家可以对照看,不过要听我先讲故事,然后再开始。
一男人M要与未婚妻F相会结婚,但两人一河相隔,M必须要借船过河才能见到F,于是他开始四处找船。
这时见一个女子L刚好有船,M跟L借,L遇到M后爱上了他,就问:我爱上你了,你爱我吗?M比较诚实,说:对不起,我有未婚妻,我不能爱你。
这么一来,L死活是不把船借给M,她的理由是:我爱你,你不爱我,这不公平,我不会借你的!M很沮丧,继续找船,刚好见一位叫S的女子,就向她借船,S说:我借给你没问题,但有个条件,我很喜欢你,你是不是喜欢我无所谓,但你必须留下陪我一晚,不然我不借你。
M很为难,L不借他船,S如果再不借他的话就过不去河与F相见了,据说这个地方只有这两条船。
为了彼岸的未婚妻,他不得不同意了S的要求,与S 有了NB。
次日,S遵守承诺把船借给了M。
见到未婚妻F后,M一直心里有事,考虑了很久,终于决定把向L 和S借船的故事跟F说了。
可惜,F听了非常伤心,一气之下与M 分了手,她觉得M不忠,不能原谅。
F失恋了,很受打击。
这时他的生活里出现了位女子E,两人也开始恋爱了,但之前的故事一直让他耿耿于坏,E问M是不是有什么话要跟她说,于是,M 一五一十地把他和L、S、F之间的故事讲了一遍。
E听了后,说,我不会介意的,这些跟我没关系。
故事讲完了,问题来了,请你把这几个人排列个次序,标准是你认为谁最好,谁第二,谁第三,第四,第五?这个M男也算在内的。
建议不要想太复杂,也不需要考虑大众看法,你认为谁做得好就是好。
看到这里请先选择好你的答案,完了往下拉看看答案。
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓答案其实很简单,就是用你的潜意识告诉你最想要的是什么。
借船过河:一个据说能看穿你的人性和欲望的心理测试

借船过河:一个据说能看穿你的人性和欲望的心理测试我10多年前认识个朋友,从国外读书回来,给我说了个心理测验《借船过河》,她说是读心理学时老师教的。
然后我拿这个测验测过无数人,都很准。
这个也不是算命,但可以让你了解自己的需要,有的人死不承认自己是这样的啊,可实际上就是这样子的。
我把这个图画下来了,大家可以对照看,不过要听我先讲故事,然后再开始。
一男人M要与未婚妻F相会结婚,但两人一河相隔,M必须要借船过河才能见到F,于是他开始四处找船。
这时见一个女子L刚好有船,M跟L借,L遇到M后爱上了他,就问:我爱上你了,你爱我吗?M比较诚实,说:对不起,我有未婚妻,我不能爱你。
这么一来,L死活是不把船借给M,她的理由是:我爱你,你不爱我,这不公平,我不会借你的!M很沮丧,继续找船,刚好见一位叫S的女子,就向她借船,S说:我借给你没问题,但有个条件,我很喜欢你,你是不是喜欢我无所谓,但你必须留下陪我一晚,不然我不借你。
M很为难,L不借他船,S如果再不借他的话就过不去河与F相见了,据说这个地方只有这两条船。
为了彼岸的未婚妻,他不得不同意了S的要求,与S有了NB。
次日,S 遵守承诺把船借给了M。
见到未婚妻F后,M一直心里有事,考虑了很久,终于决定把向L和S借船的故事跟F说了。
可惜,F听了非常伤心,一气之下与M分了手,她觉得M不忠,不能原谅。
F失恋了,很受打击。
这时他的生活里出现了位女子E,两人也开始恋爱了,但之前的故事一直让他耿耿于坏,E问M是不是有什么话要跟她说,于是,M一五一十地把他和L、S、F之间的故事讲了一遍。
E听了后,说,我不会介意的,这些跟我没关系。
故事讲完了,问题来了,请你把这几个人排列个次序,标准是你认为谁最好,谁第二,谁第三,第四,第五?这个M男也算在内的。
建议不要想太复杂,也不需要考虑大众看法,你认为谁做得好就是好。
看到这里请先选择好你的答案,完了往下拉看看答案。
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓答案其实很简单,就是用你的潜意识告诉你最想要的是什么。
数学渡河的问题

数学渡河的问题
数学渡河的问题是一个著名的逻辑谜题,其描述如下:
有一位父亲、两个儿子和一个船。
这个家庭需要渡河,但船只有两个座位。
父亲、两个儿子中的任何两个人都不能留在一起,因为父亲不能让他的儿子们彼此相遇。
每个人都必须过河。
该问题的解法是:
步骤1:父亲带着一位儿子过河,让他在河的另一侧下船。
步骤2:父亲返回原岸,带着另外一个儿子过河,与步骤一中的儿子在对岸相遇。
步骤3:父亲和这个儿子一起返回原岸,再带着另一个儿子过河,在对岸与步骤二中的儿子相遇。
步骤4:父亲和这个儿子一起返回原岸,再带着另一个儿子过河,在对岸与步骤一中的儿子相遇。
最终,父亲和两个儿子都成功过河。
夫妻过河问题

, 001 ) , 001 ) , 001 , 111 , 100 , 010 , 101 , 011 , 000 , 001 , 001 , 001 ) ) ) ) ) ) ) ) ) )
Y N N C Y Y N N N N N N Y Y Y
, 101 ) , 011 ) , 000 )
( 110 ( 101 ( 3)1 ( 011 ( 000 ( 000 ( 000 ( 100 ( 111 , 101 ) + ( 010 ( 001 ( 100 ( 010 ( 001 ( 000 ( 000 ( 000
( 3对夫妻)→(3男1女)→(3男2女)→ 对夫妻) (3男)→(3男1女)→ 1男1女 → (2男2女)→(2女)→(3女)→ 无人) (1女)→(2女)→(无人)
回1女 去 2女 去 2男 回1女 去 2女 回1女 去 2男 留1夫妻 回1夫妻
去 2女
回1女
去 2女
如果采用前次课提到的人狼羊菜问题的状 态转移法,设一个6维的向量, 态转移法,设一个6维的向量,但由于数据 比较冗长,容易出现错误, 比较冗长 , 容易出现错误 , 下面仅给出可 取状态及可取运载。 取状态及可取运载。
, 111 ) , 111 ) , 111 , 001 , 010 , 100 , 011 , 101 , 110 , 111 , 111 , 111 ) ) ) ) ) ) ) ) ) )
N N N Y Y Y Y Y Y N N N Y Y Y
, 011 ) , 101 ) , 110 )
(2)
Y N N N C C N Y N N
( 6)
(7)
( 2 ,0 ) ( 0 ,2 ) ( 2 ,0 ) ( 0 ,2 ) ( 2 , 2 ) − ( 1 ,1 ) → ( 1 ,1 ) (1 ,0 ) (1 ,2 ) ( 2 ,1 ) ( 0 ,1 ) ( 2 ,0 ) ( 2 ,2 ) ( 0 ,4 ) ( 0 ,2 ) ( 0 , 2 ) + ( 1 ,1 ) → ( 1 , 3 ) (1 ,0 ) (1 ,2 ) ( 0 ,3 ) ( 0 ,1 )
过河心里测试题

过河心里测试题在生活中,我们常常面临各种各样的选择和困难。
有时候,我们很难判断自己应该如何做出决策,或者我们不确定自己的内心真正倾向于哪个选择。
为了帮助我们更好地了解自己的内心和倾向,下面是一道具有心理测试性质的过河题目,希望通过解答这个问题,你能更好地认识自己。
题目描述:你正处于一个小镇的一侧,需要过河去到另一侧。
这个河是非常宽的,并且没有桥或其他的固定设施可以供你使用。
你注意到河旁边停着一艘小船,但船上只能容纳你和另外一位乘客。
在另一侧,你看到两个人正等待着能够用船过河的机会。
这两个人是你人生中最重要的两位人物,你必须选择其中一个人和你一起过河。
以下是两个人的简要描述:人物1:这个人是你最亲近的家人或者伴侣。
你和他/她有着你们之间无法割舍的关系。
你知道他/她对你的忠诚和爱意,无论发生什么情况都可以依靠他/她。
人物2:这个人是你非常憧憬的对手或偶像。
你对他/她非常敬仰并希望从他/她身上获得积极的影响。
这个人有着你想要的某种品质或成就。
请你回答以下问题:1. 你会选择带谁过河,人物1还是人物2?请简要说明你的选择理由。
2. 你对于没有选择的那个人会有什么感觉?你觉得他/她可能会有什么感受?3. 这个问题对你产生了什么样的启发?你从中学到了什么?以下是我对以上问题的个人回答,仅供参考:1. 我会选择带人物1过河。
因为家人或伴侣对我来说是最亲近和重要的人,我知道无论发生什么情况,他/她都会在我身边支持我和保护我。
他/她的存在给我带来了安全感和爱的滋养。
2. 我觉得没有选择的那个人可能会感到失望或者受到伤害。
因为他/她可能会认为自己在我的心中没有足够的重要性,而被另一个人物所替代。
我也会对没有选择的那个人感到内疚和不安,因为我知道我的选择对他/她来说可能会有一定的伤害。
3. 这个问题启发了我对于人际关系和价值观的思考。
它让我意识到在做出决策时,我需要权衡自己与他人之间的关系和对我有积极影响的因素。
它教会了我如何在情感和理性之间做出选择,并且提醒了我珍惜与亲人的关系。
借船过河

我10多年前认识个朋友,从国外读书回来,给我说了个心理测验《借船过河》,她说是读心理学时老师教的。
然后我拿这个测验测过无数人,都很准。
这个也不是算命,但可以让你了解自己的需要,有的人死不承认自己是这样的啊,可实际上就是这样子的。
我把这个图画下来了,大家可以对照看,不过要听我先讲故事,然后再开始。
一男人M要与未婚妻F相会结婚,但两人一河相隔,M必须要借船过河才能见到F,于是他开始四处找船。
这时见一个女子L刚好有船,M跟L借,L遇到M后爱上了他,就问:我爱上你了,你爱我吗?M比较诚实,说:对不起,我有未婚妻,我不能爱你。
这么一来,L死活是不把船借给M,她的理由是:我爱你,你不爱我,这不公平,我不会借你的!M很沮丧,继续找船,刚好见一位叫S的女子,就向她借船,S说:我借给你没问题,但有个条件,我很喜欢你,你是不是喜欢我无所谓,但你必须留下陪我一晚,不然我不借你。
M很为难,L不借他船,S如果再不借他的话就过不去河与F相见了,据说这个地方只有这两条船。
为了彼岸的未婚妻,他不得不同意了S的要求,与S有了NB。
次日,S遵守承诺把船借给了M。
见到未婚妻F后,M一直心里有事,考虑了很久,终于决定把向L和S借船的故事跟F说了。
可惜,F听了非常伤心,一气之下与M分了手,她觉得M不忠,不能原谅。
F失恋了,很受打击。
这时他的生活里出现了位女子E,两人也开始恋爱了,但之前的故事一直让他耿耿于坏,E 问M是不是有什么话要跟她说,于是,M一五一十地把他和L、S、F之间的故事讲了一遍。
E听了后,说,我不会介意的,这些跟我没关系。
故事讲完了,问题来了,请你把这几个人排列个次序,标准是你认为谁最好,谁第二,谁第三,第四,第五?这个M男也算在内的。
建议不要想太复杂,也不需要考虑大众看法,你认为谁做得好就是好。
看到这里请先选择好你的答案,完了往下拉看看答案。
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓答案其实很简单,就是用你的潜意识告诉你最想要的是什么。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题目:夫妻过河
三对夫妻要过河,河中只有一条小船,可容两人。
每个个丈夫都不愿让自己的妻子和另一个男人在一起,除非自己也在场。
(1)如何过河?有多少种渡河次数最少的方法?
(2)三对夫妻改为四对夫妻,其他条件不变,能过河吗?为什么?若船至多可容三人,能过河吗?怎么过?
数学建模
论文题目:夫妻过河问题
摘要:主要运用状态转移的方法分析类似于夫妻过河等问题。
状态转移矩阵是俄国数学家马尔科夫提出的,他在20世纪初发现:一个系统的某些因素在转移中,第n次结果只受第n-1的结果影响,即只与当前所处状态有关,而与过去状态无关。
在马尔科夫分析中,引入状态转移这个概念。
所谓状态是指客观事物可能出现或存在的状态;状态转移是指客观事物由一种状态转移到另一种状态的概率。
关键词:状态转移,状态集合。
正文:
1.建模
我们把此岸有M个男人(丈夫),F个女人(妻子)的情形称为一种状态,用一对数组(M,F)表示,注意M、F的顺序不要变,其中M、F 均为不小于0且不大于3的整数.很显然,在我们的问题中,并非所有数组所表示的状态。
(M,F) M,F∈Z,0≤M,F≤3
都是被允许的.例如在0<M<F≤3时,状态(M,F)就不允许,因为它表示必有女子在其丈夫不在场的情形下与其他男人在一起了.除去不允许状态后,剩下的就都称为允许状态.于是我们可以把本问题的允许状态集合S写出来:
S={(0,0),(0,1),(0,2),(0,3),(1,1),(2,
2),(3,3),(3,2),(3,1),(3,0),(2,1)}.
有了允许状态集S,还需要知道这些允许状态之间是如何变化的,特别是如何从三对夫妻全在此岸是的状态(3,3)一步步地变为三对夫妻全在彼岸的状态(0,0)的.这就需要讨论所谓运算(或决策),它们也是由一对有序数组表示的.因为小船每次从河的一岸驶向另一岸都使状态发生变化,故我们把小船的一次运送称为一次运算(或决策).
我们规定第n次运算dn由第n+1个状态Sn+1减去第n个状态Sn来确定,即
dn=Sn+1-Sn.
注意到小船由此岸驶向彼岸时,此岸人数由多变少,而船由彼岸驶回此岸时,此岸人数由少变多.又由于小船载乘人数不多于2人,故运算dn必然满足:
dn=(-1)n(p,q),p,q≥0且1≤p+q≤2,n∈N,
其中p,q分别表示小船离岸时船上男人与女人的数量.当Sn+1,Sn均为允许状态时,称dn为允许运算,我们把方程
Sn+1=Sn+dn
称为状态转移方程.
至此,我们已经把问题完全抽象化了.
2.解法
我们下面的任务就是利用状态转移方程来求解.实际上是要一步一步地考虑由一个允许状态加上一个允许运算,得出另一个允许状态的过程,试图寻求一条由初始状态(3,3)转为期望状态(0,0)的路径(当然对有些问题这种路径不一定存在),也就是要确定一系列的允许运算dn(n=1,2,…,m),使得
(3,3)+d1+d2+…+dm=(0,0).
由于本问题涉及的变量不多,约束条件也不多,我们可以凭简单的演算来求解.当某些问题变量较多,约束条件也较复杂时,我们可以借助计算机,以避免十分繁琐的演算.
下面是利用状态转移方程直接求解“夫妻过河”问题的一条路径:
经过决策经过11次会完成。
于是这两个问题所抽象出来的数学模型其实是一样的,解法自然也是相同的.考虑一下当问题的条件发生变化时,问题的解决会朝什么方向发展是极有意义的.很明显,夫妻数量的增加会使问题难于解答,甚至不可解,而小船载人的数量增加将大大降低问题的难度.还有所谓“人狗鸡米过河”问题,也是颇有趣味的,人、狗、鸡、米均要过河,船需人划,而船上至多还可载一物,但若人不在时,狗会吃鸡,鸡会吃米,问如何设计顺利过河方案.另外,用一定容积的若干油瓶倒油的问题也属此类问题.
下面给出状态转移问题的图解法:
当所讨论问题变量不很多时,人们也常常利用作图的方法来解决状态转移问题.例如对于“夫妻过河”问题,可以在M-F平面上标出允许状态集S中的点,而将允许运算看作是沿方格移动1格或2格,为了区别小船的往返,我们用实线表示小船由此岸至彼岸,用虚线表示小船由彼岸至此岸.于是下图就是“夫妻过河”问题的一个图解
法。
若有四对夫妻就过不了河,我们可以用穷举法,若容至三人,能过河,三对夫妻最少有7次完成。
若有四对夫妻,至少需要9次。
4.结语
状态转移问题一般并不一定有解存在,有解时解法又不一定唯一.当解法不唯一时,我们应该比较不同解法的优劣,从而确定出最优解法。
初次写建模论文,难免有不足之处,请老师批评指正。
