平行平板的多光束干涉
合集下载
22平行平板的多光束干涉
与此相反，反射光的干涉条纹则是在亮背景上的细暗条纹，由 于它不易辨别，故极少应用。
能够产生极明锐的透射光干涉条纹， 是多光束干涉的最显著和 最重要的特点。
11/8/2019
条纹宽度
It/Ii-曲线
若用条纹的半峰值全宽度
(简称半值宽度)ε=Δ表征
干涉条纹的锐度，则当
时 2m
11/8/2019
r 2 r'2 R
tt' 1 R T
11/8/2019
所有反射光在P点叠加，其合成场复振幅
E0r E01r E0lr l2
E0r1 t'tr'(2l3)E0iei(l1) l2
令 n l-2
E0r1t'tr'E0iei r'2nein
(3)频率特性
It/Ii-曲线
由t 4nhcos可知
在平板结构(n,h)给定,入射光 相邻透射光相位差处于
线方向()一定的情况下， 半宽度Δ内的光才能透
仅与波长有关。- -滤波
过平行平板。
将改写
4nhcos
c
1 2
ห้องสมุดไป่ตู้
4
nhcos
c
滤波宽度
22nhcos
也可以说干涉光强只与光束 倾角有关，这正是等倾干涉 条纹的特性。
11/8/2019
多光束干涉 装置示意图
实验装置中的透镜光轴垂 直于平板(T2-19)时
观察到的等倾条纹是一 组同心圆环。
11/8/2019
(3) 光强分布的极值条件
爱里公式
F sin2
透射光干涉条纹特点
(1)光强分布与反射率R有关
能够产生极明锐的透射光干涉条纹， 是多光束干涉的最显著和 最重要的特点。
11/8/2019
条纹宽度
It/Ii-曲线
若用条纹的半峰值全宽度
(简称半值宽度)ε=Δ表征
干涉条纹的锐度，则当
时 2m
11/8/2019
r 2 r'2 R
tt' 1 R T
11/8/2019
所有反射光在P点叠加，其合成场复振幅
E0r E01r E0lr l2
E0r1 t'tr'(2l3)E0iei(l1) l2
令 n l-2
E0r1t'tr'E0iei r'2nein
(3)频率特性
It/Ii-曲线
由t 4nhcos可知
在平板结构(n,h)给定,入射光 相邻透射光相位差处于
线方向()一定的情况下， 半宽度Δ内的光才能透
仅与波长有关。- -滤波
过平行平板。
将改写
4nhcos
c
1 2
ห้องสมุดไป่ตู้
4
nhcos
c
滤波宽度
22nhcos
也可以说干涉光强只与光束 倾角有关，这正是等倾干涉 条纹的特性。
11/8/2019
多光束干涉 装置示意图
实验装置中的透镜光轴垂 直于平板(T2-19)时
观察到的等倾条纹是一 组同心圆环。
11/8/2019
(3) 光强分布的极值条件
爱里公式
F sin2
透射光干涉条纹特点
(1)光强分布与反射率R有关
平行平板的多光束干涉及其应用1
2m和 2m＋1 m=0,1, 2,
其相应旳透射光干涉光强为：
I
t M
I
(i
)和I
t m
1 1 F
I (i)
结论：不论对透射光还是反射光，形成亮纹和暗纹旳条件与 双光束完全相同，所以条纹旳位置相同。干涉场旳对比度由 界面旳反射比来拟定。
▪ 不同反射率下透射光强度与位相差关系
▪ 不同反射率下反射光与位相差旳关系
w A(i) n0 1 n
n0
2
r，t
h
r’ ， t’
L’
p
tt' 1 r2 1
I
(t
P点光强为A：p(t )tt
) A(t) A(t)*
'r '
2( p1)
1 F
( A)(i)
1 • sin2
•
ei( p
I (i)
1)
其中
2
F
透镜焦平面上产生多光束干涉
4 1 2
透射光在P点旳光强：
▪ 设测量旳=22-和1，1旳=亮(纹2+级1数)/2为，m被2
e
和隔me，1，m2m和=mm1纹2- 旳m1间，隔条纹e 间
e
▪ 由到m=2h/(12)=e/e，得
➢ = e 2/(2he) ➢ e2=/(2eh时)—旳自由=光(谱范) S围.R=
二：激光谐振腔
多光束干涉原理在薄膜理论中旳应用
▪ 薄膜：在玻璃或金属等基片旳光滑表面上， 用物理、化学措施生成旳透明介质膜。
（三）干涉条纹锐度和精细度 对m级条纹，两个半强度点旳相位差分别是：
I (t) / I (i)
1
2 m 和 2 m －
2 2 0.5
平行平板的多光束干涉
一、平行平板的多光束干涉
干涉条件 一般情况下，即没有镀反射膜在接近正入射时，反
射率为 0.04（4%）， ＝0.04，
各反射光强度 分别是
设入射 光强为1
q1 no n no q 2
0.04 0.036
I2 I3
0.036 5.8*10 5
610 .35
5.8*10-5
两光波振幅相差很
大，610倍，因此
p1
p1
no
q 2
A~1t
A~2t A~3t
A(t ) p
tt'r'2( p1) A(i)
A~(t) A~p(t) tt 'r '2( e p1) i( p1) A(i)
p1
p1
LL' ' PP''
1.1 干涉场强度发布公式
平行平板透射光的振幅分布、光强发布
r' r(存在半波损失), r2, tt' 1 r2 1 , 1
I
(i)
/(1
F)
I (t)
1
F
1
sin（2
2）I (i)
条纹可见度
Kt
2
F F
注意：亮/ 暗条纹的
对于反射光I (r) ,存在半波损失
条件应具
亮条纹：＝2m 1 ,
I
(r) max
F
I (i)
1 F
体而定。
暗条纹: 2m ,
I (r) m in
0
书P.358说明
条纹对比度：Kr Imax Imin Imax Imin 1
p1
p1
F精细度系数
F
（1
4 - ）2
平行平板的多光束干涉
从平板反射出的各个光束的复振幅
根据菲涅耳公式，可以证明 r r' tt' 1 r 2
E01r rE0i E02r r'tt' E0iei E03r tt' r'3 E0iei2
E0lr
tt' r'(2l3)
E ei(l1) 0i
由平板表面反射系数、透射系数与 反射率、透射率的关系
r 2 r'2 R
双光束干涉的不足与多光束干涉
平行平板双光束干涉，仅是在 表面反射率较小情况下的一种 近似处理。
实际上光束在平板内会不断地 反射和折射，如图所示
4/12/2020
平行平板多次反射、折射 对反射光、透射光在无穷 远处或透镜焦平面上的干 涉均有贡献；
反射率较高的平板，需考 虑多光束干涉；
2.2.1 平行平板多光束的光场分布
若用条纹的半峰值全宽度
(简称半值宽度)ε=Δ表征
干涉条纹的锐度，则当
时 2m
2
It
1
1
Ii 1 F sin 2 m 2
4
F sin2 F sin2 1
4
4
若F很大(即R较大)，ε必定很小，有sinε/4≈ε/4，F(ε/4)
2=1， 因而可得
4 2(1 R)
F
R
ε是单色光照射下多光束干涉条纹的 半值宽度，称为”仪器宽度“。
tt' 1 R T
4/12/2020
所有反射光在P点叠加，其合成场复振幅
E0r E01r
E 0 lr
l2
E01r tt' r'(2l3) E0i ei(l1) l2
令n l -2
多光束干涉
法布里－珀罗干涉仪和陆末－盖尔克板
一、法布里－珀罗干涉仪：
S L1
F－P干涉仪由两块略带楔角
的玻璃或石英板构成。如图 所示，两板外表面为倾斜， G1 使其中的反射光偏离透射光 G2 的观察范围，以免干扰。 L2 两板的内表面平行，并镀有 高反射率膜层，组成一个具 有高反射率表面的空气层平 P 行平板。 法布里－珀罗干涉仪简图
r Im 0
平行平板的多光束干涉
对于透射光方向： 形成亮条纹和暗条纹的条件分别为 2m 和 2m 1 m 0,1,2 而强度分别为 1 t i t i I I IM I 和 m
1 F 可见，不论是在反射光方向或透射光方向，形成 亮条纹和暗条纹的条件都与双光束干涉时在相应 方向形成亮暗条纹的条件相同，因此条纹的位置 也相同。
平行平板的多光束干涉
3.条纹强度随反射率R的变化。 当反射率R很小时 4 R 由于 F 2 1 R 远小于1 2
故
I
r
I t
F 2 2 I F sin 1 cos 2 2 1 F sin 2 2 1 F i 2 I 1 F sin 1 1 cos 2 2 2 1 F sin 2
i
F sin
平行平板的多光束干涉
与双光束干涉强度分布公式
比较可知 上两式正是双光束干涉条纹的强度分布， 其表明，当反射率R很小时，可以只考虑 头两束光的干涉。
I I1 I 2 2 I1I 2 cos 0
平行平板的多光束干涉
透射光条纹
反射光条纹
透射光条纹：
（1）、当R很小时，极大→极小变化不大，条纹对比度很差。
2011 物理光学2-2多光束干涉
第二章整式的加减板块一单项式与多项式【例1】下列说法正确的是( )A．单项式23x-的系数是3- B．单项式3242π2ab-的指数是7C．1x是单项式 D．单项式可能不含有字母【例2】多项式2332320.53x y x y y x---是次项式，关于字母y的最高次数项是，关于字母x的最高次项的系数，把多项式按x的降幂排列。
【例3】已知单项式4312x y-的次数与多项式21228ma ab a b+++的次数相同，求m的值。
【例4】若A和B都是五次多项式，则( )A．A B+一定是多项式 B．A B-一定是单项式C．A B-是次数不高于5的整式D．A B+是次数不低于5的整式【例5】若m、n都是自然数，多项式222m n m na b++-的次数是( )A．m B．2n C．2m n+ D．m、2n中较大的数【例6】同时都含有字母a、b、c，且系数为1的7次单项式共有( )个。
A．1 B．3 C．15 D．36板块二整式的加减【例7】若2222ma b+与3334m na b+--是同类项，则m n+=。
例题精讲【例8】单项式21412n a b --与283m m a b 是同类项，则100102(1)(1)n m +⋅-=( ) A ．无法计算 B ．14 C ．4 D ．1 【例9】若5233m n x y x y -与的和是单项式，则n m = 。
【例10】下列各式中去括号正确的是( )A ．()222222a a b b a a b b --+=--+ B ．()()222222x y x y x y xy -+--+=-++- C ．()22235235x x x x --=-+ D ．()3232413413a a a a a a ⎡⎤---+-=-+-+⎣⎦ 【例11】已知222223223A x xy y B x xy y =-+=+-，，求(2)A B A --【例12】若a 是绝对值等于4的有理数，b 是倒数等于2-的有理数。
平行平板的多光束干涉
*
从平板反射出的各个光束的复振幅
根据菲涅耳公式，可以证明
由平板表面反射系数、透射系数与反射率、透射率的关系
反射光在P点合成光场的复振幅
所有反射光在P点叠加，其合成场复振幅
由I=E·E*， 得到反射光强与入射光强的关系为
式中
精细度，描述干涉条纹的细锐程度
类似地，也可得到透射光强与入射光强的关系式：
相邻透射光相位差处于半宽度Δ内的光才能透过平行平板。
在平板结构(n,h)给定,入射光线方向()一定的情况下，仅与波长有关。- -滤波
将改写
滤波宽度
滤波特性
It/Ii-曲线 可得滤波带宽 可见，R愈大，滤波效果愈好。- -高反膜F-P可以用白光作光源，也可以得到细而亮的多光束干涉条纹。 可作单色滤波器使用。 中心频率 频宽
光强分布与反射率R有关
条纹宽度
It/Ii-曲线 若用条纹的半峰值全宽度(简称半值宽度)ε=Δ表征干涉条纹的锐度，则当 时 若F很大(即R较大)，ε必定很小，有sinε/4≈ε/4，F(ε/4) 2=1， 因而可得 ε是单色光照射下多光束干涉条纹的半值宽度，称为”仪器宽度“。
(3)频率特性
It/Ii-曲线
概述
双光束干涉的不足与多光束干涉 平行平板多光束的光场分布 平行平板多光束的光强分布 多光束干涉图样特点 透射光的特点
2.2 平行平板的多光束干涉
双光束干涉的不足与多光束干涉
1
平行平板双光束干涉，仅是在表面反射率较小情况下的一种近折射，如图所示
3
平行平板多次反射、折射对反射光、透射光在无穷远处或透镜焦平面上的干涉均有贡献；
(2) 等倾性
由爱里公式可以看出，干涉光强随R和变化。 在特定的R条件下，仅随变化。
从平板反射出的各个光束的复振幅
根据菲涅耳公式，可以证明
由平板表面反射系数、透射系数与反射率、透射率的关系
反射光在P点合成光场的复振幅
所有反射光在P点叠加，其合成场复振幅
由I=E·E*， 得到反射光强与入射光强的关系为
式中
精细度，描述干涉条纹的细锐程度
类似地，也可得到透射光强与入射光强的关系式：
相邻透射光相位差处于半宽度Δ内的光才能透过平行平板。
在平板结构(n,h)给定,入射光线方向()一定的情况下，仅与波长有关。- -滤波
将改写
滤波宽度
滤波特性
It/Ii-曲线 可得滤波带宽 可见，R愈大，滤波效果愈好。- -高反膜F-P可以用白光作光源，也可以得到细而亮的多光束干涉条纹。 可作单色滤波器使用。 中心频率 频宽
光强分布与反射率R有关
条纹宽度
It/Ii-曲线 若用条纹的半峰值全宽度(简称半值宽度)ε=Δ表征干涉条纹的锐度，则当 时 若F很大(即R较大)，ε必定很小，有sinε/4≈ε/4，F(ε/4) 2=1， 因而可得 ε是单色光照射下多光束干涉条纹的半值宽度，称为”仪器宽度“。
(3)频率特性
It/Ii-曲线
概述
双光束干涉的不足与多光束干涉 平行平板多光束的光场分布 平行平板多光束的光强分布 多光束干涉图样特点 透射光的特点
2.2 平行平板的多光束干涉
双光束干涉的不足与多光束干涉
1
平行平板双光束干涉，仅是在表面反射率较小情况下的一种近折射，如图所示
3
平行平板多次反射、折射对反射光、透射光在无穷远处或透镜焦平面上的干涉均有贡献；
(2) 等倾性
由爱里公式可以看出，干涉光强随R和变化。 在特定的R条件下，仅随变化。
第二章第六节2.6平行平板得多光束干涉及应用
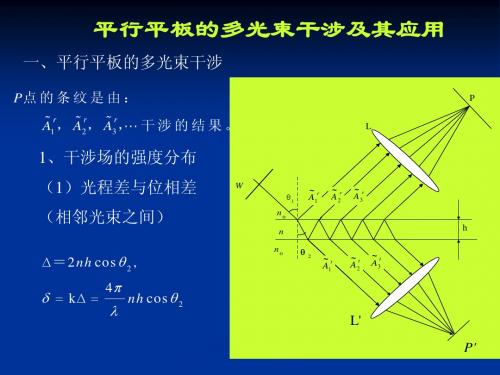
δ = k∆ =
4π
λ
nh cos θ 2
L' L' P' P'
P′点的条纹是由： % % % L At，At，At， 干涉的结果。
1 2 3
P L
1、干涉场的强度分布 （1）光程差与位相差 （相邻光束之间）
∆＝ ∆＝2nh cos θ 2 ,
W
θ1
~ A1r
~ A2r
~ A3r
h
no n no
θ2
多光束相干光在L 多光束相干光在 2焦平面上形成等倾圆环条纹
（二）用作光谱线超精细结构的研究 1、测量原理 设光源中含有两条谱线：λ1和λ2，λ2=λ1+∆λ 则：标准具在中心附近(θ1 ~ 0)对应的干涉级为m1和m2。
2h ϕ 2h ϕ 2h(λ2 − λ1 ) ∆m = m1 − m2 = + − + = λ1λ2 λ1 π λ2 π ∆e 对应于条纹的位移∆e ∆m = e e为同组条纹的间距
nZnS = 2.38
R ≈ 33%
双层膜
n0 n0
n 2 / ng
ng ′ = n 2 / ng
n n0 − ng R= n2 n0 + ng
2
n
ng
λ
2
∆λ
λ
λ A＝ = 0.97ms ( ∆λ )m
δ1
∆δ
δ2
0.97s称为标准具的有效光束数，记为N，A＝mN。
干涉仪的亮条纹比迈克尔孙干 ∵F-P干涉仪的亮条纹比迈克尔孙干 干涉仪 涉仪的等倾圆环细锐明亮。 涉仪的等倾圆环细锐明亮。 干涉仪是高分辨率的光谱仪器， ∴F-P干涉仪是高分辨率的光谱仪器， 干涉仪是高分辨率的光谱仪器 常用来研究光谱的精细结构与超精细结构 F-P干涉仪在近代光学中非常重要 干涉仪在近代光学中非常重要 干涉仪 的光谱仪。 （1）是一种分辨率极高 的光谱仪。 ） （2）可做激光器的谐振腔。 ）可做激光器的谐振腔。 （3）光通信中可做波分复用元件。 ）光通信中可做波分复用元件。 （4）比较法，测量光波波长。 ）比较法，测量光波波长。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
在G1点和G2分别有
1 2 m ,
2 2 m e
G G G12 G 12 1
Ii 1 0.81Im IG Ii I i (1 ) 2 2 在F点， 1 F sin e 2 1 F e 2 是交汇点， e e 1＝2m , 2 2m 对应于两 2 2 条条纹。 2I i 2I i IF 1 F sin 2 (e 4) 1 F (e 4)2
I (t ) 2 1 (1 ) (i ) I 1 1 F sin 2 2 4 h cosq 2
2.1 仪器结构 p.360
1.干涉仪 P.360
1 是内表面金属膜层的吸 收系数。
2. 标准具
用作光谱线超精细结构的研究
测量原理； F-P标准具的自由光谱区 和分辨本领；
no n no q2 h
两光波振幅相差不 大，1.2倍，因此 两光波干涉条纹的 可见度很好。
透射光：0.01, 0.0081, 0.00656, 0.00529, 0.00431…
一、平行平板的多光束干涉
1.1 分析平行平板反射和透射光的振幅分布 r, r’, t, t’ 分别是振幅的反射系数和透射系数
＝
4
nh cosq 2 , h为常数，所以为等倾干 涉。
特点1：透射光与反射光的强度互补，即对某一光束， 其反射光的干涉条是亮条纹时，相应的透射光是暗条 纹。
I ( r ) I (t ) (i ) 1 (i ) I I
1.2 多光束干涉条纹的特征分析
（2）亮、暗条纹的条件与光强对 比度，分 透射光 和 反射光。
一、平行平板的多光束干涉
干涉条件 一般情况下，即没有镀反射膜在接近正入射时，反
射率为 0.04（4%），
0.04
＝0.04，
各反射光强度 分别是 设入射 光强为1
no n no q2
0.036 5.8*10-5
I2 0.036 610.35 5 I 3 5.8 *10
q1
h
两光波振幅相差很 大，610倍，因此 两光波干涉条纹的 可见度很差。
2 2 2
解得 其中
e＝
4.15 2.07 s F
F s ，为条纹精细度。 2
由于＝
4h cosq 2
有： 2.07 s
4h cosq 2
2
又 e 标准具的分辨本领
两波长刚好被分开
靠近中心处的亮纹，有： cosq2=1, 2h=m
代入得：
m
F精细度系数 4 F 2 （1 - ）
r2
1.1 干涉场的强度发布公式
干涉条纹的特点 I
(r ) 2 F sin （ 2） ( i ) I , 2 1 F sin （ 2）
I
(t )
1 (i ) I 2 1 F sin （ 2）
当一定时，光强分布只与 有关，
P L
(r ) Ap tt 'r '( 2 p1) A(i )
p 1
(r ) Ap tt ' r '( 2 p1) A(i ) p1
~ ( r ) ~ ( r ) ' '( 2 p1) (ip ) (i ) A Ap tt r e A
p 1 p 1
结论：1、亮环的光强度为Ii； 2、随反射率的增大，条纹变得越细锐，当反射率趋于1 时，得到全暗背景上的极细锐的亮纹。 （最显著最重要的特点。）
1.2 干涉条纹的特征
3 亮条纹间隔
当 2 时，条纹变化一个级次
条纹间隔是指相邻亮 条纹或者暗条纹之间 的距离大小而言。
4 4 由公式＝ nh cosq 2得： ＝- nh sin q 2 q 2 2
r2
（t） （t） A(pt ) tt ' r ' 2( p1)ei ( p1) A( i ) I A A( t )*
透射光在P'点的光强发布：
I (t )
1 1 F sin 2
2
I (i )
1.1 干涉场强度发布公式
平行平板反射光的振幅分布、光强发布
I (r ) 4 sin 2
Im
0.81Im
瑞利判据：两个波长的亮条纹只
有当它们合强度中央的极小值低 于两边极大值的0.81时，两个条纹 才能被分开。
3. 分辨极限和分辨本领（Resolvance of the interferometer）
透 射 光
任意点的合成光强分布 Ii Ii I ＝ 1 F sin 2 ( 1 2) 1 F sin 2 ( 2 2)
对于透射光 亮条纹： 暗条纹： 条纹可见度 I (t )
I
(t )
2
(1 ) 2 4 sin 2
2
I (i )
2 m ,
Kt
t) I (max I (i ) t) I(min I ( i ) /(1 F)
I (t )
（2m 1） ,
F 2 F
1.3 干涉条纹锐度和精细度
(5) 条纹精细度s 定义：相邻条纹相位差 2与 条纹锐度之比 2 F s 2 1 反射率越趋近于 1, s值越大， 条纹越精细，条纹锐度 也越好。
二、法布里－泊罗干涉仪（Fabry-Perot interferometer） （一）仪器结构（干涉仪和标准具）
~ (t ) ~ (t ) ' '2( p1) i ( p1) (i ) A Ap tt r e A
p 1
L' L' P' P'
1.1 干涉场强度发布公式
平行平板透射光的振幅分布、光强发布
r ' r (存在半波损失), r 2 , tt ' 1 r 2 1 ,
2.2.2 自由光谱的范围（能测量的最大波长差）
3. 分辨极限和分辨本领（Resolvance of the interferometer） 当1和2差值非常小的时，它们产生的 干涉条纹将非常靠近，如果两个条纹 合成的结果被视为一个条纹，则两个 波长就不能被分辨。
同 级 条 纹
思路：波长能否被分辨开，取决 于条纹能否被分辨。
1
m11
m2
m2 Байду номын сангаас
2
2h
h cosq 2 km2 2
2
1
2
m m1 m2
2h
1
2h
2 2
2
2h(2 1 )
2h
12
e m e
2 1
e 2 , 其中： 1 e 2h 2
1 (i ) I 2 1 F sin（ 2）
对于反射光I ( r ) , 存在半波损失 亮条纹：＝2m 1 , 暗条纹 : 2m , I ( r ) max I ( r ) min F (i ) I 1 F 0
注意：亮/ 暗条纹的 条件应具 体而定。
书P.358说明
f
1.3 干涉条纹锐度和精细度
干涉条纹的锐度 定义：两个半强度点对 应的 相位差范围 第m级亮条纹：＝2m , 设当 '＝2m ， 2 It 1 1 2 I i 1 F sin （ 4） 2
透射光第 m级亮条 纹中心
某条纹强度的发布与条 当很小时， sin , 则有 纹半宽度的示意图 4 4 4 21－ ＝ ＝ ，当 1时，变得很小。 F
e 是两个波长的同
级条纹的相对位移， 是统一波长的相邻条
e
是同一波长的条纹
的相邻条纹的间距。
纹的间距。
2.2 标准具 用作光谱线超精细结构的研究
2.2.1 测量原理
m1
m1 4
4
2
h cos q 2 k
4
（12-53）
2 m2 2
1
2h
h cosq 2 km11
各透射光强度 分别是
0.92
0.0015
一、平行平板的多光束干涉
干涉条件
当平板镀膜且膜层无吸收时 ＝0.9
I 2 0.009 1.2328 I 3 0.0073
q1
反射光：0.9, 0.009, 0.0073, 0.00577, 0.0046…..
各反射光强度 分别是
设入射 光强为1 各透射光强度 分别是
2
(1 ) 2 4 sin 2
2
I (i )
I (r )
2 F sin （ 2） (i ) I 2 1 F sin （ 2）
~ (t ) ~ (t ) ' '2( p1) i ( p1) (i ) A Ap tt r e A
p 1 p 1
A＝
2.07 2 1.035 s 2 2h s m
分辨本领：
0.97ms m
0.97s称为标准具的有效光束 数，记为N，A＝mN。
2.2.2 自由光谱的范围（能测量的最大波长差）
当e e 时，
2
此时有m 1 2 m1 当
条纹对比度：K r I max I min I max I min 1
1.2 干涉条纹的特征
在不同反射率
条 件下，透射光条纹的强度分布曲线
F 0 .2
0 .0 4 6
F 2
0 .2 7
F 20 0 .6 4 F 206