单筋矩形截面设计资料.
单筋,矩形,正截面受弯,承载力计算

四、适用条件验算
(1) 防止少筋脆性破坏
min
min 时取 min
(2) 防止超筋脆性破坏
b或x bh0
As
bh0
max b
fc fy
A
h h0 a
b
As
Ⅰ钢筋: b 0 .614 Ⅱ钢筋: b 0 .544 Ⅲ钢筋: b 0 .518
(2)受压区合力C的作用点不变。
x1xc
1、 A1都是经验系数 凝, 土通 强过 度 6 混 查
三、基本计算公式
x 1xc
Mu
1 fc x/2 C h0
T fy As
x h0
X 0 1fcbxfyAs
M0
M
Mu
1
fcbx(h0
x )
2
x
M
Mu
fy As(h0
) 2
1 fcbh0 fyAs
ee c fc1 1 c
n
0
e 当e 0 <ec≤ ecu 时(水平段):
o
e0
ecu
c 0 fc
(4) 钢筋的应力-应变方程为:
钢筋的应力等于钢筋应变与其弹性模量的乘积,
f 但不大于强度设计值 fy 。极限拉应变取为 0.01。 y
Ese e ey fy e ey
A
Es
1
ey
弹塑性
配筋率 A s bh 0
8
开始
读
M、
b、
h、
a
、
s
f y、
、
1
f c、
A s、
f t、
m
、
in
钢筋混凝土单筋矩形截面梁例题

例题1:已知:矩形截面钢筋混凝土简支梁,计算跨度为6000mm , as=35mm 。
其上作用均布荷载设计值25 kN/m (不包括梁自重),混凝土强度等级选C20,钢筋HRB335级。
( fc =9.6 N/mm2 , ft =1.1 N/mm2 , fy =300 N/mm2 )试设计此梁。
[解](1)基本数据fc=9.6N/mm2,fy=300N/mm2 M=1/8ql 2=25N/mm ×6000mm ×6000mm/8=112500000N.mm(2)假定梁宽bh 一般取为1/10-1/15L ,即600mm-400mm ,取600mmh/b=2.0-3.5 则b=300mm (符合模数要求)(3)假定配筋率受弯构件 0.2与45ft/fy 较大值45ft/fy=45×1.1/300=0.165 取0.2(4)计算有关系数cy s c yf f bh A f f αραξ=⋅=0=0.2%×300÷(1×9.6)=0.0625 ])1(1[5.02s ξα--==0.5×[1-(1-0.0625)2]=0.0605(5)令M=Mu 计算h0mm 530.803157.645661mm300/6.910605.011250000010==⨯⨯⨯⋅==mm N mm N b f Mh c s αα (6)计算梁高h=h0+35=838mm ,取h=900mm则h/b=3满足h/b=2.0~3.5的要求(7)计算受拉钢筋0625.02-1-1==s αξ (第(4)部分已计算结果)96875.00625.05.015.012211122-11=⨯-=-=---=+=ξααγs s s 220540900300002.05107.44786596875.0300112500000mm mm h f MA s y s =⨯⨯<=⨯⨯==γ 取2540mm A s =(8)选配钢筋(9)验算适用条件(10)这样调整后,截面尺寸b 、h 变为已知情形,再按例题3计算As 。
04 单筋矩形截面正截面承载能力计算

在梁的正截面强度计算中 用等效矩形应力图代替受压 区抛物线应力图,x为等效矩 形应力图的高度,h0为截面 有效高度,它们的比 值:ξ=x/h0, ξ称为相对受压区 高度。
相对受压区高度ξ不仅反映了钢筋与混凝土的面积比(配筋率ρ), 也反映了钢筋与混凝土的材料强度比,是反映构件中两种材料配比 本质的参数。
钢筋混凝土构件在按承载能力极限状态计算时,引入下列假定: ①构件弯曲后,其截面仍保持平面,受压区混凝土平均应变和 钢筋的应变沿截面高度符合线性分布。平截面假定 ②正截面破坏时,构件受压区混凝士应力取抗压强度设计值fcd fcd,应力计算图形为矩形。等效矩形应力图 ③正截面破坏时,受弯、大偏心受压、大偏心受拉构件的受拉 主筋达到抗拉强度设计值fsd ,受拉区混凝土不参与工作(抗剪计算除外)。
2 正截面承载力计算的基本假定
以IIIa阶段作为承载力极限状态的计算依据
(l)上图为钢筋混凝土梁对应三个工作阶段的应变图。由图可见, 梁在第I阶段受压与受拉应变图呈直线分布,说明混凝土与钢筋应 变的变化规律符合平截面假定。随着弯矩的增加,当梁进入第II 阶段时,受压区混凝土压应变与受拉区钢筋拉应变的实测值均不 断增长,但应变图基本上仍是上、下两个三角形,平均应变仍符 合平截面假定。这种状况一直延续至第Ⅲ阶段,即梁破坏前。最 后,当梁破坏时,受压区混凝土边缘纤维压应变达到(或接近)混 凝上受弯时极限压应变,这标志着梁已开始破坏。
(4)由公式fsdAs=fcdbx或fsdAs(h0-x/2)=γ0Md 计算钢筋截面面积As;
(5)根据计算所得和构造要求选择钢筋直径、根数并布置,确定实际的As 实 ;实际采用的钢筋宜为计算所需钢筋截面面积的0.95~1.05倍。
(6)检查假定as是否接近实际,如误差大,重新计算(因为若as假<as实,则
第3章 §4单筋矩形截面

h0
②由(3—14)或(3—15)得到h0,再得到x的具体值;
③估计as,求出截面高度h= h0 + as ,h取整数并符合模数。至此 估计出截面b×h;
④按第(1)种情况继续计算出As并布置。
注:第②步中 h0
0 Md (1 0.5 ) fcd b
x 0,
基本 公式
x (= ) b h0 As fcd max 或= max b
bh0 fsd
(2)不少筋——防止少筋破坏
As ( ) min bh
(3—20)
(3—21)
b查表3— 2,min查附表 1— 9。
返回
二、计算方法及步骤
截面设计
任务 截面复核 1、截面设计:
§4 单筋矩形截面受弯构件
一、1、计算图式(图3—19)
α1ffcd c x = ξ h0
b
c
C =f cdbx
γ0Md
计算中性轴
h0
x 2
As
T =fsd As s
2、基本 公式
返回
x 0,
fcd bx fsd As
x M As 0, 0 M d M u fcd bx( h0 ) (3—14) 2 x M c 0, 0 M d M u fsd As ( h0 ) (3—15) 2
若 x>ξbh0,说明超筋,即ρ>ρmax,取x= ξbh0,则这时承载 力为: M f bh2 (1 0.5 ) (3—22)
u cd 0 b b
若 M u 0 Md ,则修改设计,如加大截面尺寸(加大高度 效果好于加大宽度),提高砼标号,或改用双筋。
③若第①步构造检查出ρ<ρmin,说明少筋,则应按As=ρminbh0重 新配置钢筋或修改截面(减小截面); ④若x≤ξbh0 ,则将 x代入按(3—14)或(3—15)式计算Mu
单筋矩形截面受弯构件的正截面设计概要

3.4.2 设计计算方法:
主要内容
1) 截面设计
3.4 单筋矩形截面受弯构件 的正截面承载力计算
(1) 截面设计的概念 ——做什么? (2) 截面设计的步骤 ——怎么做? 2) 截面复核 (1) 截面复核的概念——做什么? (2) 截面复核的步骤——怎么做?
n m 0 Sd 0 Gi SGi k Q1SQ1k c γQj SQjk j 2 i 1
控制截面
1) 截面设计
(2) 截面设计步骤
反之,截面尺寸 b 、 h(h0) 越 小,所需 As 就越大, ρ 增大。
经济配筋率:
梁: ρ=0.5%~1.6%
板: ρ=0.4%~0.8%
1) 截面设计
(2) 截面设计步骤 ③ 内力计算:
3.4 单筋矩形截面受弯构件 的正截面承载力计算
① 材料选择 ② 截面尺寸确定
控制截面 ?
等截面受弯构件: 弯矩组合设计值最大的截面 变截面受弯构件: 还包括截面尺寸相对较小,弯矩 组合设计值相对较大的截面 P q 弯矩组合设计值?
(2) 截面设计步骤 ① 材料选择:
3.4 单筋矩形截面受弯构件 的正截面承载力计算
公路桥梁工程中,钢筋混凝土构件的混凝土强度等级
不应低于C20;当采用400MPa级钢筋配筋时,不应 低于C25。 混凝土建议采用:C25~C40 钢筋建议采用:梁 HRB335、HRB400级钢筋 板 R235、HRB335级钢筋 (建筑工程中已取消了HPB235级钢筋,增加了HRB500级钢筋)
1) 截面设计
(2) 截面设计步骤 ② 截面尺寸确定:
第三节 单筋矩形截面受弯构件的承载力计算与截面构造汇总

弯起钢筋:
• • • •
梁中一般布置四种钢筋: 纵向受力钢筋 箍筋 弯起筋 架立钢筋
为了保证斜截面强度而设置的 一般可将纵向受力钢筋弯起而
形成 有时也专门设置弯起钢筋,以 满足纵向受力钢筋和斜截面的 需要。
架立钢筋:
c 、纵向受力钢筋
第三节 单筋矩形截面受弯构件的承载力计算与截面构造
一、基本公式与适用条件:
1、计算公式: 2、适用条件:
二、截面构造要求: 三、基本公式的应用:
1、计算公式:
1 f c bx f y As
x M M u 1 f c bx (h0 ) 2 x M M u f y As (h0 ) 2
d、梁保护层厚度
在梁截面选择配筋计算 时,
ho=h-35mm(一排钢筋) ho=h-60mm(两排钢筋)
板 :ho=h-20mm
e、纵向构造钢筋(架立筋)
固定作用:固定箍筋并与受 力钢筋连成钢筋骨架。 架立筋布置于梁的受压区, 承受由于混凝土收缩及温度 变化所产生的拉力。 如在受压区有受压纵向钢筋 时,受压钢筋可兼作架立筋 架立筋的直径与梁的跨度有 关。 梁高大于700mm时,在梁的 梁的跨度(m) 架立钢筋直径 两侧沿高度每隔300—400mm, (mm) 应设一根直径不小于10mm L<4m 不小于6mm 的纵向构造钢筋。
二、截面构造要求: (1)梁截面的构造要求: a 、梁截面形状、尺寸 • 上述要求并非严格规定,宜根据具体情况灵活掌握。
在浅梁中,宽度可适当放大。 目前常用的梁宽有:120mm、150mm、180mm、 200mm、220mm、250mm,之后以50mm的 模数递增
单筋矩形梁正截面受弯承载力计算实例
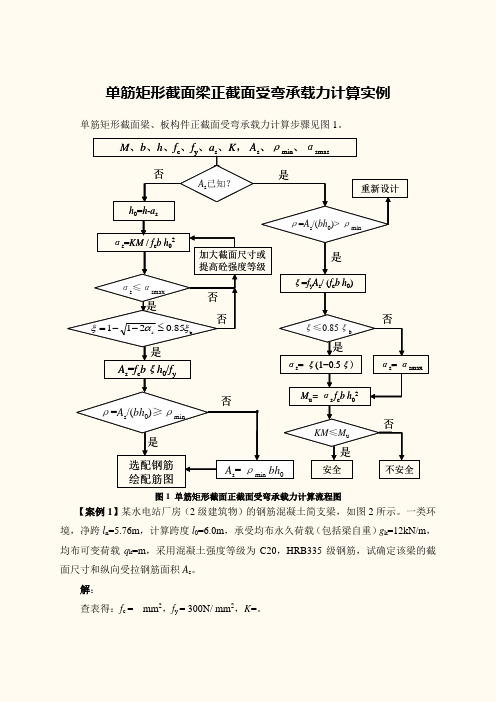
单筋矩形截面梁正截面受弯承载力计算实例单筋矩形截面梁、板构件正截面受弯承载力计算步骤见图1。
选配钢筋加大截面尺寸或是M 、b 、h 、f c 、f y 、a s 、K ,A s 、ρmin 、αsmasαs =KM / f c b h 02A s =f c b ξh 0/f ybs 85.0211ξαξ≤--=h 0=h -a s否A s = ρmin bh 0绘配筋图是是A s 已知?αs ≤αsmax提高砼强度等级ρ=A s /(bh 0)≥ρmin是ξ=f y A s / (f c b h 0)ξ≤0.85ξbαs = ξ(1−0.5ξ)M u = αs f c b h 02KM ≤M u是是安全αs = αsmax否否不安全否否否ρ=A s /(bh 0)> ρmin是重新设计图1 单筋矩形截面正截面受弯承载力计算流程图【案例1】某水电站厂房(2级建筑物)的钢筋混凝土简支梁,如图2所示。
一类环境,净跨l n =5.76m ,计算跨度l 0=6.0m ,承受均布永久荷载(包括梁自重)g k =12kN/m ,均布可变荷载q k =m ,采用混凝土强度等级为C20,HRB335级钢筋,试确定该梁的截面尺寸和纵向受拉钢筋面积A s 。
解:查表得:f c = mm 2,f y = 300N/ mm 2,K =。
(1)确定截面尺寸 由构造要求取:h =(1/8~1/12)l 0 =(1/8~1/12)×6000=750~500,取h =500mm b =(1/2~1/3)h =(1/2~1/3)×500=250~167,取b =250mm (2)内力计算M =(+ )l 02/8=(×12+×)×62 /8 = ·m (3)配筋计算取a s =40mm ,则h 0=h –a s =500–40=460mm==2c s bh f KMα248.04602506.91076.10420.126=⨯⨯⨯⨯ 290.0248.0211211s =⨯--=--=αξ<ξb =×=A s =f c bξh 0/f y =×250××460/300=1067mm 2 ρ= 1067/(250×460)=﹪>ρmin =﹪(4)选配钢筋,绘制配筋图选受拉纵筋为322(A s =1140 mm 2),需要最小梁宽b min =2c +3d +2e =2×30+ 3×22+2×25=176(mm )<250mm ,符合构造要求。
6单筋矩形截面

2某教学楼钢筋混凝土矩形截面简支梁,安全等级为二级,截面尺寸 b×h=250×550mm,承受恒载标准值10kN/m(不包括梁的自重),活荷载标准 值12kN/m,计算跨度=6m,采用C20级混凝土,HRB335级钢筋。试确定纵向 受力钢筋的数量。
3. 计算x,并判断是否属超筋梁
2M 2 148.165106 2 x h0 h 510 510 1 f c b 1.0 9.6 250
2)复核己知截面的承载力 己知:构件截面尺寸b×h,钢筋截面面积As,混凝土强度等级fc,钢筋级别 fy ,弯矩设计值M 。 求:复核截面是否安全 、弯矩承载力Mu= ?
计算步骤如下:
①确定截面有效高度h0 ②判断梁的类型 As f y
x
1 f c b
若As minbh,且x b h0 为适筋梁;
若x b h0 为超筋梁;若As minbh 为少筋梁。
③计算截面受弯承载力Mu
适筋梁 M u As f y h0 x 2
2 超筋梁 M M f bh u u, max 1 c 0 b (1 0.5b )
对少筋梁,应将其受弯承载力降低使用(已建成工程)或修改设计。 ④判断截面是否安全 若M ≤Mu ,则截面安全。
防止少筋的条件:
x xb b h0
min
AS AS ,min minbh
取x =ξbh0 ,即得到单筋矩形截面所能承受的最大弯矩的表达式:
2 M u,max 1 f c bh0 b (1 0.5 b )
混凝土受压区高度计算式: x h0
2M h 1 f c b
③ 少筋梁
配筋率小于最小配筋率的梁为少筋梁。 破坏特征:梁破坏时, 裂缝往往集中出现一条, 不但开展宽度大,而且 沿梁高延伸较高。一旦 出现裂缝,钢筋的应力 就会迅速增大并超过屈 服强度而进入强化阶段, 甚至被拉断。属于“脆 性破坏”
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
③计算钢筋截面面积As: As 1 fcbx / f y
④判断是,则不属少筋梁。
否则为少筋梁,应取As=ρminbh。
二、单筋矩形截面正截面承载力计算实例讲述
例5.1某钢筋混凝土矩形截面简支梁,构件处于 一类环境,构件安全等级为Ⅱ级计算跨度为
l0=5m,截面尺寸b×h=250×500mm,承受 楼面传来的均布恒载标准值(包括自重)gk= 6kN/m,均布活荷载标准值pk=15kN/m,采
己知:弯矩设计值M,材料强度fc、fy,截面尺寸b×h;求截面配筋As 计算步骤如下: ①确定截面有效高度h0:h0=h-as
②计算混凝土受压区高度x ,并判断是否属超筋梁
x h0
h02
2M
1 fcb
若x≤ξbh0,则不属超筋梁。 若x>ξbh0,为超筋梁,应加大截面尺寸, 或提高混凝土强度等级,或改用双筋截面。
课 题 5.4单筋矩形正截面承载力计算
学 时
1
教学目的 教学要求
了解单筋矩形正截面承载力计算的方法和步骤 ①了解单筋矩形梁正截面承载力的计算方法;
教学重点
教学难点 教学方法
单筋矩形正截面承载力的计算方法——掌握公式法计 算与步骤,了解表格法的计算方法 通过例题计算比较的形式及配合多媒体演示进行讲解
5.受弯构件正截面受弯承载力计算——截面设计(公式法)
弯矩设计值M=75kN*m,采用C20级混凝 土,HPB300级钢筋,试求受拉钢筋的截面
面积As、并绘制截面配筋图。
The End
用C20级混凝土,HRB335级钢筋,试求受拉
钢筋的截面面积As、并绘制截面配筋图。
解:见黑板
小结
通过本节学习使学生了解单筋矩形梁 正截面承载力计算的方法和步骤
作业布置
• 某钢筋混凝土矩形截面简支梁,构件处于 一类环境,构件安全等级为Ⅱ级计算跨度
为l0=5m,截面尺寸b×h=200×400mm,
