线段角单元试题组卷(02)组卷
中考数学专题复习《线段、角、相交线与平行线》专项检测题(含答案)

线段、角、相交线与平行线专项检测题一、选择题(下列每题所给的四个选项中只有一个正确答案)1.下列图形中,∠1与∠2是对顶角的是()2.下列图形中,∠2>∠1的是()3.如图,直线a∥b,∠A=38°,∠1=46°.则∠ACB的度数是()A. 84°B. 106°C. 96°D. 104°4.如图,已知AB∥CD,∠C=70°,∠F=30°,则∠A的度数为()A. 30°B. 35°C. 40°D. 45°5.如图,AB∥CD,CB平分∠ABD,若∠C=40°,则∠D的度数为()A. 90°B. 100°C. 110°D. 120°6.如图所示,已知AB∥CD,直线EF交AB于点E,交CD于点F,且EG平分∠FEB,∠1=50°,则∠2等于()A. 50°B. 60°C. 70°D. 80°7.如图,已知直线AB∥CD,直线EF与AB、CD相交于N、M两点,MG平分∠EMD,若∠BNE=30°,则∠EMG 等于()A. 15°B. 30°C. 75°D. 150°8.如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=()A. 52°B. 38°C. 42°D. 60°9.把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为()A. 125°B. 120° C . 140° D. 130°10.下列命题是真命题的是()A. 任何数的0次幂都等于1B. 顺次连接菱形四边中点的线段组成的四边形是正方形C. 图形的旋转和平移会改变图形的形状和大小D. 角平分线上的点到角两边的距离相等11.下列命题正确的是()A. 矩形的对角线互相垂直B. 两边和一角对应相等的两个三角形全等C. 分式方程x-22x-1+1=1.51-2x可化为一元一次方程x-2+(2x-1)=-1.5D. 多项式t2-16+3t因式分解为(t+4)(t-4)+3t12.下列命题中,正确的是()A. 函数y=x-3的自变量x的取值范围是x>3B. 菱形是中心对称图形,但不是轴对称图形C. 一组对边平行,另一组对边相等的四边形是平行四边形D. 三角形的外心到三角形的三个顶点的距离相等13在平面直角坐标系中,任意两点A(x1,y1),B(x2,y2),规定运算:①A⊕B=(x1+x2,y1+y2);②A⊕B=x1x2+y1y2;③当x1=x2且y1=y2时,A=B.有下列四个命题:(1)若A(1,2),B(2,-1),则A⊕B=(3,1),A⊗B=0;(2)若A⊕B=B⊕C,则A=C;(3)若A⊗B=B⊗C,则A=C;(4)对任意点A、B、C,均有(A⊕B)⊕C=A⊕(B⊕C)成立.其中正确命题的个数为()A. 1个B. 2个C. 3个D. 4个二、填空题14.若∠α的补角为76°28′,则∠α=________.15.如图,直线m∥n,△ABC为等腰直角三角形,∠BAC=90°,则∠1=________度.16.如图,AB∥CD,AD与BC交于点E,若∠B=35°,∠D=45°,则∠AEC=________.17如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=________.18如图,直线a、b被第三条直线c所截,如果a∥b,∠1=70°,那么∠3的度数是________.19.如图,l∥m,等边△ABC的顶点A在直线m上,则∠α=________.20.如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF 于点F,∠AGF=130°,则∠F=________.21.下列命题:①对角线相等的四边形是矩形;②正多边形都是轴对称图形;③通过对足球迷健康状况的调查可以了解我国公民的健康状况;④球的主视图、左视图、俯视图都是圆;⑤如果一个角的两边与另一个角的两边分别平行,那么这两个角相等,其中是真命题的有________(只需填写序号).22.下列命题:①对角线互相垂直的四边形是菱形;②点G是△ABC的重心,若中线AD=6,则AG=3;③若直线y=kx+b经过第一、二、四象限,则k<0,b>0;④定义新运算:a※b=2a-b2,若(2x)※(x-3)=0,则x=1或9;⑤抛物线y=-2x2+4x+3的顶点坐标是(1,1).其中是真命题的有________.(只填序号)参考答案1. C【解析】A.∠1、∠2没有公共顶点,不是对顶角,故A选项错误;B.∠1、∠2两边不互为反向延长线,不是对顶角,故B选项错误;C.∠1、∠2有公共顶点,两边互为反向延长线,是对顶角,故C选项正确;D.∠1、∠2两边不互为反向延长线,不是对顶角,故D选项错误.2. C【解析】根据对顶角相等,平行四边形的性质和平行线的性质,可以知道A、B、D中∠1=∠2,而在C中,三角形的一个外角大于和它不相邻的一个内角,可得∠2>∠1,故选C.3. C【解析】∵a∥b, ∴∠ABC=∠1=46°,又∵∠A=38°,∴∠ACB=180°-∠A-∠ABC=180°-38°-46°=96°.4. C【解析】∵AB∥CD,∴∠FEB=∠C=70°.∵∠FEB是△AFE的一个外角,∴∠FEB=∠A+∠F,∴∠A=∠FEB-∠F=70°-30°=40°.5. B【解析】∵AB∥CD,∴∠C=∠ABC=40°,∵CB平分∠ABD,∴∠CBD=∠ABC=40°,∴∠D=180°-∠C-∠CBD=180°-40°-40°=100°.6. D【解析】∵EG平分∠BEF,∴∠BEF=2∠1,∵∠1=50°,∴∠BEF=100°,∵AB∥CD,∴∠BEF+∠2=180°,∴∠2=180°-∠BEF=180°-100°=80°.【一题多解】∵AB∥CD,∴∠1=∠EGF,∵EG平分∠FEB,∴∠1=∠FEG,∴∠FEG=∠EGF,∴由三角形内角和为180°得,∠2=180°-2∠EGF=180°-2×50°=80°.7. A【解析】∵AB∥CD,∴∠ENB=∠EMD=30°,又∵MG平分∠EMD,∴∠EMG=∠DMG=12∠EMD=15°.8. A【解析】如解图,∵直尺的两边互相平行,∴∠3=∠2=38°,∵∠1+∠3+∠4=180°,∠4=90°,∴∠1=180°-∠4-∠3=180°-90°-38°=52°.9. D【解析】如解图,在Rt△ABC中,∠A=90°,∵∠1=40°,∴∠3=90°-∠1=50°,∴∠4=180°-∠3=130°.∵EF∥MN,∴∠2=∠4=130°.选项逐项分析正误A任何非零数的0次幂都等于1×B 顺次连接菱形四边中点的线段组成的四边形是矩形×C图形的旋转和平移不会改变图形的形状和大小×D 根据角平分线的性质可知:角平分线上一点到角两边的距离相等√选项逐项分析正误A矩形的对角线相等,不一定垂直×B 已知两边及其夹角对应相等,两个三角形才能全等×C 方程两边同乘以2x-1,得x-2+(2x-1)=-1.5√D 没有把多项式化成整式的积的形式,不是因式分解×12. D【解析】选项逐项分析正误A函数y=x-3的自变量x的取值范围是x≥3×B 菱形是中心对称图形,也是轴对称图形,两条对角线所在直线就是对称轴×C 一组对边平行,另一组对边相等的四边形可能是平行四边形,也可能是等腰梯形×D三角形的外心是三边中垂线的交点,所以到三角形的三个顶点的距离相等√13. C【解析】设C(x3,y3)序号逐项分析正误(1)若A(1,2),B(2,-1),则A⊕B=(1+2,2+(-1))=(3,1),A⊗B=1×2+2×(-1)=0√(2) A⊕B=(x1+x2,y1+y2),B⊕C=(x2+x3,y2+y3),若A⊕B=B⊕C,则,∴x1=x3,y1=y3,∴A=C√(3) A⊗B=x1x2+y1y2,B⊗C=x2x3+y2y3,若A⊗B=B⊗C,则x1x2+y1y2=x2x3+y2y3,并不能确定x1=x3,y1=y3,∴A不一定等于C×(4) (A ⊕B)⊕C =(x 1+x 2,y 1+y 2)⊕C =(x 1+x 2+x 3,y 1+y 2+y 3),A ⊕(B ⊕C)=A ⊕(x 2+x 3,y 2+y 3)=(x 1+x 2+x 3,y 1+y 2+y 3),∴(A ⊕B)⊕C =A ⊕(B ⊕C)√综上,正确命题有(1)(2)(4)共3个.14. 103°32′ 【解析】求一个角的补角,只需用180°减去它即可,但须注意进制,180°-76°28′=179°60′-76°28′=103°32′15. 45 【解析】∵△ABC 为等腰直角三角形,∠BAC =90°,∴∠ABC =45°.又∵m ∥n ,∴∠1=∠ABC =45°.16. 80° 【解析】∵AB ∥CD ,∴∠B =∠C =35°,∵∠AEC =∠C +∠D ,∴∠AEC =35°+45°=80°.【一题多解】∵AB ∥CD ,∴∠C =∠B =35°,又∵∠D =45°,∴∠CED =180°-∠C -∠D =100°.∴∠AEC =180°-∠CED =80°.17. 63°30′ 【解析】∵∠1=40°,∠2=40°,∴a ∥b, ∴∠4=180°-∠3=180°-116°30′=63°30′.18. 70° 【解析】因为a ∥b ,所以根据平行线的性质有∠1=∠2,又因为∠2和∠3为对顶角,所以∠2=∠3=70°.19. 20° 【解析】如解图,延长CB ,交直线m 于点D ,则∠CDA =40°,因为△ABC 为等边三角形,所以∠CBA =60°.根据三角形内外角的关系,得∠α=∠CBA -∠CDA =60°-40°=20°20. 9.5° 【解析】∵AB ∥CD ,∴∠BED =∠CDE =119°,∵EF 平分∠BED ,∴∠BEF =12∠BED =12×119°=59.5°,∵∠AGF =130°,∴∠EGF =180°-∠AGF =180°-130°=50°,∵∠BEF 是△EFG的外角,∴∠F=∠BEF-∠EGF=59.5°-50°=9.5°.序号逐项分析正误①对角线相等且互相平分的四边形是矩形×②正多边形都是轴对称图形√③足球迷比其他人更热爱运动,所以抽样调查的样本不具代表性×④从任意角度看球得到的平面图形都是圆√⑤如解图所示,∠1与∠2的两边分别平行,但不相等×序号逐项分析正误①对角线互相垂直平分的四边形是菱形,故①错×②重心到顶点的距离与重心到对边中点的距离之比为2∶1,画草图如解图,即AG∶GD=2∶1,若×。
七年级数学上册第4章线段角单元测试卷试题

冀教版梁山中学2021年七年级数学上册第4章?线段角?单元测试卷制卷人:歐陽文化、歐陽理複;制卷時間:二O二二年二月七日一、选择题〔一共10小题,每一小题3分,满分是30分〕1、以下说法中正确的选项是〔〕A、两点之间的所有连线中,线段最短B、射线就是直线C、两条射线组成的图形叫做角D、小于平角的角可分为锐角和钝角两类2、以下说法正确的选项是〔〕A、过一点P只能作一条直线B、直线AB和直线BA表示同一条直线C、射线AB和射线BA表示同一条射线D、射线a比直线b短3、AB=10cm,在AB的延长线上取一点C,使AC=16cm,那么线段AB的中点与AC的中点的间隔为〔〕A、5cmB、4cmC、3cmD、2cm4、按以下线段长度,可以确定点A、B、C不在同一条直线上的是〔〕A、AB=8cm,BC=19cm,AC=27cmB、AB=10cm,BC=9cm,AC=18cmC、AB=11cm,BC=21cm,AC=10cmD、AB=30cm,BC=12cm,AC=18cm5、以下图形中,无端点的是〔〕A、角平分线B、线段C、射线D、直线6、以下给出的四个语句中,结论正确的有〔〕①假如线段AB=BC,那么B是线段AC的中点;②线段和射线都可看作直线上的一局部;③大于直角的角是钝角;④如图,∠ABD也可用∠B表示.A、1个B、2个C、3个D、4个7、钟表在5点半时,它的时针和分针所成的锐角是〔〕A、15°B、70°C、75°D、90°8、钟表上12时15分钟时,时针与分针的夹角为〔〕A、90°B、82.5°C、67.5°D、60°9、∠A=40°,那么∠A的补角等于〔〕A、50°B、90°C、140°D、180°10、以下说法中正确的选项是〔〕A、8时45分,时针与分针的夹角是30°B、6时30分,时针与分针重合C、3时30分,时针与分针的夹角是90°D、3时整,时针与分针的夹角是90°二、填空题〔一共8小题,每一小题3分,满分是24分〕11、用一个钉子把一根细木条钉在墙上,木条就可能绕着钉子,原因是;当用两个钉子把木条钉在墙上时,木条就被固定住其根据是.12、如图,用“>〞、“<〞或者“=〞连接以下各式,并说明理由.AB+BC AC,AC+BC AB,BC AB+AC,理由是.13、两根细木条,一根长80厘米,另一根长130厘米,将它们其中的一端重合,放在同一条直线上,此时两根细木条的中点间的间隔是.14、0.5周角= 平角= 直角= 度.15、〔1〕57.32°=度分秒.〔2〕27°14′24″=度.16、假如∠BOA=82°,∠BOC=36°,那么∠AOC的度数是.17、如图中,∠AOB=180°,∠AOC=90°,∠DOE=90°,那么图中相等的角有对,分别为;两个角的和为90°的角有对;两个角的和为180°的角有对.18、一个锐角的余角的补角与这个锐角的差是角.三、解答题〔一共5小题,满分是46分〕19、如图,在同一个平面内有四个点A、B、C、D①画射线CD ②画直线AD ③连接AB④直线BD与直线AC相交于点O.20、如下图,点C是AB上任意一点,D、E分别是AC、CB的中点,假设AB=16,求DE的长.21、如图,用量角器量出图中∠1,∠2,∠3的度数,猜一猜它们之间有何关系?22、如下图,∠AOC比∠BOC小30°,∠AOD=∠BOD,求∠DOC的度数.23、如图,直线AB和CD相交于O点,∠COE是直角,OF平分∠AOE,∠COF=34°,求∠BOD 的度数.答案及分析:一、选择题〔一共10小题,每一小题3分,满分是30分〕1、以下说法中正确的选项是〔〕A、两点之间的所有连线中,线段最短B、射线就是直线C、两条射线组成的图形叫做角D、小于平角的角可分为锐角和钝角两类考点:直线、射线、线段;角的概念。
2022-2023学年四年级数学上册第二单元线与角检测卷(提高卷)(含答案)北师大版

绝密★启用前2022-2023学年四班级数学上册其次单元线与角检测卷(提高卷)考试时间:60分钟;满分:102分班级: 姓名:成果:留意事项:1.答题前填写好自己的班级、姓名等信息。
2.请将答案正确填写在答题区域,留意书写工整。
卷面(2分)。
我能做到书写端正,格式正确,卷面洁净。
一、认真填一填。
(每空1分,共26分)1.把上面各组直线分类:相互平行的是( ),相互垂直的是( )。
2.图中有( )条线段,( )条射线,( ) 条直线。
3.数一数,填一填。
有( )组平行线,( )组垂线。
4.从3:00走到4:00,分针转过( )°,时针转过( )°,从3:00走到3:20,分针转动了( )°,钟面上秒针旋转一周,那么分针旋转的角度是( )°。
5.观看每个钟面,并写出时针与分针形成的角的名称。
( ) ( ) ( ) ( )6.如图中,一共有( )个角,其中最大的角是最小的角的( )倍。
7.如图中,已知∠1=40°,∠2=( )°,∠3=( )°,∠4=( )°。
8.数一数下图中一共有( )条线段。
9.把一张正方形纸折成下图的样子,已知∠1=50°,则∠2=( )°。
10.在下图中,四边形ABCD 是正方形,那么,( )与AC 垂直、( )与AC 平行,DBF ∠=( )°,DOC ∠=( )°。
二、认真判一判。
(对的画√,错的画X,每题1分,共5分)1.一条射线长10000米。
( )2.角的两边越长,这个角就越大。
( )3.用6倍的放大镜看一个30°的角,这个角是平角。
( )4.我能用一副三角板拼出120°,135°,150°,15°。
( )5.一个平角减去一个锐角,得到的肯定是一个钝角。
( )三、认真选一选。
(将正确的选项填在括号内,每题1分,共5分)1.用一副三角板不能拼出()°的角。
第四章线段和角单元测试题
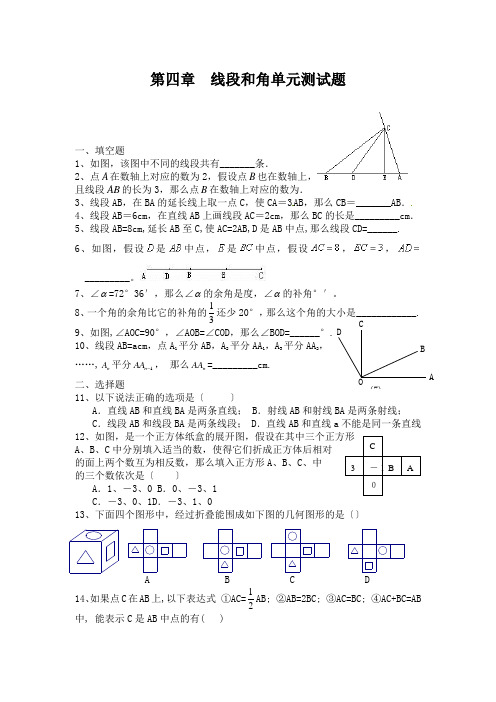
第四章 线段和角单元测试题一、填空题1、如图,该图中不同的线段共有_______条.2、点A 在数轴上对应的数为2,假设点B 也在数轴上, 且线段AB 的长为3,那么点B 在数轴上对应的数为.3、线段AB ,在BA 的延长线上取一点C ,使CA =3AB ,那么CB =_______AB .4、线段AB =6cm ,在直线AB 上画线段AC =2cm ,那么BC 的长是_________cm .5、线段AB=8cm,延长AB 至C,使AC=2AB,D 是AB 中点,那么线段CD=______.6、如图,假设是中点,是中点,假设,,_________。
7、∠α=72°36′,那么∠α的余角是度,∠α的补角°′。
8、一个角的余角比它的补角的13还少20°,那么这个角的大小是____________.9、如图,∠AOC=90°,∠AOB=∠COD ,那么∠BOD=______°.10、线段AB=acm ,点A 1平分AB ,A 2平分AA 1,A 3平分AA 2, ……,n A 平分1n AA -, 那么n AA =_________cm.二、选择题11、以下说法正确的选项是〔 〕A .直线AB 和直线BA 是两条直线; B .射线AB 和射线BA 是两条射线;C .线段AB 和线段BA 是两条线段;D .直线AB 和直线a 不能是同一条直线 12、如图,是一个正方体纸盒的展开图,假设在其中三个正方形A 、B 、C 中分别填入适当的数,使得它们折成正方体后相对的面上两个数互为相反数,那么填入正方形A 、B 、C 、中的三个数依次是〔 〕A .1、-3、0B .0、-3、1C .-3、0、1D .-3、1、013、下面四个图形中,经过折叠能围成如下图的几何图形的是〔〕14、如果点C 在AB 上,以下表达式 ①AC=12AB; ②AB=2BC; ③AC=BC; ④AC+BC=AB中, 能表示C 是AB 中点的有( )D C(7)AB AB C -1 0 315、线段AB ,延长AB 至C ,使AC=2BC ,反向延长AB 至D ,使AD=21BC , 那么线段AD 是线段AC 的〔 〕A .31B .72C .51D .4116、如图,∠1=︒15,∠AOC=︒90点B 、O 、D 在同一直线上,那么的度数为〔 〕A 75°B 15°C 105°D 165°17、在时刻8∶30时,时钟上的时针与分针间的夹角是〔〕 A 、75° B 、85° C 、70 ° D 、60°18、如上图所示,点O 为直线AB 上一点,∠AOC =∠DOE =90°, 那么图中互余角的对数为〔 〕A .2对B .3对C .4对D .5对19、两个角,它们的比是6:4,其差为36°,那么这两个角的关系是( )20、把一张报纸的一角斜折过去,使A 点落在E 点处,BC 为折痕, BD 是∠EBM 的平分线,那么∠CBD=〔 〕 A.85° B.80° C.75° D.90°三、解答题21、如图,平面上有四个点A 、B 、C 、D ,根据以下语句画图 (1)画直线AB ;作射线BC ;画线段CD ;(2)连接AD ,并将其反向延长至E ,使DE=2AD ;(3)找到一点F ,使点F 到A 、B 、C 、D 四点距离和最短 22、如图,假设CB=4㎝,DB=7㎝,且D 是AC 的中点,求线段DC 和AB 的长度.23、线段AB=14cm ,C 是AB 上一点,且AC=9cm ,O 为AB 中点,求线段OC 的长度。
初中数学线段和角的测试卷

初中数学线段和角的测试卷一、填空题。
1.线段是直的,有( )个端点;将线段向两个方向无限延长,就形成了( )线;从线段的一个端点向一个方向无限延长,就得到一条( )线。
2.从一点引出两条射线所组成的图形叫做( )。
这个点叫做它的( ),这两条射线叫做它的( )。
3.测量角的大小要用( ),直角的度数是( ),平角的度数是( ),周角的度数是( )。
4.把我们所认识的角的种类按度数从小到大排列。
( )角<( )角<( )角<( )角<( )角5.过一点可以画出( )条直线,过两点只能画出( )条直线;从一点出发可以画( )条射线。
6.1个周角=( )个平角=( )个直角;1个平角=( )个直角。
7.如果∠1和65°角正好组成一个直角,则∠1等于( );如果∠2和65°角正好组成一个平角,则∠2等于( )。
8.3时整时和( )时整时,时针和分针所成的角是直角;( )时整时,时针和分针所成的角是平角。
二、判断题。
(对的画“√”,错的画“✕”)1.直线总比射线长。
( )2.大于90°的角一定是钝角。
( )3.平角是一条直线。
( )4.任意两个锐角度数之和一定比钝角要大。
( )5.用放大镜去看90°的角,角的大小不会发生变化。
( )6.线段是直线上两点之间的部分。
( )7.过一点只能画出一条直线。
( )8.一条射线长6厘米。
( )9.过两点只能画一条直线。
( )10.两边越长,角的度数越大。
( )三、选择题。
(把正确答案的序号填在括号里)1.角的两条边是( )。
A.直线B.线段C.射线2.下面不能用三角板画出的角是( )的角。
A .15°B .70°C .105°3.丫丫画了一条长20厘米的( )。
A.直线B.射线C.线段四、分别画出90°、40°、125°的角。
五、下图中已知∠2=130°,求∠1、∠3、∠4的度数。
线段和角的单元测试

第七章测试(B)卷
一、填空题
1.点C在线段AB上,那么AC____AB.(天上“<”,“>”或“=”)
2.已知线段AB=8,点C是线段AB的中点,点D是线段BC的中点,AD=____.
3.如图:已知OB平分∠AOC,OC平分∠BOD,∠AOB=25°,那么∠AOB=____.
C.AD=4CE; D.CE= AB.
19.如图,A、O、B三点在一条直线上,OC为∠AOE的平分线,OD为∠BOE的平分线,图中共有__________对互余的角.()
A.1;B.2;
C.3;D.4.
20.用两个三角板(一个是30°的,一个是45°的)可以画出的角度是()
A.75°;B.15°;C.135°;D.115°.
5.已知线段a=4cm,b=3cm,c=2cm那么a-2b+3c=_____cm.
6.OC在∠AOB的内部,则∠COB_____∠AOB(填“<”或“>”).
7.OD是∠MON的平分线,则∠MOD=_____∠MON.
8.如图,A、O、B三点在一条直线上,图中小于180°的角共有_____个.
9.72°角的补角比它的余角大_____.
4.将一个直角3等分,每份是____度.
5.时针由3点钟走到11点,时针走了____度.
6.如图:已知AB-AC=5cm,AC:BC=2:3,AB=____cm.
7.如图:已知OC是∠AOB的平分线,图中所有角的度数和是120度,∠AOC=____度.
8.如图:已知∠AOC=∠BOD=90°,∠AOD:∠DOC=5:1,∠AOB=____度.
15.连接两点的线段叫做两点之间的距离.()
初三数学中考复习线段和角专题复习训练含答案

初三数学中考复习线段和角专题复习训练含答案1. 京广高铁全线通车,一列往复于北京和广州的火车,沿途要经过石家庄、郑州、武汉、长沙四站,铁路部门要为这趟列车预备印制车票( )A .6种B .12种C .15种D .30种2. 点A ,B ,C 在同一条数轴上,其中点A ,B 表示的数区分为-3,1,假定BC =2,那么AC 等于( )A .3B .2C .3或5D .2或63.线段AB ,画出它的中点C ,再画出BC 的中点D ,再画出AD 的中点E ,再画出AE 的中点F ,那么AF 等于AB 的( )A.14B.38C.18D.3164. 线段AB =10 cm ,点C 是直线AB 上一点,BC =4 cm ,假定M 是AC 的中点,N 是BC 的中点,那么线段MN 的长度是( )A .7 cmB .3 cmC .5 cm 或3 cmD .5 cm5. 如图,直线AB ,CD 交于点O ,射线OM 平分∠AOC ,假定∠AOC =76°,那么∠BOM 等于( )A .38°B .104°C .142°D .144°6. 学校、电影院、公园在平面图上区分用点A ,B ,C 表示,电影院在学校的正西方向,公园在学校的南偏西35°方向,那么平面图上的∠BAC 等于( )A .115°B .35°C .125°D .55°7. 一个角的补角是这个角的余角的4倍,那么这个角的大小是( )A .60°B .75°C .90°D .45°8. 如图,两块直角三角板的直角顶点O 重合在一同,且OB 恰恰平分∠COD ,那么∠AOD 的度数为( )A.20°B.150°C.135°D.105°9. 平面内两两相交的8条直线,其交点个数最少为m个,最多为n个,那么m +n等于( )A.16 B.18 C.29 D.2810. 如图,经过刨平的木板上的两个点,能弹出一条蜿蜒的墨线,而且只能弹出一条墨线,能解释这一实践运用的数学知识是________________________.11. 如图,从甲地到乙地有四条路途,其中最短的路途是____.12. 半夜闹钟响了,正在午睡的小明睁眼一看闹钟(如下图),这时分针与时针所成的角的度数是______度.13. 如下图,OE平分∠AOB,OD平分∠BOC,∠AOB=90°,∠EOD=80°,那么∠BOC的度数为_____________.15. 如图,C,D,E将线段AB分红四局部,且AC∶CD∶DE∶EB=2∶3∶4∶5,M,P,Q,N区分是AC,CD,DE,BE的中点,假定MN=a,求PQ的长.16. 如图,∠AOC=∠BOD=100°,且∠AOB∶∠AOD=2∶7,试求∠BOC的大小.17. 如图,直线AB和CD相交于点O,OM平分∠BOD,∠MON是直角,∠AOC =50°.(1)求∠AON的度数;(2)求∠DON的余角.18. 如图,数轴上点A表示的数为6,B是数轴上一点,且AB=10.动点P从点A 动身,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.(1)写出数轴上点B表示的数_______,点P表示的数_______(用含t的代数式表示)(2)动点R 从点B 动身,以每秒4个单位长度的速度沿数轴向左匀速运动,假定点P ,R 同时动身,问点P 运动多少秒时追上点R?19. 如图,∠AOB =m °,OC 是∠AOB 内的一条射线,OD 平分∠BOC ,OE 平分∠AOC .(1)求∠EOD 的度数;(2)假定其他条件不变,OC 在∠AOB 外部绕O 点转动,那么OD ,OE 的位置能否发作变化?(3)在(2)的条件下,∠EOD 的大小能否发作变化?假设不变,央求出其度数;假设变化,央求出其度数的范围.参考答案:1---9 DDDDC CACC10. 两点确定一条直线11. A12. 13513. 70°14. 70°15. 解:PQ =13a 16. 解:设∠AOB =2x ,那么∠AOD =7x ,所以∠BOD =∠AOD -∠AOB =5x =100°,所以x =20°,即∠AOB =∠COD =40°,∠AOD =140°,所以∠BOC =∠AOD -∠AOB -∠COD =140°-40°-40°=60°17. 解:(1)由于∠AOC +∠AOD =∠AOD +∠BOD =180°,所以∠BOD =∠AOC =50°,由OM 平分∠BOD ,可得∠BOM =∠DOM =25°,又由∠MON =90°,所以∠AON =180°-(∠MON +∠BOM)=180°-(90°+25°)=65°(2)由∠DON +∠DOM =∠MON =90°知∠DOM 为∠DON 的余角,故∠DON 的余角为25°18. (1) -4 6-6t(2) 解:设点P 运动x 秒时,在点C 处追上点R ,那么AC =6x ,BC =4x ,由于AC -BC =AB ,所以6x -4x =10,解得:x =5,所以点P 运动5秒时追上点R19. 解:(1)(12m)°(2)OD ,OE 的位置发作变化 (3)∠EOD 的大小坚持不变为(12m)°。
人教版苏科版小学数学—线与角(单元测试卷含答案)

一、填空题。
1.线段有(2)个端点,射线有(1)个端点。
2.(锐)角小于90°,大于90°而小于180°的角叫做(钝角)。
3.1平角=(2)直角1周角=(4)直角1周角=(2)平角4.下图中,∠1与∠2组成的角是(平)角,已知∠1=40°,那么∠2=(140°)。
5.在时钟上,时针与分针成90°是(3)时与(9)时;时针和分针形成平角的时刻是(6时)。
二、写出下面用三角尺拼出的角的度数。
(105°)(120°)(75°)三、选择题。
(在括号里填上正确答案的序号)1.过一点可以画(D)条射线。
A.1B.2C.3D.无数2.角的两条边是两条(B)。
A.直线B.射线C.线段D.曲线3.9:30,时针与分针形成的角是(B)。
A.锐角B.直角C.钝角D.平角4.在一个5倍的放大镜下看一个5°的角,看到的角是(A)。
A.5°B.25°C.30°D.45°5.可以测出长度的是(C)。
A.直线B.射线C.线段D.角的边四、给下面的角分类。
93°24°100°89°2°75°121°90°锐角直角钝角锐角:24°、2°、89°、75°直角:90°钝角:93°、100°、121°五、先量一量,再在里填上“>”或“<”。
(30°)〈(100°)(80°)〈(130°)六、量出时针与分针所成的角度。
120°60°90°七、按要求画一画。
1.以A点为顶点画一个50°的角,并在角的一边上截一条3厘米长的线段。
2.用合适的方法画出下面度数的角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.选择题(共48小题)1.已知线段AB=10cm,点C在直线AB上,且AC=2cm,则线段BC的长为()A.12cm B.8cm C.12cm或8cm D.以上均不对2.下列说法正确的是()A.经过两点可以画一条直线,并且只能画一条直线B.射线AB和射线BA是同一条射线C.两点之间,直线最短D.延长直线AB3.下列说法中正确的个数为()(1)如果AC=CB,则点C是线段AB的中点;(2)连结两点的线段叫做这两点间的距离;(3)两点之间所有连线中,线段最短;(4)射线比直线小一半;(5)平面内3条直线至少有一个交点.A.1个B.2个C.3个D.4个4.如图,下列条件中不能确定的是OC是∠AOB的平分线的是()A.∠AOC=∠BOC B.∠AOB=2∠AOCC.∠AOC+∠BOC=∠AOB D.5.54.27°可化为()A.54°16′26″B.54°28′C.54°16′15″D.54°16′12″6.过平面上四个点中的任意两点画直线,可以画出的直线共有()A.1条B.4条C.一条或四条D.1条或4条或6条7.在△ABC中,作BC边上的高,以下作图正确的是()A.B.C.D.8.如图是北京地铁的路线图,小明家住复兴门,打算趁着放假去建国门游玩,看了路线图后,小明打算乘坐①号线地铁去,认为可以节省时间,他这样做的依据是()A.垂线段最短B.两点之间,直线最短C.两点确定一条直线D.两点之间,线段最短9.下列计算错误的是()A.0.25°=900″B.125.45°=12545′C.1000″=()°D.1.5°=90′10.下列四个图中,能用∠1,∠AOB,∠O三种方法表示同一个角的是()A.B.C.D.11.在同一平面内,若∠BOA=50.3°,∠BOC=10°30′,则∠AOC的度数是()A.60.6°B.40°C.60.8°或39.8D.60.6°或40°12.如图,将两块三角尺AOB与COD的直角顶点O重合在一起,若∠AOD=4∠BOC,OE为∠BOC的平分线,则∠DOE的度数为()A.36°B.45°C.60°D.72°13.下列说法中错误的是()A.过两点有且只有一条直线B.两点之间线段的长度,叫做两点之间的距离C.若α+27°18′=90°,27.3°+β=90°,则α=βD.线段、射线、直线中,直线最长14.用一副三角尺,不能画出的角是()A.15°B.75°C.165°D.145°15.下列各数中,正确的角度互化是()A.63.5°=63°50′B.23°12′36″=23.48°C.18°18′18″=18.33°D.22.25°=22°15′16.线段AB=6cm,点C在直线AB上,且线段AC=1cm,则线段BC的长为()A.5cm B.7cm C.5cm或7cm D.以上均不对17.把2.36°用度、分、秒表示,正确的是()A.2°21'36''B.2°18'36''C.2°30'60''D.2°3'6''18.如图所示,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在()A.点A B.点B C.AB之间D.BC之间19.过某个多边形一点顶点的所有对角线,将这个多边形分成了5个三角形,则这个多边形是()A.五边形B.六边形C.七边形D.八边形20.已知点A,B,C在同一条直线上,若线段AB=3,BC=2,AC=1,则下列判断正确的是()A.点A在线段BC上B.点B在线段AC上C.点C在线段AB上D.点A在线段CB的延长线上21.如图,在直线l上顺次取A、B、C三点,使得AB=5cm,BC=3cm,如果O是线段AC的中点,那么线段OB长为()A.1cm B.1.5cm C.2cm D.4cm22.如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=20°,则∠AOB=()A.40°B.60°C.120°D.135°23.如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与AB的方向一致,则∠ECB的度数为()A.80°B.90°C.100°D.105°24.已知∠AOB=30°,自∠AOB顶点O引射线OC,若∠AOC:∠AOB=4:3,那么∠BOC的度数是()A.10°B.40°或30°C.70°D.10°或70°25.能用∠α、∠AOB、∠O三种方式表示同一个角的图形是()A.B.C.D.26.下列说法中,正确的有()①过两点有且只有一条直线,②连结两点的线段叫做两点的距离,③两点之间,线段最短,④AB=BC,则点B是线段AC的中点.A.4个B.3个C.2个D.1个27.已知:点A,B,C在同一条直线上,点M、N分别是AB、AC的中点,如果AB=10cm,AC=8cm,那么线段MN的长度为()A.6cm B.9cm C.3cm或6cm D.1cm或9cm 28.设一个锐角与这个角的补角的差的绝对值为α,则()A.0°<α<90°或90°<α<180°B.0°<α<180°C.0°<α<90°D.0°<α≤90°29.把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、B、D三点在同一直线上,BM为∠CBE的平分线,BN为∠DBE的平分线,则∠MBN的度数是()A.60°B.67.5°C.75°D.85°30.如图所示,线段AB=10,M为线段AB的中点,C为线段MB的中点,N为线段AM的一点,且MN=1,线段NC的长()A.2B.2.5C.3D.3.531.把弯曲的河道改直,能够缩短航程,这样做的道理是()A.两点之间,射线最短B.两点确定一条直线C.两点之间,直线最短D.两点之间,线段最短32.如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,则∠AOB 的度数为()A.14°B.28°C.32°D.40°33.如图所示,能用∠AOB,∠O,∠1三种方法表示同一个角的图形是()A.B.C.D.34.如图,下列说法中错误的是()A.OA的方向是东北方向B.OB的方向是北偏西30°C.OC的方向是南偏西60°D.OD的方向是南偏东30°35.平面上有三个点A,B,C,如果AB=8,AC=5,BC=3,则()A.点C在线段AB上B.点C在线段AB的延长线上C.点C在直线AB外D.不能确定36.钟表在8:25时,时针与分针的夹角是()度.A.101.5B.102.5C.120D.12537.过平面上A、B、C三点中的任意两点作直线,可作()A.1条B.3条C.1条或3条D.无数条38.如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长()A.1cm B.2cm C.4cm D.6cm39.如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=α,则∠BOE的度数为()A.ΑB.180°﹣2αC.360°﹣4αD.2α﹣60°40.用一副三角板可以画出一些指定的角,下列各角中,不能用一副三角板画出的是()A.15°B.75°C.85°D.105°41.如图所示,把一根绳子对折成线段AB,从P处把绳子剪断,已知AP=PB,若剪断后的各段绳子中最长的一段为40cm,则绳子的原长为()A.30cm B.60cm C.120cm D.60cm或120cm42.将一副三角板按如图方式摆放,则图中不存在的角度是()A.90°B.75°C.135°D.120°43.把一副三角板按照如图所示的位置摆放,则形成两个角,设分别为∠α、∠β,若已知∠α=65°,则∠β=()A.15°B.25°C.35°D.45°44.如图,已知∠AOB是直角,∠AOC是锐角,ON平分∠AOC,OM平分∠BOC,则∠MON是()A.45°B.45°+∠AOC C.60°﹣∠AOC D.不能计算45.如图,∠AOB是直角,∠COD也是直角,若∠AOC=α,则∠BOD等于()A.90°+αB.90°﹣αC.180°+αD.180°﹣α46.如图,将一副三角板的直角顶点重合,摆放在桌面上,若∠AOD=145°,则∠BOC的度数为()A.25°B.35°C.45°D.55°47.如图,∠AOC和∠DOB都是直角,如果∠AOB=150°,那么∠DOC=()A.30°B.40°C.50°D.60°48.点C在线段AB上,下列条件中不能确定点C是线段AB中点的是()A.AC=BC B.AC+BC=AB C.AB=2ACD.BC=AB二.填空题(共10小题)49.56°48′=°; 4.3°=.50.32.48°×2=度分秒.51.如图,已知∠AOB=50°,∠AOD=90°,OC平分∠AOB,则∠COD的度数是.52.用度、分、秒表示:98.42°=.53.计算77°53′26″+43°22′16″=.54.用度、分、秒表示63.27°=°′″.55.已知∠1=4°18′,∠2=4.4°,则∠1∠2.(填“大于、小于或等于)56.74.16°=°′″28°7′12″=°57.计算:28.3°﹣26°34′=°′.58.把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、B、D三点在同一直线上,BM为∠CBE的平分线,BN为∠DBE的平分线,则∠MBN的度数为.2018年11月23日王延钊的初中数学组卷参考答案与试题解析一.选择题(共48小题)1.已知线段AB=10cm,点C在直线AB上,且AC=2cm,则线段BC的长为()A.12cm B.8cm C.12cm或8cm D.以上均不对【解答】解:①如图1,点C在线段AB上时,BC=AB﹣AC=10﹣2=8cm,②如图2,点C不在线段AB上时,BC=AB+AC=10+2=12cm,所以,线段BC的长为12cm或8cm.故选:C.2.下列说法正确的是()A.经过两点可以画一条直线,并且只能画一条直线B.射线AB和射线BA是同一条射线C.两点之间,直线最短D.延长直线AB【解答】解:A、经过两点可以画一条直线,并且只能画一条直线,说法正确;B、射线AB和射线BA是同一条射线,说法错误;C、两点之间,直线最短,说法错误;D、延长直线AB,说法错误;故选:A.3.下列说法中正确的个数为()(1)如果AC=CB,则点C是线段AB的中点;(2)连结两点的线段叫做这两点间的距离;(3)两点之间所有连线中,线段最短;(4)射线比直线小一半;(5)平面内3条直线至少有一个交点.A.1个B.2个C.3个D.4个【解答】解:(1)如果AC=CB,则点C是线段AB垂直平分线上的点,原来的说法错误;(2)连结两点的线段的长度叫做这两点间的距离,原来的说法错误;(3)两点之间所有连线中,线段最短是正确的;(4)射线与直线都是无限长的,原来的说法错误;(5)平面内互相平行的3条直线没有交点,原来的说法错误.故选:A.4.如图,下列条件中不能确定的是OC是∠AOB的平分线的是()A.∠AOC=∠BOC B.∠AOB=2∠AOCC.∠AOC+∠BOC=∠AOB D.【解答】解:A、∠AOC=∠BOC能确定OC平分∠AOB,故此选项不合题意;B、∠AOB=2∠AOC能确定OC平分∠AOB,故此选项不合题意;C、∠AOC+∠COB=∠AOB不能确定OC平分∠AOB,故此选项符合题意;D、∠BOC=∠AOB,能确定OC平分∠AOB,故此选项不合题意.故选:C.5.54.27°可化为()A.54°16′26″B.54°28′C.54°16′15″D.54°16′12″【解答】解:54.27°=54°16′12″.故选:D.6.过平面上四个点中的任意两点画直线,可以画出的直线共有()A.1条B.4条C.一条或四条D.1条或4条或6条【解答】解:当四点共线时可以画一条直线;当4个点中,任何3个点都不在同一直线上时,可画6条直线.当4个点中,有3个点在同一直线上时,可画4条直线,故选:D.7.在△ABC中,作BC边上的高,以下作图正确的是()A.B.C.D.【解答】解:BC边上的高应从点A向BC引垂线,只有选项D符合条件,故选:D.8.如图是北京地铁的路线图,小明家住复兴门,打算趁着放假去建国门游玩,看了路线图后,小明打算乘坐①号线地铁去,认为可以节省时间,他这样做的依据是()A.垂线段最短B.两点之间,直线最短C.两点确定一条直线D.两点之间,线段最短【解答】解:由图可知,乘坐①号地铁走的是直线,所以节省时间的依据是两点之间线段最短.故选:D.9.下列计算错误的是()A.0.25°=900″B.125.45°=12545′C.1000″=()°D.1.5°=90′【解答】解:A、0.25°=0.25×3600″=900″,此选项正确;B、125.45°=125.45×60′=7527′,此选项错误;C、1000″=()°=()°,此选项正确;D、1.5°=1.5×60′=90′,此选项正确;故选:B.10.下列四个图中,能用∠1,∠AOB,∠O三种方法表示同一个角的是()A.B.C.D.【解答】解:A、图中的∠AOB不能用∠O表示,故本选项错误;B、图中的∠AOB不能用∠O表示,故本选项错误;C、图中∠1、∠AOB、∠O表示同一个角,故本选项正确;D、图中的∠AOB不能用∠O表示,故本选项错误;故选:C.11.在同一平面内,若∠BOA=50.3°,∠BOC=10°30′,则∠AOC的度数是()A.60.6°B.40°C.60.8°或39.8D.60.6°或40°【解答】解:∠AOC=∠BOA+∠BOC=50.3°+10°30′=50.3°+10.5°=60.8°或∠AOC=∠BOA﹣∠BOC=50.3°﹣10°30′=50.3°﹣10.5°=39.8°,故选:C.12.如图,将两块三角尺AOB与COD的直角顶点O重合在一起,若∠AOD=4∠BOC,OE为∠BOC的平分线,则∠DOE的度数为()A.36°B.45°C.60°D.72°【解答】解:∵∠AOB=90°,∠COD=90°,∴∠AOB+∠COD=180°,∵∠AOB=∠AOC+∠BOC,∠COD=∠BOC+∠BOD,∴∠AOC+∠BOC+∠BOC+∠BOD=180°,∴∠AOD+∠BOC=180°,∵∠AOD=4∠BOC,∴4∠BOC+∠BOC=180°,∴∠BOC=36°,∵OE为∠BOC的平分线,∴∠COE=∠BOC=18°,∴∠DOE=∠COD﹣∠COE=90°﹣18°=72°,故选:D.13.下列说法中错误的是()A.过两点有且只有一条直线B.两点之间线段的长度,叫做两点之间的距离C.若α+27°18′=90°,27.3°+β=90°,则α=βD.在线段、射线、直线中,直线最长【解答】解:A、过两点有且只有一条直线,正确,故本选项不符合题意;B、两点之间的线段的长度,叫两点之间的距离,正确,故本选项不符合题意;C、若α+27°18′=90°,27.3°+β=90°,则α=β,正确,故本选项不符合题意;D、线段有长度,直线和射线没有长度,错误,故本选项符合题意;故选:D.14.用一副三角尺,不能画出的角是()A.15°B.75°C.165°D.145°【解答】解:145°不能够被15整除,所以不能画出145°的角.故选:D.15.下列各数中,正确的角度互化是()A.63.5°=63°50′B.23°12′36″=23.48°C.18°18′18″=18.33°D.22.25°=22°15′【解答】解:A、63.5°=63°30′≠63°50′,故A不符合题意;B、23.48°=23°28′48″≠23°12′36″,故B不符合题意;C、18.33°=18°19′48″≠18°18′18″,故C不符合题意;D、22.25°=22°15′,故D正确,故选:D.16.已知线段AB=6cm,点C在直线AB上,且线段AC=1cm,则线段BC的长为()A.5cm B.7cm C.5cm或7cm D.以上均不对【解答】解:①点C在A、B中间时,BC=AB﹣AC=6﹣1=5(cm).②点C在点A的左边时,BC=AB+AC=6+1=7(cm).∴线段BC的长为5cm或7cm.故选:C.17.把2.36°用度、分、秒表示,正确的是()A.2°21'36''B.2°18'36''C.2°30'60''D.2°3'6''【解答】解:2.36°=2°+0.36×60′=2°21′+0.6×60″=2°21′36″,故选:A.18.如图所示,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在()A.点A B.点B C.AB之间D.BC之间【解答】解:①以点A为停靠点,则所有人的路程的和=15×300+10×900=13500(米),②以点B为停靠点,则所有人的路程的和=30×300+10×600=15000(米),③以点C为停靠点,则所有人的路程的和=30×900+15×600=36000(米),④当在AB之间停靠时,设停靠点到A的距离是m,则(0<m<100),则所有人的路程的和是:30m+15(300﹣m)+10(900﹣m)=13500+5m>13500,⑤当在BC之间停靠时,设停靠点到B的距离为n,则(0<n<200),则总路程为30(300+n)+15n+10(600﹣n)=15000+35n>13500.∴该停靠点的位置应设在点A;故选:A.19.过某个多边形一点顶点的所有对角线,将这个多边形分成了5个三角形,则这个多边形是()A.五边形B.六边形C.七边形D.八边形【解答】解:根据n边形从一个顶点出发可引出(n﹣3)条对角线,可组成n﹣2个三角形,∴n﹣2=5,即n=7.故选:C.20.已知点A,B,C在同一条直线上,若线段AB=3,BC=2,AC=1,则下列判断正确的是()A.点A在线段BC上B.点B在线段AC上C.点C在线段AB上D.点A在线段CB的延长线上【解答】解:如图,∵点A,B,C在同一条直线上,线段AB=3,BC=2,AC=1,∴点A在线段BC的延长线上,故A错误;点B在线段AC延长线上,故B错误;点C在线段AB上,故C正确;点A在线段CB的反向延长线上,故D错误;故选:C.21.如图,在直线l上顺次取A、B、C三点,使得AB=5cm,BC=3cm,如果O是线段AC的中点,那么线段OB长为()A.1cm B.1.5cm C.2cm D.4cm【解答】解:根据上图所示OB=5cm﹣OA,∵OA=(AB+BC)÷2=4cm,∴OB=1cm.故选:A.22.如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=20°,则∠AOB=()A.40°B.60°C.120°D.135°【解答】解:设∠AOC=x,则∠BOC=2x,则∠AOD=1.5x.∵∠AOD﹣∠AOC=∠COD,∴1.5x﹣x=20°,解得:x=40°.∴∠AOB=3x=120°.故选:C.23.如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与AB的方向一致,则∠ECB的度数为()A.80°B.90°C.100°D.105°【解答】解:由题意可得:AN∥FB,EC∥BD,故∠NAB=∠FBD=75°,∵∠CBF=25°,∴∠CBD=100°,则∠ECB=180°﹣100°=80°.故选:A.24.已知∠AOB=30°,自∠AOB顶点O引射线OC,若∠AOC:∠AOB=4:3,那么∠BOC的度数是()A.10°B.40°或30°C.70°D.10°或70°【解答】解:∵∠AOB=30°,∠AOC:∠AOB=4:3,∴∠AOC=40°,分为两种情况:①如图1,∠BOC=∠AOB+∠AOC=30°+40°=70°;②如图2,∠BOC=∠AOC﹣∠AOB=40°﹣30°=10°,故选:D.25.能用∠α、∠AOB、∠O三种方式表示同一个角的图形是()A.B.C.D.【解答】解:A、因为顶点O处有四个角,所以这四个角均不能用∠O表示,故本选项错误;B、因为顶点O处只有一个角,所以这个角能用∠O、∠α及∠AOB表示,故本选项正确;C、因为顶点O处有三个角,所以这三个角均不能用∠O表示,故本选项错误;D、因为∠O与∠α表示的不是同一个角,故本选项错误.故选:B.26.下列说法中,正确的有()①过两点有且只有一条直线,②连结两点的线段叫做两点的距离,③两点之间,线段最短,④AB=BC,则点B是线段AC的中点.A.4个B.3个C.2个D.1个【解答】解:①过两点有且只有一条直线,故①符合题意;②连结两点的线段的长度叫做两点的距离,故②不符合题意;③两点之间,线段最短,故③符合题意;④AB=BC,B在线段AC上,则点B是线段AC的中点,故④不符合题意;故选:C.27.已知:点A,B,C在同一条直线上,点M、N分别是AB、AC的中点,如果AB=10cm,AC=8cm,那么线段MN的长度为()A.6cm B.9cm C.3cm或6cm D.1cm或9cm 【解答】解:(1)点C在线段AB上,如:点M是线段AB的中点,点N是线段BC的中点,MB=AB=5,BN=CB=4,MN=BM﹣BN=5﹣4=1cm;(2)点C在线段AB的延长线上,如:点M是线段AB的中点,点N是线段BC的中点,MB=AB=5,BN=CB=4,MN=MB+BN=5+4=9cm,故选:D.28.设一个锐角与这个角的补角的差的绝对值为α,则()A.0°<α<90°或90°<α<180°B.0°<α<180°C.0°<α<90°D.0°<α≤90°【解答】解:设这个角的为x且0<x<90°,根据题意可知180°﹣x﹣x=α,∴α=180°﹣2x,∴180°﹣2×90°<α<180°﹣2×0°,0°<α<180°.故选:B.29.把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、B、D三点在同一直线上,BM为∠CBE的平分线,BN为∠DBE的平分线,则∠MBN的度数是()A.60°B.67.5°C.75°D.85°【解答】解:∵∠CBE=180°﹣∠ABC﹣∠DBE=180°﹣30°﹣45°=105°,BM为∠CBE 的平分线,BN为∠DBE的平分线,∴∠EBN===22.5°,=52.5°,∴∠MBN=∠MBE+∠EBN=52.5°+22.5°=75°,故选:C.30.如图所示,线段AB=10,M为线段AB的中点,C为线段MB的中点,N为线段AM的一点,且MN=1,线段NC的长()A.2B.2.5C.3D.3.5【解答】解:∵线段AB=10,M为线段AB的中点,∴MB=AB=5,∵C为线段MB的中点,∴MC=BM=2.5,∴NC=NM+MC=3.5.故选:D.31.把弯曲的河道改直,能够缩短航程,这样做的道理是()A.两点之间,射线最短B.两点确定一条直线C.两点之间,直线最短D.两点之间,线段最短【解答】解:由两点之间线段最短可知,把弯曲的河道改直,能够缩短航程,这样做根据的道理是两点之间线段最短,故选:D.32.如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,则∠AOB的度数为()A.14°B.28°C.32°D.40°【解答】解:∵已知∠BOC=2∠AOB,OD平分∠AOC,∴∠AOC=3∠AOB=2∠AOD,∴∠AOD=1.5∠AOB,∴∠AOD﹣∠AOB=0.5∠AOB=∠BOD=14°,∴∠AOB=28°,故选:B.33.如图所示,能用∠AOB,∠O,∠1三种方法表示同一个角的图形是()A.B.C.D.【解答】解:A、以O为顶点的角不止一个,不能用∠O表示,故A选项错误;B、以O为顶点的角不止一个,不能用∠O表示,故B选项错误;C、以O为顶点的角不止一个,不能用∠O表示,故C选项错误;D、能用∠1,∠AOB,∠O三种方法表示同一个角,故D选项正确.故选:D.34.如图,下列说法中错误的是()A.OA的方向是东北方向B.OB的方向是北偏西30°C.OC的方向是南偏西60°D.OD的方向是南偏东30°【解答】解:A、OA的方向是北偏东45度即东北方向,故正确;B、OB的方向是北偏西60°,故错误;C、OC的方向是南偏西60°,故正确;D、OD的方向是南偏东30°,故正确.故选:B.35.平面上有三个点A,B,C,如果AB=8,AC=5,BC=3,则()A.点C在线段AB上B.点C在线段AB的延长线上C.点C在直线AB外D.不能确定【解答】解:如图:从图中我们可以发现AC+BC=AB,所以点C在线段AB上.故选:A.36.钟表在8:25时,时针与分针的夹角是()度.A.101.5B.102.5C.120D.125【解答】解:∵时针在钟面上每分钟转0.5°,分针每分钟转6°,∴钟表上8:25时,时针与分针的夹角可以看成时针转过8时0.5°×25=12.5°,分针在数字5上.∵钟表12个数字,每相邻两个数字之间的夹角为30°,∴8:25时分针与时针的夹角3×30°+12.5°=102.5°.故选:B.37.过平面上A、B、C三点中的任意两点作直线,可作()A.1条B.3条C.1条或3条D.无数条【解答】解:如图,过平面上A、B、C三点中的任意两点作直线,可作1条或3条.故选C.38.如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长()A.1cm B.2cm C.4cm D.6cm【解答】解:点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC=2MC,BC=2CN,由线段的和差得AC﹣BC=2MC﹣2NC=2(MC﹣NC)=2×2=4cm,故选:C.39.如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=α,则∠BOE的度数为()A.αB.180°﹣2αC.360°﹣4αD.2α﹣60°【解答】解:设∠DOE=x,则∠BOE=2x,∵∠BOD=∠BOE+∠EOD,∴∠BOD=3x,∴∠AOD=180°﹣∠BOD=180°﹣3x.∵OC平分∠AOD,∴∠COD=∠AOD=(180°﹣3x)=90°﹣x.∵∠COE=∠COD+∠DOE=90°﹣x+x=90°﹣,由题意有90°﹣=α,解得x=180°﹣2α,即∠DOE=180°﹣2α,∴∠BOE=360﹣4α,故选:C.40.用一副三角板可以画出一些指定的角,下列各角中,不能用一副三角板画出的是()A.15°B.75°C.85°D.105°【解答】解:A、15°的角,45°﹣30°=15°;B、75°的角,45°+30°=75°;C、85°的角,不能直接利用三角板画出;D、105°的角,45°+60°=105°.故选:C.41.如图所示,把一根绳子对折成线段AB,从P处把绳子剪断,已知AP=PB,若剪断后的各段绳子中最长的一段为40cm,则绳子的原长为()A.30cm B.60cmC.120cm D.60cm或120cm【解答】解:设AP=xcm,则BP=2xcm,①当含有线段AP的绳子最长时,x+x=40,解得:x=20,即绳子的原长是2(x+2x)=6x=120(cm);②当含有线段BP的绳子最长时,2x+2x=40,解得:x=10,即绳子的原长是2(x+2x)=6x=60(cm);故绳长为60cm或120cm.故选:D.42.将一副三角板按如图方式摆放,则图中不存在的角度是()A.90°B.75°C.135°D.120°【解答】解:∠C=90°,∠A=60°,∠ADC=90°+45°=135°,∠ABC=30°+45°=75°,即图中存在的角度有90°,135°.60°,75°,故选:D.43.把一副三角板按照如图所示的位置摆放,则形成两个角,设分别为∠α、∠β,若已知∠α=65°,则∠β=()A.15°B.25°C.35°D.45°【解答】解:如图所示,一副三角板按照如图所示的位置摆放,则∠α+∠β+90°=180°,即∠β=180°﹣90°﹣65°=25°.故选:B.44.如图,已知∠AOB是直角,∠AOC是锐角,ON平分∠AOC,OM平分∠BOC,则∠MON是()A.45°B.45°+∠AOC C.60°﹣∠AOC D.不能计算【解答】解:∵OM平分∠BOC,ON平分∠AOC,∴∠MOC=∠BOC,∠NOC=∠AOC,∴∠MON=∠MOC﹣∠NOC=(∠BOC﹣∠AOC),=(∠BOA+∠AOC﹣∠AOC),=∠BOA,=45°.故选:A.45.如图,∠AOB是直角,∠COD也是直角,若∠AOC=α,则∠BOD等于()A.90°+αB.90°﹣αC.180°+αD.180°﹣α【解答】解:根据∠AOB是直角,∠COD也是直角,若∠AOC=α,那么∠BOC=90°﹣α,∴∠BOD=∠BOC+∠COD=90°﹣α+90°,=180°﹣α.故选:D.46.如图,将一副三角板的直角顶点重合,摆放在桌面上,若∠AOD=145°,则∠BOC的度数为()A.25°B.35°C.45°D.55°【解答】解:根据题意,易得∠AOB+∠COD=180°,即∠AOC+2∠BOC+∠BOD=180°,而∠AOD=145°,即∠AOC+∠BOC+∠BOD=145°,则∠BOC=180°﹣145°=35°;故选:B.47.如图,∠AOC和∠DOB都是直角,如果∠AOB=150°,那么∠DOC=()A.30°B.40°C.50°D.60°【解答】解:∠DOC=90°+90°﹣∠AOB=180°﹣150°=30°.故选A.48.点C在线段AB上,下列条件中不能确定点C是线段AB中点的是()A.AC=BC B.AC+BC=AB C.AB=2AC D.BC=AB【解答】解:A、AC=BC,则点C是线段AB中点;B、AC+BC=AB,则C可以是线段AB上任意一点;C、AB=2AC,则点C是线段AB中点;D、BC=AB,则点C是线段AB中点.故选:B.二.填空题(共10小题)49.56°48′=56.8°;4.3°=4°18′.【解答】解:56°48′=56.8°;4.3°=4°18′;故答案为:56.8;4°18′.50.32.48°×2=64度57分36秒.【解答】解:32.48°×2=64度57分36秒;故答案为:64;57;36.51.如图,已知∠AOB=50°,∠AOD=90°,OC平分∠AOB,则∠COD的度数是65°.【解答】解:∵∠AOB=50°,∠AOD=90°,OC平分∠AOB,∴∠BOD=∠AOD﹣∠AOB=90°﹣50°=40°,∠BOC===25°,∴∠COD=∠BOC+∠BOD=25°+40°=65°,故答案为:65°.52.用度、分、秒表示:98.42°=98°25′12″.【解答】解:98.42°=98°25′12″.故答案为:98°25′12″.53.计算77°53′26″+43°22′16″=121°15′42″.【解答】解:77°53′26″+43°22′16″=121°15′42″.故答案为:121°15′42″.54.用度、分、秒表示63.27°=63°16′12″.【解答】解:63.27°=63°+(0.27×60)′=63°+16′+(0.2×60)″=63°16′12″.∴用度、分、秒表示63.27°=63度16分12秒.故答案为:63;16;12.55.已知∠1=4°18′,∠2=4.4°,则∠1小于∠2.(填“大于、小于或等于)【解答】解:∵∠1=4°18′,∠2=4.4°=4°24′,∴∠1<∠2,故答案为:小于.56.74.16°=74°9′36″28°7′12″=28.12°【解答】解:①∵0.16°=0.16×60′=9.6′,0.6′=0.6×60″=36″,∴74.16°=74°9′36″;②∵12″=0.2′,7.2′=0.12°,∴28°7′12″=28.12°;故答案为:74,9,36;28.1257.计算:28.3°﹣26°34′=1°44′.【解答】解:原式=27°63′﹣26°34′=1°44′,故答案为:1,44.58.把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、B、D三点在同一直线上,BM为∠CBE的平分线,BN为∠DBE的平分线,则∠MBN的度数为67.5°.【解答】解:由题可得,∠ABC=45°,∠DBE=60°,∠ABD=180°,∴∠CBE=75°,又∵BM为∠CBE的平分线,BN为∠DBE的平分线,∴∠MBE=37.5°,∠EBN=30°,∴∠MBN=67.5°,故答案为:67.5°。
