粘性流体力学第七次作业
流体力学6,7,8章课后题答案

第六章 6-1解:层流状态下雷诺数Re 2000< 60.1Re 6.710vdv υ-⨯==⨯ ⇒60.120006.710v -⨯<⨯⇒62000 6.710/0.10.134(/)v m s -<⨯⨯= 即max 0.134/v m s =223max max max 0.13.140.1340.00105/ 1.05/44d Q Av v ms L sπ===⨯⨯≈=6-2解:层流状态下雷诺数Re 2000<3Re 20000.910120000.0450.1()vd d m d ρυ-=<⨯⨯⨯⇒<⇒<6-3解:3221.66100.21(/)0.13.1444Q v m s d π-⨯==≈⨯临界状态时Re 2000=52533Re Re0.210.1 1.0510(/)20001.05100.88109.2410()vd vd m s Pa s υυυμυρ---=⇒=⨯⇒==⨯⇒==⨯⨯⨯=⨯⋅ 6-4解:当输送的介质为水时:32210101270131444.(/)..Q v m s d π-⨯===⨯ 612701838632000151910..Re .vd υ-⨯===>⨯水 3015100001501...d -∆⨯== 根据雷诺数和相对粗糙度查莫迪图可知流态为水力粗糙。
当输送的介质为石油时:质量流量与水相等3310101010(/)Q kg s -=⨯⨯=31000118850.(/)Q m s == 2200118150********..(/)..Q v m s d π===⨯ 415030113184200011410..Re .vd υ-⨯===>⨯水3015100001501...d -∆⨯== 根据雷诺数和相对粗糙度查莫迪图可知流态为水力光滑。
6-5解:判断流态需先求出雷诺数()2900036009000088023144./..Re Q v m s Avd υ÷===⨯=冬季:421101./m s υ-⨯=40088021608820001110..Re ..vd υ-⨯===<⨯ ⇒ 流态为层流。
流体力学教案第7章管内流动与管路计算

第七章管内流动与管路计算在第四章中,推出的粘性流体沿管道流动的总流伯努里方程为:w 2222221111+2++=2++h gV g p z g V g p z αραρ式中h w 是粘性流体从截面1流到截面2处,单位重量流体所损失的能量,它等于所有沿程损失和局部损失之和,即:j f w h h h +=沿程损失h f 是在每段缓变流区域内单位重量流体沿流程的能量损失。
研究表明,沿程损失与单位重量流体所具有的动能和流程长度成正比,与通道的直径成反比。
gV d l h 22f λ= 该式称为达西一威斯巴赫(Darcy-Weisbach )公式。
式中λ为沿程损失系数,它与流体的粘度,流速、管道内径和管壁粗糙度等因素有关,是一个无量纲系数,除层流流动外,一般需要由试验确定。
局部损失h j 是当管道中因截面面积或流动方向的改变所引起的流动急剧变化时,单位重量流体的能量损失,通常表示为gV h 2=2j ζ 式中ζ称为局部损失系数,也是一个无量纲系数,根据引起流动的各种管件,由试验来确定。
要计算粘性流体在管道中的流动问题,需应用总流的伯努里方程。
而应用该方程的关键问题是求管道中的能量损失h w 。
总损失h w 等于各段沿程损失和局部损失之和。
若求沿程损失h f 和局部损失hj ,就必须确定沿程损失系数λ和局部损失系数ζ。
因此,确定沿程损失系数λ和局部损失系数ζ就成了本章的最关键的问题。
§7—1 圆管中的层流流动本节及以后各节所讨论的沿程损失系数的计算公式,只适用于管内充分发展的流动,而不适用于速度分布沿流程不断变化的管道入口段的流动(。
设流动为不可压流体在水平直管中的定常流动,流体充满整个管道截面,并为充分发展的层流流动。
取管道轴线与x 坐标一致。
在这样的流动中没有横向速度分量,即υ=w =0,仅有x 方的速度u 。
根据连续方程,可得0=∂∂xu (1)该式表明,u 与x 无关,仅为y 和z 的函数。
流体力学练习题流体的黏滞力和流体静力学的计算

流体力学练习题流体的黏滞力和流体静力学的计算流体力学练习题:流体的黏滞力和流体静力学的计算流体力学是研究流体在不同条件下的性质和行为的学科。
在流体力学中,黏滞力和流体静力学是两个重要的概念,它们对于我们理解流体力学的基本原理和应用具有重要的意义。
本文将围绕这两个概念展开讨论,探究黏滞力和流体静力学的计算方法和应用。
一、黏滞力的概念和计算黏滞力是指流体内部分子之间相互作用导致流体内部阻尼力的存在,它是流体内部摩擦的结果。
黏滞力的大小与流体的黏性密切相关,黏性越大,黏滞力越大。
在流体力学中,黏滞力的计算通常使用牛顿黏滞定律。
根据牛顿黏滞定律,黏滞力与流体通过的面积、速度梯度以及黏度之间存在着一定的关系。
黏滞力的计算公式如下:F = ηA(dv/dr)其中,F表示黏滞力,η表示流体的黏度,A表示流体通过的面积,dv/dr表示速度梯度。
通过这个公式,我们可以计算出流体中的黏滞力。
二、流体静力学的概念和计算流体静力学是研究流体在静止状态下受力和分压的学科。
在流体静力学中,重要的概念包括压强、表面张力和浮力等。
首先,我们来讨论流体中的压强。
根据流体静力学的基本原理,流体中的压强是由流体受到的外力和流体的密度共同决定的。
在静止的流体中,压强在各个方向上是相等的。
根据这一原理,我们可以使用以下公式计算流体中的压强:P = F/A其中,P表示压强,F表示流体受到的外力,A表示流体所受力的面积。
通过这个公式,我们可以计算出流体中的压强。
其次,我们来讨论流体中的表面张力。
表面张力是指液体表面上的分子间吸引力导致液体表面呈现出一种类似于薄膜的现象。
表面张力的大小与液体分子间相互作用力有关。
最后,我们来讨论浮力。
根据阿基米德原理,当物体浸入流体中时,流体对物体的浮力大小等于物体所排开的流体的重量。
浮力的大小与物体所受的重力和流体的密度有关。
综上所述,黏滞力和流体静力学是流体力学中的重要概念,并且在众多工程和科学领域中具有广泛的应用。
流体力学答案第七章习题及答案2 2.doc

习题及答案7 —9薄壁孔口出流,直径d=2mm,水箱水位恒定H=2m,试求: (1)孔口流量。
;⑵此孔口外接圆柱形管嘴的流量Q;(3) 管嘴收缩断面的真空。
解:(1 ) @=心顷~ j2gx2=1.22 n?/s(2) Q n = ^,A^H = 0.82^2gx2 =1.61 m3/s(3) 4 = 0.75//=0.75x2 = 1.5 mPg7 —10水箱用隔板分为A、B两室,隔板上开一孔口,其直径d 户4cm,在B室底部装有圆柱形外管嘴,其直径d2=3cm0 已知H=3m, h3=0. 5m,试求:(1) »、h2; (2)流出水箱的流量Q。
解:(1) & ="专7^ =「冬山(丑—4)=00.62 x 郴•。
町皿 = 0.82x得hi=1.07m h2=H- hFl.43m(2) Q=/Z^7^=0.62X"°:4)j2gxl.O7 =3.57 Vs7-12游泳池长25m,宽10m,水深1.5m,池底设有直径10cm 的放水孔直通排水地沟,试求放尽池水所需的时间。
V =25x10x1.5 = 375m31Qmax = M X/2^O = O^x-7rd2d2gH o =2.64xl0-2m3 解: 42Vt =——= 7.89/iQmax7-14虹吸管将A池中的水输入B池,已知长度/F3m, Z2=5m, 直径d=75mm,两池水面高差H=2m,最大超高h=1.8m,沿程阻力系数入二0.02,局部阻力系数:进口J = 0.5,转弯支=0. 2,出口J = 1。
试求流量及管道最大超高断面的真空度。
80.075 、2 2— = 3.83—2g2g 19.6x23.20 m/s3.83 (0.075)2 Q = D * = 3.20X —~ -------------- =14.13 41/s列上游水池和最大超高处的伯诺里方程 〃噫+。
3噫g +如 (I> 决如十讦+检斗l ・5H 1+-^- + 0 = H 2+0 + 0 + /Z Z Pg(d\卜勺+£+£+与+易 1 2x98000 仁 l+ --------------- =5+16.4— 9800 2g解:( 10 0.025x —— 2g I 0.025 i} i}^0.5+4+3x03+1 —=16.4—2g 2g(i +i 宙《解:列上下游水池的伯诺里方程丑+0 + 0 = ° + 0 + 0 + "『罗斋= 3.E7-16水从密闭容器A,沿直径d=25mm,长Z=10m 的管道流 入容器B,已知容器A 水面的相对压强pF2at,水面高HFlm, Hi =1 m, H2=5m,沿程阻力系数入=0.025,局部阻力系数:阀 门C a=4. 0,弯头£b=0.3,试求流量。
流体力学第七章习题答案
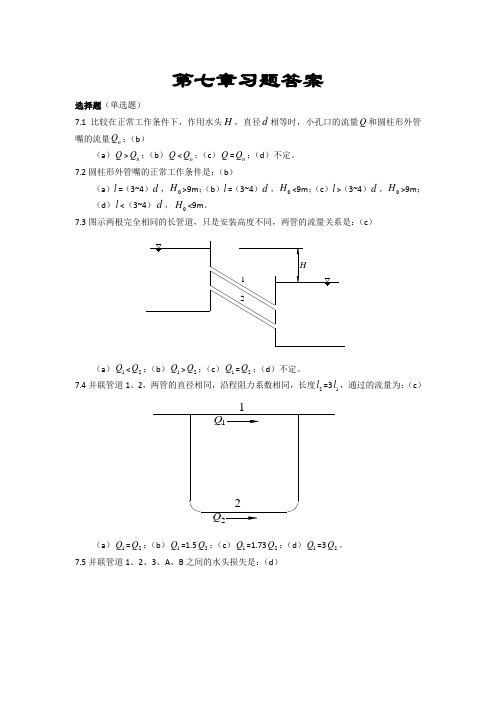
第七章习题答案选择题(单选题)7.1比较在正常工作条件下,作用水头H ,直径d 相等时,小孔口的流量Q 和圆柱形外管嘴的流量n Q :(b )(a )Q >n Q ;(b )Q <n Q ;(c )Q =n Q ;(d )不定。
7.2圆柱形外管嘴的正常工作条件是:(b )(a )l =(3~4)d ,0H >9m ;(b )l =(3~4)d ,0H <9m ;(c )l >(3~4)d ,0H >9m ;(d )l <(3~4)d ,0H <9m 。
7.3图示两根完全相同的长管道,只是安装高度不同,两管的流量关系是:(c )(a )1Q <2Q ;(b )1Q >2Q ;(c )1Q =2Q ;(d )不定。
7.4并联管道1、2,两管的直径相同,沿程阻力系数相同,长度2l =31l ,通过的流量为:(c )2(a )1Q =2Q ;(b )1Q =1.52Q ;(c )1Q =1.732Q ;(d )1Q =32Q 。
7.5并联管道1、2、3、A 、B 之间的水头损失是:(d )1(a )fAB h =1f h +2f h +3f h ;(b )fAB h =1f h +2f h ;(c )fAB h =2f h +3f h ;(d )fAB h =1f h =2f h =3f h 。
7.6长管并联管道各并联管段的:(c )(a )水头损失相等;(b )水里坡度相等;(c )总能量损失相等;(d )通过的流量相等。
7.7并联管道阀门为K 全开时各段流量为1Q 、2Q 、3Q ,现关小阀门K ,其他条件不变,流量的变化为:(c )(a )1Q 、2Q 、3Q 都减小;(b )1Q 减小,2Q 不变,3Q 减小;(c )1Q 减小,2Q 增加,3Q 减小;(d )1Q 不变,2Q 增加,3Q 减小。
7.8 有一薄壁圆形孔口,直径d 为10mm ,水头H 为2m。
流体力学课后答案第七章

流体⼒学课后答案第七章1.已知平⾯流场的速度分布为xy x u x +=2,y xy u y 522+=。
求在点(1,-1)处流体微团的线变形速度,⾓变形速度和旋转⾓速度。
解:(1)线变形速度:y x xu x x +=??=2θ 54+=??=xy y u yy θ⾓变形速度:()x y y u x u x y z +=+=222121ε旋转⾓速度:()x y x u x u x y z -=???? ????-??=222121ω将点(1,-1)代⼊可得流体微团的1=x θ,1=y θ;23/z =ε;21/z =ω2.已知有旋流动的速度场为z y u x 32+=,x z u y 32+=,y x u z 32+=。
试求旋转⾓速度,⾓变形速度和涡线⽅程。
解:旋转⾓速度:2121=???? ????-??=z u y u y z x ω 2121=??? ????-??=x u z u z x y ω 2121=???? ????-??=y u x u x yz ω⾓变形速度:2521=+=z u y u y z x ε 2521=??? ????+??=x u z u z x y ε 2521=???? ????+??=y u x u x y z ε由z y x dz dy dxωωω==积分得涡线的⽅程为:1c x y +=,2c x z +=3.已知有旋流动的速度场为22z y c u x +=,0=y u ,0=z u ,式中c 为常数,试求流场的涡量及涡线⽅程。
解:流场的涡量为:0=??-??=zu y u y z x Ω 22z y cz x u z u z x y +=??-??=Ω 22zy cy y u x u x yz +-=??-??=Ω旋转⾓速度分别为:0=x ω222zy czy +=ω 222z y cyz +-=ω则涡线的⽅程为:c dz dy z y +=??ωω即c y dz z dy +-=??可得涡线的⽅程为:c z y =+224.求沿封闭曲线2 22b y x =+,0=z 的速度环量。
国开流体力学形考任务7

国开流体力学形考任务7根据国开流体力学形考任务7中的题目,现在我们将对以下几个问题进行讨论和分析。
首先,我们将对流体力学中的材料力学进行分析。
流体力学是研究流体静力学和动力学条件下流体的运动规律的科学。
材料力学是研究材料的内部结构和性能的科学。
在流体力学中,流体的特性受到材料力学的影响,比如在研究流体的流动和压力时,需要考虑流体的黏度、密度、表面张力等特性,这些特性都与材料力学有关。
其次,我们将讨论流体力学中的流动现象。
流体力学研究的是流体在各种条件下的流动规律,比如在管道中的流体流动、河流中的水流、风的气流等。
这些流动现象都受到流体的粘滞性、惯性和压力等因素的影响,这些因素都是流体力学研究的内容。
另外,我们将对流体力学中的压力进行分析。
在流体力学中,压力是一个重要的物理量,它与流体的密度、流速和流体受到的外力有关。
在研究流体的流动时,需要考虑流体的压力分布、压力梯度和流体受到的压力力,这些都是流体力学中的重要内容。
最后,我们将对流体力学的应用进行讨论。
流体力学在工程、生物和环境等领域都有着广泛的应用,比如在航空航天工程中,需要研究飞机的气动力学,这就是流体力学的应用之一;在生物领域中,人体的血液流动和呼吸过程都是流体力学的研究对象;在环境领域中,地下水流、大气环流等自然现象都需要流体力学的研究。
综上所述,流体力学作为一门重要的物理学科,对于我们理解和应用自然界的各种现象都有着重要的作用。
通过对流体力学的研究和应用,我们可以更好地理解自然界的规律,也可以为人类的生产和生活提供更多的科学依据。
希望今后能有更多的科学家和工程师投入到流体力学的研究和应用中,为人类社会的发展和进步做出更大的贡献。
流体力学经典习题解答以及经典试卷及详细解答
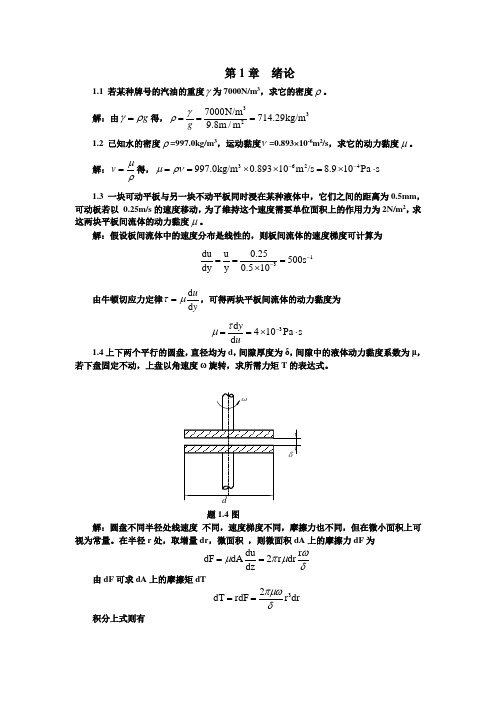
第1章 绪论1.1 若某种牌号的汽油的重度γ为7000N/m 3,求它的密度ρ。
解:由g γρ=得,3327000N/m 714.29kg/m 9.8m /m γρ===g1.2 已知水的密度ρ=997.0kg/m 3,运动黏度ν=0.893×10-6m 2/s ,求它的动力黏度μ。
解:ρμ=v 得,3624997.0kg/m 0.89310m /s 8.910Pa s μρν--==⨯⨯=⨯⋅ 1.3 一块可动平板与另一块不动平板同时浸在某种液体中,它们之间的距离为0.5mm ,可动板若以 0.25m/s 的速度移动,为了维持这个速度需要单位面积上的作用力为2N/m 2,求这两块平板间流体的动力黏度μ。
解:假设板间流体中的速度分布是线性的,则板间流体的速度梯度可计算为13du u 0.25500s dy y 0.510--===⨯ 由牛顿切应力定律d d uyτμ=,可得两块平板间流体的动力黏度为 3d 410Pa s d yuτμ-==⨯⋅1.4上下两个平行的圆盘,直径均为d ,间隙厚度为δ,间隙中的液体动力黏度系数为μ,若下盘固定不动,上盘以角速度ω旋转,求所需力矩T 的表达式。
题1.4图解:圆盘不同半径处线速度 不同,速度梯度不同,摩擦力也不同,但在微小面积上可视为常量。
在半径r 处,取增量dr ,微面积 ,则微面积dA 上的摩擦力dF 为du r dF dA2r dr dz ωμπμδ== 由dF 可求dA 上的摩擦矩dT32dT rdF r dr πμωδ==积分上式则有d 43202d T dT r dr 32πμωπμωδδ===⎰⎰1.5 如下图所示,水流在平板上运动,靠近板壁附近的流速呈抛物线形分布,E 点为抛物线端点,E 点处0d =y u ,水的运动黏度ν=1.0×10-6m 2/s ,试求y =0,2,4cm 处的切应力。
(提示:先设流速分布C By Ay u ++=2,利用给定的条件确定待定常数A 、B 、C )题1.5图解:以D 点为原点建立坐标系,设流速分布C By Ay u ++=2,由已知条件得C=0,A=-625,B=50则2u 625y 50y =-+ 由切应力公式du dy τμ=得du(1250y 50)dyτμρν==-+ y=0cm 时,221510N /m τ-=⨯;y=2cm 时,222 2.510N /m τ-=⨯;y=4cm 时,30τ= 1.6 某流体在圆筒形容器中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2.2)
其中 z z* z / L, r r * / r / ( L) 应该满足渐进衔接条件,即
r 0
lim u* ( z* , r * ) lim u ( z , r ) *
r r
(2.3) (2.4)
r* 0
lim p* ( z* , r * ) lim p( z , r )
rv u r 0 r z dU e u u 2u 1 u v u Ue ( 2 ) r z dz r r r
(2.10)
思考题 1:如何分析和判断三维流动的分离? 三维分离形成的机理与二维一样, 流动中存在逆压梯度并作用于 有粘性阻滞的边界层流动起着关键作用。但在三维流动中, 即使沿 某个方向存在压力梯度, 由于边界层内的流体还可以沿其它方向流 出, 此时边界层的流动仍可以是附着的, 所以不能将二维分离的判别 准则简单地推广应用到三维流动中[1]。 张涵信先生在调研了 Brown,Stewartson, Williams, Eichelbrenner, Oudar, Maskell, 王国璋等人的工作后归纳出三维流动分离的判定条 件为:
u 0 z 0 2u 0 xz 0
(1.1)
对于满足牛顿摩擦定律的实际流动,分离条件为:
zx 0 0
zx 0 x 0
(1.2)
[1] 张扬军, 陈乃祥. 水力机械分离流动研究[C]. 第十二次中国水电设备学术讨论会论文集. 重庆: 1995, 6-11 [2] 张涵信. 三维定常粘性流动的分离条件及分离线附近流动的性状[J]. 空气动力学学报,1985,01:112.
(2.7)
注意右边的粘性项量级,并假设 Re 2 O(1) ,可令 2 似化简为
rv u r 0 r z u u p 2u 1 u v u 2 r z z r r r p 0 r
1 ,则一阶近 Re
(2.8)
认为压强沿径向为常数,边界层内压强等于边界层外来流压强。 若将无粘流边界的压强按伯努利方程算出: p* ( z ) p0* ue*2 ( z ) / 2 ,则边 界层内的压强也等于该值。代入 N-S 方程后,化为
(2.6)
由连续方程可知,内层的无量纲径向速度为 量级,即 v O( ) ,因此 内层径向速度的量级应为 v U v ( z , r ) 将上式代入 N-S 方程,得到
rv u r 0 r z u u p 1 1 2u 1 1 u 2u v u ( ) r z z Re 2 r 2 2 r r z 2 v v 1 p 1 1 2v 1 1 v 2v 1 v (v u ) ( ) r z r Re r 2 r r z 2 r 2
rv u r 0 r z * u u 2u 1 u * due v u ue 2 r z dz r r r
(2.9)
边界条件为: a.壁面无滑移 r r0 , u v 0 b.内外区衔接条件 r , u ue* ( z ) 写回有量纲形式为
2
0 1 u u 37 (1 )dy f (1 f )d 0 U U 315
(1.3)
w u y
y 0
U
f '(0) 2
U
(1.4)
代入动量积分关系式,得
37 d 2 315 dx U
(1.5)
由定解条件 x 0, 0 ,得到
二维柱坐标下的 N-S 方程为
rv u r 0 r z u u 1 p 2u 1 u 2u v u ( 2 ) r z z r r r z 2 v v v 1 p 2v 1 v 2v v u ( 2 ) r z r r r r z 2 r 2
u y U u y 0
y
(1.1)
2u y 2
0
y
解得 a 1, b 2, c 0, d 2, e 0 所以:
u f ( ) 4 2 3 2 U
(1.2)
利用动量积分关系式来求 ,由于已得到速度分布的形式,可以得到
粘性流体力学第七次作业
班级: 热博 13 姓名:林敦 学号:2013310330
题 1:对零压力梯度平板边界层,若边界层内速度为四次多项式分布, 试用动量积分方法求边界层名义厚度、动量厚度以及壁面摩擦应力。 解: 设速度分布为 足 5 个条件:
u y 0 0 2u y 2 0
y 0
y u f ( ) a 4 b 3 c 2 d e ,其中 ,需满 U
思考题 2:某些飞机(如波音 777)或汽车上的涡流发生器的作用原 理? 解释一:将层流边界层扰动成湍流边界层,湍流边界层抗分离能 力较强,使得边界层分离点推迟,减小损失。 解释二:涡流发生器实际上是以某一安装角垂直地安装在机体表面
上的小展弦比小机翼,所以它在迎面气流中和常规机翼一样能产生翼 尖涡,但是由于其展弦比小,因此翼尖涡的强度相对较强。这种高能 量的翼尖涡与其下游的低能量边界层流动混合后,就把能量传递给了 边界层,使处于逆压梯度中的边界层流场获得附加能量后能够继续贴 附在机体表面而不致分离。这就是涡流发生器的基本工作原理。
(2.5)
将内场的无量纲形式代入柱坐标下的 N-S 方程,得到
rv u r 0 r z 1 u u p 1 1 2u 1 1 u 2u v u ( ) r z z Re 2 r 2 2 r r z 2 1 v v 1 p 1 1 2 v 1 1 v 2v 1 v v u ( ) r z r Re 2 r 2 2 r r z 2 2 r 2
1260 x x 5.84 37 U U
(1.6) (1.7)
w 0.343U 2
U x
0.343
U 2
Re x
题 2:推导细长圆柱被不可压缩流体沿纵向绕流的边界层方程。假设 所讨论的范围离前缘较远,且该处圆柱的半径与边界层厚度同量级流 动分为外区和内区。外区是无粘流,内区为边界层。 解:外区用常规尺度作无量纲化:
u U u* ( z * , r * ), v U v* ( z * , r * ), p U 2 p* ( z * , r * )
(2.1)
其中 z* z / L, r * r / L 内区暂设为:
u U u ( z , r ), v U v ( z , r ), p U 2 p ( z , r )
