五种方法求二面角及练习题
二面角四种求法_5个例题解决二面角难题

四法求二面角二面角是高考的热点内容之一,求二面角的大小应先作出它的平面角,下面介绍作二面角的平面角四种方法:定义法、垂面法、三垂线定理法、射影面积法。
(1)定义法——在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角。
注:o 点在棱上,用定义法。
(2)垂线法(三垂线定理法)——利用三垂线定理作出平面角,通过解直角三角形求角的大小。
注:o 点在一个半平面上,用三垂线定理法。
(3)垂面法——通过做二面角的棱的垂面,两条交线所成的角即为平面角。
注:点O 在二面角内,用垂面法。
(4)射影面积法——若多边形的面积是S ,它在一个平面上的射影图形面积是S`,则二面角θ的大小为COS θ= S`÷ SA 图3αβO B lO图5β α l C B A例1 如图1-125,PC⊥平面ABC,AB=BC=CA=PC,求二面角B-PA-C的平面角的正切值。
(三垂线定理法)分析由PC⊥平面ABC,知平面ABC⊥平面PAC,从而B在平面PAC上的射影在AC 上,由此可用三垂线定理作出二面角的平面角。
解∵ PC⊥平面ABC∴平面PAC⊥平面ABC,交线为AC作BD⊥AC于D点,据面面垂直性质定理,BD⊥平面PAC,作DE⊥PA于E,连BE,据三垂线定理,则BE⊥PA,从而∠BED是二面角B-PA -C的平面角。
设PC=a,依题意知三角形ABC是边长为a的正三角形,∴ D是∵PC = CA=a,∠PCA=90°,∴∠PAC=45°∴在Rt△DEA评注本题解法使用了三垂线定理来作出二面角的平面角后,再用解三角形的方法来求解。
例2 在60°二面角M-a-N内有一点P,P到平面M、平面N的距离分别为1和2,求点P到直线a的距离。
(图1-126)(垂面法)分析设PA、PB分别为点P到平面M、N的距离,过PA、PB作平面α,分别交M、N于AQ、BQ.同理,有PB⊥a,∵ PA∩PB=P,∴ a⊥面PAQB于Q又 AQ、BQ平面PAQB∴ AQ⊥a,BQ⊥a.∴∠AQB是二面角M-a-N的平面角。
二面角的几种方法及例题

二面角大小的求法(例题)二面角的类型和求法可用框图展现如下:、定义法: 甬片+—*■垂面法化T不见播型直接在二面角的棱上取一点(特殊点),分别在两个半平面内作棱的垂线,得出平面角,用定义法时,要认真观察图形的特性;例、如图,已知二面角a - a - B等于120° ,PA丄a ,A €a ,PB丄B ,B .求/ APB的大小.做OB 交线,交于点O,连接OAQ PB 平面PB 交线同理PA 交线又Q OB 交线交线面PAOB交线OA即可得AOB为面的二面角,AOB=120所以APB=60例、在四棱锥P-ABCD中, ABCD是正方形,PA!平面ABCQPA=AB=a求二面角B-PC-D的大小。
提示:VPAB VPCD,而且是直角三角形可见槻型I解法• f三垂线法A、三垂线定理法:已知二面角其中一个面内一点到一个面的垂线,用三垂线定理或逆定理作出二面角的平面角;例、在四棱锥P-ABCD中,ABCD是平行四边形,P从平面ABCD PA=AB=a / ABC=30,求二面角P-BC-A的tag 大小。
过A做AH BC,交BC于H,连接PH Q PA 面ABCDPA AB, PA BCBC 面PHAPHA为二面角在VABH中ABH=30 , AB=aAH=a/2tag PHA 2例:如图,ABCD-ABGD是长方体,侧棱AA长为1,底面为正方体且边长为2,E是棱BC勺中点,求面CD%面CD所成二面角的正切值.提示:CO DE而且是长方体! !!例、△ ABC 中,/ A=90°, AB=4 AC=3 平面 ABC 外一点 P 在平 面ABC 内的射影是AB 中点M 二面角P-AC — B 的大小为45°。
求(1) 二面角P-BC — A 的大小;(2)二面角C-PB-A 的大小 提示:角PAB 是二面角,找到每个面的直角!射影,那么PM 为面ABC 的垂线!例、如图4,平面丄平面,A =l , A € , B € ,点A 在 直线I 上的射影为A,点B 在I 的射影为B,已知AB=2AA=1,BBp/2, 求:二面角A — AB- B 的大小.提示:AA1与BB1互相垂直AF 是辅助线且垂直AB,FE 平行BB四、射影法:(面积法)利用面积射影公式S 射=S 原cos ,其中 为平面BD i' M图4角的大小,此方法不必在图形中画出平面角;例、在四棱锥P-ABCD中,ABC[为正方形,P从平面ABCD PA =AB= a,求平面PBA与平面PDC所成二面角的大小。
二面角的几种求法(很好)
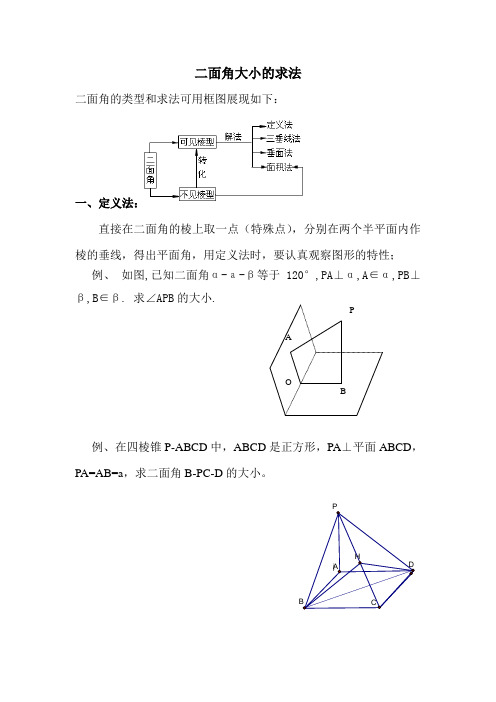
二面角大小的求法二面角的类型和求法可用框图展现如下:一、定义法:直接在二面角的棱上取一点(特殊点),分别在两个半平面内作棱的垂线,得出平面角,用定义法时,要认真观察图形的特性;例、如图,已知二面角α-а-β等于120°,PA⊥α,A∈α,PB⊥β,B∈β. 求∠APB的大小.PA=AB=a,求二面角B-PC-D的大小。
二、三垂线定理法:已知二面角其中一个面内一点到一个面的垂线,用三垂线定理或逆定理作出二面角的平面角;例、在四棱锥P-ABCD 中,ABCD 是平行四边形,PA ⊥平面ABCD ,PA=AB=a ,∠ABC=30°,求二面角P-BC-A 的大小。
例、(2003北京春)如图,ABCD-A 1B 1C 1D 1是长方体,侧棱AA 1长为1,底面为正方体且边长为2,E 是棱BC 的中点,求面C 1DE 与面CDE 所成二面角的正切值.ABCDA 1B 1C 1D 1EO例、ΔABC中,∠A=90°,AB=4,AC=3,平面ABC外一点P在平面ABC内的射影是AB中点M,二面角P—AC—B的大小为45°。
求(1)二面角P—BC—A的大小;(2)二面角C—PB—A的大小例、(2006年陕西试题)如图4,平面α⊥平面β,α∩β=l,A∈α,B∈β,点A在直线l上的射影为A1,点B在l的射影为B1,已知AB=2,AA1=1,BB1=2,求:二面角A1-AB-B1的大小.图4 B1AαβA1B LE F三、垂面法:已知二面角内一点到两个面的垂线时,过两垂线作平面与两个半平面的交线所成的角即为平面角,由此可知,二面角的平面角所在的平面与棱垂直;例、空间的点P 到二面角βα--l 的面α、β及棱l 的距离分别为4、3、3392,求二面角βα--l 的大小.四、射影法:(面积法)利用面积射影公式S 射=S 原cos θ,其中θ为平面角的大小,此方法不必在图形中画出平面角;例、在四棱锥P-ABCD 中,ABCD 为正方形,PA⊥平面ABCD ,PA =AB =a ,求平面PBA 与平面PDC 所成二面角的大小。
二面角问题求解方法大全

v1.0 可编辑可修改五法求二面角一、 定义法:从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角。
例1如图,四棱锥S ABCD -中,底面ABCD 为矩形,SD ⊥底面ABCD ,2AD =2DC SD ==,点M 在侧棱SC 上,ABM ∠=60°(I )证明:M 在侧棱SC 的中点 (II )求二面角S AMB --的大小。
练习1如图,已知四棱锥P -ABCD ,底面ABCD 为菱形,PA ⊥平面ABCD ,60ABC∠=︒,E ,F 分别是BC , PC 的中点.(Ⅰ)证明:AE ⊥PD ; (Ⅱ)若H 为PD 上的动点,EH 与平面PAD 所成最大角的正切值为62,求二面角E —AF —C 的余弦值.二、三垂线法三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.通常当点P 在一个半平面上则通常用三垂线定理法求二面角的大小。
例2. 如图,在直四棱柱ABCD-A 1B 1C 1D 1中,底面ABCD 为等腰梯形,AB111111ABCD P -ABCD60,22,2,2,3=∠====PAB PD PA AD AB ⊥AD PABPC AD A BD P -- (Ⅰ)证明:平面PBE ⊥平面PAB ;(Ⅱ)求平面PAD 和平面PBE 所成二面角(锐角)的大小.练习3已知斜三棱柱ABC —A 1B 1C 1的棱长都是a ,侧棱与底面成600的角,侧面BCC 1B 1⊥底面ABC 。
(1)求证:AC 1⊥BC ;(2)求平面AB 1C 1与平面 ABC 所成的二面角(锐角)的大小。
四、射影面积法(coss S射影)凡二面角的图形中含有可求原图形面积和该图形在另一个半平面上的射影图形面积的都可利用射影面积公式(cos 斜射S S =θ)求出二面角的大小。
二面角的几种方法及例题

二面角的几种方法及例题本页仅作为文档封面,使用时可以删除This document is for reference only-rar21 year.March二面角大小的求法(例题)二而角的类型和求法可用框图展现如下:广定义法f 三垂线法f 垂面法—面积法+]直接在二而角的棱上取一点(特殊点),分别在两个半平而内作棱的垂线,得出平而角,用定义法时,要认真观察图形的特性; 例、如图,已知二面角a - a -P 等于120°,PA 丄a ,Ae a ,PB 丄B ,BG B •求ZAPB 的大小.做OB 丄交线,交于点O,连接OAPB 丄平面0/. PB 丄交线同理PA 丄交线X ••• OB 丄交线/.交线丄面PAOB/.交线丄OA即可得ZAOB 为面a0的二面角,ZAOB=120° 所以 ZAPB=60°PA=AB=a,求二而角B-PC-D 的大小。
捉示:A PAB =A PCD ,而且是直角三角形 角 转化不见棱定义法: 例、在四棱锥P-ABCD 中,ABCD 是正方形,PA 丄平面ABCD,+可见棱型二、三垂线定理法:已知二而角其中一个面内一点到一个面的垂线,用三垂线定理或逆定理作出二而角的平而角;例、在四棱锥P-ABCD中,ABCD是平行四边形,PA丄平而ABCD, PA=AB=a, Z ABC=30°,求二面角P-BC-A 的teg 大小。
过A做AH丄BC,交BOTH,连接PH "A丄面ABCD/. PA 丄AB, PA 丄BC/. BC丄面PHA/. ZPHA为二面角在A ABH中ZABH=30°, AB=aAH=a/2tagZPHA = 2例:如图,ABCD-AiBiCiDi是长方依侧棱AAi长为2,底面为正方体且边长为2,E是棱BC的中点,求而CiDE与而CDE所成二面角的正切值.提示:CO丄DE,而且是长方体!!!A B例.A ABC 中,ZA=90° , AB二4, AC二3,平而ABC 外一点P 在平而ABC内的射影是AB中点M,二面角P—AC—B的大小为45° o求(1)二面角P—BC—A的大小;(2)二面角C—PB—A的大小提示:角PAB是二面角,找到每个面的直角!!!射影,那么PM为面ABC的垂线!例.如图4,平面a丄平而0, a。
二面角的基本求法例题及练习
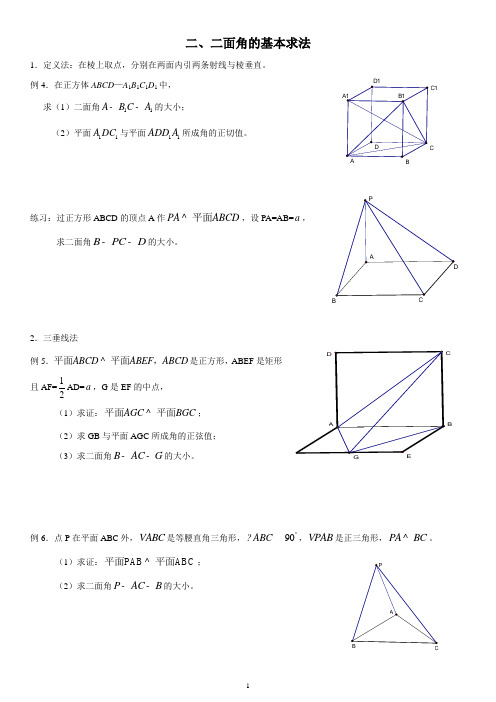
C1B二、二面角的基本求法1.定义法:在棱上取点,分别在两面内引两条射线与棱垂直。
例4.在正方体ABCD—A1B1C1D1中,求(1)二面角11A B C A--的大小;(2)平面11A DC与平面11ADD A所成角的正切值。
练习:过正方形ABCD的顶点A作PA ABCD^平面,设PA=AB=a,求二面角B PC D--的大小。
2.三垂线法例5.ABCD ABEF ABCD^平面平面,是正方形,ABEF是矩形且AF=12AD=a,G是EF的中点,(1)求证:AGC BGC^平面平面;(2)求GB与平面AGC所成角的正弦值;(3)求二面角B AC G--的大小。
例6.点P在平面ABC外,ABC是等腰直角三角形,90ABC°?,PAB是正三角形,PA BC^。
(1)求证:^平面PA B平面A BC;(2)求二面角P AC B--的大小。
练习:正方体ABCD —A 1B 1C 1D 1的棱长为1,P 是AD 的中点,求二面角1A BD P--的大小。
3.垂面法例7.SA ABC AB BC SA AB BC ^^==平面,,, (1)求证:SB BC ^;(2)求二面角C SA B --的大小; (3)求异面直线SC 与AB 所成角的余弦值。
4.无棱二面角的处理方法 (1)找棱例8.过正方形ABCD 的顶点A 作PA ABCD ^平面,设PA=AB=a , 求平面PAB 与平面PCD 所成二面角的大小。
(2)射影面积法(cos s Sq =射影)例9.正方体ABCD —A 1B 1C 1D 1的棱长为1,P 是棱1AA 的中点, 求平面11PB C 与平面ABCD 所成二面角的大小。
B1A。
五种方法求二面角及练习题之欧阳音创编

五种方法求二面角及练习题一、时间:2021.03.11创作:欧阳音二、 定义法:从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角。
1.如图,在棱长为a 的正方体ABCD —A1B1C1D1中,求:(1)二面角C1—BD —C 的正切值(2)二面角2.如图,四棱锥中,底面为矩形,底面,,,点M 在侧棱上,=60,M 在侧棱的中点ABC DADCB(1)求二面角的余弦值。
二、三垂线法:三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.通常当点P 在一个半平面上则通常用三垂线定理法求二面角的大小。
1. 如图,在直四棱柱ABCD-A B C D 中,底面ABCD 为等腰梯形,AB//CD ,AB=4, BC=CD=2, AA =2, E 、E 、F 分别是棱AD 、AA 、AB 的中点。
(1)证明:直线EE //平面FCC ;(2)求二面角B-FC -C 的余弦值。
2.如图,在四棱锥中,底面是矩形.已知.(Ⅰ)证明平面;(Ⅱ)求异面直线与所成的角的大小; (Ⅲ)求二面角的大小.三.补棱法EABCF E 1 A B 1C 1DD本法是针对在解构成二面角的两个半平面没有明确交线的求二面角题目时,要将两平面的图形补充完整,使之有明确的交线(称为补棱),然后借助前述的定义法与三垂线法解题。
即当二平面没有明确的交线时,一般用补棱法解决1.已知斜三棱柱ABC —A1B1C1的棱长都是a ,侧棱与底面成600的角,侧面BCC1B1⊥底面ABC 。
(1)求证:AC1⊥BC;(2)求平面AB1C1与平面 ABC 所成的二面角(锐角)的大小。
2:如图5,E 为正方体ABCD -A1B1C1D1的棱CC1的中点,求平面AB1E 和底面A1B1C1D1所成锐角的余弦值.3如图所示,四棱锥P-ABCD 的底面ABCD 是边长为1的菱形,∠BCD=60°,E 是CD 的中点,PA⊥底面ABCD ,PA =2.(Ⅰ)证明:平面PBE⊥平面PAB;(Ⅱ)求平面PAD 和平面PBE 所成二面角(锐ABCEDP ACBB 1C 1A 1LA 1D 1B 1C 1E DBC A图5角)的大小.角的平面角(锐角).分析平面AB1E与底面A1B1C1D1交线即二面角的棱没有给出,要找到二面角的平面角,.四、向量法向量法解立体几何中是一种十分简捷的也是非常传统的解法,可以说所有的立体几何题都可以用向量法求解,用向量法解立体几何题时,通常要建立空间直角坐标系,写出各点的坐标,然后将几何图中的线段写成用坐标法表示的向量,进行向量计算解题。
求二面角的方法专题
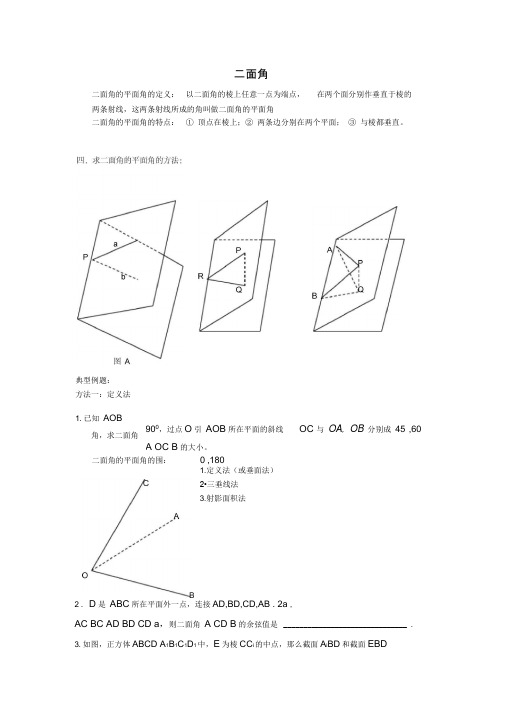
典型例题:方法一:定义法1.已知 AOB角,求二面角 900,过点O 引 AOB 所在平面的斜线 A OC B 的大小。
OC 与 OA , OB 分别成 45° ,60°二面角二面角的平面角的定义: 以二面角的棱上任意一点为端点,在两个面分别作垂直于棱的 两条射线,这两条射线所成的角叫做二面角的平面角二面角的平面角的特点: ① 顶点在棱上;② 两条边分别在两个平面; ③ 与棱都垂直。
二面角的平面角的围: 0°,180°2 . D 是 ABC 所在平面外一点,连接AD,BD,CD,AB . 2a ,AC BC AD BD CD a ,则二面角 A CD B 的余弦值是 _______________________________ .3.如图,正方体ABCD A 1B 1C 1D 1中,E 为棱CC i 的中点,那么截面A i BD 和截面EBD1.定义法(或垂面法)2•三垂线法3.射影面积法C所成的二面角为 ________________4•在 ABC 中,AB BC,SA 平面ABC ,DE 垂直平分SC ,且分别交AC,SC 于D,E ,又SA AB, SB BC ,求二面角E BD C 的大小。
5.如图,正方体ABCD A i B i C i D i 的棱长为1,P 是AD 的中点,求二面角A BD i P的大小。
6.如图,已知点P 为正方体ABCD A i B i C i D i 的棱A i B i 的中点,求二面角P AC D i的余弦值。
ABD 向上折起,使点A&如图,矩形ABCD 中,AB 6,BC 23,沿对角线BD 将 移至点P ,且P 在平面BCD 的射影0在DC 上。
1(1 )求二面角P DB C 的平面角的余弦值。
(一)3J2(2)求直线DC 与平面PBD 所成角的正弦值。
(鼻)3方法二:三垂线法:7•如图所示,平面 ABC 平面ABD, ACB 90°,CA CB,面角C BD A 的平面角的正切角为ABD 是正三角形,则二 2 3、 --- ) 3 CB大小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五种方法求二面角及练习题
定义法:
从一条直线出发的两个半平面所组成的图形叫做二面角 ,这条直线叫
做二面角的棱,这
两个半平面叫做二面角的面, 在棱上取点,分别在两面内引两条射线与棱垂直,
这两条垂线 所成的角的大小就是二面角的平面角。
1 如图,在棱长为 a 的正方体 ABC —ABCD 中,求: (1) 二面角 C -BD-C 的正切值(2)二面角B_! - BG - D
2•如图,四棱锥 S-ABCD 中,底面 ABCD 为矩形,SD _底面ABCD , AD2 ,
DC =SD =2,点M 在侧棱SC 上,.ABM =60, M 在侧棱SC 的中点
二、三垂线法:三垂线定理:在平面内的一条直线, 如果和这个平面的一条斜线的射影垂直, 那么它也和这条斜线垂直. 通常当点P 在一个半平面上则通常用三垂线定理法求二面角的大 小。
1.如图,在直四棱柱 ABCD-A 1B 1C 1D 1中,底面ABCD 为等腰梯形,AB//CD , AB=4, BC=CD=2, AA 1 =2, E 、E 1、F 分别是棱 AD 、AA 1、AB 的中点。
(1) 证明:直线EE 1//平面FCC , ; (2)求二面角B-FC 1-C 的余弦值。
(1 )求二面角S-AM -B
的余弦值。
C
C
2.女口图,在四棱锥 P - ABCD 中,底面 ABCD 是矩形.已知
AB = 3, AD = 2, PA = 2,PD = 2 •. 2, . PAB =60 .
(I)证明AD _平面PAB ;
(n)求异面直线 PC 与AD 所成的角的大小; (川)求二面角 P - BD - A 的大小.
.补棱法
本法是针对在解构成二面角的两个半平面没有明确交线的求二面角题目时, 的图形补充完整,使之有明确的交线(称为补棱),然后借助前述的定义法与三垂线法解题。
即当二平面没有明确的交线时,一般用补棱法解决
1.已知斜三棱柱 ABC —A i B i C i 的棱长都是a,侧棱与底面成600的角,侧面BCGB i 丄底面ABG
(1)求证:AG 丄BC ;
(2) 求平面ABiG 与平面ABC 所成的二面角(锐角)的大小。
2:如图5, E 为正方体 ABCD- A i B i CiDi 的棱CC 的中点,求平面 AB i E 和底面A i B i C i D i 所 成锐角的余弦值.
3如图所示,四棱锥 P-ABCD 的底面ABCD 是边长为i 的菱形,/ BCD= 60°, E 是CD 的中
点,PA 丄底面 ABCD, PA = 2.
(I)证明:平面 PBE 丄平面PAB
(n)求平面 PAD 和平面PBE 所成二面角(锐角)的大小 角的平面角(锐角)
要将两平面 C
E C i
D
E
分析平面AB I E与底面A i B i C i D i交线即二面角的棱没有给出,要找到二面角的平面角,四、向量法
向量法解立体几何中是一种十分简捷的也是非常传统的解法,可以说所有的立体几何题都可以用向量法求解,用向量法解立体几何题时,通常要建立空间直角坐标系,写出各点的坐标,然后将几何图中的线段写成用坐标法表示的向量,进行向量计算解题。
1 如图,在五面体ABCDEF中, FA —平面ABCD, AD//BC//FE,AB_ AD, M 为EC的中点,AF=AB=BC=FE=AD
2
(I) 求异面直线BF与DE所成的角的大小;
(II) 证明平面AMD _平面CDE求二面角A-CD-E的余弦值。
2、如图,在直三棱柱ABC -AB J G中,平面ABC _侧面A1ABB1.
(I)求证:AB _ BC ;
(n)若直线AC与平面A, BC所成的角为二,二面角A, - BC - A的大小
为,试判断二与「的大小关系,
3.如图,在棱长为a的正方体ABC—ABCD中,求:
(1)二面角C-BD-C的正切值(2)二面角B<! —BG —D
4•过正方形ABCD的顶点A作PA A平面ABCD,
设PA=AB=a (1)求二面角B- PC - D的大小;
(2)求二面角C-PD-A
5.如图所示,四棱锥P—ABCD的底面ABCD是边长为1的菱
E
形,/ BCA 60°, E是CD的中点,P从底面ABCD, PA= (3)
•⑴证明:BE X平面PAB
(2)求二面角A- BE—P的大小
(3)PB与面PAC的角
6如图,在底面为直角梯形的四棱锥
P -ABCD 中,AD//BC, ABC =90 ,
PA 丄平面ABCD PA =3, AD =2,AB =2j3 BC=6
(1)求证:BD-平面PAC;
⑵求二面角P _ BD - A的大小.
(3 )求二面角B-PC-A的大小
7.如图,直二面角D—AB—E中,四边形ABCD是边长为2的正方形,
AE=EB F 为CE上的点,且BF丄平面ACE.
(I)求证AE丄平面BCE
(H)求二面角B—AC—E的大小;
(川)求点D到平面ACE的距离.
8•如图,在四棱锥P ~ ABCD中,底面ABCD是矩形•已知AB = 3 , AD = 2 ,
PA = 2 , PD =2血 / PAB = 60°P
(I)证明AD —平面PAB ;
A
(n)求异面直线PC与AD所成的角的大小;
(川)求二面角P - BD - A的正切值.。
