第五章：常微分方程数值解法第一节欧拉法
第五章：常微分方程数值解法第一节欧拉法
常微分方程数值解法欧拉法
)
f ( xn1, yn1)
hL
y(k ) n 1
yn1
L
hL
k 1
y(0) n 1
yn1
Q
hL 1,
y (k 1) n 1
yn1 (k
)
在迭代公式中取极限，有
yn1 yn h f ( xn1, yn1 ) 因此yn(k1)的极限就是隐式方程的解
几何意义
y
设已知曲线上一点 Pn (xn , yn ),过该 点作弦线，斜率为(xn+1 , yn +1 ) 点的 方向场f(x,y)方向,若步长h充分小， 可用弦线和垂线x=xn+1的交点近似 曲线与垂线的交点。
式。隐式公式不能直接求解，一般需要用Euler显式公式
得到初值，然后用Euler隐式公式迭代求解。因此隐式公
式较显式公式计算复杂，但稳定性好
y0 n1
yn
h
y(k 1) n1
yn
h
f (xn , yn )
f
( xn1 ,
y(k) n1
)
收敛性
y (k 1) n 1
yn1
h
f
( xn1,
y(k ) n 1
如何求解
解析解法：（常微分方程理论）
只能求解极少一类常微分方程；实际中给定的问题不一 定是解析表达式，而是函数表，无法用解析解法。
数值解法: 求解所有的常微分方程
计算解函数 y(x) 在一系列节点 a = x0< x1<…< xn= b
处的近似值 yi y( xi ) (i 1, ... , n)
y(xn1) y(xn ) hy(xn ) y(xn ) yn
y(xn1) yn1 yn h f (xn , yn )
数值分析常微分方程的数值解法
《计算机数学基础》数值部分第五单元辅导14 常微分方程的数值解法一、重点内容 1. 欧拉公式：),...,,,(),()(1-210=⎩⎨⎧+=+=≈01+1+n k kh x x y x hf y y x y kk k k k k局部截断误差是O (h 2)。
2. 改进欧拉公式：预报－校正公式：⎪⎩⎪⎨⎧++=+=++++)],(),([2),(1111k k k k k k k k k k y x f y x f hy y y x hf y y 校正值预报值即 ))],(,(),([211k k k k k k k k y x hf y x f y x f hy y +++=++ 或表成平均的形式：⎪⎪⎪⎩⎪⎪⎪⎨⎧+21=+=+=1+1+)(),(),(c p k p k k c k k k p y y y y x hf y y y x hf y y改进欧拉法的局部截断误差是O (h 3)3. 龙格－库塔法二阶龙格－库塔法的局部截断误差是O (h 3) 三阶龙格－库塔法的局部截断误差是O (h 4) 四阶龙格−库塔法公式： )22(643211κκκκ++++=+hy y k k其中 κ1=f (x k ,y k )；κ2=f (x n +12h ，y k +21h κ1)；κ3=f (x k +12h ，y n +21h κ2)；κ4=f (x k +h ，y k +h κ3)四阶龙格－库塔法的局部截断误差是O (h 5)。
二、实例例1 用欧拉法解初值问题⎩⎨⎧1=060≤≤0--='2)().(y x xy y y ，取步长h =0.2。
计算过程保留4位小数。
解h =0.2, f (x )=－y －xy 2。
首先建立欧拉迭代格式),,)((.),(210=-420=--=+=21+k y x y y hx hy y y x hf y y k k k kk k k k k k k当k =0，x 1=0.2时，已知x 0=0,y 0=1，有y (0.2)≈y 1=0.2×1(4－0×1)＝0.8000当k ＝1，x 2=0.4时，已知x 1=0.2, y 1=0.8，有 y (0.4)≈y 2=0.2×0.8×(4－0.2×0.8)＝0.614 4 当k =2，x 3=0.6时，已知x 2=0.4,y 2=0.6144，有 y (0.6)≈y 3=0.2×0.6144×(4－0.4×0.4613)＝0.8000例2 用欧拉预报－校正公式求解初值问题⎩⎨⎧1=10=++'2)(sin y x y y y ，取步长h =0.2,计算y (0.2),y (0.4)的近似值，计算过程保留5位小数。
常微分方程的数值解法(欧拉法、改进欧拉法、泰勒方法和龙格库塔法)
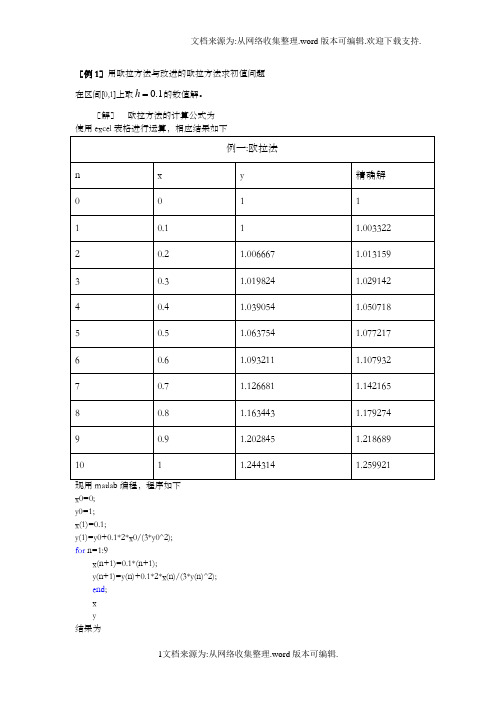
［例1］用欧拉方法与改进的欧拉方法求初值问题h 的数值解。
在区间[0,1]上取0.1［解］欧拉方法的计算公式为x0=0;y0=1;x(1)=0.1;y(1)=y0+0.1*2*x0/(3*y0^2);for n=1:9x(n+1)=0.1*(n+1);y(n+1)=y(n)+0.1*2*x(n)/(3*y(n)^2);end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0067 1.0198 1.0391 1.0638 1.0932 1.1267 1.1634 Columns 9 through 101.2028 1.2443改进的欧拉方法其计算公式为本题的精确解为()y x=x0=0;y0=1;ya(1)=y0+0.1*2*x0/(3*y0^2);y(1)=y0+0.05*(2*x0/(3*y0^2)+2*x0/(3*ya^2));for n=1:9x(n+1)=0.1*(n+1);ya(n+1)=ya(n)+0.1*2*x(n)/(3*ya(n)^2);y(n+1)=y(n)+0.05*(2*x(n)/(3*y(n)^2)+2*x(n+1)/(3*ya(n+1)^2));end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0099 1.0261 1.0479 1.0748 1.1059 1.1407 1.1783 Columns 9 through 101.2183 1.2600［例2］用泰勒方法解x＝0.1, 0.2, …, 1.0处的数值解，并与精确解进行比较。
常微分方程的数值解法
常微分方程的数值解法1. 引言常微分方程是自变量只有一个的微分方程，广泛应用于自然科学、工程技术和社会科学等领域。
由于常微分方程的解析解不易得到或难以求得，数值解法成为解决常微分方程问题的重要手段之一。
本文将介绍几种常用的常微分方程的数值解法。
2. 欧拉方法欧拉方法是最简单的一种数值解法，其具体步骤如下：- 将自变量的区间等分为n个子区间；- 在每个子区间上假设解函数为线性函数，即通过给定的初始条件在每个子区间上构造切线；- 使用切线的斜率（即导数）逼近每个子区间上的解函数，并将其作为下一个子区间的初始条件；- 重复上述过程直至达到所需的精度。
3. 改进的欧拉方法改进的欧拉方法是对欧拉方法的一种改进，主要思想是利用两个切线的斜率的平均值来逼近每个子区间上的解函数。
具体步骤如下： - 将自变量的区间等分为n个子区间；- 在每个子区间上构造两个切线，分别通过给定的初始条件和通过欧拉方法得到的下一个初始条件；- 取两个切线的斜率的平均值，将其作为该子区间上解函数的斜率，并计算下一个子区间的初始条件；- 重复上述过程直至达到所需的精度。
4. 二阶龙格-库塔方法二阶龙格-库塔方法是一种更为精确的数值解法，其基本思想是通过近似计算解函数在每个子区间上的平均斜率。
具体步骤如下： - 将自变量的区间等分为n个子区间；- 在每个子区间上计算解函数的斜率，并以该斜率的平均值近似表示该子区间上解函数的斜率；- 利用该斜率近似值计算下一个子区间的初始条件，并进一步逼近解函数；- 重复上述过程直至达到所需的精度。
5. 龙格-库塔法（四阶）龙格-库塔法是目前常用的数值解法之一，其精度较高。
四阶龙格-库塔法是其中较为常用的一种，其具体步骤如下：- 将自变量的区间等分为n个子区间；- 在每个子区间上进行多次迭代计算，得到该子区间上解函数的近似值；- 利用近似值计算每个子区间上的斜率，并以其加权平均值逼近解函数的斜率；- 计算下一个子区间的初始条件，并进一步逼近解函数；- 重复上述过程直至达到所需的精度。
第5章常微分方程数值解法
2hyxn
2h3 3!
y
yxn1
yxn1 2hyxn
h3 3
y ②
将①、②两式相减：
y
xn1
h3 yn1 3
y
——两步法局部截断误差
18
第19页/共24页
2024年8月7日
（2）梯形公式
yn1
yn
h 2
f
xn , yn
f
xn1 , yn1
yxn
hf
2
xn ,
yn1 yxn1 2hyxn ①
2024年8月7日
17
第18页/共24页
2024年8月7日
将函数用泰勒级数展开：（ h 较小， 相差不大）
yxn1
yxn
h 1!
yxn
h2 2!
yxn
h3 3!
y
yxn1
yxn
h
1!
yxn
h2
2!
yxn
h3
3!
y
yxn1
yxn1
yxn
f
xn1 , yxn1
yn1
yxn
h 2
y
xn
yxn1 ①
将函数用泰勒级数展开：
yxn1
yxn
h 1!
yxn
h2 2!
yxn
h3 3!
y ②
yxn1
yxn
h 1!
yxn
h2 2!
y ③
（ h 较小， 相差不大）
19
第20页/共24页
2024年8月7日
①、②两式相减，并代入③式：
（图示表示梯形法计算结果）
常微分方程组数值解法
常微分方程组数值解法一、引言常微分方程组是数学中的一个重要分支，它在物理、工程、生物等领域都有广泛应用。
对于一些复杂的常微分方程组，往往难以通过解析方法求解，这时候数值解法就显得尤为重要。
本文将介绍常微分方程组数值解法的相关内容。
二、数值解法的基本思想1.欧拉法欧拉法是最基础的数值解法之一，它的思想是将时间连续化，将微分方程转化为差分方程。
对于一个一阶常微分方程y'=f(x,y)，其欧拉公式为：y_{n+1}=y_n+hf(x_n,y_n)其中h为步长，x_n和y_n为第n个时间点上x和y的取值。
2.改进欧拉法改进欧拉法是对欧拉法的改良，其公式如下：y_{n+1}=y_n+\frac{h}{2}[f(x_n,y_n)+f(x_{n+1},y_n+hf(x_n,y_n))] 3.四阶龙格-库塔方法四阶龙格-库塔方法是目前最常用的数值解法之一。
其公式如下：k_1=f(x_n,y_n)k_2=f(x_n+\frac{h}{2},y_n+\frac{h}{2}k_1)k_3=f(x_n+\frac{h}{2},y_n+\frac{h}{2}k_2)k_4=f(x_n+h,y_n+hk_3)y_{n+1}=y_n+\frac{h}{6}(k_1+2k_2+2k_3+k_4)其中，k_i为中间变量。
三、常微分方程组的数值解法1.欧拉法对于一个二阶常微分方程组：\begin{cases} y'_1=f_1(x,y_1,y_2) \\ y'_2=f_2(x,y_1,y_2)\end{cases}其欧拉公式为：\begin{cases} y_{n+1,1}=y_{n,1}+hf_1(x_n,y_{n,1},y_{n,2}) \\y_{n+1,2}=y_{n,2}+hf_2(x_n,y_{n,1},y_{n,2}) \end{cases}其中，x_n和y_{n,i}(i=1, 2)为第n个时间点上x和y_i的取值。
5.1常微分方程的数值解法
5.1常微分⽅程的数值解法第五章常微分⽅程的差分⽅法⼀、教学⽬标及基本要求通过对本节课的学习，使学⽣掌握常微分⽅程、常微分⽅程⽅程组的数值解法。
⼆、教学内容及学时分配本节课主要介绍常微分⽅程的数值解法。
具体内容如下：讲授内容：欧拉公式、改进的欧拉公式。
三、教学重点难点1．教学重点：改进的欧拉公式、龙格库塔⽅法、收敛性与稳定性。
2. 教学难点：收敛性与稳定性。
四、教学中应注意的问题多媒体课堂教学为主。
适当提问，加深学⽣对概念的理解。
五、正⽂基于数值积分的求解公式：欧拉公式、改进的欧拉公式引⾔1．主要考虑如下的⼀阶常微分⽅程初值问题的求解:00()(,)()y x f x y y x y '=??=?微分⽅程的解就是求⼀个函数y=y(x)，该函数满⾜微分⽅程并且符合初值条件。
2. 例如微分⽅程:xy'-2y=4x ；初始条件: y(1)=-3。
于是可得⼀阶常微分⽅程的初始问题24(1)3y y x y ?'=+=-?。
显然函数y(x)=x 2-4x 满⾜以上条件,因⽽是该初始问题的微分⽅程的解。
3. 但是,只有⼀些特殊类型的微分⽅程问题能够得到⽤解析表达式表⽰的函数解，⽽⼤量的微分⽅程问题很难得到其解析解，有的甚⾄⽆法⽤解析表达式来表⽰。
因此，只能依赖于数值⽅法去获得微分⽅程的数值解。
4．微分⽅程的数值解：设微分⽅程问题的解y(x)的存在区间是[a,b]，初始点x 0=a ，将[a,b]进⾏划分得⼀系列节点x 0 , x 1 ,...,x n ，其中a= x 0< x 1<…< x n =b 。
y(x)的解析表达式不容易得到或根本⽆法得到，我们⽤数值⽅法求得y(x)在每个节点x k 的近似值y(x k )，即 y≈y(x k )，这样y 0 , y 1 ,...,y n 称为微分⽅程的数值解。
如果计算y n 时，只利⽤y n-1，称这种⽅法为单步法；如果在计算y n 时不仅利⽤y n-1，⽽且还要利⽤y n-2, y n-3,…, y n-r ,则称这种⽅法为r 步⽅法，也称多步法。
常微分方程欧拉算法
常微分方程欧拉算法欧拉算法的基本思想是将求解区域分割成若干小的线段，通过在每个线段上使用切线逼近原函数的值，从而得到一个近似的解。
具体而言，假设要求解的微分方程为:dy/dx = f(x, y), a ≤ x ≤ b, y(a) = y0其中f(x,y)为给定的函数，a和b为所求解区域的起点和终点，y(a)为初值条件。
将求解区域[a,b]分割为n个等长的子区间，每个子区间的长度为h=(b-a)/n。
令x_i=a+i*h和y_i=y(x_i)为第i个子区间的近似解。
对于第i个子区间，根据微分方程dy/dx = f(x, y)可以得到差分方程:(y_{i+1}-y_i)/h=f(x_i,y_i)整理得到:y_{i+1}=y_i+h*f(x_i,y_i)这就是欧拉算法的迭代公式。
通过不断迭代上述公式，可以逐步求得整个求解区域[a,b]上的近似解y_i。
欧拉算法的实现非常简单，只需要根据迭代公式进行计算即可。
具体算法如下：1. 输入所要求解的微分方程dy/dx = f(x, y)，求解区域[a, b]，初值条件y(a) = y0和分割的子区间数n。
2.计算子区间长度h=(b-a)/n。
3.初始化变量x=a和y=y0。
4.循环执行以下步骤，从i=0到n-1：(a)计算y_{i+1}=y_i+h*f(x_i,y_i)。
(b)更新x_i+1=x_i+h。
(c)将y_{i+1}作为下一个子区间的近似解，即y_i=y_{i+1}。
5.输出求得的近似解y_i。
需要注意的是，欧拉算法是一种一阶的数值方法，其精度比较有限。
当子区间长度足够小时，欧拉算法可以得到较为精确的近似解；但当子区间长度增加时，误差也会逐渐积累，从而导致求解结果的不准确。
因此，在实际应用中，需要根据具体的问题选择合适的子区间数来平衡精度和计算效率。
欧拉算法的优点是简单易懂、易于实现，并且在一些简单的微分方程求解中可以得到较好的结果。
然而，在需要高精度的求解问题中，欧拉算法显然不够优秀。
常微分方程欧拉方法
常微分方程欧拉方法常微分方程欧拉方法是一种求解常微分方程数值解的方法。
常微分方程是描述物理、工程等领域中许多现象和问题的数学模型，求解常微分方程的数值方法在实际问题中具有重要的应用价值。
欧拉方法是求解常微分方程的一种简单直观的数值方法，它的基本思想是将微分方程转化为差分方程，通过迭代计算得到数值解。
欧拉方法的基本原理是通过一阶泰勒展开近似替代微分方程中的导数项，从而将微分方程转化为差分方程。
对于一阶常微分方程dy/dx=f(x,y)，欧拉方法的迭代公式为y_(n+1) = y_n + h * f(x_n,y_n)，其中h是步长，n为迭代次数。
欧拉方法根据初始条件y_0和步长h，通过迭代计算得到一系列的近似解y_1, y_2, ..., y_n。
欧拉方法的主要优点是简单易实现，计算量较小。
它适用于求解线性常微分方程或近似线性的非线性方程，并且对于一些简单的物理问题，欧拉方法的数值解能够提供较好的近似结果。
然而，欧拉方法也存在一些局限性，由于其基于一阶近似，所以在步长较大的情况下误差较大，容易积累，导致数值解的精度下降。
因此，在使用欧拉方法时需要控制好步长大小，选择合适的迭代次数，从而保证数值解的准确性。
在实际问题中，欧拉方法可以通过多种方式进行改进。
比如改进的欧拉方法（改进的欧拉方法也被称为向前欧拉法）使用角标n+1/2的数据点估计导数，这样可以提高数值解的精度。
此外，也可以使用自适应步长策略来自动调整步长大小，从而提高数值解的准确性。
还可以结合其他数值方法，如Runge-Kutta方法等，进行数值求解。
总结起来，常微分方程欧拉方法是一种简单直观的数值求解方法，但在实际应用中需要注意步长的选择和积累误差的处理。
在对于线性常微分方程或近似线性的非线性方程的求解中，欧拉方法能够给出较好的近似解，但在复杂的非线性方程求解中，通常需要结合其他数值方法使用。
常微分方程 欧拉法
常微分方程欧拉法常微分方程是数学中的一个重要分支，它研究的是描述自然现象中变化规律的方程。
欧拉法是解常微分方程数值解法中的一种方法，它是一种基于欧拉公式的一阶数值方法，可以用于求解一些简单的常微分方程，下面我们将详细介绍欧拉法的原理和应用。
一、欧拉法的原理欧拉法是一种基于欧拉公式的一阶数值方法，它是一种比较简单的数值解法，适用于求解一些简单的常微分方程。
欧拉法的基本思想是将微分方程的求解问题转化为一个逐步逼近的问题，即将求解的区间分成若干个小区间，然后在每个小区间内用欧拉公式逐步逼近解。
欧拉公式是一个一阶泰勒公式，它的表达式为：$$y_{n+1}=y_n+hf(x_n,y_n)$$其中，$y_n$表示在$x_n$处的解，$h$表示步长，$f(x_n,y_n)$表示微分方程在$(x_n,y_n)$处的导数。
欧拉法的基本思想是根据欧拉公式逐步逼近解，即从初始点开始，依次计算每一个点的解，直到求得终止点的解。
欧拉法的步骤如下：1. 确定初始点$(x_0,y_0)$和终止点$(x_n,y_n)$以及步长$h$。
2. 根据欧拉公式计算下一个点的解$y_{n+1}$。
3. 重复步骤2，直到求得终止点的解。
二、欧拉法的应用欧拉法是一种比较简单的数值解法，适用于求解一些简单的常微分方程。
下面我们将通过一个实例来介绍欧拉法的应用。
例子：求解微分方程$y'=x+y$，$y(0)=1$在$x=1$处的解。
解：根据欧拉公式，我们可以得到：$$y_{n+1}=y_n+hf(x_n,y_n)$$将微分方程代入公式中，得到：$$y_{n+1}=y_n+h(x_n+y_n)$$根据初始条件$y(0)=1$，我们可以得到：$$y_1=y_0+h(0+1)=1+h$$$$y_2=y_1+h(1+y_1)=1+2h+h^2$$$$y_3=y_2+h(2+y_2)=1+3h+3h^2+h^3$$$$y_4=y_3+h(3+y_3)=1+4h+6h^2+4h^3+h^4$$将$h=0.1$代入上述公式中，我们可以得到：$$y_1=1.1$$$$y_2=1.21$$$$y_3=1.331$$$$y_4=1.4641$$因此，在$x=1$处的解为$y(1)=1.4641$。
常微分方程数值解算法
常微分方程数值解算法常微分方程是在物理、经济、生物、环境科学等领域中最基本的数学工具之一。
为了解决实际问题，需要求解这些方程的解。
但是，大部分常微分方程是无法求得解析解的，因此需要通过数值方法来求解。
在数值方法中，其基本思想是将微分方程化为一个逐步求解的问题。
通过离散化得到一个差分方程，然后通过数值方法求解这个差分方程。
本文将就常微分方程的数值解算法进行介绍和探讨。
1.欧拉方法欧拉方法是最基本的一种常微分方程数值解方法。
它的基本思想是将微分方程化为差分方程。
欧拉方法是一种一阶的显式方法。
通过计算当前点处的斜率即可进行逼近。
如下所示：y(t + h) = y(t) + hf(t, y(t))其中，h是步长。
f(t, y)是微分方程右边的函数。
欧拉方法的由来是其是以欧拉为名的。
这种方法的优点是简单明了，易于理解。
但是，其与真实解的误差随着步长增大而增大，误差不精，计算速度较慢等缺点也使其并非一个完美的数值解方法。
2.改进的欧拉方法改进的欧拉方法被认为是欧拉方法的一个进化版。
它是二阶数值方法，明显优于欧拉方法。
其基本思想是通过步长的平均值h/2来进行逼近。
y(t + h) = y(t) + h[ f(t, y(t)) + f(t + h, y(t) + hf(t, y(t))/2) ]其优点是能够更准确地逼近微分方程的解，只比欧拉方法多计算一些，但是其步长的误差随着步长增大而减小，并且计算速度比欧拉方法稍快。
因此，改进的欧拉方法是比欧拉方法更好的方法，效果相对较好。
3.龙格库塔方法龙格库塔方法是一种经典的数值解方法。
对于非刚性的方程可以得到较为精确的数值解。
其算法思路是利用多阶段迭代的方式，求解一些重要的插值点，并利用插值点的结果来逼近方程的解。
其公式如下：y(t + h) = y(t) + (h/6)*(k1 + 2k2 + 2k3 + k4)其中，k1 = f(t, y(t))k2 = f(t + h/2, y(t) + h/2k1)k3 = f(t + h/2, y(t) + h/2k2)k4 = f(t + h, y(t) + hk3)其优点是更精确，计算速度更快。
用欧拉方法求解常微分方程组
用欧拉方法求解常微分方程组欧拉方法是求解常微分方程组的一种数值解法。
当解析解难以求得时，我们可以通过数值方法来近似求解。
欧拉方法是一种简单粗暴的方法，它的基本思想是将微分方程在一段区间内用直线逼近，然后通过不断迭代来逼近解。
我们来看一个简单的一阶常微分方程，y’=y，初始条件为y(0)=1。
通过欧拉方法，我们可以将其离散化为y(n+1)=y(n)+hf(y(n))，其中h为步长。
我们从初始点开始，以步长h不断向前迭代，即可得到y(1)=y(0)+hy(0)=2，y(2)=y(1)+hy(1)=2.718，y(3)=y(2)+hy(2)=4.669…，一次迭代可以得到一个新的解点，通过不断迭代，我们可以逼近真正的解。
欧拉方法的原理简单易懂，但是由于直线逼近的误差会随着步长的增大而增大，所以我们需要选择合适的步长来保证精度。
此外，欧拉方法只适用于简单的一阶线性常微分方程，对于高阶、非线性方程的求解并不是很有效。
接下来，我们来看如何用欧拉方法求解二阶常微分方程。
我们将其离散化，得到y(n+1)=y(n)+hy’(n)，y’(n+1)=y’(n)+hf(y’(n),y(n))，其中y(n)表示y在第n个步长的值，y’(n)表示y’在第n个步长的值，f(y’,y)表示微分方程右侧的函数，它可以由高阶常微分方程离散化得到。
同样的，通过不断迭代，我们可以得到y(n)和y’(n)的数值解。
不难发现，欧拉方法的复杂度为O(N)，其中N表示步数，所以当步数较大时，欧拉方法的计算复杂度较高，同时误差也会增大。
因此，我们需要选择合适的步长来保证精度，一般可以使用控制误差的算法来自适应地调整步长。
总的来说，欧拉方法是一种简单易懂，实现容易的数值解法。
虽然它的精度在高精度和高维度的情况下并不是很高，但对于一些简单的常微分方程组求解还是非常有效的。
常微分方程数值解法
常微分方程数值解法常微分方程是研究函数的导数与自变量之间的关系的数学分支，广泛应用于物理、工程、生物等领域的建模与分析。
在实际问题中，我们常常遇到无法通过解析方法求得精确解的常微分方程，因此需要利用数值解法进行求解。
本文将介绍几种常用的常微分方程数值解法。
一、欧拉方法(Euler's Method)欧拉方法是最基本的数值解法之一。
它的思想是将微分方程转化为差分方程，通过逐步逼近解的方式求得数值解。
具体步骤如下：1. 将微分方程转化为差分方程：根据微分方程的定义，可以得到差分方程形式。
2. 选择步长：将自变量范围进行离散化，确定步长h。
3. 迭代计算：根据差分方程递推公式，利用前一步的数值解计算后一步的数值解。
二、改进的欧拉方法(Improved Euler's Method)改进的欧拉方法通过使用欧拉方法中的斜率来进行更准确的数值计算。
具体步骤如下：1. 计算欧拉方法的斜率：根据当前节点的数值解计算斜率。
2. 根据斜率计算改进的数值解：将得到的斜率代入欧拉方法的递推公式中，计算改进的数值解。
三、龙格-库塔方法(Runge-Kutta Method)龙格-库塔方法是一类常微分方程数值解法，其中最著名的是四阶龙格-库塔方法。
它通过计算各阶导数的加权平均值来逼近解，在精度和稳定性方面相对较高。
具体步骤如下：1. 计算每一步的斜率：根据当前节点的数值解计算每一步的斜率。
2. 计算权重：根据斜率计算各个权重。
3. 计算下一步的数值解：根据计算得到的权重，将其代入龙格-库塔方法的递推公式中，计算下一步的数值解。
四、多步法(多步差分法)多步法是需要利用多个前面节点的数值解来计算当前节点的数值解的数值方法。
常见的多步法有Adams-Bashforth法和Adams-Moulton法。
具体步骤如下：1. 选择初始值：根据差分方程的初始条件，确定初始值。
2. 迭代计算：根据递推公式，利用前面节点的数值解计算当前节点的数值解。
常微分方程初值问题的数值解法
常微分方程初值问题的数值解法在实际应用中，对于某些微分方程，我们并不能直接给出其解析解，需要通过数值方法来求得其近似解，以便更好地理解和掌握现象的本质。
常微分方程初值问题（IVP）即为一种最常见的微分方程求解问题，其求解方法有多种，本文将对常微分方程初值问题的数值解法进行较为详细的介绍。
一、欧拉法欧拉法是最基本的一种数值解法，它采用泰勒级数展开并截断低阶项，从而获得一个差分方程近似求解。
具体来讲，设 t 为独立变量，y(t) 为函数 y 关于 t 的函数，方程为：$$y'(t) = f(t, y(t)), \qquad y(t_0) = y_0$$其中 f(t,y(t)) 为已知的函数，y(t_0) 为已知的初值。
将函数 y(t) 进行泰勒级数展开：$$y(t+h) = y(t) + hf(t, y(t)) + O(h^2)$$其中 h 表示步长，O(h^2) 表示其他高阶项。
为了使误差较小，一般取步长 h 尽可能小，于是我们可以用欧拉公式表示数值解：$$y_{n+1} = y_n + hf(t_n, y_n), \qquad y_0 = y(t_0)$$欧拉法的优点是容易理解和实现，但是由于截取低阶项且使用的单步法，所以误差较大，精度较低，在具体应用时需要慎重考虑。
二、龙格-库塔法龙格-库塔法（Runge-Kutta method）是一种多步法，比欧拉法更加精确。
龙格-库塔法的主要思想是使用不同的插值多项式来计算近似解，并且将时间步长分解，每次计算需要多次求解。
以下简要介绍二阶和四阶龙格-库塔法。
二阶龙格-库塔法将时间步长 h 分解成两步 h/2，得到近似解表达式：$$\begin{aligned} k_1 &= hf(t_n, y_n)\\ k_2 &= hf(t_n+h/2,y_n+k_1/2)\\ y_{n+1} &= y_n+k_2+O(h^3)\\ \end{aligned}$$四阶龙格-库塔法四阶龙格-库塔法是龙格-库塔法中应用最为广泛的一种方法，其需要计算的中间值较多，但是具有更高的精度。
常微分方程数值解法-欧拉方法(1)
课题报告题目：常微分方程的数值解法-欧拉方法院 (系)：理学院专业：数学与信息专业指导教师：***组员：艾佳欢(组长) 邓云娜柏茜钟岩刘磊2015 年 5 月 11 日常微分方程数值解法-欧拉方法摘要：从常微分方程数值解的基本概念入手，了解最基本的数值解法--欧拉方法。
并利用欧拉方法显式隐式的特点探究如何求解微分方程，以及欧拉方法的误差分析及校正。
关键词：数值解，欧拉方法，误差，校正ABSTRACT: From the basic concept of numerical solution of ordinary differential equations, and understand the most basic numerical solution of euler method. And by using euler explicitly implicit characteristics and explore how to solve differential equations and the error analysis and correction of euler method.KEYWORDS ：arithmetic solution,Euler's method,error,revise1.初值问题数值解基本概念初值问题的数值解法，是通过微分方程离散化而给出解在某些节点上的近似值。
在[]b a ,上引入节点{}),,1(,:1100n k x x h b x x x a x k k k n nk k =-==<<<=-=称为步长。
在多数情况下，采用等步长，即),1,0(,n k kh a x nab h k =+=-=。
记准确解为)(x y ,记)(k x y 的近似值为k y ,记),(k k y x f 为k f .一阶常微分方程的初值问题⎩⎨⎧=∈=')2.1()()()1.1(),())(,()(0 x y a y b a x x y x f x y ， 若f 在{}〈+∞≤≤=y b x a D ,内连续，且满足Lip 条件：0≥∃L 使2121),(),(y y L y x f y x f -≤-，则初值问题的连续可微解)(x y 在],[b a 上唯一存在，称解)(x y 在节点i x 处的近似值)(i i x y y =为其数值解，该方法称为数值方法。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§1 Euler’s Method
y Pn+1 Pn y(x)
xn
xn+1
x
见上图， 显然，这种近似也有一定误差，
如何估计这种误差y(xn+1) yn+1 ？ 方法同上，基于Taylor展开估计局部截断误差。 但是注意，隐式公式中右边含有f(xn+1 , yn +1 ) , 由于yn +1不准确，所以不能直接用 y' (xn+1)代替f(xn+1 , yn +1 )
§1 Euler’s Method
收敛性
y
( k 1) n 1
yn 1
h (k ) f ( xn 1 , yn 1 ) f ( xn 1 , yn 1 ) 2
k 1
h hL (k ) (0) L yn 1 yn 1 y n 1 yn 1 2 2 2 hL ( k 1) 当 h 时， 1, yn yn 1 ( k ) 1 L 2 在迭代公式中取极限，有 h yn 1 yn f ( xn , yn ) f ( xn 1 , yn 1 ) 2 (k ) 因此yn 的极限就是隐式方程的解 1
y( xn ) O(h3 )
定义 若某算法的局部截断误差为 O(hp+1)，则称该算法有 p 阶精度。 欧拉法具有 1 阶精度。
§1 Euler’s Method
在第2章讨论牛顿插值公式时 介绍了差商的概念和性质， 各阶差商可以近似各阶导数，具有不同的精度， 且可以用函数值来表示。 上一章中数值微分的方法之一 就是用差商近似导数 在xn点用一阶向前差 商近似一阶导数
显然，这种近似有一定误差， 而且步长越大，误差越大， 如何估计这种误差y(xn+1) yn+1 ？
定义 在假设 yn = y(xn)，即第 n 步计算是精确的前提下，考 虑公式或方法本身带来的误差: Rn = y(xn+1) yn+1 , 称为局部 截断误差 /* local truncation error */。
method or backward Euler method*/
§1 Euler’s Method
xn+1点向后差商近似导数
y ( xn 1 ) y ( xn ) y( xn 1 ) h y ( xn 1 ) y ( xn ) hy( xn 1 )
y ( xn ) yn y ( xn 1 ) yn 1 yn h f ( xn 1 , yn 1 )
第五章 常微分方程数值解
/* Numerical Methods for Ordinary Differential Equations */
待求解的问题：一阶常微分方程的初值问题 /* Initial-Value Problem */:
dy f ( x, y) dx y ( a ) y0 x [a , b ]
欧拉法的局部截断误差： 3 h2 Rn1 y( xn1 ) yn1 [ y ( xn ) hy ( xn ) 2 y ( xn ) O(h )]
Rn+1 的主项
/* leading term */
[ yn hf ( xn , yn )]
h2 2
§1 Euler’s Method
隐式欧拉法的局部截断误差：
由微分中值定理，得 f xn 1 , yn 1 f xn 1 , y xn 1 f y xn 1 , yn 1 y xn 1 ,
在yn 1，y xn 1 之间；
如何求解
解析解法：（常微分方程理论） 只能求解极少一类常微分方程；实际中给定的问题不一 定是解析表达式，而是函数表，无法用解析解法。 数值解法: 求解所有的常微分方程 计算解函数 y(x) 在一系列节点 a = x0< x1<…< xn= b 处的近似值
yi y( xi ) (i 1, ... , n)
节点间距 hi xi 1 xi (i 0, ... , n 1) 为步长，通常采用等距节点， 即取 hi = h (常数)。 步进式：根据已知的或已求出的节点上的函数值计算 当前节点上的函数值，一步一步向前推进。因此只需 建立由已知的或已求出的节点上的函数值求当前节点 函数值的递推公式即可。
y ( xn 1 ) y ( xn ) hy ( xn )
Euler’s method
y ( xn 1 ) y ( xn ) y( xn ) h
y ( xn ) yn y ( xn 1 ) yn 1 yn h f ( xn , yn )
欧拉公式的改进： 隐式欧拉法或后退欧拉法 /* implicit Euler
yn1 yn h f ( xn , yn )
n 0, 1,...
--------Euler’s Method
几何意义
几何直观是帮助我们寻 找解决一个问题的思路 的好办法哦 亦称为欧拉折线法
/* Euler’s polygonal arc method*/
§1 Euler’s Method
隐式或后退欧拉公式
0 yn 1 yn h f ( xn , yn ) ( k 1) (k ) y y h f ( x , y n n 1 n 1 ) n 1 收敛性
由于未知数 yn+1 同时出现在等式的两边，故称为隐式 /* implicit */ 欧拉公式，而前者称为显式 /* explicit */ 欧拉公 式。隐式公式不能直接求解，一般需要用Euler显式公式 得到初值，然后用Euler隐式公式迭代求解。因此隐式公 式较显式公式计算复杂，但稳定性好
说明
§1 Euler’s Method
截断误差: 实际上，y(xn) yn， yn 也有误差，它对yn+1的误差 也有影响，见下图。但这里不考虑此误差的影响，仅考虑方 法或公式本身带来的误差，因此称为方法误差或截断误差。
局部截断误差的分析：由于假设yn = y(xn) ，即yn准确，因此 分析局部截断误差时将y(xn+1) 和 yn+1都用点xn上的信息来表 示，工具：Taylor展开。
2
1 1 hf y xn 1 ,
1 hf y xn 1 , h
f x
y
n 1
,
2
1 ( 1 x x 2 ) 1 x
§1 Euler’s Method
2 3 2 h h 2 Rn1 1 hf y xn1 , h f y xn1 , y xn y xn 3 2 h2 h3 y xn 3 f y xn1 , y xn 2 y xn 2 6 h2 Rn1 y xn o(h2 ) 2
§1 Euler’s Method
从而 Rn 1 y ( xn 1 ) yn 1 hf y xn 1 , y xn 1 yn 1 h2 h3 y xn y xn 2 3 即 1 hf x , R y n 1 n 1 h2 h3 y xn y xn 2 3
y( xn ) O(h3 )
§1 Euler’s Method
若将这两种方法进行算术平均，即可消除误差 的主要部分/*leading term*/ 而获得更高的精度,称为梯形法
梯形公式 /* trapezoid formula */
— 显、隐式两种算法的平均
h yn 1 yn [ f ( xn , yn ) f ( xn 1 , yn 1 )] 2
§1 欧拉方法 /* Euler’s Method */
§1 Euler’s Method
y ( xn 1 ) y ( xn ) hy ( xn ) y ( xn ) yn y ( xn 1 ) yn 1 yn h f ( xn , yn )
Taylor展开法
隐式欧拉法的局部截断误差： Rn1 y( xn1 ) yn1 h2 y( xn ) O(h3 )
2
即隐式欧拉公式具有 1 阶精度。
§1 Euler’s Method
比较尤拉显式公式和隐式公式及其局部截断误差
显 式 yn1 yn h f ( xn , yn ) n 0, 1,... 公 3 h2 R y ( x ) y y ( x ) O ( h ) 式 n1 n1 n1 n 2 隐 yn1 yn h f ( xn1 , yn1 ) 式 h2 公 Rn1 y( xn1 ) yn1 2 式
h2 又 f xn 1 , y xn 1 y xn 1 y xn hy xn y xn 2 yn 1 hf y xn 1 , yn 1 y xn 1 y xn 3 h hy xn h 2 y xn y xn 2 而 h2 h3 y xn 1 y xn hy xn y xn y xn 2 6
梯形法的简化计算
§1 Euler’s Method
迭代计算量大，且难以预测迭代次数。为了控制计算量，通常只迭代 一次就转入下一点的计算。用显式公式作预测，梯形公式作校正，得到如
解的存在唯一性（“常微分方程”理论）：只要 f (x, y) 在[a, b] R1 上连续，且关于 y 满足 Lipschitz 条件，即存在与 x, y 无关的常数 L 使 | f ( x, y ) f ( x, y ) | L | y y |