排队模型分析
排队模型——精选推荐
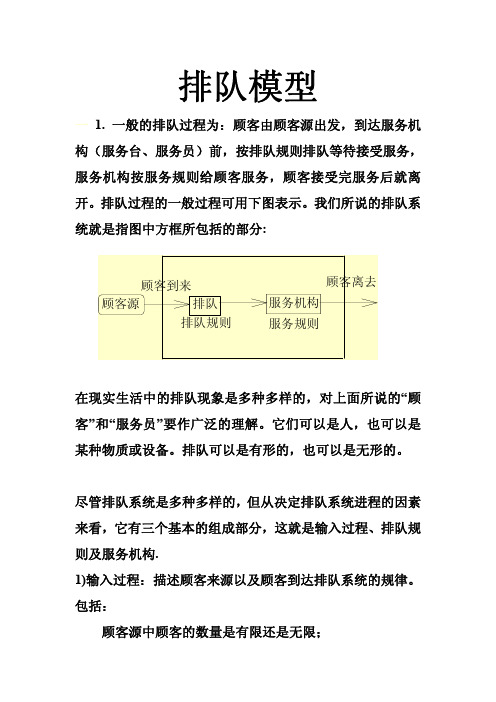
排队模型一 1. 一般的排队过程为:顾客由顾客源出发,到达服务机构(服务台、服务员)前,按排队规则排队等待接受服务,服务机构按服务规则给顾客服务,顾客接受完服务后就离开。
排队过程的一般过程可用下图表示。
我们所说的排队系统就是指图中方框所包括的部分:在现实生活中的排队现象是多种多样的,对上面所说的“顾客”和“服务员”要作广泛的理解。
它们可以是人,也可以是某种物质或设备。
排队可以是有形的,也可以是无形的。
尽管排队系统是多种多样的,但从决定排队系统进程的因素来看,它有三个基本的组成部分,这就是输入过程、排队规则及服务机构.1)输入过程:描述顾客来源以及顾客到达排队系统的规律。
包括:顾客源中顾客的数量是有限还是无限;顾客到达的方式是单个到达还是成批到达;顾客相继到达的间隔时间分布是确定型的还是随机型的,分布参数是什么,是否独立,是否平稳。
2)排队规则:描述顾客排队等待的队列和接受服务的次序。
包括:即时制还是等待制;等待制下队列的情况(是单列还是多列,顾客能不能中途退出,多列时各列间的顾客能不能相互转移);等待制下顾客接受服务的次序(先到先服务,后到先服务,随机服务,有优先权的服务)。
3)服务机构:描述服务台(员)的机构形式和工作情况。
包括:服务台(员)的数目和排列情况;服务台(员)的服务方式;服务时间是确定型的还是随机型的,分布参数是什么,是否独立,是否平稳。
2.到达和服务过程的模型2.1 到达过程的模型用表示第i 个顾客到达的时间,.i t 称为第i 个到达时间间隔.1i i T t t +=−i 我们用的特征来刻画顾客到达过程. 最常见的情况是独立同分布. 用X 表示这样的随机变量.12,,T T 12,,T T 如果X 服从参数为λ的指数分布.这时1()()i E T E X λ==即平均每隔1λ来一个顾客.换句话说,单位时间理平均有λ个顾客到来.称λ为到达速率. 用表示到时刻t 为止到达的顾客总数,则在上面的假设下()N t ()()N t P t λ∼.除了指数分布外,常用的还有爱尔朗分布,其密度函数为1()(), 0.(1)!k RxR Rx e f x x k −−=≥− 这时2(), ()i i k k E T D T R R==. k 叫形状参数, R 叫速率参数.当取λ使得R k λ=, 则爱尔朗分布可以看成是k 个独立的服从参数为λ的指数分布随机变量的和的分布.2.2服务过程的模型一般总是认为不同顾客接受服务占用的时间长短是相互独立的. 用Y表示一个客户接受服务的时间长短, 它是一个随机变量.若Y的分布是参数为μ的指数分布, 意味着一个顾客的服务时间平均为1μ. 单位时间里可以完成的平均顾客数为μ.若Y服从形状参数为k, 速率参数为R kμ=的爱尔朗分布, 则平均服务时间为1μ, 根据爱尔朗分布的性质, 可以将Y看作是k个相继子服务的总时间, 每个子服务都服从参数为1kμ的指数分布且相互独立.在排队论中,我们常用如下字母表示特定的到达时间间隔或服务时间分布:M: i.i.d. 指数分布D: i.i.d. 的确定分布E k: i.i.d. 的形参为k的爱尔朗分布GI: 到达时间间隔是i.i.d. 的某种一般分布G: 服务时间是i.i.d. 的某种一般分布在处理实际排队系统时,需要把有关的原始资料进行统计,确定顾客到达间隔和服务时间的经验分布,然后按照统计学的方法确定符合哪种理论分布。
带优先权排队论模型简介应用案例

0.325 hour
0.033 hour
0.889 hour
0.048 hour
文档仅供参考,如有不当之处,请联系改正。
案例求解 3
即
W1
=W
= Wq
+
1 m
=
Lq l
+
1 m
=
P0(l m)s r s!(1- r)2 l
+
1 m
其中
r= l sm
åé s-1 (l / m)n (l / m)s 1 ù
➢ 非强占性优先权(Nonpreemptive Priorities)——虽然一种高优先级
旳顾客到达,也不能强制让一种正在接受服务旳低优先级顾客返回排队。
➢ 强占性优先权(Preemptive Priorities)——若有高优先级旳顾客到达,
服务员即中断对低优先级顾客旳服务,并立即开始为高优先级顾客服务。
N
l = å li
i=1
r= l m
k
å 【注:】这里假设了 li < sm,
i=1
从而使其能到达稳定状态。
文档仅供参考,如有不当之处,请联系改正。
计算公式 2
抢占性优先权(基于M/M/1)
1/ m
Wk = Bk-1Bk
for k=0,1,2,…,N
文档仅供参考,如有不当之处,请联系改正。
案例求解 3
文档仅供参考,如有不当之处,请联系改正。
案ቤተ መጻሕፍቲ ባይዱ求解 3
W1-1/μ W2-1/μ W3-1/μ
Preemptive Priorities
s=1
s=2
0.024 hour
0.154 hour
排队论问题实验报告(3篇)

第1篇一、实验背景排队论是运筹学的一个重要分支,主要研究在服务系统中顾客的等待时间和服务效率等问题。
在现实生活中,排队现象无处不在,如银行、医院、超市、餐厅等。
通过对排队问题的研究,可以帮助我们优化服务系统,提高顾客满意度,降低运营成本。
本实验旨在通过模拟排队系统,探究排队论在实际问题中的应用。
二、实验目的1. 理解排队论的基本概念和原理。
2. 掌握排队模型的建立方法。
3. 熟悉排队系统参数的估计和调整。
4. 分析排队系统的性能指标,如平均等待时间、服务效率等。
5. 培养运用排队论解决实际问题的能力。
三、实验内容1. 建立排队模型本实验以银行排队系统为例,建立M/M/1排队模型。
该模型假设顾客到达服从泊松分布,服务时间服从负指数分布,服务台数量为1。
2. 参数估计根据实际数据,估计排队系统参数。
假设顾客到达率为λ=2(人/分钟),服务时间为μ=5(分钟/人)。
3. 模拟排队系统使用计算机模拟排队系统,记录顾客到达、等待、服务、离开等过程。
4. 性能分析分析排队系统的性能指标,如平均等待时间、服务效率、顾客满意度等。
四、实验步骤1. 初始化参数设置顾客到达率λ、服务时间μ、服务台数量n。
2. 生成顾客到达序列根据泊松分布生成顾客到达序列。
3. 模拟排队过程(1)当服务台空闲时,允许顾客进入队列。
(2)当顾客进入队列后,开始计时,等待服务。
(3)当服务台服务完毕,顾客离开,开始下一个顾客的服务。
4. 统计性能指标记录顾客等待时间、服务时间、顾客满意度等数据。
5. 分析结果根据实验数据,分析排队系统的性能,并提出优化建议。
五、实验结果与分析1. 平均等待时间根据模拟结果,平均等待时间为2.5分钟。
2. 服务效率服务效率为80%,即每分钟处理0.8个顾客。
3. 顾客满意度根据模拟结果,顾客满意度为85%。
4. 优化建议(1)增加服务台数量,提高服务效率。
(2)优化顾客到达率,降低顾客等待时间。
(3)调整服务时间,缩短顾客等待时间。
第3章 排队模型分析法-3-

/(k-1)
求解平稳分布
平衡方程 由正则性条件:
p1 p0 p0 2 p p p 2 2 1 2! 0 k ρ p pk-1 p0 k k k!
ρk 1 pk p0 e ρ p0 k 0 k 0 k! p0 e ρ ρk ρ pk e k! k 0,1,2,
顾客源中单个顾客的到达率为
当系统中有k个顾客的时候,顾客源中有 (m-k)个顾客,到达率为(m-k)
顾客源中的顾客数m-k (m-k)
系统内的顾客数k
0km
最大顾客数m
M/M/1/m/m的状态流图
m 0 1 (m-1) 2 (m-2) 2 m-1 m
列出状态转移平衡方程:
排队越长,进入可能性越小(令 αk=
1 k 1
);
顾客所需的服务时间序列{n,n1}独立、服从 参数为(>0)的负指数分布; 系统中只有一个服务台; 容量为无穷大,而且到达过程与服务过程彼此 独立。
2.系统状态分析
仍用N(t)表示在时刻t系统中的顾客数,令
pij(t)=P{N(t+t)=j|N(t)=i},i,j=0,1,2,… 则pij(t)的推导有
Wq(t)=P{Wq≤t}
e (t ) 1 , t0 e 1 k 1 (k 1)! j 0 j!
k 1 j
t
k 1
e 1 平均等待时间为: Wq (e 1)
5.逗留时间
类似地,顾客的逗留时间的分布函数为
W(t ) P{W t} P{Wq 0, t} P{0 W t, Wq 0}
M M C ∞排队系统模型及其应用实例分析

M M C ∞排队系统模型及其应用实例分析摘要:文章阐述了M/M/C/∞排队系统的理论基础,包括排队论的概念,排队系统的基本组成部分以及排队系统的模型。
在理论分析的基础上,文章以建行某储蓄所M/M/C/∞排队系统为例,对该系统进行分析并提出了最优解决方案。
关键词:排队论;银行储蓄所;M/M/C/∞模型;最优解1M/M/C/∞排队系统1.1排队论的概念及排队系统的组成上世纪20年代,丹麦数学家、电气工程师爱尔朗(A. K. Erlang)在用概率论方法研究电话通话问题时,开创了这门应用数学学科。
排队论主要研究各种系统的排队队长,排队的等待时间及所提供的服务等各种参数,以便求得更好的服务。
研究排队问题实质上就是研究如何平衡等待时间与服务台空闲时间。
目前,排队论已经广泛应用于通信工程、交通运输、生产与库存管理、计算机系统设计、计算机通信网络、军事作战、柔性制造系统和系统可靠性等众多领域。
任意一个排队系统都是由三个基本部分构成,即输入过程、排队规则和服务机构。
①输入过程是描述顾客来源以及顾客按什么规律达到排队系统。
②排队规则描述的顾客到达服务系统时顾客是否愿意排队,以及在排队等待情形下的服务顺序。
③服务机构描述服务台数目及服务规律。
服务机构可分为单服务台和多服务台;接受服务的顾客是成批还是单个的;服务时间服从何种分布。
1.2M/M/C/∞排队模型①排队系统模型的表示。
目前排队模型的分类采用1953年由D. G. Kendall 提出的分类方法。
他用3个字母组成的符号A/B/C表示排队系统。
为了表示其它特征有时也用4~5个字母来表示如A/B/C/D/E。
其中:A 顾客到达间隔时间的概率分布;B 服务时间的概率分布;C 服务台数目;D 系统容量限制(默认为∞);E 顾客源数目(默认为∞);概率分布的符号表示:M:泊松分布或负指数分布,D:定长分布,Ek:k阶爱尔朗分布,C:一般随机分布。
②排队系统的衡量指标。
排队论模型及实例

例10.5
某售票点有两个售票窗口,顾客按参数λ=8人/分钟的
Poisson流到达,每个窗口的售票时间均服从参数μ=5人/分 钟的负指数分布,试比较以下两种排队方案的运行指标.
(1) 顾客到达后,以1/2的概 率站成两个队列,如 右图所示:
(2) 顾客到达后排成一个队列, 顾客发现哪个窗口空时, 他就
ReQ R(1 Plost )2. (4)系统在单位时间内占用服务台(或服务员)的均值Ls
即理发店的空闲率为134顾客的损失率为279每小时进入理发店的平均顾客数为4328人理发店内的平均顾客数队长为2359人顾客在理发店的平均逗留时间是0545小时327分钟理发店里等待理发的平均顾客数等待队长为1494人顾客在理发店的平均等待时间为0345小时207分例109某工厂的机器维修中心有9名维修工因为场地限制中心内最多可以容纳12台需要维修的设备假设待修的设备按poisson过程到达平均每天4台维修设备服从负指数分布每台设备平均需要2天时间求该系统的各项参数指标
解 只需将上例LINGO程序作如下改动:R=0.6,T=1.25 即 可得到结果.程序名:exam1003.lg4.计算结果见运行.
即平均队长为3人,平均等待队长为2.25人,顾客平均逗留 时间5分钟,顾客平均等待时间为3.75分钟,系统繁忙概率 为0.75.
此时您正浏览在第18页,共47页。
• S>1的情况(M/M/S/∞) 表示有多个服务台或多名服务员服务的情况
排队论模型及实例
此时您正浏览在第1页,共47页。
排队现象是由两个方面构成,一方要求得到服务,另一方设 法给予服务。我们把要求得到服务的人或物(设备)统称为 顾客, 给予服务的服务人员或服务机构统称为服务员或服务 台。顾客与服务台就构成一个排队系统,或称为随机服务系 统。 显然缺少顾客或服务台任何一方都不会形成排队系统.
排队模型(掌握mm1,mmc,mm1k)

19 72 4 8 1 29 106 1 3 1 39 135 2 4 10
20 80 3 1 0 30 109 2 5 0 40 139 4 3 8
21 81 2 2 2 31 114 1 2 0 41 142 1
9
22 83 3 3 2 32 116 8 1 0
到达间隔分布表
到达间隔 次 (分钟) 数
1
6
2
10
3
8
4
6
5
3
6
2
7
2
8
1
9
1
10以上 1
合计 40
服务时间分布表
服务时间 次 (分钟) 数
1
10
2
10
3
7
4
5
5
4
6
2
7
1
8
1
9以上 1
合计 41
平均间隔时间: =142/40=3.55(分钟/人)
平均服务时间: 127/41=3.12(分钟/人)
平均到达率: 41/142=0.28(人/分钟)
14 52 2 9 3 24 88 5 4 6 34 121 2 6 7
15 61 1 1 0 25 92 1 3 7 35 127 1 2 3
16 62 2 3 0 26 95 3 6 5 36 129 6 1 2
17 65 1 5 0 27 101 2 4 2 37 130 3 3 7
18 70 3 2 0 28 105 2 1 0 38 133 5 2 7
三、排队模型的分类(符号表示)
我们采用Kendall记号 顾客相继到达时间间隔分布/服务时间分布/服务 台数目/排队系统允许的最大顾客容量(系统容 量)/顾客总体数量(顾客源数量)/排队规则
07:排队网络模型的性能分析
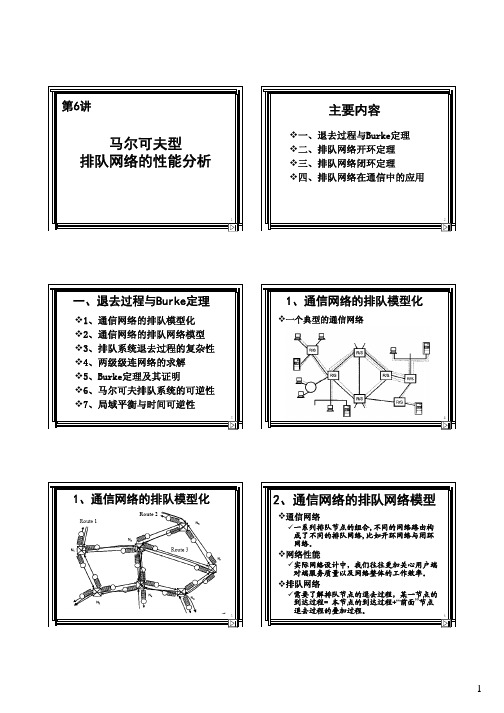
一个典型的通信网络8泊松分布过程的一个例子。
10111522 237、局部平衡与时间可逆性30312、Jackson网络-独立性假设几点独立性假设9相互独立的外部到达、泊松过程9相互独立的服务时间、负指数分布•同一个顾客在不同的排队节点遵循相互独立、且有可能不同参数的负指数分布。
9相互独立的路由策略•在某一节点接受完服务后独立地决定下一节点的路由、或者退出该排队网络。
322、Jackson网络-稳态概率()()()111212,,,,mi i j jij m m i r P I Q r r r λλλγλλλγ−=+Λ−Λ∑L L =对于节点,顾客到达率如下:用矩阵形式可以表示为:=其中:==33111212122212m m m mm m P P P P P P QPP P ⎛⎞⎜⎟⎜⎟=⎜⎟⎜⎟⎜⎟⎝⎠L L M M M M L Q矩阵的性质9对于开环网络来说,至少存在一个节点i有ri>0或者mij 1P 0>∑j=0-343、Jackson定理Jackson 定理9对于一个平稳状态的Jackson网络,在任一节点内的顾客数与其它节点的存在的顾客数无关。
9队长的概率分布Pn=P(n1,n2,…n m )等于每个单个节点队列长度概率分布的积。
353、Jackson定理()()()()()()()121122001100,,,!!!!iii i i i i i mm mn ii i i i i sn s i i i i n s s i i in i i i i ii i iP n n n p n p n p n ap n s n p n a p n s s a a s p n s s a s i a ρλµ−−−==⋅⎧≤⎪⎪=⎨⎪>⎪⎩⎛⎞=+⋅⎜⎟−⎝⎠=∑L L ,,为第个排队节点的服务者数,363、杰克逊网络通信量方程解)非奇异性,存在唯一()=-(则=令稳态总体流量:通信量方程:Q -I Q I }{},{11γλλλλγλγλij i Mi i j Mi jij i i q Q q q ==+=∑∑==iiλiγiq 11λMiM q λ38399虽然外部顾客以泊松过程到达节点i,但实际到达于第i个节点的顾客为非泊松分布过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0.6 1 0.8 那么 3 0.75
1.25
4
1
1
Q
1
1 0.75
0.57
p0
即在稳态时有57%的呼唤得到服务
A
e
1
0.6 1 0.75
0.34
即每条电话线路平均每分钟有0.34次通话
P损 1 Q 1 0.57 0.43
即约43%的呼唤不能接通
00:06:26
00:0❖6:2因6 为到达间隔时间和服务时间都具有无记忆性,因此,4
M/M/…的排队模型
❖ M/M/…的排队系统,系统中顾客数变化是一 种生灭过程
0状态代表系统有0个顾客
1状态代表系统中有1个顾客
2状态代表系统中有2个顾客
…
❖ 生灭过程的增长率和消亡率怎么确定?
增长率取决于到达率和当前系统状态
0消0:06亡:26 率取决于服务率和当前系统状态
5
增长率和消亡率的分析
❖ 假定顾客到达为强度为的泊松流,服务窗的 服务率为,服务时间服从负指数分布。考察 在t(极短)时间内,
若顾客到达间隔时间服从参数为的负指数分布, 则在t(极短)时间内有1个顾客到达的概率为 t+o(t),没有顾客到达的概率为1-t+o(t)
若服务时间服从参数为的负指数分布,则在t
状态0系统中顾客数为0 服务窗空闲 状态1 系统中有1个顾客,此顾客正在接受服务 系统顾客满服务窗忙
00:06:26
12
求解平稳分布
r
Q 0
❖ 根据马氏链、生灭过程求平稳分布的公式:
❖ 列出平p0p衡1 p方1p10程:
1 p0 1
令
p1
1
本书从现在开始用{p0,p1,p2,…}表示平稳分布
00:06:26
13
M/M/1/1的各个目标参量
v P损 p1
v 单位时间内损失的顾客数
L
p1
2
1
v 单位e 时 p间0 内1平均进入系统的顾客数
v 相求对服通务过顾能客力数之Q(比即值单)位Q 时 间e 内 被p0服 务11完的顾客数与请
v 绝对通过能力A(单A位时e 间 内p0被 1服务 完顾客的均值)
00:06:26
10
第一节 单服务窗损失制排队模型
M/M/1/1
00:06:26
11
排队模型分析
❖ M/M/1/1
❖ 顾客到达间隔时间为负指数分布,参数为, a(t) et ❖ 服务窗服务时间为负指数分布,参数为, b(t) et
损失的顾客
0
1
Q
❖ 系统最大顾客数1决定了系统状态为{0,1}
排队模型回顾
❖ 顾客到达排队系统请求服务
服
务
机
排队机构
构
如果排队系统中顾客数没有满,则进入排队系 统
如果有空闲的服务窗,则直接到服务机构接受 服务
00如:06:2果6 服务窗全部被占用,则排队等候
1
M/M..排队系统的几种可能状态
λ0= λ μ0= 0λ2= Βιβλιοθήκη μ2= 2μ00:06:26
假λ如7=此λ 系统容量为7 (M/M/3/7) λ7μ=7=0 3μ μ7= 3μ
00:06:26
14
书44页
M/M/1/1例题
❖ 设某条电话线,平均每分钟有0.6次呼唤,若 每次通话时间平均为1.25分钟,求相应的Q, A与P损
(电话业务我们通常采用M/M/…排队模型)
00:06:26
15
M/M/1/1例题
❖ 设某条电话线,平均每分钟有0.6次呼唤,若每次通话时间 平均为1.25分钟,求相应的Q,A与P损
有顾客到达,系统中顾客数加1 有顾客服务完毕,系统中顾客数减1
总之,顾客的到达和离开致使系统顾客数有变 化
❖ M/M/…的排队系统顾客数变化有什么特点?
顾客到达间隔与顾客服务时间均服从负指数分 布
❖因为顾客到达间隔时间是相互独立的,顾客接受服务 也是相互独立的,因此,之前的顾客到达情况、服务 情况不影响当前顾客数变化概率
00:06:26
7
pii(t)增 P长(t内率到达和了0个消,亡离开率了0个的) 分析
P(t内到达了k个,离开了k个,k 1) et (et ) j o(t)
1 ( j)t o(t)
当i 0时 p00 (t) P(t内到达了0个)
P(t内到达了k个,离开了k个,k 1) et o(t)
16
(极短)时间内有1个正在忙的服务窗服务完当
前顾客的概率是t+o(t), 1个正在忙的服务
0窗0:06没:26 有服务完的概率是1-t+o(t)
6
增长率和消亡率的分析 v i状态下,i状态代表排队系统中有i个顾客,假定此时有j个顾客正在 接受服务(ji),j=i 当i m, j=m 当i>m时,m为服务窗个数
2
排队模型-Kendall记号
A/B/C/D/E
C=D 损失制
顾 服服 客 务务 到 窗窗 达 服个 间 务数 隔时 时间 间的 分分 布布
00:06:26
系顾
统客
中源
允中
许顾
的客
最数
大,
顾默
客 数
认 无 穷
,
默
认
无
穷
队列长度有限 队列最大长度
C<D< 混合制 D= 等待制
3
❖ 考虑整个M排/队M系/…统的中顾排客队数的模变型化
❖ j=m,i>m 系统顾客数大于 服务窗个数时,所有服务窗都在
服务,正在接受服务的顾客数=服务窗个数
00:06:26
9
第三章 单服务窗排队模型
第一节 损失制M/M/1/1 第二节 等待制M/M/1 第三节 混合制M/M/1/m 第四节 可变服务率的M/M/1 第五节 可变输入率的M/M/1 第六节 具有不耐烦顾客的M/M/1 第七节 单服务窗闭合式M/M/1/m/m 第八节 有差错服务的M/M/1
1 t o(t)
00:06:26
8
增长率和消亡率的分析
❖ i
由 此lim,pMi,i/1M(/t…) 型li排m 队模t 型0(,t)在状 态时的增长率和消亡率为:
t0 t
t 0
t
i
lim t 0
pi ,i 1 (t ) t
lim
t 0
jt 0(t)
t
j
j是正在忙的服务窗个数
❖ j=i,im 系统顾客数少于等于服务窗数时,所有顾客都在接 受服务
pi,i1(t) P(t内到达了1个,离开了0个) P(t内到达了k个,离开了k 1个,k 2)
tet (et ) j o(t) t o(t)
pi,i1(t) P(t内到达了0个,离开了1个) P(t内到达了k个,离开了k 1个,k 1)
et C1j tet o(t)
jt o(t)
