初中数学经典试题及答案
数学初中经典试题及答案

数学初中经典试题及答案一、选择题1. 下列哪个选项是方程x^2 - 5x + 6 = 0的解?A. x = 2B. x = 3C. x = 1D. x = 4答案:A2. 如果一个三角形的两边长分别为3和4,且这两边夹角的余弦值为1/2,那么第三边的长度是多少?A. √7B. √13C. √15D. √21答案:C3. 一个数的立方根是它自身的数是?A. 0B. 1C. -1D. 以上都是答案:D二、填空题4. 一个圆的直径是10厘米,那么它的半径是______厘米。
答案:55. 一个长方体的长、宽、高分别为2米、3米、4米,那么它的体积是______立方米。
答案:24三、解答题6. 已知一个等差数列的前三项分别为2,5,8,求这个数列的第10项。
答案:第10项为27。
7. 一个矩形的长是宽的两倍,如果长增加4厘米,宽增加1厘米,那么面积增加24平方厘米,求原来矩形的长和宽。
答案:原来矩形的长为8厘米,宽为4厘米。
四、证明题8. 证明:如果一个三角形的两边相等,那么这两边所对的角也相等。
答案:设三角形ABC中,AB=AC,根据等边对等角的性质,可以得出∠B=∠C,从而证明命题成立。
五、应用题9. 一个农场主有一块矩形的土地,长是宽的3倍,如果长增加20米,宽增加10米,那么面积增加600平方米。
求原来矩形土地的长和宽。
答案:原来矩形土地的长为90米,宽为30米。
10. 一个班级有40名学生,其中男生人数是女生人数的1.5倍。
求男生和女生各有多少人。
答案:男生有24人,女生有16人。
数学初中经典试题及答案

数学初中经典试题及答案一、选择题(每题3分,共30分)1. 已知一个数的平方等于36,这个数可能是:A. 6B. -6C. 6或-6D. 以上都不是2. 一个三角形的两边长分别为3和5,第三边长为:A. 2B. 4C. 6D. 83. 计算下列表达式的值:\((-3) \times (-2)\)A. 6B. -6C. 3D. -34. 一个圆的半径为5厘米,那么它的面积是:A. 78.5平方厘米B. 25平方厘米C. 78.5平方分米D. 25平方分米5. 以下哪个是等腰三角形?A. 三边长分别为3, 4, 5B. 三边长分别为5, 5, 5C. 三边长分别为2, 3, 4D. 三边长分别为1, 2, 36. 一个数的绝对值是5,这个数可能是:A. 5B. -5C. 5或-5D. 以上都不是7. 计算下列表达式的值:\((-2)^2\)A. 4B. -4C. 2D. -28. 一个直角三角形的两条直角边长分别为6和8,那么斜边长为:A. 10B. 14C. 16D. 209. 一个数的立方等于-64,这个数是:A. 4B. -4C. 2D. -210. 计算下列表达式的值:\((-1)^3\)A. 1B. -1C. 3D. -3二、填空题(每题2分,共20分)1. 一个数的相反数是-7,这个数是________。
2. 一个数的倒数是\(\frac{1}{3}\),这个数是________。
3. 一个数的平方根是4,这个数是________。
4. 一个数的立方根是2,这个数是________。
5. 一个等差数列的首项是2,公差是3,那么第5项是________。
6. 一个等比数列的首项是3,公比是2,那么第3项是________。
7. 一个直角三角形的斜边长是10,一个直角边长是6,那么另一个直角边长是________。
8. 一个圆的直径是10厘米,那么它的周长是________厘米。
9. 一个数的绝对值是8,这个数是________或________。
初中数学几何证明经典试题(含答案)

初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF =GOGH=COCD,又CO=EO,所以CD=GF得证。
AFGCEBOD2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF =GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF =GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDB3、如图,已知四边形ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点.求证:四边形A2B2C2D2是正方形.(初二)4、已知:如图,在四边形ABCD中,AD=BC,M、NBC的延长线交MN于E、F.求证:∠DEN=∠F.D2C2B2A2D1C1B1C BD AA1经典题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.(初二)2、设MN是圆O外一直线,过O作OA⊥MN于A,自A及D、E,直线EB及CD分别交MN于P、Q.求证:AP=AQ.(初二)F3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,B 、D .求证:AB =DC ,BC =AD .(初三)经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求:∠APB 的度数.(初二)2、设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)3、设ABCD为圆内接凸四边形,求证:AB·CD+AD·BC=AC·BD.(初三)4、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a4、如图,△ABC 中,∠ABC =∠ACB =800,D、E 分别是AB 、AC 0∠EBA =200,求∠BED 的度数.经典题(一)1.如下图做GH ⊥AB,连接EO 。
初中数学几何证明经典题(含答案)
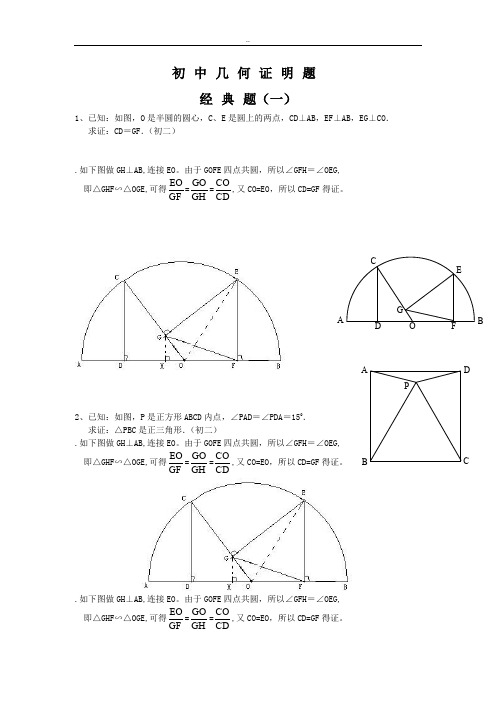
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 BF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC点P 是EF 的中点.求证:点P 到边AB 的距离等于AB的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、证:AB =DC ,BC =AD .(初三)经典1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA =200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学几何证明经典试题(含答案)
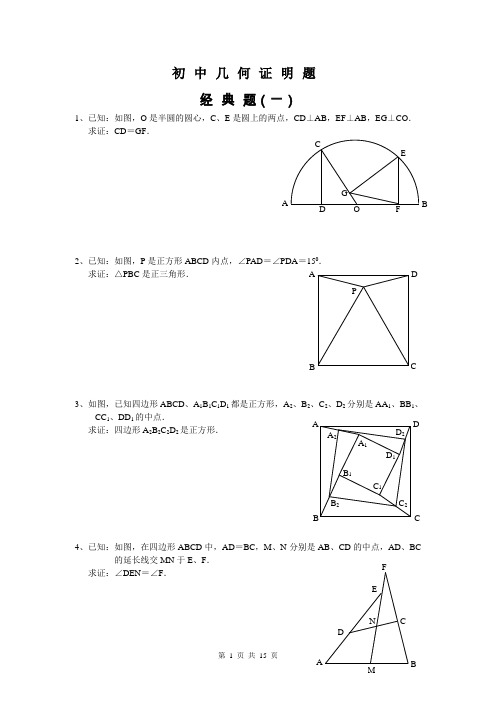
初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .3、设P 是正方形ABCD 一边求证:PA =PF .4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF B、D .求证:AB =DC ,BC =AD .经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求:∠APB 的度数.2、设P是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC·4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC , 求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDEDCB AA CBPD经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学经典几何题及答案
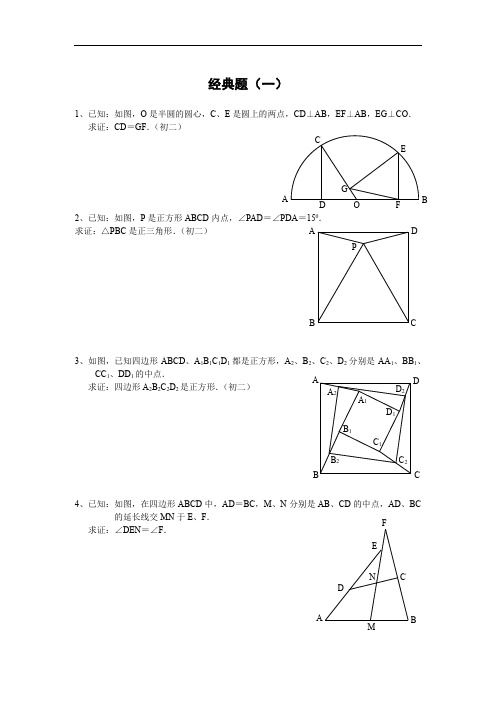
经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A FG CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 A N FE CDMBP CG FB QA D E1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE 分别交于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)· A D HE M C B O · GAO D B EC Q P NM · O Q PB DEC N M · A1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)D AF D E C B E DA CB F F EP C B A O D BFAECP1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)AP C B P A D CB CB DAFPDE CBA1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.AP CB ACBPDEDCB A A CBPD1.如下图做GH⊥AB,连接EO。
初中数学几何证明经典试题(含答案)
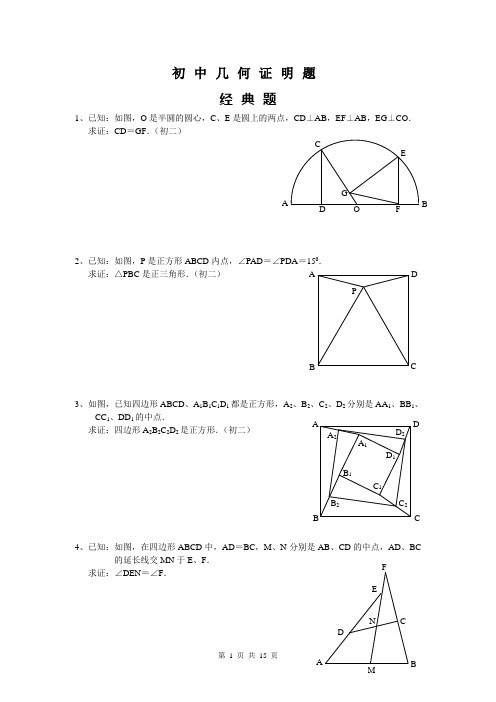
初中几何证明题经典题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC=AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC , 求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDEDCB AA CBPD经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学几何证明经典试题(含答案)

初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 A N FE CDMB · A HEOF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC求证:P A =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,D .求证:AB =DC ,BC =AD.(初三)经典1、已知:△ABC 是正三角形,P 是三角形内一点,P A =3,PB =4,求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.C BD A F PD E CB A APCBACBPDA CBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学经典试题、选择题:1、图(二)中有四条互相不平行的直线L1、L2、L3、L4所截出的七个角。
关于这七个角的度数关系,下列何者正确?()A.2=4+7 B.3=1+6C.1+4+6=180 D.2+3+5=360答案: C.2、在平行四边形ABCD中,AB=6,AD=8,∠ B 是锐角,将△ ACD沿对角线AC折叠,点D落在△ ABC所在平面内的点 E 处。
如果AE过BC的中点,则平行四边形ABCD的面积等于()A 、48 B 、10 6C 、12 7D 、24 2答案: C.3、如图,⊙ O中弦AB、CD相交于点F,AB=10,AF=2。
若CF∶DF=1∶4,则CF 的长等于()A 、2B 、 2C 、3D 、 2 2答案: B.4、如图:△ ABP与△ CDP是两个全等的等边三角形,且PA⊥PD。
有下列四个结论:①∠PBC=150;② AD∥BC;③直线PC与AB垂直;④四边形ABCD是轴对称图形。
其中正确结论的个数为()2311A 、1B 、 2C 、 3D 、 4答案: D.5、如图,在等腰 Rt △ABC 中,∠ C=90o , AC=8,F 是 AB 边上的 中点,点 D 、E 分别在 AC 、BC 边上运动,且保持 AD=CE ,连接 DE 、 DF 、EF 。
在此运动变化的过程中,下列结论: ① △ DFE 是等腰直角三角形; ② 四边形 CDFE 不可能为正方形; ③ DE 长度的最小值为 4;④ 四边形 CDFE 的面积保持不变;⑤△ CDE 面积的最大值为 8 。
其中正确的结论是( )A .①②③B .①④⑤C .①③④D .③④⑤ 答案: B.二、填空题:6、已知 0 x 1.(1) 若 x 2y 6,则 y 的最小值是 (2). 若 x 2 y 2 3 , xy 1,则 x y =.答案:(1)-3 ;(2)-1.7、用 m 根火柴可以拼成如图 1 所示的 x 个正方形,还可以拼成如图 2 所示的 2y 个正方形,那么用含 x 的代数式表示 y ,得 y = ____________ .答案:31 y = x -55 2 218、已知 m 2- 5m -1= 0,则 2m 2- 5m + 2=.m 答案: 28.9、 ____________________ 范围内的有理数经过四舍五入得到的近似数答案:大于或等于且小于 .10、如图:正方形 ABCD 中,过点 D 作 DP 交 AC 于点 M 、 交 AB 于点 N ,交 CB 的延长线于点 P ,若 MN = 1,PN = 3, 则 DM 的长为 .11、在平面直角坐标系 xOy 中,直线 y x 3 与两坐标轴围成一个△ AOB 。
现将背面完全图11、2、3、1、1的 5 张卡片洗匀后,背面朝上,从中任取一张,将相同,正面分别标有数23该卡片上的数作为点 P 的横坐标,将该数的倒数作为点 P 的纵坐标,则点 P 落在△ AOB 内的 概率为 .3答案: 3.512、某公司销售 A 、B 、C 三种产品,在去年的销售中,高新产品 C 的销售金额占总销售金额 的 40%。
由于受国际金融危机的影响,今年 A 、 B 两种产品的销售金额都将比去年减少 20%, 因而高新产品 C 是今年销售的重点。
若要使今年的总销售金额与去年持平, 那么今年高新产 品 C 的销售金额应比去年增加 %. 答案: 30.13、小明背对小亮按小列四个步骤操作:(1)分发左、中、右三堆牌,每堆牌不少于两张,且各堆牌现有的张数相同;(2)从左边一堆拿出两张,放入中间一堆; ( 3)从右边一堆拿出两张,放入中间一堆; ( 4) 左边一堆有几张牌,就从中间一堆拿几张牌放入左边一堆,当小亮知道小明操作的步骤后, 便准确地说出中间一堆牌现有的张数,你认为中间一堆牌现有的张数是 . 答案: 6.14、某同学在使用计算器求 20 个数的平均数时,错将 88 误输入为 8,那么由此求出的平均 数与实际平均数的差为 .答案: -4.三、解答题:16、若 a 、b 、c 为整数,且 a b c a 1,求 a b b c c a 的值 . 答案: 2.17、方程(2008x )2 2007 2009x 1 0 的较大根为 a ,方程 x 2 2008x 2009 0 的 较小根为 b ,求 (a b )2009 的值 .解:把原来的方程变形一下,得到:(2008x )2- ( 2008-1 )( 2008+1) X-1=020082x2- 20082x +x-1=0 20082x ( x-1 ) +( x-1 ) =0(20082x +1)( x-1 )=0x=1 或者- 1/20082,那么 a=1.第二个方程:直接十字相乘,得到: (X+1)( X-2009 ) =0 所以 X=-1 或 2009,那么 b=-1.所以 a+b=1+(-1)=0 ,即 (a b )2009 =0.15、在平面直角坐标系中,圆心 (1) (2) (3) (4) 当 当 当 当时,圆 时,圆 时,圆时,圆 O 的坐标为 O 与坐标轴有O 与坐标轴有O 与坐标轴-3 ,4),以半径 r 在坐标平面内作圆,1 个交点;2 个交点;3 个交点;4 个交点; 答案: 1)r=3 ; (2)3<r <4; 3) r=4 或 5; (4)r >4 且 r ≠5.18、在平面直角坐标系内,已知点 A (0, 6)、点 B ( 8,0),动点 P 从点 A 开始在线段 AO上以每秒 1个单位长度的速度向点 O 移动,同时动点 Q 从点 B 开始在线段 BA 上以每秒 2 个 单位长度的速度向点 A 移动,设点 P 、Q 移动的时间为 t 秒.(1) 求直线 AB 的解析式;(2) 当 t 为何值时,以点 A 、P 、 Q 为顶点的三角形△ AOB 相似?(3) 当 t=2 秒时,四边形 OPQB 的面积多少个平方单位? 解:(1) 设直线 AB 的解析式为: y=kx+b解得 kb63直线 AB 的解析式为:y x 64(2) 设点 P 、Q 移动的时间为 t 秒,OA=6,OB=8. ∴勾股定理可得, 分两种情况, ① 当△ APQ ∽△ AOB 时② 当△ AQP ∽△ AOB 时AQ AO 10 2t 6 30 , , tAP AB t 10 13 33 301331 或 t 1330时,以点 A 、P 、Q 为顶点的三角形△(3) 当 t=2 秒时,四边形 OPQB 的面积,AP=2,AQ=6过点 Q 作 QM ⊥ OA 于 M19、某中学新建了一栋 4层的教学大楼, 每层楼有 8间教室, 进出这栋大楼共有 4道门,其中两道正门大小相同,两道侧门大小也相同。
安全检查中, 对 4 道门进行了测试: 当同时开 启一道正门和两道侧门时, 2 分钟内可以通过 560 名学生;当同时开启一道正门和一道侧门 时, 4 分钟内可以通过 800 名学生。
(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生? (2)检查中发现,紧急情况时因学生拥挤,出门的效率将降低 20%。
安全检查规定:在紧急情况下全大楼的学生应在 5 分钟内通过这 4 道门安全撤离。
假设这栋教学大楼每间教室最 多有 45名学生,问:建造的这 4 道门是否符合安全规定?请说明理由。
解:(1)设平均每分钟一道正门可以通过 x 名学生,一道侧门可以通过 y 名学生,由题意得:将点 A (0, 6)、点 B (8,0)代入得6 k 0 b0 8k bAB=10 ∴ AP=t ,AQ=10-2tAP AO , t AQ AB , 10 2t1033 11AOB 相似.∴AQ QM6 QMQM=AB OB10 8△APQ 的面积为: 1 AP QM 1 2 4.822综上所述,当 t x△AMQ ∽△AOB4.8( 平方单位 ) ∴四边形 OPQB 的面积为: S △AOB -S △APQ ==( 平方单位 )2(x 2y) 5604(x y) 800 x 120 解得:y 80 答:平均每分钟一道正门可以通过120 名学生,一道侧门可以通过80 名学生。
(2)这栋楼最多有学生4×8×45=1440(名)拥挤时 5 分钟 4 道门能通过: 5 2(120 80)(1 20%)=1600(名)∵1600> 1440∴建造的 4 道门符合安全规定。
220、已知抛物线y x (m 4)x 2m 4与x轴交于点A(x1,0)、B(x2 ,0)两点,与y轴交于点C,且x1<x2,x1+2x2=0。
若点A关于y轴的对称点是点D。
(1)求过点C、B、D的抛物线的解析式;(2)若P是(1)中所求抛物线的顶点,H是这条抛物线上异于点C的另一点,且△ HBD与△CBD的面积相等,求直线PH的解析式。
x12x20x1x2m4x1x22m 4解:(1)由题意得:(m4) 2 4(2m4) m2 32 0由①②得:x12m8,x2 m4将x1 、x2 代入③得:(2m 8)( m4) 2m 4整理得:2m2 9m 14 0∴ m1 =2,m2 =7∵ x1 < x2∴ 2m 8 < m 4∴m<4 ∴ m2 =7(舍去)∴ x1=-4,x2 =2,点 C 的纵坐标为:2m 4=8∴A、B、C三点的坐标分别是A(-4,0)、B(2,0)、C(0,8)又∵点 A 与点D关于y轴对称∴D(4,0)设经过C、B、D的抛物线的解析式为:y a(x 2)(x 4)将C(0,8)代入上式得:8a(02)(0 4)∴ a=1∴所求抛物线的解析式为:y2 x 6x 822 2)∵y x 6x 8 =(x 3) ∴顶点P( 3,-1)1设点H的坐标为H(x0,y0)∵△ BCD与△ HBD的面积相等∴∣ y0∣=8∵点H只能在x 轴的上方,故y0=8将y0 =8 代入y x 6x8中得:x0=6或x0 =0(舍去)∴H(6,8)设直线PH的解析式为:y kx b则3k b16k b8解得:k=3 b =-10∴直线PH的解析式为:y3x1021、已知:如图,在直角梯形ABCD中,AD∥BC,∠ABC=90,o DE⊥ AC 于点F,交BC于点G,交AB的延长线于点E,且AE=AC。
(1)求证:BG=FG;(2)若AD=DC=,2 求AB 的长。
证明:(1)连结EC,证明略(2)证明⊿ AEC是等边三角形,AB= 322、某电视机生产厂家去年销往农村的某品牌电视机每台的售价y(元)与月份x 之间满足函数关系y 50x 2600 ,去年的月销售量p (万台)与月份x 之间成一次函数关系,其中两个月的销售情况如下表:月份1月5月销售量万台万台(1)求该品牌电视机在去年哪个月销往农村的销售金额最大?最大是多少?(2)由于受国际金融危机的影响,今年1、2 月份该品牌电视机销往农村的售价都比去年12 月份下降了m% ,且每月的销售量都比去年12 月份下降了1.5m%。
