MATLAB自定义函数及局部变量.docx
Matlab建立自定义函数的方法
Matlab建⽴⾃定义函数的⽅法
Matlab是⼀款数学商业软件，是⼀款拥有很多功能的函数软件，⽤户在使⽤这款软件的时候可以直接调⽤这些函数。
但是在实际的使⽤中，尽管Matlab提供了很多函数，但是有时候还需要⾃定义函数来解决实际情况，下⾯⼩编就以⼀个简单的例⼦来给⼤家讲解如何⾃定义函数。
⼀起去看看吧！
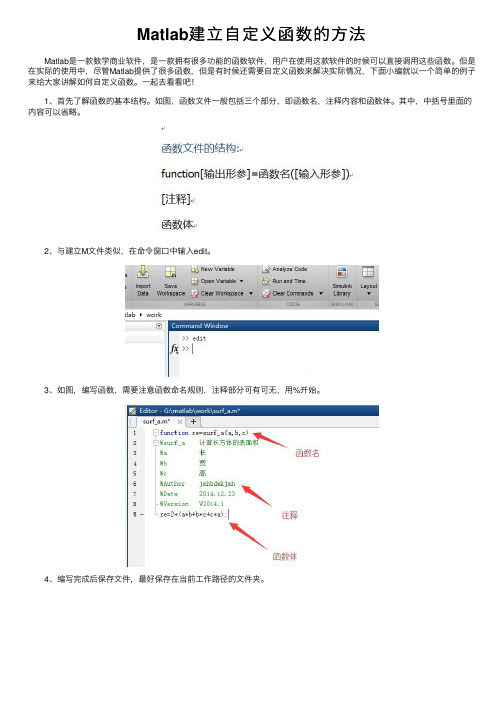
1、⾸先了解函数的基本结构。
如图，函数⽂件⼀般包括三个部分，即函数名，注释内容和函数体。
其中，中括号⾥⾯的内容可以省略。
2、与建⽴M⽂件类似，在命令窗⼝中输⼊edit。
3、如图，编写函数，需要注意函数命名规则，注释部分可有可⽆，⽤%开始。
4、编写完成后保存⽂件，最好保存在当前⼯作路径的⽂件夹。
5、函数调⽤：
如图，直接输⼊函数名，形参，就能返回计算结果。
6、查看函数说明：
和查看其它函数说明⼀样，输⼊“help 函数名” 就能看到这个函数的注释说明。
以上就是⼩编为⼤家带来的关于Matlab建⽴⾃定义函数的⽅法了；⼤家遇到同样问题的时候可以按照上述的⽅法进⾏操作，希望可以帮助到⼤家！。
Lec08_MATLAB第八讲：自定义函数的几种方式资料
9
人有了知识，就会具备各种分析能力， 明辨是非的能力。 所以我们要勤恳读书，广泛阅读， 古人说“书中自有黄金屋。 ”通过阅读科技书籍，我们能丰富知识， 培养逻辑思维能力； 通过阅读文学作品，我们能提高文学鉴赏水平， 培养文学情趣； 通过阅读报刊，我们能增长见识，扩大自己的知识面。 有许多书籍还能培养我们的道德情操， 给我们巨大的精神力量， 鼓舞我们前进。
例： f=inline('x^2+y','x','y')
y=f(2,3) 5
匿名函数
方式三：内联函数和匿名函数
匿名函数 + 函数句柄
f = @ (变量列表) 表达式
调用方式 y=f(实参列表)
例： f = @(x,y) x^2 + y;
y = f(2,3)
实参列表应与定义时的变量列表保持一致 根据实际情况，可能需要使用数组运算
方式四：符号表达式 + subs
首先定义一个符号表达式/函数，用 subs 命令调用 syms x f=1/(1+x^2);
subs(f,x,代替 x 的数值或符号)
优点：可以进行符号计算 缺点：由于使用符号运算内核，运算速度会大大降低。
8
上机作业
1、已知 Chebyshev 多项式定义如下： T0( x) 1, T1( x) x, Tn1( x) 2x Tn( x) Tn1( x), n 1, 2,K 利用符号计算，编程计算 T10(x) （注：Tn(x) 为 n 阶多项式） 程序取名 m81.m
不能与命令文件写在同一个文件中！
3
子函数
方式二：函数文件 + 子函数
MATLAB自定义函数及局部变量
MATLA自定义函数及局部变量2009-11-20 09:17在开始学习MATLA的时候并没有发现这个软件有着这么强大的功能，随着课题的不断深入，也在逼迫着自己不断的去应用新的公式并开发新的算法，这就牵涉到了如何在MATLA中自定义函数的问题，随之而来自然就是所有编程语言所面临的问题，函数调用、局部变量等等。
下面就我自己整理的一些心得与大家交流。
希望对你也有所帮助。
1、编写自定义函数时尽量分以下四部分：(1) 函数定义行：function[out1,out2,..]=filename(in1,in2,..) ，输入和输出参数个数分别由nargin和nargout两个MATLA保留的变量来给出。
(2) 第一行帮助行，以%开头，作为lookfor 指令搜索的行(3) 函数体说明及有关注解：以( %)开头，用以说明函数的作用及有关内容。
如果不希望显示某段信息，可在它的前面加空行(4) 函数体：函数体内使用的除返回和输入变量这些在function 语句中直接引用的变量以外的所有变量都是局部变量，即在该函数返回之后，这些变量会自动在MATLA的工作空间中清除掉。
如果希望这些中间变量成为在整个程序中都起作用的变量，则可以将它们设置为全局变量。
例如下面就是一个标准的自字义函数function A=myhilb(n, m)% MYHILB 是一个示范性的M-function.% A=MYHILB(N, M)会生成一个NX M 的Hilbert 矩阵A.% A=MYHILB(N会生成一个NX N 的Hilbert 矩阵.% MYHILB(N,M) 仅仅显示一个Hilbert 矩阵，而不会返回任何矩阵%这些内容在用help 时不会显示if nargout>1, error('Too many output arguments.'); endif nargin==1, m=n;elseif nargin==0 | nargin>2error('Wrong number of iutput arguments.');endA1=zeros(n,m);for i=1: nfor j=1:mA1(i,j)=1/(i+j-1);endendif nargout==1, A=A1;elseif nargout==0, disp(A1);end把该函数保存在MATLAB勺某个搜索路径中(比如work目录中),在命令窗口输入：>> help myhilbMYHILB是一个示范性的M-function.A=MYHILB(N, M)会生成一个NX M 的Hilbert 矩阵A.A=MYHILB(N会生成一个NX N 的Hilbert 矩阵.MYHILB(N,M) 仅仅显示一个Hilbert 矩阵，而不会返回任何矩阵。
matlab 定义函数
matlab 定义函数Matlab是一款强大的、功能强大的数学软件，它可以实现各种复杂数学计算任务，在很多研究领域有着广泛的应用。
它的另一个重要功能就是可以创建自定义函数，从而实现更加灵活的数学计算。
本文将介绍matlab中如何定义函数的步骤。
定义函数的步骤第一步：要定义函数，先创建一个定义函数的空白 m-file（m 文件），此m文件必须以.m为后缀名。
我们可以在matlab的命令窗口中输入“edit filename .m”，这样就可以打开一个空白的m文件，来定义自己的函数。
第二步：在m文件中，每一个定义函数都需要用“function”语句定义。
例如：```function y=f(x)y=x^2;```上面的函数定义可以读作：函数f定义，其中函数变量为x，函数值为x的平方。
第三步：当函数定义好后，保存m文件，执行函数。
这一步可以在matlab的命令行中输入“f(x)”，这样就可以计算出f(x)的值。
也可以使用图形绘制函数图形，例如：```x=-10:0.1:10;y=f(x);plot(x,y)```上面的命令表示“绘制x和f(x)之间的关系”。
函数的变形matlab也可以定义不同形式的函数，比如多元函数、指数函数、和对数函数等。
例如：多元函数：```function z=f(x,y)z=x+y;```指数函数：```function y=f(x)y=exp(x);```对数函数：```function y=f(x)y=log(x);```函数的定义以及求值定义完函数后，就可以开始求值了。
Matlab提供了多种求值方法，包括符号数值求解、全局搜索和特征值分解。
符号数值求解：通过给出函数公式，使用已有的计算方法求解函数的值。
全局搜索：在满足一定条件的函数域内，通过搜索方式求取函数的最优值。
特征值分解：可以分解函数的特征，从而实现对函数的更深入的理解和求解。
总结本文介绍了 matlab 中如何定义函数及相关求值方法，matlab 数的定义非常灵活，包括一元函数、多元函数、指数函数、和对数函数等，另外可以使用符号数值求解、全局搜索和特征值分解等方法来求取函数最优值。
matlab09自定义函数
数学实验
Matlab 自定义函数
自定义函数的五种方式
Matlab 自定义函数的五种方式
%命令 函数文件：myfile1.m 命令/函数文件 命令 函数文件： clear for t=1:10; y=mylfg(t); fprintf('%4d^(1/3) = %6.4f\n',t,y); end
调用函数时要注意实参与形参的匹配！ 调用函数时要注意实参与形参的匹配！ 实参 的匹配
%函数文件：mylfg.m 函数文件： 函数文件 function y = mylfg(x) y=x^(1/3);
命令文件/函数文件 命令文件 函数文件+ 函数文件 － 多个 M 文件 函数文件 函数文件 + 子函数 － 一个 M 文件 inline － 无需 M 文件 syms + subs 方式 － 无需 M 文件 字符串 + subs 方式 － 无需 M 文件
自定义函数方式（ 自定义函数方式（一）
方式（ ）：命令文件/函数文件 ）：命令文件 方式（1）：命令文件 函数文件 + 函数文件
diff(lfg,'x')
X
自定义函数方式（ 自定义函数方式（四）
方式（ ）： 方式（4）： syms + subs
syms 定义一个符号表达式，用 subs 命令调用 定义一个符号表达式 符号表达式， syms f x %定义符号 定义符号 f=1/(1+x^2); %定义符号表达式 定义符号表达式 subs(f,'x',代替 x 的数值或符号 代替 的数值或符号)
MATLAB之变量、函数及常用语句
１、变量命名规则：变量名的第一个字符必须是英文字母，最多包含３１个字符（包括英文字母、数字和下画线），变量中不得包含空格和标点符号，不得包含加减号。
变量名和函数区别字母的大小写，如matrix和Matrix表示两个不同的变量。
要防止它与系统的预定义变量名（如i,j,pi,eps等）、函数名（如who,length等）、保留字（如for,if,while,end等）冲突。
变量赋值用“＝”（赋值号）。
有一些变量永久驻留在工作内存中，不能再重新赋值。
这些变量见下表２、基本初等函数３、几个常用的函数4、数据文件的存储和调用在清除变量或退出MATLAB后，变量不复存在。
为了保存变量的值，可以把它们存储在数据文件中。
例如，在指令窗口中输入>>clear;x=pi/3;a=sin(x);b= cos(x);c=2*a+b执行以后，在File菜单中选Save Workspace As 存入数据文件（例如abc.mat)。
则在以后的操作中可以调用这个数据文件。
只要在File菜单中点Open操作，就可以打开这个文件。
4.1）Ｍ文件在进行复杂运算时，在指令窗口高度程序或修改指令是不方便的，因此需要从指令窗口工具栏的新建按钮或选择菜单File:New:M-Fil进入MATLAB的程序编辑器窗口，以编写自己的Ｍ文件。
Ｍ文件有二类：Ｍ脚本文件和Ｍ函数文件。
将多条MATLAB语句写在编辑器中，以扩展名为m的文件保存在某一目录中，就得到一个脚本文件。
例如在Ｍ文件编辑器中输入clear;n=1:100;s=sum%sum是求和命令（如下图），然后单击工具栏中的保存按钮，保存中选择Debug:run菜单，则会在指令窗口输出：s=5050*注：文件名与变量名的命名规则相同，Ｍ文件一般用小写字母。
尽管MATLA B区分变量名的大小写，但不区分文件名的大小写。
M 脚本文件没有参数传递功能，但Ｍ函数文件有些功能，所以Ｍ函数文件用得更为广泛。
matlab定义函数的方法
matlab定义函数的方法（原创实用版4篇）《matlab定义函数的方法》篇1在MATLAB 中，有多种方法可以定义自定义函数。
以下是几种常见的方法：1. 通过文件函数（filefunction）定义：需单独定义一个自定义函数的文件，文件名必须与函数名一致，然后在文件中使用function 关键字定义函数。
例如，定义一个名为myfunction 的函数，需要创建一个名为myfunction.m 的文件，并在文件中写入函数的定义和调用方式。
2. 通过函数文件子函数（subfunction）定义：在具有多个子函数的函数文件中，可以使用function 关键字定义子函数。
例如，在名为myfunction 的函数文件中，可以定义一个名为mysubfunction 的子函数，并在函数文件中调用该子函数。
3. 通过匿名函数（anonymous function）定义：在MATLAB 命令窗口中直接输入函数的表达式，不需要单独定义一个文件。
例如，定义一个名为myanonymous 的匿名函数，可以在命令窗口中输入以下代码：```function y = myanonymous(x)y = x^2;end4. 通过字符串subs 定义：在MATLAB 命令窗口中使用subs函数可以定义一个字符串形式的匿名函数，不需要单独定义一个文件。
例如，定义一个名为mystring 的匿名函数，可以在命令窗口中输入以下代码：```subs = @(x) x^2;```5. 通过@符号直接定义：在MATLAB 命令窗口中使用@符号可以定义一个匿名函数，不需要单独定义一个文件。
《matlab定义函数的方法》篇2在MATLAB 中，有多种方法可以定义自定义函数。
以下是其中几种常见的方法：1. 通过文件函数（filefunction）定义：需单独定义一个自定义函数的文件，文件名必须与函数名一致，然后在文件中使用function 关键字定义函数。
matlab自定义函数体中的变量计算
一、介绍在MATLAB中，自定义函数是一种非常常见且有用的编程技术。
通过自定义函数，我们可以将一系列的操作封装起来，实现代码的模块化和复用。
在自定义函数的体中，变量的计算是一个非常关键的部分。
本文将重点介绍MATLAB自定义函数体中变量的计算，包括变量的定义、赋值和运算。
二、变量的定义在MATLAB中，变量的定义遵循一定的规则，包括变量名的命名规范和数据类型的定义。
在自定义函数体中，我们需要特别注意变量的命名规范，以及避免与已有的函数名和关键字冲突。
下面是一些变量定义的示例：a = 10; 定义一个整型变量a并赋值为10b = 3.14; 定义一个浮点型变量b并赋值为3.14c = 'hello'; 定义一个字符型变量c并赋值为'hello'd = [1, 2, 3, 4]; 定义一个数组变量d并赋值为[1, 2, 3, 4]三、变量的赋值在自定义函数体中，我们经常需要给变量赋予新的数值或者进行运算后的结果。
MATLAB提供了多种方式来进行变量的赋值，包括直接赋值、运算赋值和递增递减赋值等。
下面是一些赋值的示例：a = a + 1; 将变量a的值加1后再赋给ab = b * 2; 将变量b的值乘以2后再赋给bc(2:4) = '123'; 将变量c的第2到4个字符改为'123'd = d + 1; 将变量d中的每个元素加1四、变量的运算在自定义函数体中，我们经常需要对变量进行一些运算操作，包括加减乘除、幂运算、矩阵运算等。
MATLAB提供了丰富的运算符和函数来进行变量的计算。
下面是一些运算的示例：a =b + c; 将变量b和c相加后赋给ad = sum(d); 计算变量d中所有元素的和e = exp(b); 计算变量b的指数值f = sqrt(a); 计算变量a的平方根五、总结在MATLAB自定义函数体中，变量的计算是一个非常重要的部分。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
MATLAB 口定义函数及局部变量
2009-11-20 09:17
在开始学习MATLAB的时候并没有发现这个软件有着这么强大的功能，随着课题的不断深入，也在逼迫着自己不断的去应用新的公式并开发新的算法，这就牵涉到了如何在MATLAB中口定义函数的问题，随之而来口然就是所有编程语言所面临的问题，函数调用、局部变量等等。
下面就我自己整理的一些心得与大家交流。
希望对你也有所帮助。
1、编写自定义函数时尽量分以下四部分：
(1)函数定义行：function[outl, out2,.. ]=filcname (ini, in2,..),输入和输岀参数个数分别由nargin和nargout两个MATLAB保留的变量来给岀。
(2)第一行帮助行，以%开头，作为1 ookfor指令搜索的行
(3)函数体说明及有关注解：以(%)开头，用以说明函数的作用及有关内容。
如果不希望显示某段信息，可在它的前面加空行
(4)函数体：函数体内使用的除返回和输入变量这些在function语句屮直接引用的变量以外的所有变量都是局部变量，即在该函数返回之后，这些变量会口动在MATLAB的工作空间中清除掉。
如果希望这些中间变量成为在整个程序中都起作用的变量，则可以将它们设置为全局变量。
例如卜•血就是一个标准的口字义函数。
function A=myhilb(n, m)
% MYH1LB是一个示范性的M-function・
% A=MYHILB(N, M)会生成一个NXM 的Hilbert 矩阵 A.
% A二MYHILB(N)会生成一个NXN 的Hilbert 矩阵.
% MYI1ILB(N,M)仅仅显示一个II订bert矩阵，而不会返冋任何矩阵。
%这些内容在用help时不会显示
if nargout>l, error Too many output arguments.') ; end
if nargin=l, m=n;
el seif nargin=0 nargin>2
error Wrong number of iutput arguments.');
end
Al二zeros (n, m);
for i=l: n
for j=l:m
Al(i, j)=l/(i+j-l);
end
end
if nargout~l, A=A1;
elseif nargout==0, disp(Al);
end
把该函数保存在MATLAB的某个搜索路径中(比如work目录中),在命令窗口输入：
>> help myhilb
MYH1LB是一个示范性的M-function.
A=MYH1LB(N, M)会生成一个NXM 的Hilbert 矩阵 A.
A=MYHILB(N)会生成一个NXN的H订bert矩阵.
MYHTLB(N,M)仅仅显示一个Hilbert矩阵，而不会返回任何矩阵。
>> lookfor myhilb
MYHILB是一个示范性的M-function.
2> MATLAB中全局变量与局部变量有什么区别？
答:如果一个函数内的变量没有特别声明，那么这个变量只在函数内部使用, 即为局部变量。
如果两个或多个函数共用一个变量(或者说在子程序屮也要用到主程序中的变量，注意不是参数)，那么可以用global来将它声明为全局变量。
全局变量的使用可以减少参数传递，合理利用全局变量可以提高程序执行的效率。
如果需要用到其他函数的变量。
就要利用在主程序与子程序屮分别都声明全局变量的方式实现变量的传递。
否则函数体内使用的都为局部变量。
比如下例：
3、怎样编写递归函数？
答：在建立数学模型时，经常会遇到利用递归表达的式子，这种数学表达式简单明了，在MATLAB 111实现该模型，对应的需要建立递归函数。
写一个好的递归函数，关键是找到递归的边界条件，和在中间某步骤中会发生的各种情况，然后再对应到程序中即可。
试看Hanoi塔例了：要将塔座A上的刀个鬪盘全部转移到塔座C 上，如n二1,直接把这一片移到目标柱子即可；若n>l,可以先把塔座A上的个圆盘想法转移到塔座B上，然后把塔座A上的最后一个大圆盘转移到塔座C上，最后再把塔座B上的个圆盘转移到塔座C±o把上而思想对应到递归程序屮，就得到如下代码：
function
result=hanoi(di sknum，begi npi 11 ar, mi dpi 11 ar, endpi 11 ar, sch) if disknum二二1%添加一行移动方式，递归的边界
result二[sch;1, beginpillar, cndpillar];
else%下面一句相当于把上面n-1片移到中间柱子
result=hanoi(disknum-1, beginpillar, endpillar, midpillar, sch);
%然后把最后一片移到s标柱子上
result二[result;disknum, bcginpillar, cndpillar];
%把中间当作第一•根，原來第一•根当作中间柱子，继续移动
result二hanoi(disknum-1, midpi1lar, beginpi 1lar, endpi1lar, result); end。